Comparative Assessment of the Thermal Load of a Marine Engine Operating on Alternative Fuels
Abstract
:1. Introduction
- “Part A” is derived from lignocellulosic feedstock and is expected to constitute ~77% of biodiesel by 2030, with a projected increase to ~90% by 2050;
- “Part B” is produced from non-agricultural oils and animal fats.
- Assess the thermal and mechanical load levels of cylinder–piston assemblies under nominal operating conditions, comparing them to diesel engine operations without altering the factory-set diesel operation parameters;
- Identify correlations between mechanical and thermal load factors and key combustion cycle parameters. The goal is to optimize these parameters for engines operating on a wide range of LCFs, as well as to determine the most effective strategies for reducing thermal stress in components.
2. Methodology
2.1. Properties of the Investigated Fuel Types
2.2. Thermal Loading Factors of the Components
2.3. Research Object
2.4. Variational Research Plan
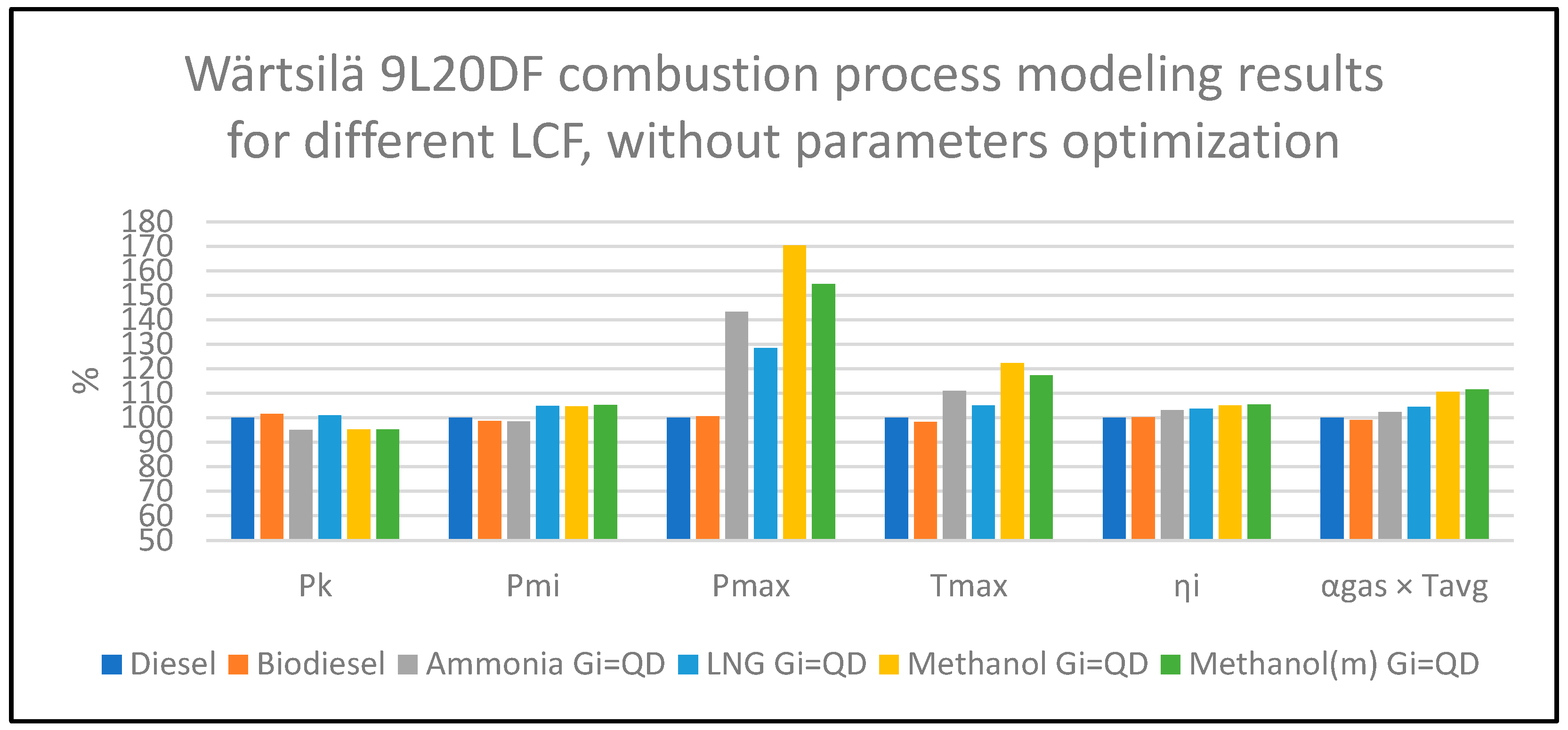
- In the first stage, the thermal load on the components was evaluated based on the multiplication of αgas av × Tavg, and the mechanical load was assessed using Pmax as an indicator. No changes were made to the adjustment parameters compared to diesel operation. The aim was to assess, through a comparative approach, the thermal and mechanical load factors of components when the engine operates on LCFs versus diesel while identifying effective directions for combustion cycle optimization;
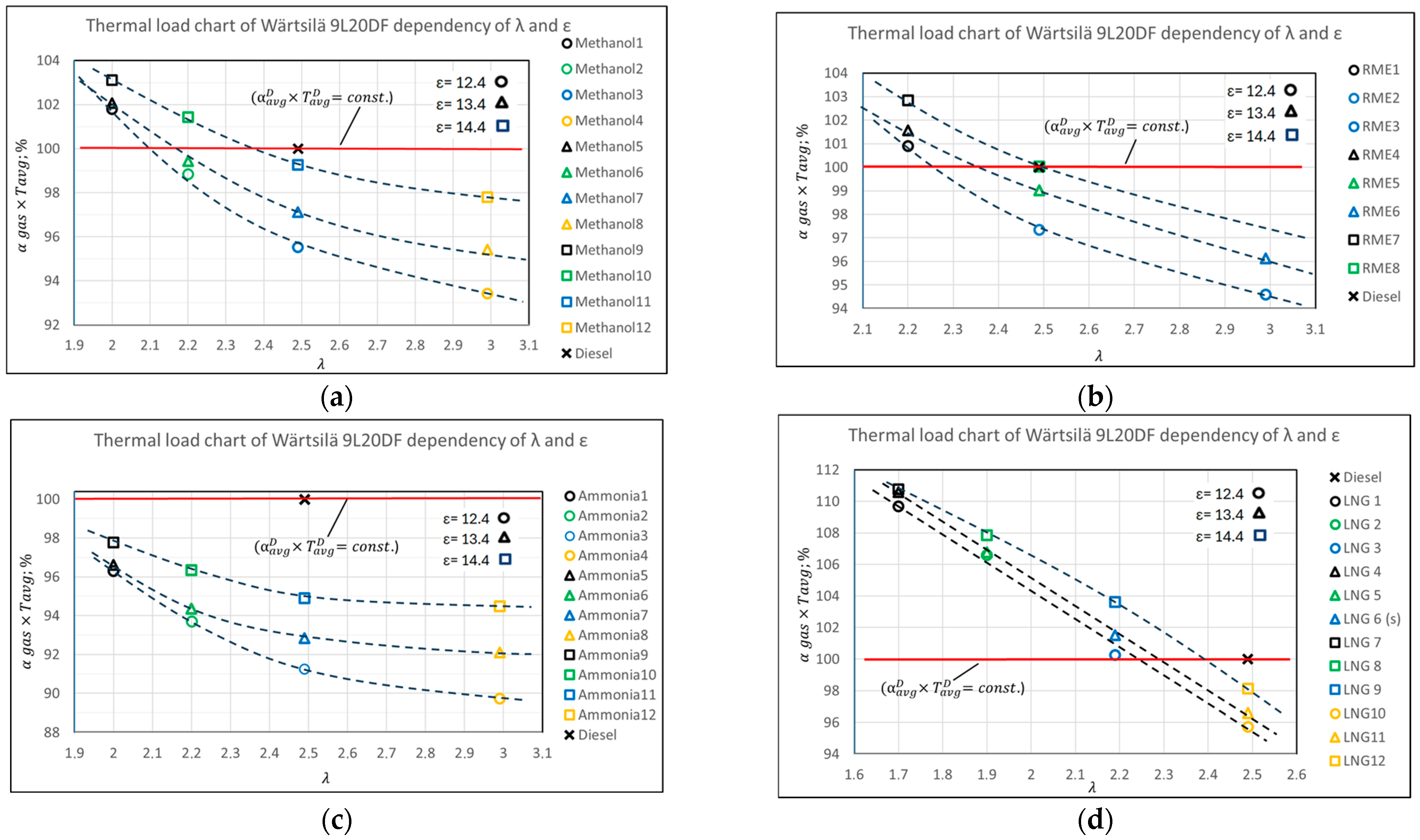
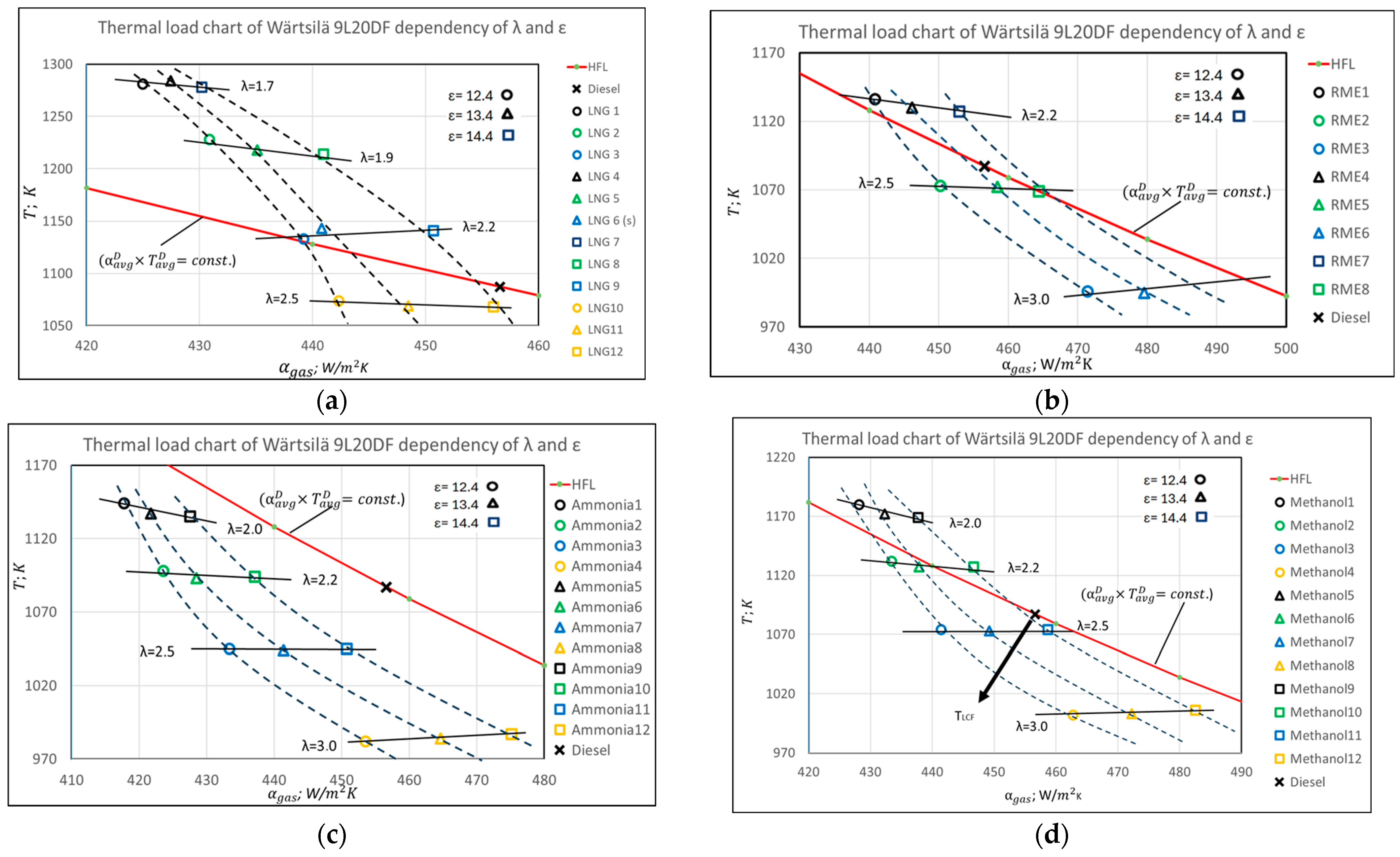
- In the second stage of the research, a detailed evaluation and optimization of the thermal load were conducted by analyzing the impact of the compression ratio (ε) and the air excess coefficient (λ) in variable models (with Pmax held constant and adjusted by modifying the combustion start angle φcomb). The objective was to validate the effectiveness of these parameters in influencing the thermal load on engine components and to generalize their application using the comparative thermal load evaluation methodology developed in [16]. The comparative assessment was graphically represented in the coordinate system of αgas and T, considering various combinations of (λ, ε)—var (Pmi-idem, Pmax-idem).
3. Results
3.1. Impact of Diesel Replacement with LCFs on Performance Parameters
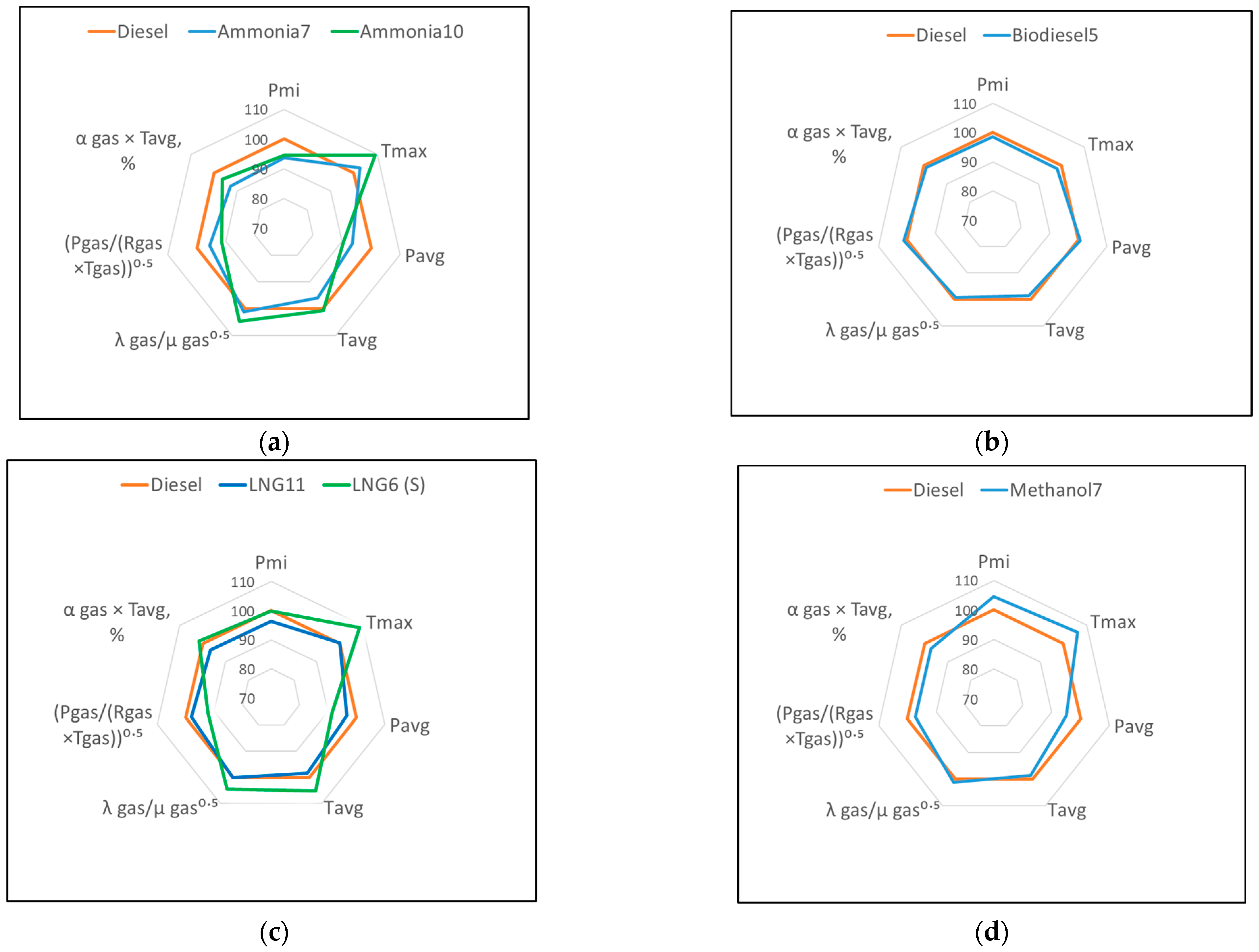
3.2. Optimization of Component Thermal Load Factors
- Increasing the excess air coefficient (λ) led to a continuous decrease in the (αgas × Tavg) criterion for biodiesel and LNG across the entire λ variation range (1.7–2.5). Meanwhile, as (ε) increased, (αgas × Tavg) also increased, indicating a rise in the thermal load on the components;
- It is important to note that the influence of (λ) on (αgas × Tavg) for methanol and ammonia was not linear: it remained roughly linear up to λ ≈ 2.5 but stabilized asymptotically for λ > 2.5. The main reason for this behavior lies in the difference in the heat release duration (φz) between ammonia and methanol, on the one hand, and biodiesel and LNG, on the other. The combustion duration φz for methanol and ammonia (40–33 crankshaft degrees) was significantly shorter than that of LNG and biodiesel (60–65 crankshaft degrees). As a result, the absolute change in φz at λ ≥ 2.5 had a lesser impact on the indicator diagram and, consequently, on (αgas × Tavg).
4. Discussion of Research Results
- By converting the engine to operate on all of the LCFs evaluated, after ensuring Pmax = idem with diesel, the thermal stress indicator (αgas × Tavg) also approached the permissible limits, similar to when the engine operates on diesel. The temperature factors were approximately 3% lower for methanol, ~7% for ammonia, ~1% for biodiesel, and ~3.5% for LNG (see Table A1 and Figure 3). Increasing the excess air coefficient λ beyond 2.5 units to reduce thermal stresses on components is not rational, as the positive effect of λ on thermal stress diminishes.
- The influence of the combustion cycle duration on (αgas × Tavg) was revealed: for fuels with relatively short combustion durations, such as ammonia and methanol, the effect on (αgas×Tavg) diminished in the λ ≥ 2.5 range, while for biodiesel and LNG, only a decreasing trend was observed.
- Alongside the αgas-based structure (widely validated across different diesel engine types), it is important to adapt the αgas formulas from other developers, primarily G. Woschni’s analytically derived expressions, which are approved for various engine fuel types [49,50]. Methodological aspects should be expanded by determining the ALFA formulas for the combustion cycle’s current parameters, Tgas and Pgas;
- Additionally, it is important to consider that operational indicators are shaped when the engine operates in characteristic cycle modes (e.g., the E3 or E2 test cycle, according to ISO 8178 for ship engines). In this context, it would be beneficial to expand the research to include partial load engine modes, where engines typically operate for extended periods. Thermal and mechanical loads on components should be assessed based on the average values of the operational cycle. When modeling the engine’s combustion cycle characteristics under partial load conditions, it will be necessary to reassess the applicability of G. Woschni’s m and φz recalibration model, taking into account the author’s observations on the inverse relationship between these parameters and λ [61], especially when compared to diesel operation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LCF | low carbon fuels; |
| GHG | greenhouse gas; |
| IMO | International Maritime Organization; |
| LNG | liquified natural gas; |
| MM | mathematical model; |
| ICE | internal combustion engine; |
| TDC | top dead center; |
| PFI | port fuel injection; |
| LHV | lower heating value; |
| CAD | crank angle degrees; |
| CPG | cylinder–piston group; |
| EGR | exhaust gas recirculation; |
| TE | thermal efficiency; |
| HDDF | high-density dual fuel; |
| SOPI | start of pre-injection; |
| ROPI | ratio of pre-injection; |
| BTDC | before top dead center; |
| CA50 | crank angle at which 50% of the heat from combustion is released; |
| CA90 | crank angle at which 90% of the heat from combustion is released; |
| CO2 | carbon dioxide; |
| CH4 | methane; |
| N2O | dinitrogen oxide; |
| NOx | nitrous oxides; |
| Tmax | maximum combustion cycle temperature (K); |
| Tk | manifold air temperature (K); |
| Tavg | combustion average temperature (K); |
| Pmax | maximum combustion cycle pressure (bar); |
| Pavg | combustion average pressure (bar); |
| Pmi | mean indicated pressure (bar); |
| Pme | break mean effective pressure (bar); |
| Pk | manifold air pressure (bar); |
| Gi | fuel injection portion; |
| ƞi | useful work coefficient; |
| φz | combustion duration (CA°); |
| φinj | fuel injection crank angle |
| φcomb | start of combustion (CA°); |
| m | heat release form factor; |
| λ | air fuel ratio; |
| αgas av | heat load coefficient during the cycle; |
| ε | engine compression ratio; |
Appendix A
| Test | Adjustable Parameters | Mathematical Modeling Results | Calculation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ε | φcomb | λ | m/φz | Pk | Pmi | Pmax | Tmax | Pavg | Tavg | ƞi | λp gas/(μgas)0.5 | αgas | αgas × Tavg. % | |
| Diesel | 13.4 | −6 | 2.5 | 1.1/65 | 4.4 | 23.8 | 177 | 1586 | 65.7 | 1087 | 0.48 | 1.11 | 457 | 100 |
| LNG 1 | 12.4 | −8 | 1.7 | 0.5/60 | 3.0 | 23.5 | 177 | 2013 | 54.0 | 1281 | 0.47 | 1.25 | 425 | 109.7 |
| LNG 2 | 12.4 | −6 | 1.9 | 0.5/60 | 3.4 | 23.7 | 178 | 1723 | 56.2 | 1228 | 0.47 | 1.22 | 431 | 106.6 |
| LNG 3 | 12.4 | −3 | 2.2 | 0.5/60 | 3.9 | 23.9 | 179 | 1726 | 59.8 | 1133 | 0.47 | 1.15 | 439 | 100.3 |
| LNG 4 | 13.4 | −5 | 1.7 | 0.5/60 | 3.0 | 23.7 | 177 | 2006 | 54.6 | 1284 | 0.47 | 1.26 | 427 | 110.6 |
| LNG 5 | 13.4 | −3 | 1.9 | 0.5/60 | 3.4 | 23.8 | 178 | 1876 | 57.3 | 1218 | 0.47 | 1.21 | 435 | 106.8 |
| LNG 6 (s) | 13.4 | 0 | 2.2 | 0.5/60 | 3.9 | 23.8 | 176 | 1723 | 60.1 | 1143 | 0.47 | 1.16 | 441 | 101.5 |
| LNG 7 | 14.4 | −2 | 1.7 | 0.5/60 | 3.0 | 23.7 | 174 | 1974 | 55.3 | 1278 | 0.47 | 1.25 | 430 | 110.8 |
| LNG 8 | 14.4 | −1 | 1.9 | 0.5/60 | 3.4 | 23.9 | 179 | 1859 | 58.8 | 1214 | 0.47 | 1.21 | 441 | 107.9 |
| LNG 9 | 14.4 | 2 | 2.2 | 0.5/60 | 3.9 | 23.8 | 176 | 1708 | 62.8 | 1141 | 0.47 | 1.16 | 451 | 103.6 |
| LNG10 | 12.4 | −2 | 2.5 | 0.5/60 | 4.2 | 23.0 | 180 | 1612 | 61.7 | 1074 | 0.48 | 1.11 | 442 | 95.7 |
| LNG11 | 13.4 | 1 | 2.5 | 0.5/60 | 4.2 | 23.0 | 177 | 1590 | 63.4 | 1069 | 0.48 | 1.11 | 448 | 96.6 |
| LNG12 | 14.4 | 3 | 2.5 | 0.5/60 | 4.2 | 22.9 | 177 | 1576 | 65.5 | 1068 | 0.47 | 1.11 | 456 | 98.1 |
| RME1 | 12.4 | −11 | 2.2 | 1.1/65 | 3.9 | 23.5 | 175 | 1701 | 60.3 | 1136 | 0.48 | 1.14 | 441 | 100.9 |
| RME2 | 12.4 | −8 | 2.5 | 1.1/65 | 4.4 | 23.4 | 174 | 1572 | 63.9 | 1073 | 0.47 | 1.10 | 450 | 97.3 |
| RME3 | 12.4 | −4 | 3.0 | 1.1/65 | 5.3 | 23.1 | 177 | 1411 | 70.6 | 996 | 0.47 | 1.06 | 471 | 94.6 |
| RME4 | 13.4 | −8 | 2.2 | 1.1/65 | 3.9 | 23.5 | 174 | 1673 | 61.8 | 1130 | 0.48 | 1.14 | 446 | 101.6 |
| RME5 | 13.4 | −6 | 2.5 | 1.1/65 | 4.4 | 23.5 | 178 | 1558 | 66.2 | 1072 | 0.48 | 1.10 | 458 | 99.0 |
| RME6 | 13.4 | −1 | 3.0 | 1.1/65 | 5.3 | 22.8 | 178 | 1392 | 73.0 | 995 | 0.46 | 1.06 | 480 | 96.1 |
| RME7 | 14.4 | −6 | 2.2 | 1.1/65 | 3.9 | 23.5 | 176 | 1657 | 63.7 | 1127 | 0.48 | 1.14 | 453 | 102.8 |
| RME8 | 14.4 | −3 | 2.5 | 1.1/65 | 4.4 | 23.2 | 175 | 1535 | 67.9 | 1069 | 0.47 | 1.10 | 464 | 100.0 |
| RME9 | 14.4 | 0 | 3.0 | 1.1/60 | 5.3 | 23.2 | 194 | 1399 | 76.6 | 1004 | 0.46 | 1.06 | 491 | 99.3 |
| Ammonia1 | 12.4 | 0 | 2.0 | 0.5/33 | 3.3 | 22.2 | 179 | 1847 | 53.6 | 1144 | 0.46 | 1.20 | 418 | 96.3 |
| Ammonia2 | 12.4 | 2 | 2.2 | 0.5/33 | 3.7 | 22.3 | 179 | 1753 | 56.0 | 1098 | 0.47 | 1.16 | 424 | 93.7 |
| Ammonia3 | 12.4 | 5 | 2.5 | 0.5/33 | 4.1 | 22.3 | 175 | 1638 | 59.3 | 1045 | 0.46 | 1.12 | 433 | 91.3 |
| Ammonia4 | 12.4 | 8 | 3.0 | 0.5/33 | 4.9 | 22.1 | 175 | 1501 | 65.5 | 982 | 0.46 | 1.08 | 454 | 89.7 |
| Ammonia5 | 13.4 | 3 | 2.0 | 0.5/33 | 3.3 | 22.3 | 177 | 1827 | 54.6 | 1137 | 0.47 | 1.20 | 422 | 96.6 |
| Ammonia6 | 13.4 | 5 | 2.2 | 0.5/33 | 3.7 | 22.3 | 175 | 1734 | 57.3 | 1093 | 0.47 | 1.16 | 428 | 94.4 |
| Ammonia7 | 13.4 | 7 | 2.5 | 0.5/33 | 4.1 | 22.3 | 175 | 1629 | 61.4 | 1044 | 0.47 | 1.12 | 441 | 92.8 |
| Ammonia7a | 13.4 | −1 | 2.5 | 0.8/50 | 4.1 | 22.3 | 177 | 1571 | 62.5 | 1049 | 0.47 | 1.13 | 445 | 94.1 |
| Ammonia8 | 13.4 | 9 | 3.0 | 0.5/33 | 4.9 | 22.3 | 181 | 1501 | 68.7 | 984 | 0.47 | 1.08 | 465 | 92.1 |
| Ammonia9 | 14.4 | 5 | 2.0 | 0.5/33 | 3.3 | 22.4 | 176 | 1816 | 56.1 | 1135 | 0.47 | 1.19 | 428 | 97.8 |
| Ammonia10 | 14.4 | 6 | 2.2 | 0.5/33 | 3.7 | 22.5 | 180 | 1733 | 59.5 | 1094 | 0.47 | 1.16 | 437 | 96.4 |
| Ammonia11 | 14.4 | 8 | 2.5 | 0.5/33 | 4.1 | 22.4 | 179 | 1628 | 64.0 | 1045 | 0.47 | 1.12 | 451 | 94.9 |
| Ammonia12 | 14.4 | 10 | 3.0 | 0.5/33 | 4.9 | 22.4 | 184 | 1500 | 71.7 | 987 | 0.47 | 1.08 | 475 | 94.5 |
| Methanol1 | 12.4 | −1 | 2.0 | 0.5/40 | 3.3 | 24.7 | 177 | 1911 | 54.9 | 1180 | 0.47 | 1.20 | 428 | 101.8 |
| Methanol2 | 12.4 | 1 | 2.2 | 0.5/40 | 3.7 | 24.8 | 175 | 1811 | 57.2 | 1132 | 0.47 | 1.17 | 433 | 98.9 |
| Methanol3 | 12.4 | 4 | 2.5 | 0.5/40 | 4.1 | 24.8 | 177 | 1694 | 60.4 | 1074 | 0.47 | 1.12 | 441 | 95.5 |
| Methanol4 | 12.4 | 7 | 3.0 | 0.5/40 | 5.0 | 24.7 | 178 | 1537 | 67.2 | 1002 | 0.47 | 1.08 | 463 | 93.4 |
| Methanol5 | 13.4 | 2 | 2.0 | 0.5/40 | 3.3 | 24.9 | 179 | 1898 | 56.0 | 1172 | 0.47 | 1.20 | 432 | 102.1 |
| Methanol6 | 13.4 | 4 | 2.2 | 0.5/40 | 3.7 | 24.9 | 177 | 1798 | 58.4 | 1127 | 0.47 | 1.16 | 438 | 99.4 |
| Methanol7 | 13.4 | 6 | 2.5 | 0.5/40 | 4.1 | 24.9 | 177 | 1683 | 62.5 | 1073 | 0.47 | 1.12 | 449 | 97.1 |
| Methanol8 | 13.4 | 9 | 3.0 | 0.5/40 | 5.0 | 24.7 | 178 | 1528 | 69.9 | 1003 | 0.47 | 1.08 | 472 | 95.4 |
| Methanol9 | 14.4 | 4 | 2.0 | 0.5/40 | 3.3 | 25.0 | 179 | 1883 | 57.4 | 1169 | 0.47 | 1.19 | 438 | 103.1 |
| Methanol10 | 14.4 | 5 | 2.2 | 0.5/40 | 3.7 | 24.9 | 175 | 1785 | 60.7 | 1127 | 0.47 | 1.16 | 447 | 101.4 |
| Methanol11 | 14.4 | 7 | 2.5 | 0.5/40 | 4.1 | 24.8 | 175 | 1671 | 65.1 | 1074 | 0.47 | 1.12 | 459 | 99.3 |
| Methanol12 | 14.4 | 10 | 3.0 | 0.5/40 | 5.0 | 24.8 | 182 | 1525 | 72.9 | 1006 | 0.47 | 1.08 | 483 | 97.8 |
| Ammonia Gi = QD | 13.4 | −6 | 2.5 | 0.8/50 | 4.1 | 22.9 | 206 | 1622 | 65.5 | 1060 | 0.48 | 1.13 | 456 | 97.5 |
| Ammonia Gi = QD | 13.4 | −6 | 2.5 | 0.5/33 | 4.1 | 23.5 | 253 | 1759 | 69.7 | 1077 | 0.49 | 1.14 | 472 | 102.3 |
| Methanol(m) Gi = QD | 13.4 | −6 | 2.5 | 0.4/30 | 4.1 | 25.0 | 273 | 1860 | 72.7 | 1114 | 0.50 | 1.16 | 497 | 111.6 |
| Methanol Gi = QD | 13.4 | −6 | 2.5 | 0.2/17 | 4.1 | 24.9 | 301 | 1940 | 75.5 | 1128 | 0.50 | 1.15 | 487 | 110.6 |
| LNG Gi = QD | 13.4 | −6 | 2.5 | 0.5/60 | 4.4 | 24.9 | 227 | 1666 | 70.9 | 1087 | 0.49 | 1.13 | 477 | 104.5 |
References
- International Maritime Organization. 2023 IMO Strategy on Reduction of GHG Emissions from Ships. Available online: https://www.imo.org/en/OurWork/Environment/Pages/2023-IMO-Strategy-on-Reduction-of-GHG-Emissions-from-Ships.aspx (accessed on 9 February 2025).
- European Commission. COM (2021) 562 Final 2021/0210 (COD). 2021. Available online: https://opac.oireachtas.ie/Data/Library3/Documents%20Laid/2021/pdf/TRAdocslaid110821_110821_152830.pdf (accessed on 9 February 2025).
- International Maritime Organization. Mandatory IGF Code for Ships Using Gases or Other Low-Flashpoint Fuels Enters into Force on 1 January 2017, Along with New Training Requirements for Seafarers Working on Those Ships. Available online: https://www.imo.org/en/MediaCentre/PressBriefings/Pages/01-IGF.aspx (accessed on 22 March 2025).
- DNV. Exploring All Options to Keep Decarbonization on Course. Available online: https://www.dnv.com/expert-story/maritime-impact/exploring-all-options-to-keep-decarbonization-on-course/ (accessed on 9 February 2025).
- DNV. Achieving the IMO Decarbonization Goals. Containership Insights. MARITIME IMPACT. 23 July 2020. Available online: https://www.dnv.com/expert-story/maritime-impact/How-newbuilds-can-comply-with-IMOs-2030-CO2-reductiontargets.html (accessed on 10 December 2023).
- International Maritime Organization. EEXI and CII—Ship Carbon Intensity and Rating System. Available online: https://www.imo.org/en/MediaCentre/HotTopics/Pages/EEXI-CII-FAQ.aspx (accessed on 22 March 2025).
- Langari, J.; Aliakbari, K.; Nejad, R.M. Failure analysis of CK45 steel crankshaft in light truck diesel engine. Eng. Fail. Anal. 2023, 145, 107045. [Google Scholar] [CrossRef]
- Venkatachalam, G.; Kumaravel, A. Experimental Investigations on the Failure of Diesel Engine Piston. Mater. Today Proc. 2019, 16, 1196–1203. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, X.; Xiang, P.; Dong, D. Analysis of thermal temperature fields and thermal stress under steady temperature field of diesel engine piston. Appl. Therm. Eng. 2017, 113, 796–812. [Google Scholar] [CrossRef]
- Cabuk, A.S. Experimental IoT study on fault detection and preventive apparatus using Node-RED ship’s main engine cooling water pump motor. Eng. Fail. Anal. 2022, 138, 106310. [Google Scholar] [CrossRef]
- Suthisripok, T.; Semsamran, P. The impact of biodiesel B100 on a small agricultural diesel engine. Tribol. Int. 2018, 128, 397–409. [Google Scholar] [CrossRef]
- Chang, J.; Güralp, O.; Filipi, Z.; Assanis, D.; Kuo, T.W.; Najt, P.; Rask, R. New Heat Transfer Correlation for an HCCI Engine Derived from Measurements of Instantaneous Surface Heat Flux. SAE Trans. 2004, 113, 1576–1593. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Chen, B.C.; Hsieh, F.C.; Ke, C.T. Heat transfer model for small-scale spark-ignition engines. Int. J. Heat Mass Transf. 2009, 52, 1875–1886. [Google Scholar] [CrossRef]
- Rabeti, M.; Ranjbar, A.A.; Jahanian, O.; Ardebili, S.M.S.; Solmaz, H. Investigation of important semi-empirical heat transfer models for a natural gas fueled HCCI engine. Energy Rep. 2021, 7, 8652–8666. [Google Scholar] [CrossRef]
- International Maritime Organization. Unified Interpretations to MARPOL ANNEX VI. MEPC.1/Circ.795/Rev.6. 2022. Available online: https://wwwcdn.imo.org/localresources/en/OurWork/Environment/Documents/Air%20pollution/MEPC.1-Circ.795-Rev.6.pdf (accessed on 19 February 2025).
- Lebedevas, S.; Milasius, E. Methodological Aspects of Assessing the Thermal Load on Diesel Engine Parts for Operation on Alternative Fuel. J. Mar. Sci. Eng. 2024, 12, 325. [Google Scholar] [CrossRef]
- Benson, R.S.; Whitehouse, N.D. Combustion in Compression Ignition Engines. In Internal Combustion Engines; Pergamon: Bergama, Turkey, 1979; pp. 69–95. [Google Scholar] [CrossRef]
- Merker, G.P.; Schwarz, C.; Stiesch, G.; Otto, F. Simulating Combustion—Simulation of Combustion and Pollutant Formation for Engine-Development; Springer: Berlin/Heidelberg, Germany, 2006; pp. 148–155. [Google Scholar]
- Stoumpos, S.; Theotokatos, G.; Boulougouris, E.; Vassalos, D.; Lazakis, I.; Livanos, G. Marine dual fuel engine modelling and parametric investigation of engine settings effect on performance-emissions trade-offs. Ocean Eng. 2018, 157, 376–386. [Google Scholar] [CrossRef]
- Ao, X.; Gan, H.; Xin, M.; Cong, Y.; Lu, D.; Guo, A.; Wang, H. Numerical investigation on the effects of pilot fuel and natural gas injection pressures on methane slip in a large marine dual-fuel engine. Energy 2024, 312, 133675. [Google Scholar] [CrossRef]
- International Maritime Organization. LNG Bunkering Development. Available online: https://futurefuels.imo.org/home/future-insight/alternative-fuels/scalability-and-sustainability/lng/ (accessed on 10 February 2025).
- Yang, D.; Wei, S.; Ma, Y.; Jiaqiang, E.; Zhao, J. Influence of critical parameters on combustion and emission characteristics of methanol/diesel dual fuel compression combustion engine. Fuel 2024, 368, 131647. [Google Scholar] [CrossRef]
- Chen, H.; Su, X.; He, J.; Xie, B. Investigation on combustion and emission characteristics of a common rail diesel engine fueled with diesel/n-pentanol/methanol blends. Energy 2019, 167, 297e311. [Google Scholar] [CrossRef]
- Deka, T.J.; Abd, M.E.; Osman, A.I.; Ali, R.I.; Baruah, D.C.; Rooney, D.W. Optimising novel methanol/diesel blends as sustainable fuel alternatives: Performance evaluation and predictive modelling. Energy Convers. Manag. 2024, 321, 118943. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, Z.; Wei, W.; Zhang, H.; Cai, W.; Dong, D.; Li, G. Multi-objective optimization of the performance for a marine methanol-diesel dual-fuel engine. Fuel 2024, 368, 131556. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, W.; Guo, L.; Zhang, H.; Jis, Z.; Qin, Z.; Zhu, G.; Yu, C.; Zhang, J. Numerical optimization of injector hole arrangement for marine methanol/diesel direct dual fuel stratification engines. Appl. Therm. Eng. 2024, 257, 124456. [Google Scholar] [CrossRef]
- Lv, J.; Sun, Y.; Zhang, Z.; Fang, Y. Optimization of operational parameters of marine methanol dual-fuel engine based on RSM-MOPSO. Process Saf. Environ. Prot. 2024, 191, 2634–2652. [Google Scholar] [CrossRef]
- Karvounis, P.; Theotokatos, G.; Patil, C.; Xiang, L.; Ding, Y. Parametric investigation of diesel–methanol dual fuel marine engines with port and direct injection. Fuel 2025, 381, 133441. [Google Scholar] [CrossRef]
- Wang, H.; Chang, Y.; Sun, K.; Jis, M.; Wang, T. Development of a reduced chemical kinetic mechanism for ammonia/diesel combustion over a wide range of ammonia energy ratios. Fuel 2025, 381, 133536. [Google Scholar] [CrossRef]
- Cheng, H.; Tang, Q.; Uddeen, K.; Huang, L.; Zheng, Z.; Turner, J.; Yao, M. The ignition mechanisms and chemical reaction kinetics of nitrogen oxide of ammonia/diesel dual-fuel engine combustion. Appl. Therm. Eng. 2024, 262, 125287. [Google Scholar] [CrossRef]
- Nie, X.; Bi, Y.; Shen, L.; Lei, J.; Wan, M.; Xiao, Y.; Chen, G. Experimental study for optimizing EGR strategy in an ammonia-diesel dual-fuel engine under different altitudes. Energy 2024, 313, 133953. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Li, X.; Li, J.; Huang, H.; Kobayashi, N. Large eddy simulation of ammonia-diesel dual fuel spray combustion: Effects of ambient condition on ignition characteristics. Che. Eng. J. 2024, 501, 157698. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Z.; Mohammed, A.E.; Dong, S.; Wang, S.; Ouyang, W.; Zhang, C.; Cheng, X. On ammonia/diesel dual-fuel combustion in optical engine. Fuel 2024, 367, 131452. [Google Scholar] [CrossRef]
- Zuo, Q.; Chen, L.; Chen, W.; Zhu, G.; Wang, z.; Ma, Y.; Shen, Z.; Lu, C. Performance analysis of ammonia energy ratio on an ammonia-diesel engine in different fuel supply modes. Fuel 2025, 384, 134038. [Google Scholar] [CrossRef]
- Drazdauskas, M.; Lebedevas, S. Numerical Study on Optimization of Combustion Cycle Parameters and Exhaust Gas Emissions in Marine Dual-Fuel Engines by Adjusting Ammonia Injection Phases. J. Mar. Sci. Eng. 2024, 12, 1340. [Google Scholar] [CrossRef]
- Lebedevas, S.; Lebedeva, G.; Gudaityte, I. Research of characteristics of working cycle of high-speed diesel engine operating on biofuels RME–E and D–RME–E. Part 1. Indicators of fuel injection system and indicative process. Transport 2013, 28, 204–213. [Google Scholar] [CrossRef]
- Ahmadi, M.G.; Shun, C.C.; Yung, K. Comparison between blended mode and fumigation mode on combustion, performance and emissions of a diesel engine fueled with ternary fuel (diesel- biodiesel- ethanol) based on engine speed. J. Energy Inst. 2019, 92, 1233e1250. [Google Scholar] [CrossRef]
- Wai, P.; Kanokkhanarat, P.; Oh, B.; Wongpattharaworakul, V.; Depaiwa, N.; Po-ngaen, W.; Chollacoop, N.; Srisurangkul, C.; Kosaka, H.; Yamakita, M.; et al. Experimental investigation of the influence of ethanol and biodiesel on common rail direct injection diesel Engine’s combustion and emission characteristics. Case Stud. Therm. Eng. 2022, 39, 102430. [Google Scholar] [CrossRef]
- Karin, P.; Tripatara, A.; Wai, P.; Oh, B.; Charoenphonphanich, C.; Chollacoop, N.; Kosaka, H. Influence of ethanol-biodiesel blends on diesel engines combustion behavior and particulate matter physicochemical characteristics. Case Stud. Chem. Environ. Eng. 2022, 6, 100249. [Google Scholar] [CrossRef]
- Blasio, D.G. Clean Fuels for Mobility; Springer: Singapore, 2022; pp. 39–179. [Google Scholar]
- Torres, D.J.; Li, Y.H.; Kong, S. Partitioning strategies for parallel KIVA-4 engine simulations. Comput. Fluids 2010, 39, 301–309. [Google Scholar] [CrossRef]
- Forgber, T.; Tosona, P.; Madlmeir, S.; Kureck, H.; Khinast, J.G.; Jajcevic, D. Extended validation and verification of XPS/AVL-Fire™, a computational CFD-DEM software platform. Powder Technol. 2020, 361, 880–893. [Google Scholar] [CrossRef]
- Lebedevas, S.; Pukalskas, S.; Daukšys, V. Mathematical modelling of indicative process parameters of dual-fuel engines with conventional fuel injection system. Transport 2020, 35, 57–67. [Google Scholar] [CrossRef]
- Lebedevas, S.; Cepaitis, T. Methodological Solutions for Predicting Energy Efficiency of Organic Rankine Cycle Waste Heat Recovery Systems Considering Technological Constraints. J. Mar. Sci. Eng. 2024, 12, 1303. [Google Scholar] [CrossRef]
- Duc, T.H.; Nhat, B.N.; Tan, P.T.; Hoang, S.D.; Quang, M.P.; Viet, T.V. Application of AVL BOOST modeling to optimize the engine working load and drivetrain transmission ratio of the diesel firefighting pump system. Heliyon 2024, 10, e41029. [Google Scholar] [CrossRef]
- Qadiri, U.; Alfantazi, A. Numerical 1-D simulations on Single-Cylinder stationary spark ignition engine using Micro-Emulsions, gasoline, and hydrogen in dual fuel mode. Cleaner Chem. Eng. 2022, 2, 100009. [Google Scholar] [CrossRef]
- Konkov, A. Diagnostics of Diesel Engine Technical Condition in Operation on the Basis of Identification of Fast Operating Processes; Admiral G.I. Nevelskoy Maritime State University: Vladivostok, Russia, 2011. [Google Scholar]
- Wiebe, I.I. The New About Working Cycle of the Engine; Mashgiz: Moscow, Russia, 1962; 271p. [Google Scholar]
- Woschni, G.; Anists, F. A method for predicting the change in the combustion process of medium-speed diesel engines under changed operating conditions. MTZ 1973, 4, 106–110. [Google Scholar]
- Woschni, G. The calculation of wall losses and the thermal load of diesel engines. MTZ 1970, 31, 491–499. [Google Scholar]
- Molodtsov, N.I.; Sokolov, P.V.; Vlasov, Y.Y. The influence of structural regulation indicators and augmentation level on heat release coefficient of gases to the surface of CPG parts. Leningr. CDERI Proc. 1975, 69, 3–17. [Google Scholar]
- Woschni, G. A Universally Applicable Equation for the Instantaneous Heat Transfer Coefficient in the Internal Combustion Engine; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1967; p. 670931. [Google Scholar]
- Wärtsilä. Available online: https://www.wartsila.com/marine/products/engines-and-generating-sets/wartsila-20 (accessed on 22 March 2025).
- Zinner, K. Results of real cycle calculations about the possibilities of influencing the efficiency of diesel engines. MTZ 1970, 31, 243–246. [Google Scholar]
- Stechkin, B.S. On the efficiency of an ideal fast combustion cycle at a finite rate of heat release. Theory, design, calculation and testing of internal combustion engines. Proc. Lab. Engines USSR Acad. Sci. 1960, 1, 61–67. [Google Scholar]
- Semenov, B.N.; Ivanchenko, N.N. Problems of increasing the fuel efficiency of diesel engines and ways to solve them. Engine Eng. 1990, 11, 3–7. [Google Scholar]
- Lebedevas, S.; Lebedeva, G.; Pikūnas, A.; Spruogis, B. A simultaneous parametric analysis of the in-cylinder processes for diesel engines. Int. J. Veh. Syst. 2011, 18, 18–45. [Google Scholar] [CrossRef]
- Kirkpatrick, A.T. Heat and Mass Transfer. In Internal Combustion Engines: Applied Thermosciences; John Wiley & Sons: Hoboken, NJ, USA, 2020; Volume 11. [Google Scholar] [CrossRef]
- Kruggel, O. Progress in the combustion technology of high performance diesel engines toward reduction of exhaust emissions without reduction of operation economy. In Proceedings of the Baden–Wurttemberg Technology Conference, Westborough, MA, USA, 2–14 June 1989; p. 14. [Google Scholar]
- Kruggel, O. Investigations into nitrogen oxide reduction on high-speed large diesel engines. MTZ Mot. 1988, 49, 22–29. [Google Scholar]
- Lebedevas, S.; Raslavičius, L.; Drazdauskas, M. Comprehensive correlation for the prediction of the heat release characteristics of diesel/CNG mixtures in a single-zone combustion model. Sustainability 2023, 15, 3722. [Google Scholar] [CrossRef]


| Fuel Type | Ammonia | Methanol | Biodiesel (RRME) | LNG | Diesel |
|---|---|---|---|---|---|
| Chemical formula | NH3 | CH3OH | CH3(CH2)nCOOCH3 | CH4 | - |
| Density when liquefied, kg/m3 | 602.8 | 792 | 890 | 430 | 832 |
| Lower calorific value, MJ/kg | 18.5 | 19.9 | 37.5 | 38.1 | 42.7 |
| Octane number | 110 | 109 | 60.6 | 107 | - |
| Cetane number | 5–7 | 5–8 | >51 | - | 47–55 |
| Ignition temperature, °C | 651 | 385 | >150 | 540 | 254–285 |
| Flame spread rate, m/s | 0.07–0.14 | 0.50 | - | 0.38 | 0.87 |
| Heat of vaporization, kJ/kg | 1370 | 1103 | 300 | 510 | 250–290 |
| C, mass fraction | 0.0 | 37.5 | 77.0 | 75.0 | 86.7 |
| H, mass fraction | 17.7 | 12.6 | 12.1 | 25.0 | 13.3 |
| O, mass fraction | 0.0 | 49.9 | 10.9 | 0.0 | 0.0 |
| N, mass fraction | 82.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| Wärtsilä 9L20DF | AE/DE | ME | |||
|---|---|---|---|---|---|
| Gas mode | Diesel mode | Gas mode | Diesel mode | ||
| Cylinder output | kW | 180 | |||
| Engine speed | rpm | 1200 | |||
| Speed mode | Constant | Variable | |||
| Engine output | kW | 1665 | |||
| Cylinder bore | mm | 200 | |||
| Stroke | mm | 280 | |||
| Compression ratio | 13.4 | ||||
| Piston displacement | l/cyl | 8.8 | |||
| Test | Parameters | |||||
|---|---|---|---|---|---|---|
| Pk, bar | Pmi, bar | Pmax, bar | Tmax, K | ηi | αgas × Tavg, % | |
| Diesel | 4.35 | 23.8 | 176.7 | 1586 | 0.476 | 100.0 |
| Biodiesel | 4.42 | 23.5 | 177.9 | 1558 | 0.476 | 99.0 |
| Ammonia Gi = QD | 4.13 | 23.5 | 253.2 | 1759 | 0.490 | 102.3 |
| Methanol Gi = QD | 4.14 | 24.9 | 301.0 | 1940 | 0.499 | 110.6 |
| Methanol (m) Gi = QD | 4.14 | 25.0 | 273.1 | 1860 | 0.502 | 111.6 |
| LNG Gi = QD | 4.39 | 24.9 | 226.9 | 1666 | 0.493 | 104.5 |
| Test | Pavg | Tavg | (λgas/μgas)0.5 | (Pgas/(Rgas × Tgas))0.5 | αgas | αgas × Tavg, % |
|---|---|---|---|---|---|---|
| Diesel | 65.7 | 1087 | 1.11 | 14.48 | 457 | 100.0 |
| Biodiesel | 66.2 | 1072 | 1.10 | 14.64 | 458 | 99.0 |
| Ammonia Gi = QD | 69.7 | 1077 | 1.14 | 14.51 | 472 | 102.3 |
| Methanol Gi = QD | 72.7 | 1114 | 1.16 | 15.09 | 497 | 110.6 |
| Methanol (m) Gi = QD | 75.5 | 1128 | 1.15 | 14.89 | 487 | 111.6 |
| LNG Gi = QD | 70.9 | 1087 | 1.13 | 14.89 | 477 | 104.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebedevas, S.; Milašius, E. Comparative Assessment of the Thermal Load of a Marine Engine Operating on Alternative Fuels. J. Mar. Sci. Eng. 2025, 13, 748. https://doi.org/10.3390/jmse13040748
Lebedevas S, Milašius E. Comparative Assessment of the Thermal Load of a Marine Engine Operating on Alternative Fuels. Journal of Marine Science and Engineering. 2025; 13(4):748. https://doi.org/10.3390/jmse13040748
Chicago/Turabian StyleLebedevas, Sergejus, and Edmonas Milašius. 2025. "Comparative Assessment of the Thermal Load of a Marine Engine Operating on Alternative Fuels" Journal of Marine Science and Engineering 13, no. 4: 748. https://doi.org/10.3390/jmse13040748
APA StyleLebedevas, S., & Milašius, E. (2025). Comparative Assessment of the Thermal Load of a Marine Engine Operating on Alternative Fuels. Journal of Marine Science and Engineering, 13(4), 748. https://doi.org/10.3390/jmse13040748







