Container Liner Shipping System Design Considering Methanol-Powered Vessels
Abstract
:1. Introduction
- Given the megatrend of the green energy transition in the shipping industry, we propose a novel bi-level programming model for addressing LSSDs. To the best of our knowledge, this is the first paper that combines bunker fuel management strategy optimization with LSSD for methanol-powered vessels. It extends the existing container liner shipping network design model by fully considering the new factors arising from fuel renewal in the liner shipping industry.
- The nonlinearity of the fuel consumption function makes it difficult to solve the lower-level model. To address this challenge, we propose the use of a model reformulation method based on a piecewise linearization approach to reconstruct the nonlinear lower-level model as a linear programming model. Then, considering the NP-hard properties of the problem, we develop a customized solution algorithm based on the framework of the genetic algorithm (GA) to explore satisfactory solutions to the model efficiently.
2. Literature Review
2.1. Traditional LSSD
2.2. Bunker Fuel Management and Green Fuel Adoption in Shipping
2.3. Research Gaps
- Bunker fuel management optimization under low-energy-density fuels, such as methanol, remains underexplored within the LSSD framework.
- More frequent bunkering requirements necessitate new strategies for liner deployment, shipping network design, and slot allocation, which are absent in current modeling frameworks.
- The impact of adopting green fuels has not yet been fully addressed in a way that considers carbon taxes and future reductions in green fuel prices.
3. Problem Description
3.1. Shipping Network Design
3.2. OD Pair and Transportation Path
3.3. Slot Allocation Scheme
3.4. Fleet Deployment, Sailing Speed, and Bunker Fuel Management
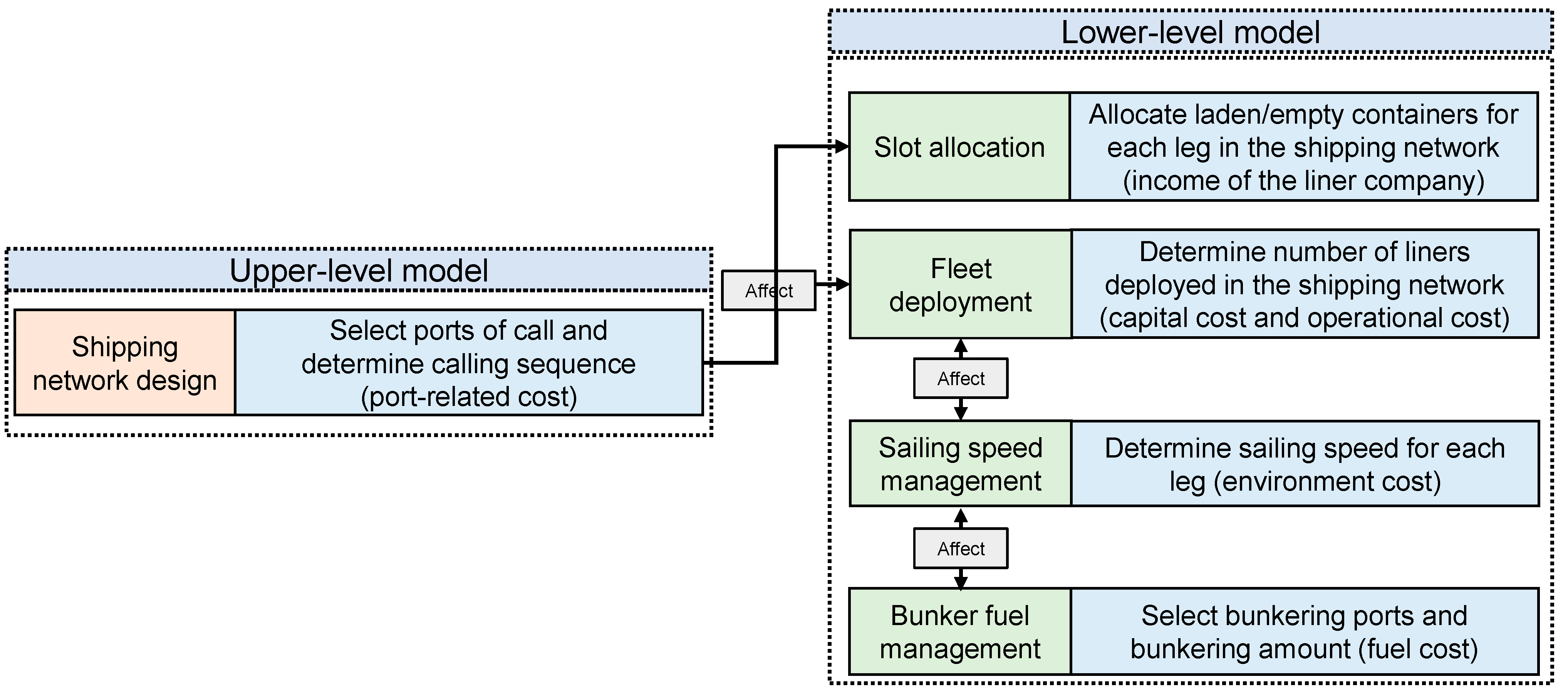
3.5. Framework of the Optimization Model
4. Model Establishment
4.1. Model Assumptions
- Shipping network structure: The shipping network consists of one trunk route (which connects hub ports and operates in a closed-loop manner) and several feeder routes (which employs a hub-and-spoke structure to connect hub ports with feeder ports). We assume that the liner company is responsible solely for the operation of trunk routes, whereas feeder routes are operated by independent feeder liner companies [1,21].
- Liner operations: We assume that the liners deployed in the fleet have the same class (i.e., capacity) and that the liner class is known. The calling frequency is set to once a week [1,20]. This assumption can be relaxed by introducing a decision variable associated with the calling frequency. Therefore, this assumption does not affect the structure of the model. All the liners deployed in this fleet sail at the same speed when they are on the same leg (e.g., leg “Port A → Port B”). However, the sailing speed may vary between different legs. The minimum and maximum sailing speeds of various types of liners are fixed and known. The liner berthing time at each port of call is fixed at 18 h.
- Bunkering feel management: The fuel price is known and fixed at each port of call, and liner companies can choose to bunker with either traditional fuel or methanol [28,42]. This assumption is introduced because the planning period of LSSD is usually 3 to 6 months, and the fuel price does not change significantly [1,21]. Moreover, liner companies usually sign agreements to guarantee stable fuel prices for a period of time to control costs in practice. Traditional fuels can be classified into several categories. For the convenience of modeling, we assume that the traditional fuel used by the liner company is very-low-sulfur fuel oil (VLSFO). The liner only bunkers at the port of call, with bunkering time included in the berthing time. To ensure navigational safety, the minimum fuel inventory in the liner’s fuel tank is set at 10% of the tank capacity.
- Fuel consumption: Owing to the lack of operational data on methanol-powered liners, we can establish a fuel consumption correction factor for methanol-powered liners that aligns with the consumption levels of HFO-powered liners. This correction factor is adjusted on the basis of the ratio of the energy density of methanol (19.9 MJ/kg) to that of HFO (40.2 MJ/kg).
- Container: in the context of container transportation, we assume that all containers transported along the shipping network are twenty feet equivalent units (TEUs), with other container sizes converted into TEUs.
4.2. Model Development
4.2.1. Upper-Level Model
4.2.2. Lower-Level Model
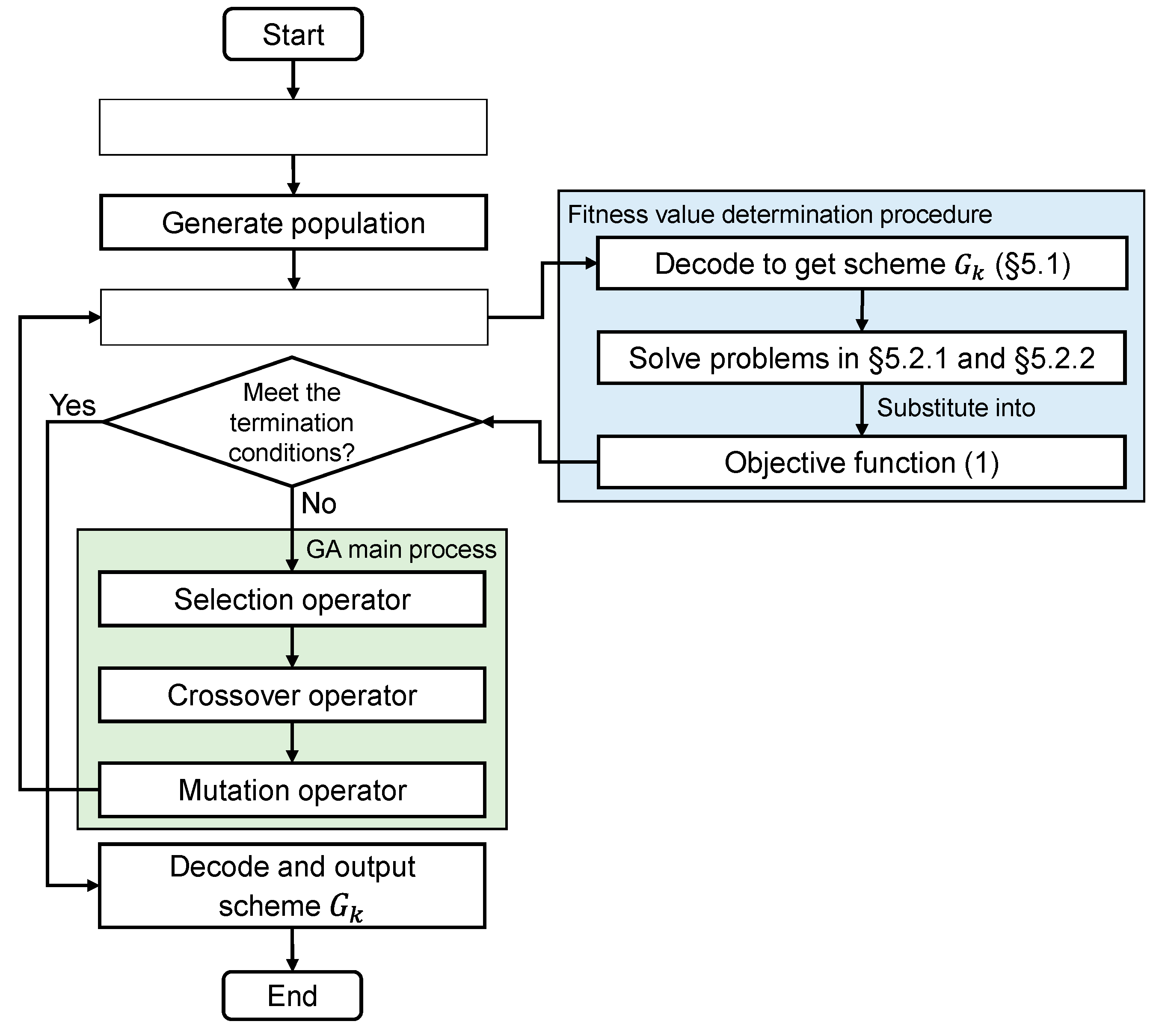
5. Solution Methodology
- For the encoding of the shipping network design scheme, we can use the optimal fleet deployment (with sailing speed management) and bunker fuel management strategies to achieve the lowest costs.
- For the encoding of the shipping network design scheme, we can optimize the slot allocation scheme to maximize profit.
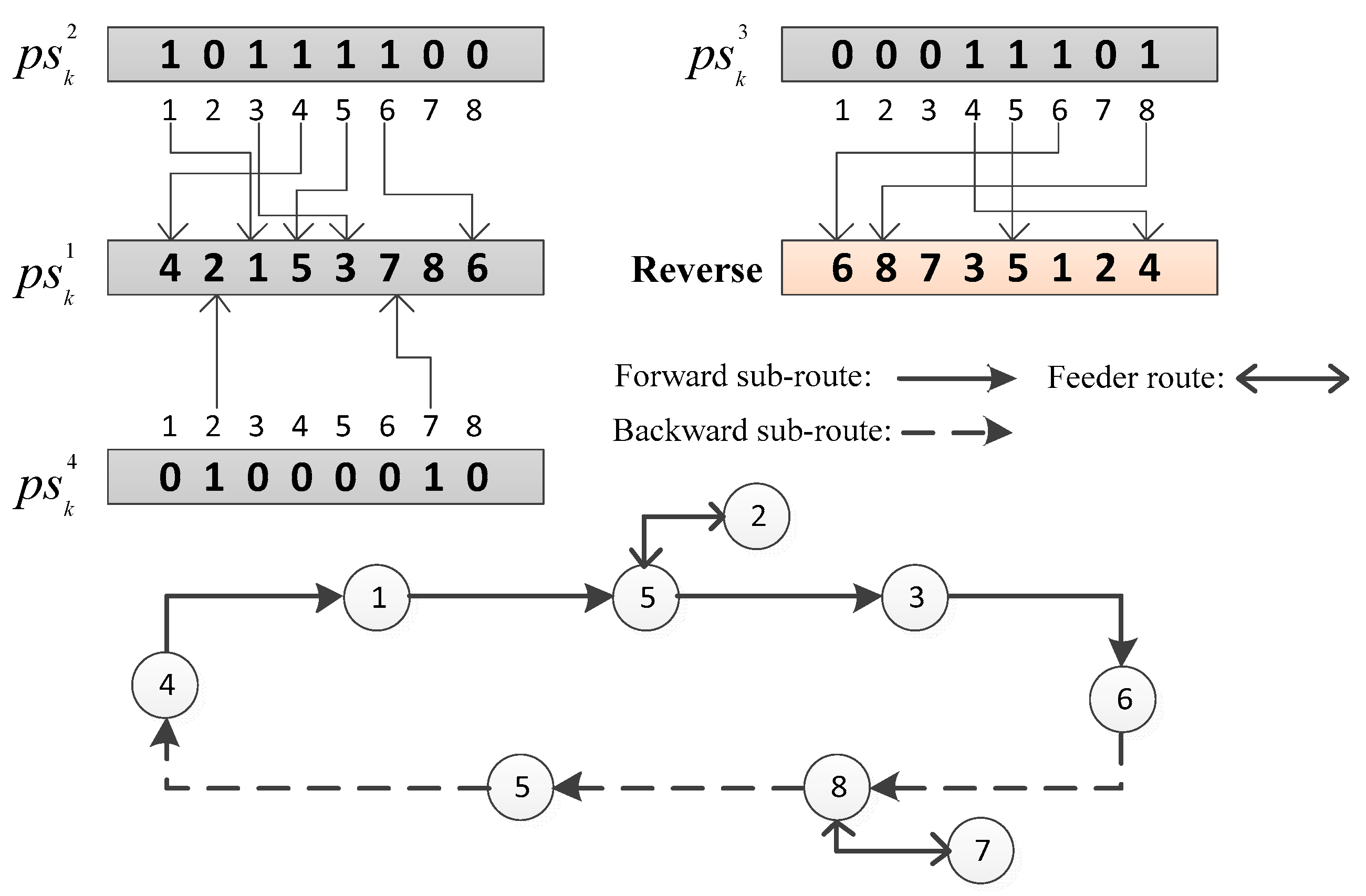
5.1. Encoding and Decoding Methods
5.2. Fitness Value Calculation
5.2.1. Optimization of Sailing Peed and Bunkering Fuel Management Strategies
5.2.2. The Optimization of the Slot Allocation Scheme
6. Numerical Experiments
6.1. Parameters and Experimental Design
6.1.1. Parameter Settings
6.1.2. Experimental Design
- (1)
- Experimental scheme design
- (2)
- Computational environment and solution process
6.2. Sensitivity Analysis
6.2.1. Sensitivity Analysis of Fuel Type
6.2.2. Sensitivity Analysis of Fuel Price
7. Conclusions
- In the comparative analysis of fuel types, we find that the optimization results for green methanol-powered liners and VLSFO-powered liners are highly consistent under the current carbon tax framework, whereas gray methanol-powered liners have significant disadvantages. This finding has important policy implications. On the one hand, the current carbon tax mechanism successfully achieves its policy goals by making green fuels and traditional fuels equally competitive in actual operation through economic means. On the other hand, the double cost pressure caused by higher fuel costs and a carbon tax may prompt the shipping industry to transition directly from traditional fuels to green fuels, bypassing gray methanol as a transitional stage. In addition, these results provide critical insights into the decarbonization pathway for the shipping industry; that is, the design of policy tools can directly influence technological choices.
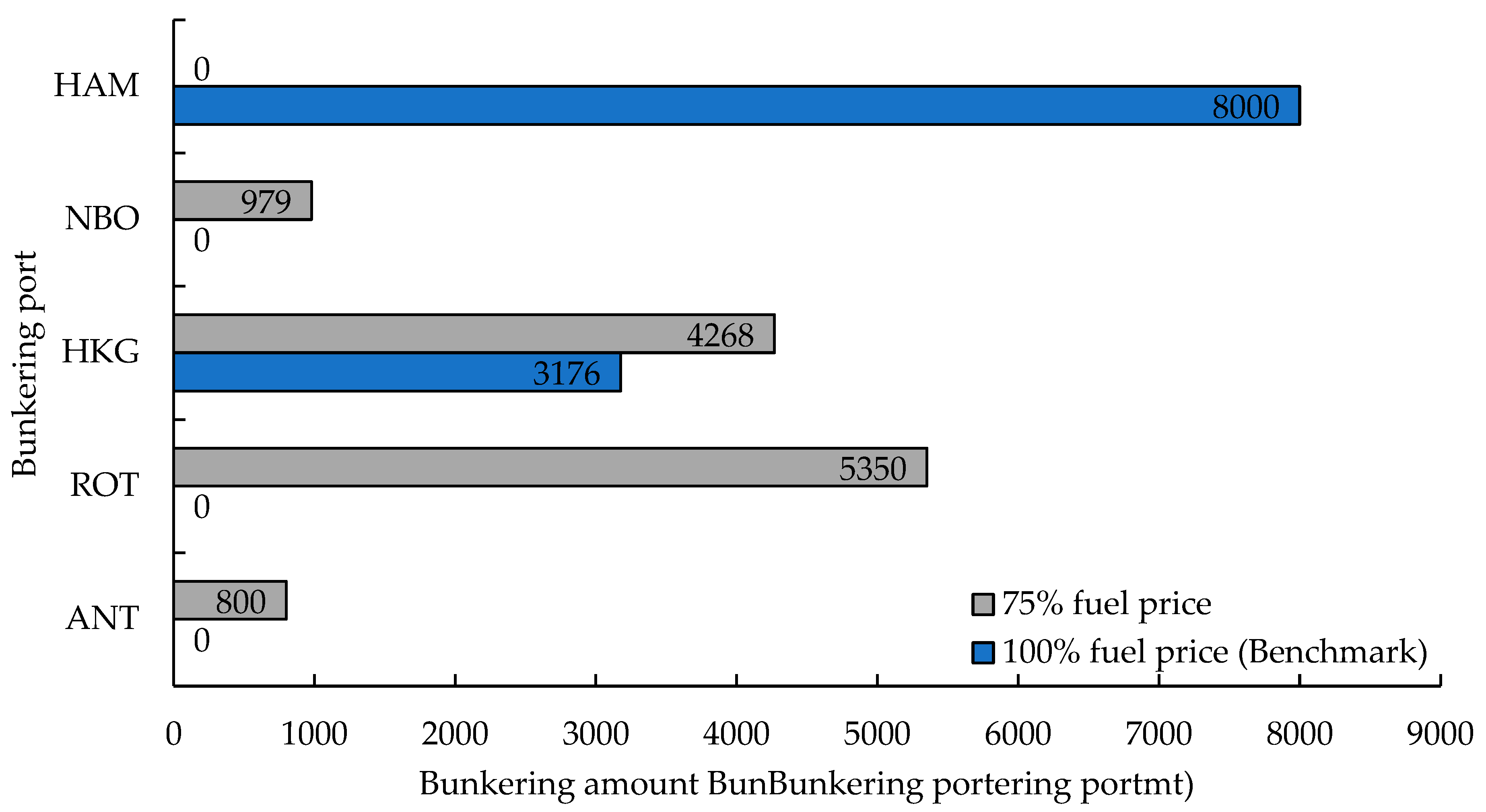
- Fuel price levels significantly impact the trade-offs that liner companies make between shipping network complexity and operational efficiency. Under the current price level, the network for 16,000 TEU liners covers only six hub ports. When the price of green methanol decreases by 25%, the number of hub ports expands to seven. Moreover, bunker fuel management strategies shift from a high concentration (with the main ports accounting for 75% of the total bunkering amount) to a more distributed model (with the main ports accounting for only 44%). This result indicates that fuel price reductions can encourage liner companies to increase competitiveness through network expansion rather than by focusing solely on cost control.
- We find a significant interaction between liner class and green transition strategies. The liners of different classes respond differently to price changes. For example, 20,000 TEU liners demonstrate a stronger potential for operational efficiency improvement after fuel price reductions, with weekly profit increasing from USD 14.17 million to USD 16.12 million (a 13.76% increase). In contrast, 16,000 TEU liners exhibit greater flexibility in shipping network optimization, with weekly profit increasing from USD 11.74 million to USD 13.91 million (an 18.48% increase). This is driven by network expansion to increase market coverage. This difference suggests that sensitivity to green fuel subsidies varies by liner class and that green transition policies should be tailored to liner classes to maximize policy effectiveness.
- Bunker fuel management strategies shift from a high-concentration model to a more distributed model. With fuel price reductions, bunker fuel management strategies exhibit decentralized characteristics, reflecting a dynamic trade-off between operational flexibility and cost control for liner companies. For example, the 16,000 TEU liners shifted from a concentrated bunkering strategy at HAM to bunkering at both ANT and ROT, whereas the 20,000 TEU liners added QIN as a bunkering hub. Decision-makers at the QIN and other Asian ports should invest in infrastructure to support the development of green fuel bunkering capabilities.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, K.; Yi, X.; Xin, X.; Zhang, T. Liner shipping network design model with carbon tax, seasonal freight rate fluctuations and empty container relocation. Sustain. Horiz. 2023, 8, 100073. [Google Scholar] [CrossRef]
- Shangguan, Y.; Tian, X.; Pang, K.-W.; Ruan, Q.; Jin, Y.; Wang, S. Navigating the green shipping: Stochastic hydrogen hub deployment in inland waterways. Transp. Res. Part D Transp. Environ. 2024, 129, 104126. [Google Scholar] [CrossRef]
- Tian, X.; Shangguan, Y.; Pang, K.-W.; Guo, Y.; Lyu, M.; Wang, S.; Huang, G.Q. Carbon emission allocation policy making in liner shipping: A novel approach toward equitable and efficient maritime sustainability. Ocean Coast. Manag. 2024, 256, 107270. [Google Scholar] [CrossRef]
- Yang, W.; Chen, X.; Liu, Y. Review and reflections of legislation and policies on shipping decarbonization under China’s “dual carbon” target. Front. Mar. Sci. 2023, 10, 1131552. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, Y.; Sun, L.; Qi, X.; Pan, X. Study on international carbon emission quota allocation of shipping industry-based on fairness and efficiency. Front. Mar. Sci. 2023, 10, 1269643. [Google Scholar] [CrossRef]
- Christiansen, M.; Hellsten, E.; Pisinger, D.; Sacramento, D.; Vilhelmsen, C. Liner shipping network design. Eur. J. Oper. Res. 2020, 286, 1–20. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Container liner fleet deployment: A systematic overview. Transp. Res. Part C Emerg. Technol. 2017, 77, 389–404. [Google Scholar] [CrossRef]
- Karsten, C.V.; Brouer, B.D.; Pisinger, D. Competitive liner shipping network design. Comput. Oper. Res. 2017, 87, 125–136. [Google Scholar] [CrossRef]
- Ting, S.-C.; Tzeng, G.-H. An optimal containership slot allocation for liner shipping revenue management. Marit. Policy Manag. 2004, 31, 199–211. [Google Scholar] [CrossRef]
- Shintani, K.; Imai, A.; Nishimura, E.; Papadimitriou, S. The container shipping network design problem with empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 39–59. [Google Scholar] [CrossRef]
- Ronen, D. Cargo ships routing and scheduling: Survey of models and problems. Eur. J. Oper. Res. 1983, 12, 119–126. [Google Scholar] [CrossRef]
- Lane, D.; Heaver, T.D.; Uyeno, D. Planning and scheduling for efficiency in liner shipping. Marit. Policy Manag. 1987, 14, 109–125. [Google Scholar]
- Rana, K.; Vickson, R.G. A model and solution algorithm for optimal routing of a time-chartered containership. Transp. Sci. 1988, 22, 83–95. [Google Scholar]
- Ronen, D. Ship scheduling: The last decade. Eur. J. Oper. Res. 1993, 71, 325–333. [Google Scholar]
- Dulebenets, M.A.; Pasha, J.; Abioye, O.F.; Kavoosi, M. Vessel scheduling in liner shipping: A critical literature review and future research needs. Flex. Serv. Manuf. J. 2021, 33, 43–106. [Google Scholar]
- Chen, J.; Ye, J.; Zhuang, C.; Qin, Q.; Shu, Y. Liner shipping alliance management: Overview and future research directions. Ocean Coast. Manag. 2022, 219, 106039. [Google Scholar]
- Elmi, Z.; Singh, P.; Meriga, V.K.; Goniewicz, K.; Borowska-Stefańska, M.; Wiśniewski, S.; Dulebenets, M.A. Uncertainties in liner shipping and ship schedule recovery: A state-of-the-art review. J. Mar. Sci. Eng. 2022, 10, 563. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, S. Optimal operating strategy for a long-haul liner service route. Eur. J. Oper. Res. 2011, 215, 105–114. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, S. Liner shipping service network design with empty container repositioning. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 695–708. [Google Scholar]
- Gao, S.; Xin, X.; Li, C.; Liu, Y.; Chen, K. Container ocean shipping network design considering carbon tax and choice inertia of cargo owners. Ocean Coast. Manag. 2022, 216, 105986. [Google Scholar]
- Xiang, Z.; Xin, X.; Zhang, T.; Chen, K.; Liu, M. Asia–Europe liner shipping network design model considering Arctic route and black carbon tax. Ocean Coast. Manag. 2025, 261, 107492. [Google Scholar] [CrossRef]
- Agarwal, R.; Ergun, Ö. Network design and allocation mechanisms for carrier alliances in liner shipping. Oper. Res. 2010, 58, 1726–1742. [Google Scholar] [CrossRef]
- Arslan, O.; Archetti, C.; Jabali, O.; Laporte, G.; Speranza, M.G. Minimum cost network design in strategic alliances. Omega 2020, 96, 102079. [Google Scholar] [CrossRef]
- Besbes, O.; Savin, S. Going bunkers: The joint route selection and refueling problem. Manuf. Serv. Oper. Manag. 2009, 11, 694–711. [Google Scholar]
- Vilhelmsen, C.; Lusby, R.; Larsen, J. Tramp ship routing and scheduling with integrated bunker optimization. EURO J. Transp. Logist. 2014, 3, 143–175. [Google Scholar] [CrossRef]
- He, P.; Jin, J.G.; Pan, W.; Chen, J. Route, speed, and bunkering optimization for LNG-fueled tramp ship with alternative bunkering ports. Ocean Eng. 2024, 305, 117957. [Google Scholar] [CrossRef]
- Omholt-Jensen, S.; Fagerholt, K.; Meisel, F. Fleet repositioning in the tramp ship routing and scheduling problem with bunker optimization: A matheuristic solution approach. Eur. J. Oper. Res. 2025, 321, 88–106. [Google Scholar] [CrossRef]
- Yao, Z.; Ng, S.H.; Lee, L.H. A study on bunker fuel management for the shipping liner services. Comput. Oper. Res. 2012, 39, 1160–1172. [Google Scholar] [CrossRef]
- Kim, H.-J.; Chang, Y.-T.; Kim, K.-T.; Kim, H.-J. An epsilon-optimal algorithm considering greenhouse gas emissions for the management of a ship’s bunker fuel. Transp. Res. Part D Transp. Environ. 2012, 17, 97–103. [Google Scholar]
- Kim, H. A Lagrangian heuristic for determining the speed and bunkering port of a ship. J. Oper. Res. Soc. 2014, 65, 747–754. [Google Scholar]
- Sheng, X.; Lee, L.H.; Chew, E.P. Dynamic determination of vessel speed and selection of bunkering ports for liner shipping under stochastic environment. OR Spectr. 2014, 36, 455–480. [Google Scholar]
- Meng, Q.; Wang, S.; Lee, C.-Y. A tailored branch-and-price approach for a joint tramp ship routing and bunkering problem. Transp. Res. Part B: Methodol. 2015, 72, 1–19. [Google Scholar]
- Zhen, L.; Wang, S.; Zhuge, D. Dynamic programming for optimal ship refueling decision. Transp. Res. Part E Logist. Transp. Rev. 2017, 100, 63–74. [Google Scholar]
- Aydin, N.; Lee, H.; Mansouri, S.A. Speed optimization and bunkering in liner shipping in the presence of uncertain service times and time windows at ports. Eur. J. Oper. Res. 2017, 259, 143–154. [Google Scholar]
- De, A.; Choudhary, A.; Turkay, M.; Tiwari, M.K. Bunkering policies for a fuel bunker management problem for liner shipping networks. Eur. J. Oper. Res. 2021, 289, 927–939. [Google Scholar]
- Wang, H.; Liu, Y.; Wang, S.; Zhen, L. Optimal Ship Deployment and Sailing Speed under Alternative Fuels. J. Mar. Sci. Eng. 2023, 11, 1809. [Google Scholar] [CrossRef]
- Svanberg, M.; Ellis, J.; Lundgren, J.; Landälv, I. Renewable methanol as a fuel for the shipping industry. Renew. Sustain. Energy Rev. 2018, 94, 1217–1228. [Google Scholar]
- Parris, D.; Spinthiropoulos, K.; Ragazou, K.; Giovou, A.; Tsanaktsidis, C. Methanol, a Plugin Marine Fuel for Green House Gas Reduction—A Review. Energies 2024, 17, 605. [Google Scholar] [CrossRef]
- Gao, T.; Tian, J.; Liu, C.; Huang, C.; Wu, H.; Yuan, Z. A model for speed and fuel refueling strategy of methanol dual-fuel liners with emission control areas. Transp. Policy 2025, 161, 1–16. [Google Scholar]
- Chen, K.; Lu, Q.; Xin, X.; Yang, Z.; Zhu, L.; Xu, Q. Optimization of empty container allocation for inland freight stations considering stochastic demand. Ocean Coast. Manag. 2022, 230, 106366. [Google Scholar]
- Li, Z.; Wang, L.; Wang, G.; Xin, X.; Chen, K.; Zhang, T. Investment and subsidy strategy for low-carbon port operation with blockchain adoption. Ocean Coast. Manag. 2024, 248, 106966. [Google Scholar]
- De, A.; Wang, J.; Tiwari, M.K. Fuel bunker management strategies within sustainable container shipping operation considering disruption and recovery policies. IEEE Trans. Eng. Manag. 2019, 68, 1089–1111. [Google Scholar]




| Sets | |
|---|---|
| P | Set of all candidate ports of call, indexed by i or j |
| Set of all shipping network design schemes, indexed by n | |
| Set of fuel type, indexed by k | |
| Set of liner class, indexed by s | |
| in the shipping network design scheme , indexed by b | |
| Set of ports of call associated with network design scheme n | |
| Set of legs whose head node is port i in network design scheme n | |
| Set of legs whose tail node is port i in network design scheme n | |
| Parameters | |
| OD pair with origin port i and destination port j | |
| in shipping network design scheme | |
| in shipping network design scheme | |
| in network design scheme | |
| , and 0 otherwise | |
| Liner berthing time at port i | |
| fuel at port i | |
| is located | |
| Fuel consumption–carbon emission conversion factor for type k fuel | |
| Fuel consumption coefficient associated with type k fuel | |
| Minimum fuel inventory required for fuel tank of a class k liner | |
| Capacity of fuel tank for a class k liner | |
| Liner capacity | |
| Minimum/maximum sailing speed allowed | |
| Fuel consumption at port i in shipping network design scheme n | |
| Annual construction (i.e., purchase) cost for a class s liner | |
| Fixed cost incurred by liner bunkers at the port i | |
| Decision variables | |
| Binary variable, 1, if shipping network design scheme is selected by the liner company, 0 otherwise | |
| Binary variable, 1 if port i is selected for bunkering in shipping network design scheme n, 0 otherwise | |
| in shipping network design scheme | |
| Bunkering amount at port i in shipping network design scheme n | |
| Fuel inventory after bunkering at port i in shipping network design scheme n | |
| in shipping network design scheme n | |
| in shipping network design scheme | |
| in shipping network design scheme | |
| in shipping network design scheme | |
| in shipping network design scheme | |
| Number of liners deployed in the liner fleet | |
| in shipping network design scheme | |
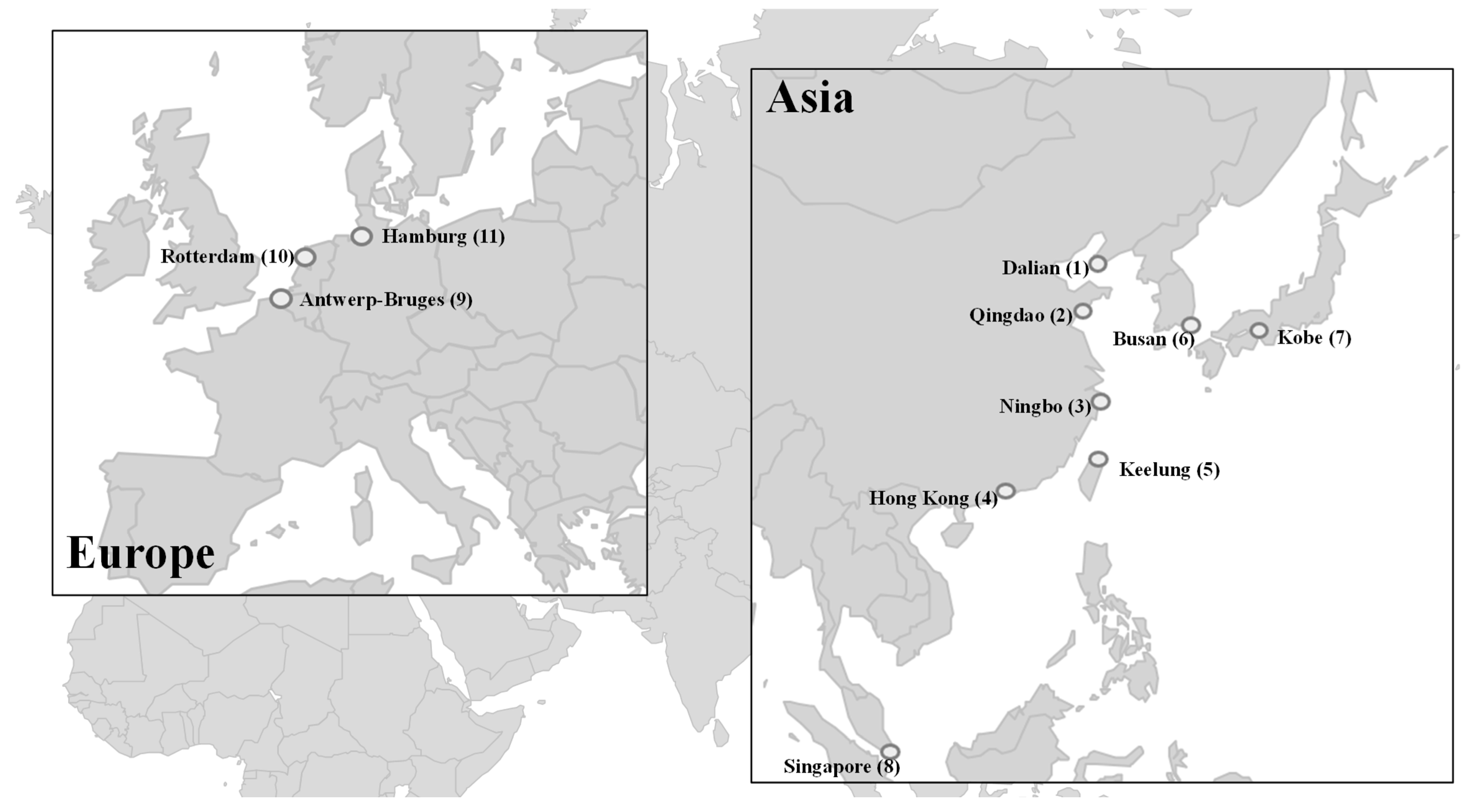
| No. | Port Name | Port Code | Area |
|---|---|---|---|
| 1 | Port of Dalian | DAL | Asia |
| 2 | Port of Qingdao | QIN | |
| 3 | Port of Ningbo | NBO | |
| 4 | Port of Hong Kong | HKG | |
| 5 | Port of Keelung | KEE | |
| 6 | Port of Busan | BUS | |
| 7 | Port of Kobe | KOB | |
| 8 | Port of Singapore | SGP | |
| 9 | Port of Antwerp-Bruges | ANT | Europe |
| 10 | Port of Rotterdam | ROT | |
| 11 | Port of Hamburg | HAM |
| Liner Class | Fuel Tank Capacity (×104 mt) | Fixed Cost (×104 USD/Week) | (kn) | (kn) | ||
|---|---|---|---|---|---|---|
| 16,000 TEU | 0.8 | 57.4 | 0.0386 | 0.0180 | 15.0 | 26.0 |
| 20,000 TEU | 1.0 | 60.9 | 0.0439 | 0.0205 |
| Fuel Type | Port | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DAL | QIN | NBO | HKG | KEE | BUS | KOB | SGP | ANT | ROT | HAM | |
| VLSFO | 629 | 635 | 639 | 612 | 613 | 626 | 685 | 604 | 552 | 549 | 572 |
| Gray methanol | 338 | 341 | 345 | 353 | 351 | 345 | 348 | 359 | 350 | 339 | 339 |
| Green methanol | 696 | 699 | 703 | 702 | 709 | 704 | 707 | 714 | 699 | 697 | 697 |
| Liner Class | Fuel Type | Trunk Route | Feeder Routes | Weekly Revenue (×106 USD) |
|---|---|---|---|---|
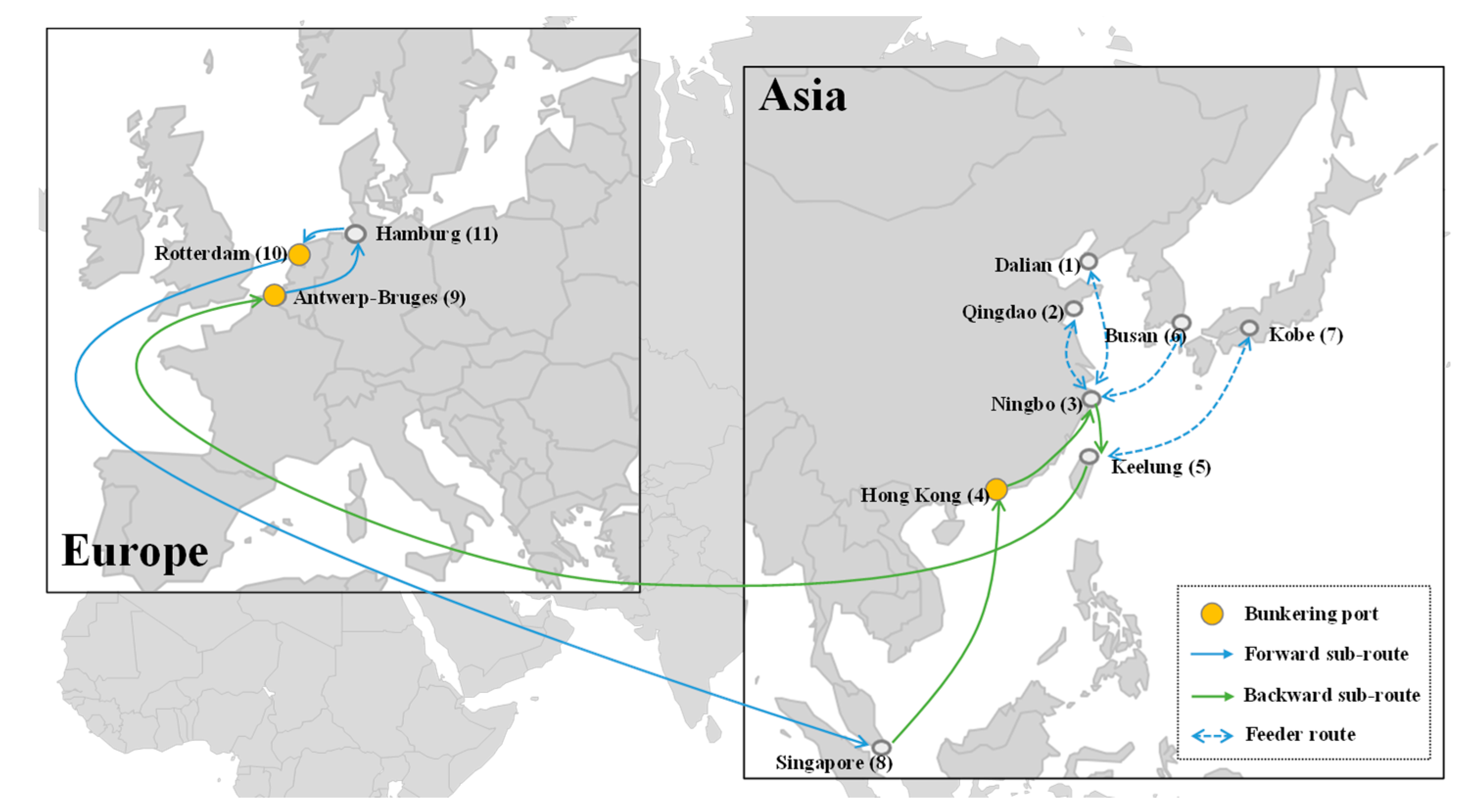
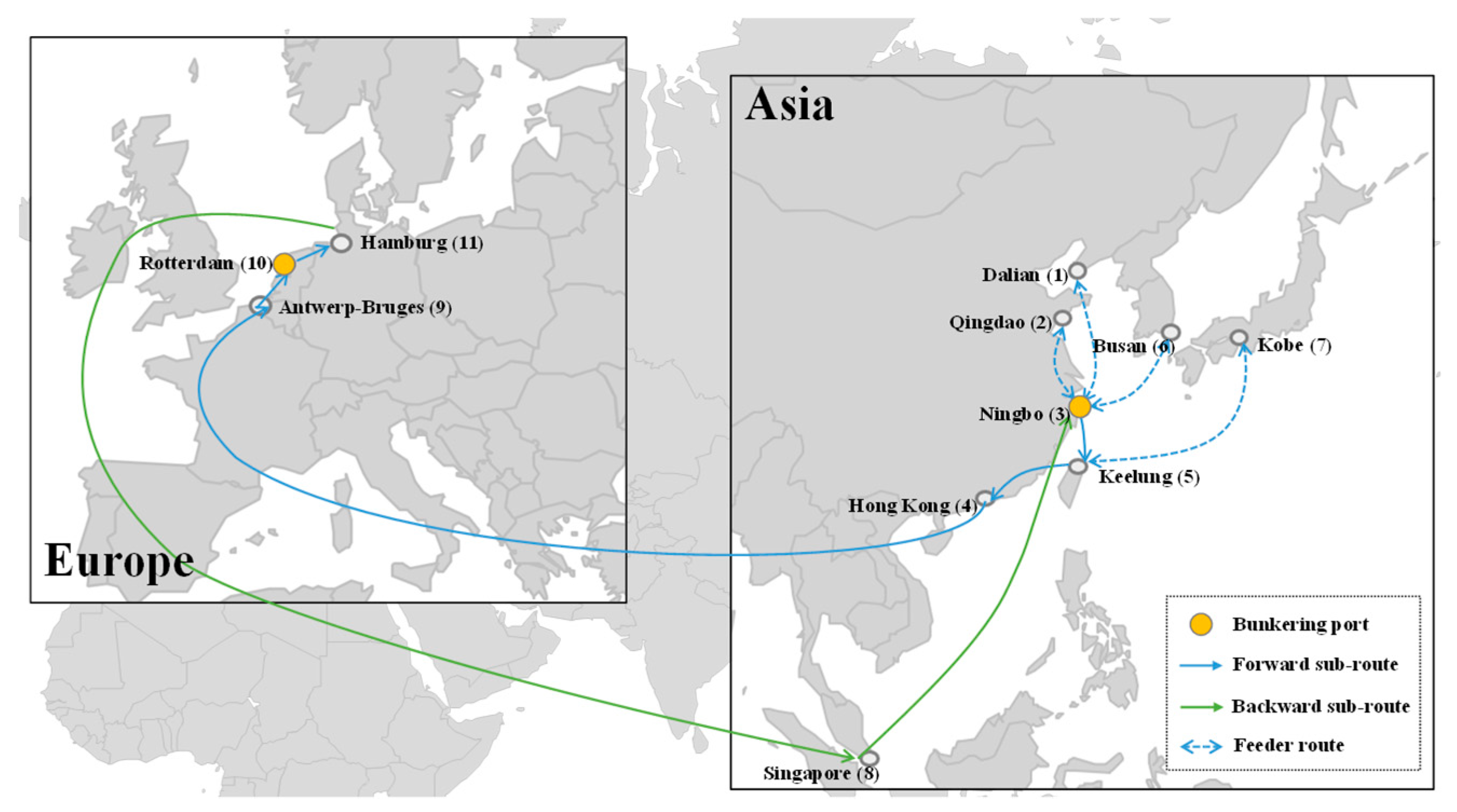
| 16,000 TEU | Green methanol | ANT → HAM → ROT → SGP → HKG → NBO → KEE → ANT | DAL + QIN + BUS NBO KOB KEE | 15.89 |
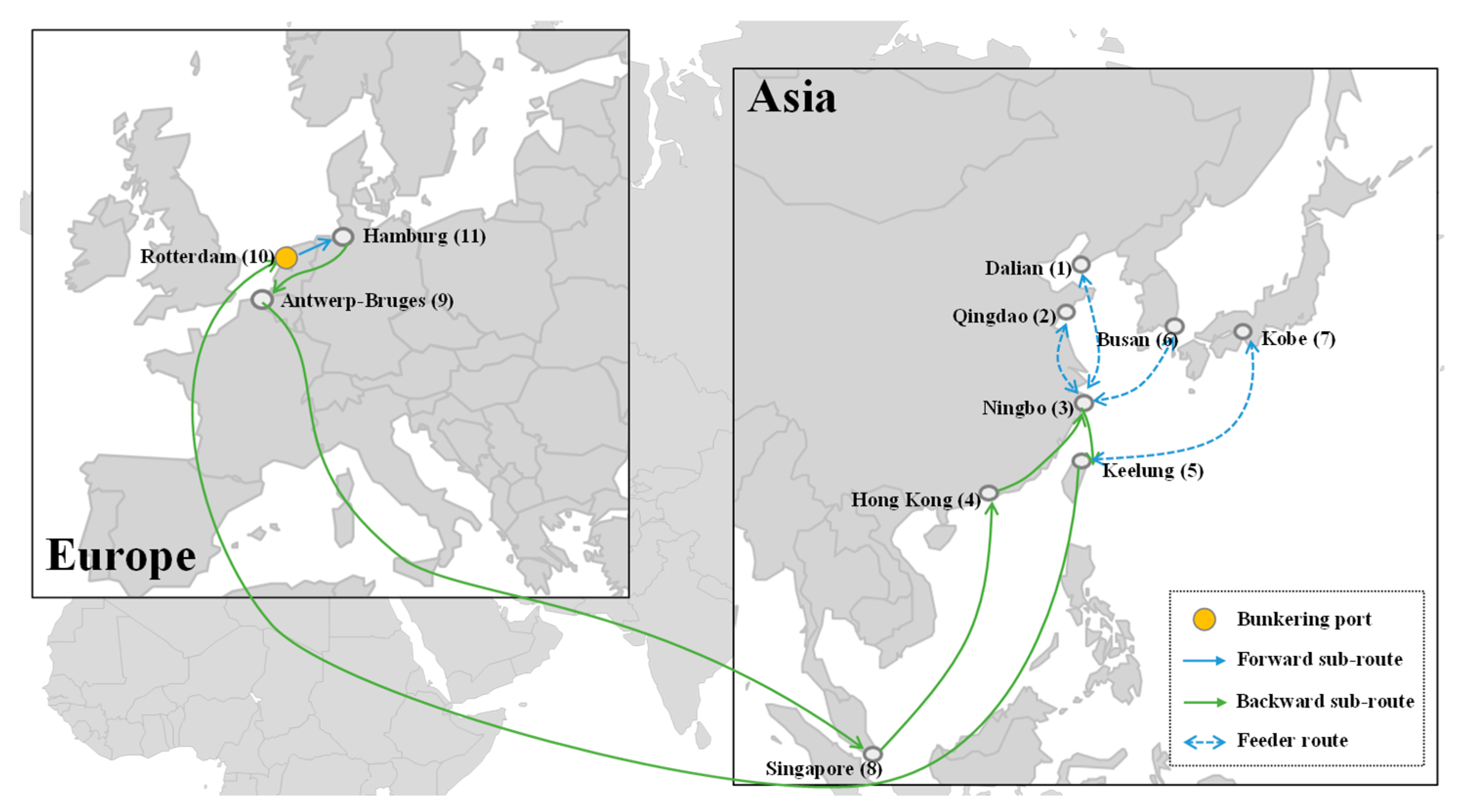
| Gray methanol | KEE → HKG → ROT → HAM → SGP → NBO → BUS → KEE | DAL + QIN NBO KOB KEE ANT HAM | 14.82 | |
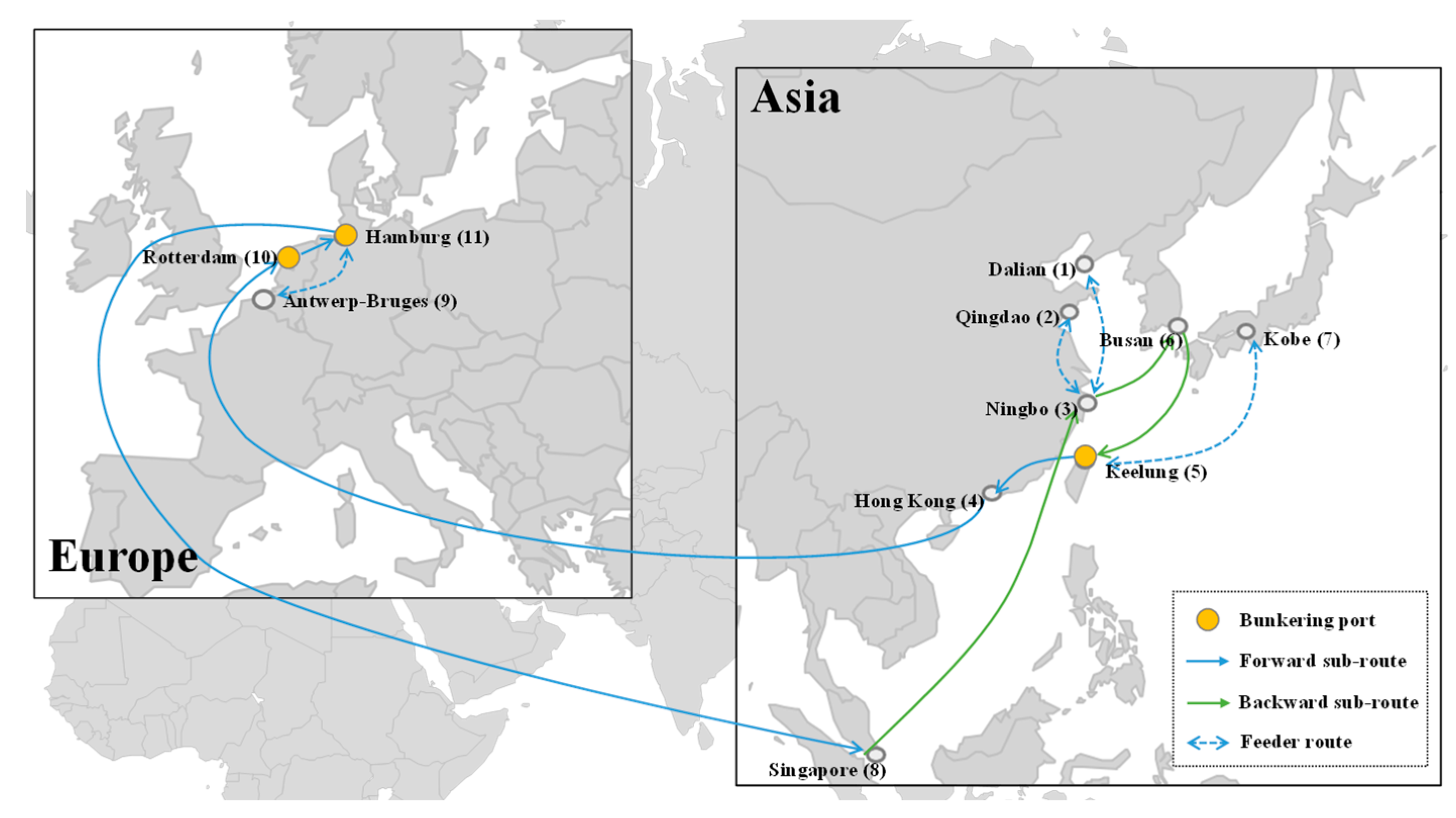
| VLSFO | ROT → HAM → ANT → SGP → HKG → NBO → KEE → ROT | DAL + QIN + BUS NBO KOB KEE | 15.88 | |
| 20,000 TEU | Green methanol | NBO → KEE → ROT → HAM → ANT → SGP → HKG → NBO | DAL + QIN + BUS
NBO KOB KEE | 19.42 |
| Gray methanol | NBO → KEE → HKG → ANT → ROT → HAM → SGP → NBO | DAL + QIN + BUS NBO KOB KEE | 18.54 | |
| VLSFO | NBO → BUS → KEE → HKG → ROT → HAM → ANT → SGP → NBO | DAL + QIN NBO KOB KEE | 19.23 |
| Line Class | Fuel Type | Bunkering Amount (×104 mt) | Bunkering Ports | Number of Liners | Average Sailing Speed (kn) | Fuel Cost (×106 USD) |
|---|---|---|---|---|---|---|
| 16,000 TEU | Green methanol | 10.42 | ANT, ROT, HKG | 9 | 15.34 | 36.50 |
| Gray methanol | 11.73 | KEE, ROT, HAM | 9 | 16.77 | 40.33 | |
| VLSFO | 4.93 | ROT | 9 | 15.25 | 27.07 | |
| 20,000 TEU | Green methanol | 12.16 | NBO, ROT, HAM | 9 | 16.23 | 42.53 |
| Gray methanol | 11.66 | NBO, ROT | 9 | 15.46 | 39.91 | |
| VLSFO | 6.53 | NBO, KEE, HKG, ROT | 9 | 16.27 | 38.03 |
| Fuel Type | Liner Class | Trunk Route | Feeder Routes | Weekly Revenue (×106 USD) |
|---|---|---|---|---|
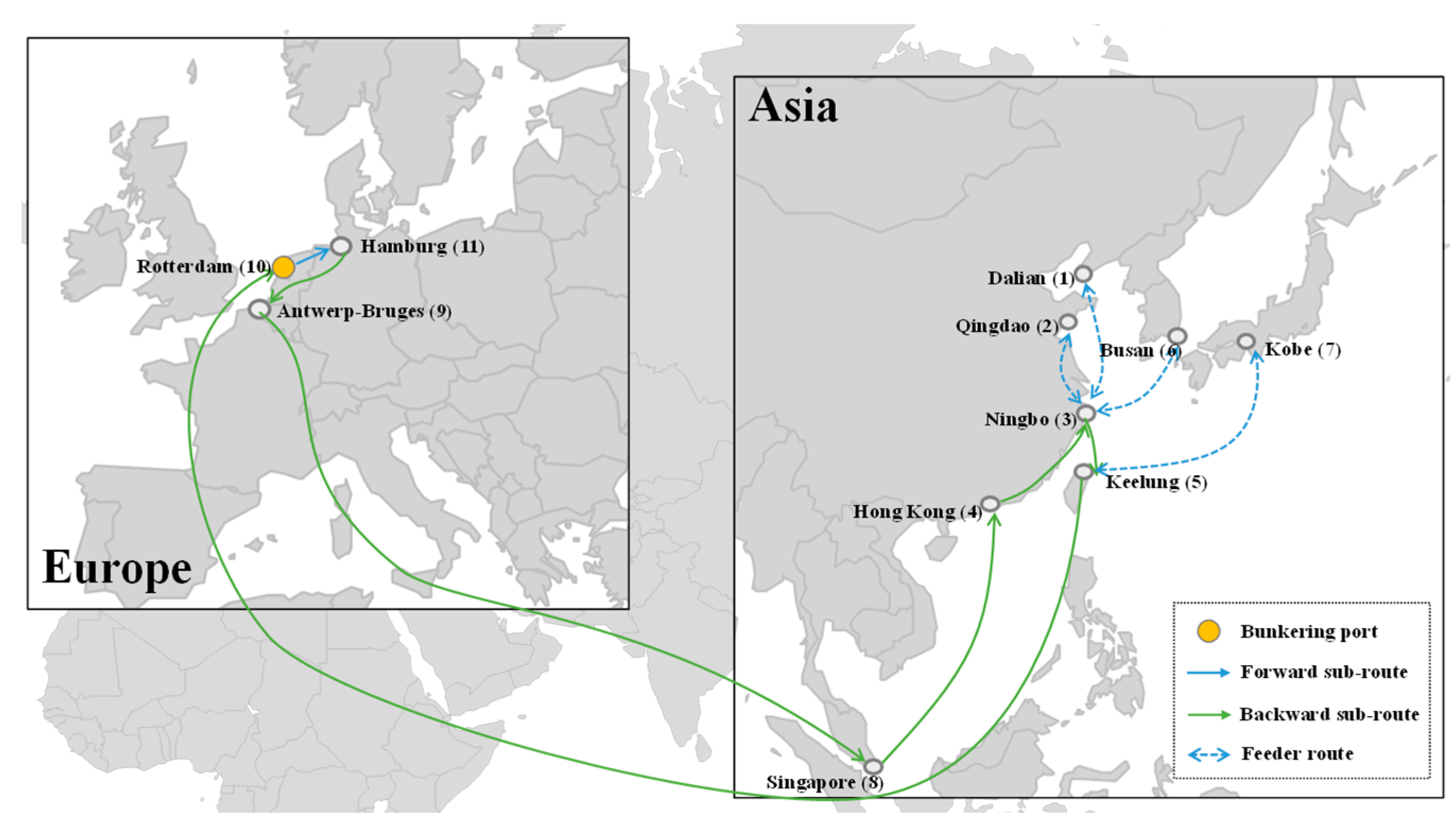
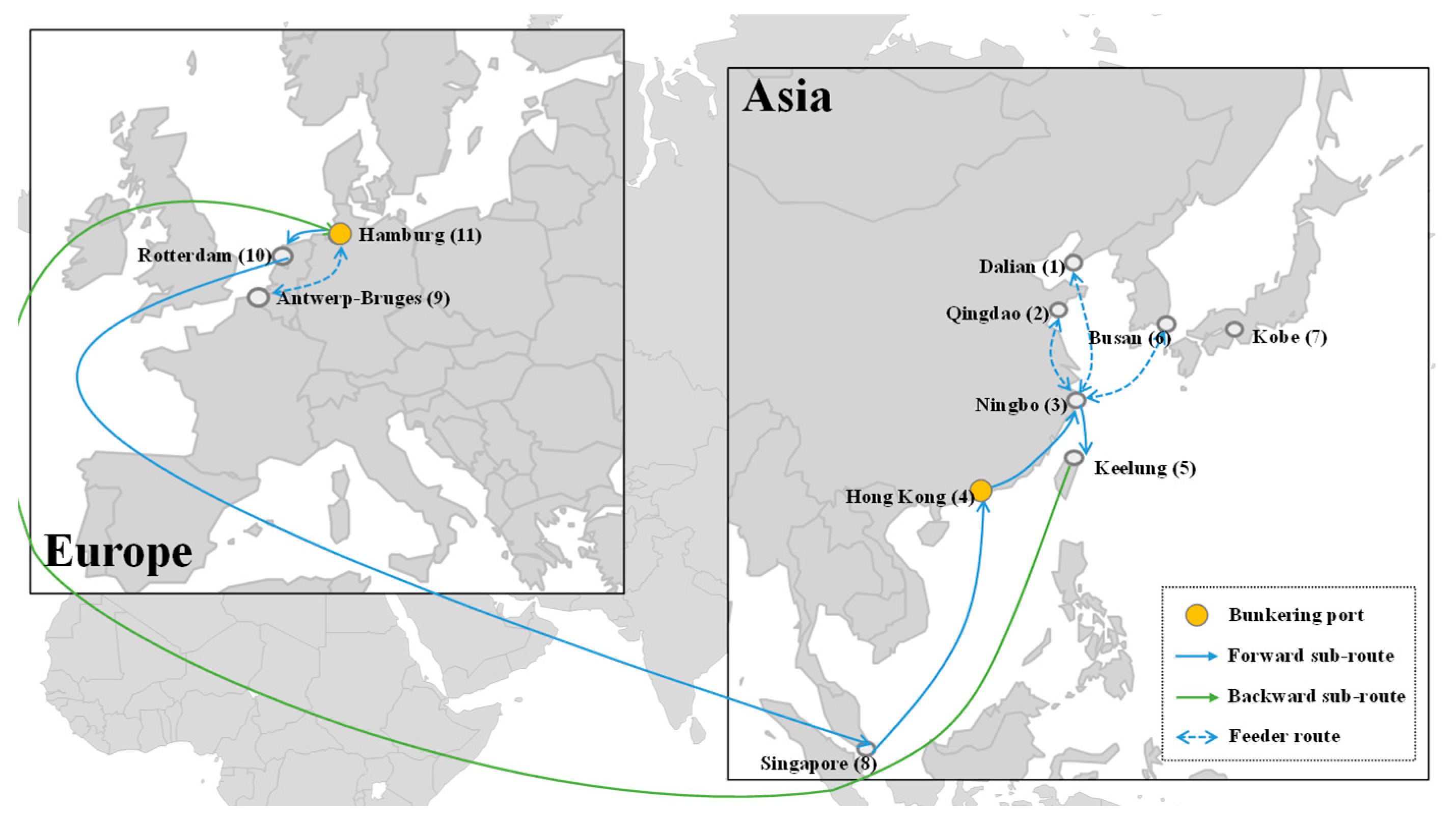
| Green methanol | 16,000 TEU | HAM → ROT → SGP → HKG → NBO → KEE → HAM | DAL + QIN + BUS NBO ANT HAM | 11.74 |
| 20,000 TEU | ANT → ROT → SGP → HKG → KEE → NBO → HKG → ANT | DAL + QIN + BUS NBO KOB KEE HAM ROT | 14.17 |
| Fuel Type | Liner Class | Bunkering Amount (×104 mt) | Bunkering Ports | Number of Liners | Average Speed (kn) | Fuel Cost (×106 USD) |
|---|---|---|---|---|---|---|
| Green methanol | 16,000 TEU | 10.06 | HAM, HKG | 9 | 15.16 | 70.25 |
| 20,000 TEU | 10.89 | ANT, ROT, HKG | 9 | 15.25 | 76.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yu, X.; Shang, J.; Chen, K.; Xin, X.; Zhang, W.; Yu, S. Container Liner Shipping System Design Considering Methanol-Powered Vessels. J. Mar. Sci. Eng. 2025, 13, 709. https://doi.org/10.3390/jmse13040709
Li Z, Yu X, Shang J, Chen K, Xin X, Zhang W, Yu S. Container Liner Shipping System Design Considering Methanol-Powered Vessels. Journal of Marine Science and Engineering. 2025; 13(4):709. https://doi.org/10.3390/jmse13040709
Chicago/Turabian StyleLi, Zhaokun, Xinke Yu, Jianning Shang, Kang Chen, Xu Xin, Wei Zhang, and Shaoqiang Yu. 2025. "Container Liner Shipping System Design Considering Methanol-Powered Vessels" Journal of Marine Science and Engineering 13, no. 4: 709. https://doi.org/10.3390/jmse13040709
APA StyleLi, Z., Yu, X., Shang, J., Chen, K., Xin, X., Zhang, W., & Yu, S. (2025). Container Liner Shipping System Design Considering Methanol-Powered Vessels. Journal of Marine Science and Engineering, 13(4), 709. https://doi.org/10.3390/jmse13040709







