Internal Tide Generation and Propagation in the Sulu Sea Under the Influence of Circulation
Abstract
1. Introduction
2. Data and Methods
2.1. Remote Sensing Data
2.2. Model Setup and Validation
2.3. Energy Diagnostic
2.4. Ray-Tracing Method
3. Results
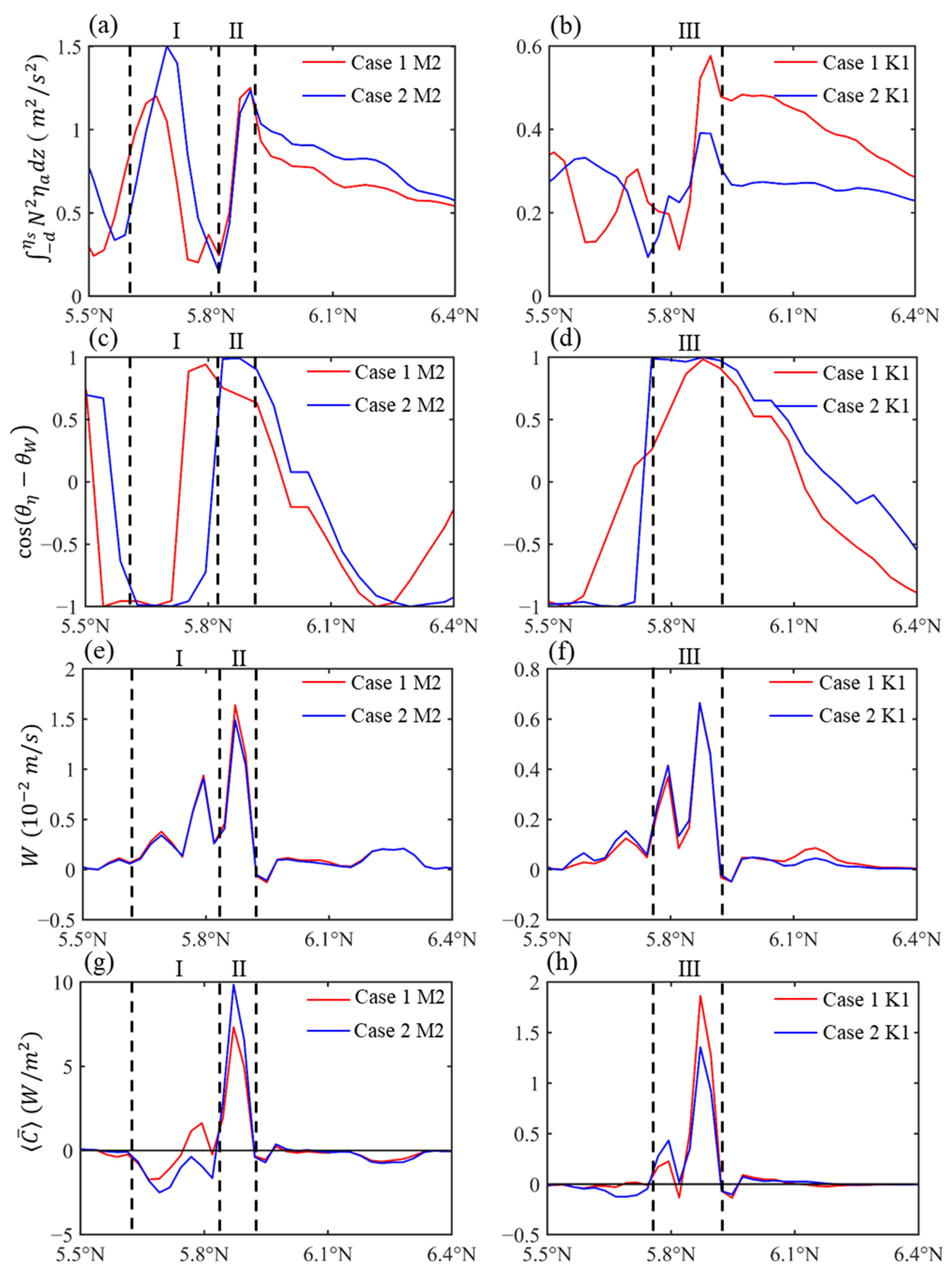
3.1. Modulation of Circulation on IT Generation
3.2. Modulation of Circulation on IT Propagation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alford, M.H. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 2003, 423, 159–162. [Google Scholar] [CrossRef]
- Zhao, Z.; Alford, M.H.; Girton, J.B.; Rainville, L.; Simmons, H.L. Global Observations of Open-Ocean Mode-1 M2 Internal Tides. J. Phys. Oceanogr. 2016, 46, 1657–1684. [Google Scholar] [CrossRef]
- Rudnick, D.L.; Boyd, T.J.; Brainard, R.E.; Carter, G.S.; Egbert, G.D.; Gregg, M.C.; Holloway, P.E.; Klymak, J.M.; Kunze, E.; Lee, C.M.; et al. From Tides to Mixing Along the Hawaiian Ridge. Science 2003, 301, 355–357. [Google Scholar] [CrossRef] [PubMed]
- Floor, J.W.; Auclair, F.; Marsaleix, P. Energy transfers in internal tide generation, propagation and dissipation in the deep ocean. Ocean Model. 2011, 38, 22–40. [Google Scholar] [CrossRef]
- Munk, W.; Wunsch, C. Abyssal recipes II: Energetics of tidal and wind mixing. Deep Sea Res. Part I Oceanogr. Res. Pap. 1998, 45, 1977–2010. [Google Scholar] [CrossRef]
- Wunsch, C.; Ferrari, R. Vertical Mixing, Energy, and the General Circulation of the Oceans. Annu. Rev. Fluid Mech. 2004, 36, 281–314. [Google Scholar] [CrossRef]
- Apel, J.R.; Holbrook, J.R.; Liu, A.K.; Tsai, J.J. The Sulu Sea Internal Soliton Experiment. J. Phys. Oceanogr. 1985, 15, 1625–1651. [Google Scholar] [CrossRef]
- Liu, B.; D’Sa, E.J. Oceanic Internal Waves in the Sulu–Celebes Sea Under Sunglint and Moonglint. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6119–6129. [Google Scholar] [CrossRef]
- Nagai, T.; Hibiya, T. Internal tides and associated vertical mixing in the Indonesian Archipelago. J. Geophys. Res. Ocean. 2015, 120, 3373–3390. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, Z.; Feng, M.; Li, Q.; Zhang, P.; You, J.; Gao, S.; Yin, B. Satellite Investigation of Semidiurnal Internal Tides in the Sulu-Sulawesi Seas. Remote Sens. 2021, 13, 2530. [Google Scholar] [CrossRef]
- Rainville, L.; Pinkel, R. Propagation of Low-Mode Internal Waves through the Ocean. J. Phys. Oceanogr. 2006, 36, 1220–1236. [Google Scholar] [CrossRef]
- Ponte, A.L.; Klein, P. Incoherent signature of internal tides on sea level in idealized numerical simulations. Geophys. Res. Lett. 2015, 42, 1520–1526. [Google Scholar] [CrossRef]
- Masunaga, E.; Uchiyama, Y.; Suzue, Y.; Yamazaki, H. Dynamics of Internal Tides Over a Shallow Ridge Investigated with a High-Resolution Downscaling Regional Ocean Model. Geophys. Res. Lett. 2018, 45, 3550–3558. [Google Scholar] [CrossRef]
- Rainville, L.; Lee, C.M.; Rudnick, D.L.; Yang, K. Propagation of internal tides generated near Luzon Strait: Observations from autonomous gliders. J. Geophys. Res. Ocean. 2013, 118, 4125–4138. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.R.; Chao, S.; Chang, M.; Farmer, D.M.; Fringer, O.B.; et al. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef]
- Duda, T.F.; Lin, Y.; Buijsman, M.; Newhall, A.E. Internal Tidal Modal Ray Refraction and Energy Ducting in Baroclinic Gulf Stream Currents. J. Phys. Oceanogr. 2018, 48, 1969–1993. [Google Scholar] [CrossRef]
- Masunaga, E.; Uchiyama, Y.; Yamazaki, H. Strong Internal Waves Generated by the Interaction of the Kuroshio and Tides over a Shallow Ridge. J. Phys. Oceanogr. 2019, 49, 2917–2934. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Liu, Z.; McWilliams, J.C.; Gan, J. Insight Into the Dynamics of the Radiating Internal Tide Associated With the Kuroshio Current. J. Geophys. Res. Ocean. 2021, 126, e2020JC017018. [Google Scholar] [CrossRef]
- Tang, G.; Deng, Z.; Chen, R.; Xiu, F. Effects of the Kuroshio on internal tides in the Luzon Strait: A model study. Front. Mar. Sci. 2023, 9, 995601. [Google Scholar] [CrossRef]
- Park, J.; Watts, D.R. Internal Tides in the Southwestern Japan/East Sea. J. Phys. Oceanogr. 2006, 36, 22–34. [Google Scholar] [CrossRef]
- Kerry, C.G.; Powell, B.S.; Carter, G.S. The Impact of Subtidal Circulation on Internal Tide Generation and Propagation in the Philippine Sea. J. Phys. Oceanogr. 2014, 44, 1386–1405. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Z.; Zhang, Z.; Yang, Y.; Zhou, C.; Yang, Q.; Zhao, W.; Tian, J. Role of Mesoscale Eddies in Modulating the Semidiurnal Internal Tide: Observation Results in the Northern South China Sea. J. Phys. Oceanogr. 2018, 48, 1749–1770. [Google Scholar] [CrossRef]
- Cai, T.; Zhao, Z.; D’Asaro, E.; Wang, J.; Fu, L. Internal Tide Variability Off Central California: Multiple Sources, Seasonality, and Eddying Background. J. Geophys. Res. Ocean. 2024, 129, e2024JC020892. [Google Scholar] [CrossRef]
- Fan, L.; Sun, H.; Yang, Q.; Li, J. Numerical investigation of interaction between anticyclonic eddy and semidiurnal internal tide in the northeastern South China Sea. Ocean Sci. 2024, 20, 241–264. [Google Scholar] [CrossRef]
- Cai, S.; He, Y.; Wang, S.; Long, X. Seasonal upper circulation in the Sulu Sea from satellite altimetry data and a numerical model. J. Geophys. Res. Ocean. 2009, 114, C03026. [Google Scholar] [CrossRef]
- Han, W.; Moore, A.M.; Levin, J.; Zhang, B.; Arango, H.G.; Curchitser, E.; Di Lorenzo, E.; Gordon, A.L.; Lin, J. Seasonal surface ocean circulation and dynamics in the Philippine Archipelago region during 2004–2008. Dyn. Atmos. Ocean. 2009, 47, 114–137. [Google Scholar] [CrossRef]
- Metzger, E.J.; Hurlburt, H.E. The Nondeterministic Nature of Kuroshio Penetration and Eddy Shedding in the South China Sea. J. Phys. Oceanogr. 2001, 31, 1712–1732. [Google Scholar] [CrossRef]
- Qu, T.; Kim, Y.Y.; Yaremchuk, M.; Tozuka, T.; Ishida, A.; Yamagata, T. Can Luzon Strait Transport Play a Role in Conveying the Impact of ENSO to the South China Sea? J. Clim. 2004, 17, 3644–3657. [Google Scholar] [CrossRef]
- Qu, T.; Song, Y.T. Mindoro Strait and Sibutu Passage transports estimated from satellite data. Geophys. Res. Lett. 2009, 36, L09601. [Google Scholar] [CrossRef]
- Gordon, A.L.; Huber, B.A.; Metzger, E.J.; Susanto, R.D.; Hurlburt, H.E.; Adi, T.R. South China Sea throughflow impact on the Indonesian throughflow. Geophys. Res. Lett. 2012, 39, L11602. [Google Scholar] [CrossRef]
- Xie, J.; Du, H.; Gong, Y.; Niu, J.; He, Y.; Chen, Z.; Liu, G.; Liu, L.; Zhang, L.; Cai, S. The role of seasonal circulation in the variability of dynamic parameters of internal solitary waves in the Sulu Sea. Prog. Oceanogr. 2023, 217, 103100. [Google Scholar] [CrossRef]
- Gopalakrishnan, G.; Cornuelle, B.D.; Hoteit, I.; Rudnick, D.L.; Owens, W.B. State estimates and forecasts of the loop current in the Gulf of Mexico using the MITgcm and its adjoint. J. Geophys. Res. Ocean. 2013, 118, 3292–3314. [Google Scholar] [CrossRef]
- Fu, H.; Wu, X.; Li, W.; Zhang, L.; Liu, K.; Dan, B. Improving the accuracy of barotropic and internal tides embedded in a high-resolution global ocean circulation model of MITgcm. Ocean Model. 2021, 162, 101809. [Google Scholar] [CrossRef]
- Min, W.; Li, Q.; Xu, Z.; Wang, Y.; Li, D.; Zhang, P.; Robertson, R.; Yin, B. High-resolution, non-hydrostatic simulation of internal tides and solitary waves in the southern East China Sea. Ocean Model. 2023, 181, 102141. [Google Scholar] [CrossRef]
- Kang, D.; Fringer, O. Energetics of Barotropic and Baroclinic Tides in the Monterey Bay Area. J. Phys. Oceanogr. 2012, 42, 272–290. [Google Scholar] [CrossRef]
- Zilberman, N.V.; Becker, J.M.; Merrifield, M.A.; Carter, G.S. Model Estimates of M2 Internal Tide Generation over Mid-Atlantic Ridge Topography. J. Phys. Oceanogr. 2009, 39, 2635–2651. [Google Scholar] [CrossRef]
- Kelly, S.M.; Nash, J.D. Internal-tide generation and destruction by shoaling internal tides. Geophys. Res. Lett. 2010, 37, L23611. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, S.; Cao, A.; Xie, J.; Song, J.; Guo, X. Refraction of the M2 internal tides by mesoscale eddies in the South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2023, 192, 103946. [Google Scholar] [CrossRef]

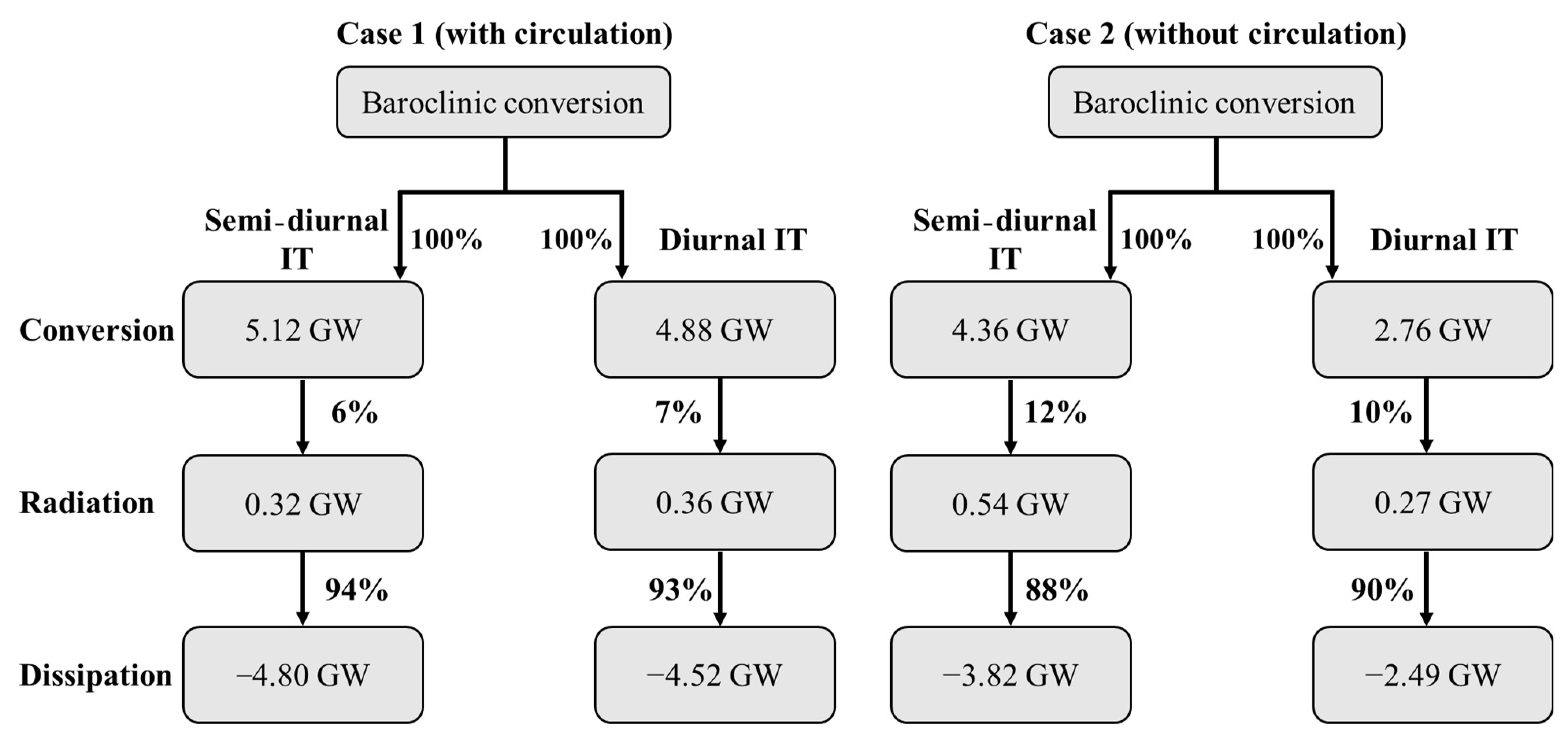


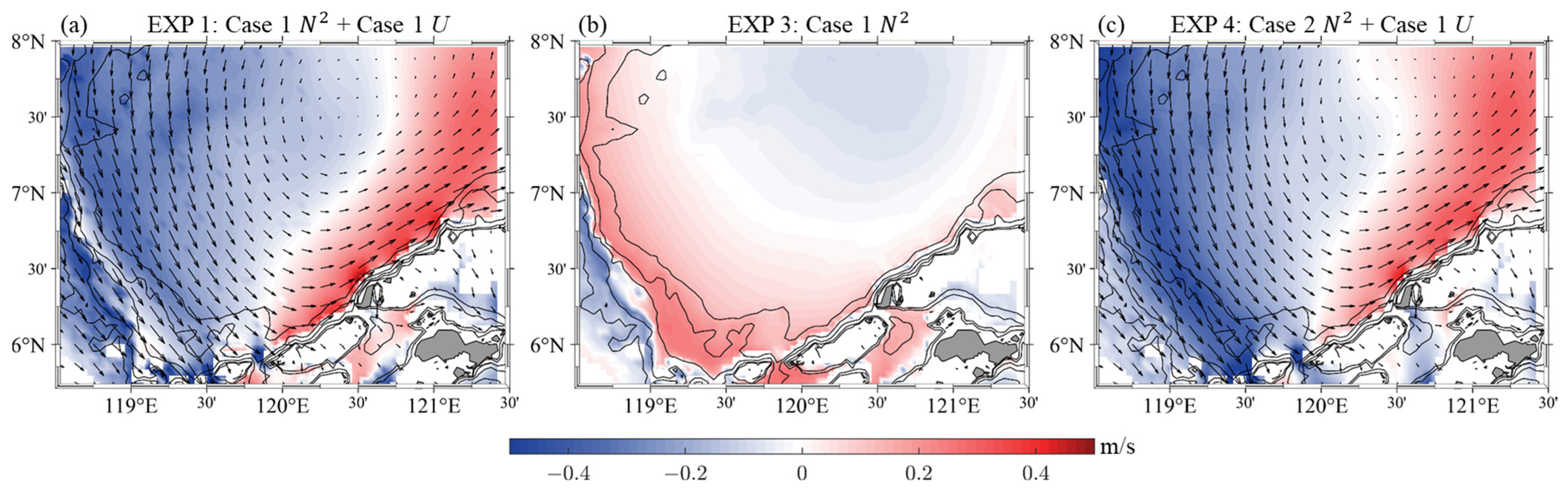
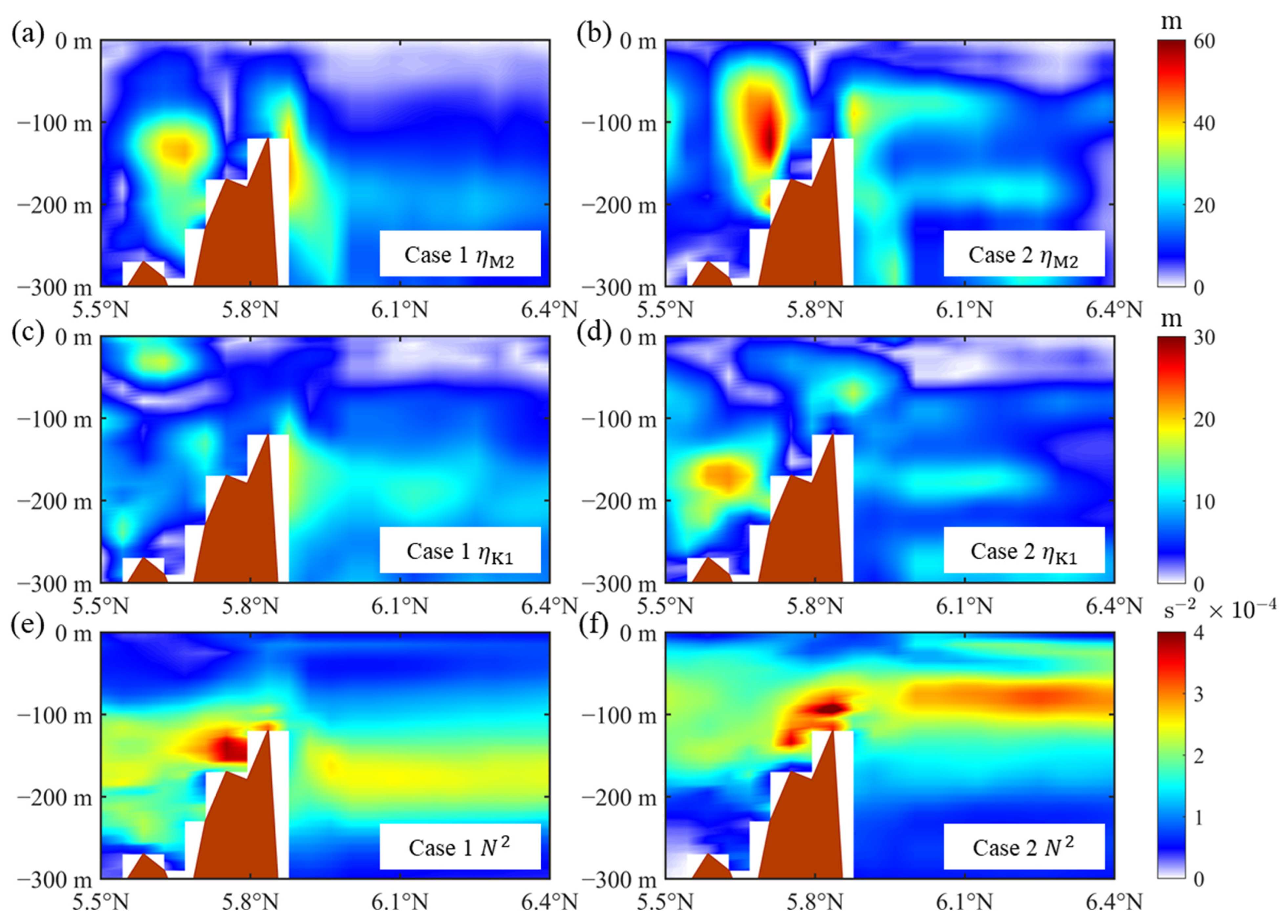
| Range | Resolution | Forcing | Simulation Time | |
|---|---|---|---|---|
| Case 1 | 3–27° N 107–130° E | Horizontal: 1/24° × 1/24° Vertical: from 10 m near the sea surface to 300 m near the seabed. | (1) Atmospheric forcing; (2) Open boundary forcing of temperature, salinity, and currents; (3) Open boundary tidal forcing; | (1) A four-year circulation simulation starting from 1 January 2014. (2) Building on the circulation model, a 130-day coupled circulation and IT simulation starting from 16 November 2016. |
| Case 2 | 3–27° N 107–130° E | Horizontal: 1/24° × 1/24° Vertical: from 10 m near the sea surface to 300 m near the seabed. | Open Boundary tidal forcing; | A 130-day IT simulation starting from 16 November 2016. |
| EXP 1 | EXP 2 | EXP 3 | EXP 4 | EXP 5 | EXP 6 | EXP 7 | EXP 8 | |
|---|---|---|---|---|---|---|---|---|
| IT components | M2 | M2 | M2 | M2 | K1 | K1 | K1 | K1 |
| Stratification () | Case 1 | Case 2 | Case 1 | Case 2 | Case 1 | Case 2 | Case 1 | Case 2 |
| Background currents () | Case 1 | – | – | Case 1 | Case 1 | – | – | Case 1 |
| Semi-Diurnal IT | Diurnal IT | |||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 1 | Case 2 | |
| Positive conversion (GW) | 7.31 | 9.37 | 6.02 | 3.53 |
| negative conversion (GW) | −2.20 | −5.01 | −1.14 | −0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, Y.; Yang, Y.; Wang, C.; Li, H.; Li, J.; Huang, X. Internal Tide Generation and Propagation in the Sulu Sea Under the Influence of Circulation. J. Mar. Sci. Eng. 2025, 13, 806. https://doi.org/10.3390/jmse13040806
Rong Y, Yang Y, Wang C, Li H, Li J, Huang X. Internal Tide Generation and Propagation in the Sulu Sea Under the Influence of Circulation. Journal of Marine Science and Engineering. 2025; 13(4):806. https://doi.org/10.3390/jmse13040806
Chicago/Turabian StyleRong, Yuhao, Yunchao Yang, Chao Wang, Heng Li, Jiahui Li, and Xiaodong Huang. 2025. "Internal Tide Generation and Propagation in the Sulu Sea Under the Influence of Circulation" Journal of Marine Science and Engineering 13, no. 4: 806. https://doi.org/10.3390/jmse13040806
APA StyleRong, Y., Yang, Y., Wang, C., Li, H., Li, J., & Huang, X. (2025). Internal Tide Generation and Propagation in the Sulu Sea Under the Influence of Circulation. Journal of Marine Science and Engineering, 13(4), 806. https://doi.org/10.3390/jmse13040806






