Research on Characteristics of the Hermite–Gaussian Correlated Vortex Beam
Abstract
1. Introduction
2. Propagation of the HGCVB in Oceanic Turbulence
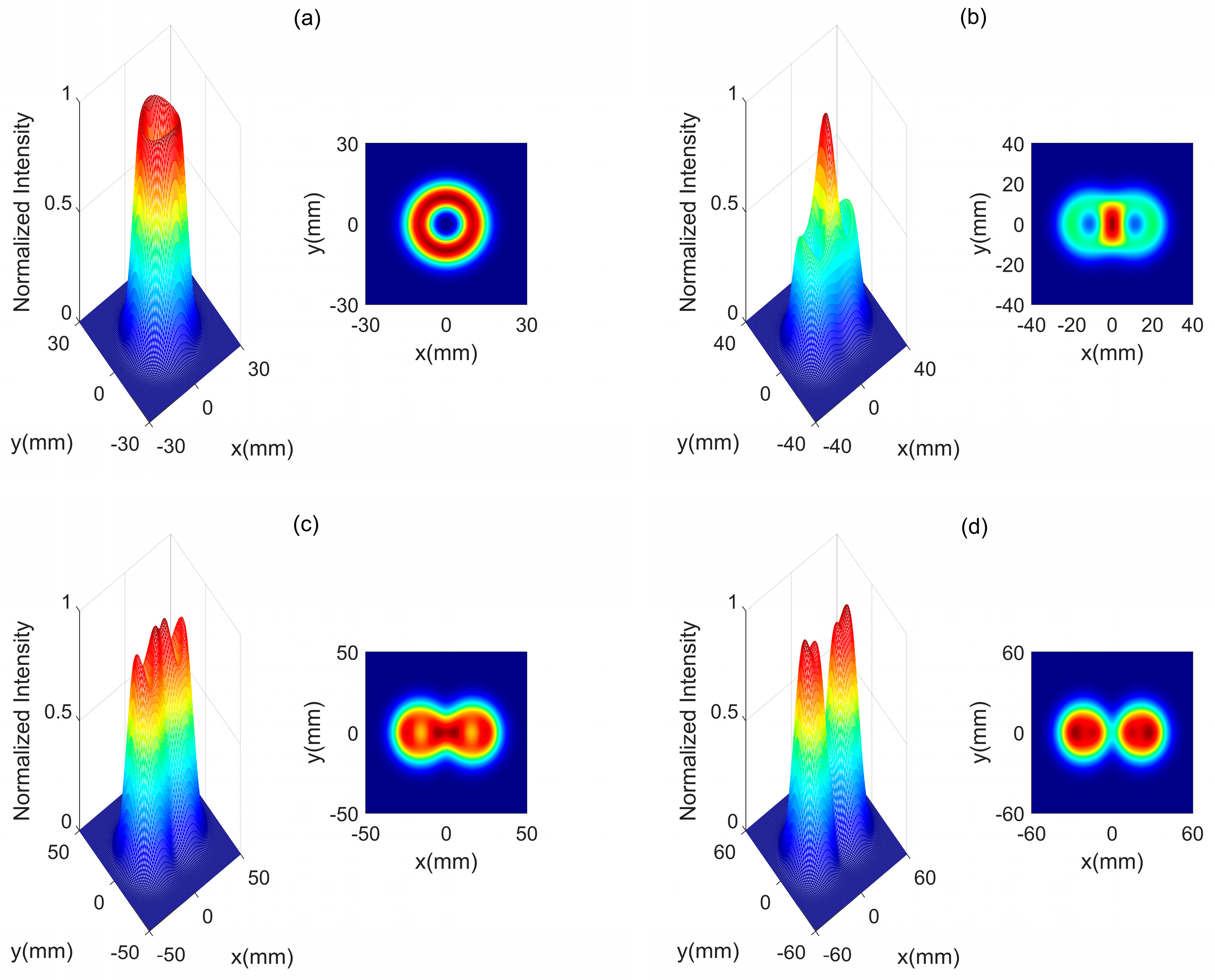
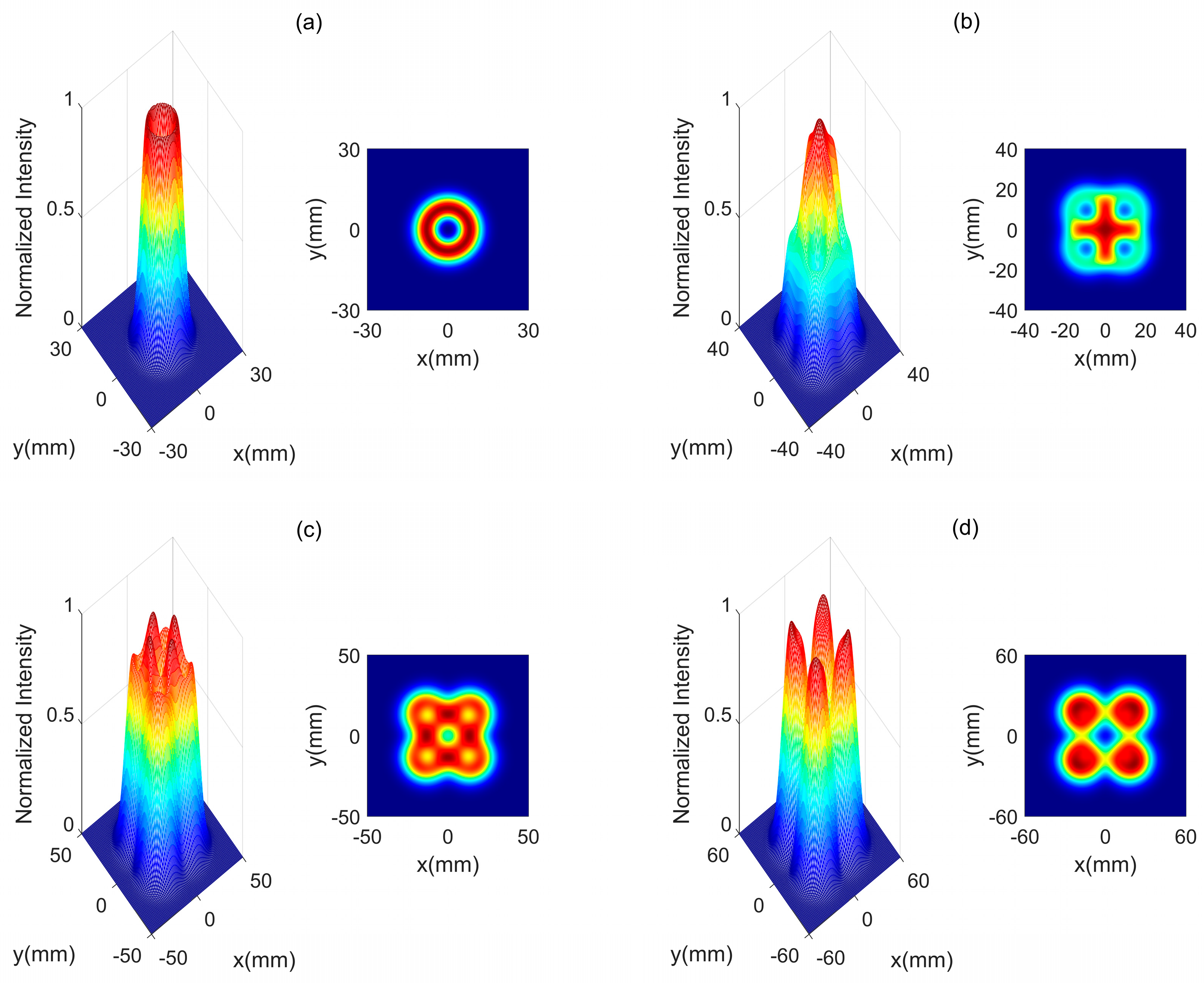
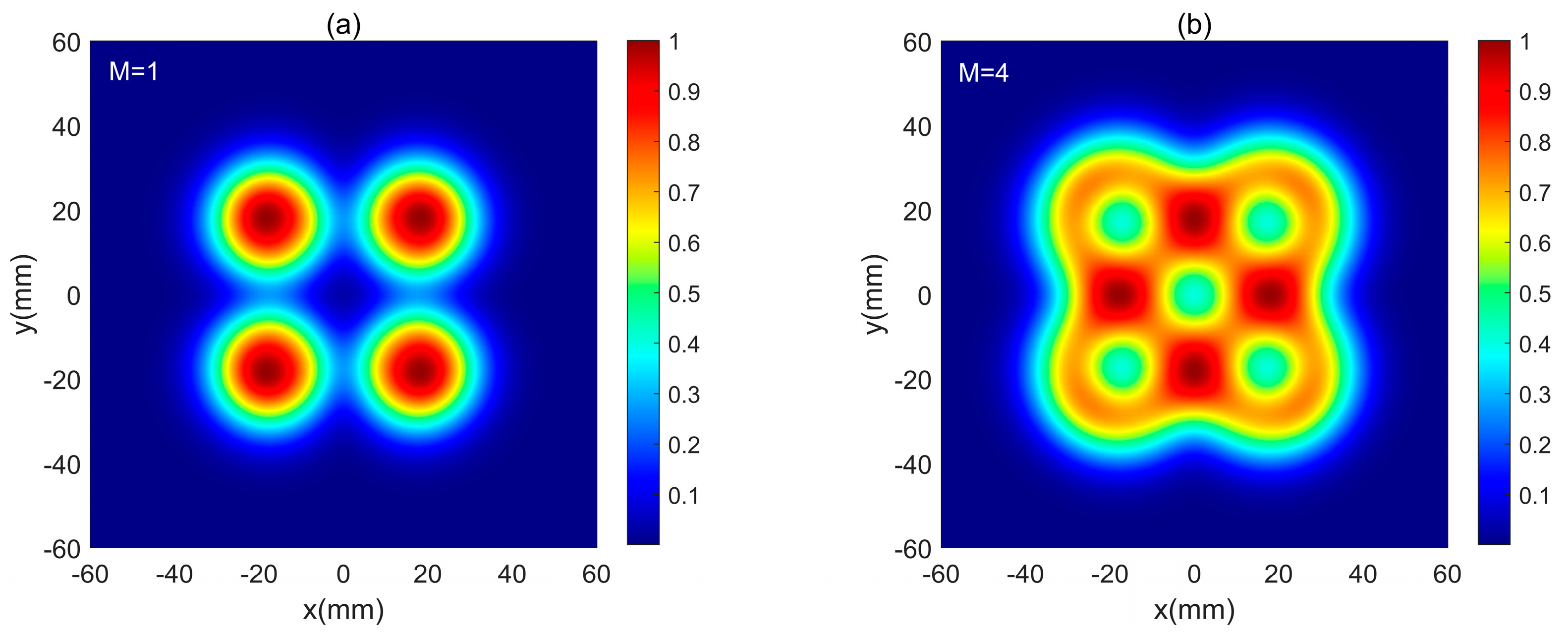
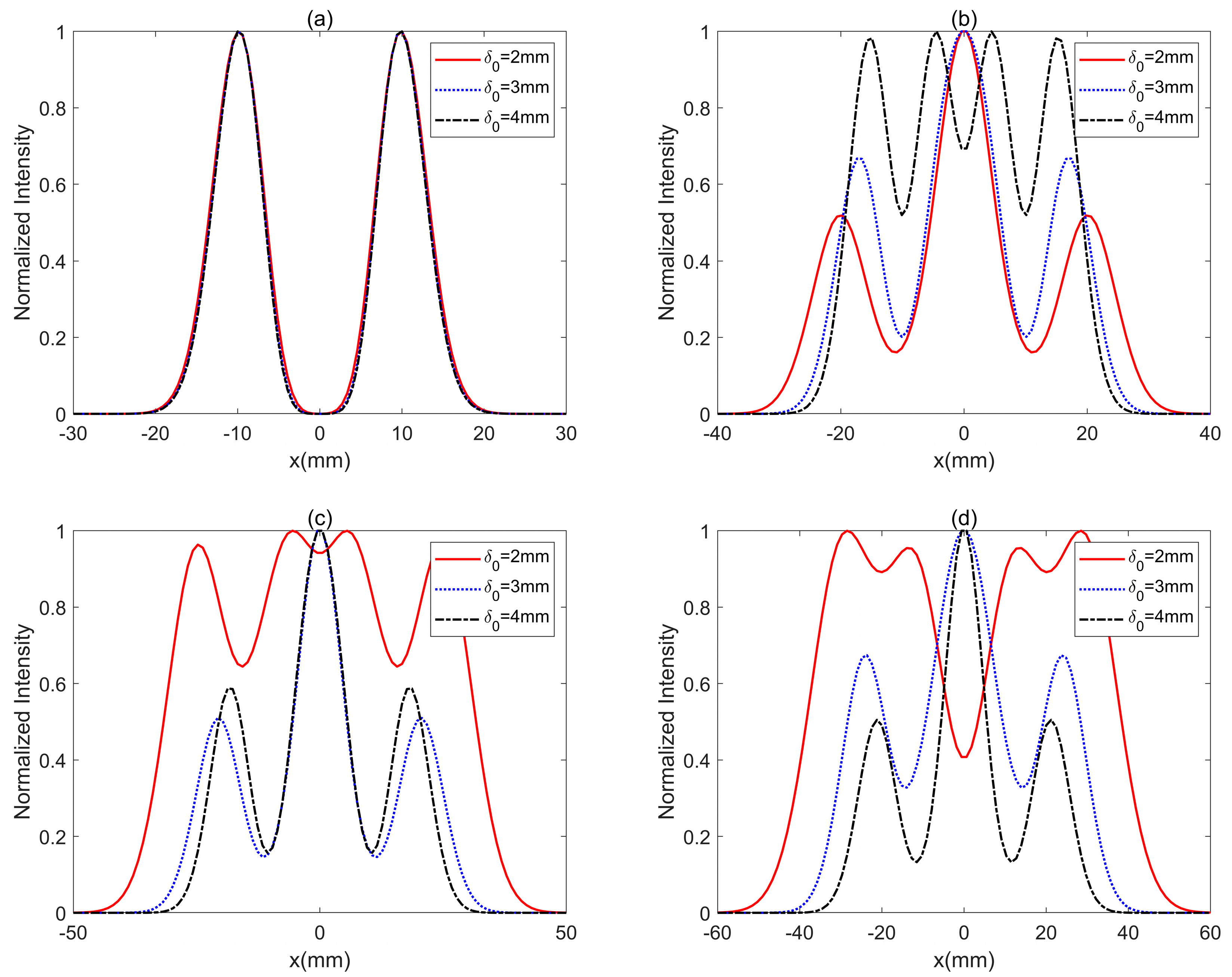
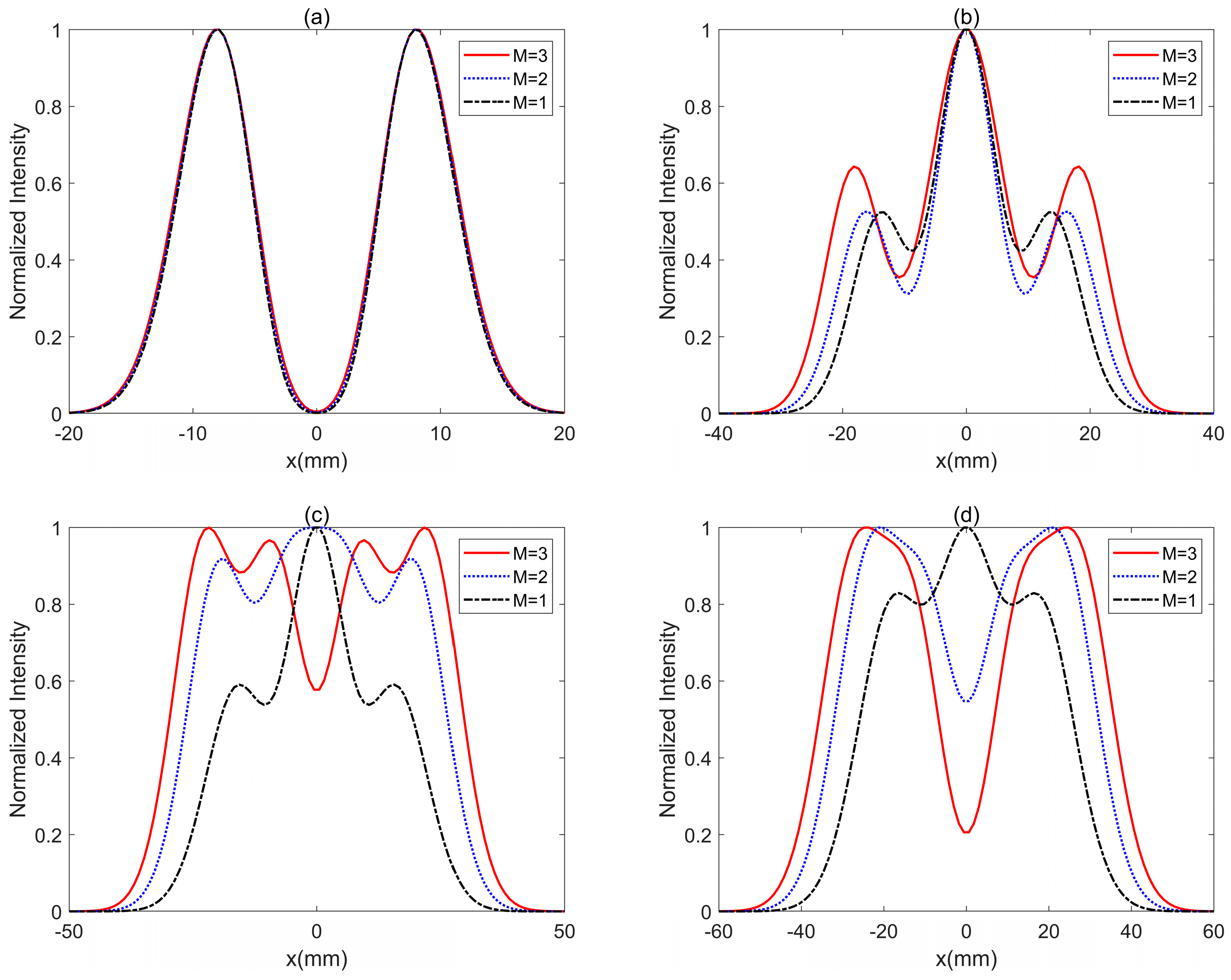
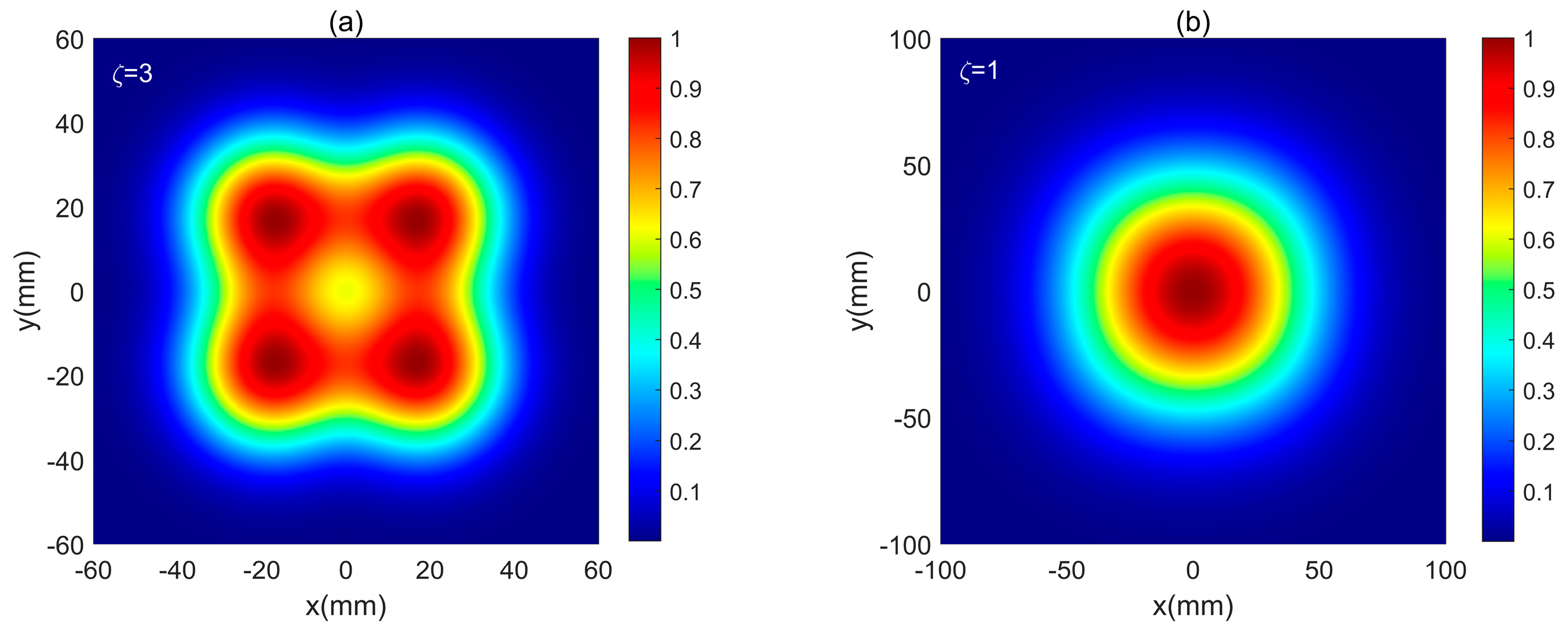
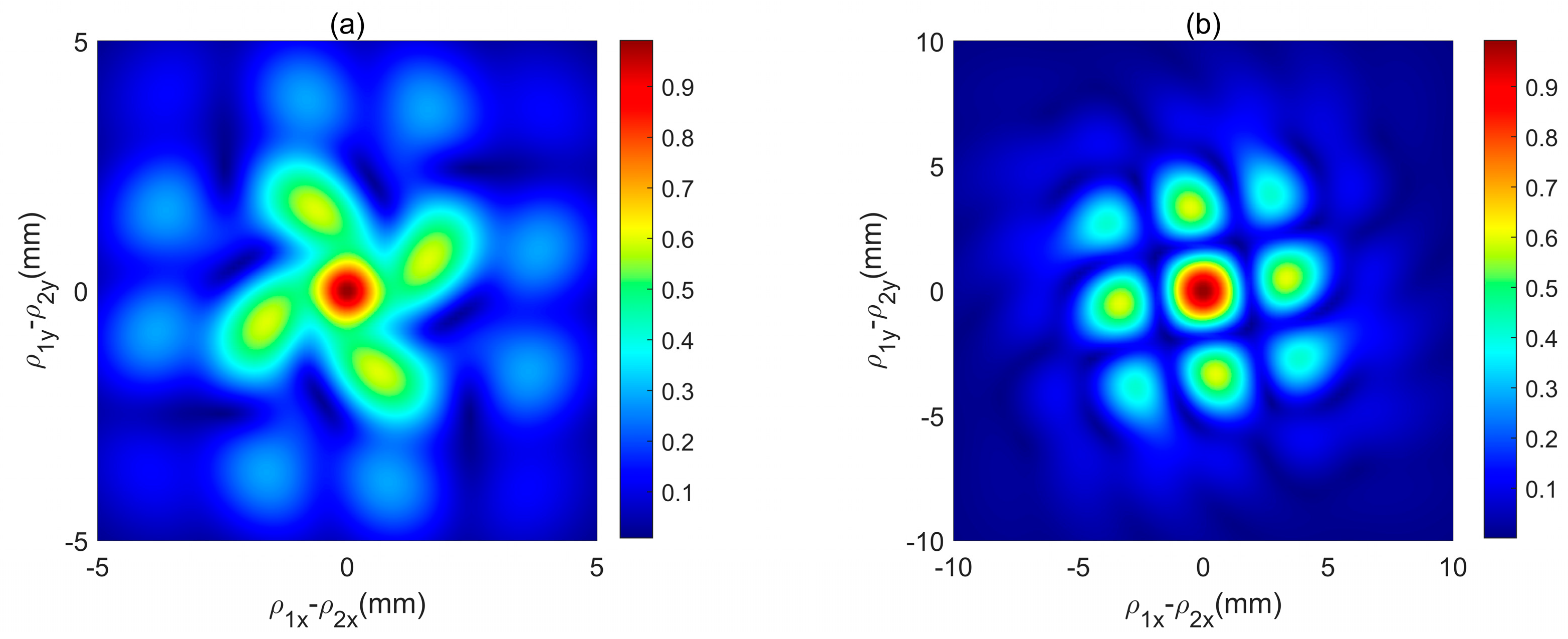
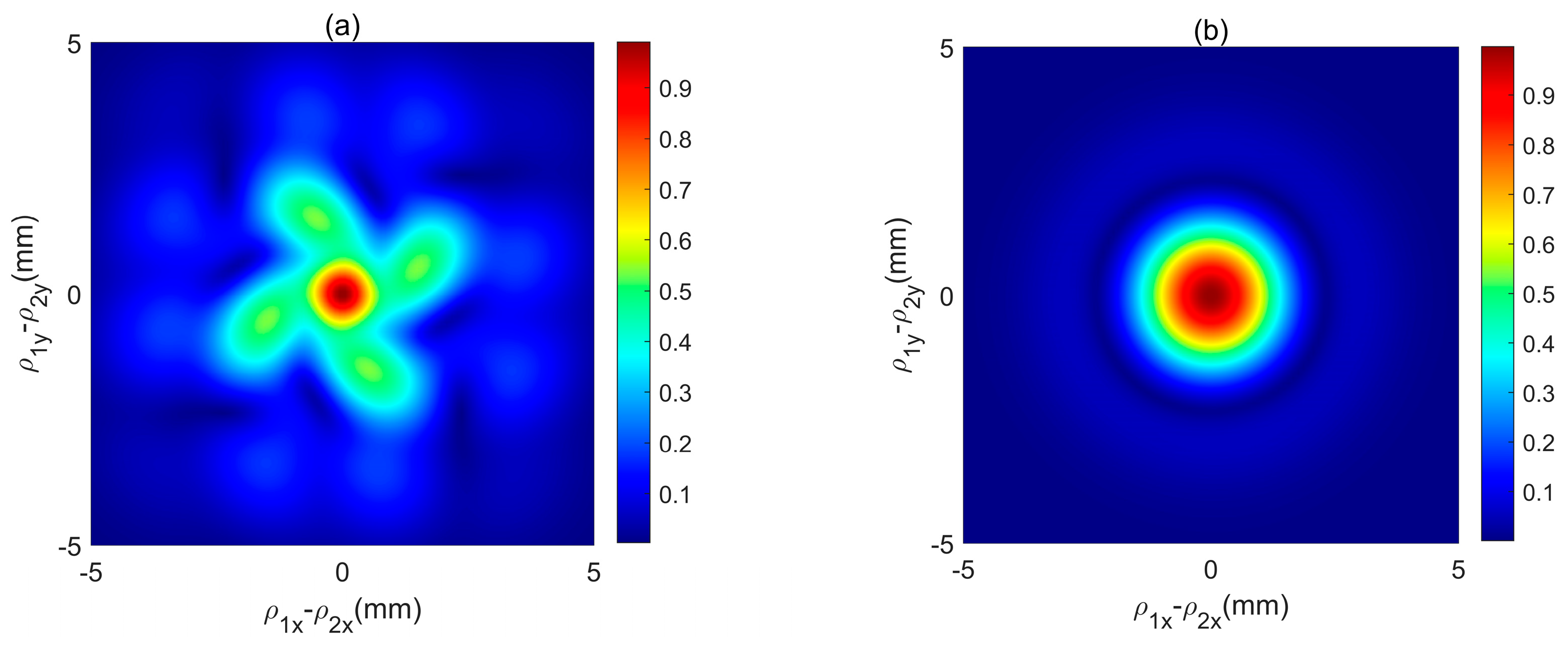
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HGCVB | Hermite-Gaussian correlated vortex beam |
| PCB | Partially coherent beam |
| GSM | Gaussian-Schell model |
| LGC | Laguerre-Gaussian correlated |
| HGC | Hermite-Gaussian correlated |
| CSD | Cross-spectral density |
| DOC | Degree of coherence |
References
- Baykal, Y.; Ata, Y.; Gökçe, M.C. Underwater turbulence, its effects on optical wireless communication and imaging: A review. Opt. Laser Technol. 2022, 156, 108624. [Google Scholar] [CrossRef]
- Korotkova, O. Light Propagation in a Turbulent Ocean. Prog. Opt. 2019, 64, 1–43. [Google Scholar]
- Baykal, Y. Scintillation index in strong oceanic turbulence. Opt. Commun. 2016, 375, 15–18. [Google Scholar] [CrossRef]
- Yousefi, M.; Golmohammady, S.; Mashal, A.; Kashani, F.D. Analyzing the propagation behavior of scintillation index and bit error rate of a partially coherent flat-topped laser beam in oceanic turbulence. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2015, 32, 1982–1992. [Google Scholar] [CrossRef] [PubMed]
- Gerçekcioğlu, H.; Baykal, Y. Laser beam scintillations of LIDAR operating in weak oceanic turbulence. J. Opt. Soc. Am. B 2022, 40, A44–A50. [Google Scholar] [CrossRef]
- Ata, Y. Structure function, coherence length, and angle-of-arrival variance for Gaussian beam propagation in turbulent waters. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2022, 39, 63–71. [Google Scholar] [CrossRef]
- Bayraktar, M. Average intensity of astigmatic hyperbolic sinusoidal Gaussian beam propagating in oceanic turbulence. Phys. Scr. 2020, 96, 025501. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Chang, H.; Huang, J.; Zhu, X.; Cai, Y.; Yu, J. Second-Order Statistics of Self-Splitting Structured Beams in Oceanic Turbulence. Photonics 2023, 10, 339. [Google Scholar] [CrossRef]
- Yi, X.; Ban, K.; Liu, H.; Ata, Y.; Cheng, M.; Zhang, L. Aperture-Averaged Angle-of-Arrival Fluctuations in Oceanic Turbulence of Arbitrary Strength. IEEE Trans. Antennas Propag. 2024, 72, 2631–2642. [Google Scholar] [CrossRef]
- Gerçekcioğlu, H.; Baykal, Y. Bit error rate of M-pulse position modulated laser beams for vertical links operating in weak oceanic turbulence. J. Opt. 2024, 26, 105602. [Google Scholar] [CrossRef]
- Jo, J.-H.; Ri, O.-H.; Ju, T.Y.; Pak, K.-M.; Ri, S.-G.; Hong, K.-C.; Hyon Jang, S. Effect of oceanic turbulence on the spectral changes of diffracted chirped Gaussian pulsed beam. Opt. Laser Technol. 2022, 153, 108200. [Google Scholar] [CrossRef]
- Liu, D.J.; Wang, Y.C.; Wang, G.Q.; Yin, H.M.; Wang, J.R. The influence of oceanic turbulence on the spectral properties of chirped Gaussian pulsed beam. Opt. Laser Technol. 2016, 82, 76–81. [Google Scholar] [CrossRef]
- Ata, Y.; Baykal, Y.; Gökçe, M.C. Analysis of Optical Wireless MIMO Communication in Underwater Medium. IEEE Internet Things J. 2024, 11, 20660–20672. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, P.; He, S.; Dai, H.; Fan, Y.; Wang, Y.; Tong, S. Average capacity of an underwater wireless communication link with the quasi-Airy hypergeometric-Gaussian vortex beam based on a modified channel model. Opt. Express 2023, 31, 24067–24084. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.H.; Wang, F.; Cai, Y.J. Partially coherent light beam shaping via complex spatial coherence structure engineering. Adv. Phys.-X 2022, 7, 2009742. [Google Scholar] [CrossRef]
- Wu, Y.Q.; Zhang, Y.X.; Li, Y.; Hu, Z.D. Beam wander of Gaussian-Schell model beams propagating through oceanic turbulence. Opt. Commun. 2016, 371, 59–66. [Google Scholar] [CrossRef]
- Chen, L.; Wang, G.; Yin, Y.; Zhong, H.; Liu, D.; Wang, Y. Partially Coherent Off-Axis Double Vortex Beam and Its Properties in Oceanic Turbulence. Photonics 2024, 11, 20. [Google Scholar] [CrossRef]
- Luo, B.; Wu, G.H.; Yin, L.F.; Gui, Z.C.; Tian, Y.H. Propagation of optical coherence lattices in oceanic turbulence. Opt. Commun. 2018, 425, 80–84. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. Properties of a random electromagnetic multi-Gaussian Schell-model vortex beam in oceanic turbulence. Appl. Phys. B 2018, 124, 176. [Google Scholar] [CrossRef]
- Du, H.; Ding, G.; Du, X.; Xiong, Z.; Wang, S.; Liu, Q.; Feng, H.; Wang, S. Propagation Characteristics of Rectangular Hermite-Gaussian Array Beams Through Oceanic and Atmospheric Turbulence. IEEE Photonics J 2023, 15, 6300107. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, H.; Wang, G.; Yin, H.; Wang, Y. Radial phased-locked multi-Gaussian Schell-model beam array and its properties in oceanic turbulence. Opt. Laser Technol. 2020, 124, 106003. [Google Scholar] [CrossRef]
- Liang, C.; Khosravi, R.; Liang, X.; Kacerovská, B.; Monfared, Y.E. Standard and elegant higher-order Laguerre–Gaussian correlated Schell-model beams. J. Opt. 2019, 21, 085607. [Google Scholar] [CrossRef]
- Chen, Y.H.; Liu, L.; Wang, F.; Zhao, C.L.; Cai, Y.J. Elliptical Laguerre-Gaussian correlated Schell-model beam. Opt. Express 2014, 22, 13975–13987. [Google Scholar] [CrossRef]
- Wang, J.; Ke, X.; Wang, M. Evolution of phase singularities of Laguerre–Gaussian Schell-model vortex beam. J. Opt. 2020, 22, 115602. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wang, F.; Zhao, C.L.; Cai, Y.J. Experimental demonstration of a Laguerre-Gaussian correlated Schell-model vortex beam. Opt. Express 2014, 22, 5826–5838. [Google Scholar] [CrossRef]
- Korotkova, O.; Sahin, S.; Shchepakina, E. Multi-Gaussian Schell-model beams. J. Opt. Soc. Am. A 2012, 29, 2159–2164. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Liu, L.; Zhao, C.L.; Cai, Y.J. Multi-Gaussian Schell-model vortex beam. Phys. Lett. A 2014, 378, 750–754. [Google Scholar] [CrossRef]
- Chen, Y.H.; Gu, J.X.; Wang, F.; Cai, Y.J. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2015, 91, 013823. [Google Scholar] [CrossRef]
- Liu, L.; Wang, H.; Liu, L.; Dong, Y.; Wang, F.; Hoenders, B.J.; Chen, Y.; Cai, Y.; Peng, X. Propagation Properties of a Twisted Hermite-Gaussian Correlated Schell-Model Beam in Free Space. Front. Phys. 2022, 10, 847649. [Google Scholar] [CrossRef]
- Zhao, X.-C.; Zhang, L.; Lin, R.; Lin, S.-Q.; Zhu, X.-L.; Cai, Y.-J.; Yu, J.-Y. Hermite Non-Uniformly Correlated Array Beams and Its Propagation Properties. Chin. Phys. Lett. 2020, 37, 124202. [Google Scholar] [CrossRef]
- Jeffrey, A.; Dai, H.H. Handbook of Mathematical Formulas and Integrals, 4th ed.; Academic Press Inc.: Cambridge, MA, USA, 2008. [Google Scholar]
- Wang, X.; Wang, L.; Zhao, S. Propagation Properties of an Off-Axis Hollow Gaussian-Schell Model Vortex Beam in Anisotropic Oceanic Turbulence. J. Mar. Sci. Eng. 2021, 9, 1139. [Google Scholar] [CrossRef]
- Chen, M.Y.; Zhang, Y.X. Effects of anisotropic oceanic turbulence on the propagation of the OAM mode of a partially coherent modified Bessel correlated vortex beam. Wave Random Complex 2019, 29, 694–705. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, R.; Liu, D.; Yin, Y.; Zhong, H.; Wang, Y.; Wang, G. Research on Characteristics of the Hermite–Gaussian Correlated Vortex Beam. J. Mar. Sci. Eng. 2025, 13, 814. https://doi.org/10.3390/jmse13040814
Cong R, Liu D, Yin Y, Zhong H, Wang Y, Wang G. Research on Characteristics of the Hermite–Gaussian Correlated Vortex Beam. Journal of Marine Science and Engineering. 2025; 13(4):814. https://doi.org/10.3390/jmse13040814
Chicago/Turabian StyleCong, Rui, Dajun Liu, Yan Yin, Haiyang Zhong, Yaochuan Wang, and Guiqiu Wang. 2025. "Research on Characteristics of the Hermite–Gaussian Correlated Vortex Beam" Journal of Marine Science and Engineering 13, no. 4: 814. https://doi.org/10.3390/jmse13040814
APA StyleCong, R., Liu, D., Yin, Y., Zhong, H., Wang, Y., & Wang, G. (2025). Research on Characteristics of the Hermite–Gaussian Correlated Vortex Beam. Journal of Marine Science and Engineering, 13(4), 814. https://doi.org/10.3390/jmse13040814





