Projected 21st Century Coastal Flooding in the Southern California Bight. Part 1: Development of the Third Generation CoSMoS Model

Abstract

Due to the effects of climate change over the course of the next century, the combination of rising sea levels, severe storms, and coastal change will threaten the sustainability of coastal communities, development, and ecosystems as we know them today. To clearly identify coastal vulnerabilities and develop appropriate adaptation strategies due to projected increased levels of coastal flooding and erosion, coastal managers need local-scale hazards projections using the best available climate and coastal science. In collaboration with leading scientists world-wide, the USGS designed the Coastal Storm Modeling System (CoSMoS) to assess the coastal impacts of climate change for the California coast, including the combination of sea-level rise, storms, and coastal change. In this project, we directly address the needs of coastal resource managers in Southern California by integrating a vast range of global climate change projections in a thorough and comprehensive numerical modeling framework. In Part 1 of a two-part submission on CoSMoS, methods and the latest improvements are discussed, and an example of hazard projections is presented.

1. Introduction

With over 600 million people living in the coastal zone worldwide [1], changes in sea-level and atmospheric conditions, including winds, sea-level pressures (SLPs), and precipitation [2], represent significant potential hazards. As such, changes will affect coastal erosion and flood patterns [3], increasing development and populations in these areas [1] will exasperate vulnerabilities and exposure unless methods to identify future hazards are developed and appropriate mitigation and adaptation strategies implemented.

Global Climate Models (GCMs) are often the best tools to evaluate potential changes in large-scale conditions and hazards. The coarse resolution and inability of GCMs to represent meso-scale conditions essential for local coastal impact studies [4], however, make downscaling of GCMs necessary [5] for community-scale coastal hazard identification. Several studies have conducted regional downscaling of GCMs for evaluation of changes in future storm surges and wave conditions of interest to coastal communities [6,7,8,9,10]. However, only a few have translated that work to the coastal zone and developed flood hazard maps from the combined impacts of projected sea-level rise (SLR), wave setup and runup, storm surge, and other coastal water level contributors.

One such study is the Coastal Storm Modeling System (CoSMoS) [11,12], a physics-based numerical modeling approach developed to comprehensively assess future coastal flooding risk by integrating SLR, dynamic water levels, and shoreline change. CoSMoS yields detailed hazards projections through a series of nested hydrodynamic models of increasing resolution that are applied to a 2 m resolution digital elevation model (DEM) to depict high-resolution storm-induced coastal flooding over large geographic regions. It has already been used by local emergency managers and planning councils to assess the exposure of 95% of the 26 million coastal residents in the state of California. The prototype system, developed for the California coast by USGS in collaboration with Deltares, uses swell computed with the global WaveWatchIII numerical wave model, the TOPEX/Poseidon satellite altimetry-based global tide model, and atmospheric forcing data from GCMs, to determine regional wave and water-level boundary conditions. These physical processes are dynamically downscaled using a series of nested SWAN (Simulating Waves Nearshore, Delft University of Technology) and Delft3D-FLOW numerical models that are linked at the coast to tightly spaced XBeach (eXtreme Beach) cross-shore profile models [11]. That first iteration of CoSMoS focused on evaluating flood hazards associated with historical storms and two SLR scenarios as well as a hypothetical extreme storm [13]. That initial work was expanded upon across the greater San Francisco Bay Area and up to Pt. Arena by including 40 SLR and storm scenarios, and incorporating downscaled atmospheric forcing and river discharge within San Francisco Bay [14,15,16]. Since then, further improvements and enhancements to the overall modeling system have been made to incorporate long-term shoreline change, better represent spatially-variable coastal storm responses, and integrate additional contributions to coastal flood levels.

Building upon earlier implementations, we present work showcasing the development of the third generation of CoSMoS in Southern California. This latest generation of explicit, numerically-derived flooding includes several new developments and modeling improvements: (1) high resolution grids for better representation of harbors, lagoons, bays, estuaries, and overland flow; (2) fluvial discharges that might locally impede and amplify flooding associated with coastal storms; (3) long-term morphodynamic change (i.e., beach change and cliff/bluff retreat) and its effect on coastal flooding projections; (4) uncertainty associated with terrain models, numerical model errors and vertical land motion; and (5) alterations to coastal storm intensity and frequency associated with a changing climate. Resulting model projections include flood extent, depth, duration, uncertainty, water elevation, wave run-up, maximum wave height, maximum current velocity, and long-term shoreline change and bluff retreat.

The objectives of this manuscript, Part 1 of 2, are to present the global-to-local scale downscaling methodology of the latest generation of CoSMoS, used to define flood hazards and assess the exposure of people, property, and infrastructure to future SLR and coastal storms in the Southern California Bight. This includes presentation and discussion of: (1) the modeling architecture; (2) the required model system inputs; (3) the inclusion of fluvial discharge; (4) the incorporation of long-term shoreline change and cliff retreat; and (5) the resultant generation of local-scale coastal hazards. Evaluation of the resulting hazards, exposure and vulnerability associated with various SLR scenarios combined with the full spectrum of plausible future coastal storms, variations in coastal response, and ecological and economic exposure that are available in web tools are detailed in Part 2 [17].

2. Materials and Methods

2.1. Study Area

Five counties comprise the coast of Southern California, extending from the U.S./Mexican Border to Point Conception: Santa Barbara, Ventura, Los Angeles, Orange, and San Diego Counties (Figure 1). The 500 km stretch of coast is an active, complex tectonic setting along the Pacific and North American plate boundary, resulting in much of the Southern California Bight (SCB) being fronted by a narrow continental shelf, a series of islands, beaches often backed by semi-resistant bedrock sea cliffs, and a highly irregular complex bathymetry that hosts a plethora of submerged seamounts, troughs, and canyons [18,19]. The deep-water wave climate is transformed to a more complicated nearshore wave field by the numerous seamounts, knolls, canyons, and the Channel Islands [20,21,22,23]. The islands block waves approaching from many directions, yielding a large shadow zone of wave energy. Additionally, complex shallow water bathymetry adjacent to the islands, seamounts and canyons, scatters, focuses, and dissipates wave energy, resulting in highly variable wave energy distribution patterns along the coast. Although swell dominates nearshore wave energy, locally-generated seas contribute as much as ~40% to the total wave energy spectrum [24,25].

Tides are mixed, semi-diurnal, with a mean diurnal range of 1.7 m [26]. Offshore significant wave height can reach ~8 m during the most extreme events [27], and therefore even with dissipation across the shelf, wave-driven water levels (i.e., set-up and runup) are still the dominant contributors to extreme coastal water levels across the region, contributing as much as 3 m to the total water level, while storm surge and El-Niño-driven water level anomalies rarely contribute more than ~20–30 cm each [28,29].

The heavily urbanized region hosts one of the largest economies in the United States, with a coastal county population of 17 million. Many vulnerable coastal areas are presently protected by sea walls or other flood and erosion defenses designed to withstand present-day storm impacts. Thus, the efficacy of these defenses against SLR or the combined effects of storms and SLR is questionable.

The coincident occurrence of storm-driven elevated water levels with high astronomic tides yield the greatest flooding [30,31]. Whereas astronomic tide ranges along the open coast are well predicted and not expected to significantly vary over the 21st century compared to historical levels [32], rates of SLR and the frequency and magnitude of storm-generated water levels are less well-constrained, and thus are the main foci of this study.

2.2. Modeling Framework

The third generation of CoSMoS, CoSMoS v. 3.0, is comprised of one global-scale wave model and a suite of regional and local scale models that simulate coastal hazards in response to projections of 21st century waves, storm surge, anomalous variations in water levels, river discharge, tides, and SLR (Figure 2). A total of 40 scenarios, resulting from the combination of ten sea levels, three storm conditions, and one background condition (i.e., daily average wave conditions), were simulated. Because scientific consensus on the magnitude and rate of SLR projections is constantly evolving [33,34,35,36,37,38,39], CoSMoS does not use a SLR rate projection or curve. Rather, CoSMoS uses discrete amounts of SLR, ranging from 0 m to 2 m, at 0.25 m increments, plus an additional 5 m extreme. Conceptually, SLR is not tied to a specific period in CoSMoS, but rather a range of discrete SLR values are chosen to illustrate conditions under various climate scenario assumptions and time periods. Future storm conditions represent the 1-year, 20-year, and 100-year return level coastal storm events, as derived and downscaled from winds, sea-level pressures (SLPs), and sea-surface temperatures (SSTs) of the RCP (Representative Concentration Pathway) 4.5, GFDL-ESM2M global climate model (GCM). Thus, the full suite of projections spans plausible SLR and 21st century storm conditions for an array of planning horizons and uses.

Summarizing the CoSMoS approach, at the global scale, GCM wind fields developed for the Coupled Model Intercomparison Project Phase 5 (CMIP5) [40] are fed into the WaveWatchIII (WWIII) [41] global wave model (see Section 2.2.1 for details). A higher-resolution, nested WWIII model produces a regional time-series of 21st century wave conditions across a range of models and climate scenarios at the edge of the continental shelf for the western U.S. coast [42].

Scaling down, select wave conditions from the regional scale are subsequently fed into a series of nested, higher resolution, coupled hydrodynamic and wave models (i.e., Delft3D-FLOW and SWAN) [43,44] that dynamically-downscale waves across the shelf to the nearshore in conjunction with astronomic tides and storm surge (see Section 2.2.3 for details). Nested model simulations include atmospheric pressures and winds [14,45], local river discharge, and seasonal water-level anomalies. Highest resolution grids (~10–20 m) are used to simulate overland flows in areas surrounding protected embayments. Along the open coast, cross-shore XBeach [46,47] models are used every 100–200 m in the along-shore direction to explicitly simulate wave set-up and swash (i.e., run-up) due to infragravity waves, a key driver of extreme water levels during storm events on dissipative beaches [48]. Modeled flood levels are ultimately interpolated onto regularly spaced grids and differenced from a 2 m resolution DEM [49] to generate local-scale flood projections and identify vulnerable areas not hydraulically connected to the open ocean but wetted by the numerical model.

The explicit CoSMoS downscaling approach summarized above, from a global to local scale, is computationally expensive and thus does not lend itself to simulating extensive, 100-year-long continuous time-series. Instead, the model system is run for pre-determined storm scenarios of interest, such as the 1-year or 100-year storm event, in combination with SLR amounts. These storms are first identified from time-series of total water level proxies (TWL_px) at the shore (see Section 2.2.2 and Section 2.2.3). The 21st century TWL_px time series are computed using a linear super-position of the major processes contributing to the overall total water level, to efficiently estimate coastal water level impacts and identify extreme events. The identified events define the boundary conditions for subsequent detailed numerical modeling with CoSMoS.

TWL_px time series are also used to force a cliff recession and shoreline change model, both of which were developed for this study (Section 2.2.2). The data-driven sandy beach evolution [50,51] and cliff retreat [52,53] models are run at thousands of cross-shore transects spaced approximately 100 m apart along the coast. Both models use shoreline positions and oceanographic forcing to calibrate a suite of equations and develop robust relationships between forcing parameters and coastal response. Results from the two models provide time-varying beach shoreline and cliff positions, defined as the mean-high-water (MHW) line and top of the cliff, respectively, that are used to evolve cross-shore profiles [54] (Section 2.2.2.5) extracted from the underlying 2-m resolution DEM [49]. Evolved profiles illustrating projected cliff retreat and beach change are used to modify the three-dimensional DEM prior to running the thirty-six scenarios that incorporate future SLR (SLR 0.25 m and higher) using the approach of the CoSMoS system described above.

Each of the aforementioned components is detailed in the following subsections, with emphasis on the newest inclusions for Southern California.

2.2.1. Inclusion of Swell Waves and GCM Selection

Previous versions of CoSMoS [11,12] included swell wave projections as boundary forcing, derived from four GCMs [42]. However, with the additional complexity and inclusion of local wave generation, storm surge, and efforts to capture the range of storm impact responses, it was necessary to identify one GCM for use in this version of CoSMoS. Thus, internal physical consistency (between derived swell projections, simulated wind waves, simulated storm surge, etc.) within the model system is maintained for all included processes. Therefore, an appropriate GCM was selected based on comparisons to wave buoy observations (using GCM winds from 1976 through 2010). The Earth-system model from National Ocean and Atmospheric Administration (NOAA) Geophysical Fluid Dynamics Laboratory (GFDL-ESM2M) was shown to best represent observed wave conditions in the extremes (winter H_s rmsd of 7–17 cm, extreme H_s bias < 5 cm, D_p < 7° ± 0.5°) based on wave simulations along the California coast [42]. Lower percentile waves were somewhat underestimated with a bias of about 25 cm, commensurate with other global scale models. As GCM-driven wave projections associated with the RCP4.5 emissions scenario resulted in higher waves, and more extreme coastal wave climates, compared to RCP8.5 for the study region [8,42], GFDL-ESM2M RCP4.5 was selected to illustrate representative storm events. All further GCM-downscaling across the Southern California Bight used the GFDL-ESM2M RCP4.5 model scenario.

Downscaled wind and SLP fields used in this version of CoSMoS were produced and obtained from Scripps Institution of Oceanography [14,45,55]. For model validation and hindcast runs, data from California Reanalysis Downscaling at 10 km (CaRD10) was used; CaRD10 is a reconstruction of the high-spatial resolution/high-temporal scale analysis of atmosphere and land covering the state of California for global change studies [55]. For future periods, data fields from Localized Constructed Analogs (LOCA, 2011–2100 at 2.5° × 1.5°, 3-hourly resolution, derived from GFDL-ESM2M RCP 4.5) was used. Unique to LOCA’s approach, a multiscale matching scheme [45] is used to select appropriate analogs from historical libraries, constructed from CaRD10 datasets.

To obtain global-scale wave projections, a WWIII model [41] was applied over a near-global grid (NWWIII, latitude 80° S–80° N) with 1° × 1.25° spatial resolution, and a one-way nested Eastern North Pacific (ENP) grid of 0.25° spatial resolution (~23.6 to 27.7 km at latitude 32° N). Details of model settings are found in Appendix A.

For further use in CoSMoS v 3.0, GFDL-ESM2M RCP4.5 wave projections [42] were extracted at the Scripps Institution of Oceanography California Data Information Program (CDIP) buoy 067 (33.221° N, 119.881° W) offshore the SCB (Figure 3). CDIP 067 is located offshore the shelf and has a robust historical record. Conditions at this location served as regional offshore conditions for deriving nearshore wave time series, nearshore TWL_px, and boundary conditions in higher-resolution nested models, in Section 2.2.2, Section 2.2.3, and Section 2.2.3.3, respectively. Return periods of offshore wave height are summarized in

Table 1. Projected and observed deep-water waves at buoy CDIP067. A Generalized Pareto Distribution (GPD) was fit through the wave data and in the case of the observation data, extrapolated for return periods greater than the length of the time-series. Listed T_p and D_p are the means of all instances for which the shown H_s ± 0.1 m occurred.

Parameter	1-year	5-year	10-year	20-year	50-year	100-year
GFDL-ESM2M (full 100 years up to year 2100) (Tp and Dp are means of all Hs ± 0.1 m)
Hs (m)	4.93	5.93	6.25	6.5	6.76	6.91
Tp (s)	16	16	17	17	16	17
Dp (deg)	294	292	291	282	282	284
Observed (September 1996 through December 2017)
Hs (m)	6.04	7.21	7.47	7.65	7.79	7.86
Tp (s)	15	16	14	17	No data	No data
Dp (deg)	299	296	305	306	No data	No data

. Of note, these values are ~1 m lower than measured waves at the same location where a maximum significant wave height of 7.76 m (wave period, T_p = 14.3 s) was observed on 28 December 2006. While swell waves are projected to be lower in the 21st Century for this region compared to the recent past, the wave period is projected to increase and the incidence angle to be more southerly [42,56]. More southerly incidence angles and longer wave periods are related to the intensification of Southern Ocean wave generation, a consistent feature in global climate model predictions [57,58]. The projected decrease of extreme wave heights is thought to be related to a poleward shift in North Pacific extra-tropical storm tracks [8,31,59].

2.2.2. Modeling Long-Term Shoreline Change

Two data-driven models to simulate cliff retreat and sandy beach evolution were developed for this study. The two models and supporting wave data are briefly described in the following subsections to illustrate function and position within the CoSMoS approach. Several different management scenarios involving beach nourishment and the existence and maintenance of hard structures to limit erosion were simulated with both the cliff recession and sandy shoreline change models. Further details can be found in respective references for individual models [50,51,52,53].

2.2.2.1. Initial Elevation

The 2-m CoNED DEM was constructed from recent bare-earth topographic and bathymetric lidar and multi- and single-beam sonar datasets [49]. The seamless topobathymetric DEM was constructed to define the shape of nearshore, beach, and cliff surfaces as accurately as possible, utilizing dozens of the most recent bathymetric and topographic datasets available at the time of generation. The vast majority of the data were derived from the Coastal California Data Merge Project which includes lidar data collected from 2009 to 2011 and multi-beam bathymetry collected between 1996 and 2011 extending out to the three nautical mile limit of California’s state waters [60]. Harbors and some void areas in the nearshore were filled in with bathymetry from either more recent multi-beam surveys, 1/3 arc-second NOAA coastal relief model data, or single-beam bathymetry. The DEM is used as initial conditions and calibration data in two long-term coastal change models (Section 2.2.2.3 and Section 2.2.2.4) that are run prior to the CoSMoS flood model, in addition to defining grid elevations for hydrodynamic and wave models (Section 2.2.3). Combined long-term shoreline changes are applied two-dimensionally to alter the DEM for SLR scenarios and are used in local-scale Tier III transect models (Section 2.2.3.4 and Section 2.2.3.5).

2.2.2.2. Nearshore Wave Time Series and Water Level Proxies

Both cliff and shoreline change models were forced with hindcast (1980–2010) and projected (2010–2100) wave time series developed by Hegermiller et al. [61,62]. The hindcast was generated from high resolution SWAN model runs that capture changes in the wave field due to wave refraction across complex bathymetry and shadowing, focusing, diffraction, and dissipation of wave energy by islands. The model was forced at the open boundaries by intermediate-depth Wave Information Study (WIS) [63] wave time-series located landward of the Channel Islands, and by CaRD10 near-surface wind fields [55]. Three-hourly wave parameters (significant wave heights, mean wave period, peak wave period, mean wave direction, and peak wave direction) were output at 4802 points along the 10 m bathymetric contour every ~100 m in the alongshore direction, coincident with offshore ends of cross-shore transects used in the long-term cliff/sandy beach models and XBeach simulations (Figure 2). The hindcast was validated against 23 co-located CDIP buoys and found to behave reasonably well with an RMSE of 27 cm. See Hegermiller et al. [61] for further details and data.

To relate nearshore wave parameters to deep-water wave conditions, the 30-year hindcast time-series was correlated with deep-water waves at the CDIP067 to generate a look-up-table [61]. The look-up-table, in conjunction with the dynamically downscaled waves and winds (GFDL-ESM2M RCP 4.5) as the forcing fields (WWIII; Section 2.2.1), was used to derive nearshore wave parameters for the aforementioned nearshore points at three-hourly intervals out to the year 2100.

To identify significant coastal storm events, in terms of coastal flooding impacts at the shore, a proxy of total water levels (TWL_px) was developed from the nearshore wave time series. To efficiently estimate TWL_px, wave runup (R_2%) was empirically computed from the hindcast and projected wave time-series [61,62], and then linearly super-imposed onto empirically derived time-series of storm surge (SS) [64] and other water level anomalies (SLA):

$$TW{L}_{px}=R_{2\%}+SS+SLA$$

(1)

Further details on generation and limitations of TWL_px can be found in Erikson et al. [64]; see Section 2.2.3.1 for use of TWL_px for storm selection. Conditional dependencies are accounted for using internally-consistent boundary conditions from a single GCM (GFDL-ESM2M RCP 4.5), the choice of which is justified above in Section 2.2.1.

While CoSMoS outputs use discrete amounts of SLR (see Section 2.2), specific SLR rates were used in long-term cliff and sandy beach models, with simulation end times (representing long-term morphodynamic change) matching overall CoSMoS SLR amounts. These rates are necessary as long-term cliff and sandy beach models were run for the entire 21st century period, unlike CoSMoS simulations. SLR scenarios for the coastal cliff/beach projections were represented with a second-order polynomial curve (see [51] for details) that reached 1 m or greater by the year 2100, relative to 2000 (Figure 4, modified from [51]). To align with CoSMoS SLR amounts of 0.25 m, 0.50 m and 0.75 m, long-term morphodynamic change simulations were simulated until 01 January 2044, 2069, and 2088, respectively, based on the National Research Council values developed for Southern California [34]. Cliff/beach SLR scenarios are in line with the range of long-term predictions from the 4th California Climate Assessment [37] (Figure 4) and other studies [33,65,66]. The 0.93 m scenario is a regional sea-level projection developed specifically for Southern California by the National Research Council [34].

2.2.2.3. Coastal Cliff Retreat Model

Cliff retreat, defined as the landward movement of the cliff-top edge, is projected at each applicable transect in SCB using a multi-model ensemble of up to seven models that relate sea-cliff retreat to wave impacts using the hindcast and projected wave time series (Section 2.2.2.2), SLR, historical cliff behavior, and cross-shore geometry [67,68,69,70,71]. Mean long-term historic cliff retreat rates during ~1930–2000 calculated by the USGS National Shoreline Assessment were used to calibrate the models. The multi-model ensemble mitigates limitations of a single model and, therefore, can develop more robust predictions. Included models can be classified into two general groups: (1) simple 1-D models relating wave impacts to cliff retreat; and (2) 2-D transect models that include a discretized, evolving profile of nearshore and cliff morphology. The ensemble approach uses a weighted mean among all model outputs, giving preference to models with the least uncertainty [52,53].

The cliff-retreat model results in time-averaged cliff edge positions and rates for each SLR scenario, at all applicable SCB transects. Projections include two management scenarios considering the existence or non-existence of hard structures that limit cliff erosion. Considered structures and armoring locations were obtained from the California Coastal Commission [72] and aerial photographs from the California Coastal Records Project [73].

Included models do not explicitly distinguish between soft rock and hard rock coasts because they represent only basic physical interactions between waves and cliffs that are common to both morphologies. Smaller-scale details, such as vertical variations in rock strength on the cliff face [74] and seasonal variations in beach width and height, are not explicitly represented. Neither are dynamics related to seasonal beach erosion [75] and talus deposition and subsequent removal [76,77]. Finally, while rainfall can affect sea cliff evolution in parts of Southern California [78], CoSMoS cliff-retreat projections focus on wave-driven erosion, because relationships between rainfall, groundwater, and cliff failures are not well established. Rainfall-induced cliff erosion and other factors that might affect cliff retreat rates, such as jointing, fractures, and groundwater flow, are, however, implicitly included in the historical cliff retreat rates used to calibrate the models.

2.2.2.4. Sandy Beach Shoreline Change Model

The CoSMoS-COAST sandy shoreline change model [51] combines geographic information, management scenarios, and forcing conditions (due to waves and SLR) with three process-based models that compute: (1) wave-driven longshore transport [50]; (2) cross-shore transport due to waves [75]; and (3) cross-shore transport due to SLR [79]. CoSMoS-COAST integrates the process-based models with historical shoreline observation via an Extended Kalman Filter data assimilation method [80]. The model uses historical shoreline positions and oceanographic observations to calibrate a suite of equations and develop robust relationships between forcing parameters and shoreline response and project these relationships into the future [51].

The projected time-series of nearshore waves [61,62] and water levels (Section 2.2.2.2), combined with sea-level rates of change, were used to model one-dimensional shoreline change (represented by position of the mean high water (MHW) line) to the year 2100 at all applicable SCB transects. Four different management scenarios, representing the combinations of existing/no beach nourishment and the existence/non-existence of hard structures that limit erosion (i.e., “hold the line” on erosion) were considered. In the latter scenario, erosion was limited to a fixed polyline digitized from aerial photos accessible in Google Earth [81] representing the division of beach and urban infrastructure.

As the process-based models referenced above assume an equilibrium beach profile, changes in the profile shape are not computed in CoSMoS-COAST, which outputs shoreline positions and uncertainty (see [51] for details). Contributing to uncertainty, natural and anthropogenic sediment supply for management scenarios is also estimated from limited shoreline data throughout the region.

2.2.2.5. Combining Long-Term Morphodynamic Change

Projections of shoreline change and cliff retreat were combined to illustrate long-term morphodynamic change within CoSMoS. This was done by evolving the present-day (0 m SLR) cross-shore profiles to reflect the projected shoreline change (as illustrated by the MHW contour change) and cliff retreat for each SLR scenario. Details of the profile evolution scheme were presented by Erikson et al. [54]. Only projections from one management scenario were used for incorporating of long-term morphodynamic change: beach nourishment would cease but that existing cliff armoring and flood/beach protection infrastructure remains in place (i.e., the “hold-the-line” scenario). The resulting “evolved” profiles were used in simulations of runup and event-based morphodynamic change with the Tier III XBeach model (Section 2.2.3.5). Additionally, the 4000+ evolved profiles along the SCB were merged together to modify the 3-dimensional DEM for each CoSMoS SLR scenario. Projected elevation changes (ΔZ at each geographic coordinate) along each transect were blended at 10 m spacing between each profile, to interpolate the results of discrete beach/cliff responses along shore. These higher-density elevation changes were spatially interpolated to create a two-dimensional elevation adjustment, altering the present-day DEM to reflect long-term shoreline change for each SLR scenario. This DEM was used in final fine-scale flood projections and mapping potential hazards (Section 2.3).

2.2.3. Core Flood Model Architecture

In contrast to the TWL proxies (Section 2.2.2.2) that were computed to aid in identification of extreme storms (following subsection) and to provide temporally continuous boundary conditions for the cliff recession and shoreline change models (Section 2.2.2.3 and Section 2.2.2.4), flood hazard modeling is done explicitly and deterministically with a suite of numerical models accounting for changes in water levels, waves, currents and resulting interactions between them (Figure 2). For all flood hazard simulations, projected deep water wave conditions, computed with the global scale wave model (Section 2.2.1), are propagated to shore with a suite of regional (Tier I) and local (Tiers II and III) models that additionally simulate regional and local wave growth (seas) in combination with event-driven morphodynamic change and water level changes due to astronomic tides, winds, sea-level pressure, steric effects, and sea-level rise. The nested framework (Tier I–Tier III) was run separately for multiple identified storm events (Section 2.2.3.1) and SLR.

The regional Tier I model consists of one Delft3D hydrodynamic FLOW grid for computation of currents and water level variations (astronomic tides, storm surge, and steric effects) and one SWAN grid for computation of wave generation and propagation across the continental shelf. The highest grid resolution is 1.2 km × 2.5 km nearshore. Wave conditions from the global wave model are applied at the open-boundaries of the SWAN model. The FLOW and SWAN models are two-way coupled, so that wave-current interaction is accounted for.

Employing high-resolution grids for simultaneous fine-scale modeling of the entire study area was not feasible given model and computational limitations; Tier II simulations were therefore segmented into 11 sections covering the SCB. Each sub-model consists of two SWAN grids and multiple FLOW grids of variable resolution, with the finest resolution of 5 m × 15 m in nearshore regions. Wave and water level time-series from the Tier I model are applied at the open boundaries of each Tier II sub-model (Section 2.2.3.4). Tier II simulations also included river discharges to capture impacts of potential riverine backflow at the coast.

Tier III consists of over 4000 cross-shore XBeach transect models (highest resolution of 5 m) simulating event-driven morphodynamic change, water level variations, and infragravity wave runup every ~100 m alongshore (Section 2.2.3.5). Wave runup is the maximum vertical extent of wave uprush on a beach or structure above the still water level, and in cases where infragravity waves exist, the reach of wave runup can be significantly further inland compared to wave runup driven by shorter incident waves [46,47]. The U.S. west coast is particularly susceptible to infragravity wave runup due to the prevalence of breaking long-period swell (low wave steepness) across wide, mildly sloping (dissipative) beaches that result in a shoreward decay of incident wave energy and accompanying growth of infragravity energy.

2.2.3.1. Storm Event Selection

The CoSMoS framework is computationally expensive, therefore a full 21st century simulation is infeasible. Additionally, as major contributors to coastal water levels such as astronomic tides and storms are independent processes, a century-long simulation may not fully characterize potential flood risk, as the timing between high tide occurrences and storm impacts would be necessary. Therefore, future storm events are identified a priori in CoSMoS; these events are then run with Tiers I–III, synched to representative spring tide cycles.

The storm selection process employs the same TWL proxies used as forcing for the cliff recession and shoreline change models (Section 2.2.2). Proxies do not account for variations in water levels due to astronomic tides and SLR, as they are independent of atmospheric conditions. It is recognized, however, that nearshore wave heights and R_2% are affected by tidal stage and currents, and non-linear interactions can be important [82]. As runup is the dominant contribution to TWL_px (over 85%), it is unlikely that selection of extreme storm events would be significantly impacted. Additionally, these components are accounted for in the more detailed CoSMoS model simulations.

In keeping with the approach of identifying coastal storms with specific recurrence intervals (Section 2.2.1), the ranked 1-year, 20-year, and 100-year future coastal storm events, derived from the 100-year TWL time series at the shore, were identified at each nearshore transect location (4802 sites). Event results were clustered with a k-means algorithm to delineate coherent coastal segments which had similar return period water levels for specific storms; see Erikson et al. [64] for more details on identification methodology. Clustering of extreme events showed that the more severe but rare coastal flood events (e.g., the 100-year event) occur for most of the region from the same storm event. In contrast, different storms from varying directions were responsible for the less severe, but more frequent, local coastal flood events (Figure 5). To this end, two 100-year storms were identified (February 2044 and March 2059), two 20-year storms (February 2025 and February 2095), and three 1-year storms (March 2020, December 2056, and January 2097). Upon completion of 1-year storm simulations using the entire train of models (Tier I–Tier III resolving detailed flow dynamics and wave-current interaction) for a range of SLRs, results showed a single 1-year storm (March 2020) consistently yielded the highest water levels throughout the SCB; thus, 1-year projections use contributions from only this event. Event conditions are summarized for each of the identified storms in

Table 2. Boundary conditions associated with each modeled scenario.

Scenario	Hs, Meters	Tp, Seconds	Dp, Degrees	SLA, Meters	Minimum SLP (Kilopascal)	Maximum Wind Speed, Meters/Second
Background	1.75	12	286	0	NA	NA
1-year storm 1	4.39	16	284	0.16	100.56	22.8
20-year storm 1	5.86	18	281	0.18	100.79	22.3
20-year storm 2	6.13	18	292	0.24	100.41	28.7
100-year storm 1	6.20	16	264	0.19	100.43	26.6
100-year storm 2	6.80	18	287	0.23	98.67	30.3

. For each identified event, associated event conditions are applied as follows: deep water wave conditions (H_s, T_p, and D_p) applied at all open boundaries of the Tier I wave grid; SLA applied uniformly to all model domains; and downscaled time- and space-varying SLP and wind fields applied to all domains synched such that minimum SLP in the region coincided with high tide water levels.

2.2.3.2. Fluvial Discharge Model

CoSMoS incorporated discharges from 37 coastal rivers in the SCB considered most relevant in influencing coastal flooding (

Table 3. Primary and sub-ordinate rivers within the Southern California study area.

Primary Stream	Sub-Ordinate Stream
Atascedero	Jalama, Gaviota, Refugio, El Capitan, Devereux, Goleta
Mission Creek	Arroyo Burro, Mission, Carpinteria, Rincon
Ventura	Santa Clara
Calleguas	Malibu
Santa Margarita	San Juan, San Mateo, San Onofre, Los Flores, San Luis Rey, Buena Vista, Agua Hedionda, Batiquitos, San Elijo, Del Mar, Pensaquitos, San Diego, Sweetwater, Otay, Tijuana
Rio Hondo	Ballona, Dominguez, Bolsa Chica, Newport Bay
Santa Ana	Los Angeles, San Gabriel

; Figure 6); discharges are included in Tier II sub-models. At the time of this study, no available time series of 21st century discharge rates associated with this project’s RCP scenario exist, and therefore discharge projections were developed. The approach does not erroneously assume that a 100-year fluvial discharge event coincides with a 100-year coastal storm event for the simulation period [83], but instead employs atmospheric patterns common to both events with the aim to obtain more realistic joint occurrences.

Rivers were initially separated into two groups: (1) primary gauged rivers for which relationships between peak flows and an independent atmospheric variable (from downscaled GCM) are identified; and (2) subordinate river for which relations with assigned primary rivers were used to estimate future flows.

Seven gauged rivers for which identifiable relationship between peak flows and SLPs were attainable (Table 3) were labeled as “primary/parent representations” within the SCB. As many as 15 sub-ordinate rivers were assigned to each of these primary rivers using previous studies that have evaluated similar relationships [84]. Exceptions are the Rio Hondo and Santa Ana Rivers, for which sub-ordinate rivers and tributaries were assigned as shown in Figure 6 due to the urbanized lowland nature of the former and contrasting mountainous and dammed Santa Ana watershed. See Appendix A for details on discharge data sources.

To estimate future peak discharge rates, and relate them to coincident storm events, observation-based least-squares linear regression equations relating peak discharges to SLPs were developed. Using these relationships with future SLPs, from the GFDL-ESM2M RCP4.5 GCM as the predictor, future rates consistent with storm event physics are established. Several variants of SLPs were tested against observed peak discharge rates (99.95th percentile flow rate) measured at the seven primary USGS gauging sites. Reasonably strong linear relationships (0.50 ≤ r ≤ 0.99, 0.001 ≤ p-value ≤ 0.076) were found between maximum SLP gradients (ΔSLP) and peak discharge. To find the most appropriate predictor, ΔSLP (from CaRD10 reanalysis) were compared over one, three and five days prior to peak discharge and within 0.667°, 1°, and 5° radii of the gauging station. Best fits were obtained with the three-day window and 0.67° search radius for all but two gauging sites (Santa Ana and Santa Margarita; best fit of 1.0° radius). The greater search radius of the Santa Ana and Santa Margarita Rivers is consistent with the larger watershed areas (~>3 times) associated with each of these rivers compared to the five other watersheds.

Discharge projections of smaller, subordinate rivers within the SCB watersheds were derived using area-normalized flow rate relationship [16]

$$Q_i^{21}=R_{Primary}^{21}·A^i$$

(2)

where and $Q_i^{21}$ is the projected discharge rate (m³/s) of subordinate river i, $A^i$ is the watershed area (m²) associated with river i, and $R_{Primary}^{21}$ is the area-normalized projected flow of the corresponding primary river.

An idealized dimensionless hydrograph was developed from nine gauging station discharge records throughout the study area. These stations had data available at 15 min or smaller sampling resolution and at least three events exceeding the 99.95th percentile during the record period. Events exceeding the 99.95th percentile were selected, normalized by the peak flow, $Q^{Historical}$, and fit with a lognormal distribution. Lognormal distributions are often used to develop unit hydrographs as they have been shown to predict peak flows and time to peak well [85]. The mean of the mean and mean variance of all nine fitted distributions were used to define the idealized hydrograph in Figure 7. The hydrograph is skewed toward rapid initial increases in flow and subsequent slower rates of decreasing discharge rates. The total duration is on the order of 0.7 days (17 h) for flows that exceed 10% of the peak discharge.

Simulations were constructed such that peak discharge was synched with peak tide levels and surge (i.e., minimum SLP) conditions. Winds fields, resultant waves, and fluvial discharge parametrization from the same downscaled GCM were thus dictated by the timing of the SLP low. Most USGS gauging stations are upstream of tidal influence; model discharge points were placed at gauge locations within applicable CoSMoS Delft3D domains (Figure 7). Discharge points were placed in the upmost position in the domain for the few cases where gauge locations were outside model boundaries.

2.2.3.3. Regional-Scale Wave and Hydrodynamic Model (Tier I)

The WAVE and FLOW modules of the Delft3D version 4.01.00 were used to simulate waves and hydrodynamics, respectively. The WAVE module allows for two-way coupling (communication) between wave computations and FLOW hydrodynamics simulating waves with the numerical model SWAN. SWAN is a commonly used third-generation spectral wave model specifically developed for nearshore wave simulations that account for propagation, refraction, dissipation, and depth-induced breaking [44,86]. Delft3D-FLOW, developed by WL/Delft Hydraulics and Delft University of Technology, is a widely used numerical model that calculates non-steady flows and transport phenomena resulting from tidal and meteorological forcing [43].

Tier I SWAN and FLOW models consist of identical structured curvilinear grids that extend from shore to ~200 km offshore in water depths >1000 m and range in resolution from 1.2 km × 2.5 km in the nearshore to 3.5 km × 5 km in the offshore (dashed black line in Figure 3; black line in Figure 8). The two-way coupled model was run in a spherical coordinate system and with FLOW in a vertically-averaged mode (2DH). Spatially varying astronomic tidal amplitudes and phases derived from the Oregon State University TOPEX/Poseidon global tide database [87] were applied along all open boundaries.

SLA due to large-scale meteorological and oceanographic processes unrelated to storms, were applied along all open boundaries of the Tier I FLOW grid. Elevated SLA are often observed in conjunction with El Niño events [28,29,88] and yield water levels of 10–20 cm above normal for several months [89]. In an effort to maintain simplicity, measured SLAs were correlated with sea surface temperature anomalies (SSTAs) for the same time periods. These relationships were used with projected GFDL-ESM2M SSTs to estimate future variations in SLAs, as described in [34].

Space- and time-varying wind (split into eastward and northward components) and SLP fields (see Section 2.2.1) were applied to all grid cells at each model time-step. The wind and SLP fields were input as equidistant points spaced 10 km apart and interpolated within the Delft3D model to the SWAN and FLOW grids. An average pressure of 101.3 kilopascals was applied to the open boundaries of the meteorological grid.

Deep water wave parameters (H_s, T_p, and D_p), obtained with the WWIII model for the CDIP067 buoy and each identified storm event (Section 2.2.3.1), were applied along all open boundaries of the Tier I SWAN grid. Wave direction is critical to accurate simulations of wave propagation from deep-water to the nearshore in the complex SCB region [22]. However, as alongshore variations in deep-water wave forcing available with the WWIII model outputs were small, particularly with respect to incident wave directions, non-varying wave boundary forcing is applied to the Tier I model.

2.2.3.4. Local-Scale 2D Wave and Hydrodynamic Model (Tier II)

Tier II consists of 11 local-scale sub-models to cover the SCB, each consisting of two SWAN grids and multiple FLOW grids (Figure 8). Physical overlap exists between sub-models along-shore extents to avoid erroneous boundary effects in regions of interest.

Each Tier II hydrodynamic FLOW sub-model consists of one “outer” grid and multiple two-way coupled “domain decomposition” (DD) structured grids. DD allows for local grid refinement where higher resolution (~10–50 m) is needed to adequately simulate the physical processes and resolve detailed flow dynamics and overland flood extents. Communication between the grids takes place along internal boundaries where higher-resolution grids are refined by three or five times that of the connected grid. This DD technique allows for two-way communication between the grids and for simultaneous simulation of multiple domains.

In the landward direction, Tier II DD FLOW grids extend to the 10 m topographic contour; exceptions exist where channels (e.g., the Los Angeles River) or other low-lying regions extend multiple kilometers inland. The number of DD FLOW grids ranges from 4 to 13, depending on local geography, bathymetry, and overall landscape. Grid resolution ranges from approximately 130 m × 145 m (across and along-shore, respectively) in the offshore region to as fine as 5 m × 15 m in the nearshore and overland regions.

Wave computations are done with the SWAN model using two grids for each Tier II sub-model: one larger grid covering the same area as the “outer” FLOW grid and a second finer-resolution two-way coupled nearshore nested grid. The nearshore SWAN grids extend from at least the 30 m isobath to well inland of the present day shoreline. The landward extension is included to allow for wave computations of the higher SLR scenarios. See Appendix A for details on settings.

Water level and Neumann time-series extracted from Tier I simulations were applied to the shore parallel and lateral open boundaries of each Tier II “sub-model outer” grid, respectively (one-way nesting). Several of the sub-models proved to be unstable with lateral Neumann boundaries; for those cases, one or both of the lateral boundaries were converted to water level time-series or left unassigned. The extracted time series from Tier I included variations due to tides, SLAs and spatially-varying storm surge. To account for further, local contributions of winds and SLPs to storm surge related wind-setup at the shore and local inverse barometer effects (IBE, rise or depression of water levels in response to atmospheric pressure gradients), the same 10 km hourly-resolution winds used in Tier I are also applied to each grid cell in the Tier II sub-models.

2.2.3.5. Local-Scale 1D Wave and Hydrodynamic Model (Tier III)

Nearshore hydrodynamics, wave setup, total wave runup and event-based erosion were simulated with the XBeach (eXtreme Beach) version 1.21.3667 (2014) model [46,47]. XBeach is a morphodynamic storm impact model specifically designed to simulate beach and dune erosion, overwash, and flooding of sandy coasts. XBeach was run in a profile mode, at 4466 cross-shore transects numbered consecutively from 1 at the U.S./Mexico border to 4802, north of Point Conception (Figure 3). Profiles across harbor mouths, inlets, etc. were excluded from simulations. Each of the profiles extend from the approximate −15 m isobath to at least 10 m above NAVD88 (truncated in cases where a lagoon or other waterway exists on the landward end of the profile). Cross-shore profiles obtained from the DEM (see Section 2.2.2.1) were re-sampled using an algorithm that evaluates long wave resolution at the offshore boundary, depth-to-grid-size ratio, and grid size smoothness constraints to obtain optimum grid resolution while reducing computation times. Final profile grid resolutions are between 25 m and 35 m in the offshore and 5 m in shallow nearshore and land regions. Further details on settings are provided in Erikson et al. [54] and Appendix A.

Time-series of water levels (hourly) and waves (20-min intervals) extracted from completed Tier II runs were applied at the seaward ends of each of the transect models. Water-level variations represented the cumulative effect of astronomic tides, storm surge (including inverse barometric effects and wind setup), SLAs, and SLR. Neumann boundaries set to zero were used along the lateral boundaries: a condition that has been shown to work well with quasi-stationary situations where the coast can be assumed to be uniform alongshore outside the model domain [46,47].

Within each simulation, morphodynamic change due to the storm event is computed along the profile transect. The event-based erosion extent simulated by XBeach is dependent on the hydrodynamics across the entire active and wetted profile, bordered on the landward side by the runup extent.

2.3. Determination of Flood Extents and Uncertainty

Flood extents were determined in two ways: (1) from the landward-most wet grid cell in the high-resolution Delft3D grids in embayments; and (2) from maximum sustained water levels calculated with XBeach cross-shore models along the open coast. The frequency-filtered sustained water levels (constant water levels of durations longer than 1 min) are intended to capture the wave setup at the shore, which is the increase in mean water level above the still water line due to the transfer of momentum by breaking waves. Maximum runup, computed with the Tier III XBeach model, are also output as part of the CoSMoS results, but are mapped as single points and are not included in the flood footprint (see Section 4). Mapped outputs are done in this way to distinguish between shorter duration wave runup which, depending on the beach slope, may only constitute a couple of centimeters of intermittent standing water. Except where overtopping occurs or at a narrow beach that fronts a near vertical cliff or wall, sustained water levels and flood extents are seaward of the maximum runup.

Melding of flood extents simulated with the XBeach and Delft3D high resolution models was done by interpolating (linear Delaunay Triangulation) resulting water level elevations onto a common 2 m resolution square mesh (within the Mathworks Matlab environment). In some areas, such as Mission Beach in San Diego County, where both XBeach and high resolution grids exist to capture flooding from either or both the landward or seaward side, XBeach results were given precedence. Because of Tier III transect model spacing, areas between transects contain interpolated flood depths and extents and are not exact representations of model outputs.

This post-processing step was done for all storms simulated as part of a given scenario. For the 20-year storm for example, two individual storm events were modeled to ensure that local effects, such as shoreline orientation with respect to incident storm direction, were taken into account. For those cases where more than one storm was modeled, all resulting 2 m gridded flood maps were overlain and maximum water levels saved at each grid cell to generate a single, composite flood map for a given scenario.

Resulting water-elevation surfaces were differenced from the high resolution DEM to isolate areas where the water level exceeds topographic elevations, indicating flooding. For scenarios that include SLR, 2 m DEMs that incorporate long-term morphodynamic changes were used (Section 2.2.2.5).

The resulting flood maps were then processed to exclude isolated wetted areas not hydraulically connected to the ocean; these disconnected areas were flagged as low-lying vulnerable areas below the flood elevation. To note, culverts or other manmade and natural underground pathways, not physically captured in the DEM, between coastal waters and land are not accounted for in the modeling and flood projection.

Maps of associated maximum flood durations, velocities, and wave heights were processed in a similar manner to that of the flood depths and extents in that they were gridded onto a common 2 m mesh and then combined. Data that fell outside the flood map extents were removed so that the footprints of all data layers are consistent.

2.3.1. Uncertainty

Uncertainties in the numerical model outputs and DEM measurements were combined with estimates of vertical land motion (VLM, Section 2.3.2) to produce spatially varying offsets that were added/subtracted to/from the modeled flood elevations to produce maps of flood potential; essentially spatially-characterizing the vertical uncertainty from the model. This was done for each of the 40 scenarios, yielding maximum and minimum potential flood extents (the upper and lower bounds of total uncertainty) for each flood projection. Models compared well to available observation stations within the SCB (Section 3), but model comparisons remain limited for the size and scope of the study area and may not address spatial variability of error. Therefore, a much larger value of ±50 cm was used to represent model uncertainty. This larger value was used in an effort to mitigate for the low number of available and tested storms compared to the geographic scope. Uncertainties associated with the baseline DEM were set at ±0.18 m, equivalent to the 95% confidence level for topographic lidar measurements in open terrain [90].

2.3.2. Vertical Land Motion

Spatially variable measurements of vertical land motion based on GPS data and statistical and physical tectonic models, largely attributed to tectonic movement of the San Andreas Fault System from Howell et al. [91], were also incorporated into uncertainty. For each SLR scenario, spatially variable, 1 km resolution rasters of uplift and subsidence values were derived from Howell et al. [91]. For consistency with long-term cliff/beach projections, uplift and subsidence rates were applied through year 2100 for all SLR amounts above 1.0 m, while earlier time frames (2044/2069/2088) were used for lower SLR scenarios, as described in Section 2.2.2.2. The corresponding amounts of uplift and subsidence were then added to or subtracted from the baseline DEM to account for uncertainty due to vertical land motion.

Maximum rates of uplift (0.4 mm/year) and subsidence (0.6 mm/year) within our study area equate to a maximum of 3.4 cm of uplift and 5.2 cm of subsidence for the 1 m SLR scenario. In the future, these rates could be refined using more spatially-resolved data sources (e.g., InSAR) to complement the GPS data which are fairly sparse along the Southern California coast. However, in general, even the highest rates of vertical motions that have been recorded in the San Francisco Bay Area [92] and more locally in the Santa Ynez mountains [93] rarely exceed more than 2 and 6 mm/year, respectively, and therefore are quite small relative to the expected rates of SLR by the middle and end of the 21st century.

3. Results—Model Validation

The model setup and simulation scheme were tested by comparing model outputs to observed water level variations due to astronomic tides and non-tidal residuals (storm surge and other anomalous water levels), wave heights, wave runup, and short-term morphologic change.

The root-mean-square-difference (rmsd) and bias were calculated,

$$rmsd={\left[\frac{{\sum }_{i=1}^N{\left(ob{s}_i-md{l}_i\right)}^2}{N}\right]}^{1/2}$$

(3)

$$bias=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N\left(md{l}_i-ob{s}_i\right)$$

(4)

where obs is the observation data, mdl is the model data, i is the individual time point data, and N is the total number of time-points analyzed. The rmsd represents the standard deviation of the residuals (difference between the observed and modeled values), the bias describes the model’s overall offset from observations. Regarding flood extents, an extreme paucity of region-scale spatially-varying flood data exist for model comparisons. Certain temporally-limited datasets have been painstakingly collected for specific locations [94], but comparisons of flood extents across the study area is infeasible at the current time.

The model’s ability to replicate tidal variations was tested over a month-long time-period (October to November 2010) to capture full variations in spring and neap cycles. Modeled tidal variations were compared to NOAA predicted tides at the four tide-stations within the SCB: La Jolla (station ID: 941030), Los Angeles (station ID: 9410660), Santa Monica (station ID: 9410840), and Santa Barbara (station ID: 9411340). Comparisons between time-series of the modeled and predicted tides are very good at all four stations, being less than 6 cm for both the rmsd and bias (Figure 9).

Wave model accuracy was tested against the January 2010 storm by comparing hindcast wave heights, periods, and directions to observed values at 18 buoys within the Southern California Bight (see Figure 8 for buoy locations; Figure 10 for observation-model comparisons; and

Table B1. Comparison of modeled and measured waves for the January 2010 validation storm. Grid refers to either Tier I or a Tier II grid abbreviation (Figure 8).

NDBC ID	CDIP ID	Lat (Degrees N)	Lon (Degrees W)	Grid	Significant Wave Height		Peak Wave Period		Peak Wave Direction
					rms, Meters	Skill	rms, Seconds	Skill	rms, Degrees	Count
46086	-	32.49083	118.03472	Tier I	0.37	0.92	2.02	0.62	-	982
46069	-	33.67444	120.21167	Tier I	0.60	0.96	2.57	0.66	-	93
46054	-	34.26472	120.47694	Tier I	0.62	0.91	1.81	0.61	-	981
46053	-	34.25250	119.85333	gc, is	0.25	0.75	1.88	0.63	-	978
46025	-	33.74944	119.05278	Tier I	0.28	0.76	2.19	0.55	-	983
46221	28	33.85500	118.63400	mk	0.25	0.83	2.36	0.53	1.7	1966
46242	43	33.21980	117.43940	cb, ty	0.19	0.55	3.08	0.51	1.2	1614
46224	45	33.17778	117.47215	cb, ty	0.27	0.74	2.66	0.48	1.5	1944
46219	67	33.22480	119.88180	Tier I	0.67	0.79	1.82	0.69	2.2	1964
46215	76	35.20382	120.85931	Tier I	0.50	0.89	2.25	0.60	2.0	1968
46222	92	33.61791	118.31701	mk	0.27	0.88	2.09	0.58	2.3	1963
46231	93	32.74700	117.37000	sd	0.31	0.90	2.20	0.55	2.4	1968
46223	96	33.45800	117.76700	cb	0.25	0.79	2.30	0.52	1.9	1947
46225	100	32.93342	117.39083	cb	0.27	0.84	2.37	0.54	1.9	1968
46216	107	34.33300	119.80300	gc, is	0.29	0.88	1.79	0.54	2.0	1968
46217	111	34.16692	119.43465	gc, is	0.22	0.69	2.26	0.50	2.3	1941
46241	161	33.00300	117.29200	cb, ty	0.25	0.71	2.27	0.56	1.9	1968
46238	167	33.76000	119.55000	Tier I	0.51	0.89	1.78	0.62	2.3	1967

in Appendix B for full comparisons). In addition to rms values, non-dimensional Wilmott skill scores are used to aid in quantifying model skill of wave simulations [95]. See Appendix B for complete skill scores.

The model’s ability to simulate wave heights across the area is generally good to great (Wilmott skill ranging 0.69 to 0.96, Table A1), and in conjunction with the rmsd values, shows that model performance increases with the finer Tier II grids. Rmsd values range 19–51 cm for the Tier II grids and 28–67 cm for the Tier I grids. Peak wave directions are quite good with rmsd values less than 3°. Peak wave periods are modeled with good to fair skill (0.48 < skill < 0.69). The lower peak wave period skill compared to wave height skill is likely a reflection of the “jumpy” nature of peak wave periods in multimodal regions such as SCB [25]. Skill scores of mean wave period are likely to show better performance, but are not listed here as it is the peak periods that are used for boundary conditions to Tier III XBeach models.

Wave runup was evaluated by running XBeach for a time-period of available runup measurements at Ocean Beach, just south of the Golden Gate near San Francisco in central California. Runup measurements were obtained during 3-h daylight intervals in May 2006 when offshore waves ranged between 1–2 m and peak wave periods up to 14s (at NDBC buoy 46026) using a camera system [96]. The foreshore beach slope was mild with an average slope of 0.03. Computed rms values between the observed and modeled runup height for four separate 3-h periods ranged 10–16 cm [96].

4. Discussion—Projected Hazards Case Study: Del Mar, California

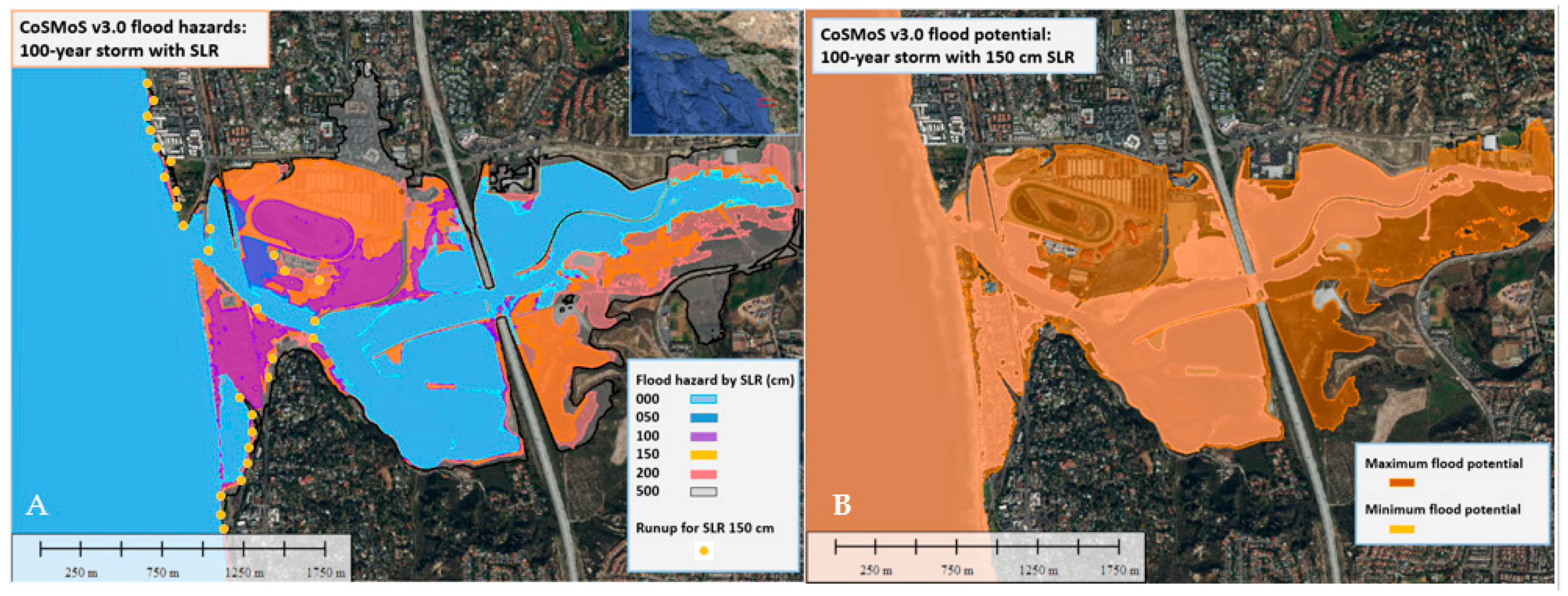
Changes in flood extents and hazards between scenarios can be investigated to determine thresholds and hotspots of vulnerability with respect to SLR and storm intensity. To highlight the significance of dynamic storm contributions to flood risks, and the incorporation of these processes in CoSMoS, results for Del Mar, California, are showcased.

Looking across this community, the storm-related impacts of flooding are clearly visible (Figure 11) for all SLR scenarios. Considering SLR-related flooding only, 0.8 km² of Del Mar is impacted with SLR of 150 cm (Figure 12). Notably, however, flood extents from a 100-year storm for the same SLR impact more than twice the area than when considering SLR alone, underlining the importance of dynamically-driven water levels in coastal flooding. This is especially true for lower amounts of SLR, probable in the beginning to middle of the 21st century. With higher amounts of SLR, flood extents reach the extent of the lagoon basin and the surrounding high terrain, limiting further exposure. Taking a closer look at the local scale, identification of specific at-risk features and locations are clearly ascertained. Runup points, illustrating landward wave-driven wetted extents, show even more extensive effects inland. In contrast, CoSMoS flood extents signify presence of 1–2 cm of water for at least a minute, to demonstrate a more representative impact of flooding. Runup is sometimes used as the TWL at shore to drive flood illustrations in other vulnerability models [97] despite potentially limited volumes of seawater associated with the uppermost and intermittent swash. However, as wave-driven wetting and flooding projections are separated in CoSMoS results, users can either include or isolate impacts as appropriate for their site, planning needs, and level of risk tolerance.

Considering uncertainty illustrated in flood potential (Figure 11), marsh areas are particularly vulnerable. The low-elevation stretches of marsh show significant increases in vulnerability with maximum flood potential, or the upper range of model uncertainty and DEM accuracy. As elevation-data collection methods for the DEM showed the greatest uncertainty in regions of densely-vegetated parcels such as marsh areas, due to the inability of lidar at penetrating the thick plant matter [98], this uncertainty should be incorporated for any risk or adaptation study. For comprehensive analyses of risk, runup and flood potential (uncertainty) should be considered, in addition to explicit flood projections.

Looking at long-term shoreline change hazards around the lagoon entrance to Del Mar, existing beaches appear particularly vulnerable for conditions at or greater than 150 cm (Figure 13). Long-term projections indicate beaches retrograde landward to existing breakwater and urban infrastructure for all SLR scenarios above 150 cm. However, impacts may occur sooner, as locations for the SLR 100 cm show significant retrograding, coming to within less than 7 m of this urban boundary for much of the beach area shown. Similarly, cliff retreat for the bluffs north of the lagoon entrance show ~40 m of landward regression for the same SLR 150 cm scenario; greater erosion is seen for higher SLR scenarios. The subsequent impacts of this cliff erosion, as incorporated into long-term profile and DEM evolution, can be seen in the flooding projections, as flood extents progress inland along the bluff-backed coastline for each consecutive SLR scenario.

An extensive presentation and discussion of projected hazards across the SCB, to include examination of spatial variation in flood extents and contributions to flood hazards, is presented in Part 2 of this manuscript [17].

5. Conclusions

The overarching concept of CoSMoS is to leverage projections of global climate patterns over the 21st century from the most recent (CMIP5) Global Climate Models (GCMs). Coarse resolution GCM projections are downscaled to the local level and used as boundary conditions to sophisticated ocean modeling tools that simulate complex physics to accurately predict local coastal water levels and flooding for the full range of expected SLR (n = 10: 0–2 m in 0.25 m increments, and 5 m) and storm scenarios (n = 4: average daily/background conditions, annual, 20-year and 100-year). Resulting model projections include spatially explicit estimates of flood extent, depth, duration, uncertainty, water elevation, wave runup, maximum wave height, maximum current velocity, and long-term shoreline change and bluff retreat.

This latest version of CoSMoS has incorporated several additional contributions to coastal water levels and change. Fluvial discharge projections have been included in the hydrodynamic simulations, to capture effects of back-flooding at 37 river mouths in the SCB. Wind setup, locally-generated waves, and other wind-driven processes are inclusively simulated with dynamically downscaled SLPs and winds. Long-term morphodynamic change, derived from century-scale sandy beach and cliff retreat projections, is captured and used in hydrodynamic simulations of future conditions. By including these projections, driven by a range of SLR and wave conditions, a more comprehensive hazards projection is achieved.

Long-term shoreline change models do not include feedback between beach and cliff erosion, however. This feedback is important for complex sediment systems, such as in the study area and other portions of California. Additionally, the profile evolution scheme does not capture along-shore transport and full redistribution of sediment. Future studies will include effort to address feedback between the cliff and shore models, as well as improved profile evolution algorithms.

The inclusion of fluvial discharge is an important addition for river areas along the coast. Several studies suggest the joint probability of co-occurrence between coastally-driven water levels and river flood events are not directly proportional [99,100]. CoSMoS includes estimates of fluvial discharge based on the selected storms’ SLP gradient intensity, not a direct hydrologic projection. In addition, the hydrographs used in the simulations are idealized and peak fluvial discharges are first-order estimates. The simple model employed is efficient and appropriate for inclusion in the prescribed wave-driven flood scenarios. However, the model system would benefit from realizations of discharges for a given storm using improved atmospheric relationships. Similarly, pluvial flooding, related to the intensity and duration of precipitation, can be an important contribution of flooding for many coastal urban areas. Pluvial components are not included, as it is currently beyond the scope of the modeling system; however, such events are likely attributed to atmospheric rivers in California, [101] and the co-occurrence of these phenomena with extreme coastal wave events is currently being investigated.

Additionally, future development of CoSMoS aims to better capture overland flow and flood projections in overtopping and spill-over situations. While several types of overland flow models exists, models are limited in: (1) ability resolve high-resolution flow over large, complex regions; (2) public/open-source access; or (3) interoperability with other parts of the CoSMoS framework. Feasible options for future CoSMoS developments involve the use of flexible-mesh hydrodynamic models and which may also account for infragravity components.

Although the limitations exist for the models and computations contributing to this storm modeling system, CoSMoS provides a comprehensive, physically-consistent, and explicit projection of coastal hazards for the 21st century. Hazard projections are adaptable and scalable, covering a large region with high-resolution projections for a wide range of SLR and storm conditions, to meet the needs of varied users and interests involved in community-scale planning. The thorough modeling approach presented here is designed to provide the necessary data to fully assess potential coastal risks with our changing climate, and make decisions to mitigate and act.