Failure of Grass Covered Flood Defences with Roads on Top Due to Wave Overtopping: A Probabilistic Assessment Method
Abstract
:1. Introduction
2. Theoretical Background
2.1. Shear Stress Excess ()
2.2. Erosion Model as a Function of
3. Millingen aan de Rijn Wave Overtopping Experiment with a Road on Top
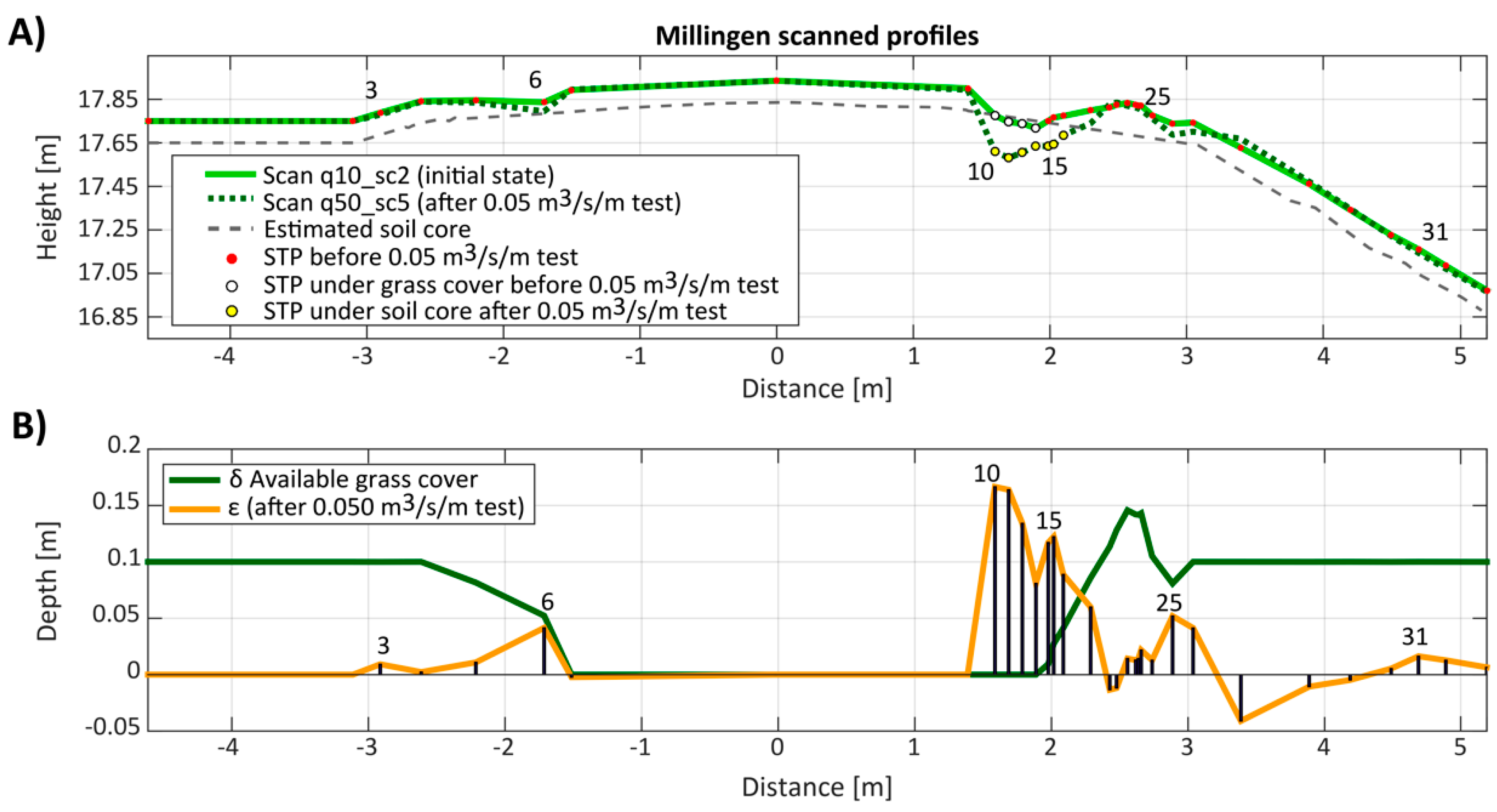
3.1. Millingen Experiment Part I: Scour Measurements
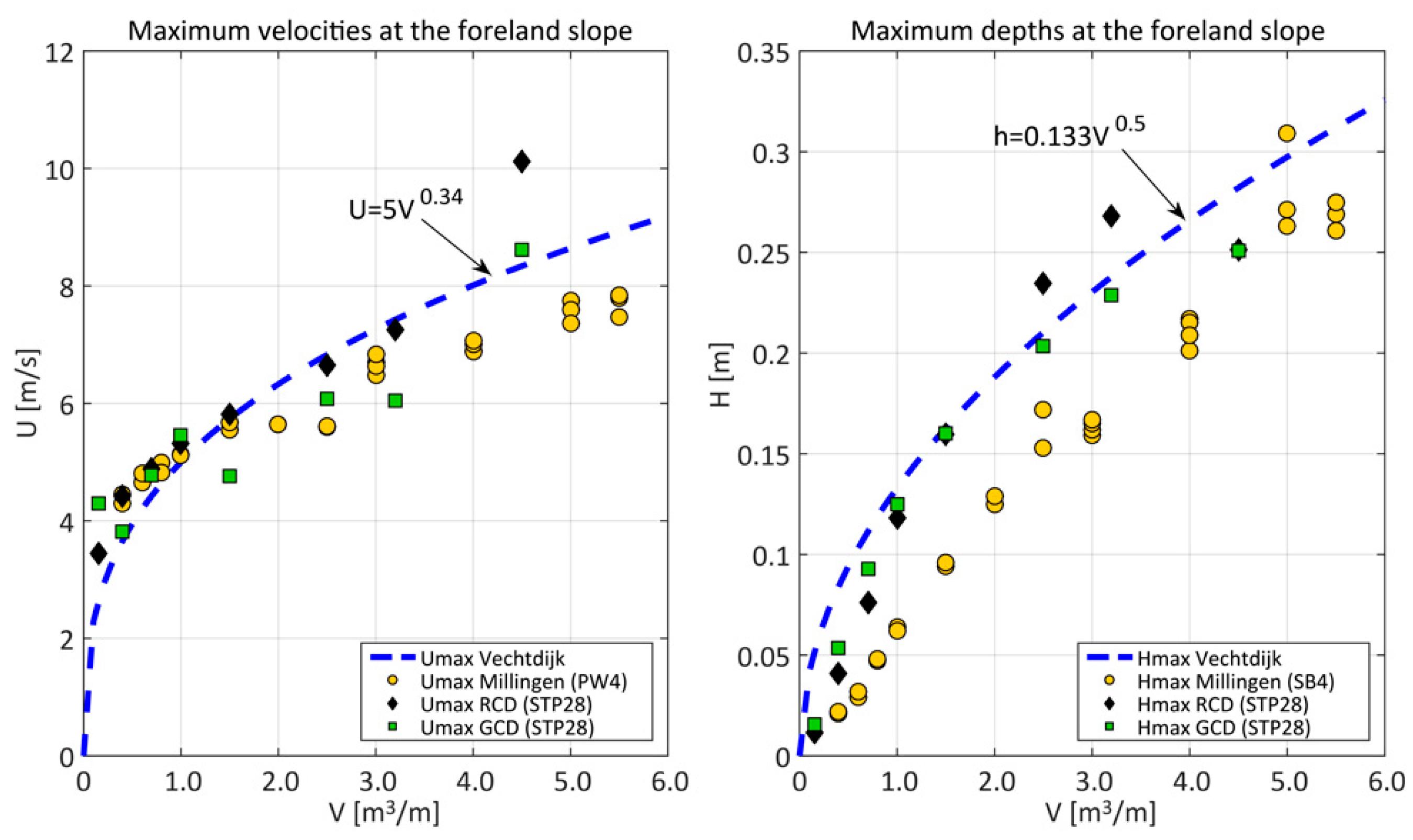
3.2. Millingen Experiment Part II: Flow Depths and Velocity Measurements
4. Methodology
4.1. CFD Models
4.2. Emulator Surfaces Construction
4.3. Functions
4.4. Probabilistic Safety Assessment
5. Results
5.1. CFD Calibration and Validation
5.2. Effects of Turbulence on the Excess Shear Stress
5.3. CE Curves Calculated from Millingen Measurements
5.4. Scour Depth Profiles
5.5. Probability of Failure
6. Discussion
6.1. Uncertainties in the Modelling Process
6.2. Sensitivity to the Grass Quality Estimation
6.3. Applications of the Probabilistic Method
7. Conclusions and Recommendations
- The dike with a road showed higher probabilities (5 × 10−5 > Pf > 1 × 10−4) of failure with respect to a dike without a road (Pf <1 × 10−6) if realistic grass quality distribution was assumed. The probability of failure in the zones where higher initial deterioration was observed (e.g., locations immediately next to the road and over the vertex) is significantly higher with respect to the remaining part of the dike. Yet, these locations also correspond to spots where higher turbulence was observed with respect to the remaining part of the locations along the dike profile. However, if good quality grass was present all along the dike, both dike cases will present very low failure probabilities along the slope and the vertex (Pf < 5 × 10−5).
- Local erosion depth is highly influenced by the momentum of the water volume, which is reduced (energy dissipation) by a rough surface such as grass. If a road is present, both the smoother asphalt surface and the resultant bottom irregularities (possibly derived by traffic and material change) increase the scour potential for failure along the crest and the slope with respect to the dike without a road as they influence the generated and dissipated turbulence (kinetic energy) and its variability (turbulence intensities).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. CFD Validation on the Crest

Appendix B. CFD Validation for the Slope
Appendix C. CFD Validation for Overtopping Duration

References
- Aguilar-López, J.P. Probabilistic Safety Assessment of Multi-Functional Flood Defences; Twente University: Enschede, The Netherlands, 2016. [Google Scholar]
- Hemer, M.A.; Fan, Y.; Mori, N.; Semedo, A.; Wang, X.L. Projected changes in wave climate from a multi-model ensemble. Nat. Clim. Chang. 2013, 3, 471–476. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Alexander, L.V.; Allen, S.K.; Bindoff, N.L.; Bréon, F.-M.; Church, J.A.; Cubasch, U.; Emori, S. Technical summary. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 33–115. [Google Scholar]
- Middelkoop, H.; Daamen, K.; Gellens, D.; Grabs, W.; Kwadijk, J.C.; Lang, H.; Parmet, B.W.; Schädler, B.; Schulla, J.; Wilke, K. Impact of climate change on hydrological regimes and water resources management in the rhine basin. Clim. Chang. 2001, 49, 105–128. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.; Stive, M.J. Estimating coastal recession due to sea level rise: Beyond the bruun rule. Clim. Chang. 2012, 110, 561–574. [Google Scholar] [CrossRef]
- Jongejan, R.; Ranasinghe, R.; Wainwright, D.; Callaghan, D.P.; Reyns, J. Drawing the line on coastline recession risk. Ocean Coast. Manag. 2016, 122, 87–94. [Google Scholar] [CrossRef]
- Naulin, M.; Kortenhaus, A.; Oumeraci, H. Reliability-based flood defense analysis in an integrated risk assessment. Coast. Eng. J. 2015, 57. [Google Scholar] [CrossRef]
- Vrijling, J.K. Probabilistic design of water defense systems in the netherlands. Reliabil. Eng. Syst. Saf. 2001, 74, 337–344. [Google Scholar] [CrossRef]
- Lee, C.-E.; Kwon, H.J. Reliability analysis and evaluation of partial safety factors for random wave overtopping. KSCE J. Civ. Eng. 2009, 13. [Google Scholar] [CrossRef]
- Victor, L.; Van der Meer, J.W.; Troch, P. Probability distribution of individual wave overtopping volumes for smooth impermeable steep slopes with low crest freeboards. Coast. Eng. 2012, 64, 87–101. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Technical Report Wave Run-Up and Wave Overtopping at Dikes; Rijkswaterstaat, DWW: Utrecht, The Netherlands, 2002. [Google Scholar]
- Pullen, T.; Allsop, N.; Bruce, T.; Kortenhaus, A.; Sch, H.; Van der Meer, J. Eurotop: Wave Overtopping of Sea Defences and Related Structures: Assessment Manual; Environment Agency: Bristol, UK, 2007.
- Franco, L.; De Gerloni, M.; Van der Meer, J. Wave overtopping on vertical and composite breakwaters. Coast. Eng. Proc. 1994. [Google Scholar] [CrossRef]
- Dean, R.G.; Rosati, J.D.; Walton, T.L.; Edge, B.L. Erosional equivalences of levees: Steady and intermittent wave overtopping. Ocean Eng. 2010, 37, 104–113. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Hardeman, B.; Steendam, G.J.; Schuttrumpf, H.; Verheij, H.J. Flow depths and velocities at crest and landward slope of a dike, in theory and with the wave overtopping simulator. Coast. Eng. Proc. 2010, 1. [Google Scholar] [CrossRef]
- Steendam, G.J.; Van Hoven, A.; Van der Meer, J.; Hoffmans, G. Wave overtopping simulator tests on transitions and obstacles at grass covered slopes of dikes. Coast. Eng. Proc. 2014, 1. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M.; van Hoven, A.; Harderman, B.; Verheij, H. Erosion of grass covers at transitions and objects on dikes. In Proceedings of the 7th International Conference on Scour and Erosion, Perth, Australia, 2–4 December 2015; Cheng, L., Drapper, S., An, H., Eds.; Taylor and Francis Group: Perth, Australia, 2015. [Google Scholar]
- Hoffmans, G.J.C.M.; Akkerman, G.J.; Verheij, H.; Van Hoven, A.; Van der Meer, J. The erodibility of grassed inner dike slopes against wave overtopping. ASCE 2008, 3224–3236. [Google Scholar] [CrossRef]
- Verheij, H.J.; Meijer, D.G.; Kruse, G.A.M.; Smith, G.M.; Vesseur, M. Onderzoek Naar de Sterkte van Graszoden van Rivierdijken; Deltares (WL): Delft, The Netherlands, 1995. [Google Scholar]
- Hewlett, H.; Boorman, L.A.; Bramley, L. Design of Reinforced Grass Waterways; Construction Industry Research and Information Association: London, UK, 1987. [Google Scholar]
- Trung, L. Overtopping on Grass Covered Dikes: Resistance and Failure of the Inner Slopes; TU Delft, Delft University of Technology: Delft, The Netherlands, 2014. [Google Scholar]
- Schüttrumpf, H.; Oumeraci, H. Layer thicknesses and velocities of wave overtopping flow at seadikes. Coast. Eng. 2005, 52, 473–495. [Google Scholar] [CrossRef]
- Kobayashi, N.; Weitzner, H. Erosion of a seaward dike slope by wave action. J. Waterw. Port Coast. Ocean Eng. 2014, 141. [Google Scholar] [CrossRef]
- Quang, T.T.; Oumeraci, H. Numerical modelling of wave overtopping-induced erosion of grassed inner sea-dike slopes. Nat. Hazards 2012, 63, 417–447. [Google Scholar] [CrossRef]
- Ribberink, J.S. Bed-load transport for steady flows and unsteady oscillatory flows. Coast. Eng. 1998, 34, 59–82. [Google Scholar] [CrossRef]
- Bomers, A.; Lopez, J.A.; Warmink, J.J.; Hulscher, S.J. Modelling effects of an asphalt road at a dike crest on dike cover erosion onset during wave overtopping. Nat. Hazards 2018, 1–30. [Google Scholar] [CrossRef]
- Castelletti, A.; Galelli, S.; Ratto, M.; Soncini-Sessa, R.; Young, P.C. A general framework for dynamic emulation modelling in environmental problems. Environ. Model. Softw. 2012, 34, 5–18. [Google Scholar] [CrossRef]
- Razavi, S.T.; Bryan, A.; Burn Donald, H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Duncan, A.; Chen, A.S.; Keedwell, E.; Djordjevic, S.; Savic, D. Urban Flood Prediction in Real-Time from Weather Radar and Rainfall Data Using Artificial Neural Networks; International Association of Hydrological Sciences: Exeter, UK, 2011. [Google Scholar]
- Aguilar-Lopez, J.P.; Van Andel, S.J.; Werner, M.; Solomatine, D.P. Hydrodynamic and water quality surrogate modelling for reservoir operation. In Proceedings of the 11th IWA/IAHR International Conference on Hydroinformatics, New York, NY, USA, 17–21 August 2014. [Google Scholar]
- Kingston, G.B.; Rajabalinejad, M.; Ben, P.G.; Van Gelder, P.H.A.J.M. Computational intelligence methods for the efficient reliability analysis of complex flood defence structures. Struct. Saf. 2011, 33, 64–73. [Google Scholar] [CrossRef]
- Aguilar-López, J.P.; Warmink, J.J.; Schielen, R.M.J.; Hulscher, S.J.M.H. Data-driven surrogate models for flood defence failure estiamtion: “Jarillon de calí”. In Proceedings of the 11th IWA/IAHR International Conference on Hydroinformatics, New York, NY, USA, 17–21 August 2014. [Google Scholar]
- Aguilar-López, J.P.; Warmink, J.J.; Schielen, R.M.J.; Hulscher, S.J.M.H. Piping erosion safety assessment of flood defences founded over sewer pipes. Eur. J. Environ. Civ. Eng. 2016, 1–29. [Google Scholar] [CrossRef]
- Van Gent, M.R.A.; van den Boogaard, H.F.P.; Pozueta, B.; Medina, J.R. Neural network modelling of wave overtopping at coastal structures. Coast. Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef]
- Bomers, A.; Aguilar-López, J.P.; Warmink, J.J.; Hulscher, S.J.M.H. Modelling erosion development during wave overtopping of an asphalt road covered dike. In Proceedings of the FLOODrisk 2016 3rd European Conference on Flood Risk Management, Innovation, Implementation and Integration, Lyon, France, 16–21 October 2016. [Google Scholar]
- Hoffmans, G.J.C.M. The Influence of Turbulence on Soil Erosion; Eburon Uitgeverij BV: Delft, The Netherlands, 2012. [Google Scholar]
- Hughes, S.A. Adaptation of the Levee Erosional Equivalence Method for the Hurricane Storm Damage Risk Reduction System (Hsdrrs); DTIC Document: Fort Belvoir, VA, USA, 2011. [Google Scholar]
- Partheniades, E. Erosion and deposition of cohesive soils. J. Hydraul. Div. 1965, 91, 105–139. [Google Scholar]
- Verheij, H.J.; Hoffmans, G.J.C.M.; van der meer, J. Evaluation and Model Development, Grass Erosion Test at the Rhine Dike; Deltares: Delft, The Netherlands, 2015. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- COMSOL. The Comsol CFD Module User's Guide (Version 5.2); COMSOL: Stockholm, Sweden, 2015. [Google Scholar]
- Marriott, M.J.; Jayaratne, R. Hydraulic Roughness–Links Between Manning’s Coefficient, Nikuradse’s Equivalent Sand Roughness and Bed Grain Size; UEL: London, UK, 2010. [Google Scholar]
- Te Chow, V. Open Channel Hydraulics; McGraw-Hill: London, UK, 1959. [Google Scholar]
- Jansen, R.B. Advanced dam Engineering for Design, Construction, and Rehabilitation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bakker, J.; Melis, R.; Mom, R. Factual Report: Overslagproeven Rivierenland; INFRAM: Dutch, The Netherlands, 2013. [Google Scholar]
- Van der Meer, J.W.; Van Hovern, A.; Paulissen, M.; Steendam, G.J.; Verheij, H.J.; Hoffmans, G.J.C.M.; Kruse, G.A.M. Handreiking Toetsen Grasbekledingen op Dijken TBV Het Opstellen van het Beheerdersoordeel (bo) in de Verlengde Derde Toetsronde; Rijkswaterstaat, Waterdienst: Utrecht, The Netherlands, 2012. [Google Scholar]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Piontkowitz, T. Erograss: Failure of Grass Cover Layers at Seaward and Shoreward Dike Slopes. Design, Construction and Performance; Danish Coastal Inspectorate: Copenhagen, Denmark, 2009. [Google Scholar]
- Van der Meer, J.W.; Janssen, J.; Hydraulics, D. Wave Run-Up and Wave Overtopping at Dikes and Revetments; Delft Hydraulics: Delft, The Netherlands, 1994. [Google Scholar]
- Hughes, S.A.; Thornton, C.I.; Van der Meer, J.W.; Scholl, B.N. Improvements in describing wave overtopping processes. Coast. Eng. Proc. 2012, 1. [Google Scholar] [CrossRef]
- Van Loon-Steensma, J.M.; Vellinga, P. Robust, multifunctional flood defenses in the dutch rural riverine area. Nat. Hazards Earth Syst. Sci. 2014, 14, 1085–1098. [Google Scholar] [CrossRef]














| Experiment Part I | |||
|---|---|---|---|
| Overtopping Discharge | Interval 1 Interval | Scanning Instant | Profile Scan Label |
| [m3/s/m] | [min] | [min] | [min] |
| Initial state | 0 | 0 | q0_t0 |
| 0.001 | 72 | 72 | q1_sc1 |
| 0.010 | 180 | 252 | q10_sc1 |
| 0.010 | 180 | 432 | q10_sc2 2 |
| 0.050 | 60 | 492 | q50_sc1 |
| 0.050 | 60 | 552 | q50_sc2 |
| 0.050 | 60 | 612 | q50_sc3 |
| 0.050 | 60 | 672 | q50_sc4 |
| 0.050 | 180 | 852 | q50_sc5 2 |
| 0.100 | 100 | 952 | q100_sc1 |
| 0.100 | 120 | 1072 | q100_sc2 |
| [m] | Source | ||
|---|---|---|---|
| Surface | [s/m1/3] | [m] | - |
| Asphalt | 0.016 | 0.0047 | [39] |
| Grass | 0.025 | 0.0680 | [39] |
| Steel | 0.017 | 0.0068 | [43] |
| Rubble/Clay | 0.026 | 0.0670 | [43] |
| Geotextile 1 | 0.024 | 0.0660 | [44] |
| [m3/s/m] | |||||||
|---|---|---|---|---|---|---|---|
| 0.0001 | 0.001 | 0.010 | 0.020 | 0.050 | 0.075 | 0.100 | |
| [h] | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| [m] | 2.99 | 2.20 | 1.40 | 1.17 | 0.85 | 0.71 | 0.61 |
| Slope [-] | 1:3 | 1:3 | 1:3 | 1:3 | 1:3 | 1:3 | 1:3 |
| [-] | 6545 | 6545 | 6545 | 6545 | 6545 | 6545 | 6545 |
| [-] | 65 | 458 | 2291 | 3142 | 4451 | 4974 | 5367 |
| [-] | 0.01 | 0.07 | 0.35 | 0.48 | 0.68 | 0.76 | 0.82 |
| 1 [m3/m] | 0.21 | 0.46 | 0.94 | 1.27 | 1.91 | 2.35 | 2.72 |
| Good | Poor | Average | Good | ||
|---|---|---|---|---|---|
| Distribution | [-] | Log-norm | Log-norm | Log-norm | Log-norm |
| mean | [m/s] | 0.85 | 3 | 4 | 6.5 |
| CoV | [-] | 0.1 | 0.3 | 0.3 | 0.3 |
| QCF | [-] | - | 1.5 | 1 | 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-López, J.P.; Warmink, J.J.; Bomers, A.; Schielen, R.M.J.; Hulscher, S.J.M.H. Failure of Grass Covered Flood Defences with Roads on Top Due to Wave Overtopping: A Probabilistic Assessment Method. J. Mar. Sci. Eng. 2018, 6, 74. https://doi.org/10.3390/jmse6030074
Aguilar-López JP, Warmink JJ, Bomers A, Schielen RMJ, Hulscher SJMH. Failure of Grass Covered Flood Defences with Roads on Top Due to Wave Overtopping: A Probabilistic Assessment Method. Journal of Marine Science and Engineering. 2018; 6(3):74. https://doi.org/10.3390/jmse6030074
Chicago/Turabian StyleAguilar-López, Juan P., Jord J. Warmink, Anouk Bomers, Ralph M. J. Schielen, and Suzanne J. M. H. Hulscher. 2018. "Failure of Grass Covered Flood Defences with Roads on Top Due to Wave Overtopping: A Probabilistic Assessment Method" Journal of Marine Science and Engineering 6, no. 3: 74. https://doi.org/10.3390/jmse6030074
APA StyleAguilar-López, J. P., Warmink, J. J., Bomers, A., Schielen, R. M. J., & Hulscher, S. J. M. H. (2018). Failure of Grass Covered Flood Defences with Roads on Top Due to Wave Overtopping: A Probabilistic Assessment Method. Journal of Marine Science and Engineering, 6(3), 74. https://doi.org/10.3390/jmse6030074







