Experimental and Numerical Model Investigations of the Underwater Towing of a Subsea Module
Abstract
:1. Introduction
2. Tests Using a Physical Model
2.1. Geometry and General Parameters
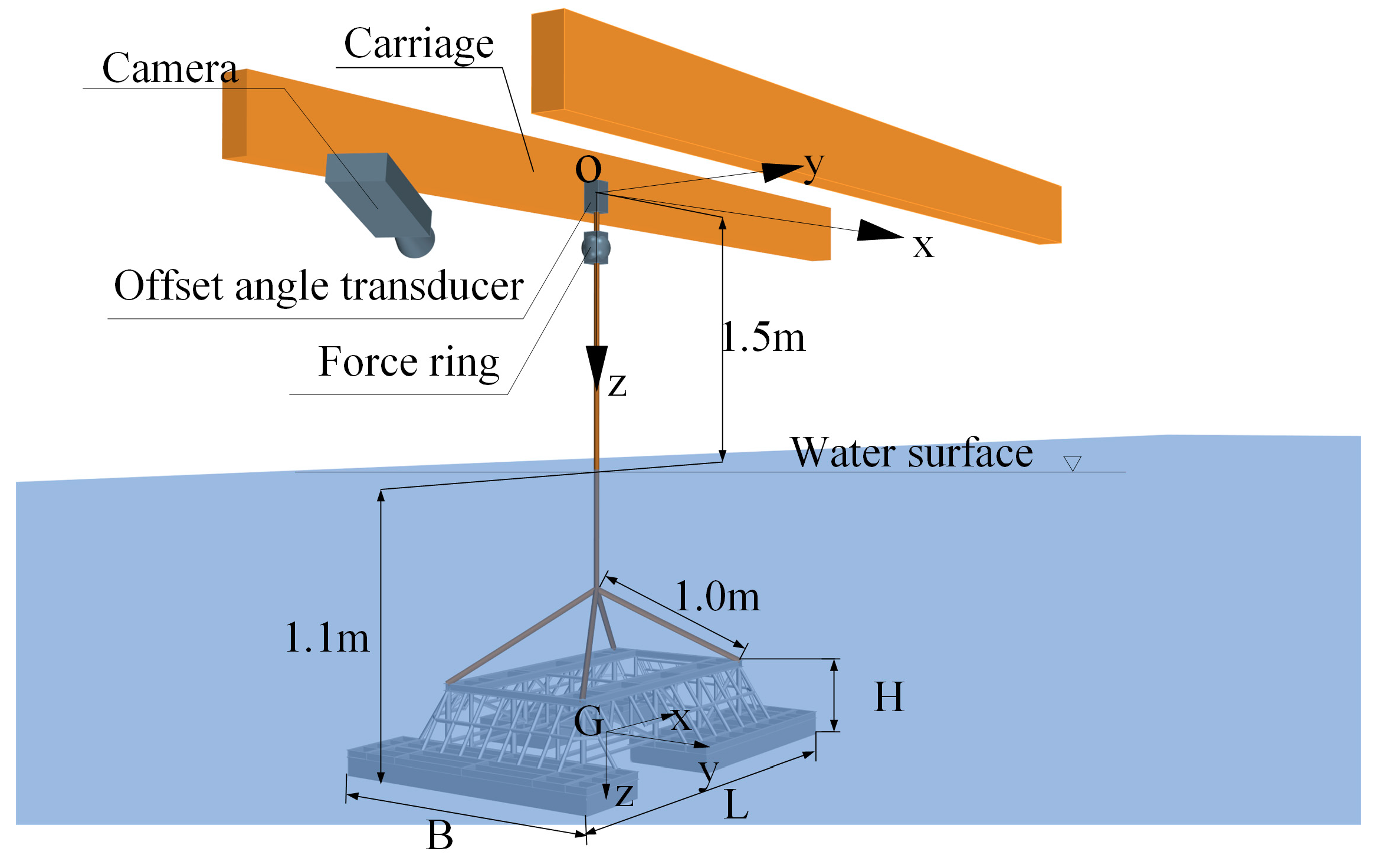
2.2. Experimental Setup
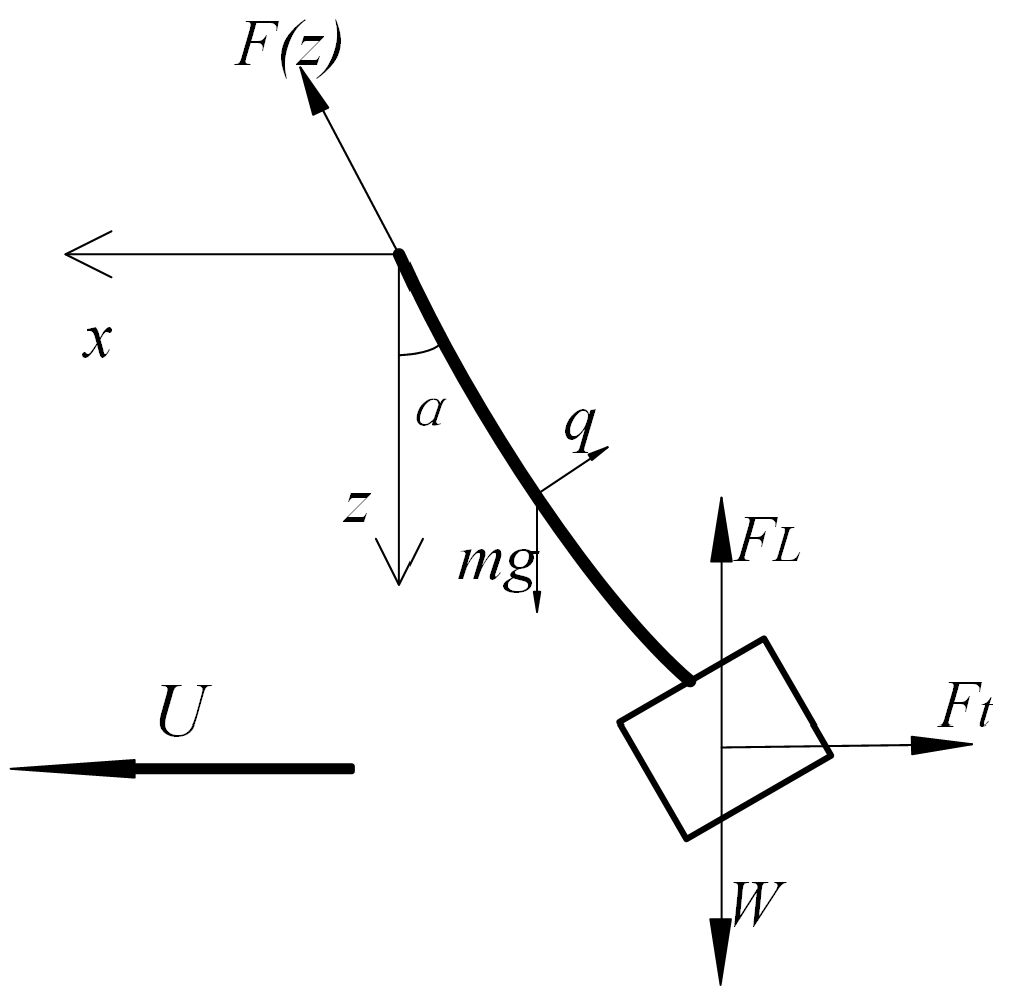
2.3. Physical Modeling of the Module
2.4. Experimental Results
3. Numerical Simulations
3.1. Mathematical and Numerical Models
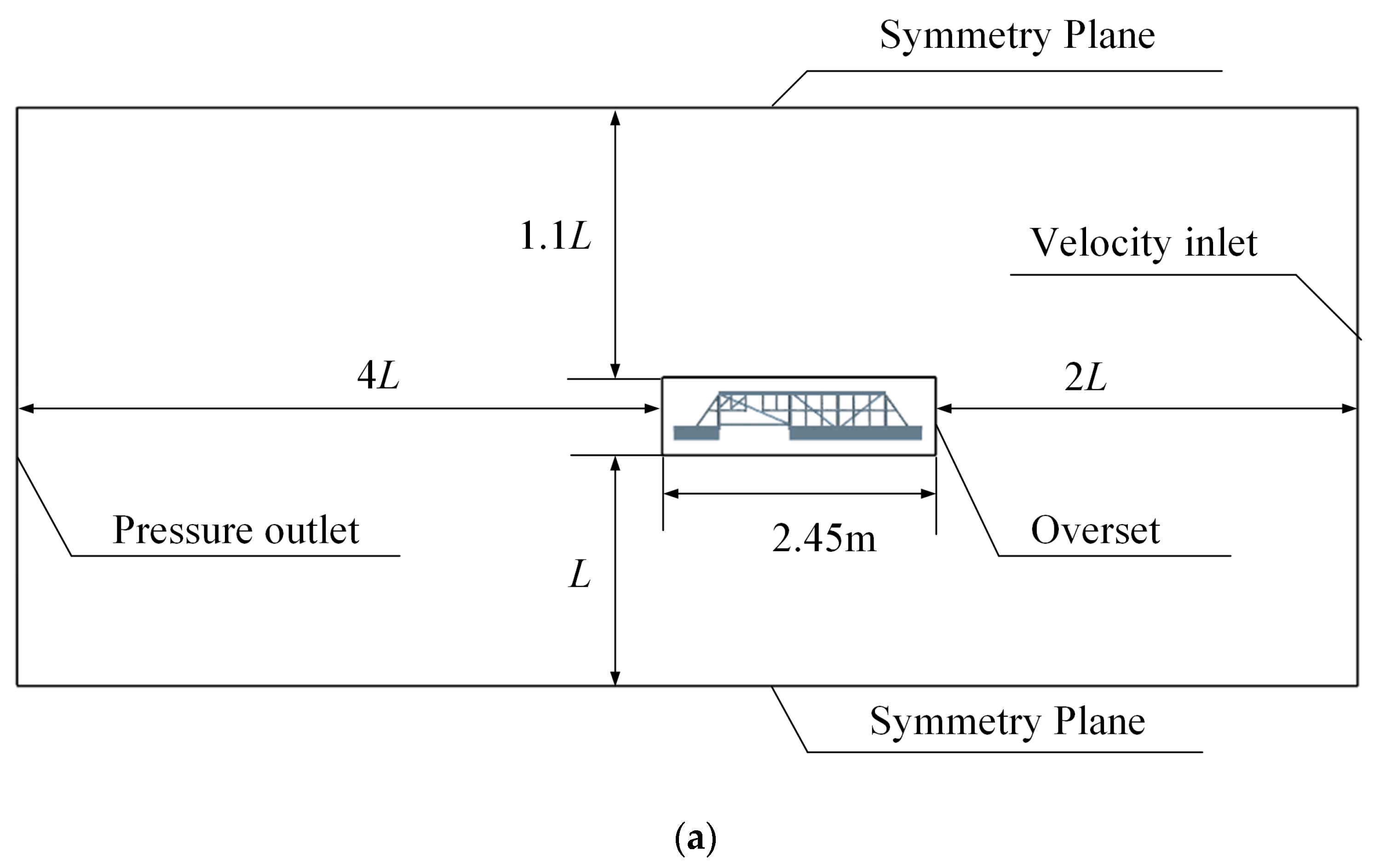
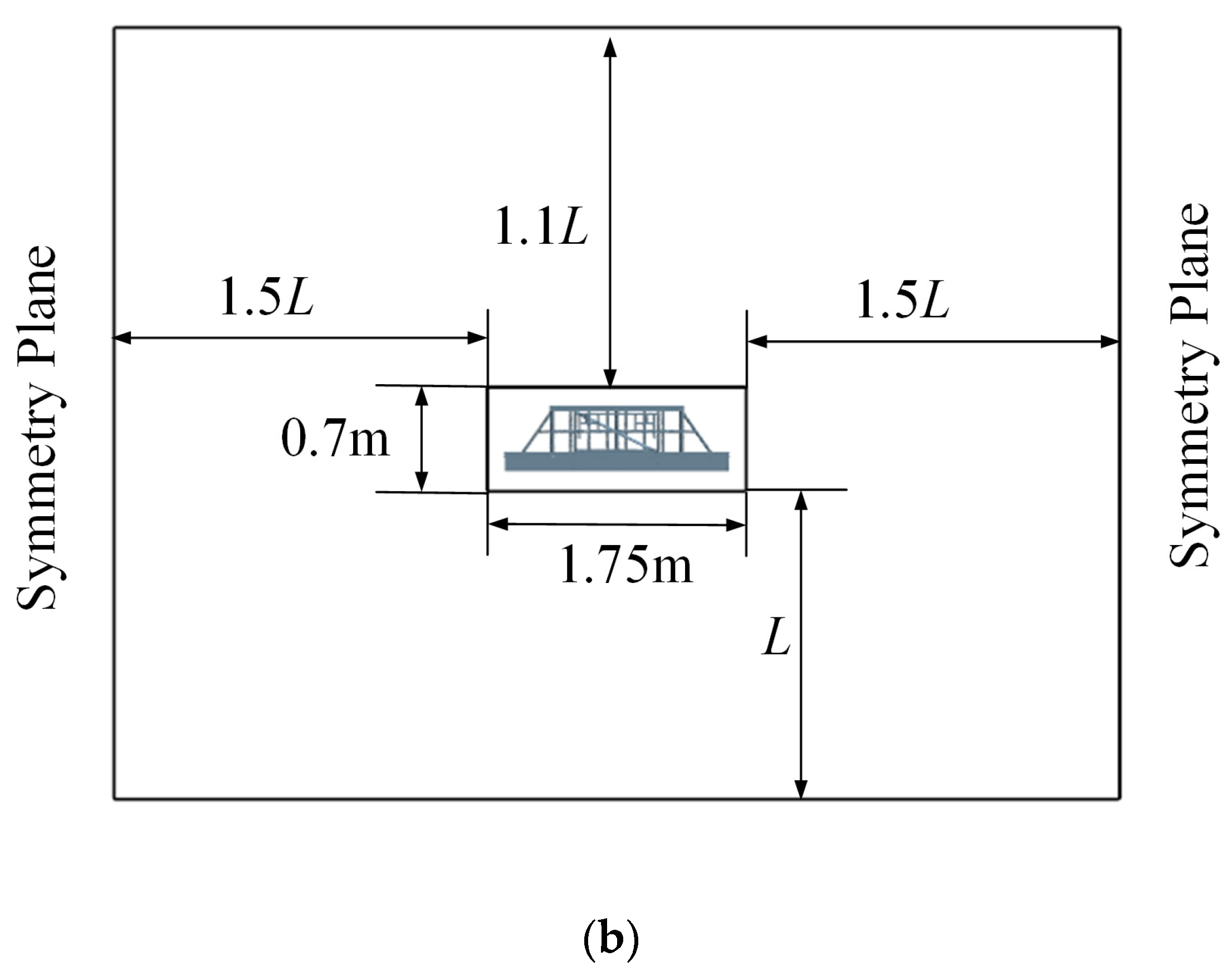
3.2. Boundary Conditions
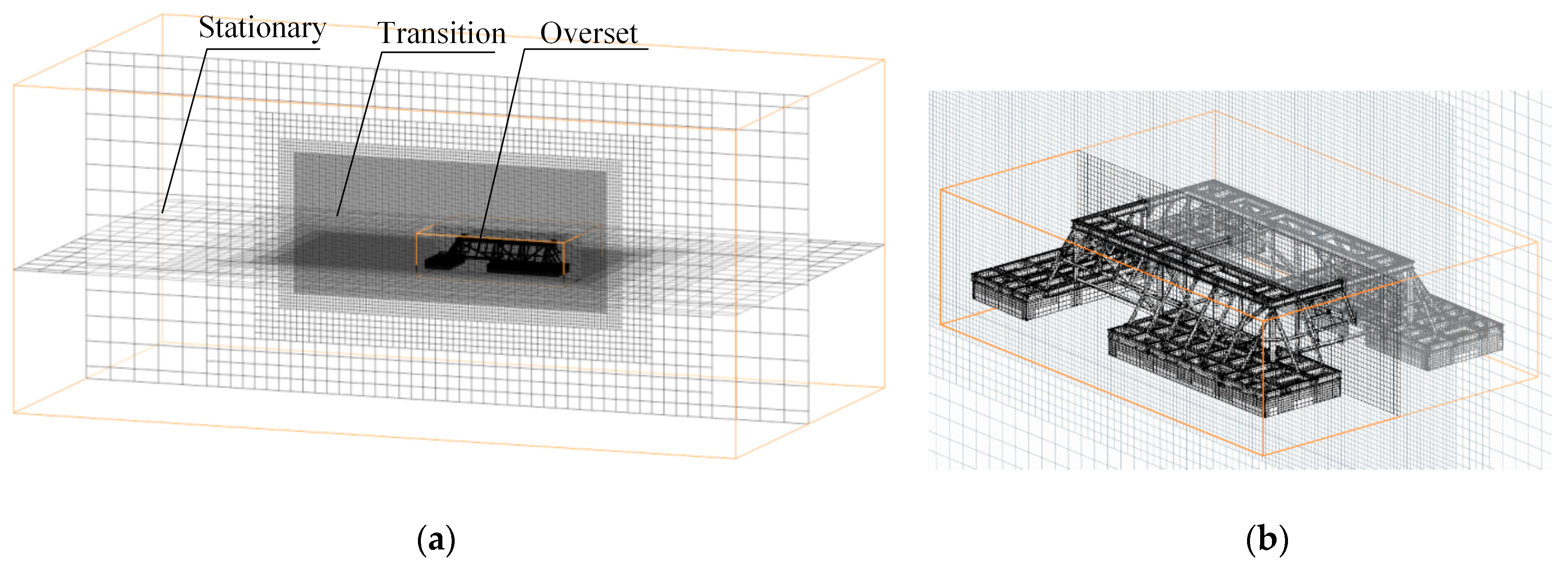
3.3. Mesh Generation
4. Result and Discussion
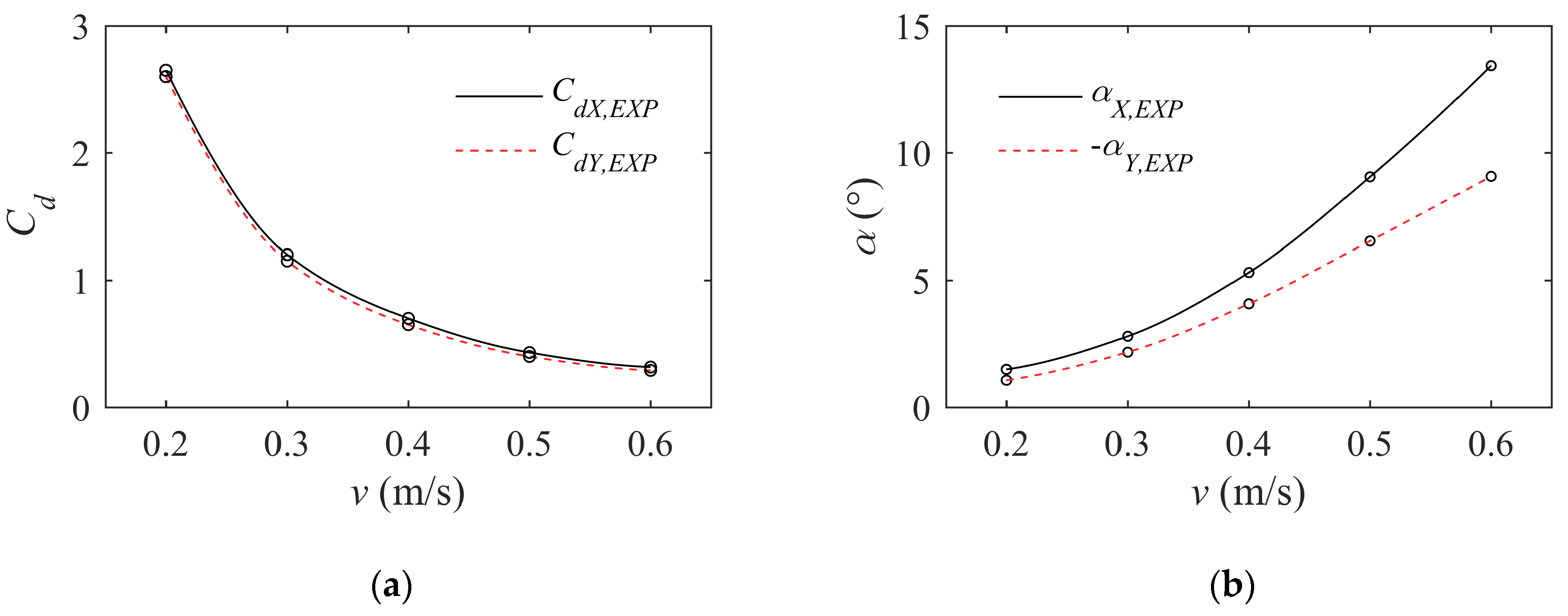
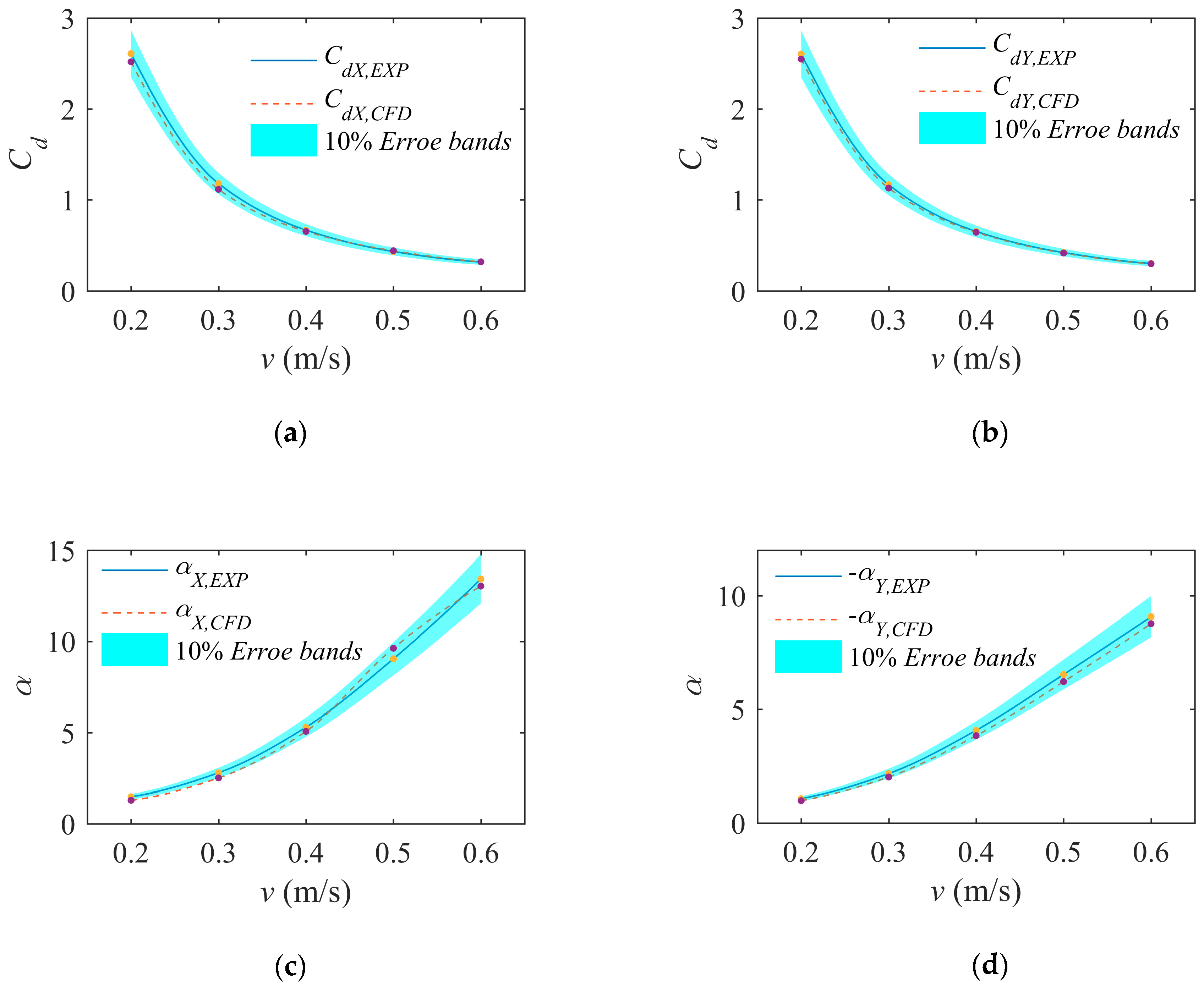
4.1. Validation of Numerical Prediction
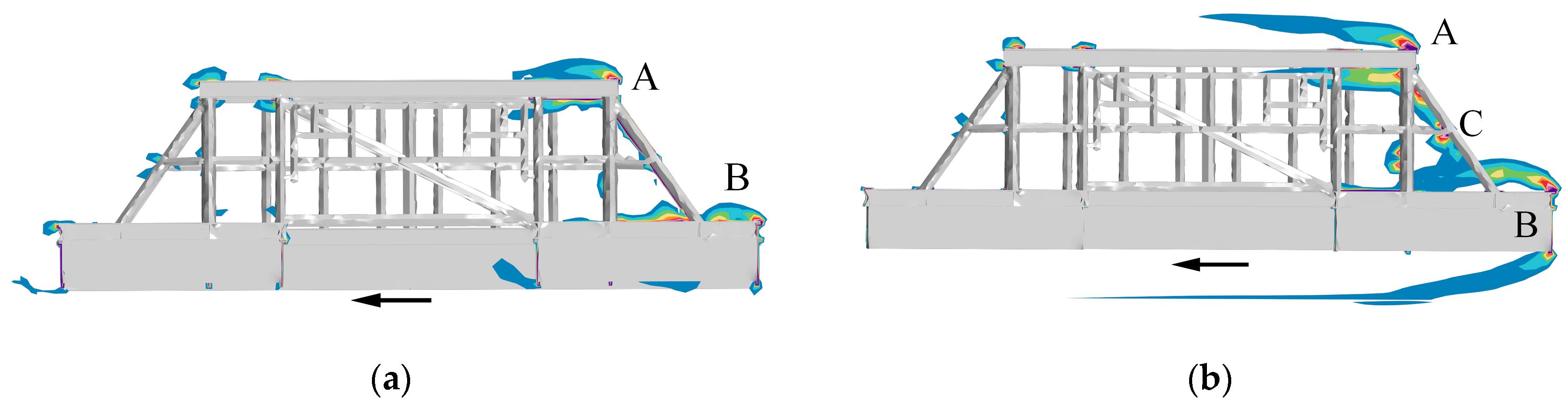
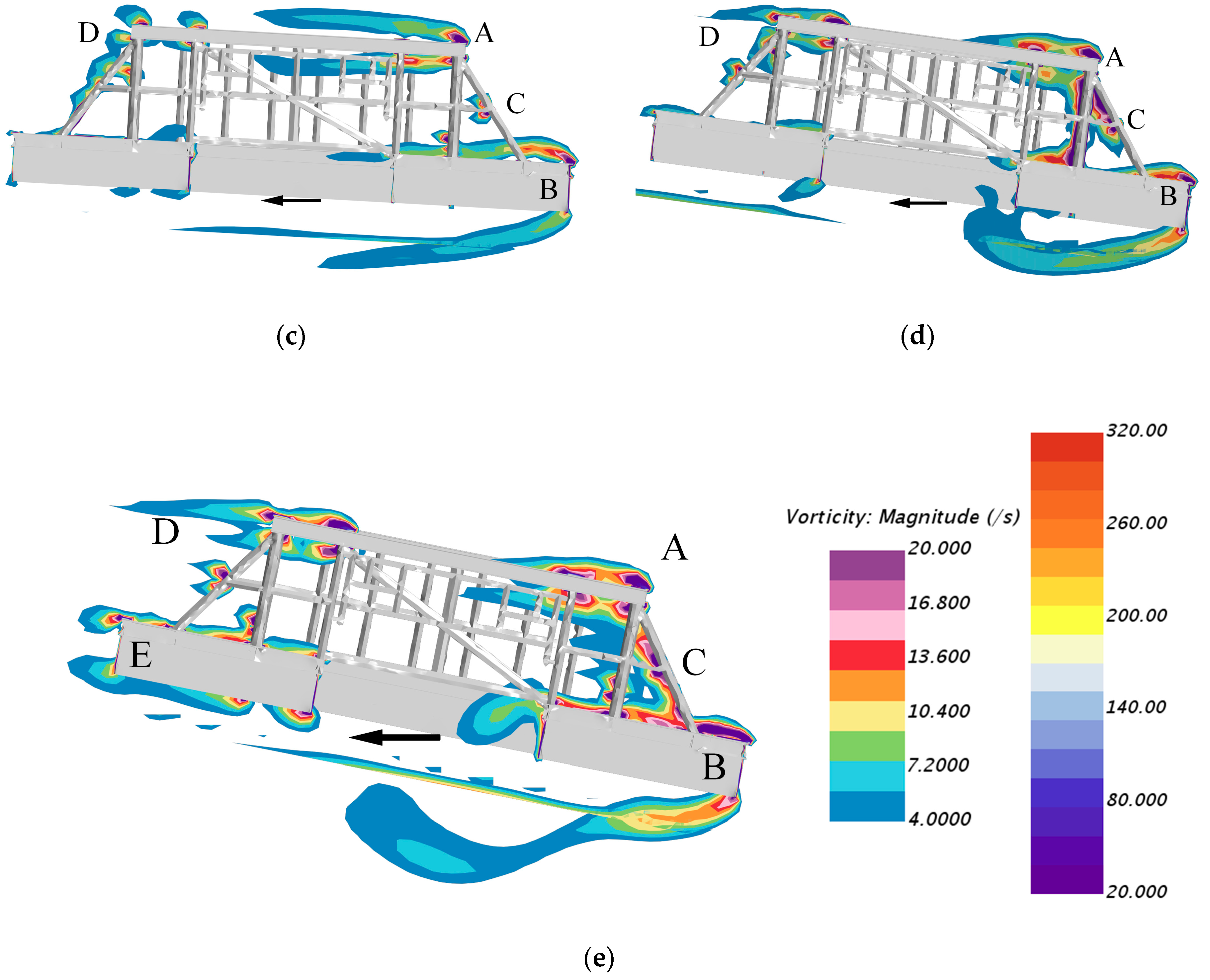
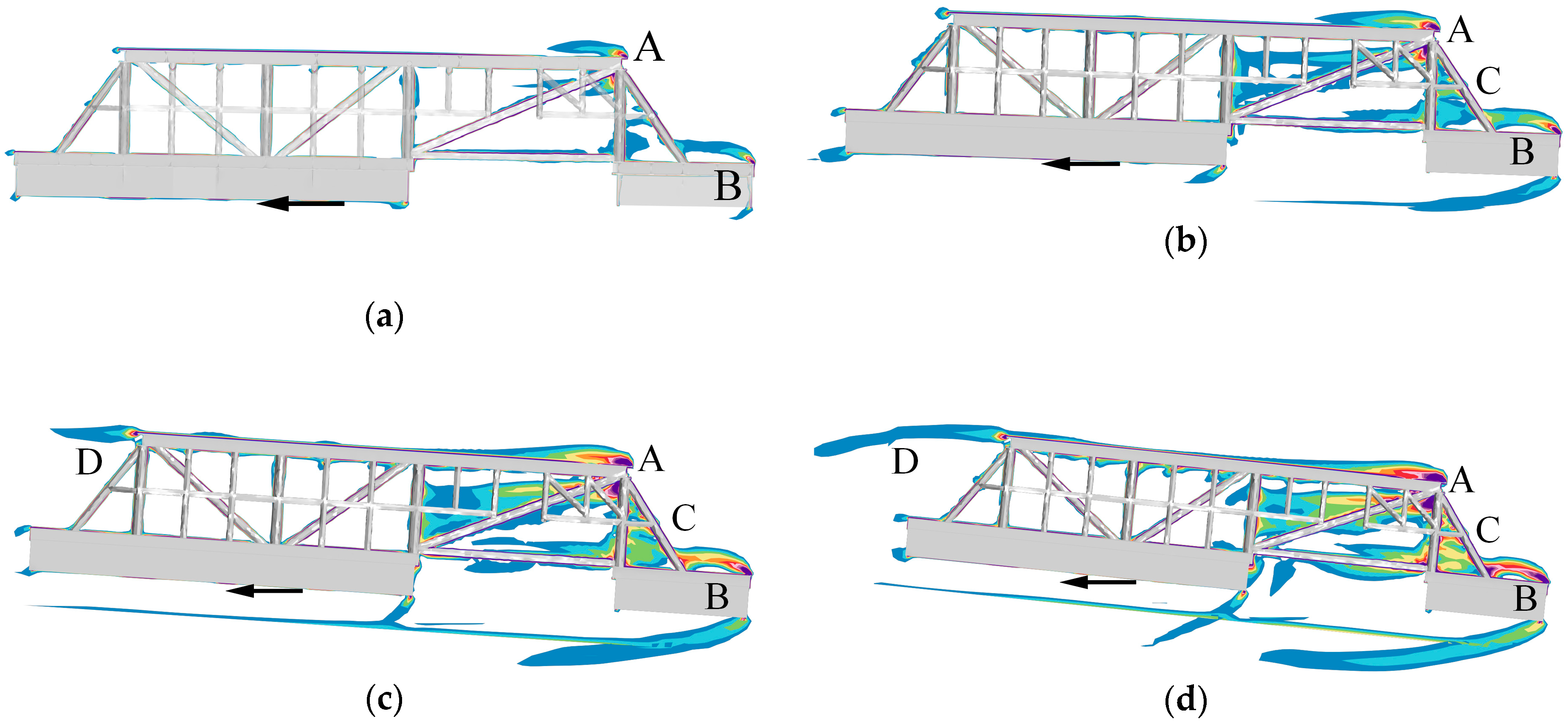
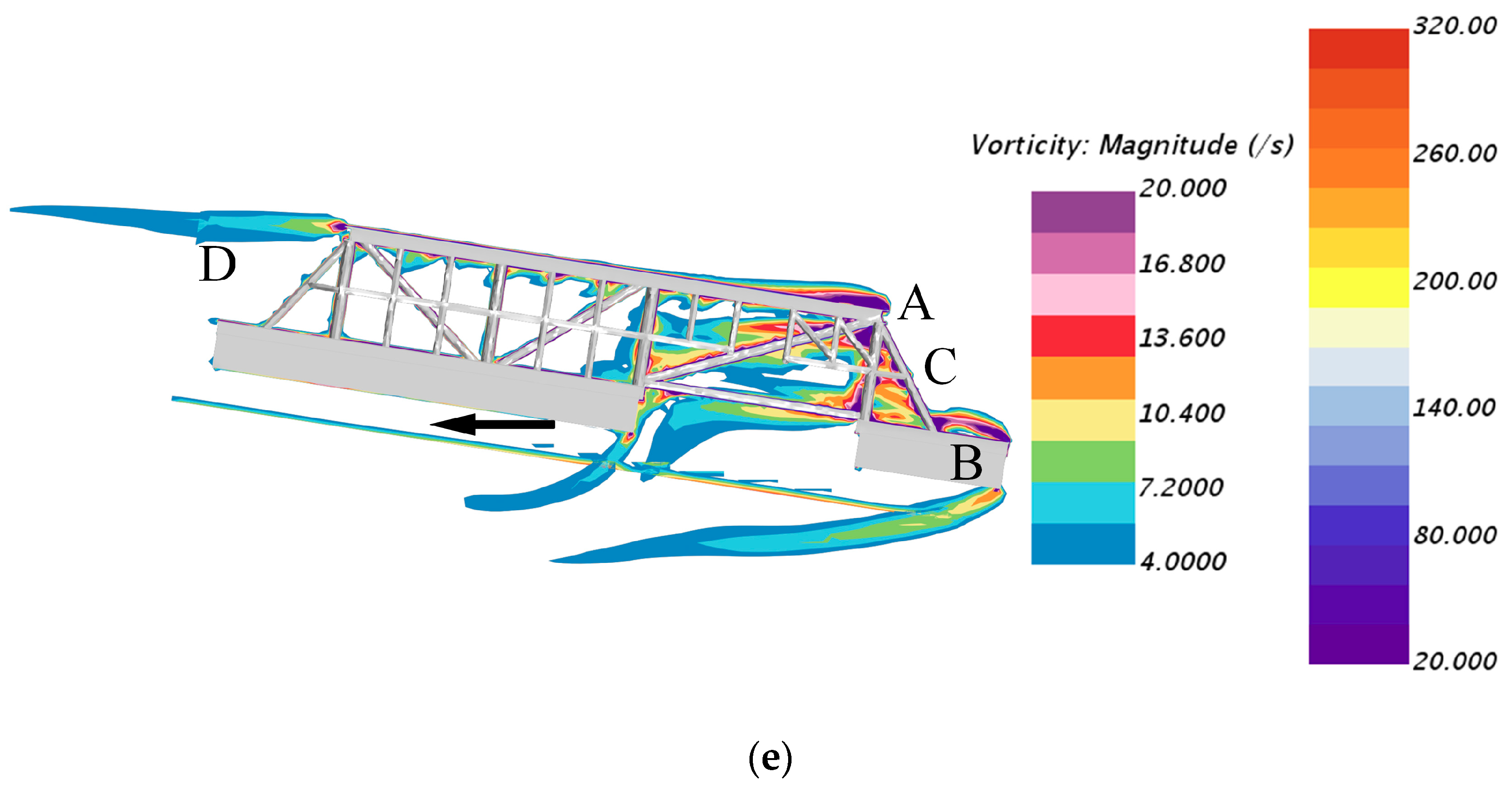
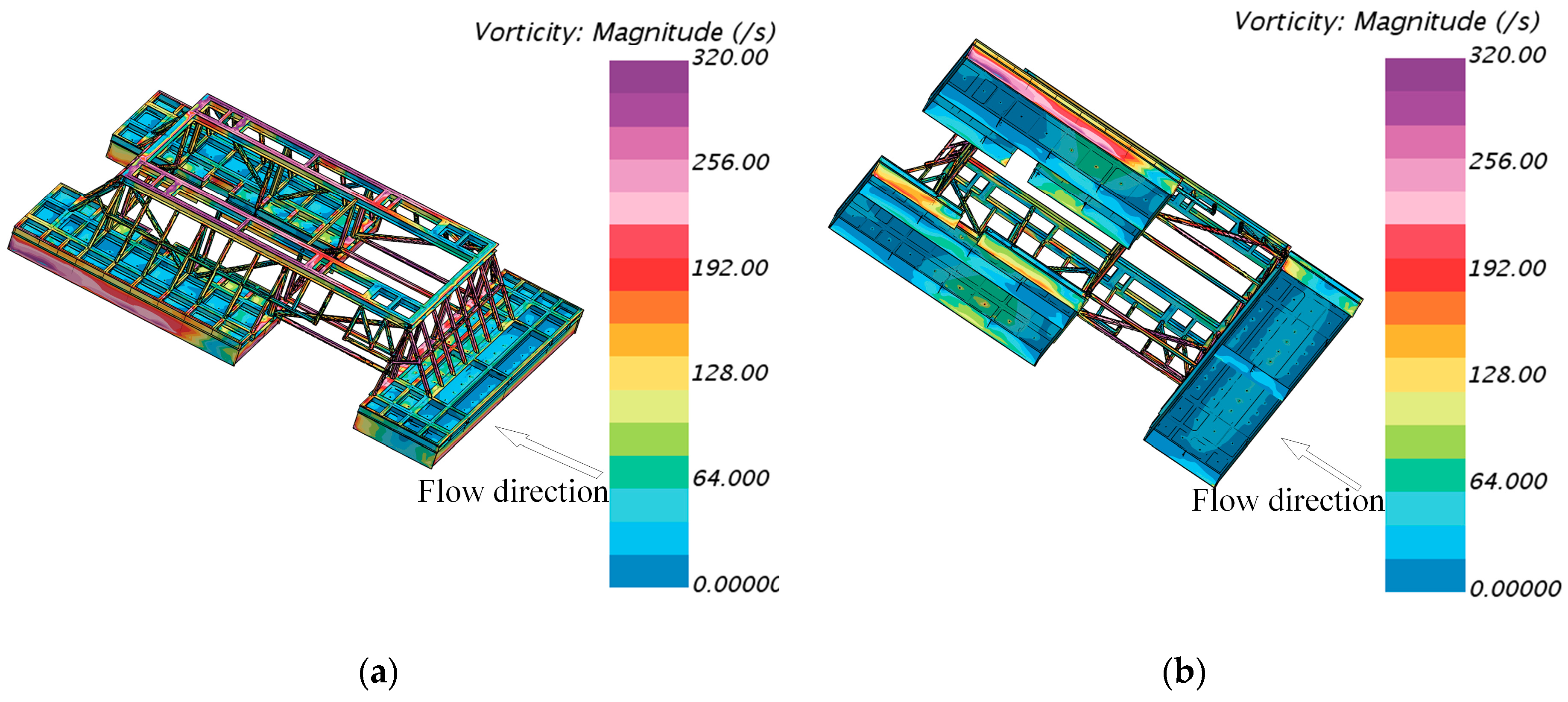
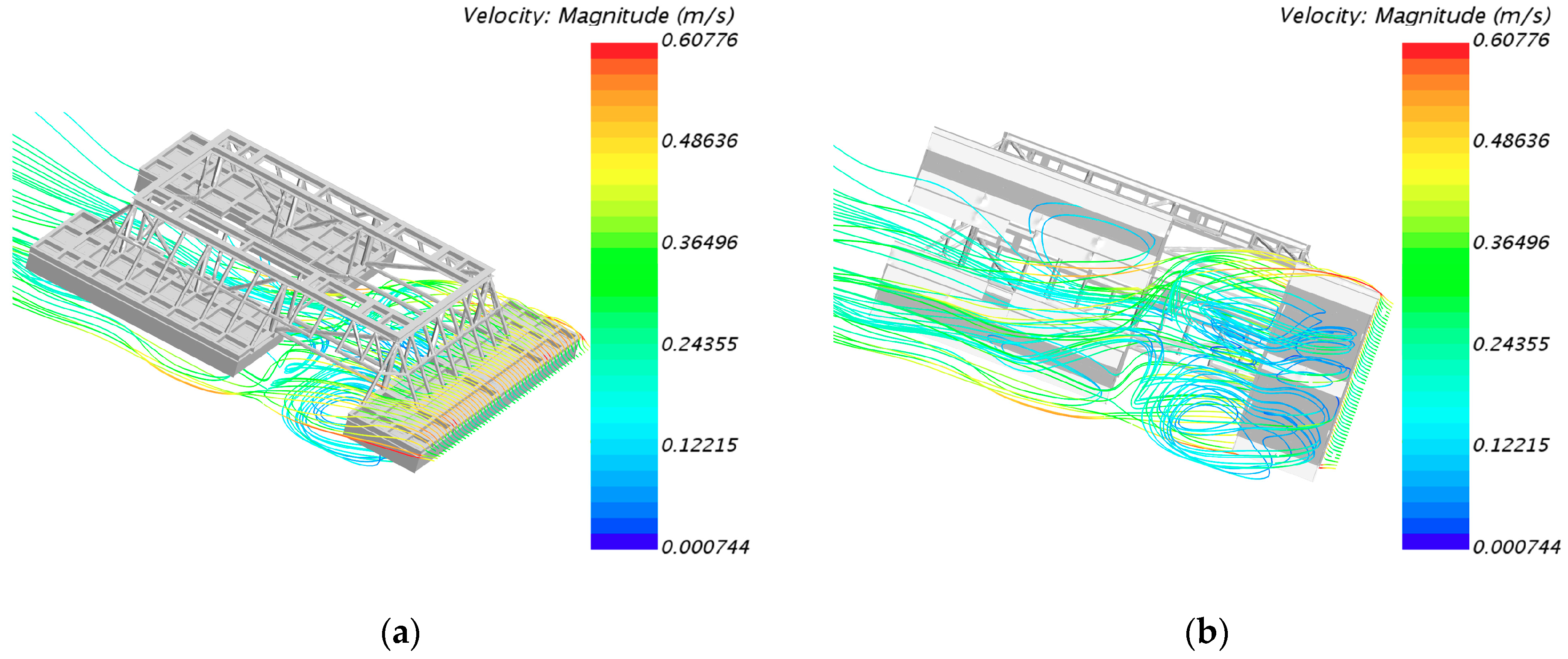
4.2. Detailed Vorticity Field Analysis
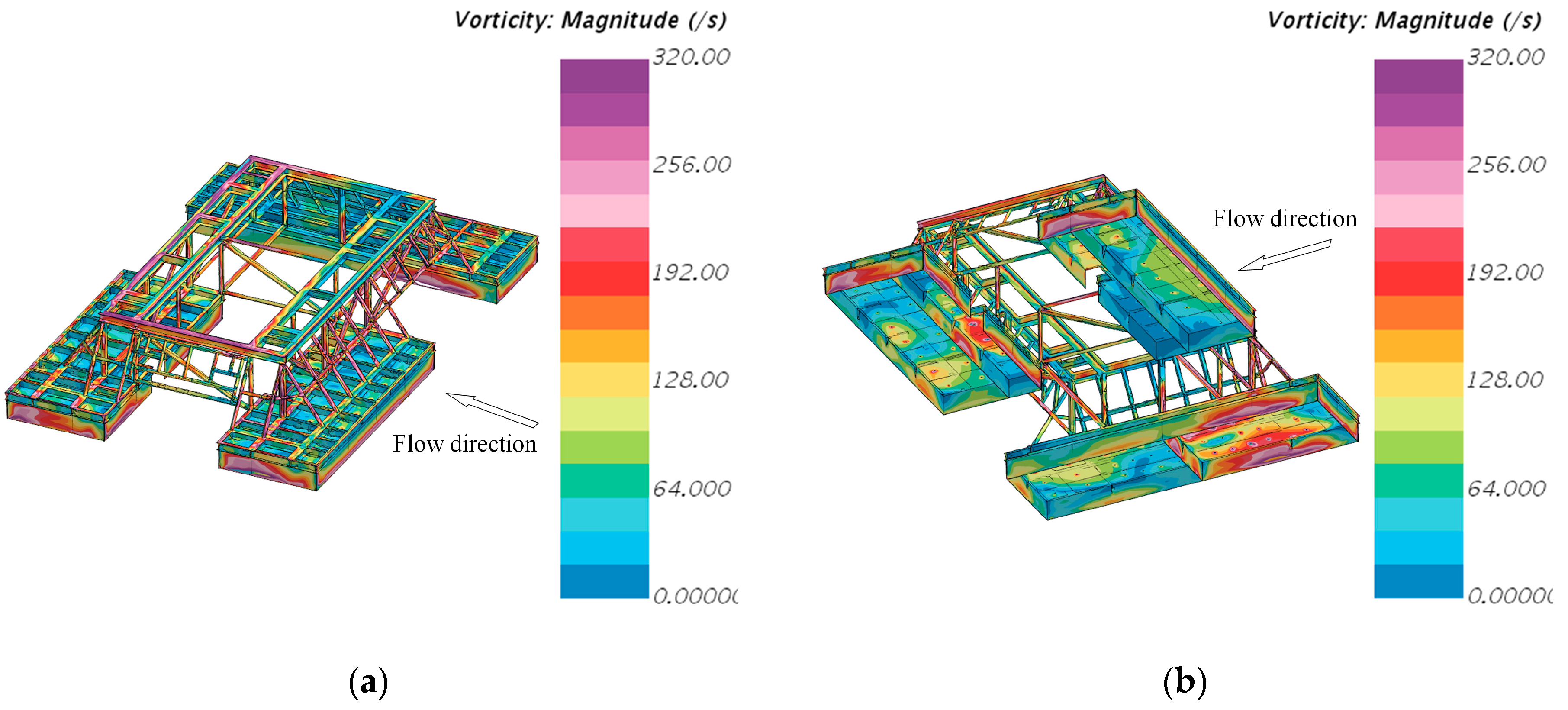
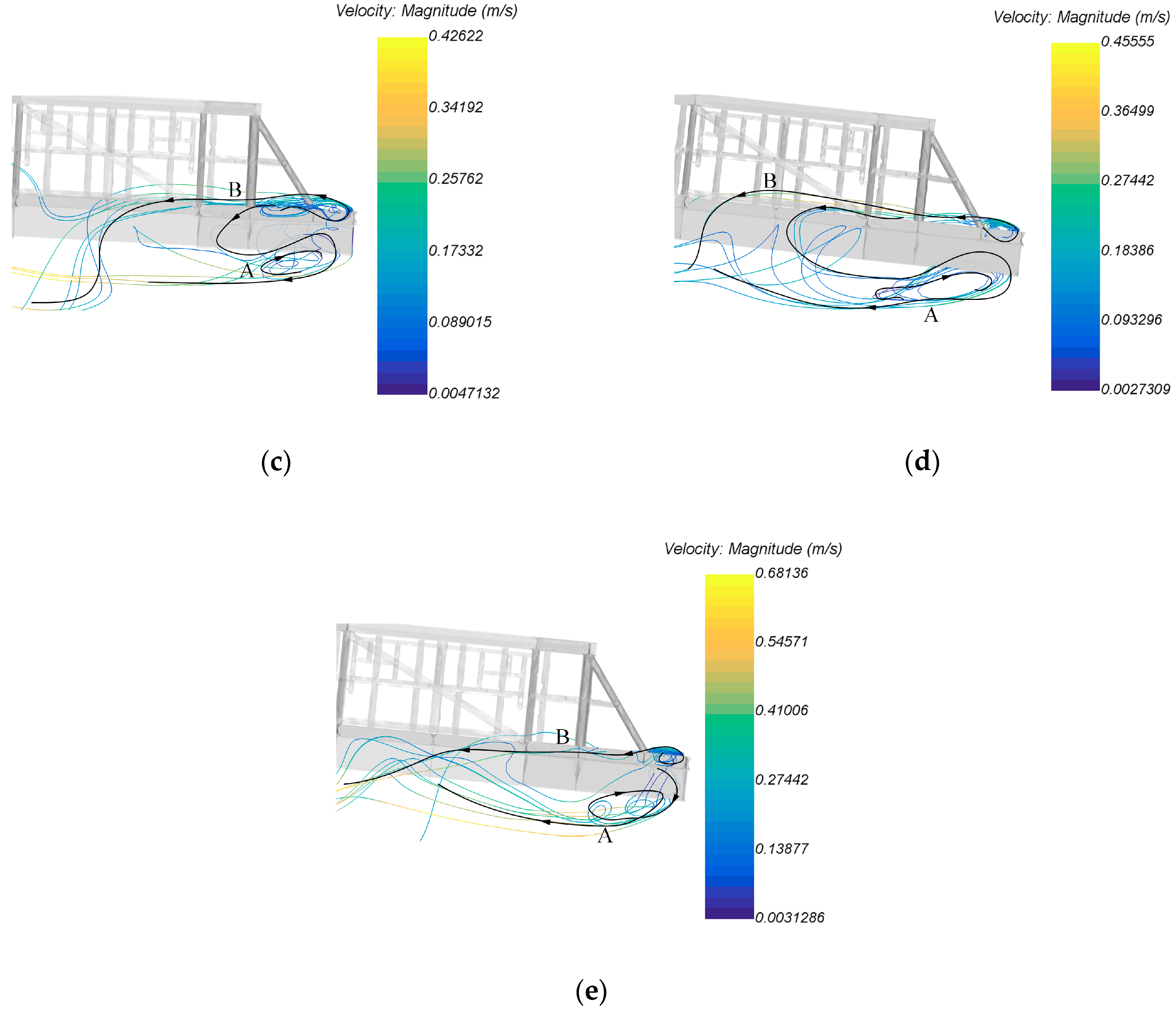
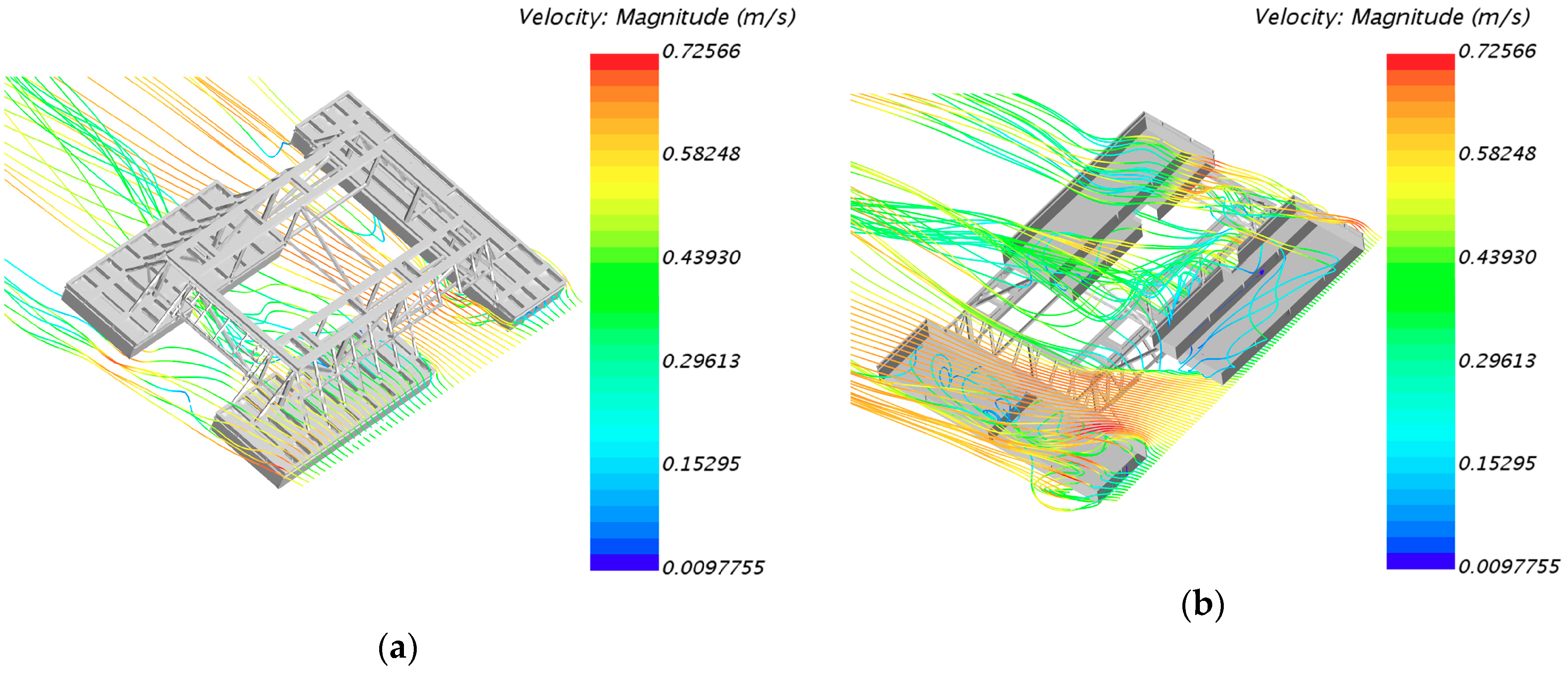
4.3. Detailed Flow Patterns Analysis
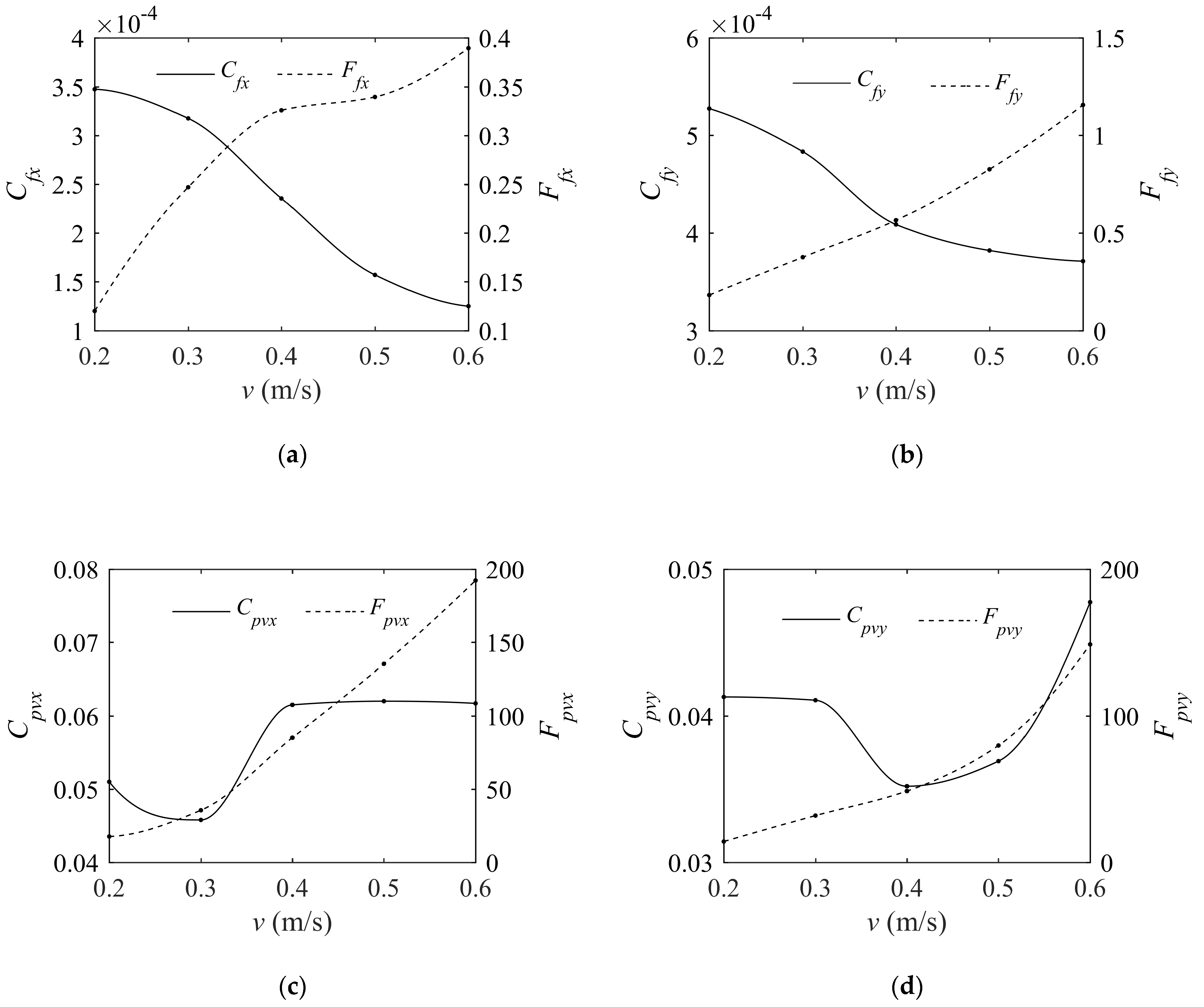
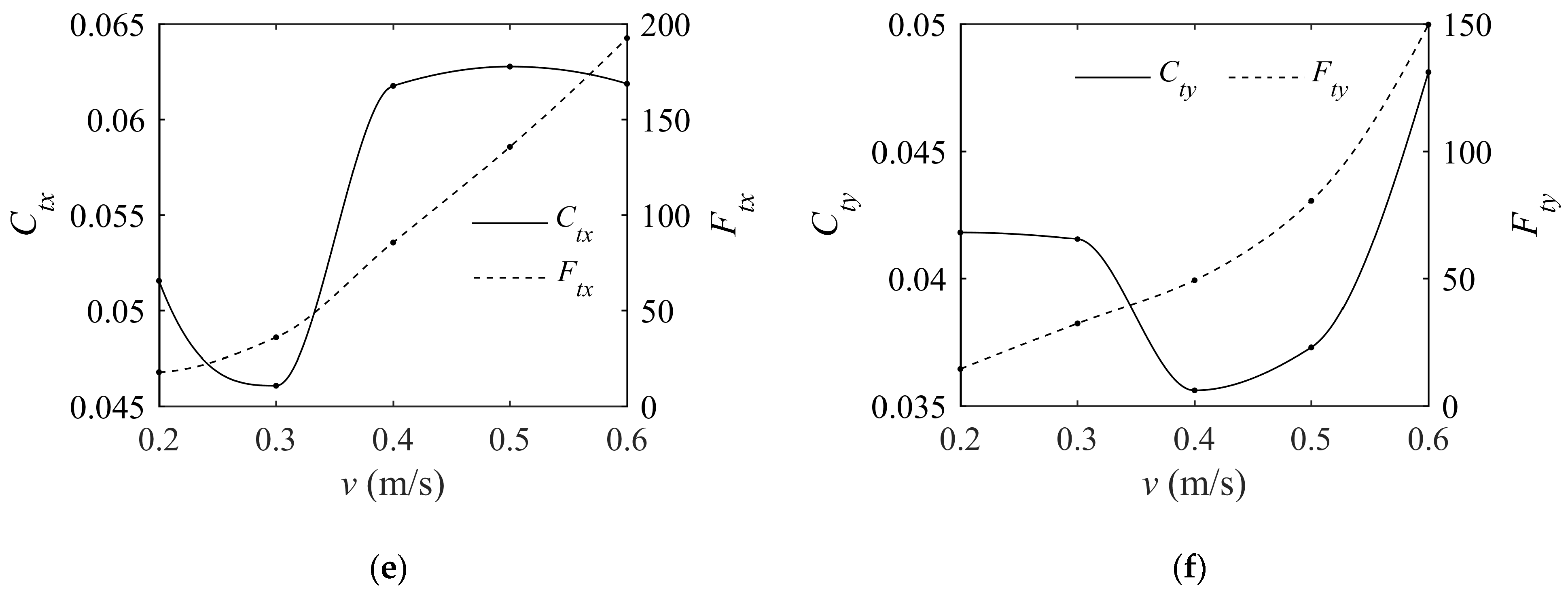
4.4. Resistance Component Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nam, B.W.; Kim, N.W.; Hong, S.Y. Experimental and numerical study on coupled motion responses of a floating crane vessel and a lifted subsea manifold in deep water. Int. J. Naval Archit. Ocean Eng. 2017, 9, 552–567. [Google Scholar] [CrossRef]
- Ramos, R.V.; Camponogara, E.; Martins, F.F.V.J. Design optimization of oilfield subsea infrastructures with manifold placement and pipeline layout. Comput. Chem. Eng. 2018, 108, 163–178. [Google Scholar] [CrossRef]
- Neto, E.D.A.; Jacovazzo, B.M.; Correa, F.N.; Jacob, B.P. Numerical evaluation of a subsea equipment installation method designed to avoid resonant responses. Appl. Ocean Res. 2019, 88, 288–305. [Google Scholar] [CrossRef]
- Olsen, T.A. Subsurface Towing of Heavy Module. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 6 January 2011. [Google Scholar]
- Risoey, T.; Mork, H.; Johnsgard, H.; Gramnaes, J. The pencil buoy method—A subsurface transportation and installation method. Offshore Technol. Conf. 2007, 30, 1–7. [Google Scholar] [CrossRef]
- Yamazu, T.; Haraguchi, K.; Inoue, T.; Arai, K. Development of a Highly Flexible and High-Resolution Deep-Towed Streamer. J. Mar. Sci. Eng. 2019, 7, 254. [Google Scholar] [CrossRef]
- Jacobsen, T. Subsurface Towing of a Subsea Module. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 6 June 2010. [Google Scholar]
- Kang, W.H.; Zhang, C.; Yu, J. Stochastic extreme motion analysis of jack-up responses during wet towing. Ocean Eng. 2016, 111, 56–66. [Google Scholar] [CrossRef]
- Zhang, P.; Peng, Y.; Ding, H.; Hu, R.; Shi, J. Numerical analysis of offshore integrated meteorological mast for wind farms during wet towing transportation. Ocean Eng. 2019, 188, 106271–106283. [Google Scholar] [CrossRef]
- Ding, H.; Hu, R.; Le, C. Towing Operation Methods of Offshore Integrated Meteorological Mast for Offshore Wind Farms. J. Mar. Sci. Eng. 2019, 7, 100. [Google Scholar] [CrossRef]
- Rattanasiri, P.; Wilson, P.A.; Phillips, A.B. Numerical investigation of a fleet of towed AUVs. Ocean Eng. 2014, 80, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Ye, J.; Yang, C.; Chen, Y.; Tian, H.; Xiong, X. Experimental study on a controllable underwater towed system. Ocean Eng. 2005, 32, 1803–1817. [Google Scholar] [CrossRef]
- Go, G.; Ahn, H.T. Hydrodynamic derivative determination based on CFD and motion simulation for a tow-fish. Appl. Ocean Res. 2019, 82, 191–209. [Google Scholar] [CrossRef]
- Sun, F.J.; Zhu, Z.H.; LaRosa, M. Dynamic modeling of cable towed body using nodal position finite element method. Ocean Eng. 2011, 38, 529–540. [Google Scholar] [CrossRef]
- Wu, J.; Chwang, A.T. Experimental investigation on a two-part underwater towed system. Ocean Eng. 2001, 28, 735–750. [Google Scholar] [CrossRef]
- Wu, J.; Chwang, A.T. Investigation on a two-part underwater manoeuvrable towed system. Ocean Eng. 2001, 28, 1079–1096. [Google Scholar] [CrossRef]
- Wu, J.; Chwang, A.T. A hydrodynamic model of a two-part underwater towed system. Ocean Eng. 2000, 27, 455–472. [Google Scholar] [CrossRef]
- Jacobsen, T.; Leira, B.J. Numerical and experimental studies of submerged towing of a subsea template. Ocean Eng. 2012, 42, 147–154. [Google Scholar] [CrossRef]
- Elkafas, A.G.; Elgohary, M.M.; Zeid, A.E. Numerical study on the hydrodynamic drag force of a container ship model. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- STAR-CCM+ Users’ Guide Version 13.04. In CD-Adapco, Computational Dynamics-Analysis & Design; Application Company Ltd.: Melville, NY, USA, 2018.
- Zhang, X.; Lin, Z.; Mancini, S.; Li, P.; Li, Z.; Liu, F. A Numerical Investigation on the Flooding Process of Multiple Compartments Based on the Volume of Fluid Method. J. Mar. Sci. Eng. 2019, 7, 211. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, H.; Zou, J.; Hu, A.; Yang, J. Experimental and numerical investigations on hydrodynamic and aerodynamic characteristics of the tunnel of planing trimaran. Appl. Ocean Res. 2017, 63, 1–10. [Google Scholar] [CrossRef]
- Gao, T.; Wang, Y.; Pang, Y.; Chen, Q.; Tang, Y. A time-efficient CFD approach for hydrodynamic coefficient determination and model simplification of submarine. Ocean Eng. 2018, 154, 16–26. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, H.; Zhou, Q. Numerical Prediction of Submarine Hydrodynamic Coefficients using CFD Simulation. J. Hydrodyn. 2012, 24, 840–847. [Google Scholar] [CrossRef]
- Saranjam, B. Experimental and numerical investigation of an unsteady supercavitating moving body. Ocean Eng. 2013, 59, 9–14. [Google Scholar] [CrossRef]
- Maki, K.J.; Broglia, R.; Doctors, L.J.; Di Mascio, A. Numerical investigation of the components of calm-water resistance of a surface-effect ship. Ocean Eng. 2013, 72, 375–385. [Google Scholar] [CrossRef]
- Molin, B. Hydrodynamique Des Structures Offshore, 1st ed.; National Defense Industry Press: Beijing, China, 2012; pp. 100–103. [Google Scholar]
- Cantwell, B.; Coles, D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 1983, 136, 321–374. [Google Scholar] [CrossRef] [Green Version]



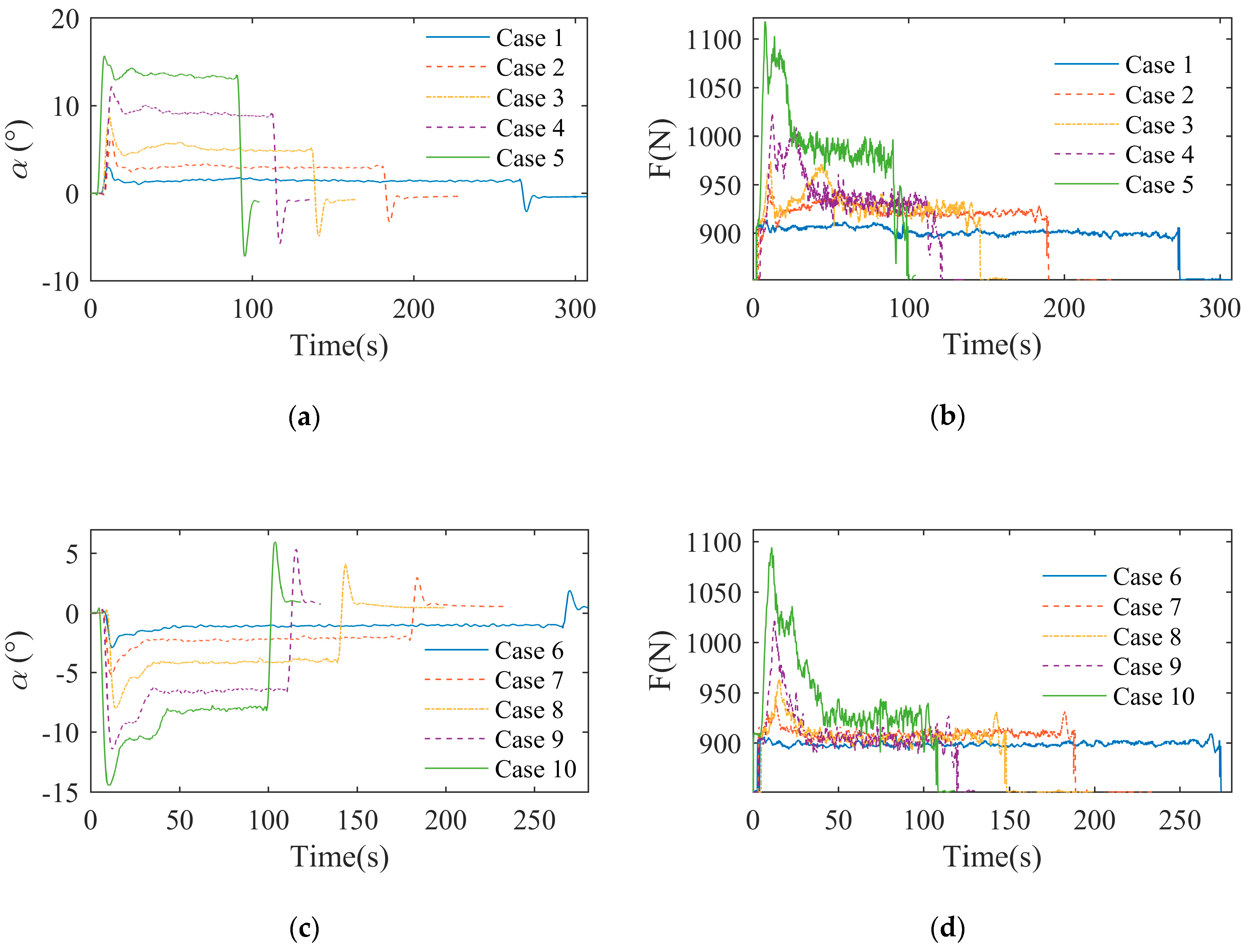




| Towing Direction: X | Velocity/m·s−1 | Towing Direction: Y | Velocity/m·s−1 |
|---|---|---|---|
| Case 1 | 0.2 | Case 6 | −0.2 |
| Case 2 | 0.3 | Case 7 | −0.3 |
| Case 3 | 0.4 | Case 8 | −0.4 |
| Case 4 | 0.5 | Case 9 | −0.5 |
| Case 5 | 0.6 | Case 10 | −0.6 |
| Velocity/m·s−1 | ||||||
|---|---|---|---|---|---|---|
| 0.2 | 2.607 | 2.603 | 0.15 | 1.490 | 1.063 | 28.7 |
| 0.3 | 1.180 | 1.167 | 1.1 | 2.794 | 2.168 | 22.4 |
| 0.4 | 0.667 | 0.652 | 2.2 | 5.301 | 4.072 | 23.2 |
| 0.5 | 0.431 | 0.419 | 2.8 | 9.053 | 6.535 | 27.8 |
| 0.6 | 0.316 | 0.299 | 5.4 | 13.430 | 9.073 | 32.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zan, Y.; Guo, R.; Yuan, L.; Wu, Z. Experimental and Numerical Model Investigations of the Underwater Towing of a Subsea Module. J. Mar. Sci. Eng. 2019, 7, 384. https://doi.org/10.3390/jmse7110384
Zan Y, Guo R, Yuan L, Wu Z. Experimental and Numerical Model Investigations of the Underwater Towing of a Subsea Module. Journal of Marine Science and Engineering. 2019; 7(11):384. https://doi.org/10.3390/jmse7110384
Chicago/Turabian StyleZan, Yingfei, Ruinan Guo, Lihao Yuan, and Zhaohui Wu. 2019. "Experimental and Numerical Model Investigations of the Underwater Towing of a Subsea Module" Journal of Marine Science and Engineering 7, no. 11: 384. https://doi.org/10.3390/jmse7110384
APA StyleZan, Y., Guo, R., Yuan, L., & Wu, Z. (2019). Experimental and Numerical Model Investigations of the Underwater Towing of a Subsea Module. Journal of Marine Science and Engineering, 7(11), 384. https://doi.org/10.3390/jmse7110384





