Loads and Response of a Tension Leg Platform Wind Turbine with Non-Rotating Blades: An Experimental Study
Abstract
:1. Introduction
2. Materials and Methods
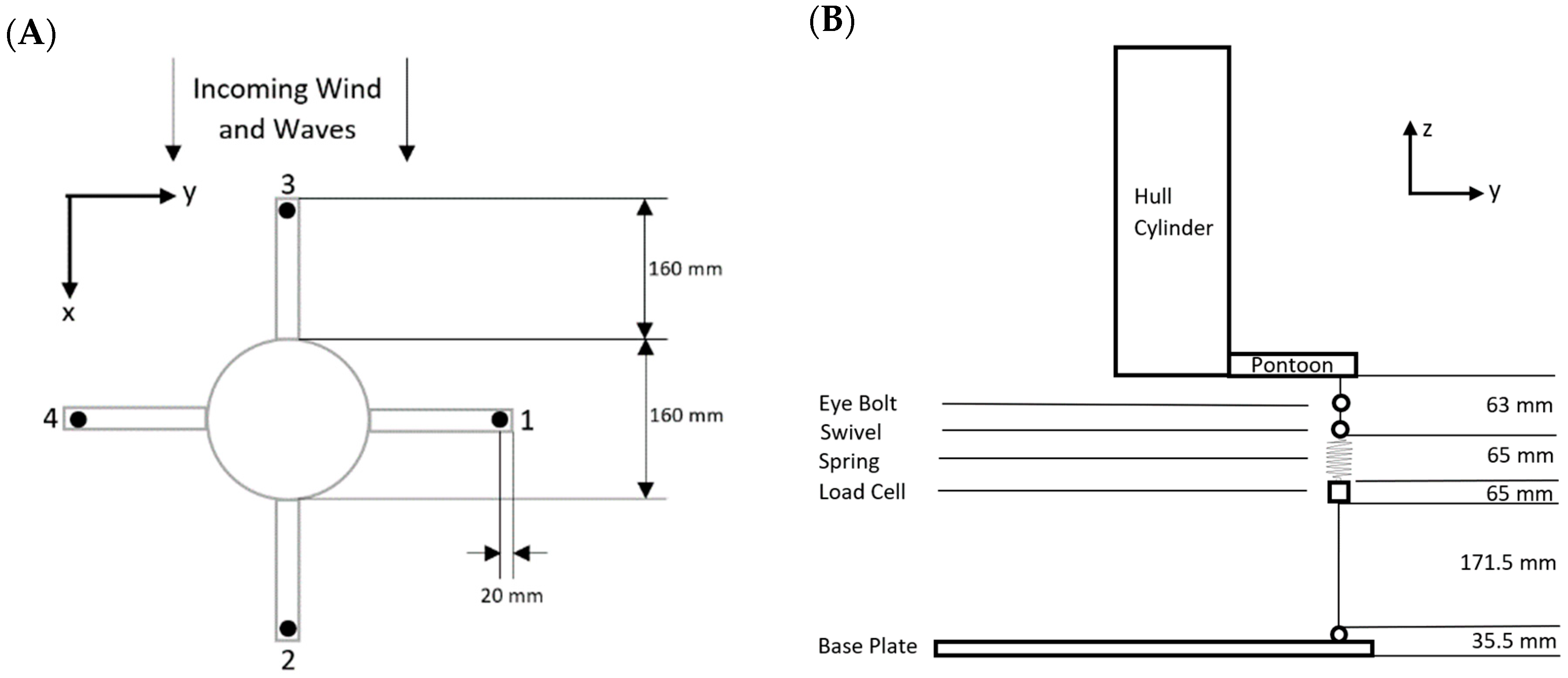
2.1. TLP Model Description
2.2. Turbine Model Description
2.3. TLPWT Model Construction
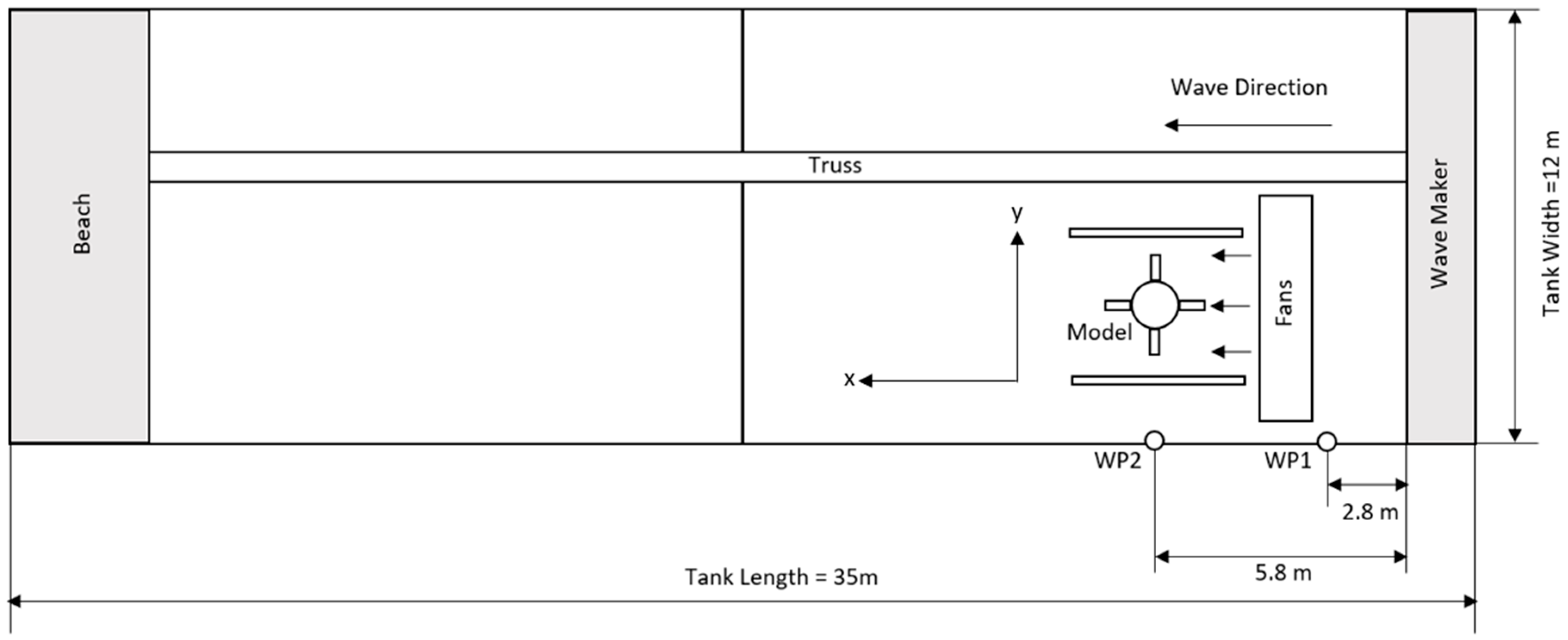
2.4. Experimental Setup and Test Matrix
3. Model Calibrations
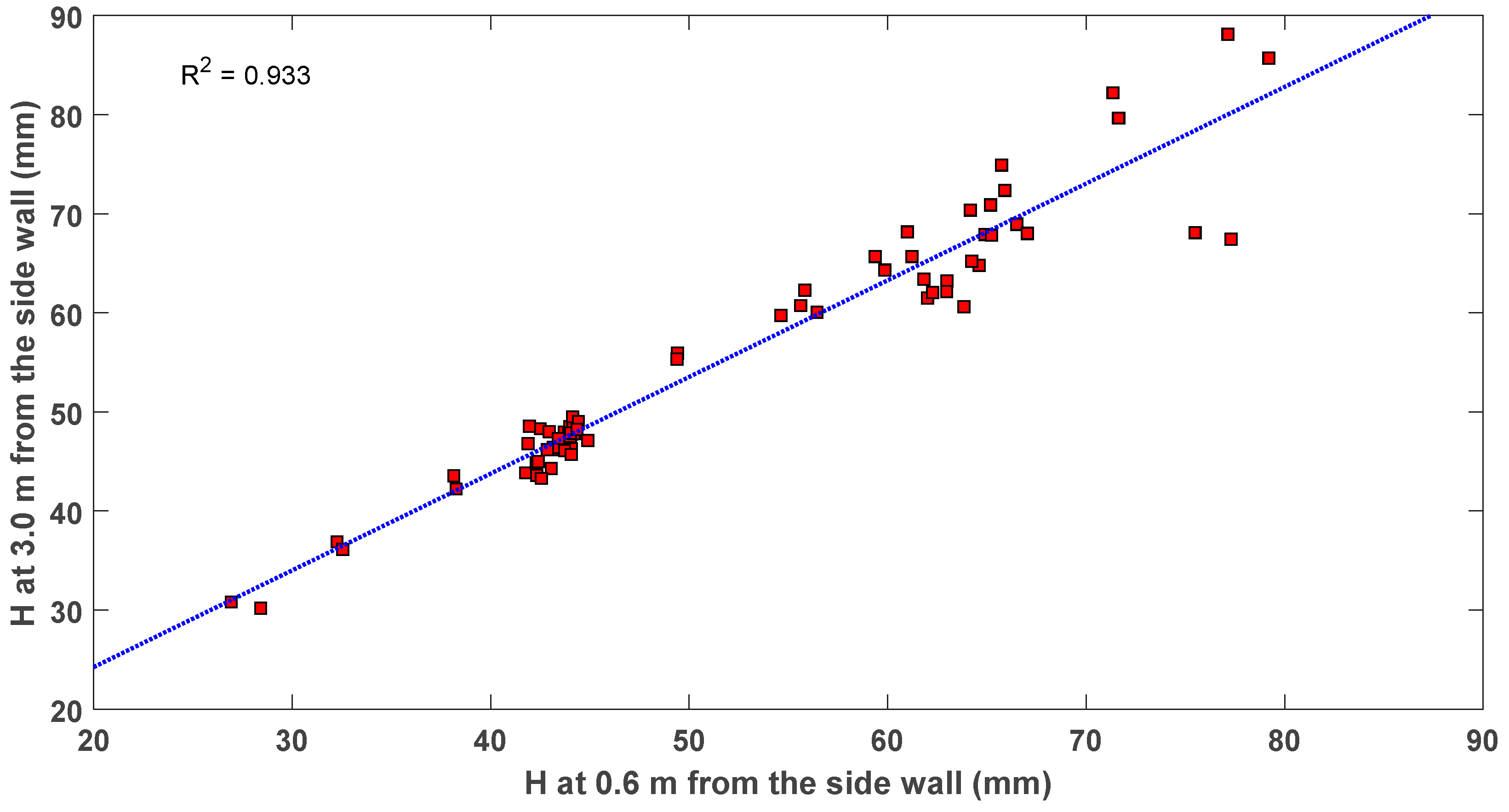
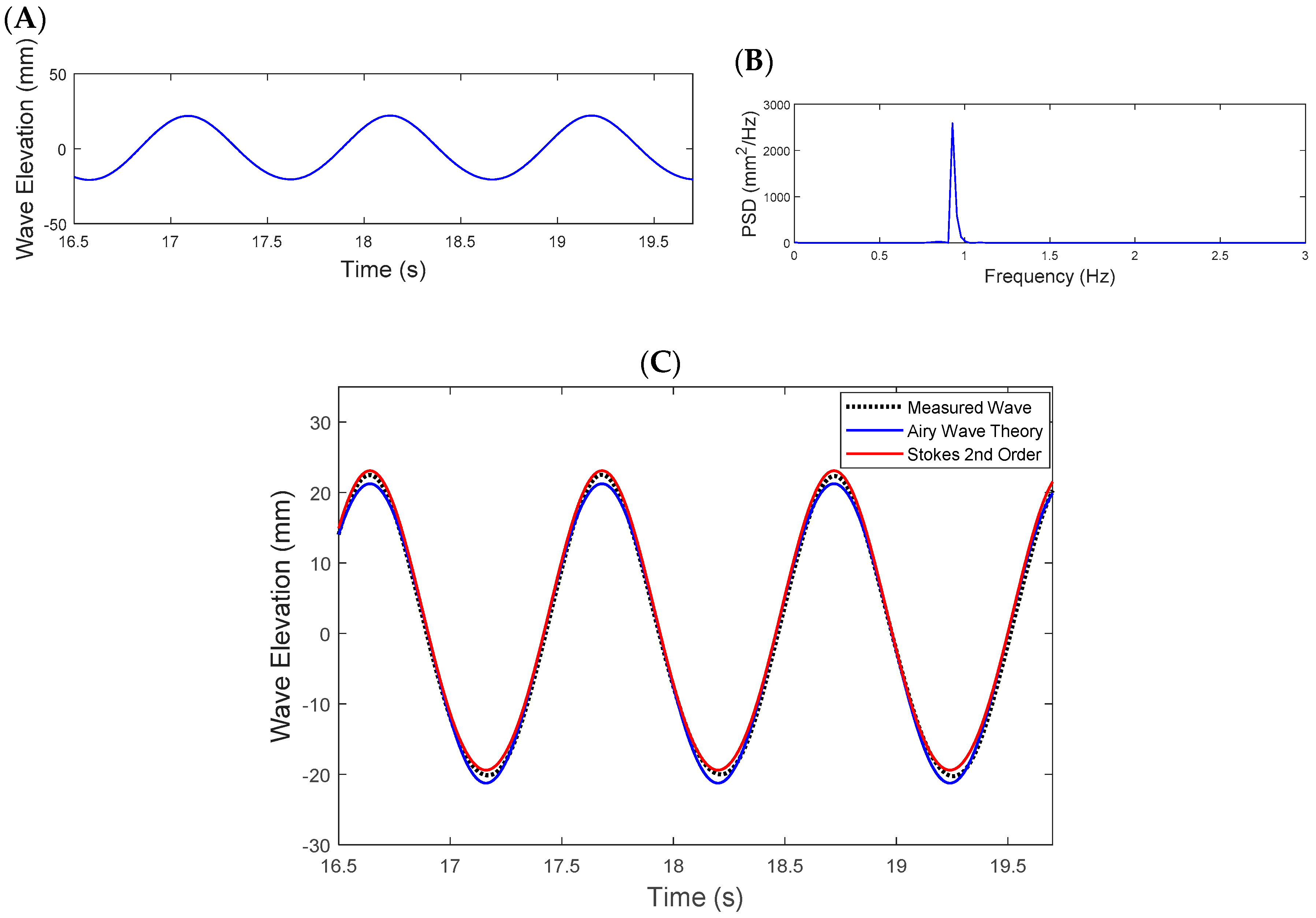
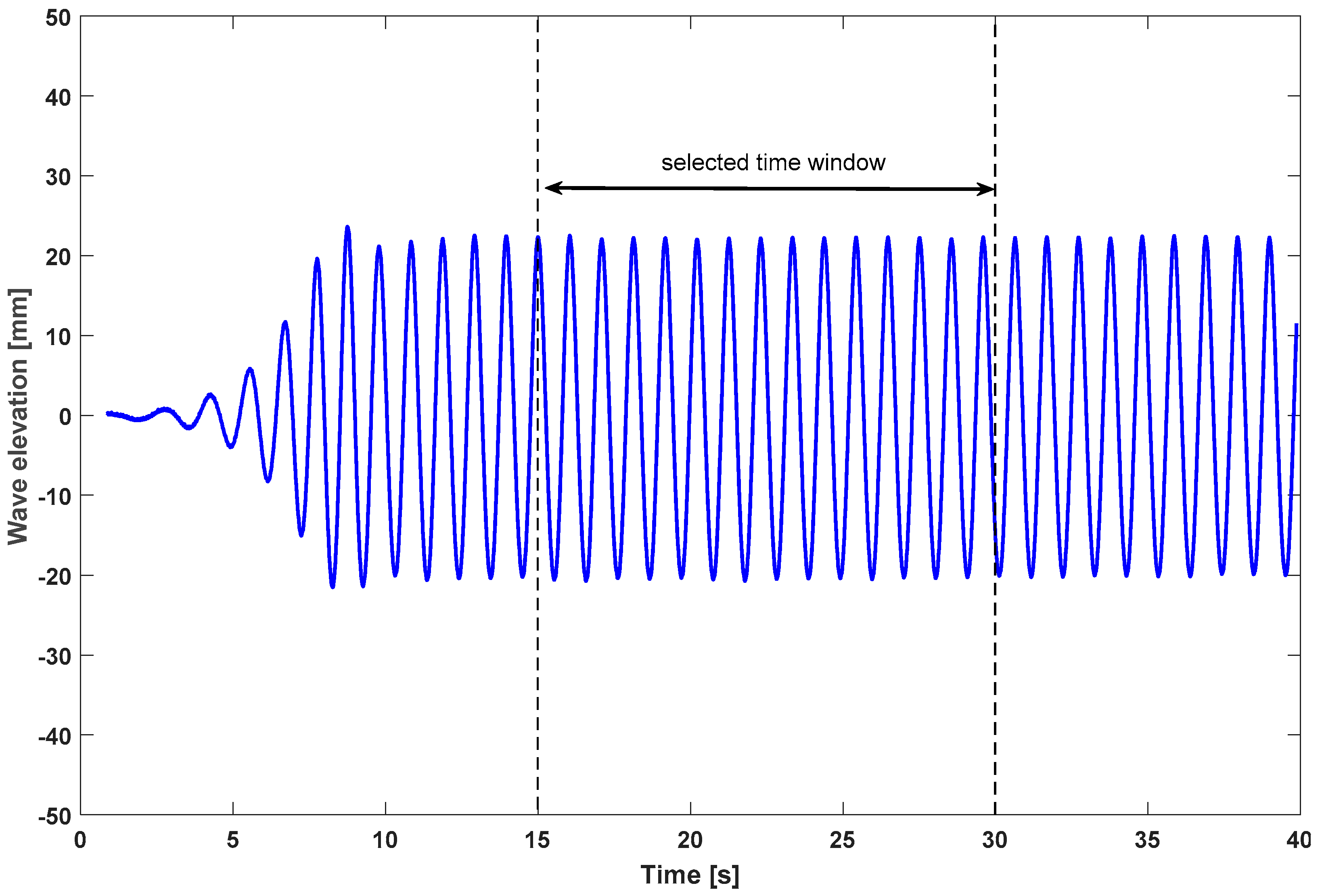
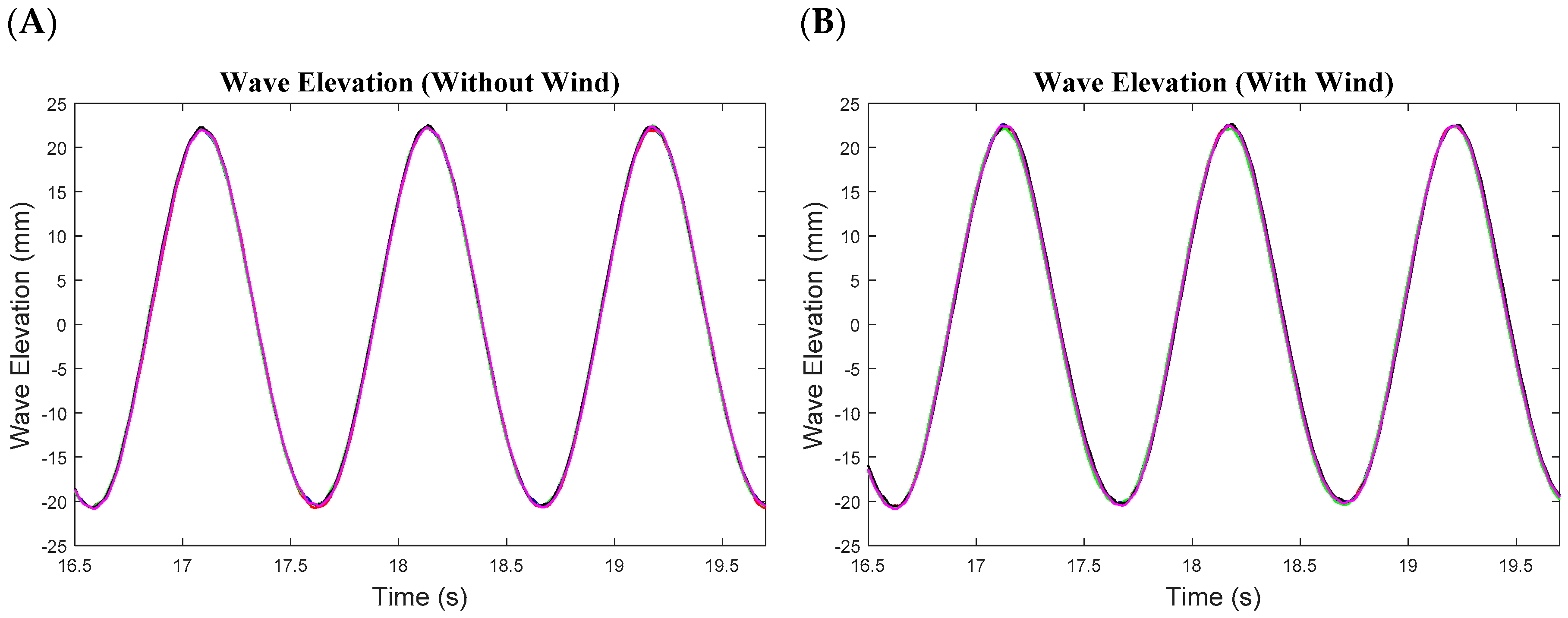
3.1. Wave Calibration
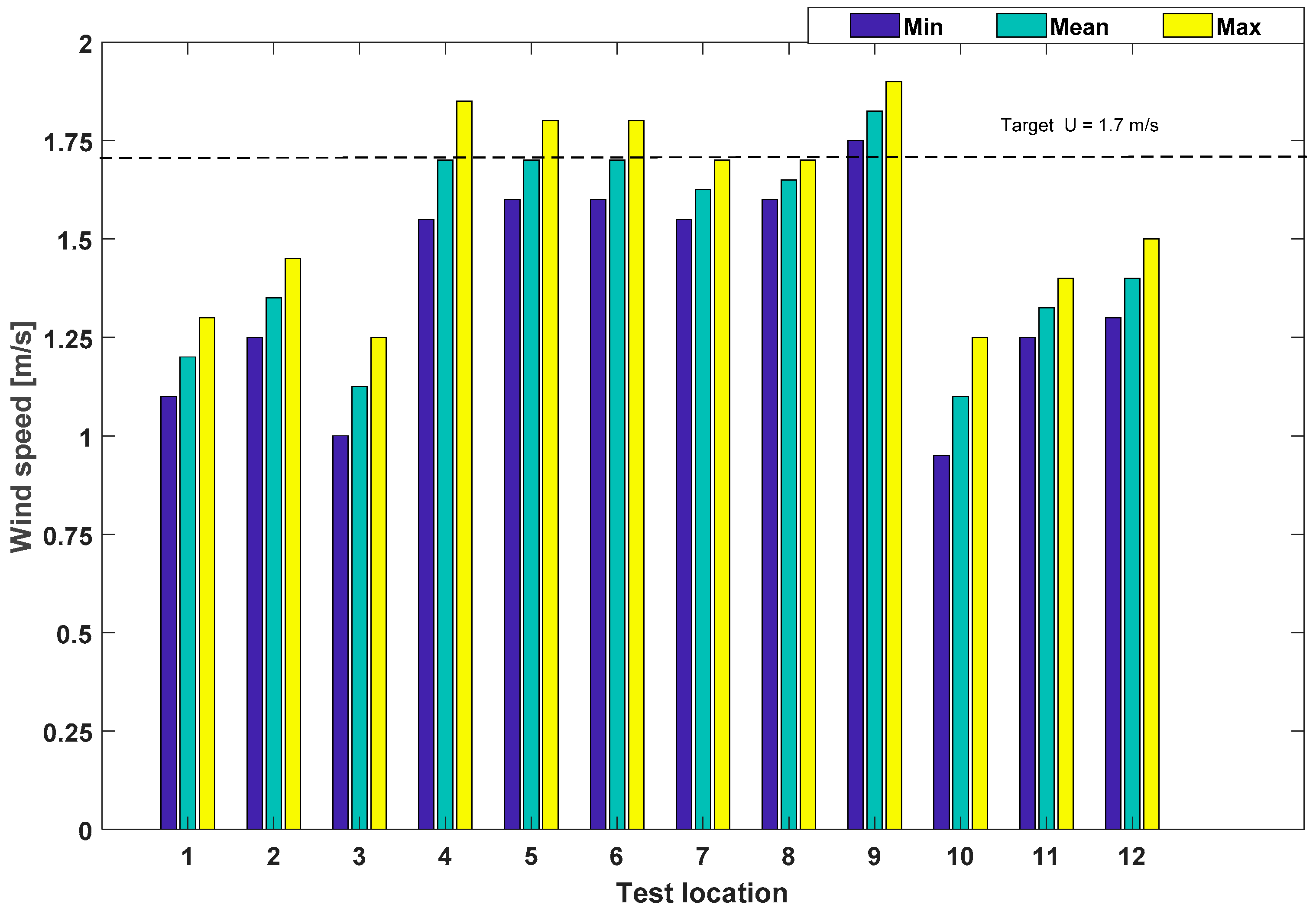
3.2. Wind Calibration
3.3. Free Decay Tests
3.4. Data Analysis
4. Results and Discussion
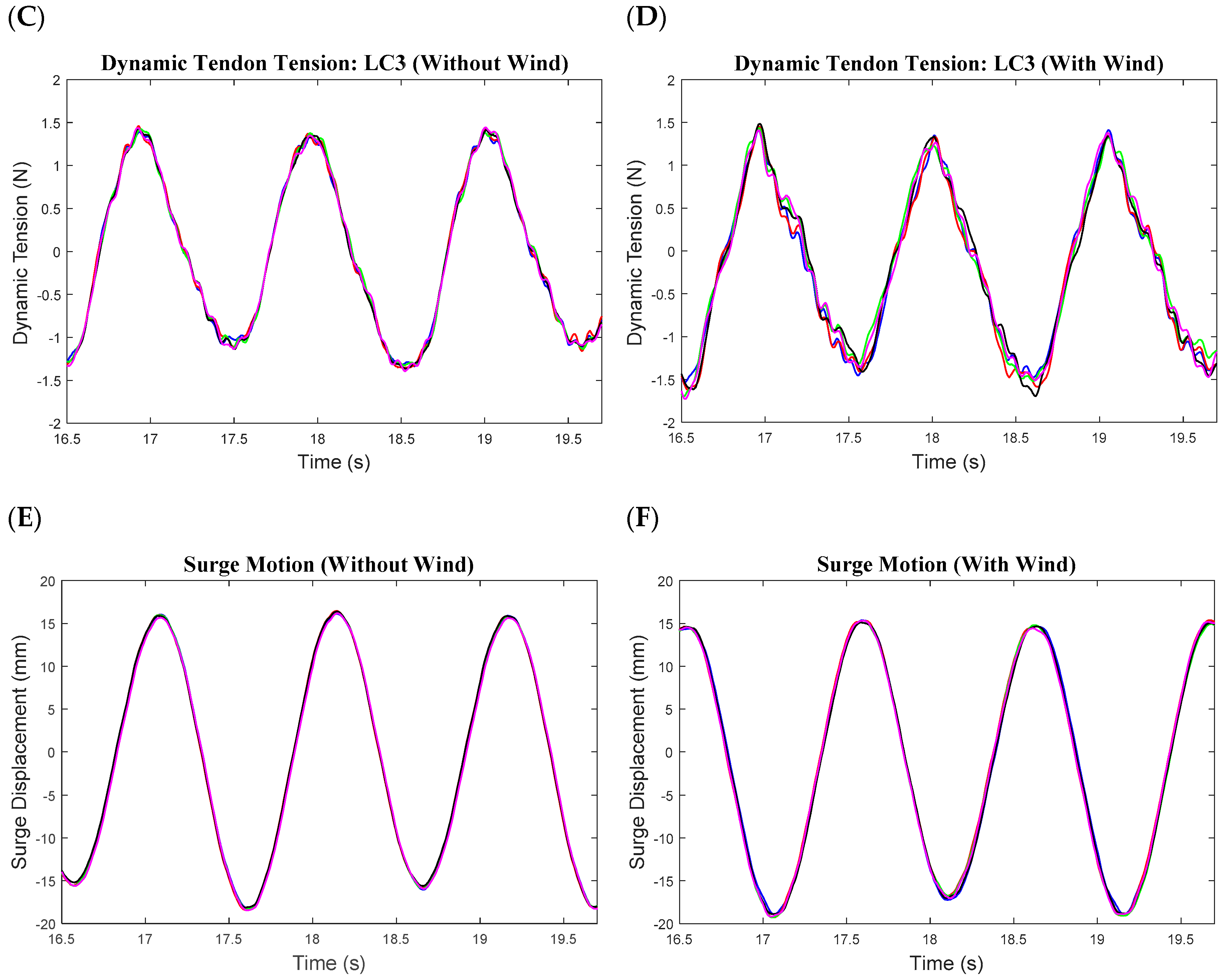
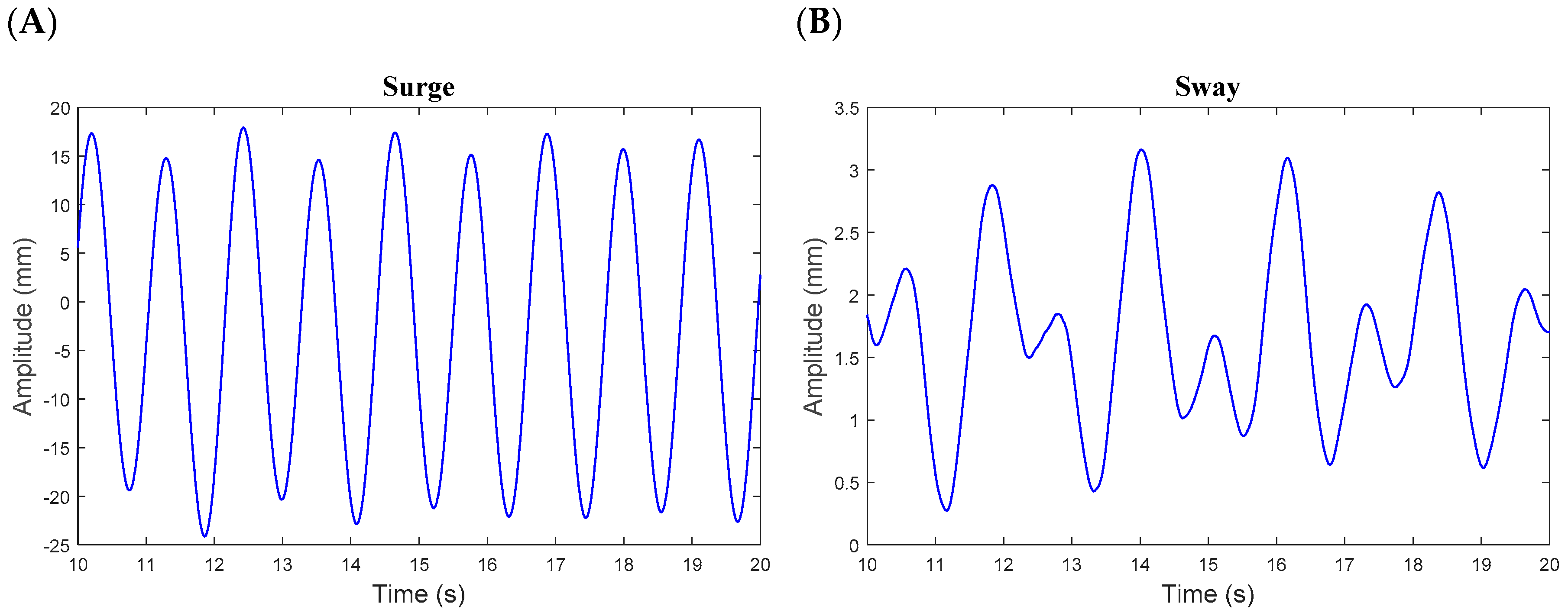
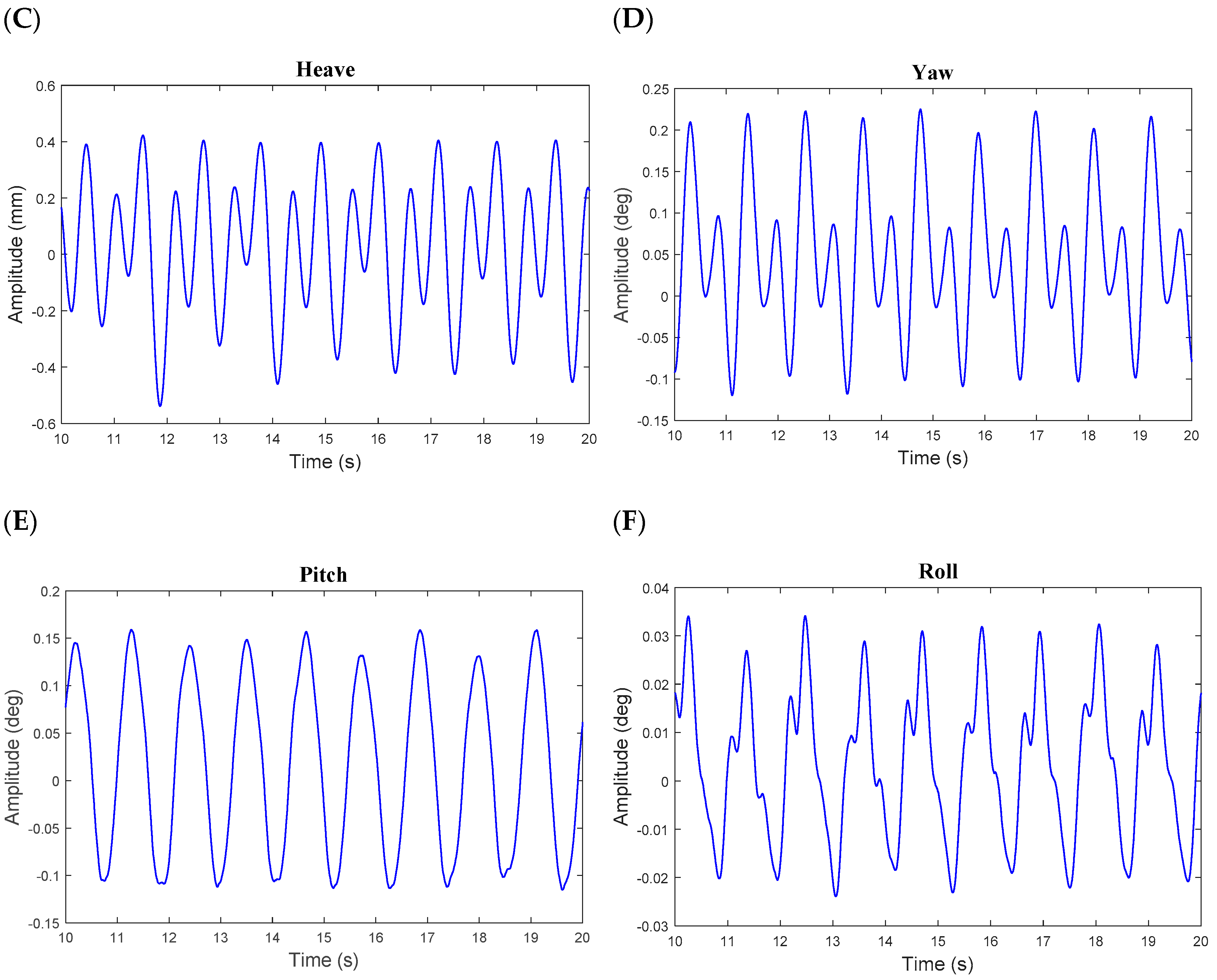
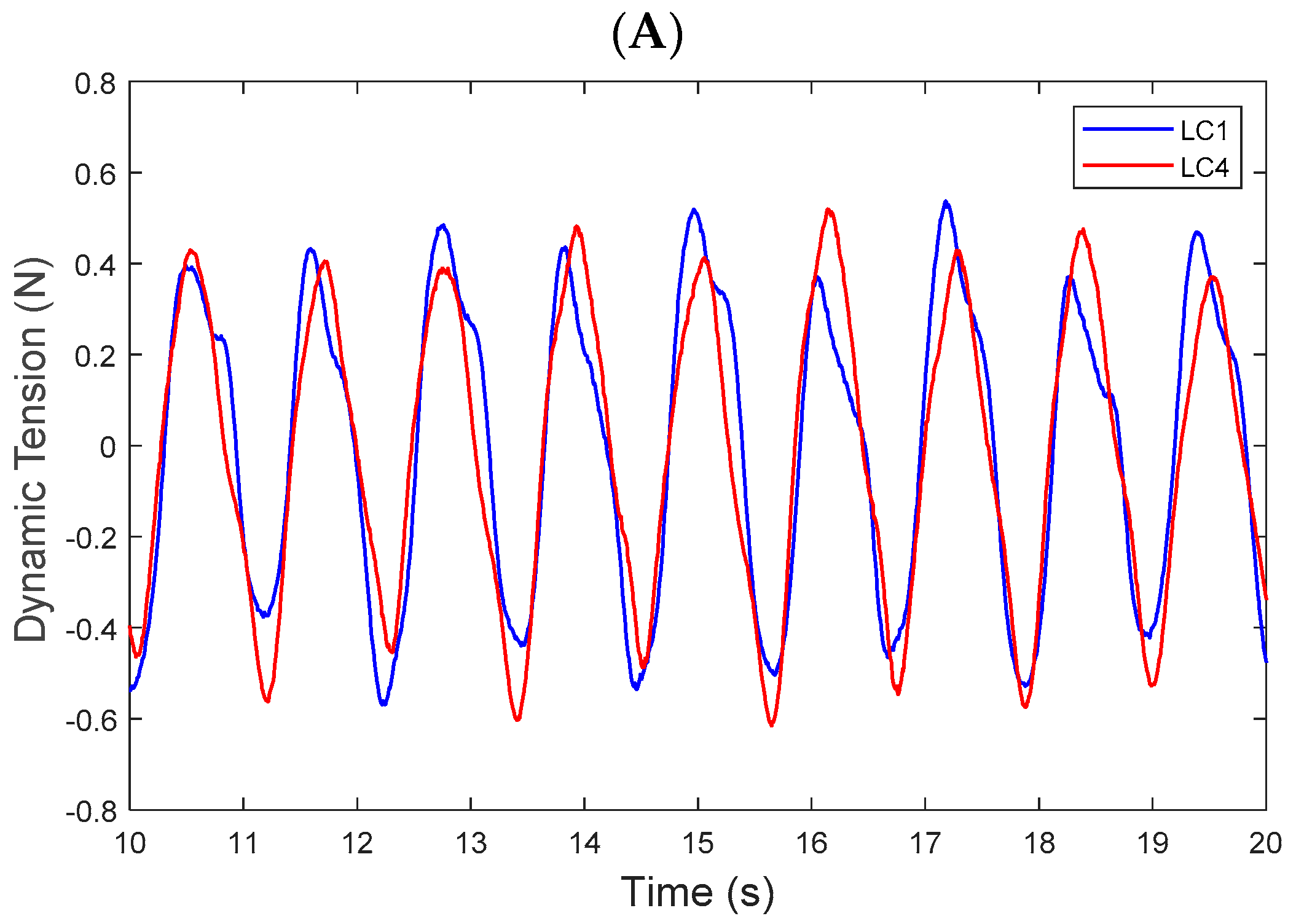
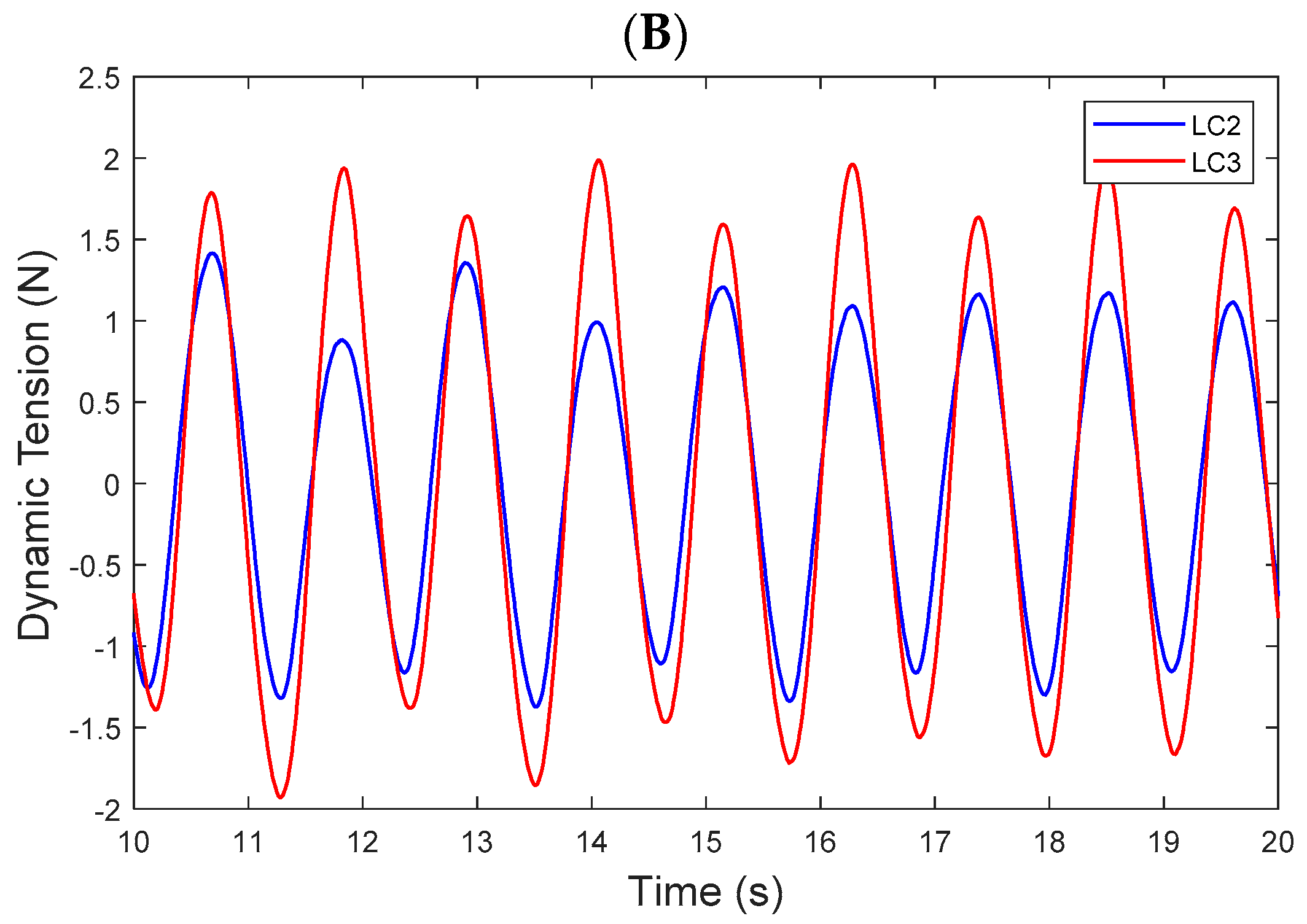
4.1. Time Series of Motion and Tendon Responses
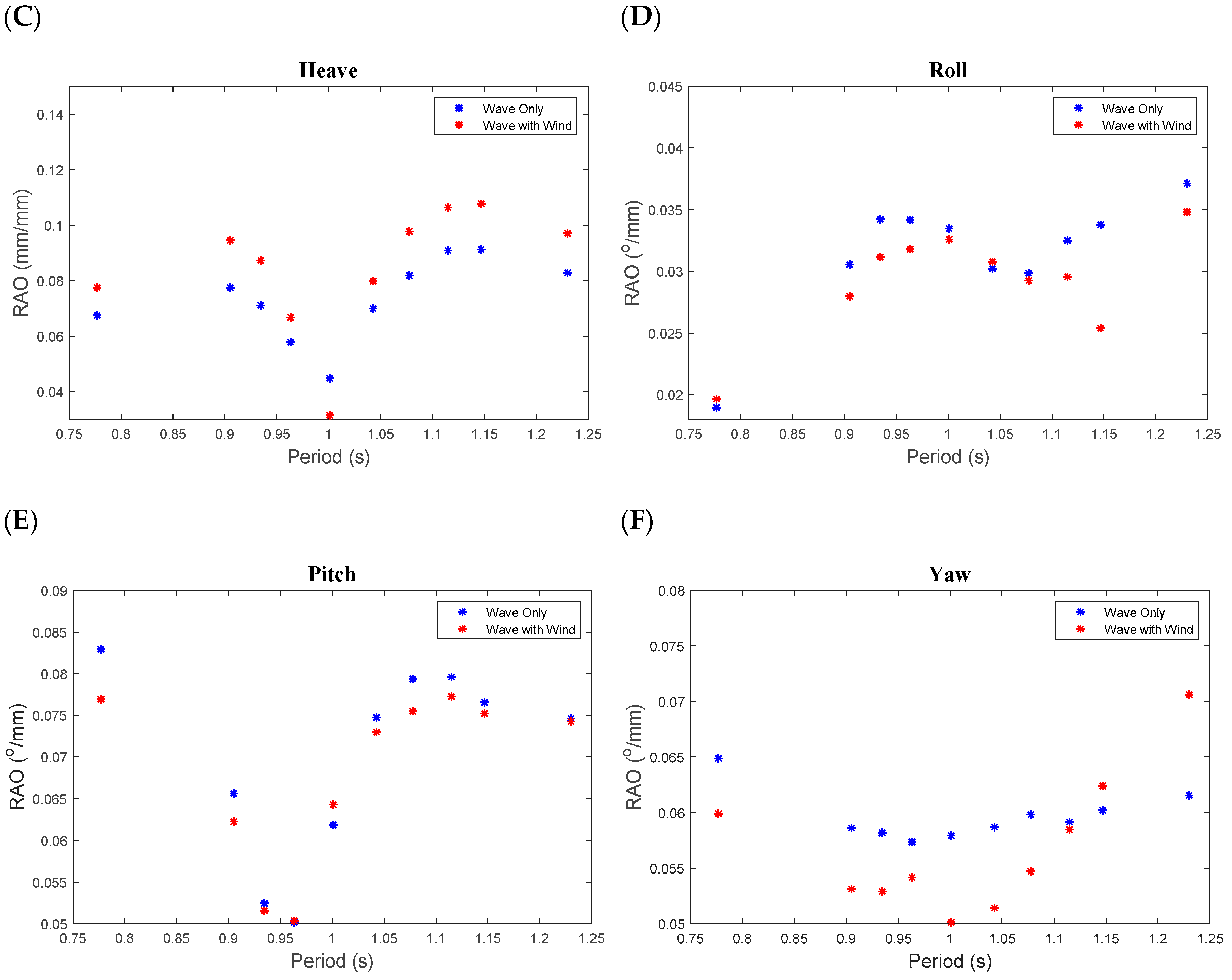
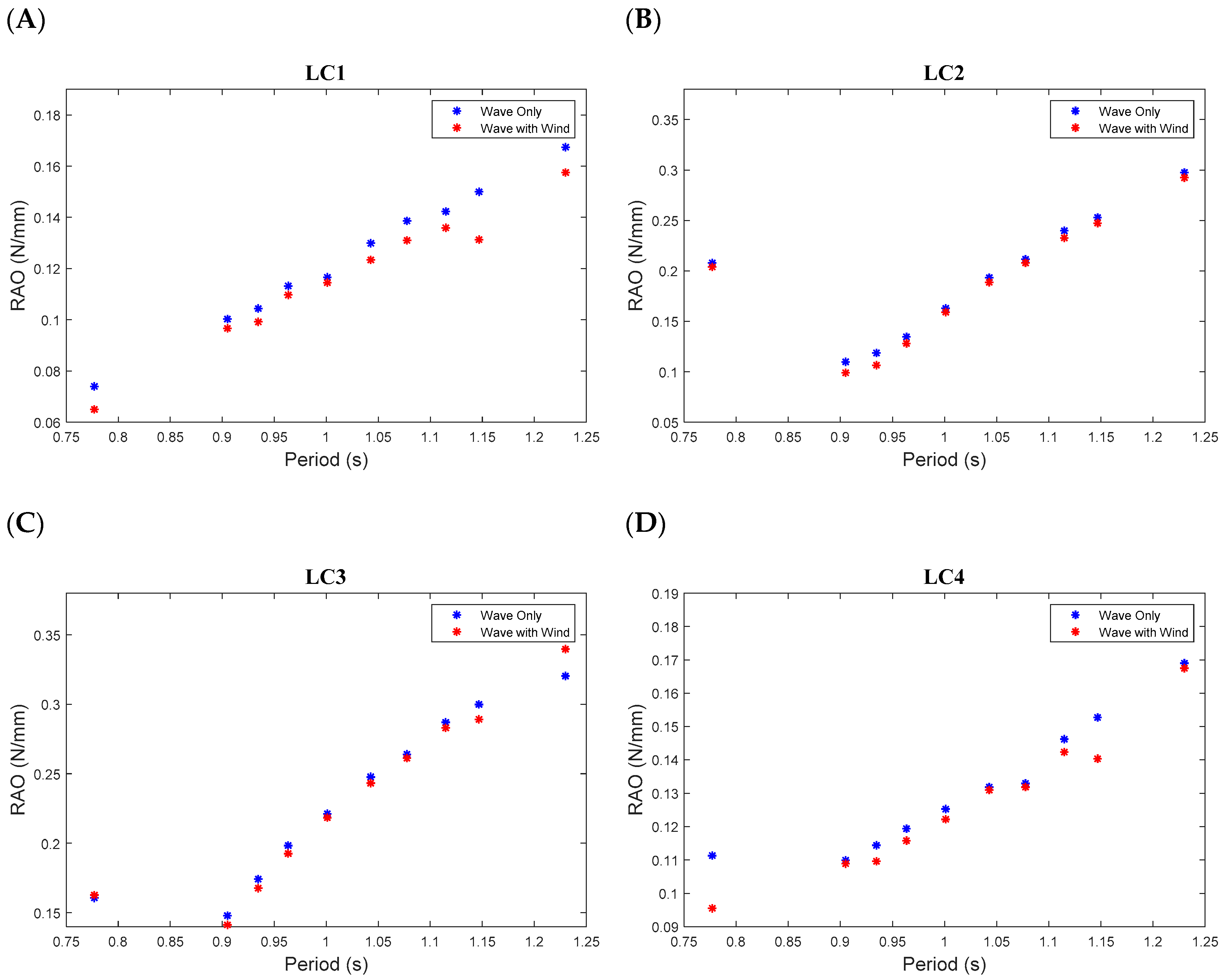
4.2. Response Amplitude Operators (RAOs)
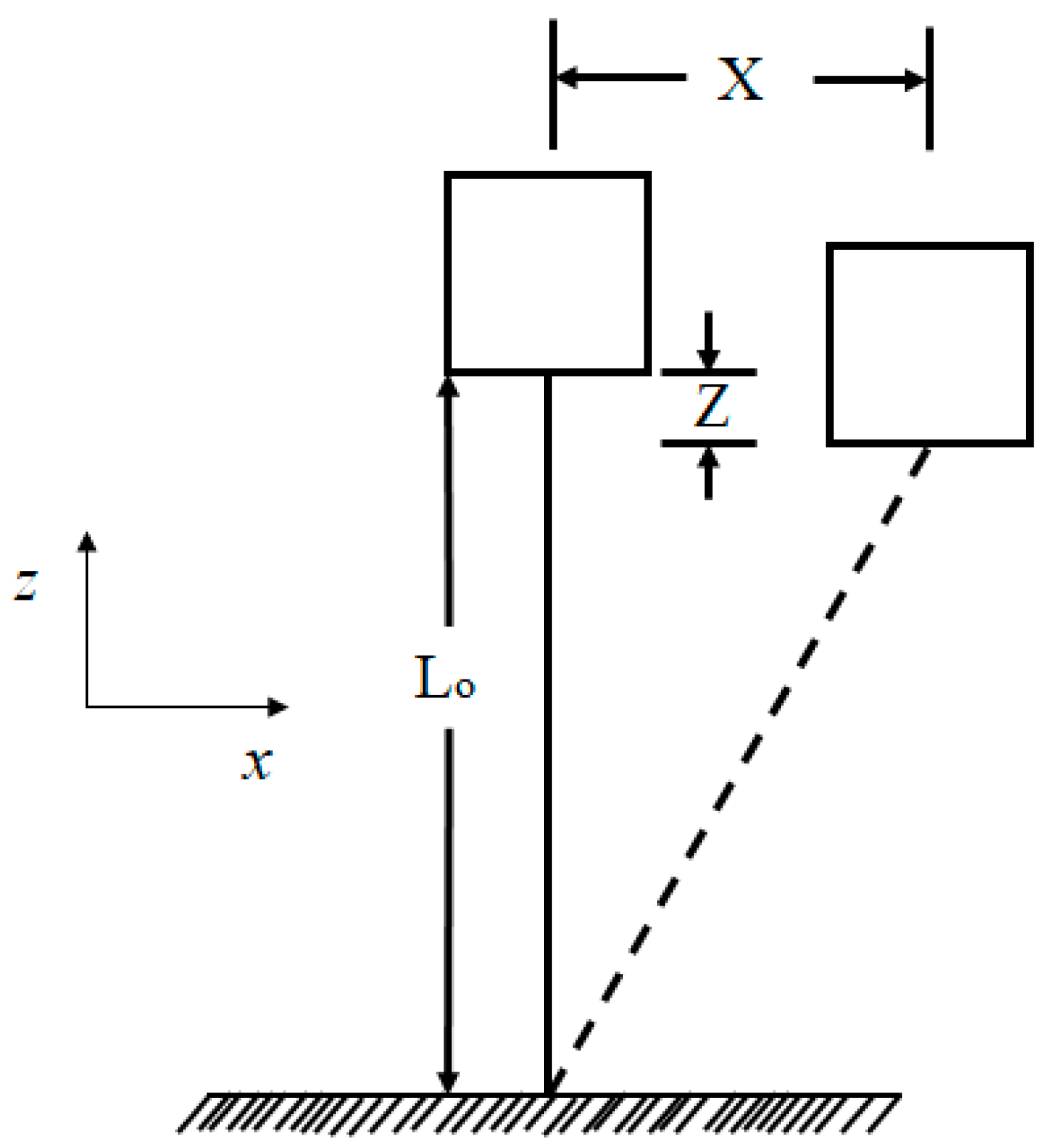
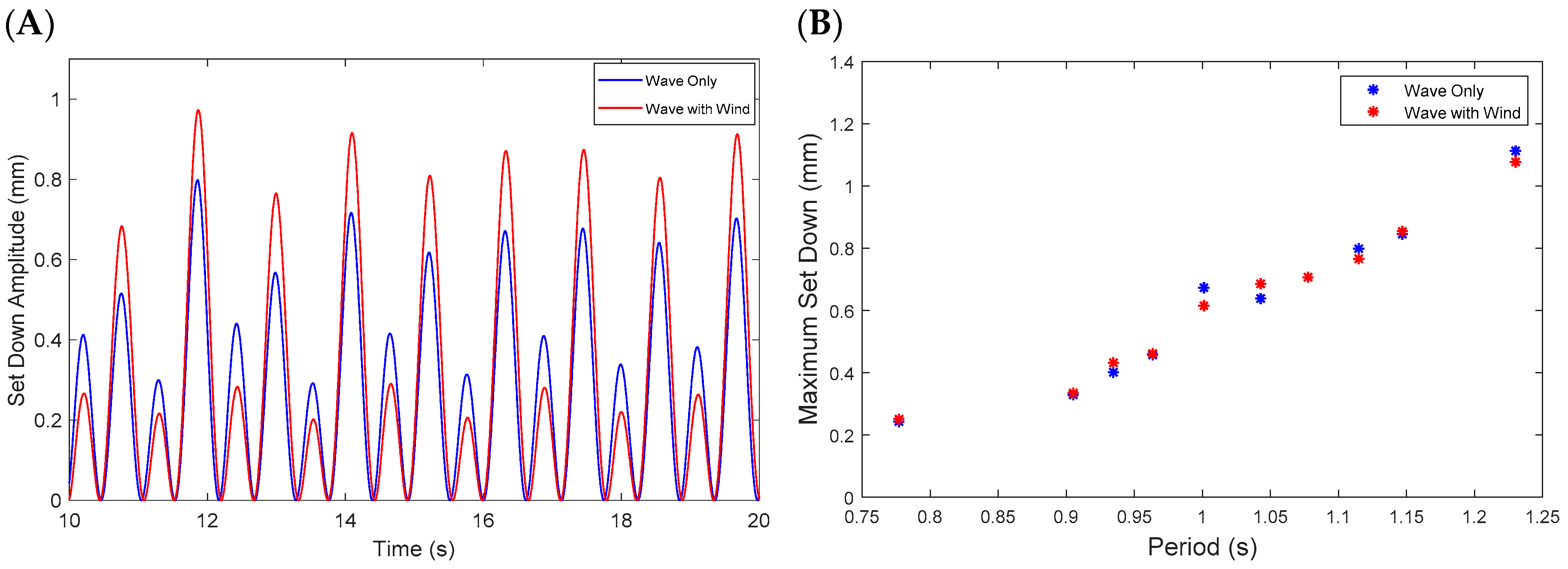
4.3. Model’s Offset Versus Set-Down
5. Conclusions and Recommendations
- Several free decay tests were performed to evaluate the natural periods of the model in the key degrees of freedom including surge, heave, pitch, and yaw. The natural periods in the surge and pitch motions evaluated from the decay tests had a relatively close agreement to the theoretical values. Furthermore, the natural periods in the surge, heave, and pitch degrees of freedom were all outside the range of 6–20 s, whilst the yaw natural period fell inside this range. As the yaw control of the nacelle is typically used to orient the turbine towards the predominant wind direction, such a situation could lead to an increase in the yaw motion if excited by waves. Therefore, it is recommended to investigate the effect of yaw motion on the performance of a TLPWT.
- The tested TLPWT model showed typical motion responses to that of generalised TLP systems with significant surge offsets along with stiff heave and pitch motions. The maximum magnitudes for the RAOs of surge motion and all tendons occurred at the longest wave period of 1.23 s (~13.0 s at full-scale) tested in this study.
- There was evidence that static wind loading on the turbine structure had some impact on the motions and tendon response, particularly in the heave direction, with an average increase of 13.1% in motion magnitude for the tested wind conditions. The wind had a negligible effect on the surge motion and slightly decreased the tendon tensions in all tendons.
- The results also showed the set-down magnitudes amounting to approximately 2–5% of the offset. Furthermore, the waves are the dominant factor contributing to the set-down of the TLPWT, with a minimal contribution from the static wind forcing.
- As the environmental condition tested in this study is considered a mild to moderate sea state, it should be stressed that it is unlikely that the maximum motions and loads of the model were captured during these tests. A testing in a survivability sea state condition would likely provide such information. It is therefore recommended that further testing into the survivability of the TLPWT should be performed. Furthermore, the use of a drag plate instead of the static rotor tested in this study can be investigated in future studies, as the thrust distribution would be more uniform. The results of this study could be used for calibrating numerical tools such as CFD codes which can then be used for further investigations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Notations
| AMC | Australian Maritime College |
| CFD | Computational Fluid Dynamics |
| CV | Coefficient of Variation (%) |
| D | Column diameter (m) |
| d | Water depth (m) |
| EC | Environmental Condition |
| FAST | Fatigue, Aerodynamics, Structures, and Turbulence |
| FFT | Fast Fourier Transform |
| FOWT | Floating Offshore Wind Turbine |
| H | Wave height (m) |
| Hmax | Maximum wave height (m) |
| Hs | Significant wave height (m) |
| Ixx | Mass Moment of Inertia about x-axis (kg·mm2) |
| Iyy | Mass Moment of Inertia about y-axis (kg·mm2) |
| KB | Vertical distance measured from the model’s keel to the centre of buoyancy (m) |
| KG | Vertical distance measured from the model’s keel to the VCG (m) |
| L | Wave length (m) |
| LC | Load Cell |
| Lo | Original tendon length (m) |
| m | Mean value (vary) |
| MIT | Massachusetts Institute of Technology |
| MTB | Model Test Basin |
| MW | Mega Watt |
| NREL | National Renewable Energy Laboratory |
| NRMSE | Normalised Root Mean Square Error |
| PSD | Power Spectral Density (m2/Hz) |
| R2 | Correlation coefficient (-) |
| RAO | Response Amplitude Operator |
| t | Time (s) |
| T | Wave period (s) |
| TLP | Tension Leg Platform |
| Tn | Natural period (s) |
| Tp | Peak period (s) |
| U | Mean wind speed (m/s) |
| VCG | Vertical Centre of Gravity |
| WP | Wave Probe |
| X | Horizontal offset (m) |
| Z | Set-down (m) |
| σ | Standard deviation (vary) |
References
- Breton, S.-P.; Moe, G. Status, plans and technologies for offshore wind turbines in Europe and North America. Renew. Energy 2009, 34, 646–654. [Google Scholar] [CrossRef]
- IRENA. Renewable Capacity Statistics 2018; The International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2018. [Google Scholar]
- Global Wind Energy Council (GWEC). Global Wind Report: Annual Market Update 2017. Available online: https://www.tuulivoimayhdistys.fi/filebank/1191-GWEC_Global_Wind_Report_April_2018.pdf (accessed on 31 December 2018).
- Wang, X.; Zeng, X.; Li, J.; Yang, X.; Wang, H. A review on recent advancements of substructures for offshore wind turbines. Energy Convers. Manag. 2018, 158, 103–119. [Google Scholar] [CrossRef]
- Arshad, M.; O’Kelly, B.C. Offshore wind-turbine structures: A review. Proc. Inst. Civ. Eng. Energy 2013, 166, 139–152. [Google Scholar] [CrossRef]
- Doherty, P.; Gavin, K. Laterally loaded monopile design for offshore wind farms. Proc. ICE-Energy 2011, 165, 7–17. [Google Scholar] [CrossRef]
- Sclavounos, P.; Tracy, C.; Lee, S. Floating offshore wind turbines: Responses in a seastate pareto optimal designs and economic assessment. In Proceedings of the ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; American Society of Mechanical Engineers: New York, NY, USA, 2008. [Google Scholar]
- Wang, C.; Utsunomiya, T.; Wee, S.; Choo, Y. Research on floating wind turbines: A literature survey. IES J. Part A Civ. Struct. Eng. 2010, 3, 267–277. [Google Scholar] [CrossRef]
- Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tension Leg Platform with a Comparison to Other Floating Turbine Concepts: April 2009; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Koo, B.J.; Goupee, A.J.; Kimball, R.W.; Lambrakos, K.F. Model tests for a floating wind turbine on three different floaters. J. Offshore Mech. Arct. Eng. 2014, 136, 020907. [Google Scholar] [CrossRef]
- Skaare, B.; Hanson, T.D.; Nielsen, F.G.; Yttervik, R.; Hansen, A.M.; Thomsen, K.; Larsen, T.J. Integrated Dynamic Analysis of Floating Offshore Wind Turbines. In Proceedings of the 2007 European Wind Energy Conference and Exhibition, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Abdussamie, N.; Drobyshevski, Y.; Ojeda, R.; Thomas, G.; Amin, W. Experimental investigation of wave-in-deck impact events on a TLP model. Ocean Eng. 2017, 142, 541–562. [Google Scholar] [CrossRef]
- Hore, J.; Abdussamie, N.; Ojeda, R.; Penesis, I. Experimental investigation into the hydrodynamic performance of a TLP-OWC device. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Bachynski, E.E.; Moan, T. Design considerations for tension leg platform wind turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Sclavounos, P.; Lee, S.; DiPietro, J.; Potenza, G.; Caramuscio, P.; De Michele, G. Floating offshore wind turbines: tension leg platform and taught leg buoy concepts supporting 3-5 MW wind turbines. In Proceedings of the European Wind Energy Conference, Warsaw, Poland, 20–23 April 2010. [Google Scholar]
- Xu, N.; Zhang, J. Pitch/Roll Static Stability of Tension Leg Platforms. In Proceedings of the ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; American Society of Mechanical Engineers: New York, NY, USA, 2010. [Google Scholar]
- Halkyard, J. Floating Offshore Platform Design, in Handbook of Offshore Engineering; Elsevier: Amsterdam, The Netherlands, 2005; pp. 419–661. [Google Scholar]
- Nihei, Y.; Iijima, K.; Murai, M.; Ikoma, T. A comparative study of motion performance of four different FOWT designs in combined wind and wave loads. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Chakrabarti, S.K. Offshore Structure Modeling; World Scientific: Singapore, 1994; Volume 9. [Google Scholar]
- Low, Y. Frequency domain analysis of a tension leg platform with statistical linearization of the tendon restoring forces. Mar. Struct. 2009, 22, 480–503. [Google Scholar] [CrossRef]
- Srinivasan, C.; Gaurav, G.; Serino, G.; Miranda, S. Ringing and springing response of triangular TLPs. Int. Shipbuild. Prog. 2011, 58, 141–163. [Google Scholar]
- Matsui, T.; Sakoh, Y.; Nozu, T. Second-order sum-frequency oscillations of tension-leg platforms: Prediction and measurement. Appl. Ocean Res. 1993, 15, 107–118. [Google Scholar] [CrossRef]
- Feng, W.H.; Hua, F.Y.; Yang, L. Dynamic analysis of a tension leg platform for offshore wind turbines. J. Power Technol. 2014, 94, 42–49. [Google Scholar]
- Nihei, Y.; Matsuura, M.; Murai, M.; Iijima, K.; Ikoma, T. New Design Proposal for the TLP Type Offshore Wind Turbines. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; The American Society of Mechanical Engineers (ASME): Nantes, France, 2013. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report No. NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Kimball, R.; Goupee, A.J.; Fowler, M.J.; de Ridder, E.-J.; Helder, J. Wind/wave basin verification of a performance-matched scale-model wind turbine on a floating offshore wind turbine platform. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Tracy, C.C.H. Parametric Design of Floating Wind Turbines; Massachusetts Institute of Technology: Cambridge, MA, USA, 2007. [Google Scholar]
- Oguz, E.; Clelland, D.; Day, A.H.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and numerical analysis of a TLP floating offshore wind turbine. Ocean Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; Technical Report NREL/TP-500-41958; National Renewable Energy Laboratory: Golden, CO, USA, 2008.
- Bachynski, E.E. Design and Dynamic Analysis of Tension Leg Platform Wind Turbines. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, March 2014. [Google Scholar]
- Nihei, Y.; Fujioka, H. Motion characteristics of TLP type offshore wind turbine in waves and wind. In Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; American Society of Mechanical Engineers: New York, NY, USA, 2010. [Google Scholar]
- Martin, H.R.; Kimball, R.W.; Viselli, A.M.; Goupee, A.J. Methodology for wind/wave basin testing of floating offshore wind turbines. J. Offshore Mech. Arct. Eng. 2014, 136, 020905. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, J.; He, Y. Preliminary design of a multi-column TLP foundation for a 5-MW offshore wind turbine. Energies 2012, 5, 3874–3891. [Google Scholar] [CrossRef]
- Zamora-Rodriguez, R.; Gomez-Alonso, P.; Amate-Lopez, J.; De-Diego-Martin, V.; Dinoi, P.; Simos, A.N.; Souto-Iglesias, A. Model scale analysis of a TLP floating offshore wind turbine. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: San Francisco, CA, USA, 2014. [Google Scholar]
- Hansen, A.M.; Laugesen, R.; Bredmose, H.; Mikkelsen, R.; Psichogios, N. Small scale experimental study of the dynamic response of a tension leg platform wind turbine. J. Renew. Sustain. Energy 2014, 6, 053108. [Google Scholar] [CrossRef]
- DNV. Recommended Practice DNV-RP-C205: Environmental Conditions and Environmental Loads; DNV: Oslo, Norway, 2010. [Google Scholar]
- Chia, C.K.W. Experimental Investigation into Extreme Wave Impact on a TLP Offshore Wind Turbine. In National Centre for Maritime Engineering & Hydrodynamics; University of Tasmania: Launceston, Australia, 2017. [Google Scholar]
- Banks, M.; Abdussamie, N. The response of a semisubmersible model under focused wave groups: Experimental investigation. J. Ocean Eng. Sci. 2017, 2, 161–171. [Google Scholar] [CrossRef]
- Groves, B.; Abdussamie, N. Generation of rogue waves at model scale. J. Ocean Eng. Sci. 2019, in press. [Google Scholar] [CrossRef]
- Qualysis. Qualisys Motion Tracking System. 2018. Available online: https://www.qualisys.com/ (accessed on 31 December 2018).
- Chakrabarti, S.K. Hydrodynamics of Offshore Structures; WIT Press: Southampton, UK, 1987. [Google Scholar]
- Naess, A.; Moan, T. Stochastic Dynamics of Marine Structures; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Abdussamie, N.; Ojeda, R.; Drobyshevski, Y.; Thomas, G.; Amin, W. Dynamic behaviour of a TLP in waves: CFD versus model tests. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Abdussamie, N. Towards Reliable Prediction of Wave-in-Deck Loads and Response of Offshore Structures. Ph.D. Thesis, University of Tasmania, Launceston, Australia, June 2016. [Google Scholar]
- Demirbilek, Z. Design formulae for offset, set down and tether loads of a tension leg platform (TLP). Ocean Eng. 1990, 17, 517–523. [Google Scholar] [CrossRef]
- DNVGL. Floating Wind Turbine Structures—Standard—DNVGL-ST-0119; DNV.GL: Høvik, Norway, 2018. [Google Scholar]

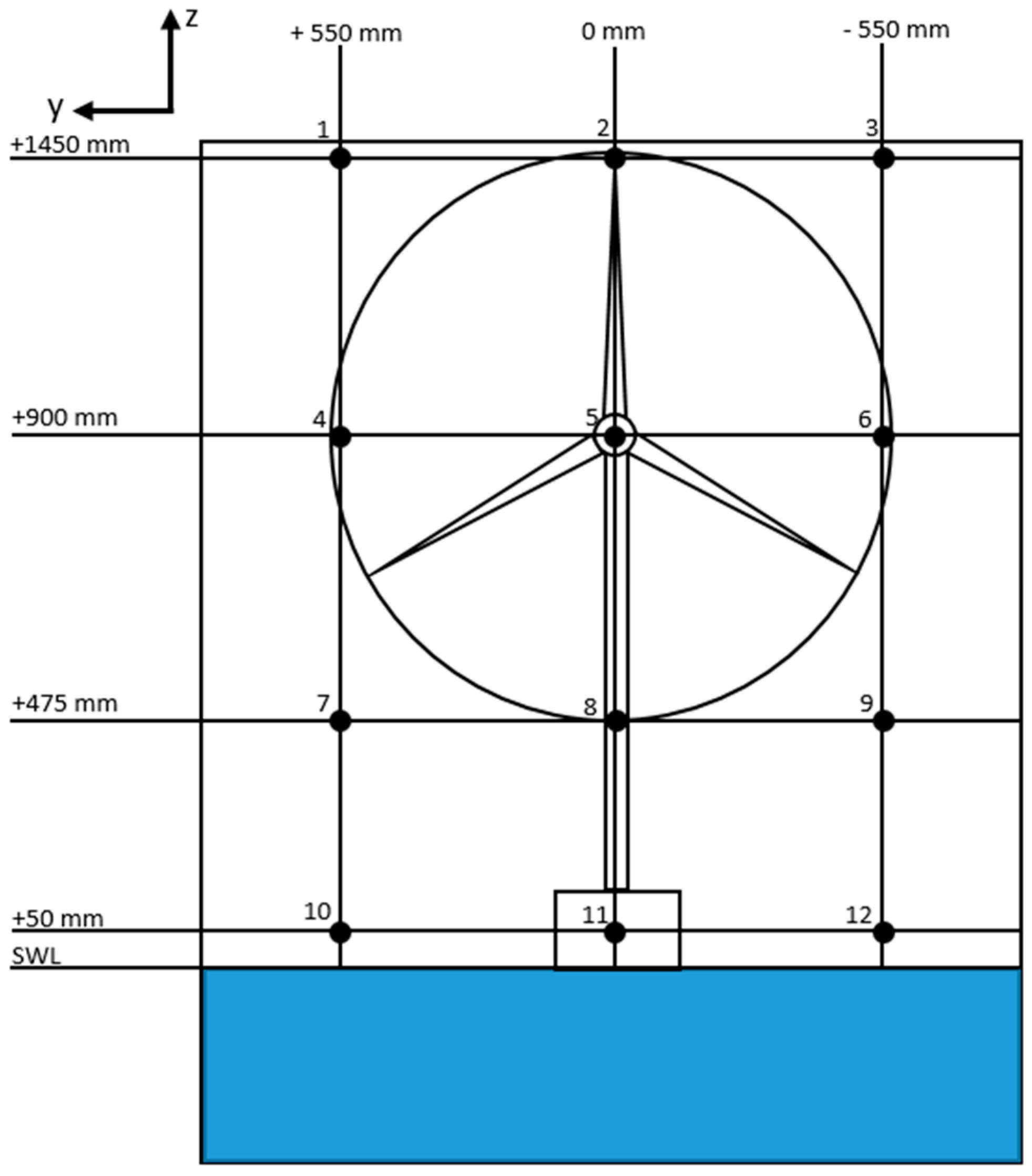


| Parameter | Planned | Tested Model-Scale | Reference for Planned Full-Scale Values | |
|---|---|---|---|---|
| Full-Scale | Model-Scale | |||
| Hull column diameter | 18.00 m | 160.71 mm | 160.00 mm | Bachynski and Moan [14] |
| Hull column height | 52.60 m | 469.64 mm | 600.00 mm | Bachynski and Moan [14] |
| Draft | 47.89 m | 427.59 mm | 500.00 mm | Matha [9] |
| Freeboard | 5.00 m | 44.64 mm | 100.00 mm | Matha [9] |
| Pontoon length | 18.00 m | 160.71 mm | 160.00 mm | Bachynski and Moan [14] |
| Pontoon width | 2.40 m | 21.42 mm | 21.70 mm | Bachynski and Moan [14] |
| Pontoon height | 2.40 m | 21.42 mm | 21.70 mm | Bachynski and Moan [14] |
| Hull structural mass | - | - | 2.63 kg | - |
| Ballast mass | - | - | 1.82 kg | - |
| Total pre-tension | - | - | 5.11 kg | - |
| Volumetric displacement | 11.80 × 107 m3 | 8.44 × 106 mm3 | 1.04 × 107 mm3 | Bachynski and Moan [14] |
| Water depth | 150.00 m | 1.34 m | 0.90m | Bachynski and Moan [14] |
| Parameter | Planned | Tested Model-Scale | Reference for Planned Full-Scale Values | |
|---|---|---|---|---|
| Full-Scale | Model-Scale | |||
| Tower height | 90.00 m | 803.00 mm | 800.00 mm | Matha [9] |
| Tower bottom diameter | 6.00 m | 53.50 mm | 53.30 mm | |
| Tower top diameter | 3.87 m | 34.50 mm | 34.50 mm | |
| Hub height | 90.00 m | 803.00 mm | 800.00 mm | |
| Rotor hub diameter | 3.00 m | 26.70 mm | 35.00 mm | |
| Rotor diameter | 126.00 m | 1.12 m | 1.13 m | |
| Overhang | 5.00 m | 44.60 mm | 45.00 mm | |
| Blade length | 61.50 m | 549.00 mm | 550.00 mm | |
| Tower mass | 3.47 × 105 kg | 247.00 g | 246.00 g | |
| Nacelle mass | 2.40 × 105 kg | 171.00 g | 170.00 g | |
| Rotor mass | 1.10 × 103 kg | 78.20 g | 160.00 g | |
| Model Component | Material | Mass (g) |
|---|---|---|
| Hull cylinder | Polyvinyl Chloride (PVC) | 1890 |
| External pontoons | Timber | 72.00 (each) |
| Bottom and top caps | Polyvinyl Chloride (PVC) | 173.00 (each) |
| Ballast | Lead | 1866.00 |
| Turbine | PLA plastic | 576.00 |
| Qualisys probes | - | 50.00 |
| Tendon lines | 7-Strand, coated steel wire | - |
| Parameter | Value | Unit |
|---|---|---|
| Vertical Centre of Gravity (KG) | 0.29 | m |
| Vertical Centre of Buoyancy (KB) | 0.24 | m |
| Mass Moment of Inertia about x-axis, Ixx | 9.71 × 105 | kg·mm2 |
| Mass Moment of Inertia about y-axis, Iyy | 9.79 × 105 | kg·mm2 |
| Mass Moment of Inertia about z-axis, Izz | 3.26 × 104 | kg·mm2 |
| Parameter | Full-Scale | Model-Scale |
|---|---|---|
| Significant wave height, Hs (m) | 4.40 | 0.039 |
| Peak wave period, Tp (s) | 10.60 | 1.00 |
| Mean wind speed at hub, U (m/s) | 18.00 | 1.70 |
| Condition | H (m) | T (s) | Condition | H (m) | H/Hs (-) | T (s) |
|---|---|---|---|---|---|---|
| 1 | 0.039 | 1.230 | 11 | 0.025 | 0.641 | 1.000 |
| 2 | 1.147 | 12 | 0.030 | 0.769 | ||
| 3 | 1.115 | 13 | 0.035 | 0.897 | ||
| 4 | 1.078 | 14 | 0.040 | 1.026 | ||
| 5 | 1.043 | 15 | 0.045 | 1.154 | ||
| 6 | 1.000 | 16 | 0.050 | 1.282 | ||
| 7 | 0.963 | 17 | 0.055 | 1.410 | ||
| 8 | 0.935 | 18 | 0.060 | 1.539 | ||
| 9 | 0.905 | 19 | 0.065 | 1.667 | ||
| 10 | 0.777 | 20 | 0.070 | 1.795 |
| Degree of Freedom | Predicted Tn (s) | Measured Tn (s) | Full-Scale Equivalent Tn (s) |
|---|---|---|---|
| Surge | 2.113 | 2.078 | 21.99 |
| Heave | 0.213 | 0.256 | 2.71 |
| Pitch | 0.243 | 0.260 | 2.75 |
| Yaw | 0.675 | 0.586 | 6.20 |
| Run | WP2 (mm) | LC3 (N) | Qualisys, X (mm) | |||
|---|---|---|---|---|---|---|
| Max | Min | Max | Min | Max | Min | |
| Run 1 | 22.24 | −20.73 | 1.41 | −1.33 | 16.14 | −18.19 |
| Run 2 | 22.26 | −20.77 | 1.44 | −1.36 | 16.46 | −18.23 |
| Run 3 | 22.47 | −20.75 | 1.42 | −1.33 | 16.34 | −18.23 |
| Run 4 | 22.50 | −20.75 | 1.42 | −1.37 | 16.39 | −18.14 |
| Run 5 | 22.36 | −20.86 | 1.44 | −1.38 | 16.18 | −18.48 |
| Mean, m | 22.37 | −20.77 | 1.43 | −1.35 | 16.30 | −18.25 |
| Standard deviation, σ | 0.12 | 0.05 | 0.01 | 0.02 | 0.14 | 0.13 |
| CV (%) | 0.54 | 0.24 | 0.70 | 1.48 | 0.86 | 0.71 |
| NRMSE (%) | 0.47 | 0.22 | 0.88 | 1.55 | 0.75 | 0.65 |
| R2 (-) | 0.9926 | 0.9745 | 0.9978 | |||
| Run | WP2 (mm) | LC3 (N) | Qualisys, X (mm) | |||
|---|---|---|---|---|---|---|
| Max | Min | Max | Min | Max | Min | |
| Run 1 | 22.61 | −20.64 | 1.36 | −1.46 | 15.38 | −18.92 |
| Run 2 | 22.52 | −20.55 | 1.39 | −1.56 | 15.29 | −19.29 |
| Run 3 | 22.33 | −20.75 | 1.38 | −1.48 | 15.33 | −19.29 |
| Run 4 | 22.63 | −20.57 | 1.43 | −1.66 | 15.11 | −18.90 |
| Run 5 | 22.48 | −20.50 | 1.36 | −1.49 | 15.33 | −19.18 |
| Mean, m | 22.55 | −20.60 | 1.38 | −1.53 | 15.28 | −19.12 |
| Standard deviation, σ | 0.12 | 0.10 | 0.03 | 0.08 | 0.10 | 0.19 |
| CV (%) | 0.53 | 0.49 | 2.17 | 5.23 | 0.65 | 0.99 |
| NRMSE (%) | 0.50 | 0.42 | 1.89 | 4.79 | 0.61 | 0.91 |
| R2 (-) | 0.9997 | 0.9993 | 0.9994 | |||
| RAO Parameter | Max RAO (Wave Only) | Max RAO (Wave and Wind) | Wind Effect |
|---|---|---|---|
| Surge motion | 1.091 mm/mm | 1.102 mm/mm | 1.0% |
| LC1 | 0.167 N/mm | 0.158 N/mm | −6.0% |
| LC2 | 0.298 N/mm | 0.292 N/mm | −2.0% |
| LC3 | 0.320 N/mm | 0.340 N/mm | 6.0% |
| LC4 | 0.169 N/mm | 0.168 N/mm | −1.0% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murfet, T.; Abdussamie, N. Loads and Response of a Tension Leg Platform Wind Turbine with Non-Rotating Blades: An Experimental Study. J. Mar. Sci. Eng. 2019, 7, 56. https://doi.org/10.3390/jmse7030056
Murfet T, Abdussamie N. Loads and Response of a Tension Leg Platform Wind Turbine with Non-Rotating Blades: An Experimental Study. Journal of Marine Science and Engineering. 2019; 7(3):56. https://doi.org/10.3390/jmse7030056
Chicago/Turabian StyleMurfet, Timothy, and Nagi Abdussamie. 2019. "Loads and Response of a Tension Leg Platform Wind Turbine with Non-Rotating Blades: An Experimental Study" Journal of Marine Science and Engineering 7, no. 3: 56. https://doi.org/10.3390/jmse7030056
APA StyleMurfet, T., & Abdussamie, N. (2019). Loads and Response of a Tension Leg Platform Wind Turbine with Non-Rotating Blades: An Experimental Study. Journal of Marine Science and Engineering, 7(3), 56. https://doi.org/10.3390/jmse7030056






