Parametric Study of Tsunamis Generated by Earthquakes and Landslides
Abstract
:1. Introduction
2. Experimental Investigation
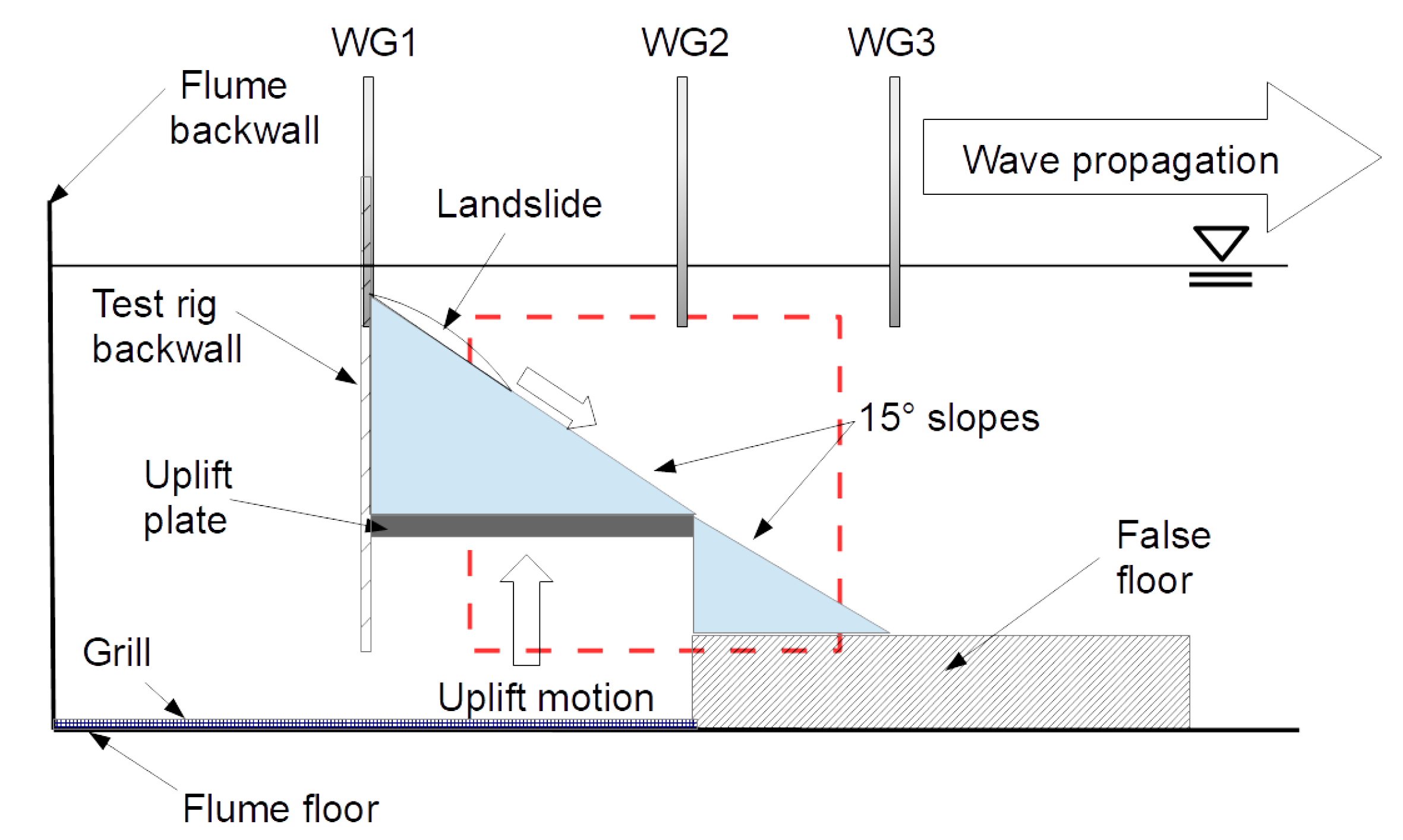
2.1. Experimental Setup
2.2. Fault Rupture Mechanism
2.3. Landslide Models
2.3.1. Solid Block Landslide
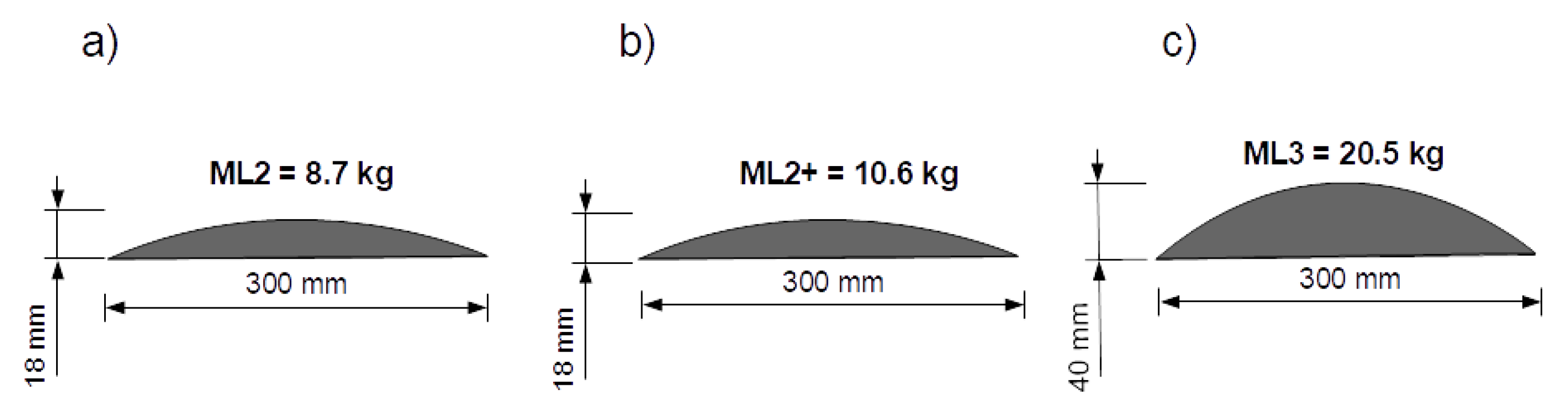
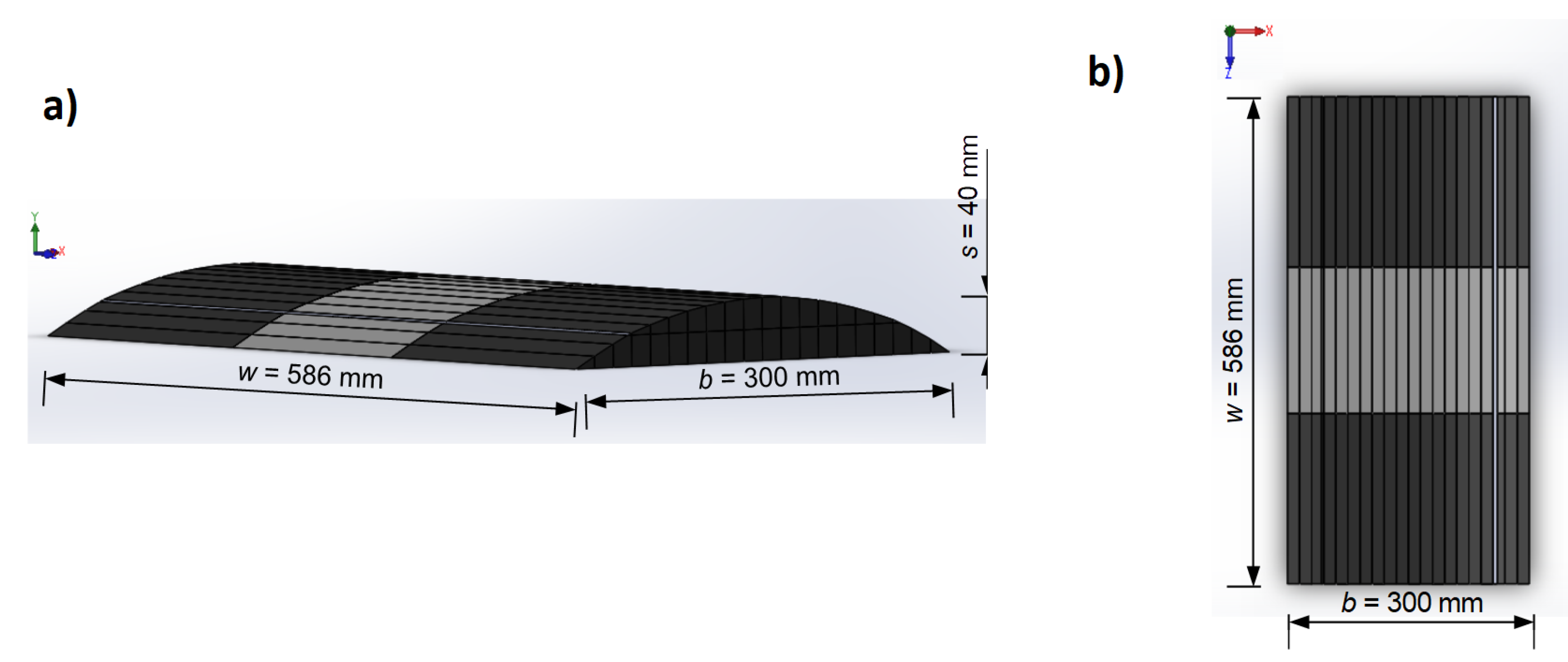
2.3.2. Modular Landslide
3. Results
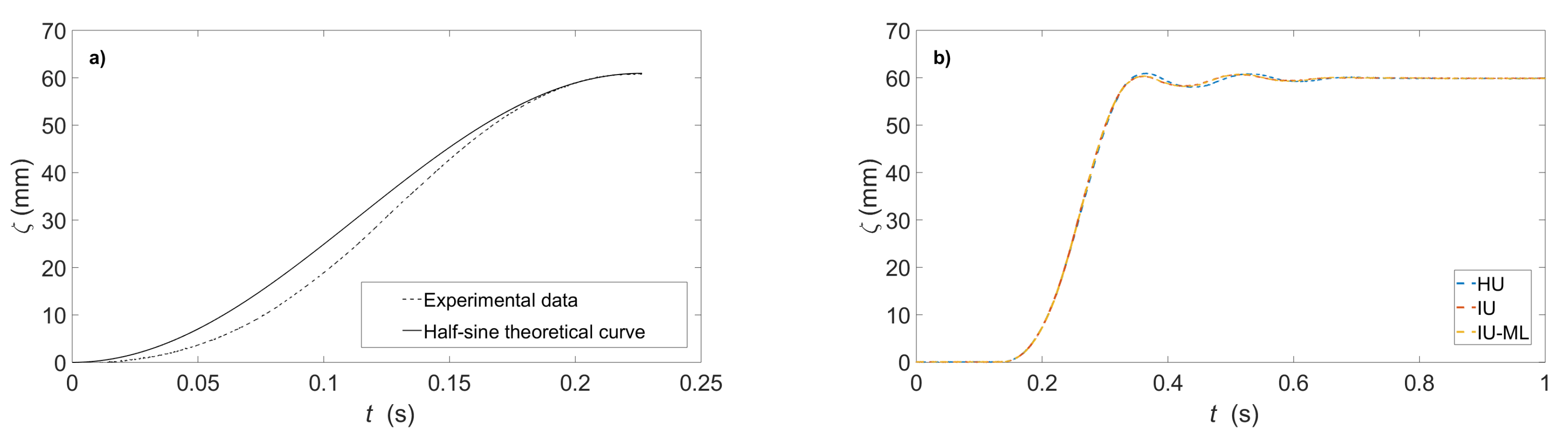
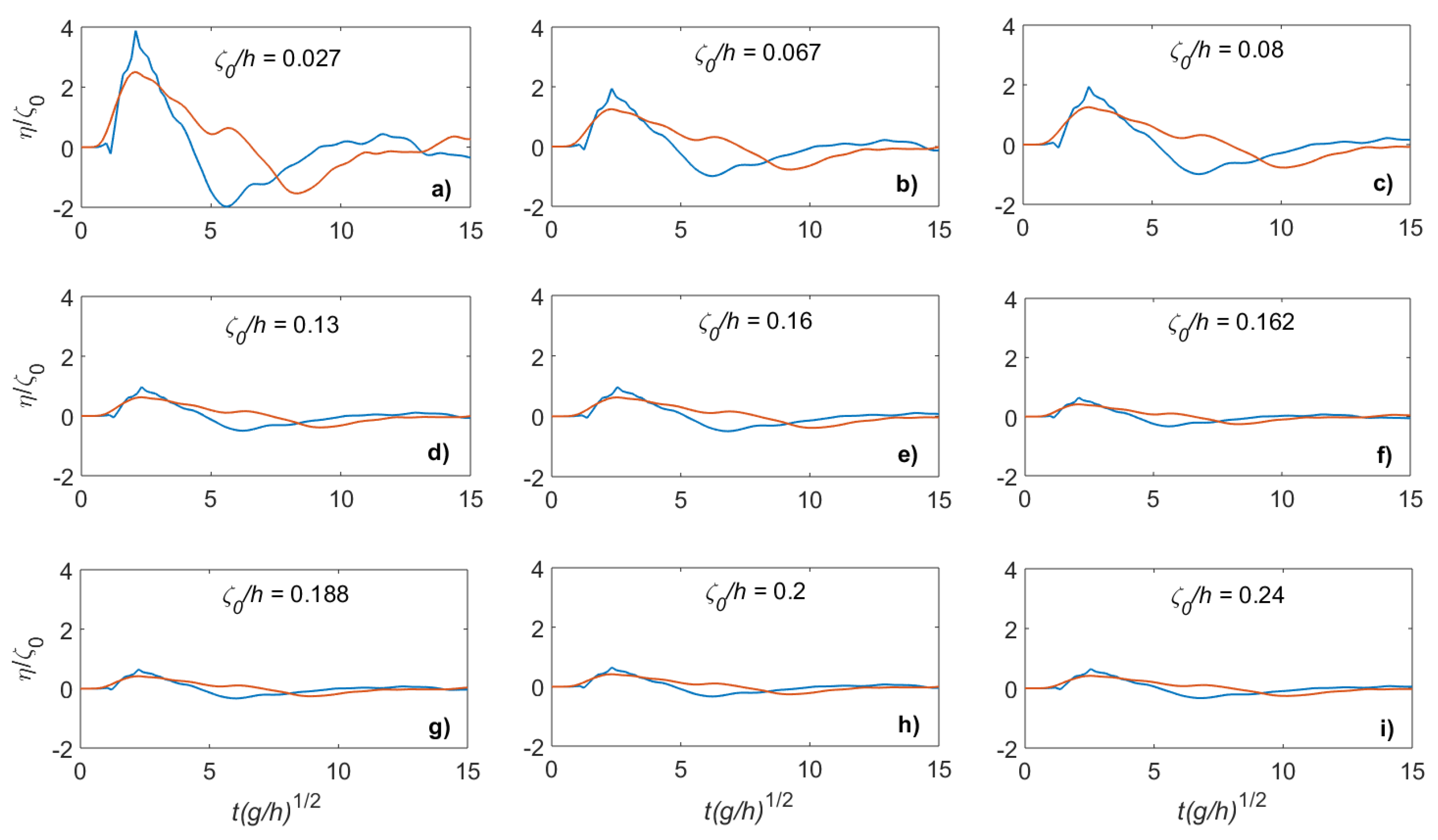
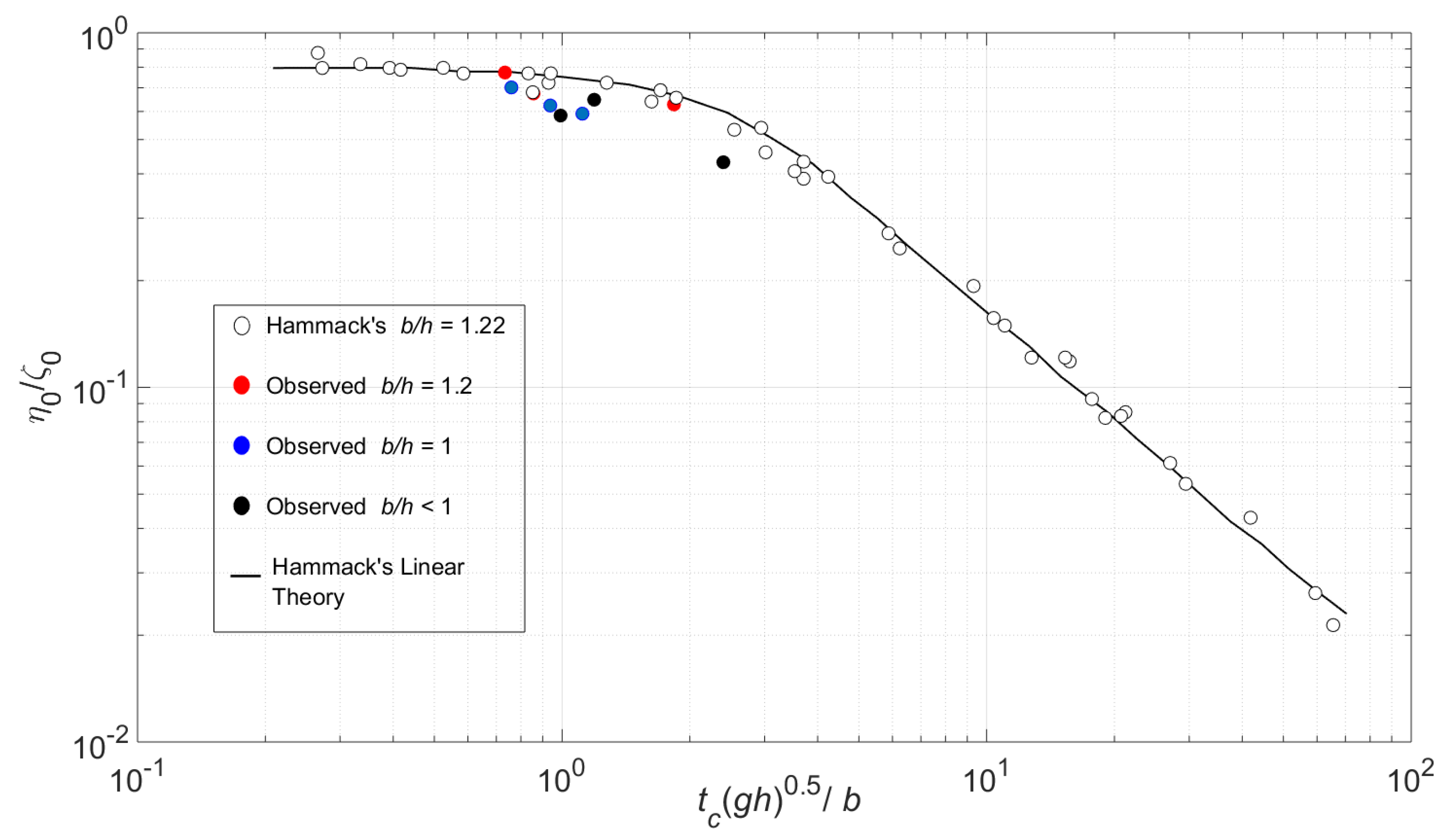
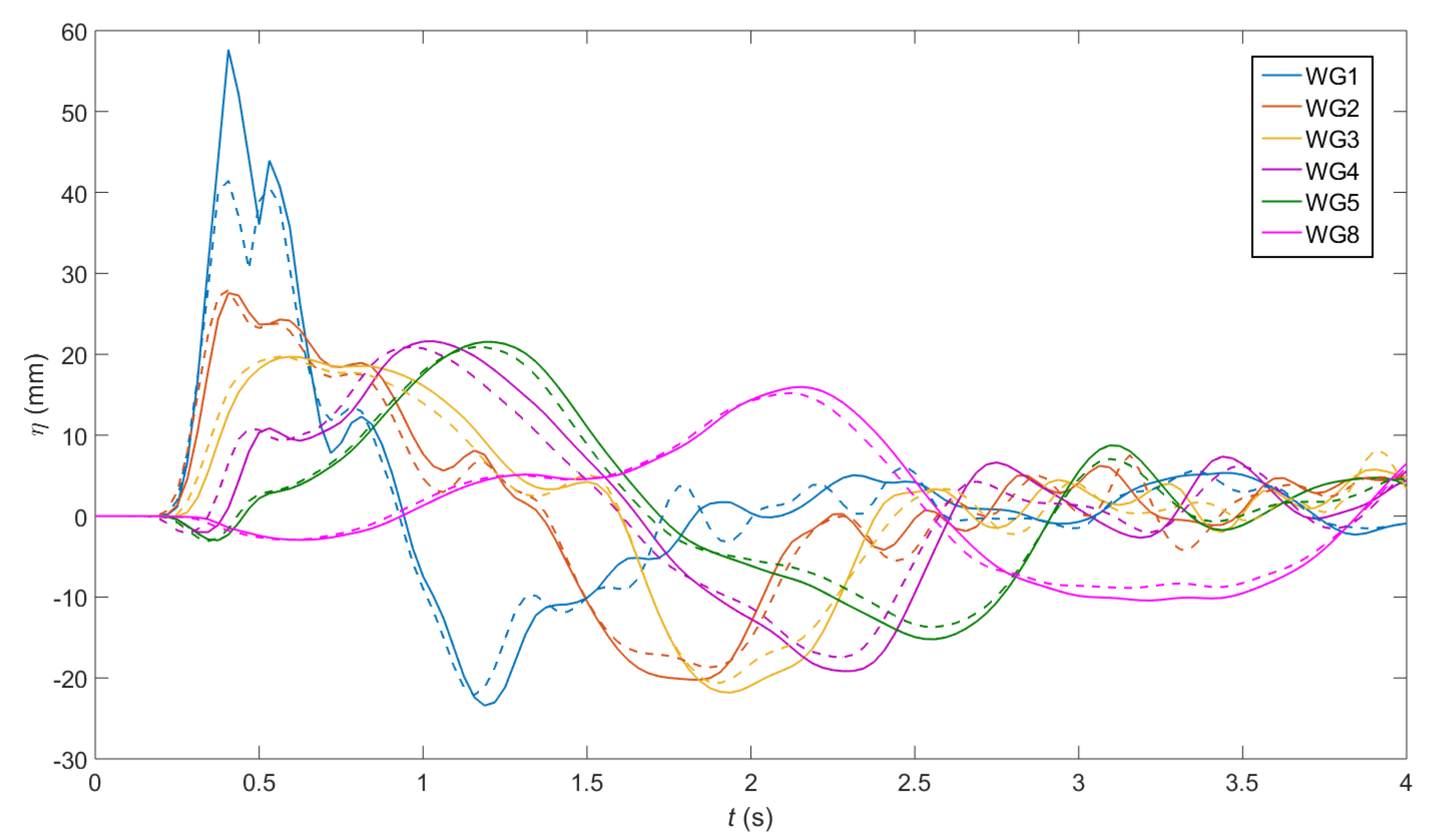
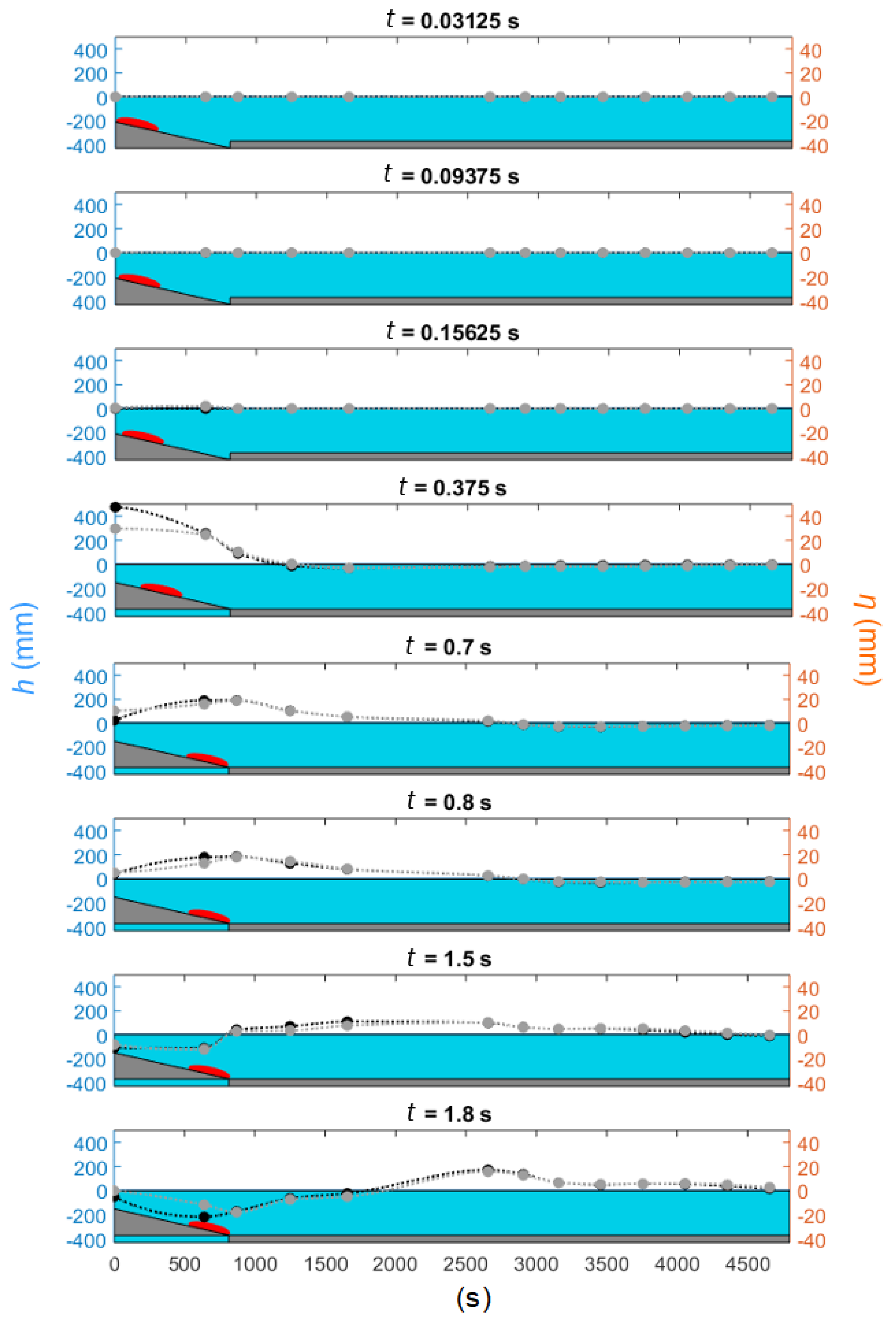
3.1. Description of Fault Rupture Motion
3.2. Description of Solid Block Motion
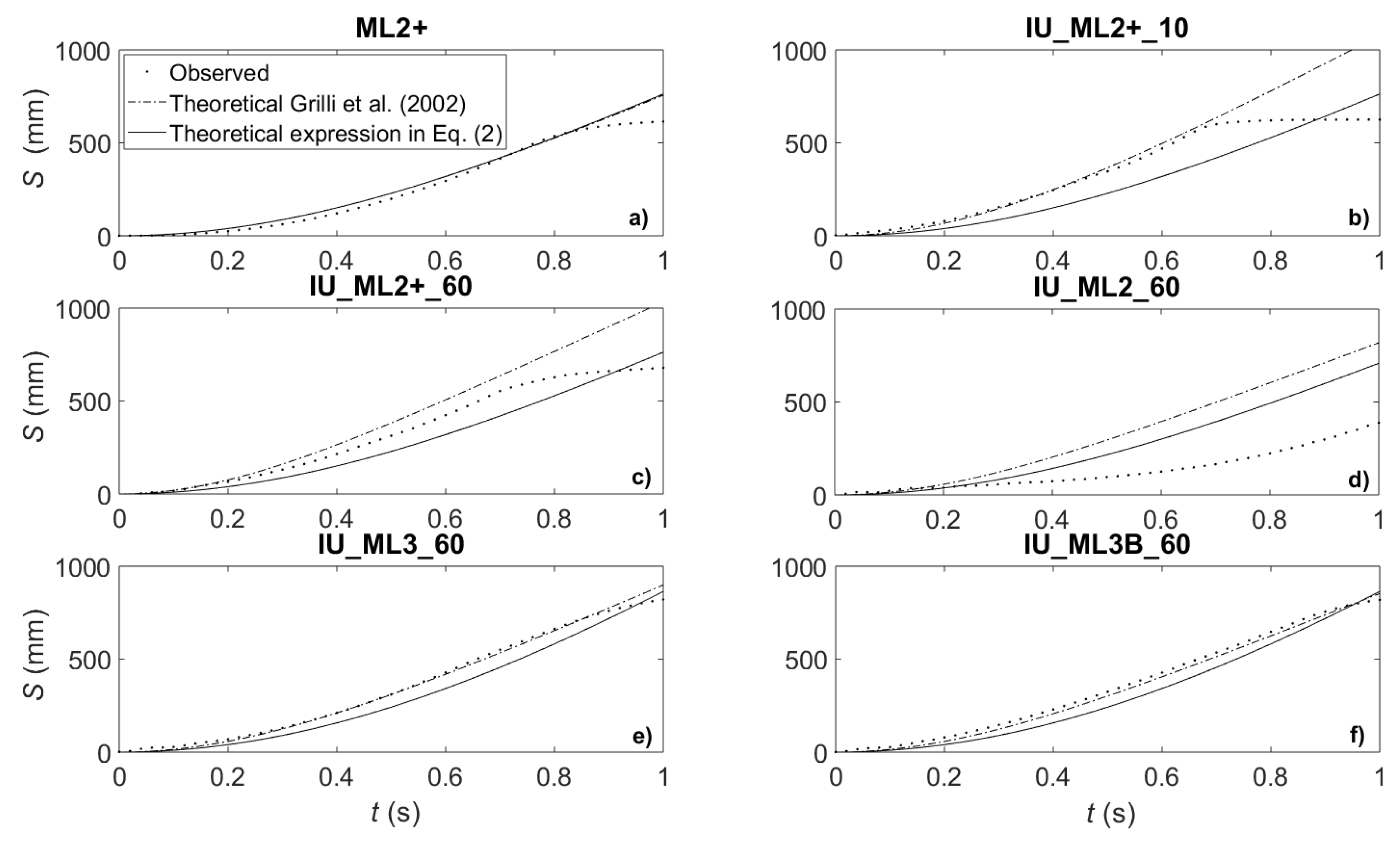
- Both theoretical approximations of landslide position show good agreement with the observed data for the landslide-only test (Figure 7a), until the point at which the landslide model experiences a change in geometry of the slope, not modelled by the theory.
- Whilst the ML2+ models (Figure 7a–c) stopped before transitioning onto the horizontal floor, the lighter model ML2 (Figure 7d) exhibited aquaplaning motion, travelling beyond the end of the slope. This resulted in longer travel times. The larger and heavier landslides ML3 and ML3B (Figure 7e,f), also exhibited longer travel times as they travelled beyond the end of the slope, due in part to their increased momentum and possibly due to deformation of the models (see final point).
- The effect of increasing uplift size on the ML2+ landslide position is also evident from these tests. The smallest uplift of 10 mm (Figure 7b), has measurements that are in very good agreement with the theoretical approximation of Grilli et al. [33], but rather poor agreement with the theoretical approximation from the present study. However, for a 60 mm uplift, observations from the same landslide model now have worse agreement with Grilli et al. [33], though match the present theory more closely than for the smaller uplift. It is worth noting that neither of the theoretical approximations took into account the uplift motion in their formulation.
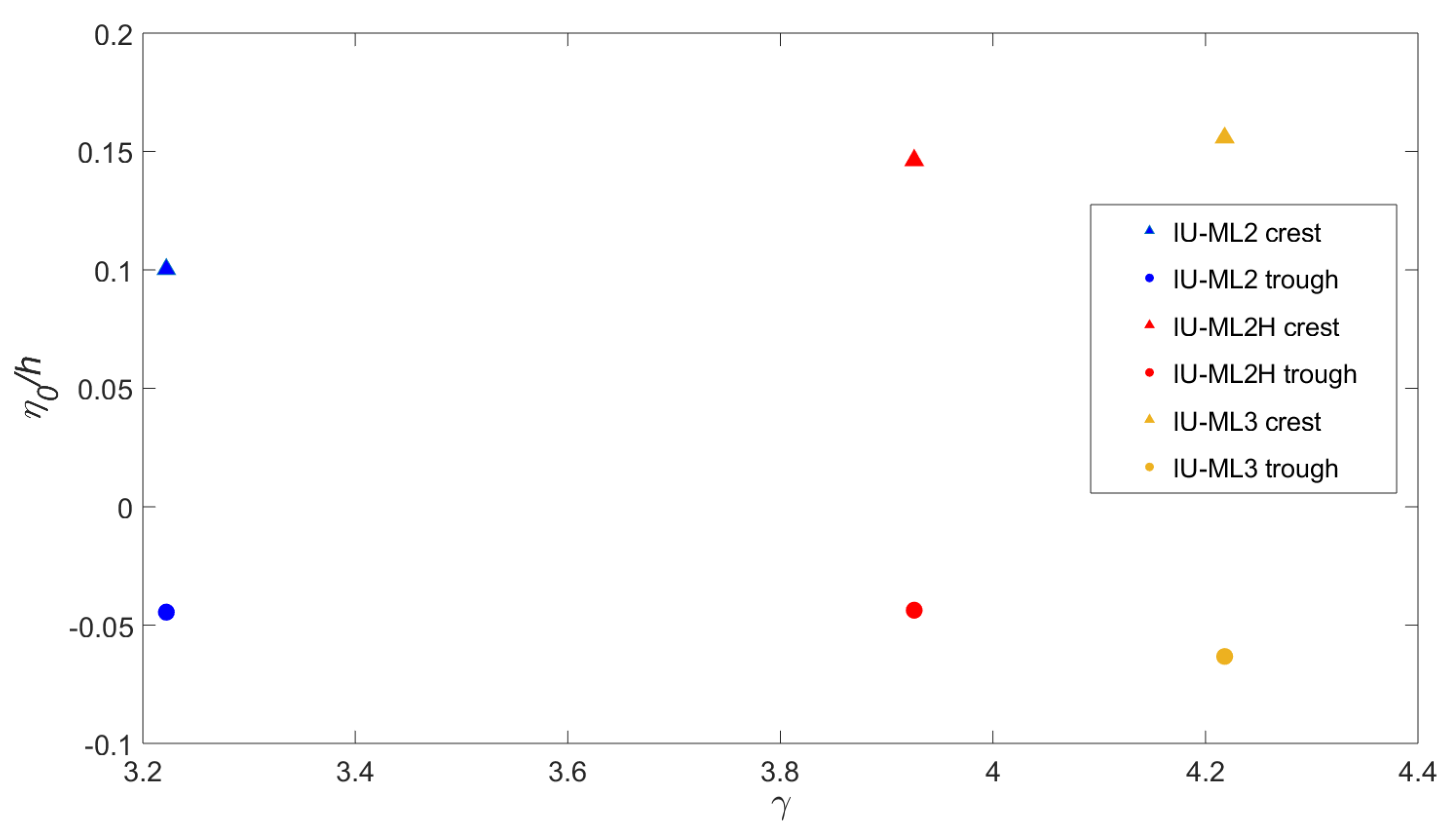
- The landslide weight was seen to have a large effect on the level of agreement of the measured and theoretical predictions. For the same uplift magnitude of 60 mm, the lightest model ML2 (Figure 7c) exhibits the worst agreement, the medium mass model ML2+ (Figure 7b) exhibits slightly better agreement, and the largest model ML3 (Figure 7e) shows by far the best agreement. N.B. Model ML3 was thicker as well as heavier.
- As described in Section 2.3, ML3 consisted of twenty slices which were joined together with tape, which flexed as the landslide hit the end of the slope, enabling it to slightly adapt its shape as it moved onto the horizontal bed. For the case of the granular landslide ML3B (Figure 7f), the landslide is seen to travel slightly more slowly than ML3 (Figure 7e), possibly due to the spreading effect of the individual slices of ML3B during its motion, as opposed to ML3, which remained as a whole.
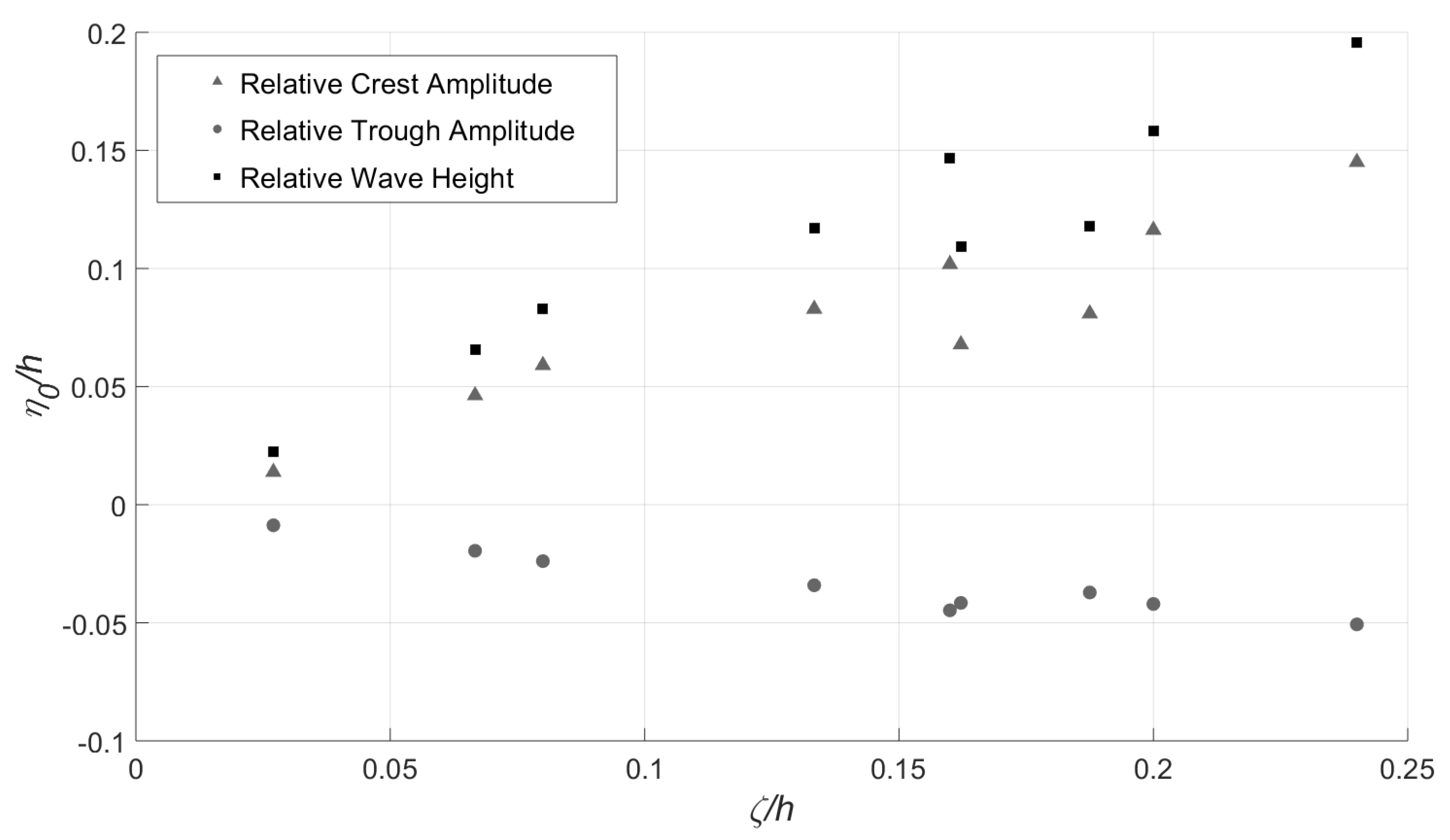
3.3. Effect of the Uplift Displacement on the Generated Wave
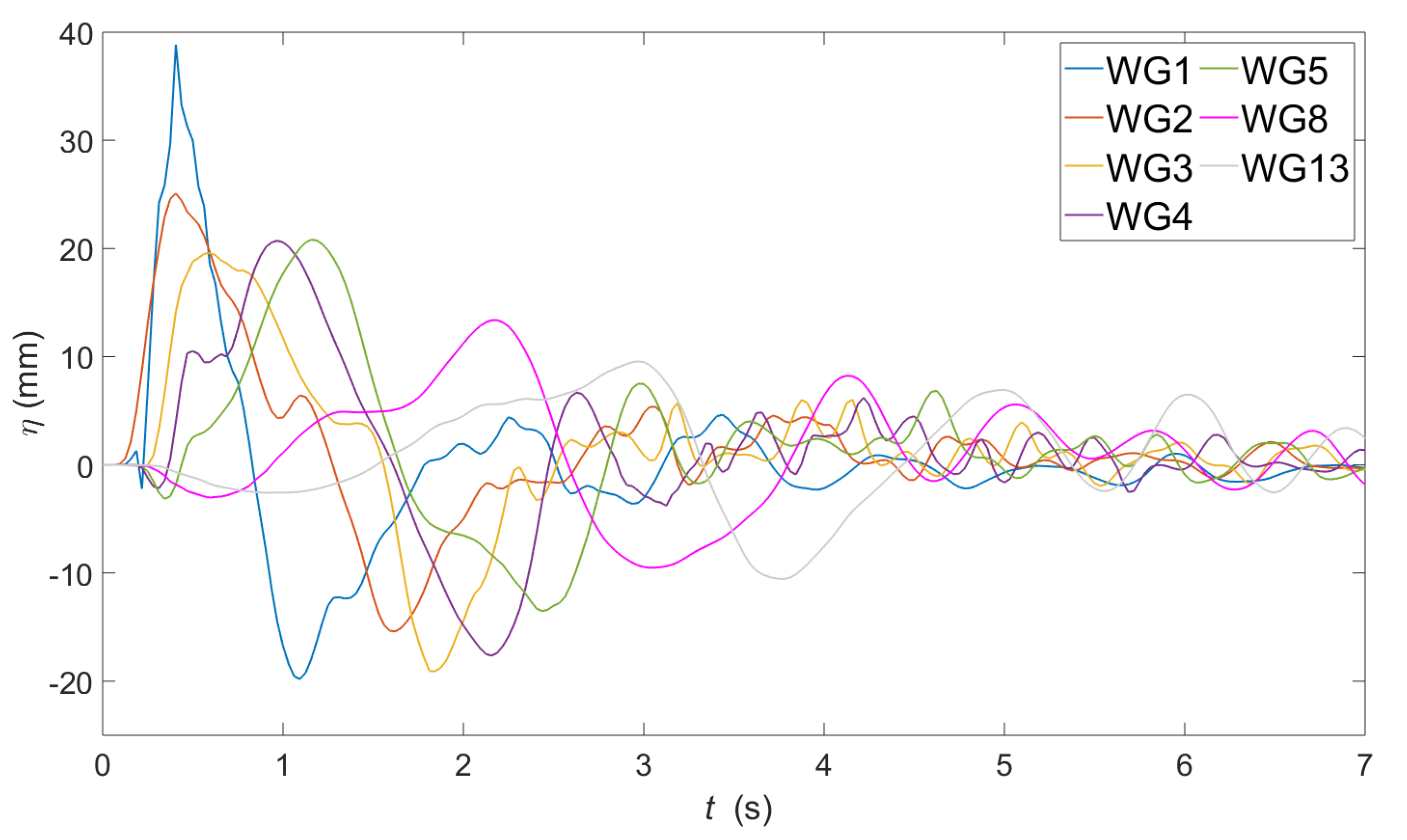
3.4. Effect of the Landslide Motion and Geometry on the Generated Wave
3.5. Effect of a Coupled Mechanism on the Generated Wave
4. Discussion
Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
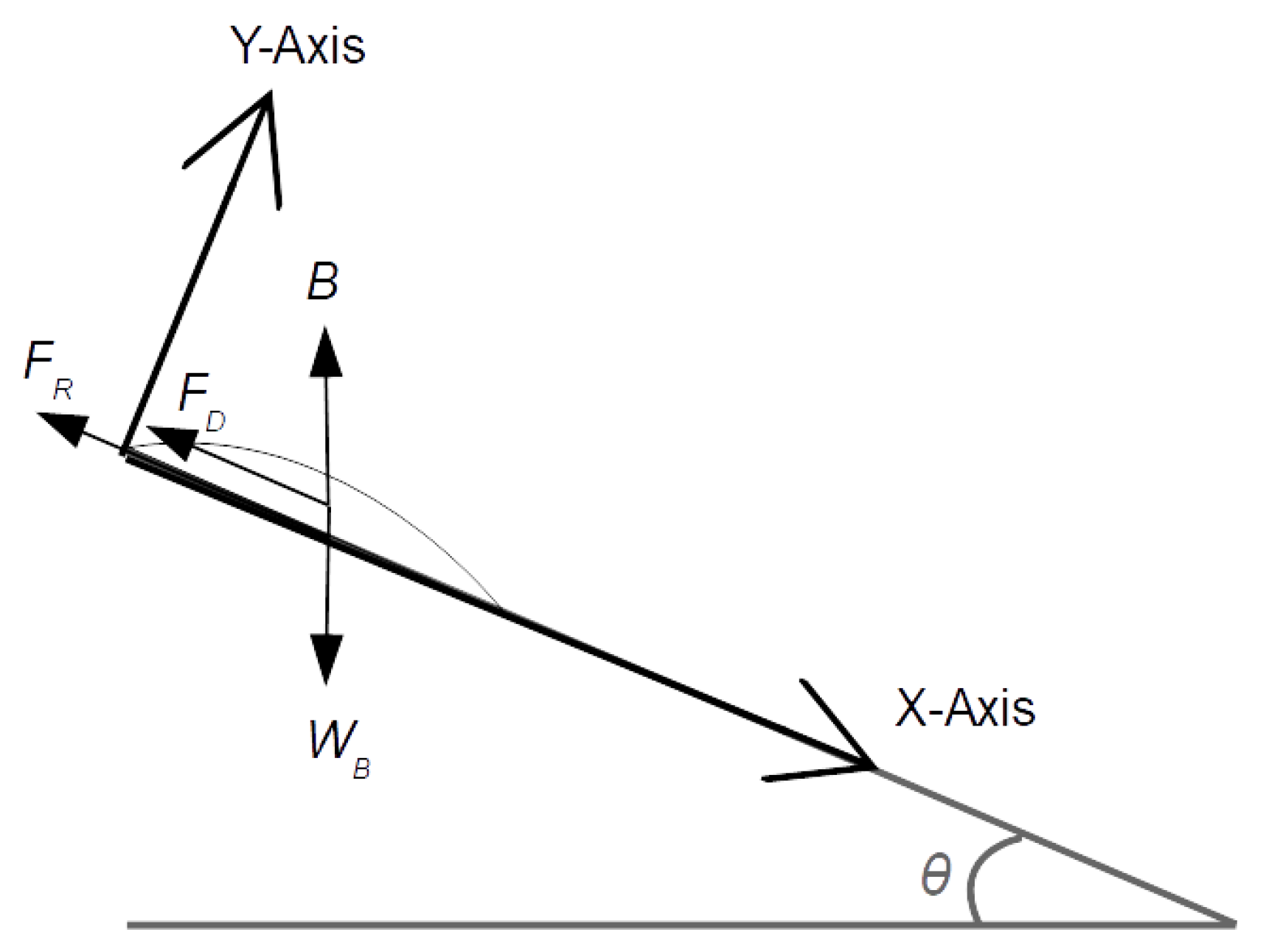
Appendix A. Theoretical Formulation for Landslide Motion
References
- Okal, E.A. Seismic parameters controlling far-field tsunami amplitudes: A review. Nat. Hazards 1988, 1, 67–96. [Google Scholar] [CrossRef]
- Kajiura, K. Tsunami source, energy and directivity of wave radiation. Bull. Earthq. Res. Inst. 1970, 48, 835–869. [Google Scholar]
- Fine, I.V.; Rabinovich, A.B.; Bornhold, B.D.; Thomson, R.E.; Kulikov, E.A. The Grand Banks landslide-generated tsunami of November 18, 1929: Preliminary analysis and numerical modeling. Mar. Geol. 2005, 215, 45–57. [Google Scholar] [CrossRef]
- Kawata, Y.; Benson, B.C.; Borrero, J.C.; Borrero, J.L.; Davies, H.L.; Lange, W.P.; Imamura, F.; Letz, H.; Nott, J.; Synolakis, C.E. Tsunami in Papua New Guinea was as intense as first thought. Eos Trans. Am. Geophys. Union 1999, 80, 101–105. [Google Scholar] [CrossRef]
- Tappin, D.R.; Watts, P.; McMurtry, G.M.; Matsumoto, T. Offshore evidence on the source of the 1998 Papua New Guinea tsunami: A sediment slump. In Proceedings of the International Tsunami Symposium, Seattle, WA, USA, 7–10 August 2001; Volume 175, pp. 381–388. [Google Scholar]
- Synolakis, C.E.; Bardet, J.P.; Borrero, J.C.; Davies, H.L.; Okal, E.A.; Silver, E.A.; Sweet, S.; Tappin, D.R. The slump origin of the 1998 Papua New Guinea Tsunami. Proc. R. Soc. Math. Phys. Eng. Sci. 2002, 458, 763–789. [Google Scholar] [CrossRef]
- Heinrich, P.; Guibourg, S.; Roche, R. Numerical modeling of the 1960 Chilean tsunami. Impact on French Polynesia. Phys. Chem. Earth 1996, 21, 19–25. [Google Scholar] [CrossRef]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Todorovska, M.I.; Trifunac, M.D. Generation of tsunamis by a slowly spreading uplift of the sea floor. Soil Dyn. Earthq. Eng. 2001, 21, 151–167. [Google Scholar] [CrossRef]
- Kowalik, Z.; Knight, W.; Logan, T.; Whitmore, P. The tsunami of 26 December, 2004: Numerical modeling and energy considerations. Pure Appl. Geophys. 2007, 164, 379–393. [Google Scholar] [CrossRef]
- Hammack, J.L. A note on tsunamis: Their generation and propagation in an ocean of uniform depth. J. Fluid Mech. 1973, 60, 769–799. [Google Scholar] [CrossRef]
- Iwasaki, S. Experimental study of a tsunami generated by a horizontal motion of a sloping bottom. Bull. Earthq. Res. Inst. 1982, 57, 239–262. [Google Scholar]
- Jamin, T.; Gordillo, L.; Ruiz-Chavarria, G.; Berhanu, M.; Falcon, E. Experiments on generation of surface waves by an underwater moving bottom. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Impulse product parameter in landslide generated impulse waves. J. Waterw. Port Coast. Ocean. Eng. 2010, 136, 145–155. [Google Scholar] [CrossRef]
- Heller, V.; Spinneken, J. Improved landslide-tsunami prediction: Effects of block model parameters and slide model. J. Geophys. Res. Ocean. 2013, 118, 1489–1507. [Google Scholar] [CrossRef]
- Heller, V.; Bruggemann, M.; Spinneken, J.; Rogers, B.D. Composite modelling of subaerial landslide–tsunamis in different water body geometries and novel insight into slide and wave kinematics. Coast. Eng. 2016, 109, 20–41. [Google Scholar] [CrossRef]
- Evers, F.M.; Hager, W. Generation and spatial propagation of landslide generated impulse waves. Coast. Eng. Proc. 2017, 1, 13. [Google Scholar] [CrossRef]
- Assier-Rzadkieaicz, S.; Heinrich, P.; Sabatier, P.C.; Savoye, B.; Bourillet, J.F. Numerical modelling of a landslide-generated tsunami: The 1979 Nice event. Pure Appl. Geophys. 2000, 157, 1707–1727. [Google Scholar] [CrossRef]
- Tinti, S.; Pagnoni, G.; Zaniboni, F. The landslides and tsunamis of the 30th of December 2002 in Stromboli analysed through numerical simulations. Bull. Volcanol. 2006, 68, 462–479. [Google Scholar] [CrossRef]
- Heinrich, P.; Piatanesi, A.; Hébert, H. Numerical modelling of tsunami generation and propagation from submarine slumps: The 1998 Papua New Guinea event. Geophys. J. Int. 2001, 145, 97–111. [Google Scholar] [CrossRef]
- Lynett, P.; Liu, P.L.F. A numerical study of submarine-landslide-generated waves and run-up. Proc. R. Soc. Math. Phys. Eng. Sci. 2002, 458, 2885–2910. [Google Scholar] [CrossRef]
- Bondevik, S.; Løvholt, F.; Harbitz, C.; Mangerud, J.; Dawson, A.; Svendsen, J.I. The Storegga Slide tsunami—Comparing field observations with numerical simulations. In Ormen Lange—An Integrated Study for Safe Field Development in the Storegga Submarine Area; Elsevier: New York, NY, USA, 2005; pp. 195–208. [Google Scholar]
- Watts, P. Tsunami features of solid block underwater landslides. J. Waterw. Port Coast. Ocean. Eng. 2000, 2, 144–152. [Google Scholar] [CrossRef]
- Sue, L.P. Modelling of Tsunami Generated by Submarine Landslides. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2007. [Google Scholar]
- Van Nieuwkoop, J.C.C. Experimental and Numerical Modelling of Tsunami Waves Generated by Landslides. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Wiegel, R.L. Laboratory studies of gravity waves generated by the movement of a submerged body. Eos Trans. Am. Geophys. Union 1955, 36, 759–774. [Google Scholar] [CrossRef]
- Watts, P.; Grilli, S.T. Underwater landslide shape, motion, deformation, and tsunami generation. Int. Offshore Polar Eng. Conf. 2003, 5, 364–371. [Google Scholar]
- Heller, V.; Hager, W.H. Wave types of landslide generated impulse waves. Ocean. Eng. 2011, 38, 630–640. [Google Scholar] [CrossRef]
- Mohammed, F.; Fritz, H.M. Physical modeling of tsunamis generated by three-dimensional deformable granular landslides. J. Geophys. Res. Ocean. 2012, 118, 3221. [Google Scholar] [CrossRef]
- Hammack, J.L. Tsunamis—A Model of Their Generation and Propagation. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1972. [Google Scholar]
- Philip, W.; Fumihiko, I.; Aaron, B.; Grilli, S.T. Benchmark cases for tsunamis generated by underwater landslides. In Proceedings of the Fourth International Symposium on Ocean Wave Measurement and Analysis, San Francisco, CA, USA, 2–6 September 2001. [Google Scholar] [CrossRef]
- Perez del Postigo, N.; Raby, A.; Whittaker, C.; Boulton, S.J. Tsunami generation by combined fault rupture and landsliding. In Proceedings of the 7th International Conference on the Application of Physical Modelling in Coastal and Port Engineering and Science (Coastlab18), Santander, Spain, 22–26 May 2018; pp. 1–10. [Google Scholar]
- Grilli, S.T.; Vogelmann, S.; Watts, P. Development of a 3D numerical wave tank for modeling tsunami generation by underwater landslides. Eng. Anal. Bound. Elem. 2002, 26, 301–313. [Google Scholar] [CrossRef]
- Whittaker, C.; Nokes, R.; Davidson, M. Tsunami forcing by a low Froude number landslide. Environ. Fluid Mech. 2015, 15, 1215–1239. [Google Scholar] [CrossRef]
- Wana, R.; Perez, N.; Hughes, J.; Graham, D.; Raby, A.; Whittaker, C. Smoothed Particle Hydrodynamics (SPH) modelling of tsunami waves generated by a fault rupture. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2019. [Google Scholar]
- Heller, V.; Hager, W.H.; Minor, H.E. Scale effects in subaerial landslide generated impulse waves. Exp. Fluids 2008, 44, 691–703. [Google Scholar] [CrossRef]



| WG1 | WG2 | WG3 | WG4 | WG5 | WG6 | WG7 | WG8 | WG9 | WG10 | WG11 | WG12 | WG13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (m) | 0 | 0.64 | 0.87 | 1.25 | 1.657 | 2.657 | 2.907 | 3.157 | 3.457 | 3.757 | 4.047 | 4.357 | 4.657 |
| 0.77 | 0.08 | 1.2 | 6.63 |
| 0.67 | 0.16 | 1.2 | 6.75 |
| 0.62 | 0.24 | 1.2 | 10.16 |
| 0.71 | 0.06 | 1.0 | 7.69 |
| 0.62 | 0.13 | 1.0 | 9.30 |
| 0.59 | 0.20 | 1.0 | 7.38 |
| 0.43 | 0.19 | 0.94 | 0.09 |
| 0.58 | 0.03 | 0.81 | 2.54 |
| 0.64 | 0.16 | 0.81 | 2.54 |
| Model | Mass (kg) | (m/s) | (m) | (s) | Reynolds Number | Froude Number | |||
|---|---|---|---|---|---|---|---|---|---|
| ML2 | 8.7 | 1.09 | 0.40 | 0.36 | 3.22 | 0.7 | 0.15 | 3.23 | 0.64 |
| ML2+ | 10.6 | 1.35 | 0.45 | 0.34 | 3.93 | 0.7 | 0.15 | 4.04 | 0.78 |
| ML3 | 20.5 | 1.26 | 0.53 | 0.42 | 4.22 | 0.75 | 0.15 | 3.79 | 0.74 |
| ML3B | 20.5 | 1.16 | 0.45 | 0.39 | 4.22 | 0.75 | 0.15 | 3.49 | 0.68 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez del Postigo Prieto, N.; Raby, A.; Whittaker, C.; Boulton, S.J. Parametric Study of Tsunamis Generated by Earthquakes and Landslides. J. Mar. Sci. Eng. 2019, 7, 154. https://doi.org/10.3390/jmse7050154
Perez del Postigo Prieto N, Raby A, Whittaker C, Boulton SJ. Parametric Study of Tsunamis Generated by Earthquakes and Landslides. Journal of Marine Science and Engineering. 2019; 7(5):154. https://doi.org/10.3390/jmse7050154
Chicago/Turabian StylePerez del Postigo Prieto, Natalia, Alison Raby, Colin Whittaker, and Sarah J. Boulton. 2019. "Parametric Study of Tsunamis Generated by Earthquakes and Landslides" Journal of Marine Science and Engineering 7, no. 5: 154. https://doi.org/10.3390/jmse7050154
APA StylePerez del Postigo Prieto, N., Raby, A., Whittaker, C., & Boulton, S. J. (2019). Parametric Study of Tsunamis Generated by Earthquakes and Landslides. Journal of Marine Science and Engineering, 7(5), 154. https://doi.org/10.3390/jmse7050154





