Simulation of the Behavior of a Ship Hull under Grounding: Effect of Applied Element Size on Structural Crashworthiness
Abstract
:1. Introduction
2. Brief Review of Pioneering Works
2.1. Structural Performance Studies
2.2. Methods for the Simulation of Impact Phenomena
3. Analysis Methods
3.1. Calculation Algorithm
3.2. Geometry and Material
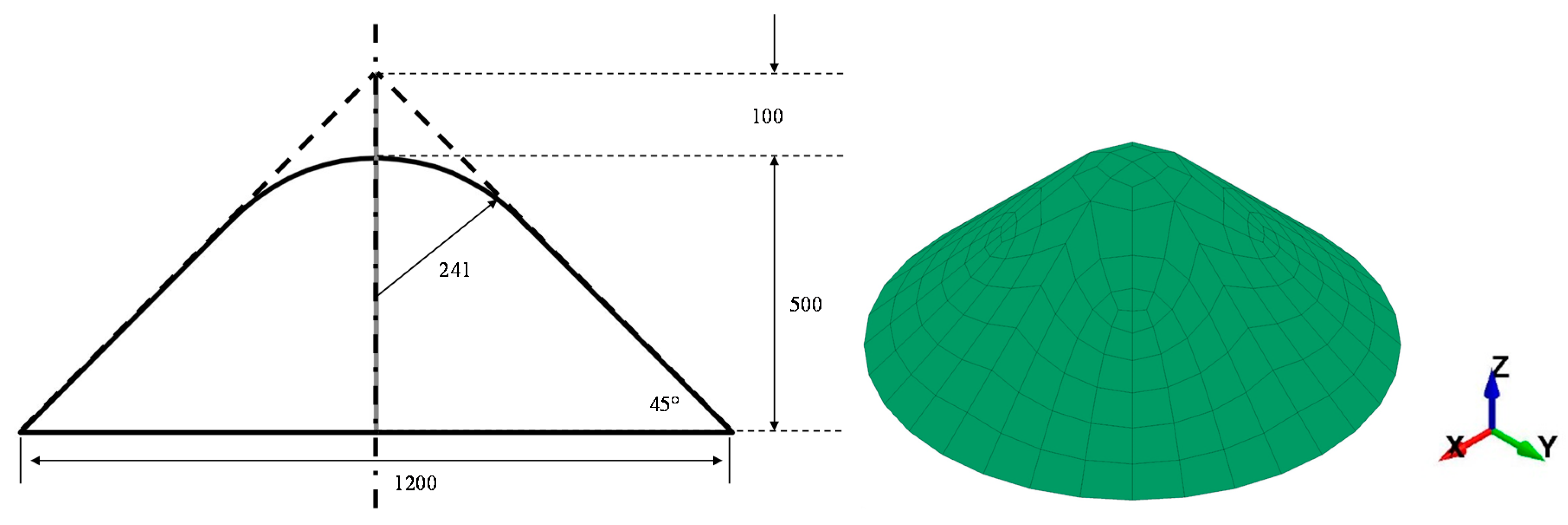
3.3. Rock Parameters
3.4. Design of Accident Scenario
4. Structural Crashworthiness of Tanker
4.1. Internal Energy
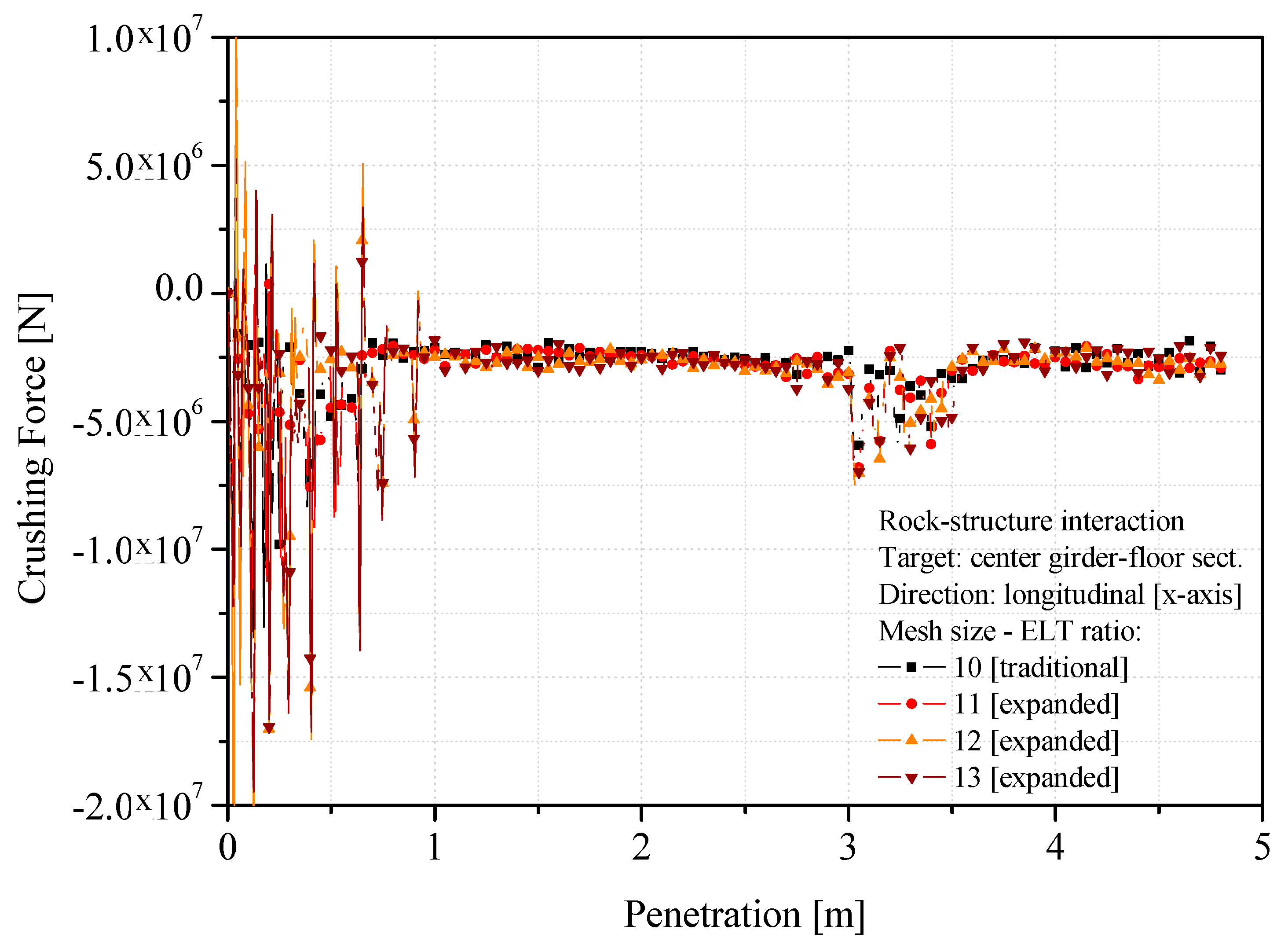
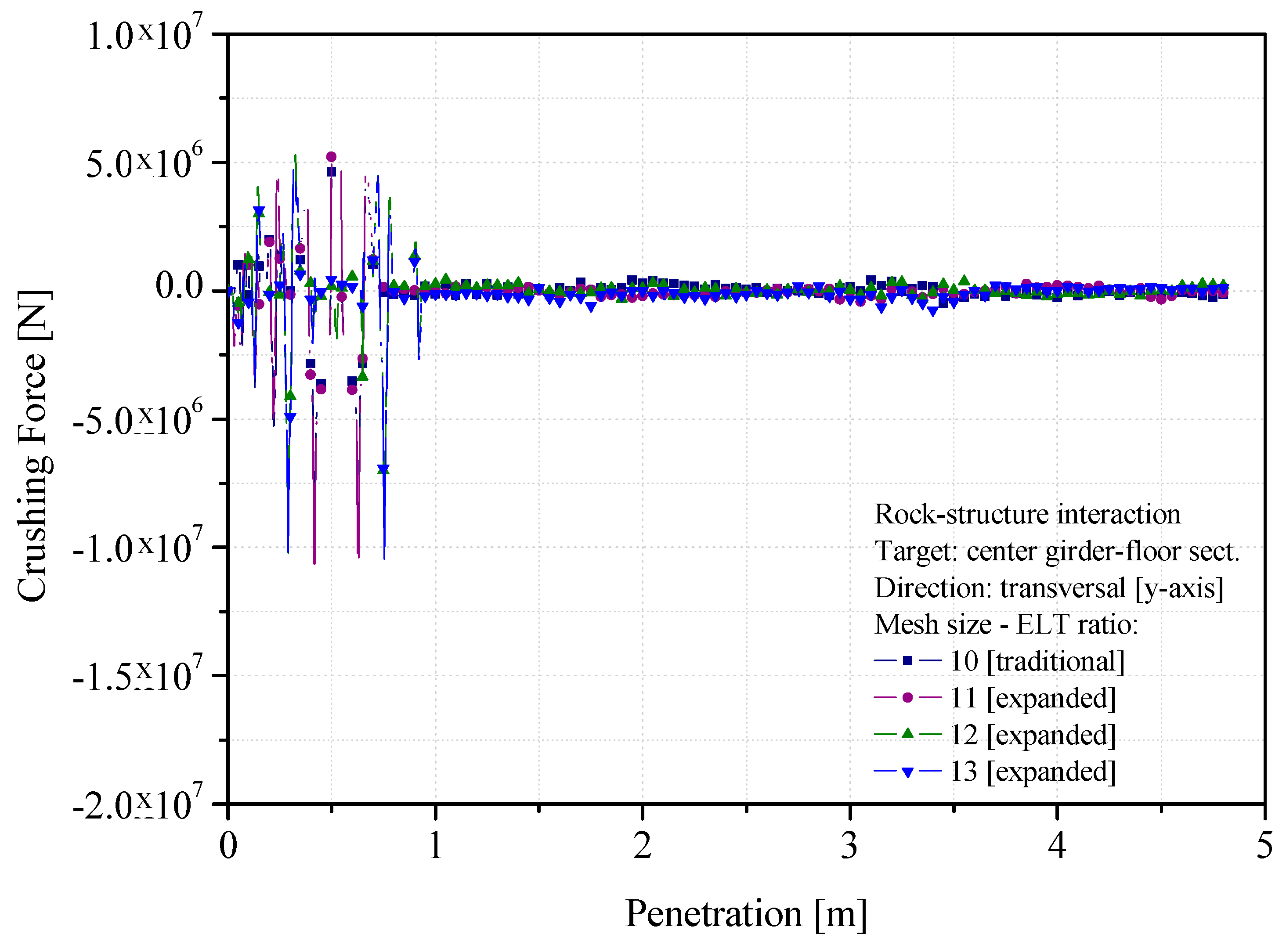
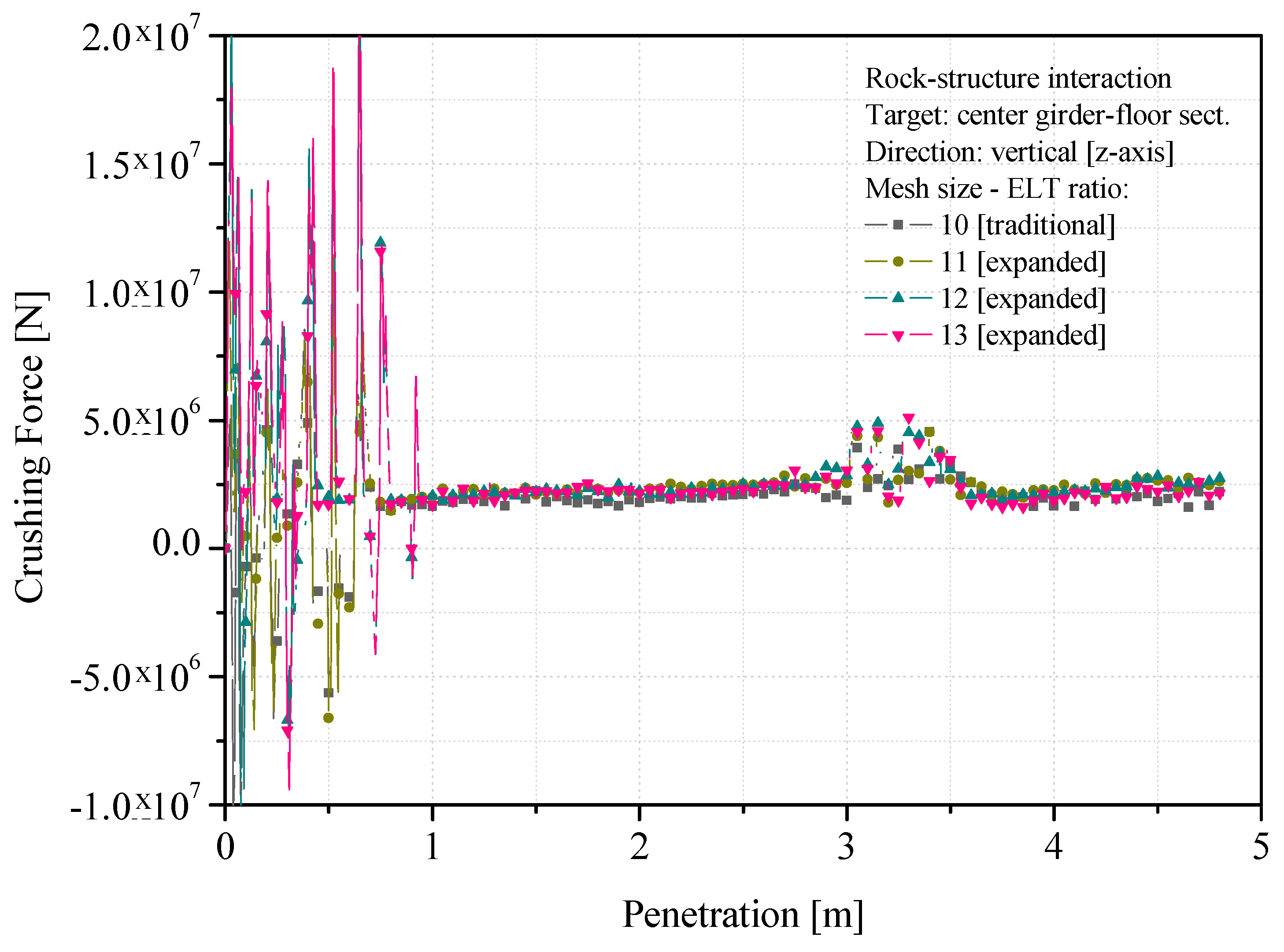
4.2. Crushing Force
4.3. Damage Pattern
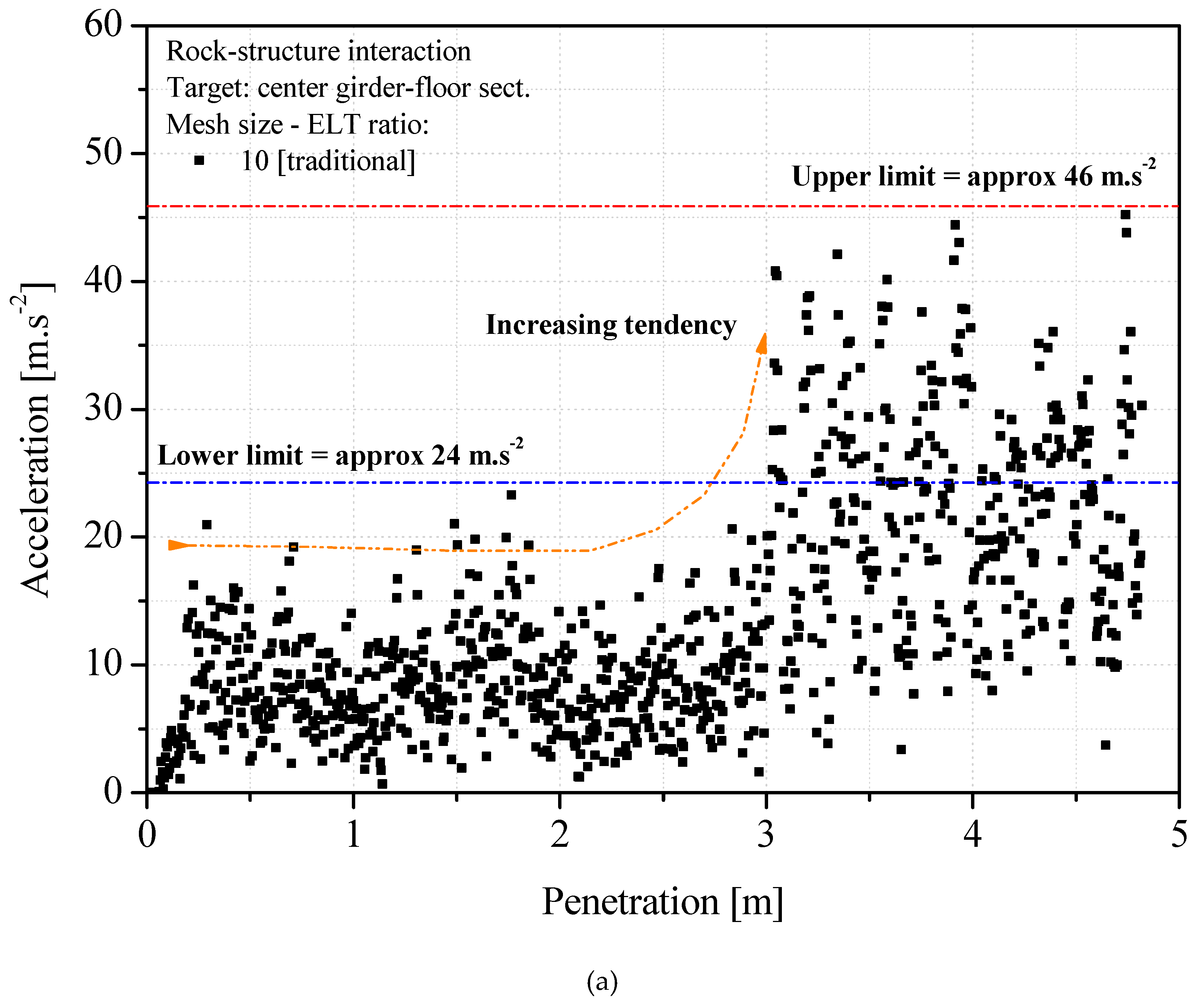
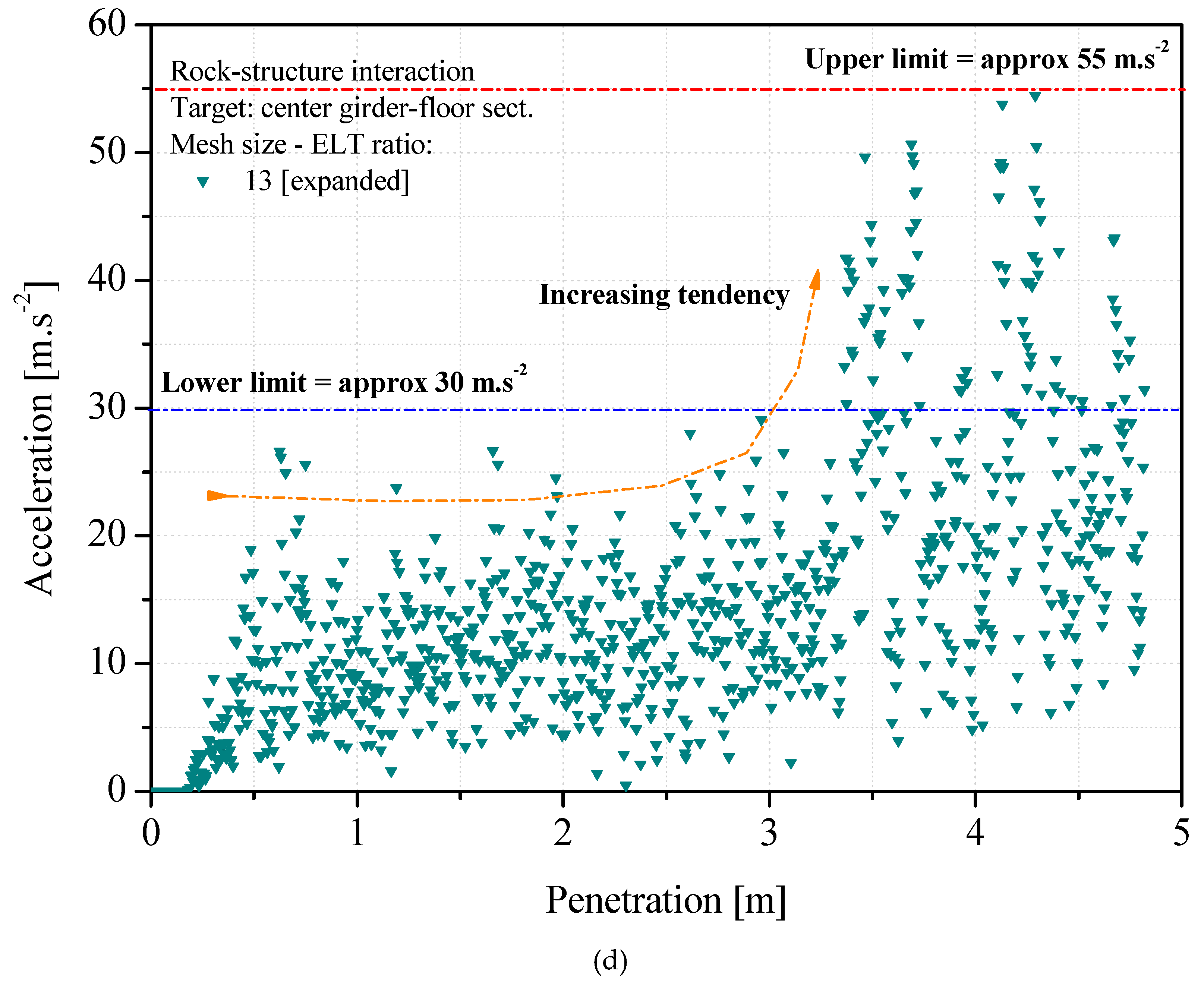
4.4. Structural Acceleration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tabri, K.; Matusiak, J.; Varsta, P. Sloshing interaction in ship collisions—An experimental and numerical study. Ocean Eng. 2009, 36, 1366–1376. [Google Scholar] [CrossRef]
- Pedersen, P.T. Review and application of ship collision and grounding analysis procedures. Mar. Struct. 2010, 23, 241–262. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Muttaqie, T.; Sohn, J.M.; Bae, D.M. Nonlinear analysis of inter-island RoRo under impact: Effects of selected collision’s parameters on the crashworthy double-side structures. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 248. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Alsos, H.S.; Amdahl, J. On the resistance of tanker bottom structures during stranding. Mar. Struct. 2007, 20, 218–237. [Google Scholar] [CrossRef]
- Kõrgesaar, M. The effect of low stress triaxialities and deformation paths on ductile fracture simulations of large shell structures. Mar. Struct. 2019, 63, 45–64. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Bahatmaka, A.; Cho, J.H.; Sohn, J.M.; Bae, D.M.; Samuel, S.; Cao, B. Analysis of Structural Crashworthiness on a Non-Ice Class Tanker during Stranding Accounting for the Sailing Routes; Soares, C.G., Teixeira, A.P., Eds.; Taylor & Francis Group: London, UK, 2018. [Google Scholar]
- Ozguc, O.; Das, P.K.; Barltrop, N. A comparative study on the structural integrity of single and double side skin bulk carriers under collision damage. Mar. Struct. 2005, 18, 511–547. [Google Scholar] [CrossRef]
- Haris, S.; Amdahl, J. Analysis of ship–ship collision damage accounting for bow and side deformation interaction. Mar. Struct. 2013, 32, 18–48. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Bae, D.M.; Sohn, J.M.; Zakki, A.F.; Cao, B.; Cho, J.H. Effects of the rebounding of a striking ship on structural crashworthiness during ship-ship collision. Thin-Walled Struct. 2017, 115, 225–239. [Google Scholar] [CrossRef]
- Yu, Z.; Hu, Z.; Amdahl, J.; Liu, Y. Investigation on structural performance predictions of double-bottom tankers during shoal grounding accidents. Mar. Struct. 2013, 33, 188–213. [Google Scholar] [CrossRef]
- Sormunen, O.V.E.; Kõrgesaar, M.; Tabri, K.; Heinvee, M.; Urbel, A.; Kujala, P. Comparing rock shape models in grounding damage modelling. Mar. Struct. 2016, 50, 205–223. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Bae, D.M.; Cho, J.H.; Sohn, J.M. Characteristic of double bottom responses under powered-hard grounding scenario with idealised rock indenter. Int. J. Struct. Eng. 2018, 9, 130–144. [Google Scholar] [CrossRef]
- Qiankun, J.; Gangyi, D. A finite element analysis of ship sections subjected to underwater explosion. Int. J. Impact Eng. 2011, 38, 558–566. [Google Scholar] [CrossRef]
- Ming, F.R.; Zhang, A.M.; Xue, Y.Z.; Wang, S.P. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions. Ocean Eng. 2016, 117, 359–382. [Google Scholar] [CrossRef]
- Minorsky, V.U. An analysis of ship collision with reference to protection of nuclear power ships. J. Ship Res. 1958, 3, 1–4. [Google Scholar]
- Woisin, G. Design against collision. Schiff Hafen 1979, 31, 1059–1069. [Google Scholar]
- Simonsen, B.C.; Törnqvist, R. Experimental and numerical modelling of ductile crack propagation in large-scale shell structures. Mar. Struct. 2004, 17, 1–27. [Google Scholar] [CrossRef]
- Alsos, H.S.; Amdahl, J. On the resistance to penetration of stiffened plates, Part I—Experiments. Int. J. Impact Eng. 2009, 36, 799–807. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Bae, D.M.; Sohn, J.M.; Zakki, A.F.; Cao, B.; Wang, Q. Analysis of structural damage on the struck ship under side collision scenario. Alex. Eng. J. 2018, 57, 1761–1771. [Google Scholar] [CrossRef]
- Reardon, P.; Sprung, J.L. Validation of Minorsky’s ship collision model and use of the model to estimate the probability of damaging a radioactive material transportation cask during a ship collision. In Proceedings of the International Conference on Design and Methodologies for Collision and Grounding Protection of Ships, San Francisco, CA, USA, 22–23 August 1996. [Google Scholar]
- Zhiqiang, H.; Jørgen, A.; Lin, H. Verification of a simplified analytical method for predictions of ship groundings over large contact surfaces by numerical simulations. Mar. Struct. 2011, 24, 436–458. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Sohn, J.M.; Bae, D.M.; Setiyawan, A. Crashworthiness assessment of thin-walled bottom structures during powered-hard grounding accidents. In Proceedings of the ASME 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar] [CrossRef]
- AbuBakar, A.; Dow, R.S. Simulation of ship grounding damage using the finite element method. Int. J. Solids Struct. 2013, 50, 623–636. [Google Scholar] [CrossRef] [Green Version]
- Zong, Z.; Zhao, Y.; Li, H. A numerical study of whole ship structural damage resulting from close-in underwater explosion shock. Mar. Struct. 2013, 31, 24–43. [Google Scholar] [CrossRef]
- ANSYS. ANSYS LS-DYNA User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- ANSYS. ANSYS Mechanical APDL Element Reference; ANSYS, Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Camargo, F.V.D. Survey on experimental and numerical approaches to model underwater explosions. J. Mar. Sci. Eng. 2019, 7, 15. [Google Scholar] [CrossRef]
- Zhang, S. The Mechanics of Ship Collisions; Technical University of Denmark: Lyngby, Denmark, 1999. [Google Scholar]
- Wierzbicki, T.; Thomas, P. Closed form solution for wedge cutting force through thin metal sheets. Int. J. Mech. Sci. 1993, 35, 209–229. [Google Scholar] [CrossRef]
- Simonsen, B.C.; Wierzbicki, T. Plasticity, fracture and friction in steady state plate cutting. Int. J. Impact Eng. 1998, 21, 387–411. [Google Scholar] [CrossRef]
- Lamb, T.; Brown, R.L. The size and speed of tankers: Recent improvements in construction. Naval Eng. J. 1952, 64, 161–168. [Google Scholar] [CrossRef]
- Törnqvist, R. Design of Crashworthy Ship Structures; Technical University of Denmark: Lyngby, Denmark, 2003. [Google Scholar]
- Prabowo, A.R. Crashworthiness Assessment of Ship Structures under Collision and Grounding; Pukyong National University: Busan, South Korea, 2018. [Google Scholar]
- Prusty, B.G.; Satsangi, S.K. Analysis of stiffened shell for ships and ocean structures by finite element method. Ocean Eng. 2001, 28, 621–638. [Google Scholar] [CrossRef]






| Author | Phenomenon | Subject | Conclusions |
|---|---|---|---|
| Ozguc et al. [8] | Collision | Bulk carrier | The collision energy absorption capability depends on the thickness of structural parts, such as the outer and inner shells and side stringers. |
| Haris and Amdahl [9] | Collision | Shuttle tanker | Collisions in which both ships deform. The damage and energy dissipation switches between ships during the collision. |
| Prabowo et al. [10] | Collision | Passenger ship; Tanker; Reefer cargo | It was demonstrated that the structural crashworthiness of the struck ship during rebounding was different than for fully stuck cases. |
| Author | Phenomenon | Subject | Conclusions |
|---|---|---|---|
| Yu et al. [11] | Grounding | Tanker | Up to an indentation of 90% of the double-bottom height, other double-bottom structural components contribute little to the total energy dissipation during distortion; therefore, it can be neglected. |
| Sormunen et al. [12] | Grounding | Tanker | The relationship between the volume of damaged material and the real rock area or model projected area was found to be linear for the whole grounding simulation and less than the vertical phase of the grounding model. |
| Prabowo et al. [13] | Grounding | Tanker | The bottom shell was found to be the component which experienced the highest plastic deformation during grounding. |
| Qiankun and Gangyi [14] | Explosion | Idealized as 1/4 of the ship section | The effects of alpha damping to the velocity response were investigated, with the alpha damping significantly reducing at later times and low frequency response considering the effects of hydrodynamic drag. |
| Ming et al. [15] | Explosion | Idealized as a stiffened plate | The detonation wave propagates into the water and the hull plate; therefore, an instantaneous high-pressure is produced on the plate, which is up to 700–800 MPa in a zone whose radius is close to the radius of the charge. The stiffeners seem to have no response during this process. |
| Author | Phenomenon | Method | Conclusions |
|---|---|---|---|
| Prabowo et al. [20] | Collision | Finite element method | Implementation of a wider double hull was considered a good option to increase safety; however, the ship’s capacity would be reduced. |
| Reardon and Sprung [21] | Collision | Empirical approach | Minorsky’s ship collision model was validated and the probability of damaging a radioactive material during collision was estimated. |
| Author | Phenomenon | Method | Conclusions |
|---|---|---|---|
| Zhiqiang et al. [22] | Grounding | Simplified approach; Finite element method | Notably, the vertical component of the grounding force induced heave and pitch motions of the hull. Initial contact was likely to take place in the bow area, where the hull responds most readily to pitch motions. |
| Prabowo et al. [23] | Grounding | Scaled experiment; Finite element method | It was found that the plate tended to provide more resistance in perpendicular grounding, while the internal energy of the stiffener was dominant during oblique groundings. |
| Abubakar and Dow [24] | Grounding | Scaled experiment; Finite element method | The effect of grounding was highly localized in all simulations, with high stress contours only occurring in the area close to the impact. |
| Zong et al. [25] | Explosion | Scaled experiment; Finite element method | Damage modes were classified according to the standoff distance between the charge and the ship. This is helpful for the analysis of the surface of the ship when subjected to underwater explosion. |
| No. | Parameter | Description |
|---|---|---|
| 1 | Vessel type | Chemical tanker |
| 2 | Structural arrangement | Double hull |
| 3 | Specific class | Non-ice operations |
| 4 | Total length (m) | 144 |
| 5 | Width (m) | 22.6 |
| 6 | Depth (m) | 12.5 |
| 7 | Draft (m) | 9.2 |
| No. | Property/Parameter | Description |
|---|---|---|
| 1 | Material model | Plastic-kinematic model |
| 2 | Element type | Shell |
| 3 | Characteristic | Deformable |
| 4 | Density (kg m−3) | 7850 |
| 5 | Elastic modulus (MPa) | 210,000 |
| 6 | Poisson’s ratio | 0.3 |
| 7 | Yield strength (MPa) | 315 |
| 8 | Hardening exponent | 0 |
| 9 | Cowper–Symonds Parameter 1 (C; s−1) | 3200 |
| 10 | Cowper–Symonds Parameter 2 (p) | 5 |
| 11 | Failure strain | 0.2 |
| 12 | Axial constraint | All displacements |
| 13 | Rotational constraint | All rotations |
| No. | Property/Parameter | Description |
|---|---|---|
| 1 | Material model | Rigid |
| 2 | Element type | Solid |
| 3 | Characteristic | Undeformable |
| 4 | Density (kg m−3) | 4002 |
| 5 | Elastic modulus (MPa) | 147,000 |
| 6 | Poisson’s ratio | 0.281 |
| 7 | Axial constraint | y- and z-axis displacements |
| 8 | Rotational constraint | All rotations |
| No. | Selected Ratio | No. of Elements | Simulation Time (s) |
|---|---|---|---|
| 1 | 10 (traditional) | >127,000 | ±4500 |
| 2 | 11 (expanded) | >93,000 | ±2400 |
| 3 | 12 (expanded) | >87,000 | ±2700 |
| 4 | 13 (expanded) | >73,000 | ±1448 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prabowo, A.R.; Putranto, T.; Sohn, J.M. Simulation of the Behavior of a Ship Hull under Grounding: Effect of Applied Element Size on Structural Crashworthiness. J. Mar. Sci. Eng. 2019, 7, 270. https://doi.org/10.3390/jmse7080270
Prabowo AR, Putranto T, Sohn JM. Simulation of the Behavior of a Ship Hull under Grounding: Effect of Applied Element Size on Structural Crashworthiness. Journal of Marine Science and Engineering. 2019; 7(8):270. https://doi.org/10.3390/jmse7080270
Chicago/Turabian StylePrabowo, Aditya Rio, Teguh Putranto, and Jung Min Sohn. 2019. "Simulation of the Behavior of a Ship Hull under Grounding: Effect of Applied Element Size on Structural Crashworthiness" Journal of Marine Science and Engineering 7, no. 8: 270. https://doi.org/10.3390/jmse7080270
APA StylePrabowo, A. R., Putranto, T., & Sohn, J. M. (2019). Simulation of the Behavior of a Ship Hull under Grounding: Effect of Applied Element Size on Structural Crashworthiness. Journal of Marine Science and Engineering, 7(8), 270. https://doi.org/10.3390/jmse7080270






