Modeling Storm Surge Attenuation by an Integrated Nature-Based and Engineered Flood Defense System in the Scheldt Estuary (Belgium)
Abstract
:1. Introduction
2. Materials and Methods
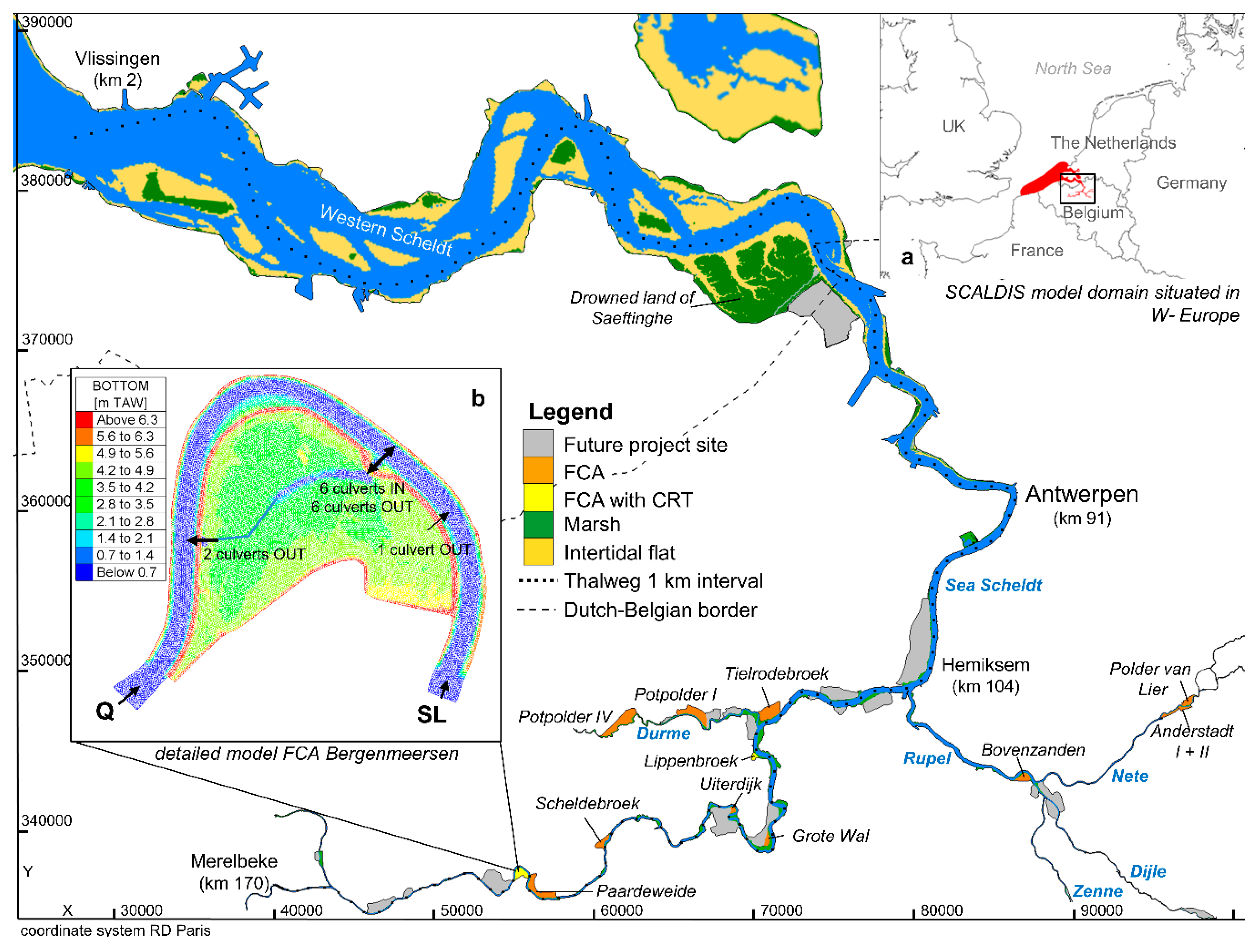
2.1. Study Case
2.1.1. The Scheldt Estuary
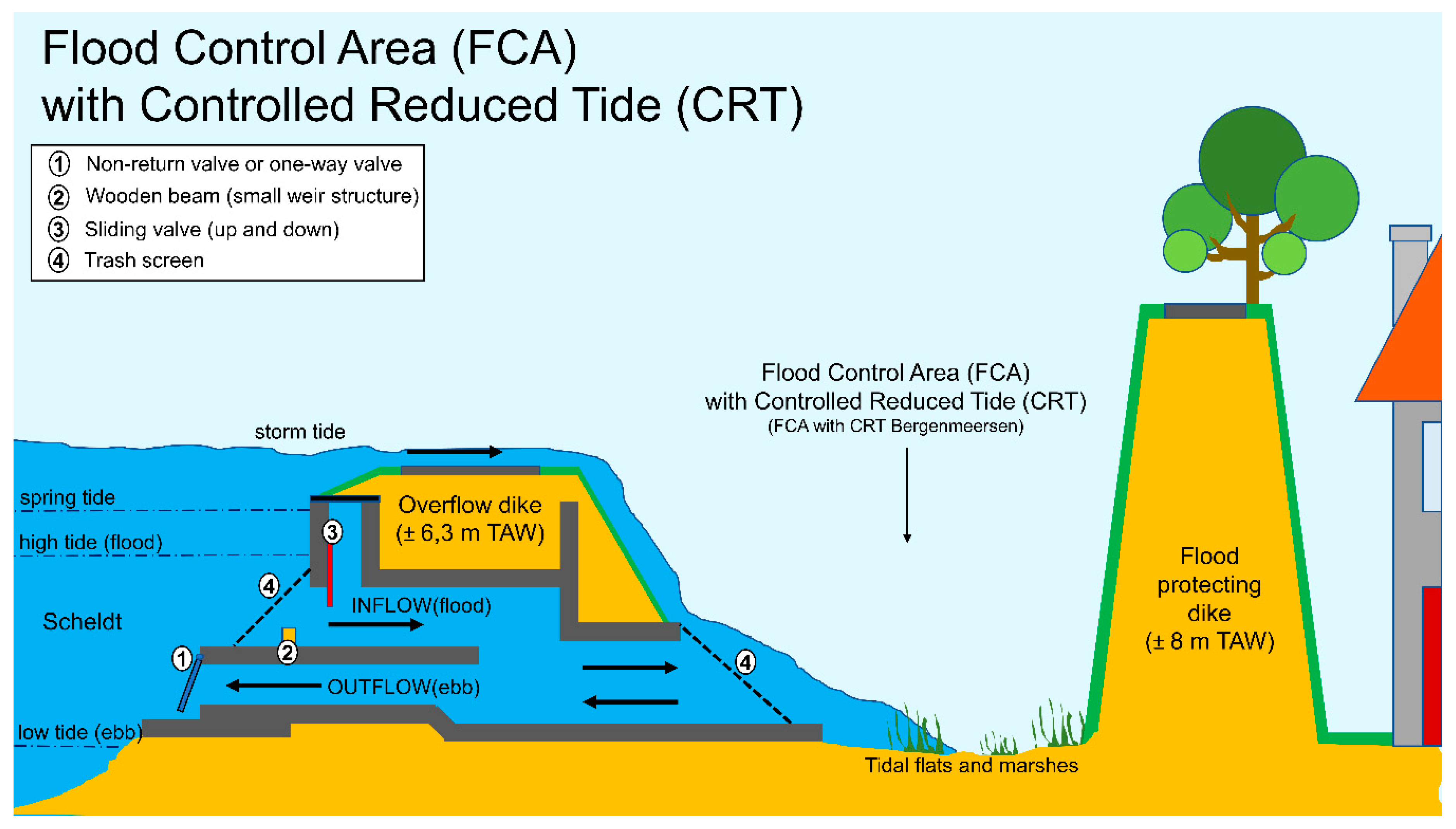
2.1.2. FCAs and CRT
2.2. TELEMAC-3D Model: SCALDIS
2.3. Model Implementation of Culvert Flow
2.3.1. Different Types of Flow
2.3.2. Reformulation of the Equations for Model Implementation
2.3.3. Different Head Loss Coefficients
- (1)
- The entrance head loss represents the head loss due to the contraction of the flow at the entrance of the culvert. An abrupt contraction at the culvert entrance causes a head loss due to the deceleration of the flow immediately after the vena contracta. A head loss coefficient C1, of which the value is a function of the diameter ratio after and before the contraction, is proposed by [48]. For a culvert between a river and a floodplain, the contraction can be seen as very large, estimating the entrance head loss coefficient to be 0.5 according to [48]. Bodhaine [46] noticed that the entrance head loss coefficient C1 for flow type 5 had to be lowered comparatively with the other flow types. The calculated discharge seemed to be overestimated when the default equation was used. Therefore, a correction coefficient C5 is multiplied with entrance head loss coefficient C1 when flow type 5 occurs. An exact value for C5 is not given but according to Bodhaine [46] this coefficient lies in the following interval: 4 ≤ C5 ≤ 10.
- (2)
- The head loss due to pillars inside the culvert: Sometimes, at the entrance of culverts, the flow is divided into two sections by a pillar. This pillar causes additional head loss and is taken into account. According to [48], the head loss coefficient Cp to account for a pillar is given by:where Lp is the thickness of the pillar; b is the distance between two consecutive pillars; and β is a coefficient dependent on the cross-sectional area of the pillar and according to Bodhaine [46] β equals 2.42 for rectangular pillars and 1.67 for rounded pillars; θ stands for the angle of the pillar with the horizontal plane. In most cases, this angle will be 90° and sin θ will be equal to 1.
- (3)
- The head loss due to internal friction: The head loss coefficient C2 takes the head loss inside the culvert due to internal friction into account and is calculated according to [49]:where L is the length of the culvert; n is the Manning Strickler roughness coefficient; R is the wet cross-sectional area in the culvert.
- (4)
- The exit head loss: C3 represents the head loss coefficient due to expansion of the flow exiting the culvert. It is calculated according to [49]:where As and As2 are the sections just in- and outside the downstream end of the culvert.
- (5)
- The head loss due to non-return or one-way valve: All outflow culverts have non-return valves on the estuary side to prevent water from entering the FCA (see number 1 in Figure 2). Depending on the opening, the valve will cause more or less head loss. CV represents the head loss coefficient due to the presence of a non-return valve. For a flap gate valve rotating around hinges at its upper edge, values for CV were obtained experimentally by [48]. Four values for CV are given in Table 3 according to the opening of the valve.like for head loss coefficient C1, a correction coefficient CV5 is multiplied with the head loss coefficient CV to take into account the increase of the head loss when applying flow type 5. Through a number of laboratory experiments with a physical scale-model at Flanders Hydraulics Research, the value for this coefficient was determined to be 1.5 [45].
- (6)
- The head loss due to the presence of a trash screen: Trash screens in front of the inflow and outflow culverts prevent garbage, drift wood, and plant debris from clogging the culverts (indicated by number 4 in Figure 2). The head loss due to the presence of these screens can be estimated by its relationship with the velocity head through the net flow area. The head loss coefficient CT accounting for the presence of a trash screen can be calculated according to [50]:where the ratio of net flow area, Anet, to gross rack area, Agross, is given by AT:
- (7)
- Wooden beams in front of the inflow culvert to function as a small weir: The height of these wooden beams is used to fine tune the moment the flow enters the FCA during flood in the estuary (indicated by number 2 in Figure 2). This structure will not be taken into account with the head loss. Instead, on the side where this wooden weir structure is present, the bottom level of the culvert will be set equal to the top of this wooden weir. For the entrance diameter or opening of the culvert, the height of the small weir will be subtracted from the height of the culvert. This structure makes the overall modelling of the culvert discharge more complicated. However, this assumption provides the correct time of water inflow in an FCA with CRT in the calculations.
- (8)
- Downward sliding valves to close the culvert: Sliding valves were designed to close the culvert for maintenance or to prevent inflow in an FCA with CRT in case of a storm surge. However, in practice, these valves are often used to smother the inflow of the culverts (indicated by number 3 in Figure 2). No additional head loss coefficient is defined for these valves. The length over which these valves are let down is subtracted from the culvert height in the calculations.
2.4. FCA with CRT Bergenmeersen: Detailed 3D Hydrodynamic Model
2.4.1. FCA with CRT Bergenmeersen
2.4.2. Detailed 3D Hydrodynamic Model
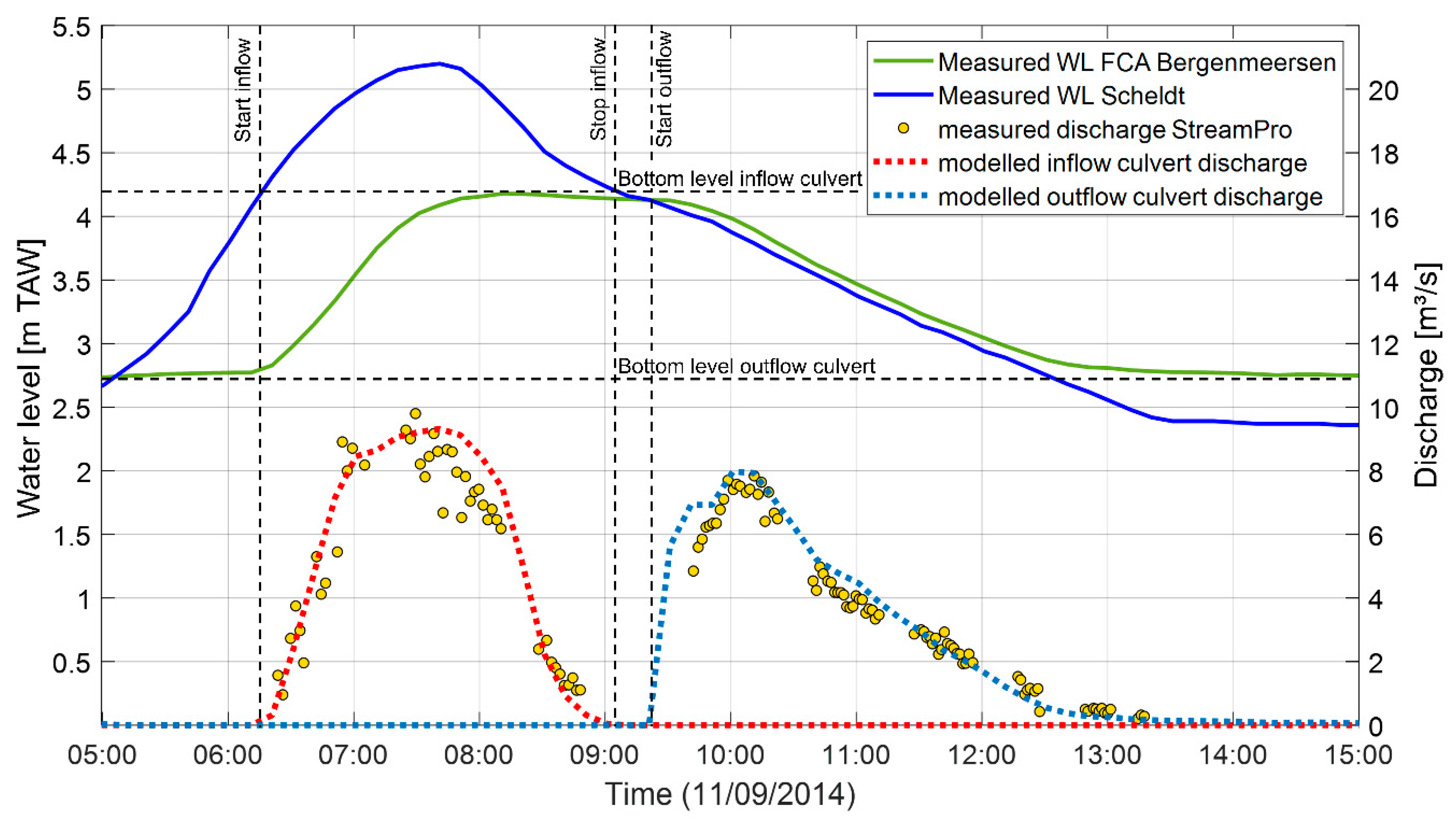
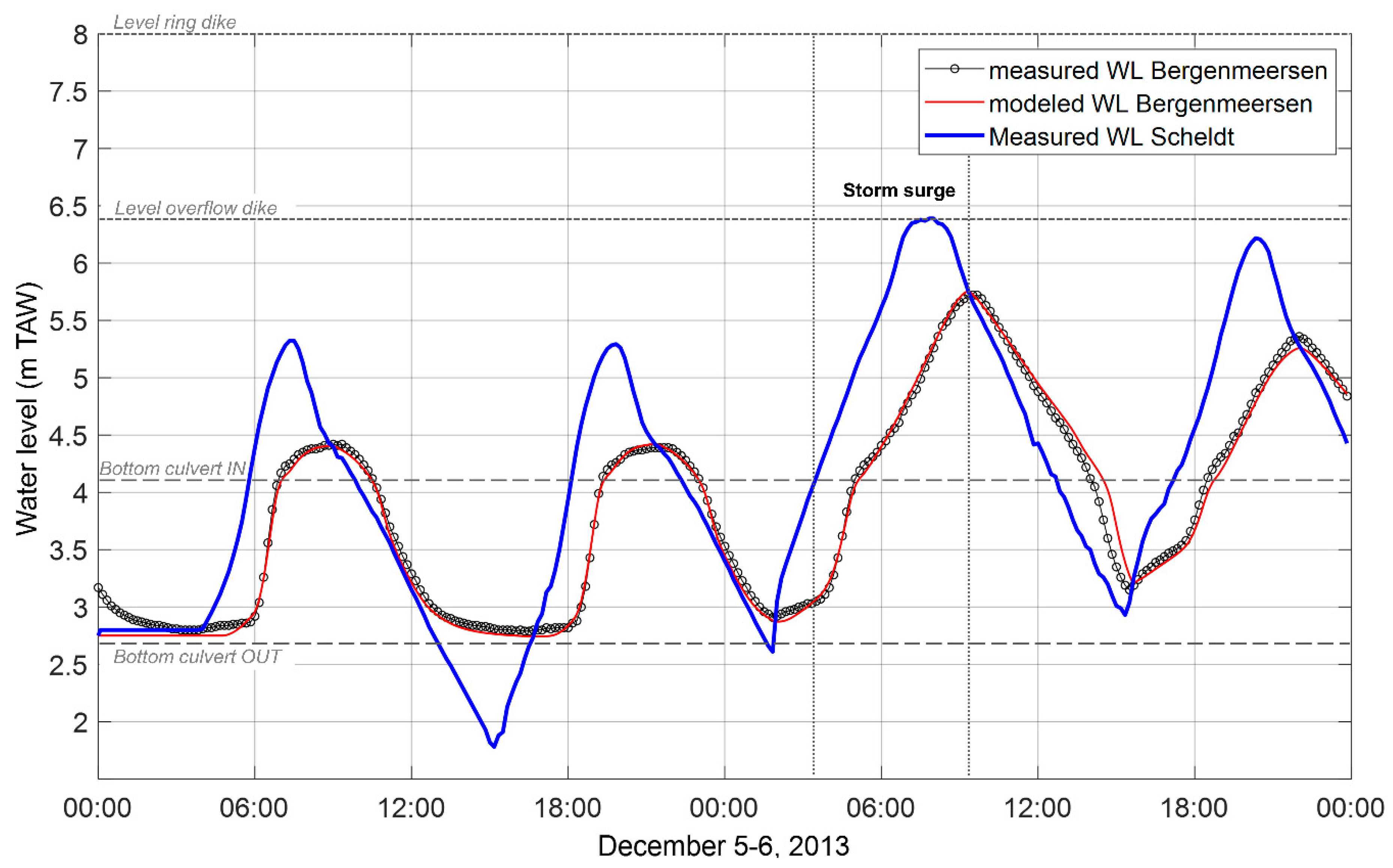
2.4.3. Validation of the Bergenmeersen Culverts Flow Model
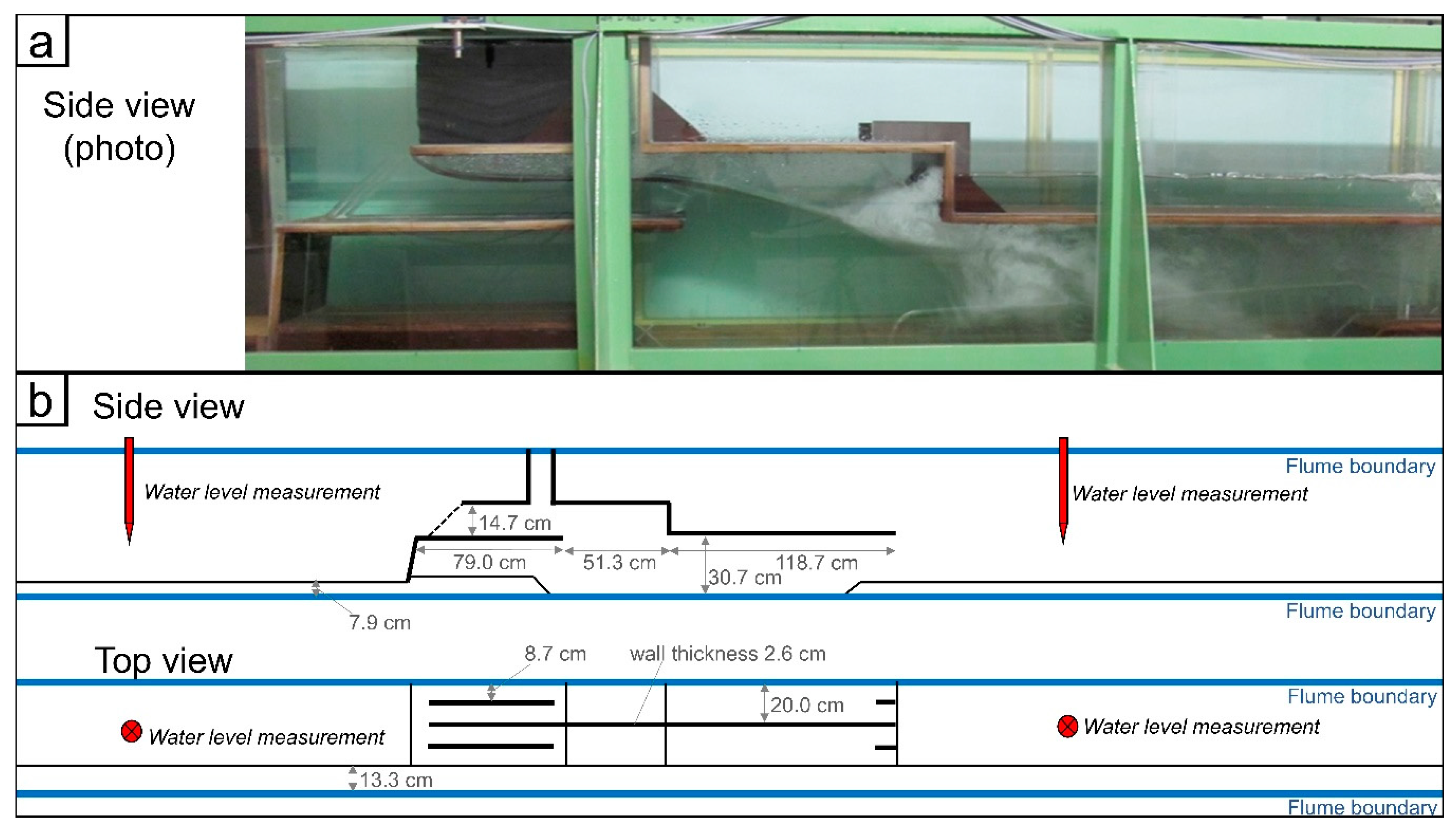
2.5. Physical Scale Model
2.5.1. Scale Model Geometry
2.5.2. Scale Model Tests Setup
2.5.3. Culvert Parameters
2.6. Hindcast of Storm Surge and Impact of FCA in the Scheldt Estuary
- (1)
- Scenario 1 will hindcast the storm surge of 6 December 2013 as it was. All FCAs that were active at that time are active in the model. This scenario will tell how well the model can simulate this storm surge and it will be used as a reference to compare the other two scenarios with.
- (2)
- Scenario 2 starts from scenario 1 for which the largest intertidal marsh area in the estuary (the so-called Drowned Land of Saeftinghe, for location see Figure 1) is removed from the model domain. Its effect on storm surge attenuation was already demonstrated in [19,55]. This scenario is added to compare the impact of a large natural marsh on storm surge attenuation within the estuary with the impact of several smaller FCAs. This marsh was removed from the model domain by increasing its bottom level to a point where it cannot be flooded anymore.
- (3)
- Scenario 3 starts from scenario 2 for which all FCAs are removed from the model domain.
3. Results
3.1. Bergenmeersen Detailed 3D Model Validation
3.2. Physical Scale Model Tests
3.3. SCALDIS Estuary Scale Storm Surge Simulations
4. Discussion
4.1. Storm Surge Height Reduction by FCAs
4.2. Culvert Flow Implementation in TELEMAC
4.3. Detailed 3D Model FCA Bergenmeersen
4.4. Physical Scale Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Practical Implementation of the Culvert Equations into TELEMAC
- I1: mesh node number of culvert on side 1;
- I2: mesh node number of the culvert on side 2;
- CE1: entrance head loss coefficient for the culvert on side 1 (this corresponds to the head loss coefficient C1);
- CE2: entrance head loss coefficient for the culvert on side 2 (this corresponds to the head loss coefficient C1);
- CS1: exit head loss coefficient for the culvert on side 1 (this corresponds to the head loss coefficient C3);
- CS2: exit head loss coefficient for the culvert on side 2 (this corresponds to the head loss coefficient C3);
- LARG: the width of the culvert;
- HAUT1: height of the culvert on side 1;
- CLP: coefficient to restrict the flow direction (0 both directions are possible; 1 = only flow from side 1 to 2; 2 = only flow from side 2 to 1; 3 = no flow);
- L: linear head loss coefficient used only when OPTBUSE = 1; If OPTBUSE = 2, L is calculated;
- RD1: culvert bottom elevation on side 1 (z1);
- RD2: culvert bottom elevation on side 2 (z2);
- CV: head loss coefficient when a valve is present;
- C56: factor to differentiate between flow types 5 and 6;
- CV5: correction factor for CV when flow type 5 is used;
- C5: correction factor for CE1 and CE2 with flow type 5;
- TRASH: head loss coefficient when trash screens are present;
- HAUT2: height of the culvert on side 2;
- FRIC Manning Strickler friction coefficient;
- LONG: length of the culvert;
- CIR: indicates whether the culvert is rectangular (=0) or circular (=1); in case of a circular culvert the height is taken to calculate the wet section.


Appendix B. Model Parameters Culverts
| Parameter | Inflow Culverts | Outflow Culverts | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |
| CE1 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| CE2 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| CS1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| CS2 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| LARG | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 |
| HAUT1 | 0.35 | 0.35 | 0.35 | 0.45 | 0.25 | 0.35 | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 |
| CLP | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| RD1 | 4.5 | 4.5 | 4.35 | 4.2 | 4.2 | 4.2 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 |
| RD2 | 4.2 | 4.2 | 4.2 | 4.2 | 4.2 | 4.2 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 |
| CV | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| C56 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| CV5 | 0 | 0 | 0 | 0 | 0 | 0 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| C5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| TRASH | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| HAUT2 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 |
| FRIC | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 | 0.015 |
| LONG | 1 | 1 | 1 | 1 | 1 | 1 | 9 | 9 | 9 | 9 | 9 | 9 |
| CIR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Parameter | Inflow Culverts | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| CE1 | 0.5 | 0.5 | 0.5 | 0.5 |
| CE2 | 0.5 | 0.5 | 0.5 | 0.5 |
| CS1 | 0.2 | 0.2 | 0.2 | 0.2 |
| CS2 | 0.2 | 0.2 | 0.2 | 0.2 |
| LARG | 0.087 | 0.087 | 0.087 | 0.087 |
| HAUT1 | 0.147 | 0.147 | 0.147 | 0.147 |
| CLP | 1 | 1 | 1 | 1 |
| RD1 | 0.313 | 0.313 | 0.313 | 0.313 |
| RD2 | 0.313 | 0.313 | 0.313 | 0.313 |
| CV | 0 | 0 | 0 | 0 |
| C56 | 10 | 10 | 10 | 10 |
| CV5 | 0 | 0 | 0 | 0 |
| C5 | 6 | 6 | 6 | 6 |
| TRASH | 0 | 0 | 0 | 0 |
| HAUT2 | 0.147 | 0.147 | 0.147 | 0.147 |
| FRIC | 0.012 | 0.012 | 0.012 | 0.012 |
| LONG | 0.6 | 0.6 | 0.6 | 0.6 |
| CIR | 0 | 0 | 0 | 0 |
References
- Resio, D.T.; Westerink, J.J. Modeling the physics of storm surges. Phys. Today 2008, 61, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Hanson, S.; Nicholls, R.; Ranger, N.; Hallegatte, S.; Corfee-Morlot, J.; Herweijer, C.; Chateau, J. A global ranking of port cities with high exposure to climate extremes. Clim. Chang. 2011, 104, 89–111. [Google Scholar] [CrossRef] [Green Version]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Hanson, S.; Herweijer, C.; Patmore, N.; Hallegatte, S.; Corfee-Morlot, J.; Chateau, J.; Muir-Wood, R. Ranking the World’s Cities Most Exposed to Coastal Flooding Today and in the Future; OECD Environment Working Paper No. 1 (ENV/WKP(2007)1; OECD: Paris, France, 2007. [Google Scholar]
- Dangendorf, S.; Wahl, T.; Nilson, E.; Klein, B.; Jensen, J. A new atmospheric proxy for sea level variability in the southeastern North Sea: Observations and future ensemble projections. Clim. Dyn. 2014, 43, 447–467. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.R. Changes in tropical cyclone number, duration, and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [Green Version]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Projected Atlantic hurricane surge threat from rising temperatures. Proc. Natl. Acad. Sci. USA 2013, 110, 5369–5373. [Google Scholar] [CrossRef] [Green Version]
- McGranahan, G.; Balk, D.L.; Anderson, B. The rising tide: Assessing the risks of climate change and human settlements in low elevation coastal zones. Environ. Urban. 2007, 19, 17–37. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Nicolai, M., Okem, A., Petzold, J., et al., Eds.; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Morris, R.L.; Konlechner, T.M.; Ghisalberti, M.; Swearer, S.E. From grey to green: Efficacy of eco-engineering solutions for nature-based coastal defense. Glob. Chang. Biol. 2018, 24, 1827–1842. [Google Scholar] [CrossRef]
- Sutton-Grier, A.E.; Wowk, K.; Bamford, H. Future of our coasts: The potential for natural and hybrid infrastructure to enhance the resilience of our coastal communities, economies and ecosystems. Environ. Sci. Policy 2015, 51, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Leonardi, N.; Camacina, I.; Donatelli, C.; Ganju, N.K.; Plater, A.J.; Schuerch, M.; Temmerman, S. Dynamic interactions between coastal storms and salt marshes: A review. Geomorphology 2018, 301, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defense in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef] [PubMed]
- Haddad, J.; Lawler, S.; Ferreira, C.M. Assessing the relevance of wetlands for storm surge protection: A coupled hydrodynamic and geospatial framework. Nat. Hazards 2016, 80, 839–861. [Google Scholar] [CrossRef]
- Lawler, S.; Haddad, J.; Ferreira, C.M. Sensitivity considerations and the impact of spatial scaling for storm surge modeling in wetlands of the Mid-Atlantic region. Ocean Coast. Manag. 2016, 134, 226–238. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.Q.; Zhang, K.Q.; Li, Y.P.; Xie, L. Numerical study of the sensitivity of mangroves in reducing storm surge and flooding to hurricane characteristics in southern Florida. Cont. Shelf Res. 2013, 64, 51–65. [Google Scholar] [CrossRef]
- Marsooli, R.; Orton, P.M.; Georgas, N.; Blumberg, A.F. Three-dimensional hydrodynamic modeling of coastal flood mitigation by wetlands. Coast. Eng. 2016, 111, 83–94. [Google Scholar] [CrossRef]
- Stark, J.; Van Oyen, T.; Meire, P.; Temmerman, S. Observations of tidal and storm surge attenuation in a large tidal marsh. Limnol. Oceanogr. 2015, 60, 1371–1381. [Google Scholar] [CrossRef]
- Smolders, S.; Plancke, Y.; Ides, S.; Meire, P.; Temmerman, S. Role of intertidal wetlands for tidal and storm tide attenuation along a confined estuary: A model study. Nat. Hazards Earth Syst. Sci. 2015, 15, 1659–1675. [Google Scholar] [CrossRef] [Green Version]
- Debernard, J.B.; Røed, L.P. Future wind, wave and storm surge climate in the Northern Seas: A revisit. Tellus 2008, 60, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Woth, K.; Weisse, R.; Von Storch, H. Climate change and North Sea storm surge extremes: An ensemble study of storm surge extremes expected in a changed climate projected by four different regional climate models. Ocean Dyn. 2006, 56, 3–15. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 47, 3171–3190. [Google Scholar] [CrossRef] [Green Version]
- Spencer, T.; Brooks, S.M.; Evans, B.R.; Tempest, J.A.; Möller, I. Southern North Sea storm surge event of 5 December 2013: Water levels, waves and coastal impacts. Earth Sci. Rev. 2015, 146, 120–145. [Google Scholar] [CrossRef] [Green Version]
- Jensen, J.; Arns, A.; Wahl, T. Yet another 100yr storm surge event: The role of individual storm surges on design water levels. J. Mar. Sci. Technol. 2015, 23, 882–887. [Google Scholar] [CrossRef]
- Wadey, M.P.; Haigh, I.D.; Nicholls, R.J.; Brown, J.M.; Horsburgh, K.; Carrol, B.; Gallop, S.L.; Mason, T.; Bradshaw, E. A comparison of the 31 January–1 February 1953 and 5–6 December 2013 coastal flood events around the UK. Front. Mar. Sci. 2015, 2, 84. [Google Scholar] [CrossRef] [Green Version]
- Meire, P.; Dauwe, W.; Maris, T.; Peeters, P.; Coen, L.; Deschamps, M.; Rutten, J.; Temmerman, S. Sigma plan proves efficiency. ECSA Bull. 2014, 62, 19–23. [Google Scholar]
- Kroos, J. Stormvloedrapport van 5 t/m 7 December 2013: Sint Nicolaasvloed 2013 (Verslag van de Stormvloed); Rijkswaterstaat, Watermanagementcentrum: Utrecht, The Netherlands, 2014; Available online: http://resolver.tudelft.nl/uuid:4d028320-7dfa-46a6-ab77-f79bdccce98c (accessed on 17 December 2019).
- Horner, R.W. The Thames tidal flood risk—the need for the barrier: A review of its design and construction. Q. J. Eng. Geol. Hydrogeol. 1984, 17, 199–206. [Google Scholar] [CrossRef]
- Gerritsen, H. What Happened in 1953? The Big Flood in the Netherlands in Retrospect; Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences; Royal Society: London, UK, 2005; Volume 363, pp. 1271–1291. [Google Scholar] [CrossRef]
- Anonymus. Geactualiseerd Sigmaplan voor Veiligheid en Natuurlijkheid in Het Bekken van de Zeeschelde: Synthesenota; Report Flemish Waterways Administration: Antwerpen, Belgium, 2006. [Google Scholar]
- Maris, T.; Cox, T.; Temmerman, S.; De Vleeschauwer, P.; Van Damme, S.; De Mulder, T.; Van den Bergh, E.; Meire, P. Tuning the tide: Creating ecological conditions for tidal marsh development in a flood control area. Hydrobiologia 2007, 588, 31–43. [Google Scholar] [CrossRef]
- Meire, P.; Ysebaert, T.; Van Damme, S.; Van den Bergh, E.; Maris, T.; Struyf, E. The Scheldt estuary: A description of a changing ecosystem. Hydrobiologia 2005, 540, 1–11. [Google Scholar] [CrossRef]
- Beauchard, O.; Jacobs, S.; Cox, T.J.S.; Maris, T.; Vrebos, D.; Van Braeckel, A.; Meire, P. A new technique for tidal habitat restoration: Evaluation of its hydrological potentials. Ecol. Eng. 2011, 37, 1849–1858. [Google Scholar] [CrossRef]
- Jacobs, S.; Beauchard, O.; Struyf, E.; Cox, T.J.S.; Maris, T.; Meire, P. Restoration of tidal freshwater vegetation using controlled reduced tide (CRT) along the Schelde Estuary (Belgium). Estuar. Coast. Shelf Sci. 2009, 85, 368–376. [Google Scholar] [CrossRef]
- Broekx, S.; Smets, S.; Liekens, I.; Bulckaen, D.; De Nocker, L. Designing a long-term flood risk management plan for the Scheldt estuary using a risk-based approach. Nat. Hazards 2011, 57, 45–266. [Google Scholar] [CrossRef]
- Smolders, S.; Leroy, A.; Teles, M.J.; Maximova, T.; Vanlede, J. Culverts modelling in TELEMAC-2D and TELEMAC-3D. In Proceedings of the XXIIIrd TELEMAC-MASCARET User Conference, Paris, France, 11–13 October 2016. [Google Scholar]
- Baeyens, W.; van Eck, B.; Lambert, C.; Wollast, R.; Goeyens, L. General description of the Scheldt estuary. Hydrobiologia 1997, 366, 1–14. [Google Scholar] [CrossRef]
- Van Damme, S.; Struyf, E.; Maris, T.; Ysebaert, T.; Dehairs, F.; Tackx, M.; Heip, C.; Meire, P. Spatial and temporal patterns of water quality along the estuarine salinity gradient of the Scheldt estuary (Belgium and The Netherlands): Results of an integrated monitoring approach. Hydrobiologia 2005, 540, 29–45. [Google Scholar] [CrossRef]
- Cox, T.; Maris, T.; De Vleeschauwer, P.; De Mulder, T.; Soetaert, K.; Meire, P. Flood control areas as an opportunity to restore estuarine habitat. Ecol. Eng. 2006, 28, 55–63. [Google Scholar] [CrossRef]
- Boumans, R.M.J.; Burdick, D.M.; Dionne, M. Modelling habitat change in salt marshes after tidal restoration. Restor. Ecol. 2002, 10, 543–555. [Google Scholar] [CrossRef] [Green Version]
- De Mulder, T.; Vercruysse, J.; Verelst, K.; Peeters, P. Inlet sluices for flood control areas with controlled reduced tide in the Scheldt estuary: An overview. In Proceedings of the International Workshop on Hydraulic Design of Low-Head Structures, Aachen, Germany, 20–22 February 2013; Bung, D.B., Pagliara, S., Eds.; Bundesanstalt für Wasserbau (BAW): Karlsruhe, Germany, 2013; pp. 43–53. [Google Scholar]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007; ISBN 9780470035580. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows; IAHR Monographs Series; CRC Press: Boca Raton, FL, USA, 1993; p. 293. ISBN 9789054101185. [Google Scholar]
- Smagorinsky, J. General simulation experiments with the primitive equations: 1 the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Smolders, S.; Maximova, T.; Vanlede, J.; Plancke, Y.; Verwaest, T.; Mostaert, F. Integraal Plan Bovenzeeschelde: Subreport 1—SCALDIS: A 3D Hydrodynamic Model for the Scheldt Estuary; Version 5.0. WL Rapporten 2016 13_131; Flanders Hydraulics Research: Antwerp, Belgium, 2016; Available online: http://documentatiecentrum.watlab.be/imis.php?module=ref&refid=261397 (accessed on 17 December 2019).
- Bodhaine, G. Measurement of Peak Discharge at Culverts by Indirect Methods; Chapter A3. U.S Geological Survey Techniques of Water-Resources Investigations; United States Government Publishing Office: Washington, DC, USA, 1968.
- Carlier, M. Hydraulique Générale et Appliquéé; No. BOOK. 1972; Librairie Eyrolles: Paris, France, 1972. [Google Scholar]
- Larock, B.E.; Jeppson, R.W.; Watters, Z.G. Hydraulics of Pipeline Systems; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Lencastre, A. Manuel D’hydraulique Générale; Librairie Eyrolles: Paris, France, 1961. [Google Scholar]
- Wahl, T.L. Trash Control Structures and Equipment: A Literature Review and Survey of Bureau of Reclamation Experience; United States Department of the Interior, Bureau of Reclamation, Hydraulics Branch, Research and Laboratory Services Division: Denver, CO, USA, 1992.
- De Beukelaer-Dossche, M.; Decleyre, D. (Eds.) Bergenmeersen: Construction of a Flood Control Area with Controlled Reduced Tide as Part of the Sigma Plan; Waterways and Sea Canal (W&SC)/Agency for Nature and Forest (ANB): Antwerp/Brussels, Belgium, 2013; Volume 136, ISBN 9789040303432. [Google Scholar]
- Vercruysse, J.; Visser, K.P.; Peeters, P.; Mostaert, F. Sigmaplan—Vismigratie Gereduceerde Getijdegebieden: Opmeting van Helling Terugslagklep en Debiet te Bergenmeersen; Versie 4.0. WL Rapporten 2016, 15_034; Waterbouwkundig Laboratorium: Antwerpen, België, 2016. [Google Scholar]
- Gaslikova, L.; Grabemann, I.; Groll, N. Changes in North Sea storm surge conditions for four transient future climate realizations. Nat. Hazards 2013, 66, 1501–1518. [Google Scholar] [CrossRef] [Green Version]
- Temmerman, S.; De Vries, M.B.; Bouma, T.J. Coastal marsh die-off and reduced attenuation of coastal floods: A model analysis. Glob. Planet. Chang. 2012, 92–93, 267–274. [Google Scholar] [CrossRef]
- Stark, J.; Smolders, S.; Meire, P.; Temmerman, S. Impact of intertidal area characteristics on estuarine tidal hydrodynamics: A modelling study for the Scheldt Estuary. Estuar. Coast. Shelf Sci. 2017, 198, 138–155. [Google Scholar] [CrossRef]
- Masselink, G.; Hanley, M.E.; Halwyn, A.C.; Blake, W.; Kingston, K.; Newton, T.; Williams, M. Evaluation of salt marsh restoration by means of self-regulating tidal gate–Avon estuary, South Devon, UK. Ecol. Eng. 2017, 106, 174–190. [Google Scholar] [CrossRef]
- Montgomery, J.M.; Bryan, K.R.; Mullarney, J.C.; Horstman, E.M. Attenuation of storm surges by coastal mangroves. Geophys. Res. Lett. 2019, 46, 2680–2689. [Google Scholar] [CrossRef] [Green Version]
- Shepard, C.C.; Crain, C.M.; Beck, M.W. The protective role of coastal marshes: A systematic review and meta-analysis. PLoS ONE 2011, 6, e27374. [Google Scholar] [CrossRef]
- Reed, D.; van Wesenbeeck, B.; Herman, P.M.; Meselhe, E. Tidal flat-wetland systems as flood defenses: Understanding biogeomorphic controls. Estuar. Coast. Shelf Sci. 2018, 213, 269–282. [Google Scholar] [CrossRef]
- French, J.R. Hydrodynamic modelling of estuarine flood defense realignment as an adaptive management response to sea-level rise. J. Coast. Res. 2008, 24, 1–12. [Google Scholar] [CrossRef]
- Esteves, L.S. Is managed realignment a sustainable long-term coastal management approach? J. Coast. Res. 2013, 65, 933–938. [Google Scholar] [CrossRef]
- Smolders, S.; Vercruysse, J.; Visser, K.P.; Henderick, A.; Coen, L.; Mostaert, F. Sigmaplan—Vismigratie Gereduceerde Getijdegebieden: Bepalen Debiet in-en Uitwatering GOG-GGG Bergenmeersen en Bazel; Versie 3.0. WL Rapporten, 16_094_1; Waterbouwkundig Laboratorium: Antwerpen, Belgium, 2018. [Google Scholar]


| Flow Type | Discharge Equation | Occurs When |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
| Flow Type | Discharge Equation | Occurs When |
|---|---|---|
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
| Valve Position | Wide Open | ¾ Open | ½ Open | ¼ Open |
|---|---|---|---|---|
| CV | 0.2 | 1. | 5.6 | 17 |
| Set # | Upstream Water Level | Downstream Water Level | Upstream Water Level | Downstream Water Level |
|---|---|---|---|---|
| (Reality) | (Reality) | (Model) | (Model) | |
| [m TAW] | [m TAW] | [m] | [m] | |
| 1 | 4 | 3 | 0.361 | 0.293 |
| 2 | 5 | 3 | 0.429 | 0.291 |
| 3 | 6 | 3 | 0.494 | 0.293 |
| 4 | 7 | 3 | 0.559 | 0.291 |
| 5 | 8 | 3 | 0.626 | 0.292 |
| 6 | 7 | 6 | 0.560 | 0.492 |
| Set # | Upstream Water Level | Downstream Water Level | No Trash Screen | Trash Screen | ||||
|---|---|---|---|---|---|---|---|---|
| Model [m] | Model [m] | Measured Q [m3/s] | Calculated Q [m3/s] | Difference [%] | Measured Q [m3/s] | Calculated Q [m3/s] | Difference [%] | |
| 1 | 0.361 | 0.293 | 0.006 | 0.006 | 0 | 0.005 | 0.005 | 0 |
| 2 | 0.429 | 0.291 | 0.025 | 0.025 | 0 | 0.023 | 0.022 | −4.3 |
| 3 | 0.494 | 0.293 | 0.050 | 0.049 | −2 | 0.046 | 0.043 | −6.5 |
| 4 | 0.559 | 0.291 | 0.063 | 0.063 | 0 | 0.060 | 0.060 | 0 |
| 5 | 0.626 | 0.292 | 0.076 | 0.071 | −6.6 | 0.073 | 0.068 | −6.8 |
| 6 | 0.56 | 0.492 | 0.061 | 0.062 | 1.6 | 0.057 | 0.054 | −5.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smolders, S.; João Teles, M.; Leroy, A.; Maximova, T.; Meire, P.; Temmerman, S. Modeling Storm Surge Attenuation by an Integrated Nature-Based and Engineered Flood Defense System in the Scheldt Estuary (Belgium). J. Mar. Sci. Eng. 2020, 8, 27. https://doi.org/10.3390/jmse8010027
Smolders S, João Teles M, Leroy A, Maximova T, Meire P, Temmerman S. Modeling Storm Surge Attenuation by an Integrated Nature-Based and Engineered Flood Defense System in the Scheldt Estuary (Belgium). Journal of Marine Science and Engineering. 2020; 8(1):27. https://doi.org/10.3390/jmse8010027
Chicago/Turabian StyleSmolders, Sven, Maria João Teles, Agnès Leroy, Tatiana Maximova, Patrick Meire, and Stijn Temmerman. 2020. "Modeling Storm Surge Attenuation by an Integrated Nature-Based and Engineered Flood Defense System in the Scheldt Estuary (Belgium)" Journal of Marine Science and Engineering 8, no. 1: 27. https://doi.org/10.3390/jmse8010027
APA StyleSmolders, S., João Teles, M., Leroy, A., Maximova, T., Meire, P., & Temmerman, S. (2020). Modeling Storm Surge Attenuation by an Integrated Nature-Based and Engineered Flood Defense System in the Scheldt Estuary (Belgium). Journal of Marine Science and Engineering, 8(1), 27. https://doi.org/10.3390/jmse8010027






