Influence of Tidal Current, Wind, and Wave in Hebei Spirit Oil Spill Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.2. Field Observation
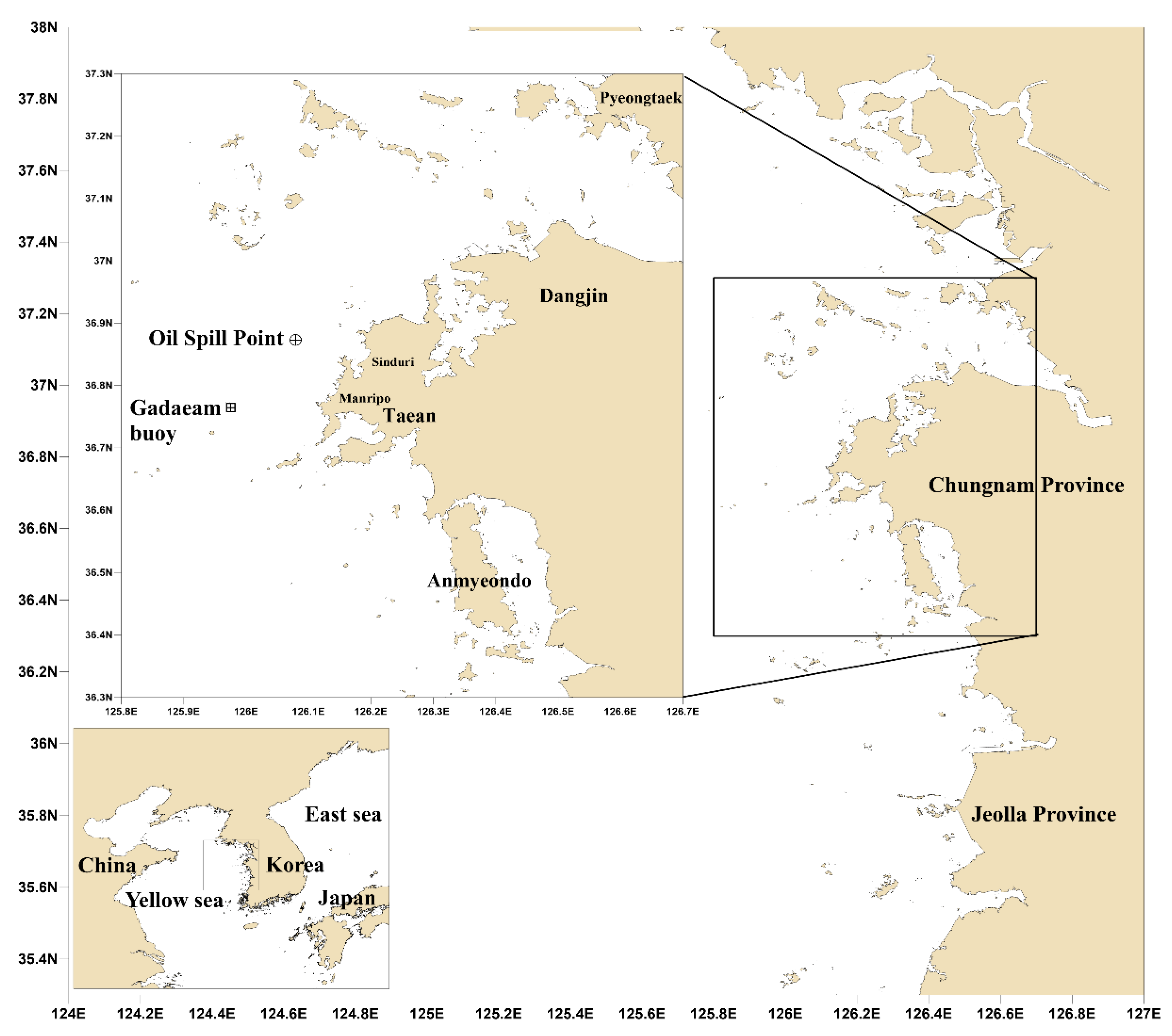
2.2.1. Satellite Image
2.2.2. Wind Observation
2.2.3. Wave Observation
3. Results
3.1. Verification of the Tidal Model
3.2. Tide and Wind Numerical Experiment
3.3. Wave Numerical Experiment
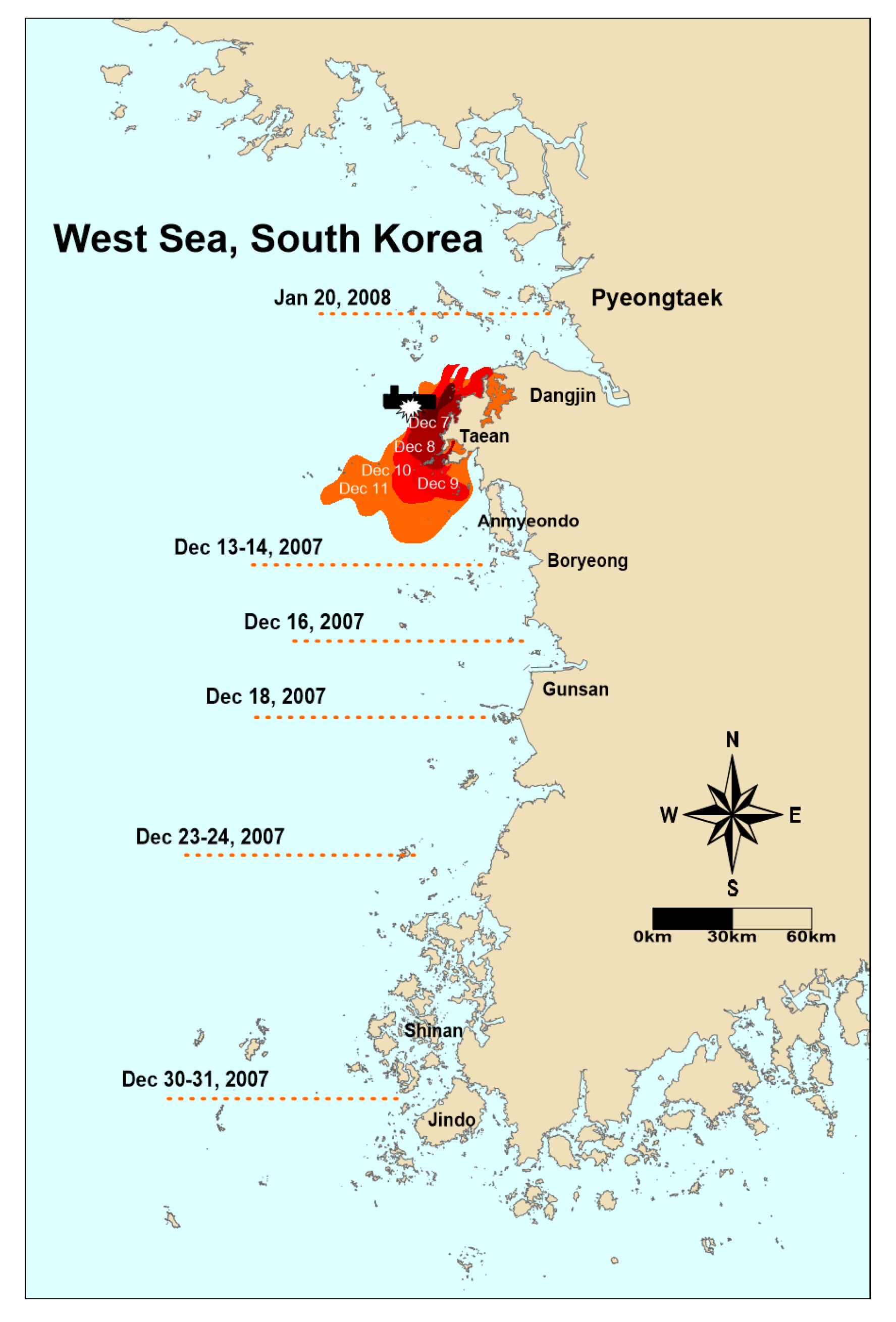
3.4. Oil Spill Numerical Experiment
3.4.1. Oil Spill Distribution Considering Tidal Currents (Case 1)
3.4.2. Oil Spill Distribution Considering Tidal and Wind Drift Currents (Case 2)
3.4.3. Oil Spill Distribution Considering Tidal, Wind Drift, and Stokes Drift Currents (Case 3)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Report of Investigation into the Collision between the Hong Kong Registered Ship “Hebei Spirit” and Korean Crane Barge “Samsung No.1” on 7 December 2007. Hong Kong Special Administrative Department, Marine Department, Marine Accident Investigation Section. Available online: https://www.mardep.gov.hk/en/publication/pdf/mai071207a_f.pdf (accessed on 27 December 2019).
- Korea Coast Guard (KCG). Korea Coast Guard 2008 White Paper; Korea Coast Guard: Seoul, Korea, 2008. [Google Scholar]
- Seo, S.W. Hydraulic Characteristics and Prediction Technology of Taean Oil Spill Diffusion. Korean Soc. Coast. Ocean Eng. 2008, 1, 53–64. (In Korean) [Google Scholar]
- Kim, C.S.; Cho, Y.K.; Choi, B.J.; Jung, K.T.; You, S.H. Improving a prediction system for oil spills in the Yellow Sea: Effect of tides on subtidal flow. Mar. Pollut. Bull. 2013, 68, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Kim, T.H.; Yang, C.S.; Oh, J.H.; Ouchi, K. Analysis of the Contribution of Wind Drift Factor to Oil Slick Movement under Strong Tidal Condition: Hebei Spirit Oil Spill Case. PLoS ONE 2014, 9, e87393. [Google Scholar] [CrossRef]
- Lee, J.L.; Lee, D.Y.; Kim, I.C. Numerical Modeling of Wave Effect on Hebei Spirit Oil Spill (2007), Taean, Korea. J. Coast. Res. 2009, 56, 836–840. [Google Scholar]
- Yim, U.H.; Ha, S.Y.; An, J.G.; Won, J.H.; Han, G.M.; Hong, S.H.; Kim, M.K.; Jung, J.H.; Shim, W.J. Fingerprint and weathering characteristics of stranded oils after the Hebei Spirit oil spill. J. Hazard. Mater. 2011, 197, 60–69. [Google Scholar] [CrossRef]
- Kim, T.S.; Park, K.A.; Li, X.; Lee, M.J.; Hong, S.W.; Lyu, S.J.; Nam, S.Y. Detection of the Hebei Spirit oil spill on SAR imagery and its temporal evolution in a coastal region of the Yellow Sea. Adv. Space Res. 2015, 56, 1079–1093. [Google Scholar] [CrossRef]
- Kim, M.K.; Han, S.H.; Won, J.H.; Yim, U.H.; Jung, J.H.; Ha, S.Y.; An, J.G.; Joo, C.K.; Kim, E.S.; Han, G.M.; et al. Petroleum hydrocarbon contaminations in the intertidal seawater after the Hebei Spirit oil spill effect of tidal cycle on the TPH concentrations and the chromatographic characterization of seawater extracts. Water Res. 2013, 47, 758–768. [Google Scholar] [CrossRef]
- Kim, D.H.; Yang, G.G.; Min, S.J.; Koh, C.H. Social and ecological impacts of the Hebei Spirit oil spill on the west coast of Korea: Implications for compensation and recovery. Ocean Coast. Manag. 2014, 102, 533–544. [Google Scholar] [CrossRef]
- Samaras, A.G.; De Dominicis, M.; Archetti, R.; Lamberti, A.; Pinardi, N. Towards improving the representation of beaching in oil spill models: A case study. Mar. Pollut. Bull. 2014, 88, 91–101. [Google Scholar] [CrossRef]
- De Dominicis, M.; Pinardi, N.; Zodiatis, G.; Lardner, R. MEDSLIK-II, a Lagrangian marine surface oil spill model for short-term forecasting—Part 1: Theory. Geosci. Model. Dev. 2013, 6, 1851–1869. [Google Scholar] [CrossRef] [Green Version]
- Grisolia-Santos, D.; Spaulding, M.L. The influence of oil particle size distribution as an initial condition in oil spill random walk models. In Oil and Hydrocarbon Spills, Modeling, Analysis and Control II; Rodríguez, G., Brebbia, C., Eds.; WIT Press: Southampton, UK, 2000; Volume 44, pp. 19–28. [Google Scholar]
- Hamrick, J.M. A three dimensional environmental fluid dynamics computer code: Theoretical and computational aspects. In Special Report in Applied Marine Science and Ocean. Engineering; Virginia Institute of Marine Science, College of William and Mary: Williamsburg, VA, USA, 1992; No. 317; 63p. [Google Scholar]
- Kuo, A.Y.; Shen, J.; Hamrick, J.M. The effect of acceleration on bottom shear stress in tidal estuaries. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 75–83. [Google Scholar] [CrossRef]
- Shen, J.; Boon, J.D.; Kuo, A.Y. A modeling study of a tidal intrusion front and its impact on larval dispersion in the James River estuary, Virginia. Estuaries 1999, 22, 681–692. [Google Scholar] [CrossRef]
- Moustafa, M.Z.; Hamrick, J.M. Calibration of the wetland hydrodynamic model to the Everglades nutrient removal project. Water Qual. Ecosyst. Model. 2000, 1, 141–167. [Google Scholar] [CrossRef]
- Ji, Z.G.; Hamrick, J.H.; Pagenkopf, J. Sediment and metals modeling in shallow river. J. Environ. Eng. 2002, 128, 105–119. [Google Scholar] [CrossRef]
- Wool, T.A.; Davie, S.R.; Rodriguez, H.N. Development of three-dimensional hydrodynamic and water quality models to support TMDL decision process for the Neuse River estuary, North Carolina. J. Water Resour. Plan. Manag. 2003, 129, 295–306. [Google Scholar] [CrossRef]
- Zou, R.; Carter, S.; Shoemaker, L.; Parker, A.; Henry, T. Integrated hydrodynamic and water quality modeling system to support nutrient total maximum daily load development for Wissahickon Creek, Pennsylvania. J. Environ. Eng. 2006, 132, 555–566. [Google Scholar] [CrossRef]
- Craig, P.M. User’s Manual for EFDC Explorer: A Pre/Post Processor for the Environmental Fluid Dynamics Code; Dynamic Solutions, LLC: Knoxville, TN, USA, 2010. [Google Scholar]
- Mellor, G.L.; Yamamda, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, Part I: Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions, Part II: Verification. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Rusu, E.; Conley, D.C.; Coelho, E.F. A hybrid framework for predicting waves and longshore currents. J. Mar. Syst. 2008, 69, 59–73. [Google Scholar] [CrossRef]
- Oh, S.H.; Suh, K.D.; Son, S.Y.; Lee, D.Y. Performance comparison of spectral wave models based on different governing equations including wave breaking. KSCE J. Civ. Eng. 2009, 13, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Stokes, G.G. On the theory of oscillatory waves. Math. Phys. Pap. 1880, 1, 197–229. [Google Scholar]
















| Location | Tidal Components | Amplitude (cm) | Phase (degree) | Error | |||
|---|---|---|---|---|---|---|---|
| Observed | Computed | Observed | Computed | Amplitude | Phase | ||
| T-1 | M2 | 231.6 | 231.8 | 106.6 | 115.5 | 0.2 | 8.9 |
| S2 | 90.1 | 88.1 | 155.1 | 160.9 | −2.0 | 5.8 | |
| K1 | 34.7 | 36.2 | 287.0 | 288.0 | 1.5 | 1.0 | |
| O1 | 28.5 | 27.3 | 257.0 | 260.3 | −1.2 | 3.3 | |
| T-2 | M2 | 211.1 | 207.5 | 95.4 | 94.2 | −3.6 | −1.2 |
| S2 | 81.0 | 78.7 | 138.8 | 137.8 | −2.3 | −1.0 | |
| K1 | 35.8 | 33.3 | 280.1 | 278.8 | −2.5 | −1.3 | |
| O1 | 26.8 | 24.4 | 252.1 | 250.6 | −2.4 | −1.5 | |
| T-3 | M2 | 215.7 | 215.5 | 90.0 | 89.3 | −0.2 | −0.7 |
| S2 | 83.3 | 81.7 | 133.7 | 133.8 | −1.6 | 0.1 | |
| K1 | 35.2 | 34.1 | 277.5 | 275.7 | −1.1 | −1.8 | |
| O1 | 26.3 | 25.2 | 249.4 | 247.5 | −1.1 | −1.9 | |
| Tidal Velocity Components | U-components | V-components | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Amplitude (cm/s) | Phase (degree) | Error | Amplitude (cm/s) | Phase (degree) | Error | ||||
| Amplitude | Phase | Amplitude | Phase | ||||||
| M2 | Observed | 34.5 | 66.0 | −4.7 | −13.4 | 94.5 | 53.2 | 3.5 | −4.8 |
| Computed | 29.8 | 52.6 | 98.0 | 48.4 | |||||
| S2 | Observed | 16.0 | 112.6 | −4.7 | −19.3 | 36.0 | 93.1 | −1.3 | −6.3 |
| Computed | 11.3 | 93.3 | 34.7 | 86.8 | |||||
| K1 | Observed | 5.4 | 239.7 | −2.1 | −37.0 | 9.8 | 207.8 | −1.2 | −5.1 |
| Computed | 3.3 | 202.7 | 8.6 | 202.7 | |||||
| O1 | Observed | 3.8 | 192.5 | −1.4 | −25.2 | 6.4 | 158.9 | −0.4 | −1.4 |
| Computed | 2.4 | 167.3 | 6.0 | 157.5 | |||||
| Tidal Velocity Components | U-components | V-components | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Amplitude (cm/s) | Phase (degree) | Error | Amplitude (cm/s) | Phase (degree) | Error | ||||
| Amplitude | Phase | Amplitude | Phase | ||||||
| M2 | Observed | 59.4 | 36.3 | −10.3 | −3.9 | 57.5 | 38.6 | 16.3 | −5.3 |
| Computed | 49.1 | 32.4 | 73.8 | 33.3 | |||||
| S2 | Observed | 23.1 | 87.8 | −6.4 | −13.2 | 22.0 | 87.3 | 2.3 | −13.7 |
| Computed | 16.7 | 74.6 | 24.3 | 73.6 | |||||
| K1 | Observed | 5.3 | 213.1 | −1.6 | −27.5 | 5.2 | 204.2 | 0.0 | −18.6 |
| Computed | 3.7 | 185.6 | 5.2 | 185.6 | |||||
| O1 | Observed | 3.4 | 178.4 | −0.9 | −25.1 | 3.0 | 168.3 | 0.4 | −23.6 |
| Computed | 2.5 | 153.3 | 3.4 | 144.7 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.-H.; Kim, T.-G.; Cho, Y.-H. Influence of Tidal Current, Wind, and Wave in Hebei Spirit Oil Spill Modeling. J. Mar. Sci. Eng. 2020, 8, 69. https://doi.org/10.3390/jmse8020069
Lee K-H, Kim T-G, Cho Y-H. Influence of Tidal Current, Wind, and Wave in Hebei Spirit Oil Spill Modeling. Journal of Marine Science and Engineering. 2020; 8(2):69. https://doi.org/10.3390/jmse8020069
Chicago/Turabian StyleLee, Kwang-Ho, Tag-Gyeom Kim, and Yong-Hwan Cho. 2020. "Influence of Tidal Current, Wind, and Wave in Hebei Spirit Oil Spill Modeling" Journal of Marine Science and Engineering 8, no. 2: 69. https://doi.org/10.3390/jmse8020069
APA StyleLee, K.-H., Kim, T.-G., & Cho, Y.-H. (2020). Influence of Tidal Current, Wind, and Wave in Hebei Spirit Oil Spill Modeling. Journal of Marine Science and Engineering, 8(2), 69. https://doi.org/10.3390/jmse8020069





