Establishing an Integrated Permanent Sea-Level Monitoring Infrastructure towards the Implementation of Maritime Spatial Planning in Cyprus
Abstract
:1. Introduction
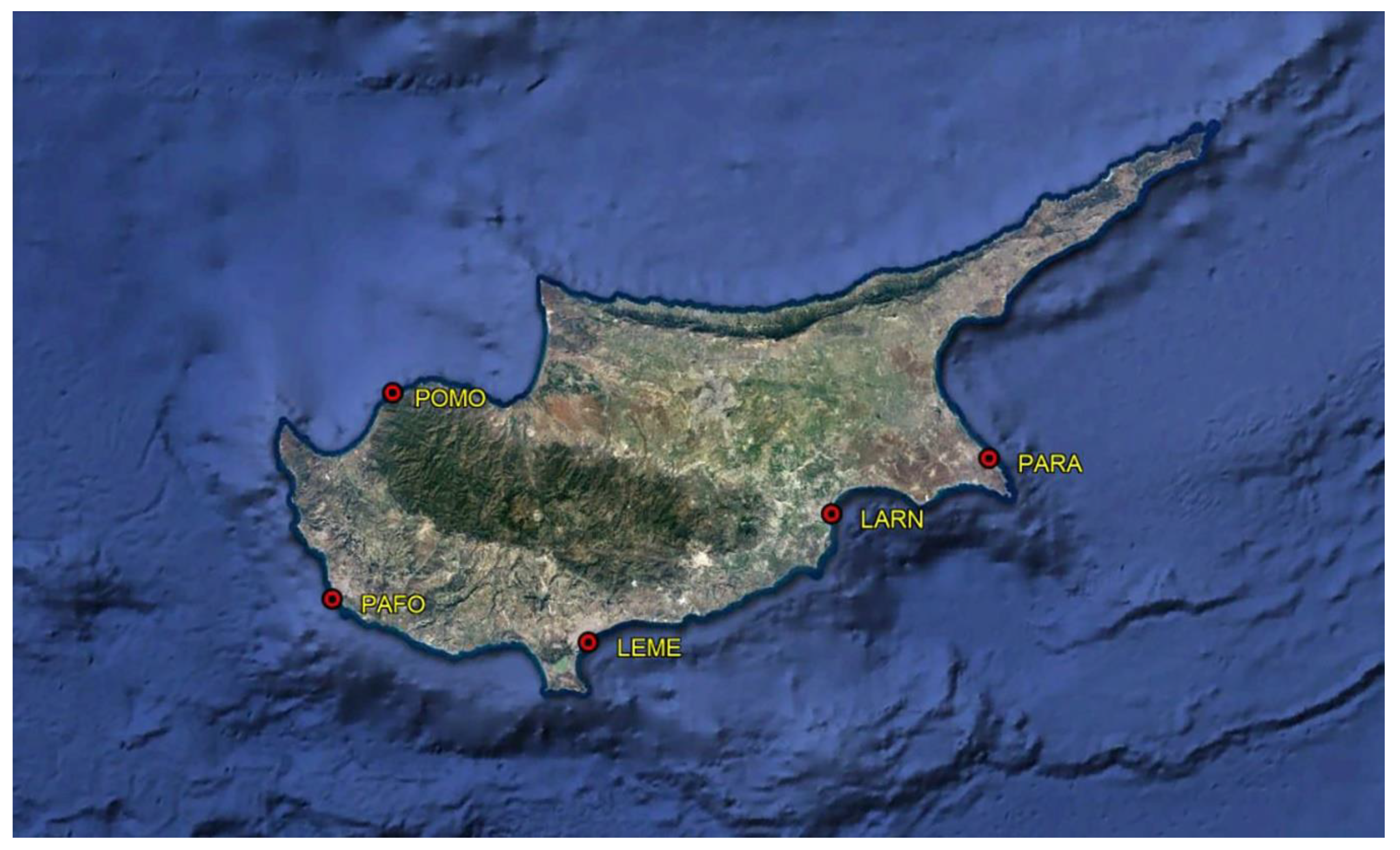
- A description of the Cyprus National TG Network (PYTHEAS) and the processes that were involved during the establishment of the infrastructure;
- The determination of local tidal data in Cyprus using sea-level measurements for the period 2017–2019;
- The transfer of the tidal data to the reference TG station in Limasol.
2. Methodology
2.1. The Establishment of the National Tide Gauge Station Network (PYTHEAS)
- Accessibility: The benchmark must enable easy and unobstructed access for future geodetic and surveying works.
- Resilience: The benchmark must be installed at a location with the least chance of destruction or future obstruction.
2.2. Determination of Tidal Levels
2.2.1. TG Data Pre-Processing and QC
- Tide gauge stability check: A time threshold of 5 min was defined, as suggested in [14] during which, if the value of the sea-level height remains constant then it indicates a structural instability of the tide gauge. In essence, the software scans for the occurrence of identical sea-level values over the specified timespan. This assessment is mostly applied to stilling well gauges. However, for the sake of completion, it was incorporated in the QC module.
- Outlier detection check: Large outliers are removed by specifying minimum and maximum thresholds. Significantly low or high values usually occur in cases of obstruction of the tide radar (e.g., a boat parking directly below the sensor) or some extreme event (e.g., storm surge). In such cases, outliers (blunders) will appear for a limited amount of time and will exhibit no periodicity. The thresholds initially used in this research were set as the upper and lower staff gauge limits. At the same time, a check is performed for any sudden change in the gradient of the data, which can be an indication of invalid measurements.
2.3. Estimation of the Astronomical Impact and Computation of Tidal Levels
2.4. Tidal Data Transfer
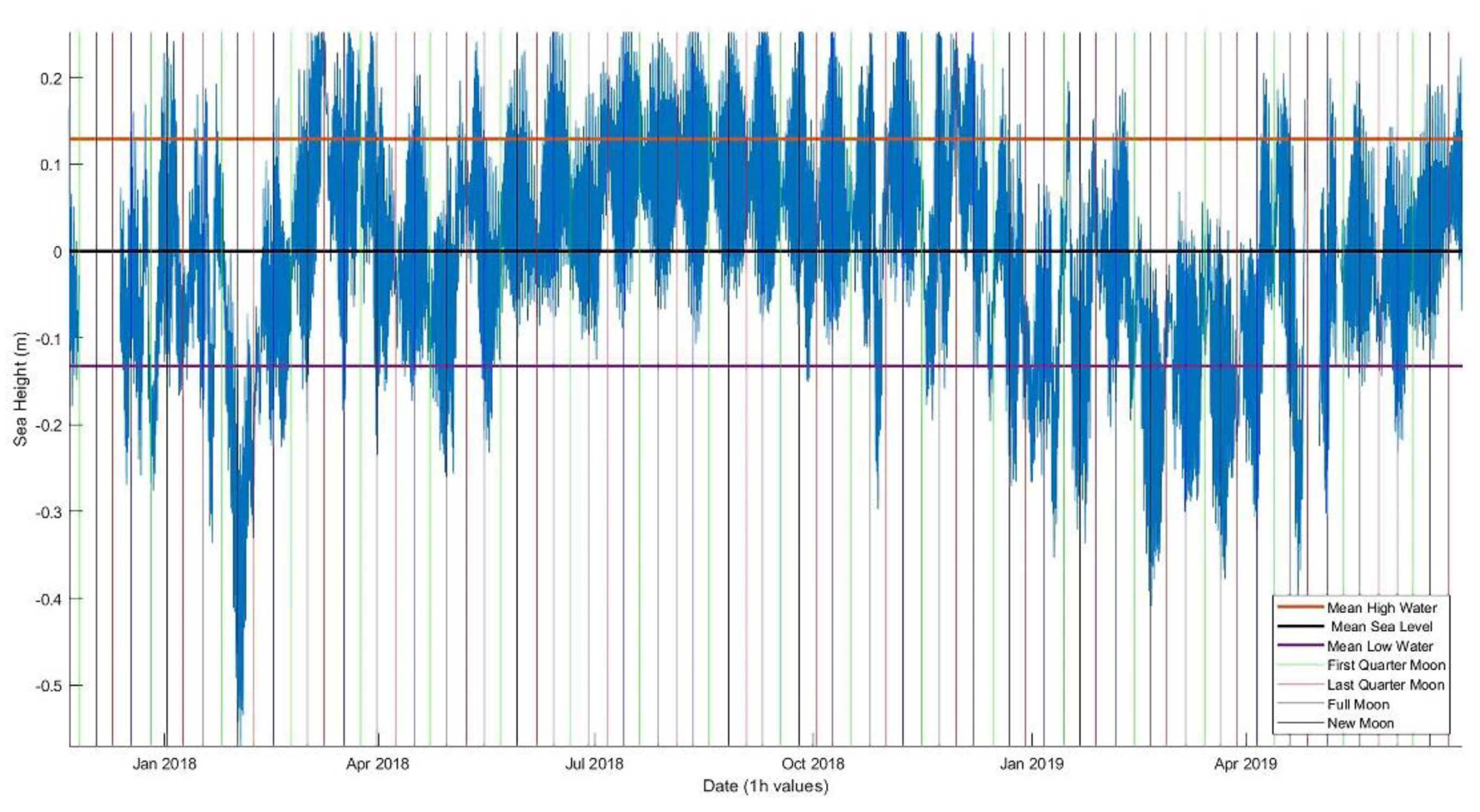
3. Results
4. Discussion
5. Conclusions
- The establishment of a procedure for the physical installation and referencing of TG’s;
- The definition of the methodology for the QC of the observations and the calculation of local tidal data. Α microtidal range of 0.303 to 0.261 was determined and a difference of 1 cm in the MTL and MSL data between the auxiliary stations and the reference TG.
- The definition of a common tidal level, which will be used for the determination of a benchmark to study MSLR and MSL variability;
- The calculation of the astronomical influence, and indirectly, the meteorological residuals that affect the sea elevation of Cyprus. The astronomical influence was estimated to contribute approximately 59% (~8 cm) to sea elevation, while the remaining portion is attributed to meteorological residuals (41% or approximately 5 cm).
Author Contributions
Funding
Conflicts of Interest
References
- Ehler, C.; Douvere, F. Marine Spatial Planning: A step-by-step approach toward ecosystem-based management. In Intergovernmental Oceanographic Commission and Man and the Biosphere Programme; IOC Manual and Guides No. 53; ICAM Dossier No. 6; UNESCO: Paris, France, 2009. (In English) [Google Scholar]
- Douvere, F. The importance of marine spatial planning in advancing ecosystem-based sea use management. Mar. Policy 2008, 32, 762–771. [Google Scholar] [CrossRef]
- Coastance. Eu Project Coastance Report Phase B2–B3, Component 3: Regional Action Strategies for Coastal Zone Adaptation to Climate Change; Conseil général de l’Hérault,Pôle Développement Durable, Direction du Développement Littoral et Maritime: Montpellier, France, 2012; pp. 1–3. [Google Scholar]
- Consortium for Ocean Leadership. Science Requirements for Marine Spatial Planning; Consortium for Ocean Leadership: Washington, DC, USA, 2009; pp. 1–4. [Google Scholar]
- Ehler, C. A Guide to Evaluating Marine Spatial Plans; MarXiv: Santa Barbara, CA, USA, 2017; p. 41. [Google Scholar]
- Hadjimitsis, D.; Agapiou, A.; Themistocleous, K.; Mettas, C.; Evagorou, E.; Soulis, G.; Xagoraris, Z.; Pilikou, M.; Aliouris, K.; Ioannou, N. Maritime spatial planning in Cyprus. Open Geosci. 2016, 8, 653–661. [Google Scholar] [CrossRef] [Green Version]
- UNESCO, IOC. Manual on Sea-level Measurements and Interpretation; Manual Guides, JCOMM Technical Report No. 31; UNESCO: Paris, France, 2006; Volume IV. [Google Scholar]
- UNESCO, IOC. Manual on sea level measurement and interpretation. In Intergovernmental Oceanographic Commission, Manuals and Guides 14; UNESCO: Paris, France, 1985; p. 83. [Google Scholar]
- ROSEN, D.S. Medgloss-mediterranean and black sea regional sea level monitoring network: Update of activities and progress. In Proceedings of the 11th Session of the IOC/UNESCO Group of Experts on the Global Sea Level Observing System (GLOSS), Paris, France, 13–15 May 2009. [Google Scholar]
- Agresti, V. Effects of Tidal Motion on the Mediterranean Sea General Circulation. Ph.D. Thesis, Alma Mater Studiorum Università di Bologna, Bologna, Italy, 2018. [Google Scholar]
- Bonaduce, A.; Pinardi, N.; Oddo, P.; Spada, G.; Gilles Larnicol, G. Sea-level variability in the Mediterranean Sea from altimetry and tide gauges. Clim. Dyn. 2016, 47, 2851–2866. [Google Scholar] [CrossRef] [Green Version]
- Operating Instructions Radar Level Sensor OTT RLS. Available online: https://www.otthydromet.com/en/p-ott-rls-radar-level-sensor/6310900192S#resources (accessed on 19 July 2020).
- User Manual Smart Weather Sensors. Available online: https://www.lufft.com/download/manual-lufft-wsxxx-weather-sensor-en/ (accessed on 19 July 2020).
- Pérez, B.; Álvarez Fanjul, E.; Pérez, S.; de Alfonso, M.; Vela, J. Use of tide gauge data in operational oceanography and sea level hazard warning systems. J. Oper. Oceanogr. 2013, 6, 1–18. [Google Scholar] [CrossRef]
- Doodson, A.T.; Warburg, H.D. Admiralty Manual of Tides; HM Stationery Office: Richmond, UK, 1941. [Google Scholar]
- Doodson, A.T. The Harmonic Development of the Tide-Generating Potential. Proc. R. Soc. Lond. Ser. A 1921, 100, 305–329. [Google Scholar]
- Pugh, D.T. Tides, Surges and Mean Sea Level; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1987.
- Shirahata, K.; Shuhei, Y.; Takeo, T.; Satoshi, I. Digital filters to eliminate or separate tidal components in groundwater observation time-series data. Jpn. Agric. Res. Q. JARQ 50 2016, 50, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Parker, B.B. The Response of Massachusetts Bay to Wind Stress. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1975. [Google Scholar]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2014; pp. 20–21. [Google Scholar]
- Groves, G.W. Numerical filters for discrimination against tidal periodicities. Eos Trans. Am. Geophys. Union 1955, 36, 1073–1084. [Google Scholar] [CrossRef]
- Boon, J.D. Secrets of the Tide: Tide and Tidal Current Analysis and Predictions, Storm Surges and Sea Level Trends; Elsevier: Amsterdam, The Netherlands, 2013; pp. 60–66. [Google Scholar]
- Rossiter, J.R. A routine method of obtaining monthly and annual values of sea level from tidal records. Int. Hydrogr. Rev. 1961, 38, 42–45. [Google Scholar]
- Foreman, M.G.G. Manual for Tidal Heights Analysis and Prediction; Institute of Ocean Sciences: Patricia Bay, BC, Canada, 1979. [Google Scholar]
- Consoli, S.; Recupero, D.R.; Zavarella, V. A survey on tidal analysis and forecasting methods for Tsunami detection. arXiv 2014, arXiv:1403.0135. [Google Scholar]
- Le Provost, C. Ocean tides. In International Geophysics; Academic Press: Cambridge, MA, USA, 2001; Volume 69, pp. 267–303. [Google Scholar]
- Parker, B.B. Tidal Analysis and Prediction; NOAA Special Publication NOS CO-OPS 3; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2007. [Google Scholar]
- Godin, G. The Analysis of Tides; No. 551.4708 G6; University of Toronto: Toronto, ON, Canada, 1972. [Google Scholar]
- Amiruddin, A.M.; Haigh, I.D.; Tsimplis, M.N.; Calafat, F.M.; Dangendorf, S. The seasonal cycle and variability of sea level in the South China Sea. J. Geophys. Res. Oceans 2015, 120, 5490–5513. [Google Scholar] [CrossRef] [Green Version]
- Leatherman, S.P.; Zhang, K.; Douglas, B.C. Sea level rise shown to drive coastal erosion. Eos Trans. Am. Geophys.Union 2000, 81, 55–57. [Google Scholar] [CrossRef]















| Station | Radar TG | Weather Station | GNSS Receiver | GNSS Antenna |
|---|---|---|---|---|
| LARN | OTT RLS | Gill MaxiMet GMX500 | Trimble® Alloy | Trimble® Zephyr 3 |
| PAFO | OTT RLS | Gill MaxiMet GMX500 | Trimble® Alloy | Trimble® Zephyr 3 |
| POMO | OTT RLS | Gill MaxiMet GMX500 | Trimble® Alloy | Trimble® Zephyr 3 |
| PARA | OTT RLS | Gill MaxiMet GMX500 | Trimble® Alloy | Trimble® Zephyr 3 |
| LEME | OTT RLS | Lufft WS500 | Leica GRX 1200 + GNSS | Leica AR25 |
| Station | Observation Period | Number of Observations | ACCEPTED | REJECTED |
|---|---|---|---|---|
| LARN | 21/11/2017 00:00–31/10/2019 23:59 | 1015859 | 1013623 (99.88%) | 2236 (0.22%) |
| PAFO | 24/11/2017 00:00–31/10/2019 23:59 | 930334 | 929073 (99.87%) | 1261 (0.13%) |
| POMO | 22/11/2017 00:00–30/06/2019 23:59 | 808688 | 794725 (98.83%) | 13963 (1.7%) |
| PARA | 13/12/2017 00:00–30/06/2019 23:59 | 812301 | 811002 (99.84%) | 1299 (0.16%) |
| LEME | 01/01/2018 00:00–31/10/2019 23:59 | 963228 | 963167 (99.99%) | 61 (0.006%) |
| Station | MSL | MHW | MLW | MHHW | MLLW | HHW | LLW | MTL | ATI |
|---|---|---|---|---|---|---|---|---|---|
| LARN | 1.073 | 0.141 | −0.141 | 0.163 | −0.156 | 0.3651 | −0.6335 | 0.141 | 0.084 |
| LEME | 1.353 | 0.133 | −0.133 | 0.155 | −0.150 | 0.3522 | −0.5990 | 0.133 | 0.084 |
| PAFO | 1.194 | 0.136 | −0.135 | 0.159 | −0.151 | 0.3381 | −0.5929 | 0.135 | 0.078 |
| POMO | 1.022 | 0.129 | −0.132 | 0.149 | −0.149 | 0.3175 | −0.5665 | 0.130 | 0.066 |
| PARA | 1.195 | 0.153 | −0.150 | 0.177 | −0.169 | 0.3825 | −0.6142 | 0.151 | 0.093 |
| Station | Mean ΔMSL | Mean ΔMTL | ΔMSL Std. Deviation | ΔMTL Std. Deviation |
|---|---|---|---|---|
| PARA | 0.011 | −0.012 | 0.072 | 0.074 |
| PAFO | −0.016 | −0.013 | 0.091 | 0.072 |
| POMO | −0.009 | −0.012 | 0.071 | 0.074 |
| LARN | −0.010 | −0.014 | 0.089 | 0.044 |
| Station | LLW According to Local MSL | Adjusted LLW |
|---|---|---|
| PARA | −0.614 | −0.603 |
| PAFO | −0.593 | −0.609 |
| POMO | −0.567 | −0.575 |
| LARN | −0.633 | −0.644 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danezis, C.; Nikolaidis, M.; Mettas, C.; Hadjimitsis, D.G.; Kokosis, G.; Kleanthous, C. Establishing an Integrated Permanent Sea-Level Monitoring Infrastructure towards the Implementation of Maritime Spatial Planning in Cyprus. J. Mar. Sci. Eng. 2020, 8, 861. https://doi.org/10.3390/jmse8110861
Danezis C, Nikolaidis M, Mettas C, Hadjimitsis DG, Kokosis G, Kleanthous C. Establishing an Integrated Permanent Sea-Level Monitoring Infrastructure towards the Implementation of Maritime Spatial Planning in Cyprus. Journal of Marine Science and Engineering. 2020; 8(11):861. https://doi.org/10.3390/jmse8110861
Chicago/Turabian StyleDanezis, Chris, Marios Nikolaidis, Christodoulos Mettas, Diofantos G. Hadjimitsis, Georgios Kokosis, and Chrysanthi Kleanthous. 2020. "Establishing an Integrated Permanent Sea-Level Monitoring Infrastructure towards the Implementation of Maritime Spatial Planning in Cyprus" Journal of Marine Science and Engineering 8, no. 11: 861. https://doi.org/10.3390/jmse8110861
APA StyleDanezis, C., Nikolaidis, M., Mettas, C., Hadjimitsis, D. G., Kokosis, G., & Kleanthous, C. (2020). Establishing an Integrated Permanent Sea-Level Monitoring Infrastructure towards the Implementation of Maritime Spatial Planning in Cyprus. Journal of Marine Science and Engineering, 8(11), 861. https://doi.org/10.3390/jmse8110861







