A Locking Sweeping Method Based Path Planning for Unmanned Surface Vehicles in Dynamic Maritime Environments

Abstract

Unmanned surface vehicles (USVs) are new marine intelligent platforms that can autonomously operate in various ocean environments with intelligent decision-making capability. As one of key technologies enabling such a capability, path planning algorithms underpin the navigation and motion control of USVs by providing optimized navigational trajectories. To accommodate complex maritime environments that include various static/moving obstacles, it is important to develop a computational efficient path planning algorithm for USVs so that real-time operation can be effectively carried out. This paper therefore proposes a new algorithm based on the fast sweeping method, named the locking sweeping method (LSM). Compared with other conventional path planning algorithms, the proposed LSM has an improved computational efficiency and can be well applied in dynamic environments that have multiple moving obstacles. When generating an optimal collision-free path, moving obstacles are modelled with ship domains that are calculated based upon ships’ velocities. To evaluate the effectiveness of the algorithm, particularly the capacity in dealing with practical environments, three different sets of simulations were undertaken in environments built using electronic nautical charts (ENCs). Results show that the proposed algorithm can effectively cope with complex maritime traffic scenarios by generating smooth and safe trajectories.

1. Introduction

In recent years, the exploration and exploitation of the ocean have received increasing attention. This has been underpinned by advances in technologies such as robotics and autonomous systems (RASs). Unmanned surface vehicles (USVs), as a new type of marine RAS, have become a global research focus due to their wide applications in both civil and military fields. Compared with manned surface ships, USVs have advantages such as rapid operation responses, high level of adaptability, and improved autonomy [1,2,3,4,5]. The core modules of USVs include sensor, communication, motion control, and decision processing modules. These modules work collaboratively to achieve autonomous navigation for USVs (autonomy refers to the ability to interact with the external environment). One of the most important aspects of USVs is their ability to select a safe and effective motion mode according to information describing the surrounding environment. Such a capability is referred to as path planning technology, which is a key autonomous decision-making functionality and forms the basis of the navigation and motion control of a USV.

1.1. Literature Review

According to the different types of available environmental information, path planning of USVs can be divided into: (1) global path planning based on global information and (2) local path planning based on local sensor information. Local path planning can be regarded as short-range online path planning that acquires information of close-range ships according to the automatic identification system (AIS) marine radar or other sensing devices. Common local path planning methods include the dynamic window approach (DWA), velocity obstacle (VO), artificial potential field (APF), and intelligent optimization algorithms.

Seder et al. [6] improved the original DWA [7] by combining a heuristic D* algorithm to address collision avoidance with moving obstacles. More specifically, dynamic obstacles were modelled using a mobile grid, and a virtual obstacle was then constructed by predicting the location of the collision point between a mobile robot and dynamic obstacles to achieve local collision avoidance for the robot. Tang et al. [8] proposed the OAABHW algorithm on the basis of the DWA, which transformed dynamic windows into heading and velocity windows, and constructed two functions to select the collision avoidance velocity and collision avoidance direction. Zhang et al. [9] combined the SARSA online strategy reinforcement learning algorithm on the basis of Tang’s study and proposed an adaptive collision avoidance algorithm for USVs. A compensated course angle is calculated to reduce the disturbance generated by sea winds and currents to improve the collision avoidance performance of USVs.

Bandyophadyay et al. [10] proposed a reactive obstacle avoidance algorithm on the basis of VO [11] for USVs. They tested the algorithm in a port area in Singapore where USVs are allowed to navigate with a maximum speed of 5 knots. Kuwata et al. [12] presented a maritime navigation algorithm for avoiding hazards and obeying COLREGs using the VO, which calculated the distance of closest point of approach (DCPA) and the time of closest point of approach (TCPA) using the relative velocity. When both the DCPA and the TCPA pass the given safety threshold, a collision is deemed to exist. By constructing a cost function, a velocity vector that can minimize the cost function was selected from a feasible velocity space as the obstacle-avoidance velocity vector. Wu et al. [13] analyzed the angular relationship between the relative velocities and relative positions of a USV and obstacles. They proposed an autonomous collision avoidance algorithm based on the VO and considered the influence of winds, waves, and currents. Zhang et al. [14] proposed a dynamic obstacle avoidance algorithm for USVs by combining the VO with the DWA.

The APF algorithm [15] is widely used in USV path planning due to advantages of simple structure, high real-time performance, and efficient and smooth path planning capability. However, the APF algorithm is prone to the local minimum problem, which makes it unable to “escape from” the local minimum point to reach the target point. To solve this problem, Xue et al. [16] addressed the local minimum problem by introducing virtual target points; however, this increased the computation time. Lyu et al. [17] obtained the path by introducing a virtual force, and then added the appropriate function and safety requirements to the corresponding virtual force according to the COLREGs to control the ship’s collision avoidance behavior. Chen et al. [18] established new repulsion and gravitational field functions, in which the gravitational field increased with the oscillation function. When a USV falls into local minimum points, it will randomly change the direction of the gravitational field to break the balance and escape the local minimum point. However, the generated path is random and not optimal. Wu et al. [19] used the APF model to describe the probability distribution of USV collision, using historical AIS data to obtain the track distribution of different key road sections. The nonlinear optimization of historical AIS data was carried out to determine the parameters of the APF model, and then the best path of the APF model was solved using the A* algorithm. However, they only considered the repulsion of obstacles to form the potential energy field. To determine a suitable path, they also needed to set a linear reference path from the starting point to the end point.

Garrido et al. [20] used the fast marching method (FMM) to construct the potential field. This differs from the traditional artificial potential field method which combines the repulsion field with the gravitational field to generate the total potential field. The FMM generates the potential field by simulating the propagation of electromagnetic waves, and the generated potential field can effectively avoid the local minimum problem. Gomez et al. [21] further improved the FMM to the fast marching square method (FMSM) to enhance the safety of the planned trajectory. Liu et al. [22,23,24] further improved the FMM algorithm by combining it with collision risk assessment for ships [25] and proposed the constrained FMM to solve the dynamic obstacle avoidance problem for USVs. However, the FMM works on a grid space; the finer the grid space, the lower the computational efficiency. In addition, FMM uses a narrow band to expand wavefronts, and the minimum time-of-arrival point in the narrow band should be selected in an iterative way making the amount of computation required to complete the expansion of the narrow band in the whole calculation area huge. A variation of FMM is the fast sweeping method (FSM) with improved computational efficiency. Zhao et al. [26] proposed the FSM to solve first-order nonlinear hyperbolic partial differential equations and proved the monotony and stability of the method. Qian et al. [27] improved this method and used it to solve the time-of-arrival function equation. Lan et al. [28] extended this method for the calculation of seismic wave time-of-arrival on an undulating surface.

1.2. Discussions on USVs Path Planning

In summary of the above discussion, the FMM-based motion planning and its variations have dominated in recent years in USV autonomous navigation. Compared with other types of algorithms (such as DWA, VO, and APF), FMM can provide advantages of the absence of local minima problem, guaranteed smoothness of the generated trajectory, and completeness of the algorithm output [21]. In terms of the computational time of FMM, it can be argued that relatively fast computational speed can be achieved in low dimensional space and on small grid maps.

However, it also should be noted that using the FMM to calculate trajectories in complex environments still requires substantial iterations, which hinders the computational efficiency. In particular, when the FMM is expanded into the FMSM algorithm, such an issue is even more significant because the FMSM requires the FMM to be summed twice. As a consequence, in maritime environments the FMM or FMSM should be implemented with the appropriate modifications required to make the algorithms more suitable in large-scale spaces.

Another important issue with the status quo of USV path planning is the lack of algorithm validations in a simulation environment containing practical information. For example, many simulation experiments [29,30,31] have been conducted in simple self-constructed environments rather than real ocean environments. Computer-based simulation environments should be established based on practical maritime navigation information, such as electrical nautical charts (ENCs).

To address the abovementioned issues, this paper proposes an improved algorithm, named the locking sweeping method (LSM), based on the fast sweeping method (FSM). Compared with the FMM, the LSM has an improved computational speed, particularly when a planning space has a large number of grid points. Highlights of this paper can be summarized as:

(1) To better solve the path planning problem of USVs, this paper applied a locking sweeping method (LSM) based on the FSM. The LSM has increased computational efficiency compared with the conventional FMM and FSM. Such an advantage provides the proposed method with better compliance with the real-time requirements of USV path planning.

(2) The LSM can extract information from a real navigation map to construct a grid map that accurately reflects static and dynamic obstacles, and the planned path can be used as the guidance track for practical navigation, which is verified by a static global simulation test.

(3) The LSM was adopted to model dynamic behaviors of moving ships for collision avoidance. The feasibility was verified by simulation experiments in various dynamic environments.

(4) All simulation environments were constructed using electronic nautical charts (ENCs) and additional information, such as moving ships, were superimposed. The generated trajectory consists of geodetic coordinates, which can be directly used as navigation waypoints for vessels. This will create a seamless interface when the developed algorithms are applied to a real navigation scenario where ENCs are intensively used.

The remainder of the paper is organized as follows. Section 2 specifically introduces the FSM and LSM algorithms, and compares the computational efficiency of the FMM, FSM, and LSM. Section 3 describes fundamentals of the LSM proposed in this paper and the algorithm that models static and dynamic obstacles. Section 4 introduces the USV path planning algorithms. The proposed algorithms and methods are verified in computer-based simulations in Section 5. Section 6 concludes the paper and discusses future work.

2. Fundamental Methodologies

Because the FMM has been widely used in USV path planning [22,23,24] and shares a common fundamental in its generation of a potential field, it is important to first introduce the details of the FMM. In a grid map, the FMM generates a potential field by simulating the propagation of an electromagnetic wave from a starting point (such a process can be mathematically expressed using the Eikonal equation which is explained in Section 2.1). As the wave traverses the map, the value of each node records the time-of-arrival of electromagnetic waves. Because the interface begins propagating from the start point, the time-of-arrival of the start point is therefore the lowest and is equal to zero. The time-of-arrival values at other points increase as the electromagnetic wave advances, and reach their highest value at the end point. The details of FMM are provided in [20].

The complexity of FMM is $\mathit{O}\left(n\log n\right)$ [32], where n represents the total number of cells of a grid map. It can be seen that with the increase in space size, the calculation efficiency will decrease. In a marine application, because of the expansion of USVs’ task scope, which requires the execution of small-scale fine tasks, there is increasing demand for the development of an efficient path planning algorithm suitable for real-time operation in large environments. This paper therefore proposes to use an LSM based on the FSM to achieve path planning for USVs.

2.1. Fast Sweeping Method (FSM)

The fast sweeping method (FSM) is an iterative algorithm which computes the time-of-arrival field by successively sweeping (traversing) the whole grid following a specific order, and using the Gauss–Seidel iterative method to solve the discretized equations of the nonlinear upwind scheme [26,33]. Each Gauss–Seidel iteration is called a sweep, and each sweep solves the time-of-arrival field propagating in a certain direction. For example, in the case of solving a two-dimensional time-of-arrival field, the whole space can be divided into four groups: top right, top left, bottom left, and bottom right (first, second, third, and fourth quadrants, respectively), and an iterative calculation process takes place in these four directions in a sequence as:

1. $i=1:nx,j=1:ny$

2. $i=nx:1,j=1:ny$

3. $i=nx:1,j=ny:1$

4. $i=1:nx,j=ny:1$

where, $nx$ is the number of grid points in the $x$ direction, and $ny$ is the number of grid points in the $y$ direction, as shown in Figure 1.

As stated previously, a propagation of an electromagnetic wave can be expressed using the Eikonal equation in a two-dimensional isotropic medium as:

$${\left(\frac{\partial t}{\partial x}\right)}^2+{\left(\frac{\partial t}{\partial y}\right)}^2=s^2\left(x,y\right),\left(x,y\right)\in \Omega$$

(1)

where $t$ is the time-of-arrival, $s(x,y)$ is the slowness (reciprocal of the velocity), and $\Omega$ is the model space. The upwind difference scheme of the discrete Eikonal equation is:

$${\left[{\left(t_{i,j}^h-t_{xmin}^h\right)}^{+}\right]}^2+{\left[{\left(t_{i,j}^h-t_{ymin}^h\right)}^{+}\right]}^2=s_{i,j}^2{h}^2$$

(2)

where $t_{xmin}^h=\min \left(t_{i-1,j}^h,t_{i+1,j}^h\right)$, $t_{ymin}^h=\min \left(t_{i,j-1}^h,t_{i,j+1}^h\right)$, and $h$ is the spatial lag, and:

$${\left(f\right)}^{+}=\{\begin{array}{c}f,f>0,\\ 0,f\le 0.\end{array}$$

(3)

The time-of-arrival field of the entire model space can be solved by combining the upwind difference scheme and Gauss–Seidel iteration. For example, in the first quadrant, the time-of-arrival $t_{i,j}^h$ of $(i,j)$ only depends on the time-of-arrival $t_{i-1,j}^h$ of its left point $(i-1,j)$ and the time-of-arrival $t_{i,j-1}^h$ of its lower point $(i,j-1)$, both of which calculate the correct values because they can be recursively traced back to the initial point in the first sweep. In this way, after the first sweep, the correct time-of-arrival of all of the nodes in the positive half-axis in the first quadrant (the time-of-arrivals of all nodes on the positive x-axis and y-axis depend only on the time-of-arrivals of their left or lower points, respectively) can be obtained. Similarly, after the second sweep, the time-of-arrivals of all nodes on the negative x-axis and positive y-axis in the second quadrant can also be obtained. The time-of-arrivals of all nodes in the first quadrant reaches the minimum and satisfies the discrete equations with their values remaining unchanged in the second sweep. Under the same argument, after the third and fourth sweep, all nodes in the third and fourth quadrant also obtain the correct time-of-arrivals. The entire process is shown in Figure 2, and the solution of Equation (1) can be obtained as:

$$t_{i,j}=\{\begin{array}{c}\min (t_{xmin},t_{ymin})+s_{i,j}h,\left|t_{xmin}-t_{ymin}\right|\ge s_{i,j}h,\\ \frac{t_{xmin}+t_{ymin}+\sqrt{2s_{i,j}{}^2{h}^2-{\left(t_{xmin}-t_{ymin}\right)}^2}}{2},\left|t_{xmin}-t_{ymin}\right|<s_{i,j}h.\end{array}$$

(4)

When there are obstacles in a model space (as shown in Figure 3), it is necessary to carry out multiple iterations until all nodes $\left|t^{new}-t^{old}\right|\le \delta$ ($\delta$ is the minimum value to determine whether to stop an iteration) in the model field achieve iterative convergence. The time-of-arrival field shown in Figure 4 was calculated after three iterations, forming a potential field with the starting point as the source. In this potential field, the value of each node represents the time-of-arrival of the node, which is between 0 and 1. It is assumed that the model space is isotropic (the slowness of sweeping is the same in the entire model space). Then, the time-of-arrival of the interface is proportional to the distance between the current node and the starting point. The time-of-arrival of the starting point is the minimum value in the whole model space, which is 0. The obstacle area in the model space is an inaccessible area of the sweeping with its time-of-arrival having the maximum value of 1. The gradient descent method was applied to the potential field established by the FSM. By following the descending direction of the gradient, the shortest barrier-free path from the current point to the starting point can be found.

The pseudocode of the FSM algorithm is shown in Algorithm 1. $S$ is the set of nodes in the grid map that need to be evaluated. Function FSMComputeT() is used to compute potential field. Function JudgeConvergence() is used to judge the convergence of potential field. The variable $SweepDirections$ is the set of sweeping directions; if the $SweepDirections=\left[1,1\right]$ vector is given, where 1 (−1) means a forwards (backwards) sweep in that axis, the four sweep directions will be represented as:

$$\begin{gathered} 1:[1,1]2:[-1,1] \\ 3:[-1,-1]4:[1,-1] \end{gathered}$$

(5)

Algorithm 1. Fast Sweeping Method Algorithm.

Input: potential field ($T$), initial point ($P_{initial}$), $S$, grid map($X$), $SweepDirections$ Initialization: 1. $T_{\mathrm{i}}\leftarrow \infty ,\forall x_{\mathrm{i}}\in X$ 2. $T.P_{initial}\leftarrow 0$ Sweeping: 3. stop←False 4. while stop ≠ True do 5.    for k = 1:4 do 6.      $T$←FSMComputeT($SweepDirection{s}_{\mathrm{k}}$, $S$, $P_{initial}$, $T$) 7.   end for 8.   Ture←JudgeConvergence ($T$) 9.   stop←Ture 10. end while 11. return $T$

The FSM carries out as many grid iterations as necessary until the value for every node has converged. Because no ordering of the data is used, the evaluation of each node is $\mathit{O}\left(1\right)$. As there are n node and t iterations, the total computational complexity of FSM is $\mathit{O}\left(nt\right)$ [34]. In comparison, the total computational complexity of FMM is $\mathit{O}\left(n\log n\right)$. Hence, in a simple environment, the calculation efficiency of FSM is higher than that of FMM, but as the complexity of the environment increases, more iterations will be required, which causes the calculation efficiency of FSM to gradually decrease until it is exceeded by FMM.

2.2. Locking Sweeping Method (LSM)

As can be seen from Figure 4a, after the first iteration of FSM, nodes in some areas within the small circle can be assigned with correct values, which remain unchanged for the rest of the process and do not need to be recalculated. Such a feature is especially useful for USVs when the operating environment is complex and requires multiple FSM iterations to construct a potential field. Therefore, this paper adopts the locking sweeping method (LSM) [34,35] to construct potential fields.

In the LSM, we maintain a locking structure at each point. All points that should be calculated will be unlocked, and points that do not require calculation (points where calculations would yield no useful information) will be locked. The details of the LSM are as follows:

• Step 1: Set initial arrival time at all points to infinity; set arrival time to 0 for sources
• Step 2: Set the obstacle area node with the locked state and other nodes with the unlocked state
• Step 3: Perform the LSM algorithm. If a point is locked, proceed to the next one without computing anything. If a point is unlocked, compute the arrival time at it using Equation (4)
• Step 4: Determine whether the value of the node converges, if so, change the locking state of the node to locking, otherwise do nothing
• Step 5: When all nodes in the interface are locked, stop the iteration

This method has the advantage of fast skipping over points that do not need recalculation, which can greatly improve the efficiency of constructing the potential field for a complex environment. The pseudocode of the LSM algorithm is shown in Algorithm 2. In $L$, the node value = 1 represents a locked node; the arrival time needs to be computed for other nodes with an unlocked state in the interface. The function LSMComputeT( ) is used to compute the potential field.

Algorithm 2. Locking Sweeping Method Algorithm.

Input: potential field ($T$), initial point ($P_{initial}$), locking map($L$), grid map($X$), $SweepDirections$ Initialization: 1. $T_{\mathrm{i}}\leftarrow \infty ,\forall x_{\mathrm{i}}\in X$ 2. $T.P_{initial}\leftarrow 0$ 3. $L_{\mathrm{i}}\leftarrow 0,\forall x_{\mathrm{i}}\in X$ 4. if $x_i$ belongs to the obstacle area then 5.  $L_{\mathrm{i}}\leftarrow 1$ 6. end if Sweeping: 7. stop←False 8. while stop ≠ True do 9.   for k = 1:4 do 10.     $T$←LSMComputeT ($SweepDirection{s}_{\mathrm{k}}$, $L$, $P_{initial}$, $T$) 11.     if the value of $x_i$ converges then 12.      $L_{\mathrm{i}}$←1 13.     end if 14.   end for 15.   if $L_{\mathrm{i}}=1,\forall x_{\mathrm{i}}\in X$ do 16.     stop←True 17.   end if 18. end while 19. return $T$

The process to solve the time-of-arrival field of Figure 3 using the LSM is shown in Figure 5. The figure on the left shows the calculation results after each iteration, and the figure on the right shows the locked state of the nodes in the model space. Spaces in white represent unlocked nodes and black spaces represent locked nodes, which the next iteration will skip. Before the first iteration, the locked area of the model space was the obstacle area. It can be seen from the figure on the right that the dimension of the unlocked area was greatly reduced after each iteration. After the third iteration, all nodes in the model space are locked, and the results in the left figure are output and the iteration terminates. Compared with the three iterations of the FSM, LSM improves the calculation efficiency by preventing a large amount of unnecessary calculation.

3. Planning Space Representation Based on LSM

In path planning problems, regardless of the type of unmanned vehicle and application situation, navigation safety always has the highest priority. To plan a safe path, it is very important to provide a reasonable abstraction of the navigation environment. This is especially true for marine environments because they involve a large number of uncertain environmental factors. A sufficiently safe distance should always be maintained between USVs and obstacles (both static and dynamic). Hence, in this section, an LSM-based map representation method for both static environments and dynamic obstacles is described.

3.1. Static Obstacles Representation

The LSM is directly used for the path planning for USVs. However, its disadvantage is that the generated path is too close to the obstacle, which is not suitable for the navigational safety of USVs. Therefore, to maintain a certain distance between USVs and static obstacles, the LSM was used to establish a safe area between the static obstacles and USVs, compress the global sweep results into a fixed area, and complete the static environment representation.

For example, a working environment of USVs is shown in Figure 6, which is an electronic chart of the Dalian sea area. The coordinates of this area are 121.571° E to 122.029° E and 38.8167° N to 39.0667° N. The original electronic chart was transferred to a grid chart to form the binary image as shown in Figure 7, where the black area represents areas with static obstacles, such as land and islands, and the white area represents the navigation sea area. The boundary nodes in the extracted binary image were set as the initial sweep points, i.e., the value is 0. The LSM algorithm was used to sweep the entire interface iteratively until the numerical convergence of all the nodes is obtained. Then, the resulting time-of-arrival field was processed numerically. The final potential field shows that the value of the obstacle area is 1. The farther from the static obstacle, the smaller the value until it becomes 0, as shown in Figure 8. Considering these values as indicators of security at a given point, a node with a larger value indicates that the current position may be relatively close to the obstacle boundary with low safety. The closer the boundary, the larger the value, forming a potential field zone that prevents USVs from approaching. Therefore, USVs should sail in areas with small or 0 values to ensure navigation safety.

For the entire planning space, most areas can guarantee a safe operation of unmanned vehicles. In this case, a certain value can be used as a threshold to intercept the static environment potential energy diagram, which can then be normalized to complete the static environment representation based on the LSM. The threshold is an adjustable parameter that can be selected according to different needs. The environmental model generated by different thresholds is shown in Figure 9. The blue area, i.e., the area with a value of 0, is a safe and feasible area for USVs. Two points are selected as the starting point and the end point of the path, and the path from the starting point to the end point is obtained in the map processed by different thresholds with the results shown in Figure 10. It can be seen from the figure that the planned path is different at different thresholds. A threshold value of 0.95 can better reflect the shape of the original environment, and ensure a safe distance between the feasible area and obstacle boundary, and the length of the planned path is the shortest. Specific selection criteria for thresholds will be discussed in future work. In the subsequent simulation test, the threshold value was set to 0.95 when the environmental model was processed with the threshold value.

3.2. Dynamic Obstacles Representation

To avoid a collision between USVs and dynamic obstacles or other ships, the concept of a safety area is often introduced in path planning research [35]. The safety area, i.e., a ship domain in international regulations for avoiding collisions at sea, refers to the area around a target that other moving objects are forbidden to enter. The shape of the ship domain is usually circular, and its center is located at the instantaneous position of a ship. However, in the path planning problem for USVs, a circular ship safety field is often impractical, especially when a USV is traveling at high speed, and the collision risk in the bow direction is greater than that in the side and stern directions. To fully accommodate such a requirement, Tam and Bucknall [25] proposed a new ship domain assessment method, in which a ship domain is generated and able to alter its shape according to the specific velocity. Therefore, in this paper the ship domain proposed in [25] was adopted.

The LSM was used to simulate the ship safety field based on ship speed, and the sweeping of the LSM was carried out in a specific space rather than in the whole model space. Because the number of sweep points was greatly reduced, the computational time of the LSM is relatively short, which improves the dynamic collision avoidance ability. The specific working process is similar to that of the static environment. The USV boundary node was extracted as the initial point. Then, the LSM was used to construct the ship’s safety field. When the USV travels at low speed, the ship safety area will be closer to the circle. In contrast, when the USV is traveling at high speed, the ship safety area is more similar to a semi-ellipse [22].

The ship dimensions corresponding to different speeds were obtained by Equations (6) and (8). The former was used to calculate the stern part in the ship field, while the latter was used to calculate the bow part in the ship field. The stern part in the ship field is defined as:

$${\mathrm{SA}}_{Aft}=\{\begin{array}{cc}\hfill r_{aft}& \mathrm{if}{r}_{aft}\ge r_{min}\hfill \\ \hfill r_{min}& \mathrm{otherwise}.\hfill \end{array}$$

(6)

where $r_{min}$ is the minimum distance of the ship when it is safe to travel. $r_{aft}$ is the radius of the second half of the safety area, which is defined as:

$$r_{aft}=\{\begin{array}{cc}\mathrm{velocity}\times \mathrm{time}\hfill & \mathrm{if}\mathrm{velocity}\times \mathrm{Time}<\mathrm{DisLimit},\hfill \\ 2\times \mathrm{DisLimit}-\left(\mathrm{velocity}\times \mathrm{time}\right)\hfill & \mathrm{otherwise}.\hfill \end{array}$$

(7)

where $\mathrm{velocity}$ is the speed of the ship, and $\mathrm{time}$ is the unit time, which is used to determine the area swept by the ship during this time period. In this study, $\mathrm{time}$ in $r_{aft}$ is defined as 1 min; $\mathrm{DisLimit}$ is a predefined scalar property that limits the maximum allowable safe zone radius for the side and stern sections.

The bow part of the ship field is defined as:

$${\mathrm{SA}}_{fore}=\{\begin{array}{cc}\mathrm{velocity}\times \mathrm{time}\hfill & \mathrm{if}\mathrm{velocity}\times \mathrm{Time}<\mathrm{DisLimit},\hfill \\ r_{\min }\hfill & \mathrm{otherwise}.\hfill \end{array}$$

(8)

As the speed of the ship increases, its maneuverability will gradually decrease. Therefore, to ensure the safety of ships under high-speed navigation, emphasis should be placed on the forward area of ships, particularly in situations of head-on and crossing collisions.

In the process of algorithm iteration, the ship domain is set as the obstacle region having the value of 1; however, to indicate the target ship collision risk, the LSM was used to sweep the target ship domain. The value of the target ship domain ranges from 1 to 0, and the closer the value to 0, the greater the collision risk, as shown in Figure 11. At low speed, the safety area has a circular shape. At this time, the target ship has high maneuverability and low-speed inertia, meaning it can easily turn in any direction. Hence, the collision risk is evenly distributed around the ship. At high speed, the maneuverability of the ship is relatively poor; hence, the target ship is more likely to travel in the direction of the velocity. The bow area has greater risk of collision, and the safety area has an elliptical shape following its velocity vector.

4. USV Path Planning Algorithm

The flowchart of the USV path planning algorithm is shown in Figure 12. In this algorithm, a static environment model and a dynamic obstacle model were constructed using the LSM. A potential field with the mission end point as the initial point was constructed and superposed to obtain the overall potential field. Then, the gradient descent method was used to obtain the shortest path from the starting point to the end point of the task along the gradient descent direction of the potential field.

• Step 1: First, the task environment map is transferred to a grid map, and the LSM is used to generate the static environment field, as shown in Figure 13a. During the entire planning process, the static environment remains unchanged, and the generated field matrix can be recorded as $M_{static}$ and stored for later simulation.
• Step 2: On the basis of $M_{static}$, the static full potential field was obtained using LSM, with the goal of the task as the initial point of sweeping, as shown in Figure 13b. The generated field matrix is recorded as $M_{PF}$.
• Step 3: Within each control period t, according to the instantaneous position and speed of the dynamic obstacle, LSM was used to model the dynamic target, and the results were normalized to obtain the dynamic obstacle field map, as shown in Figure 14. The generated map matrix is recorded as $M_{dynamic}$.
• Step 4: The final environmental potential field matrix $M_{total}$ is obtained by superposing $M_{dynamic}$ and $M_{PF}$, as shown in Figure 15.
• Step 5: According to the instantaneous position and speed of a USV, the gradient descent method was applied in $M_{total}$ to obtain the path planning point, and the USV sailed toward the planning point.
• Step 6: If the USV reaches the mission goal, then the cycle ends; otherwise, go back to Step 3.

Compared with the potential field generated by the APF method, the potential field generated by the LSM has a single global minimum located at the initial point. Compared with the traditional FMM and FSM, the LSM uses less computational time. The accuracy of three methods is also the same; hence, the LSM is more efficient than other the methods.

5. Simulation Results and Discussions

In this section, simulation results are provided to demonstrate the performance of the proposed algorithm. Simulations are first conducted to compare the FMM, FSM, and LSM algorithms to show the computing efficiency provided by the LSM with the comparisons carried out in free spaces, areas with simple obstacles, and practical maritime environments. The second set of tests are carried out using ENC information from Dalian sea area with the results showing that trajectories can always be well generated to avoid both complex static and dynamic obstacles. All simulations were carried out using MATLAB.

5.1. Comparison Results of FMM, FSM, and LSM

The FMM, FSM, and LSM were used to calculate the time-of-arrival field of model spaces without obstacles. The results (time) for the experiments are shown in Figure 16. The x-axis represents the pixel size of the model space, and the y-axis represents the calculation time. It can be seen that with the increase in the size of the model space, the calculation efficiency of the FMM declines rapidly, for which the calculation speed is always the slowest among the three methods. The LSM provides the best calculation performance in different sizes of model space.

Another comparison of the FMM, FSM and LSM was undertaken in an environment with barriers as shown in Figure 17 to assess their performances in dealing with obstacles. An example of the time-of-arrival field computed by the LSM is shown in Figure 18. The numerical comparison results considering the computational time are shown in Figure 19. It can be seen that the FMM takes the most computational time when the number of barriers is small. However, when more barriers exist in the environment, the computational time of the FSM will decrease rapidly because more iterations are required for calculation. Overall, the LSM has the best performance because its computational time is the lowest in all settings.

The last comparison of the FMM, FSM and LSM was carried out in an environment extracted from a practical navigation area in Dalian sea as shown in Figure 20a. An example of the time-of-arrival field computed by the LSM is shown in Figure 20b. By undertaking the comparison in the same environment but with different environment resolutions, the performances of the three methods with regards to their computational time are shown in Figure 21. In the case of low precision, where the resolution is less than 500 × 500 pixels, the calculation time of the LSM is slightly lower than that of the FSM and FMM. When the resolution of the environment is increased, the computational efficiencies of three methods gradually decrease. However, the FMM has the fastest decline, and the LSM has the least change. When the environment has the resolution of 4000 × 4000 pixels, the computation time of LSM is about half that of FSM and one third that of FMM. Therefore, the LSM is used to construct the potential energy field and complete the path planning of USVs in this paper.

5.2. Simulation Results of USVs Path Planning in Practical Environments

To verify the algorithm, a variety of simulation experiments were conducted on the MATLAB simulation platform, including: (1) the static simulation of USVs in the global environment, (2) the local collision avoidance simulation of USVs, and (3) dynamic simulation combining the previous two conditions. In all simulations, the ENC of Dalian sea area (shown in Figure 6) was used as the environmental model. As mentioned previously, the ENC was first converted to a corresponding binary map as the input for the path planning algorithm. Position information of both USVs and other ships was expressed in geodetic coordinates. In addition, the coordinates of navigation waypoints can be directly extracted from the generated path for ships in practical maritime environments.

Simulation results are presented to demonstrate how the trajectory was generated to address two fundamental requirements: (1) generating a safe global trajectory connecting the start and end points in a static environment; (2) generating a collision-free local trajectory to avoid both the dynamic and static obstacles. It should be noted that, as stated in [20], when using the LSM (or the level set method-based algorithm in general) for generating a trajectory, a path with the shortest distance can also be found provided such a solution exists. Therefore, in this paper, this characteristic has not been discussed and readers can refer to [20,22,26] for more detailed discussion.

5.2.1. Global Static Planning Simulation

In the global static planning simulation, the Dalian sea area was adopted as the planning space. The starting point of a USV was set to be (121.8389° E, 38.8455° N), marked by a red dot. The goal of the mission is (121.6076° E, 38.9992° N), marked by a red asterisk. The sailing speed of the USV is constant with a value of 10 knots. The global environment is shown in Figure 22.

Using the LSM again in Figure 22 to obtain the potential field for path planning, unlike the generated static environment, this sweep takes the goal of the task as the initial point, and iteratively sweeps the entire interface. To ensure the navigation safety of the USV, the obstacle area and the color gradient narrow band are the areas that cannot be accessed by the sweeping. The final result is shown in Figure 23.

In Figure 23, the white area represents the static obstacles and the color gradient narrow band represents the anti-collision area. In addition, there is a blue to brown color gradient wave zone from the goal, indicating the potential field that the USV should follow when sailing in the safe area. The gradient descent method was used to solve the optimal path in the potential field, and an obstacle-free path from the origin to the goal was obtained, as shown in Figure 24. The geodetic coordinates of the waypoint of the path can be sampled and obtained by means of an electronic chart, with longitude and latitude of some key navigation points show in

Table 1. Geodetic coordinates of key navigation points in the global static planning path.

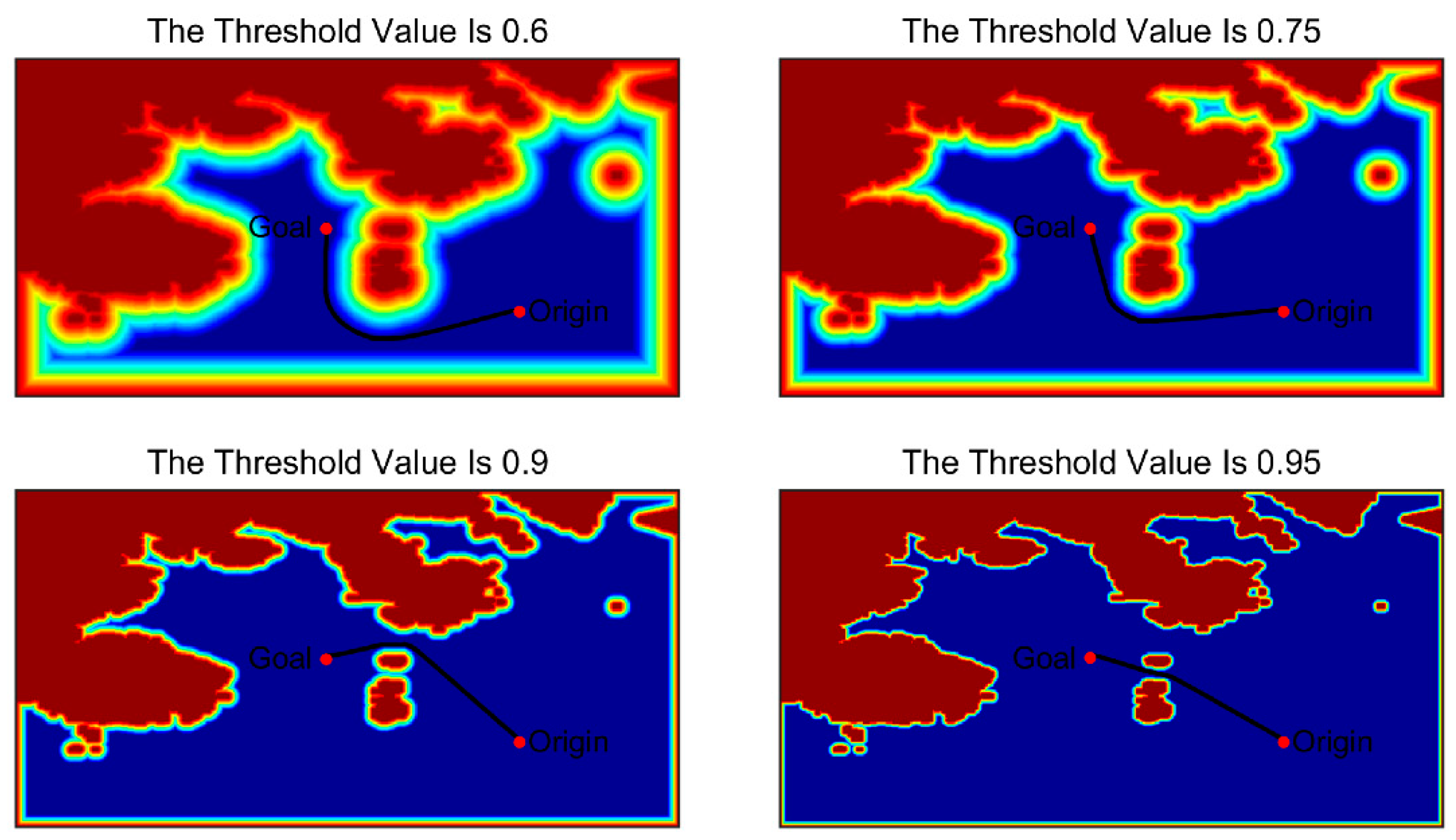
Point Number	Geodetic Coordinate
origin	(121.8389, 38.8455)
point 1	(121.9071, 38.8673)
point 2	(121.9116, 38.8786)
point 3	(121.9139, 38.9036)
point 4	(121.8744, 38.9261)
point 5	(121.8235, 38.9348)
point 6	(121.6947, 38.9967)
point 7	(121.6317, 39.0173)
point 8	(121.6002, 39.0111)
goal	(121.6076, 38.9992)

.

As can be seen in Figure 24, the USV started from the bay, sailed across the strait to the Bohai Sea, and finally reached the end point at the back of the island. The path generated in the process is smooth, and under the premise of ensuring a safe distance from the coast boundary, the path length was minimized. This method avoids the local minimum problem of the traditional APF and realizes a point-to-point global path planning in a complex environment.

5.2.2. Local Dynamic Programming Simulation

Local dynamic collision avoidance planning simulation was carried out in a dynamic environment with multiple moving ships, and a part of the Dalian sea area was used as the working area. The USV sailed from (121.6443° E, 39.0467° N) to (121.6512° E, 38.8967° N) at a speed of 16 knots. Three virtual ships—Obs1, Obs2, and Obs3—were added to the process, with speeds of 8, 14, and 20 knots, respectively. The initial condition of the task is shown in Figure 25.

In Figure 25a, the blue dot represents the start point of the USV and the mobile ships, the red dotted line represents the navigation route of the three mobile ships, and the red asterisk represents the mission goal of the USV. Figure 25b shows the potential field distribution in the task space. The color of the potential field gradually darkens from blue to brown. The blue area near the goal means that the potential field tends to be 0. The farther from the goal, the darker the color and the larger the node value. The safety field of mobile ships proves that the algorithm can adjust the ship safety field according to the speed. The speed of Obs1 is relatively small, and the ship field is shown as a circular area. The speeds of Obs2 and Obs3 are relatively large, and the ship field is shown as a semi-elliptical shape, in which the speed of Obs3 is greater than that of Obs2; hence, the field shape of Obs3 is more slender, and the center of gravity for collision avoidance is located nearer the bow. The entire moving trajectory of the USV is shown in Figure 26.

In Figure 26, the left figure shows the planned path of the USV and the position of all of the ships. The right figure is the potential field map corresponding to the left figure. The potential field map was used to plan the navigation path of the USV. Figure 25 shows that the line between the origin and goal of the USV passes through Obs1; hence, the USV must first overtake Obs1. Simulation cycle 5 is shown in Figure 26a. At this time, the USV moves to the right of Obs1 and attempts to overtake it from the right. The potential field shows that the USV is traveling at the edge of the Obs1 security area, which ensures the ship’s safe navigation. In simulation cycle 9, as shown in Figure 26b, the USV has completed the overtaking operation and sailed towards the mission goal along the gradient descent direction. At this time, the USV has approached the ship safety field of Obs2 and formed a crossing situation with Obs2. The USV turned left and sailed to the position shown in simulation cycle 10 (Figure 26c); it then sailed to the rear of Obs2 to avoid the risk of collision. After determining the removal of the collision risk, it adjusted the navigation direction and continued to sail towards the goal, until it formed a head-on situation with Obs3. Figure 26d shows that in simulation cycle 14, the USV sailed towards the right to avoid the incoming Obs3, and completed the evasive action in simulation cycle 16 (Figure 26e). In simulation cycle 26 (Figure 26f), the USV reached the goal and completed the entire mission.

From the navigation path of the unmanned vehicle on the left of Figure 26, it can be seen that the avoidance treatment methods of the unmanned vehicle for the three collision situations (head-on, crossing, and overtaking) during the whole voyage, and the evasive path is reasonable. The figure on the right shows that the overall trajectory of the USV is always outside the ship safety field of the moving ship, and maintains a safe distance from static obstacles; this proves that the USV can effectively avoid dynamic obstacles and ensure navigation safety.

5.2.3. Simulation of Tasks in a Dynamic Environment with Multiple Moving Ships

The simulation space adopted was the whole Dalian sea area, as shown in Figure 13. The USV performed the task in Section 5.1, and sailed from (121.8389° E, 38.8455° N) to (121.6076° E, 38.9992° N) at a speed of 16 knots. Three virtual ships, Obs1, Obs2, and Obs3, were added to the process with speeds of 8, 16, and 24 knots, respectively. The initial situation of the task is shown in Figure 27.

In Figure 27, the USV should start from the bay and cross more than half of the sea to achieve the goal of the mission at the bottom left of the chart. Figure 27 clearly shows the potential field of the USV in the safe driving area and the safety area of the moving ship to facilitate the planning of the correct navigation path of the USV. The entire moving trajectory of the USV is shown in Figure 28.

In Figure 28, the USV starts from the origin and completes the overtaking of Obs1 in the bay (Figure 28a,b). It uses evasive action to address the head-on situation with Obs3 (Figure 28c,d) and the crossing situation with Obs2 (Figure 28e,f). In simulation cycle 85, the USV achieved the goal of the mission. The overall navigation path of the USV is shown in Figure 28g. The overall navigation path is relatively smooth. The USV maintained a sufficiently safe distance from static obstacles during the course of the operation, and always sailed outside the safety field of the moving ship to avoid dynamic obstacles.

Compared with the static global planning of the USV in Section 5.1, the tasks performed by the USV are the same. The trajectory in Figure 28g is similar to that in Figure 24 overall. It can be seen that there is no redundant action, and necessary evasive action is taken in the course of the USV’s route. This proves that the stability of the algorithm is high, and that the USV does not take adverse maneuvers when using the proposed algorithm.

6. Conclusions and Future Work

In this paper, a new method based on the LSM was proposed to address the path planning problem of USVs in practical maritime environments with both static and dynamic obstacles. Compared with other conventional methods, such as the FMM and the FSM algorithms, the LSM has the advantage of fast computational speed, which enables the proposed algorithm to efficiently model the planning environment and generate an optimized trajectory in real time. In addition, generated trajectories are guaranteed to be safe and smooth, which facilitates trajectory following and tracking for USVs. To validate the performance of the proposed algorithms, three sets of different simulations were carried out. To improve the practicability of the tests, all simulation environments were constructed using the ENC information from the Dalian sea area. The simulation results demonstrate that the proposed path planning algorithm generates optimized paths to avoid both static and dynamic obstacles. Furthermore, because of the adoption of ENC information, the generated trajectory consists of geodetic coordinates that can be directly used for practical maritime navigation.

In future work, one direction will be to improve the LSM algorithm so that route planning for multi-USV formation applications can be achieved. Compared with single vehicle planning, more complex planning requirements, such as coordination and collaboration within the formation, should be considered and addressed. Another interesting direction would be to introduce an environmental interference model and a USV control model to achieve autonomous navigation capability for USVs. Information communication and exchange between different functioning modules should be accommodated. Furthermore, when dealing with moving obstacles, COLREGs regulations can be further integrated into the proposed algorithm. This can be potentially achieved by adding a “COLREGs compliant potential field” that is superimposed on the conventional potential field generated by the LSM to guide USVs to avoid dynamic obstacles according to the rules.