The Optimization Process for Seaside Operations at Medium-Sized Container Terminals with a Multi-Quay Layout
Abstract
:1. Introduction
2. Literature Overview
2.1. General Problem Survey Papers
2.2. Berth Allocation and Crane Allocation as Isolated Problems in Related Papers
2.3. Integrated Solutions
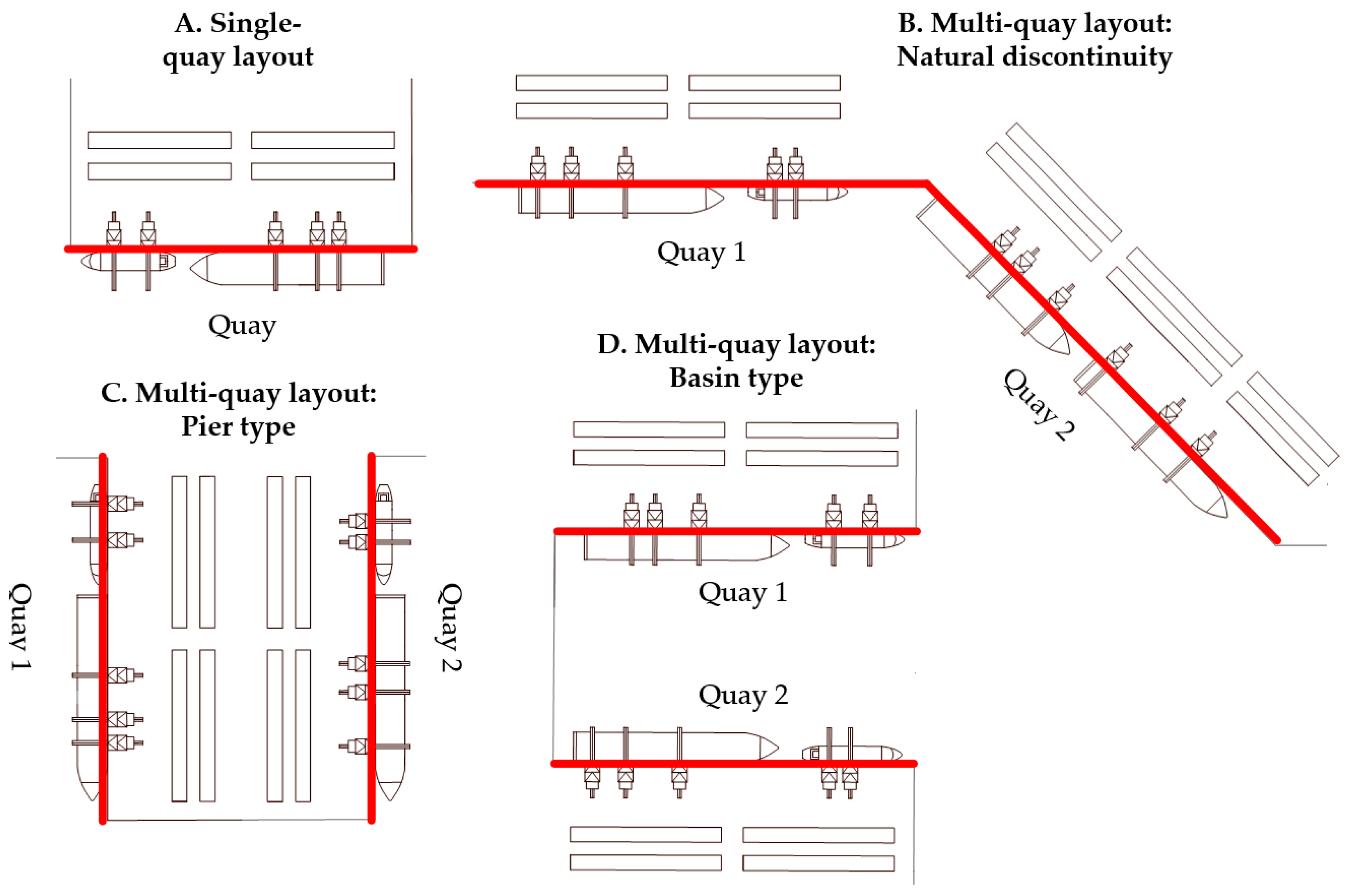
2.4. Papers Where a Multi-Quay or Multi-Terminal Environment Is Considered
3. Problem Description and Methodology
3.1. Problem Description
- The availability of quay cranes (number of QCs to be assigned);
- Transport demand (number of containers);
- The distribution of containers across the ships’ holds/bays, or stowage plan;
- Crane production and utilization factor.
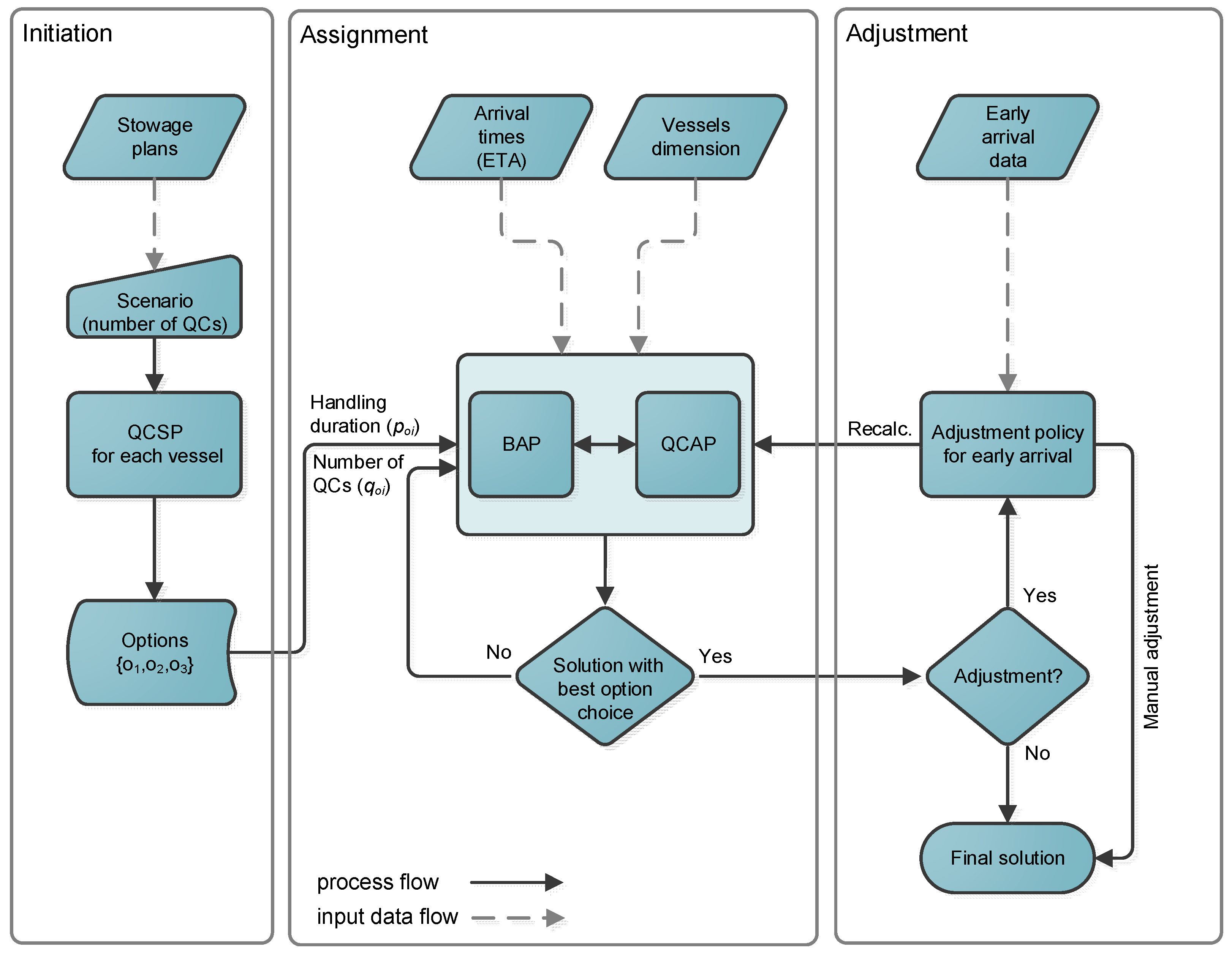
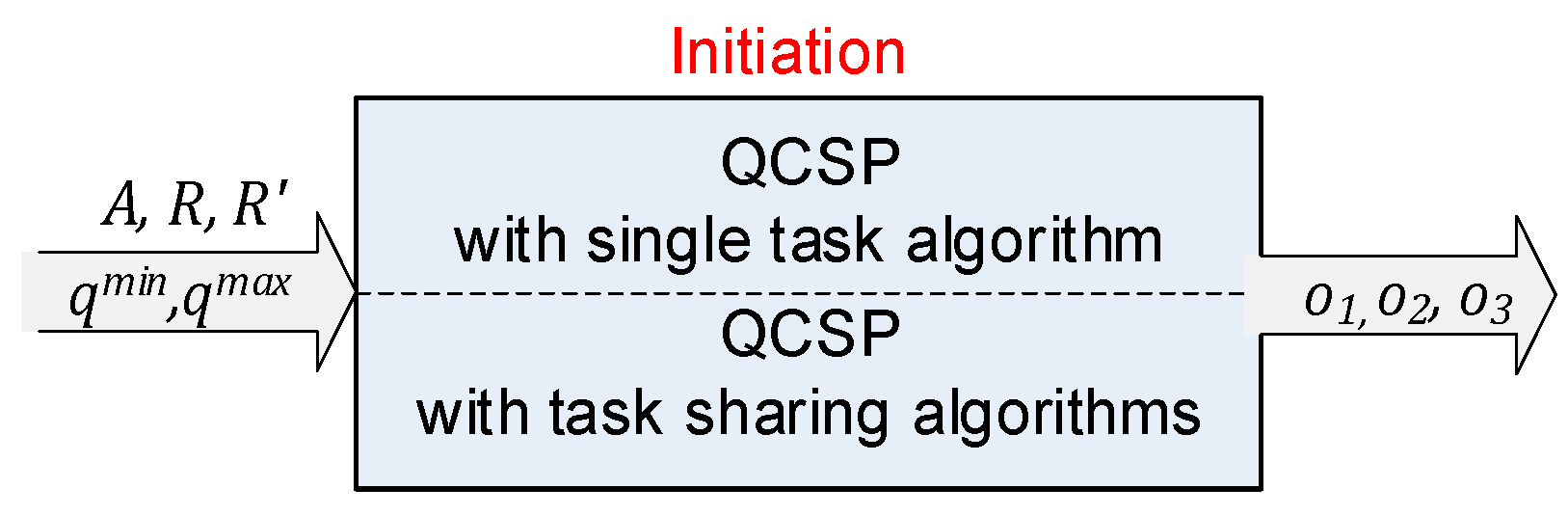
3.2. Methodology
4. Model Formulation
4.1. Assumptions
- Berths are divided into segments and marked from the outer to the inner side of the quay;
- Vessels are always berthed with a bow on the outer side of the quay;
- All berths are available, there are no depth restrictions;
- There are no priority vessels, all vessels have the same priority;
- Safety distances between the ships are ignored or may be incorporated into ships’ length;
- Maneuvering time and preparation times are considered as constant and are integrated with waiting and processing times;
- The number of assigned cranes is constant during the handling process;
- The allocated crane can be moved to another task (bay) before the previous one is completed;
- There is one terminal operator for both quays that offers the public service;
- There is a mutual agreement between the shipping company and the terminal operator where a policy for the port service exists.
4.2. Parameters and Variables
| Indices | |
| i, j | the index for vessels |
| k | the index for quays/terminals |
| t | the index for time windows |
| v | the index for scenarios |
| Sets | |
| V | set of vessels, V = {1, 2, …, n} |
| W | set of quays or terminals, W = {1, 2, …, m} |
| S | set of operational scenarios, S = {O1, O2, O3} |
| T | set of time windows, T = {1, 2, …, H} |
| Parameters | |
| ai | estimated time of arrival of the vessel i, . |
| li | length of the vessel i expressed in required berth positions, |
| ciw | unit cost of lost time due to waiting for free berth of the vessel i, |
| cie | unit cost of speed-up due to earlier arrival policy of the vessel i, |
| ωik | quay logistic cost coefficient for the vessel i if berthing at the quay k, , |
| WLk | length of the quay or terminal k, |
| QCk | number of quay cranes available at the quay/terminal k, |
| H | planning horizon |
| M | big integer number |
| Auxiliary variables | |
| piv | processing time or handling time of the vessel i in the scenario v, , |
| qiv | number of quay cranes assigned in the scenario v, , . |
| Decision variables | |
| bi | starting berth position of the vessel i, . |
| si | berthing time (start of handling operations) of the vessel i, |
| di | departure time of the vessel i, |
| wi | waiting time for free berth of the vessel i, |
| ei | time savings if earlier arrival is possible of the vessel i, |
| xik | set to 1 if vessel i is berthed on quay k, and 0 otherwise, , |
| yij | set to 1 if , and 0 if , |
| zij | set to 1 if , and 0 if |
| oiv | set to 1 if vessel i is processing according to scenario v, and 0 otherwise, , |
| rit | set to 1 if vessel i is processing in time windows t, and 0 otherwise, , |
| ritkv | set to 1 if vessel i is processing in time windows t at quay k according to scenario v, and 0 otherwise, , , , |
4.3. Objective Function
5. Experiment and Analysis of Results
5.1. Experiment Setup
- If increasing the number of cranes does not bring improvement in processing time, the corresponding scenario is excluded from the selection;
- If more than three scenarios are qualified, three of them with the best score (lower processing time) are selected;
- If there are less than three scenarios qualified, a dummy option with a big integer value for processing time is inserted to prevent it from being further considered as the option.
- Number of quays = 2;
- Number of cranes or each quay/terminal = 5;
- Length of each quay = 15;
- All unit costs = 1;
- Quay logistic cost coefficient = equal for both terminals = 1.
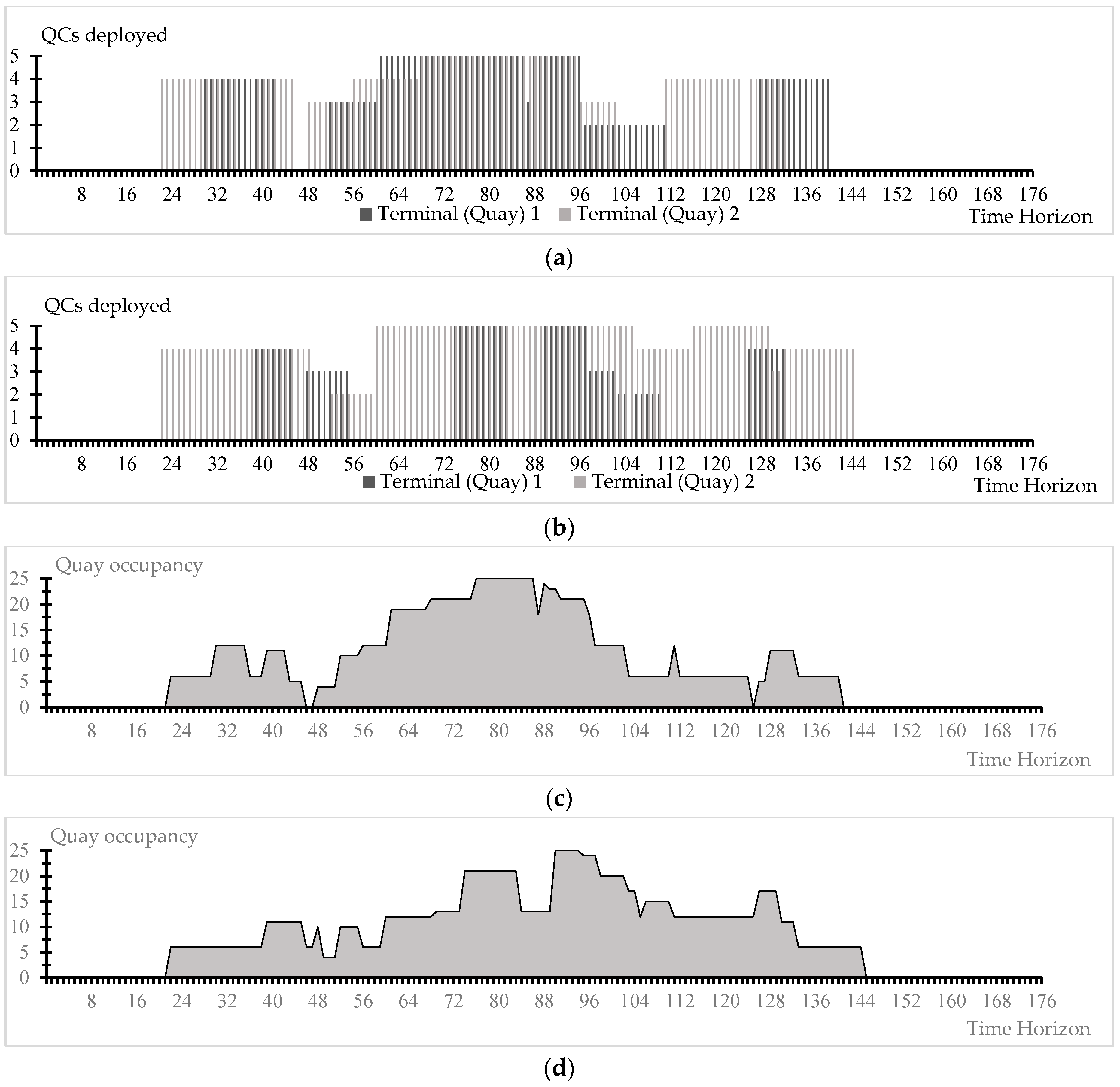
5.2. Results
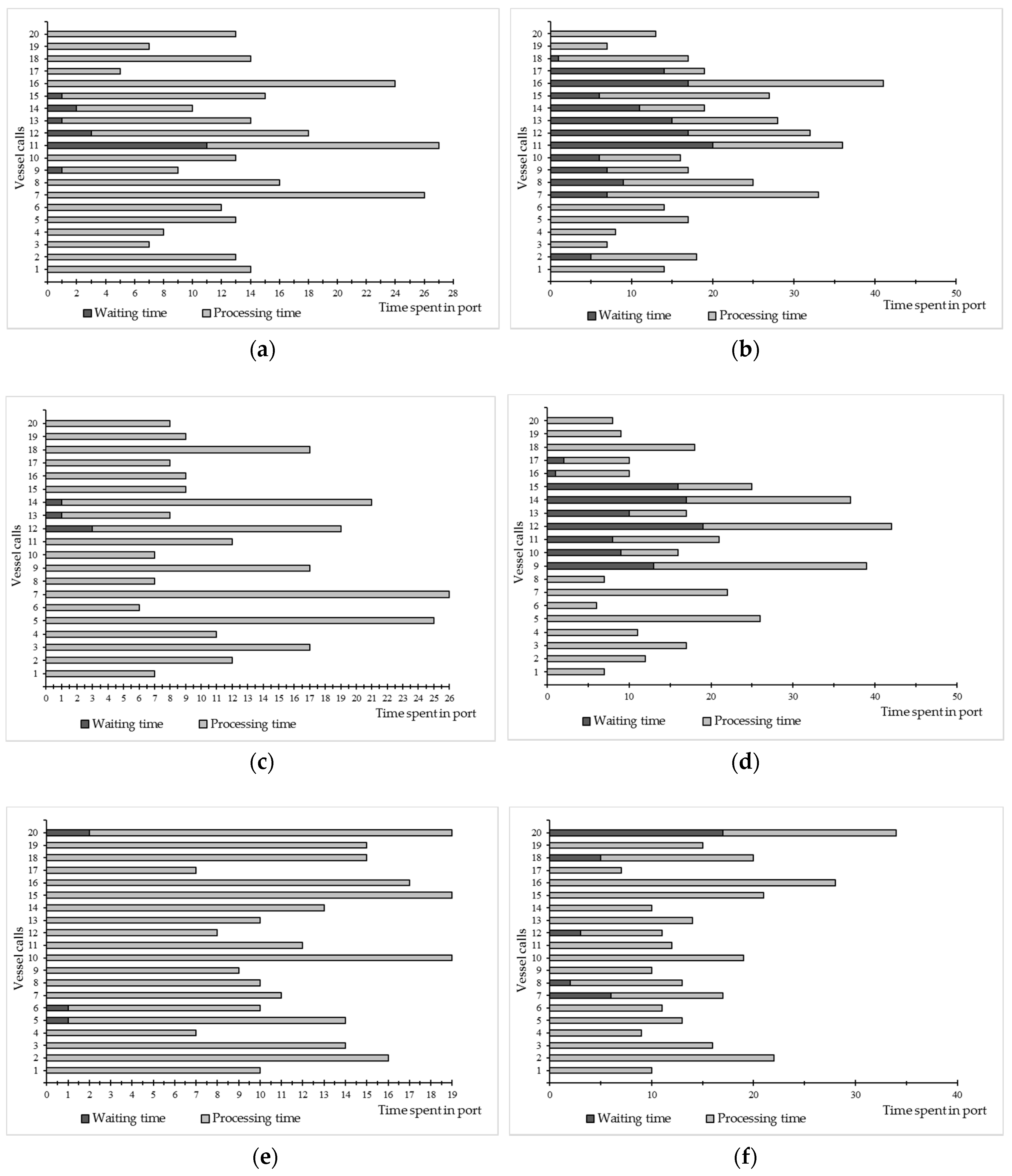
5.3. Utilization Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Vessel Arrivals | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Seed = 400 | Seed = 700 | |||||||||||
| λ = 3.2 | λ = 3.5 | λ = 3.2 | λ = 3.5 | Number of Cranes | Processing Time | |||||||
| n | a(1) | a(2) | a(3) | a(4) | l | opt1 | opt2 | opt3 | opt1 | opt2 | opt3 | TEU |
| 1 | 12 | 11 | 6 | 6 | 5 | 2 | 3 | 4 | 16 | 11 | 10 | 874 |
| 2 | 26 | 24 | 8 | 8 | 6 | 1 | 2 | 3 | 43 | 22 | 16 | 1157 |
| 3 | 29 | 27 | 31 | 29 | 6 | 2 | 3 | 4 | 24 | 16 | 14 | 1310 |
| 4 | 38 | 35 | 34 | 32 | 3 | 1 | 2 | M | 9 | 7 | M | 229 |
| 5 | 39 | 36 | 39 | 37 | 4 | 1 | 2 | M | 24 | 13 | M | 648 |
| 6 | 39 | 36 | 40 | 38 | 4 | 1 | 2 | 3 | 22 | 11 | 9 | 598 |
| 7 | 45 | 41 | 50 | 47 | 4 | 1 | 2 | 3 | 28 | 14 | 11 | 741 |
| 8 | 51 | 47 | 51 | 48 | 4 | 1 | 2 | 3 | 22 | 11 | 10 | 589 |
| 9 | 70 | 64 | 65 | 61 | 5 | 2 | 3 | 4 | 15 | 10 | 9 | 792 |
| 10 | 71 | 65 | 66 | 62 | 6 | 1 | 2 | 3 | 46 | 23 | 19 | 1247 |
| 11 | 76 | 69 | 77 | 72 | 4 | 1 | 2 | M | 20 | 12 | M | 548 |
| 12 | 78 | 71 | 79 | 74 | 3 | 1 | M | M | 8 | M | M | 210 |
| 13 | 82 | 75 | 81 | 76 | 5 | 1 | 2 | 3 | 27 | 14 | 10 | 724 |
| 14 | 90 | 82 | 94 | 87 | 3 | 1 | 2 | M | 13 | 10 | M | 359 |
| 15 | 96 | 88 | 99 | 91 | 7 | 2 | 3 | 4 | 32 | 21 | 19 | 1706 |
| 16 | 98 | 89 | 101 | 93 | 6 | 2 | 3 | 4 | 28 | 19 | 17 | 1492 |
| 17 | 112 | 102 | 119 | 109 | 4 | 1 | 2 | 3 | 19 | 10 | 7 | 516 |
| 18 | 114 | 104 | 120 | 109 | 6 | 2 | 3 | 4 | 23 | 15 | 12 | 1228 |
| 19 | 115 | 104 | 132 | 120 | 5 | 1 | 2 | 3 | 29 | 15 | 14 | 791 |
| 20 | 118 | 107 | 151 | 137 | 7 | 3 | 4 | 5 | 25 | 19 | 17 | 2023 |
| 21 | 140 | 127 | 157 | 142 | 6 | 2 | 3 | 4 | 23 | 15 | 14 | 1221 |
| 22 | 140 | 127 | 166 | 150 | 6 | 2 | 3 | 4 | 21 | 14 | 13 | 1126 |
| 23 | 145 | 132 | 176 | 159 | 5 | 2 | 3 | 4 | 12 | 8 | 7 | 624 |
| 24 | 150 | 137 | 186 | 168 | 4 | 1 | 2 | 3 | 24 | 12 | 8 | 638 |
| 25 | 157 | 143 | 190 | 172 | 6 | 1 | 2 | 3 | 33 | 17 | 13 | 904 |
| 26 | 160 | 146 | 199 | 180 | 6 | 2 | 3 | 4 | 21 | 14 | 12 | 1123 |
| 27 | 163 | 149 | 200 | 181 | 7 | 2 | 3 | M | 26 | 20 | M | 1384 |
| 28 | 175 | 160 | 204 | 185 | 6 | 2 | 3 | M | 22 | 16 | M | 1185 |
| 29 | 178 | 162 | 206 | 187 | 4 | 1 | 2 | 3 | 19 | 10 | 8 | 518 |
| 30 | 218 | 199 | 207 | 188 | 4 | 1 | 2 | 3 | 25 | 13 | 10 | 680 |
| 31 | 222 | 202 | 209 | 190 | 6 | 2 | 3 | 4 | 23 | 16 | 14 | 1251 |
| 32 | 231 | 210 | 212 | 193 | 5 | 1 | 2 | 3 | 31 | 15 | 14 | 824 |
| 33 | 238 | 216 | 214 | 195 | 3 | 1 | 2 | M | 13 | 10 | M | 354 |
| 34 | 241 | 218 | 218 | 199 | 4 | 1 | 2 | 3 | 16 | 8 | 7 | 423 |
| 35 | 248 | 225 | 227 | 207 | 6 | 2 | 3 | 4 | 21 | 14 | 13 | 1113 |
| 36 | 250 | 227 | 228 | 208 | 6 | 2 | 3 | M | 24 | 19 | M | 1311 |
| 37 | 257 | 233 | 231 | 211 | 3 | 1 | 2 | M | 10 | 5 | M | 271 |
| 38 | 260 | 235 | 253 | 231 | 6 | 2 | 3 | 4 | 24 | 16 | 14 | 1293 |
| 39 | 269 | 243 | 269 | 246 | 5 | 2 | 3 | 4 | 13 | 9 | 7 | 719 |
| 40 | 277 | 250 | 271 | 248 | 6 | 2 | 3 | 4 | 22 | 15 | 13 | 1187 |
| 41 | 284 | 256 | 272 | 249 | 3 | 1 | 2 | M | 10 | 6 | M | 256 |
| 42 | 294 | 265 | 289 | 265 | 5 | 1 | 2 | 3 | 30 | 15 | 13 | 813 |
| 43 | 301 | 271 | 292 | 268 | 5 | 1 | 2 | 3 | 33 | 17 | 16 | 899 |
| 44 | 304 | 273 | 300 | 275 | 3 | 1 | 2 | M | 11 | 8 | M | 299 |
| 45 | 314 | 282 | 311 | 285 | 3 | 1 | 2 | M | 13 | 10 | M | 354 |
| 46 | 316 | 284 | 311 | 285 | 5 | 1 | 2 | 3 | 27 | 14 | 9 | 729 |
| 47 | 317 | 285 | 313 | 287 | 6 | 2 | 3 | 4 | 25 | 17 | 15 | 1335 |
| 48 | 323 | 291 | 322 | 295 | 4 | 1 | 2 | 3 | 23 | 11 | 10 | 604 |
| 49 | 330 | 297 | 327 | 300 | 3 | 1 | 2 | M | 11 | 6 | M | 295 |
| 50 | 341 | 307 | 327 | 300 | 6 | 1 | 2 | 3 | 42 | 21 | 18 | 1126 |
| 51 | 342 | 308 | 328 | 301 | 3 | 1 | 2 | M | 12 | 8 | M | 330 |
| 52 | 349 | 314 | 349 | 320 | 5 | 2 | 3 | 4 | 17 | 12 | 11 | 928 |
| 53 | 357 | 321 | 351 | 321 | 7 | 2 | 3 | M | 33 | 22 | M | 1768 |
| 54 | 364 | 327 | 353 | 323 | 4 | 1 | 2 | 3 | 24 | 12 | 10 | 647 |
| 55 | 370 | 332 | 363 | 332 | 3 | 1 | 2 | M | 13 | 8 | M | 348 |
| 56 | 383 | 344 | 365 | 334 | 3 | 1 | 2 | M | 7 | 5 | M | 188 |
| 57 | 384 | 345 | 377 | 345 | 5 | 1 | 2 | 3 | 24 | 12 | 8 | 638 |
| 58 | 386 | 347 | 394 | 361 | 3 | 1 | 2 | M | 12 | 7 | M | 324 |
| 59 | 398 | 358 | 396 | 363 | 5 | 1 | 2 | 3 | 38 | 19 | 13 | 1008 |
| 60 | 414 | 372 | 398 | 364 | 6 | 2 | 3 | 4 | 20 | 13 | 10 | 1048 |
| 61 | 417 | 375 | 419 | 384 | 5 | 1 | 2 | M | 28 | 14 | M | 745 |
| 62 | 429 | 386 | 420 | 385 | 5 | 1 | 2 | 3 | 28 | 14 | 13 | 750 |
| 63 | 453 | 408 | 423 | 388 | 3 | 1 | 2 | M | 12 | 9 | M | 329 |
| 64 | 455 | 410 | 433 | 397 | 4 | 1 | 2 | M | 17 | 12 | M | 454 |
| 65 | 457 | 411 | 458 | 420 | 6 | 1 | 2 | 3 | 44 | 22 | 16 | 1185 |
| 66 | 477 | 429 | 461 | 423 | 4 | 1 | 2 | M | 22 | 11 | M | 588 |
| 67 | 488 | 439 | 464 | 426 | 5 | 1 | 2 | 3 | 31 | 16 | 11 | 832 |
| 68 | 490 | 441 | 475 | 436 | 5 | 2 | 3 | 4 | 17 | 11 | 10 | 902 |
| 69 | 526 | 473 | 476 | 437 | 3 | 1 | 2 | M | 12 | 7 | M | 321 |
| 70 | 536 | 482 | 488 | 448 | 5 | 1 | 2 | 3 | 22 | 11 | 9 | 592 |
| 71 | 544 | 489 | 488 | 448 | 6 | 2 | 3 | 4 | 22 | 15 | 14 | 1165 |
| 72 | 546 | 491 | 498 | 457 | 5 | 1 | 2 | 3 | 35 | 18 | 14 | 935 |
| 73 | 560 | 504 | 524 | 481 | 6 | 2 | 3 | M | 25 | 21 | M | 1336 |
| 74 | 575 | 518 | 576 | 528 | 4 | 1 | 2 | 3 | 25 | 12 | 10 | 661 |
| 75 | 589 | 531 | 603 | 553 | 5 | 1 | 2 | 3 | 31 | 16 | 13 | 836 |
| 76 | 603 | 544 | 604 | 554 | 4 | 1 | 2 | 3 | 22 | 11 | 8 | 596 |
| 77 | 615 | 555 | 607 | 557 | 7 | 2 | 3 | 4 | 25 | 17 | 13 | 1357 |
| 78 | 616 | 556 | 607 | 557 | 4 | 1 | 2 | 3 | 20 | 10 | 9 | 543 |
| 79 | 619 | 558 | 630 | 578 | 5 | 1 | 2 | 3 | 37 | 18 | 13 | 986 |
| 80 | 627 | 566 | 638 | 585 | 5 | 1 | 2 | 3 | 40 | 20 | 14 | 1075 |
| 81 | 632 | 570 | 639 | 586 | 4 | 1 | 2 | 3 | 19 | 10 | 7 | 517 |
| 82 | 635 | 573 | 647 | 593 | 5 | 1 | 2 | 3 | 28 | 14 | 12 | 754 |
| 83 | 635 | 573 | 657 | 602 | 6 | 1 | 2 | 3 | 49 | 24 | 17 | 1309 |
| 84 | 645 | 582 | 675 | 618 | 5 | 2 | 3 | 4 | 18 | 12 | 11 | 980 |
| 85 | 650 | 587 | 689 | 631 | 6 | 2 | 3 | M | 26 | 25 | M | 1370 |
| 86 | 658 | 595 | 694 | 635 | 3 | 1 | 2 | M | 10 | 6 | M | 257 |
| 87 | 666 | 602 | 699 | 640 | 6 | 2 | 3 | M | 26 | 22 | M | 1387 |
| 88 | 678 | 613 | 701 | 641 | 3 | 1 | 2 | M | 12 | 7 | M | 315 |
| 89 | 705 | 638 | 702 | 642 | 6 | 2 | 3 | M | 26 | 17 | M | 1381 |
| 90 | 731 | 662 | 706 | 645 | 3 | 1 | 2 | M | 10 | 7 | M | 257 |
| 91 | 743 | 673 | 713 | 651 | 6 | 2 | 3 | 4 | 19 | 13 | 12 | 1026 |
| 92 | 761 | 689 | 715 | 653 | 6 | 1 | 2 | 3 | 46 | 23 | 16 | 1243 |
| 93 | 768 | 696 | 724 | 661 | 3 | 1 | 2 | M | 10 | 7 | M | 268 |
| 94 | 772 | 700 | 724 | 661 | 7 | 2 | 3 | M | 29 | 20 | M | 1535 |
| 95 | 784 | 711 | 725 | 662 | 3 | 1 | 2 | M | 10 | 9 | M | 270 |
| 96 | 791 | 718 | 740 | 676 | 4 | 1 | 2 | 3 | 19 | 10 | 9 | 514 |
| 97 | 795 | 722 | 748 | 683 | 3 | 1 | 2 | M | 10 | 8 | M | 278 |
| 98 | 796 | 723 | 753 | 688 | 5 | 1 | 2 | 3 | 37 | 18 | 17 | 984 |
| 99 | 797 | 724 | 761 | 695 | 5 | 1 | 2 | 3 | 28 | 14 | 9 | 738 |
| 100 | 825 | 750 | 771 | 704 | 5 | 2 | 3 | 4 | 15 | 10 | 8 | 823 |
| QC | 1 | 2 | 3 | 4 | 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Full | Split | Full | Split | Full | Split | Full | Split | Full | Split | |
| 1 | 32.5 | 32.5 | 16.66 | 16.27 | 12.47 | 10.84 | 10.12 | 10.12 | 10.12 | 10.12 |
| 2 | 42.98 | 42.98 | 21.85 | 21.5 | 16.31 | 16.32 | 16.31 | 16.32 | 16.31 | 16.32 |
| 3 | 48.64 | 48.64 | 24.4 | 24.32 | 16.99 | 16.27 | 13.65 | 13.54 | 13.65 | 13.52 |
| 4 | 8.53 | 8.53 | 6.52 | 6.54 | 6.52 | 6.53 | 6.52 | 6.53 | 6.52 | 6.53 |
| 5 | 24.13 | 24.13 | 12.54 | 12.54 | 12.54 | 12.54 | 12.54 | 12.54 | 12.54 | 12.54 |
| 6 | 22.26 | 22.26 | 12.15 | 11.13 | 8.82 | 8.82 | 8.82 | 8.82 | 8.82 | 8.82 |
| 7 | 27.53 | 27.53 | 14.36 | 13.77 | 11.6 | 10.61 | 10.6 | 10.6 | 10.6 | 10.6 |
| 8 | 21.91 | 21.91 | 11.82 | 10.97 | 9.47 | 9.47 | 9.47 | 9.47 | 9.47 | 9.46 |
| 9 | 29.45 | 29.45 | 15.04 | 14.73 | 10.7 | 9.82 | 8.49 | 8.49 | 8.49 | 8.49 |
| 10 | 46.29 | 46.29 | 24.09 | 23.15 | 18.76 | 18.76 | 18.76 | 18.76 | 18.76 | 18.76 |
| 11 | 20.37 | 20.37 | 11.81 | 11.81 | 11.83 | 11.83 | 11.83 | 11.83 | 11.83 | 11.83 |
| 12 | 7.81 | 7.81 | 7.81 | 7.81 | 7.81 | 7.81 | 7.81 | 7.81 | 7.81 | 7.81 |
| 13 | 26.92 | 26.92 | 13.88 | 13.46 | 10.12 | 10.08 | 10.07 | 10.07 | 10.07 | 10.07 |
| 14 | 13.32 | 13.32 | 10.15 | 10.15 | 10.15 | 10.15 | 10.15 | 10.15 | 10.15 | 10.15 |
| 15 | 63.34 | 63.34 | 31.71 | 31.71 | 23.59 | 21.12 | 18.75 | 18.75 | 18.73 | 18.73 |
| 16 | 55.38 | 55.38 | 28.62 | 27.7 | 19.96 | 18.48 | 17.04 | 17.05 | 17.04 | 17.05 |
| 17 | 19.22 | 19.22 | 10.02 | 9.61 | 7.47 | 6.59 | 6.59 | 6.59 | 6.59 | 6.59 |
| 18 | 45.62 | 45.62 | 22.87 | 22.87 | 16.45 | 15.27 | 12.98 | 11.46 | 10.54 | 10.23 |
| 19 | 29.38 | 29.38 | 15.03 | 14.69 | 14.32 | 14.32 | 14.32 | 14.32 | 14.32 | 14.32 |
| 20 | 75.1 | 75.1 | 37.92 | 37.59 | 25.82 | 25.07 | 21.02 | 18.79 | 16.85 | 16.43 |
| 21 | 45.32 | 45.32 | 22.73 | 22.73 | 15.88 | 15.11 | 13.64 | 13.64 | 13.64 | 13.62 |
| 22 | 41.86 | 41.86 | 22.49 | 20.93 | 15.77 | 13.95 | 12.52 | 12.52 | 12.52 | 12.52 |
| 23 | 23.25 | 23.25 | 12.08 | 11.63 | 8.4 | 7.75 | 7.1 | 7.1 | 7.1 | 7.1 |
| 24 | 23.73 | 23.73 | 13.14 | 11.87 | 10.55 | 8.02 | 8.01 | 8.01 | 8.01 | 8.01 |
| 25 | 33.37 | 33.37 | 16.96 | 16.7 | 12.64 | 12.66 | 12.66 | 12.65 | 12.66 | 12.66 |
| 26 | 41.7 | 41.7 | 21.5 | 20.85 | 15.26 | 13.9 | 11.82 | 11.83 | 11.82 | 11.83 |
| 27 | 51.45 | 51.45 | 25.83 | 25.83 | 19.55 | 19.55 | 19.55 | 19.55 | 19.55 | 19.55 |
| 28 | 44.02 | 44.02 | 22.86 | 22.02 | 16.53 | 16.12 | 16.12 | 16.12 | 16.12 | 16.12 |
| 29 | 19.3 | 19.3 | 9.89 | 9.67 | 7.76 | 7.76 | 7.76 | 7.76 | 7.76 | 7.76 |
| 30 | 25.26 | 25.26 | 12.82 | 12.7 | 9.42 | 9.42 | 9.42 | 9.42 | 9.42 | 9.42 |
| 31 | 46.46 | 46.46 | 23.63 | 23.26 | 16.02 | 15.49 | 13.62 | 13.63 | 13.63 | 13.62 |
| 32 | 30.63 | 30.63 | 15.39 | 15.33 | 13.9 | 13.9 | 13.9 | 13.9 | 13.9 | 13.9 |
| 33 | 13.12 | 13.12 | 10.37 | 10.37 | 10.37 | 10.37 | 10.37 | 10.37 | 10.37 | 10.37 |
| 34 | 15.75 | 15.75 | 8.49 | 7.88 | 7.3 | 7.29 | 7.3 | 7.29 | 7.3 | 7.29 |
| 35 | 41.33 | 41.33 | 21.01 | 20.7 | 14.42 | 13.78 | 13.09 | 13.09 | 13.09 | 13.09 |
| 36 | 48.68 | 48.68 | 24.53 | 24.36 | 18.61 | 18.61 | 18.59 | 18.61 | 18.59 | 18.61 |
| 37 | 10.09 | 10.09 | 5.57 | 5.04 | 4.97 | 4.48 | 4.97 | 4.48 | 4.97 | 4.48 |
| 38 | 48.03 | 48.03 | 24.05 | 24.05 | 17.23 | 16.04 | 14.37 | 13.81 | 13.81 | 13.78 |
| 39 | 26.77 | 26.77 | 13.47 | 13.38 | 9.77 | 8.92 | 7.32 | 7.31 | 7.32 | 7.31 |
| 40 | 44.12 | 44.12 | 22.12 | 22.11 | 15.23 | 14.71 | 13.05 | 13.05 | 13.05 | 13.05 |
| 41 | 9.53 | 9.53 | 5.89 | 5.88 | 5.89 | 5.88 | 5.89 | 5.88 | 5.89 | 5.88 |
| 42 | 30.25 | 30.25 | 15.29 | 15.13 | 12.69 | 12.69 | 12.69 | 12.69 | 12.69 | 12.69 |
| 43 | 33.41 | 33.41 | 17.04 | 16.71 | 15.93 | 15.93 | 15.93 | 15.93 | 15.93 | 15.93 |
| 44 | 11.14 | 11.14 | 7.59 | 7.59 | 7.59 | 7.59 | 7.59 | 7.59 | 7.59 | 7.59 |
| 45 | 13.16 | 13.16 | 9.62 | 9.62 | 9.62 | 9.62 | 9.62 | 9.62 | 9.62 | 9.62 |
| 46 | 27.13 | 27.13 | 13.74 | 13.64 | 10.11 | 9.16 | 9.14 | 9.16 | 9.14 | 9.16 |
| 47 | 49.56 | 49.56 | 26.35 | 24.78 | 19.52 | 16.58 | 16.38 | 15.21 | 15.18 | 15.18 |
| 48 | 22.43 | 22.43 | 11.53 | 11.22 | 10.21 | 10.22 | 10.22 | 10.22 | 10.22 | 10.22 |
| 49 | 10.96 | 10.96 | 6.14 | 6.14 | 6.14 | 6.14 | 6.14 | 6.14 | 6.14 | 6.14 |
| 50 | 41.87 | 41.87 | 21.88 | 20.93 | 19.14 | 18.01 | 18 | 18 | 18.01 | 18 |
| 51 | 12.26 | 12.26 | 7.97 | 7.97 | 7.97 | 7.97 | 7.97 | 7.97 | 7.97 | 7.97 |
| 52 | 34.5 | 34.5 | 17.5 | 17.25 | 12.29 | 11.5 | 10.89 | 10.91 | 10.89 | 10.91 |
| 53 | 65.66 | 65.66 | 33.28 | 32.84 | 23.24 | 22.24 | 22.23 | 22.23 | 22.23 | 22.23 |
| 54 | 24.04 | 24.04 | 12.06 | 12.02 | 10.39 | 10.39 | 10.39 | 10.39 | 10.39 | 10.39 |
| 55 | 12.94 | 12.94 | 7.4 | 7.41 | 7.4 | 7.42 | 7.4 | 7.42 | 7.4 | 7.42 |
| 56 | 7.01 | 7.01 | 4.53 | 4.53 | 4.53 | 4.53 | 4.53 | 4.53 | 4.53 | 4.53 |
| 57 | 23.76 | 23.76 | 12.36 | 11.89 | 8.2 | 7.97 | 7.97 | 7.97 | 7.97 | 7.97 |
| 58 | 12.04 | 12.04 | 6.9 | 6.9 | 6.9 | 6.9 | 6.9 | 6.9 | 6.9 | 6.9 |
| 59 | 37.46 | 37.46 | 18.96 | 18.73 | 13.19 | 13.19 | 13.19 | 13.19 | 13.19 | 13.19 |
| 60 | 38.95 | 38.95 | 19.6 | 19.48 | 13.57 | 12.98 | 10.51 | 10.24 | 10.22 | 10.22 |
| 61 | 27.68 | 27.68 | 15.17 | 13.84 | 13.78 | 13.78 | 13.78 | 13.77 | 13.78 | 13.77 |
| 62 | 27.88 | 27.88 | 14.23 | 13.94 | 12.47 | 12.45 | 12.47 | 12.45 | 12.47 | 12.45 |
| 63 | 12.23 | 12.23 | 8.6 | 8.6 | 8.6 | 8.6 | 8.6 | 8.6 | 8.6 | 8.6 |
| 64 | 16.92 | 16.92 | 12 | 12.01 | 12.01 | 12.01 | 12.01 | 12.01 | 12.01 | 12.01 |
| 65 | 44 | 44 | 22.64 | 22.01 | 15.81 | 15.81 | 15.81 | 15.81 | 15.81 | 15.79 |
| 66 | 21.86 | 21.86 | 11.41 | 11.39 | 11.39 | 11.38 | 11.39 | 11.38 | 11.39 | 11.38 |
| 67 | 30.9 | 30.9 | 16.82 | 15.45 | 11.21 | 11.1 | 11.1 | 11.1 | 11.1 | 11.09 |
| 68 | 33.51 | 33.51 | 16.99 | 16.78 | 12.73 | 11.17 | 9.87 | 9.87 | 9.87 | 9.87 |
| 69 | 11.92 | 11.92 | 6.74 | 6.75 | 6.74 | 6.74 | 6.74 | 6.74 | 6.74 | 6.74 |
| 70 | 22.05 | 22.05 | 11.05 | 11.05 | 9.04 | 9.04 | 9.04 | 9.04 | 9.04 | 9.04 |
| 71 | 43.26 | 43.26 | 22.53 | 21.64 | 15.71 | 14.42 | 13.85 | 13.85 | 13.85 | 13.85 |
| 72 | 34.73 | 34.73 | 17.57 | 17.41 | 14.25 | 14.25 | 14.27 | 14.25 | 14.27 | 14.25 |
| 73 | 49.58 | 49.58 | 25.65 | 24.79 | 20.45 | 20.45 | 20.45 | 20.45 | 20.45 | 20.45 |
| 74 | 24.57 | 24.57 | 12.74 | 12.28 | 10.22 | 10.22 | 10.22 | 10.22 | 10.22 | 10.22 |
| 75 | 31.09 | 31.09 | 16.42 | 15.55 | 13.13 | 13.13 | 13.13 | 13.13 | 13.13 | 13.13 |
| 76 | 22.18 | 22.18 | 11.57 | 11.09 | 8.85 | 7.84 | 7.84 | 7.84 | 7.84 | 7.84 |
| 77 | 50.43 | 50.43 | 25.62 | 25.31 | 18.03 | 16.82 | 13.28 | 13.28 | 13.26 | 13.28 |
| 78 | 20.21 | 20.21 | 10.62 | 10.11 | 8.7 | 8.72 | 8.7 | 8.72 | 8.7 | 8.72 |
| 79 | 36.66 | 36.66 | 18.99 | 18.33 | 13.23 | 12.95 | 12.96 | 12.95 | 12.96 | 12.96 |
| 80 | 39.94 | 39.94 | 20.03 | 20.05 | 14.29 | 14.18 | 14.17 | 14.18 | 14.17 | 14.17 |
| 81 | 19.23 | 19.23 | 9.64 | 9.62 | 6.68 | 6.68 | 6.68 | 6.68 | 6.68 | 6.68 |
| 82 | 28.05 | 28.05 | 14.05 | 14.03 | 11.42 | 11.42 | 11.41 | 11.42 | 11.41 | 11.42 |
| 83 | 48.63 | 48.63 | 25.6 | 24.32 | 17.05 | 17.05 | 17.05 | 17.03 | 17.05 | 17.03 |
| 84 | 36.41 | 36.41 | 18.63 | 18.2 | 12.9 | 12.14 | 11.1 | 11.1 | 11.1 | 11.1 |
| 85 | 50.88 | 50.88 | 26.14 | 25.44 | 24.51 | 24.51 | 24.51 | 24.5 | 24.51 | 24.5 |
| 86 | 9.55 | 9.55 | 5.47 | 5.47 | 5.47 | 5.47 | 5.47 | 5.47 | 5.47 | 5.47 |
| 87 | 51.51 | 51.51 | 26.62 | 25.79 | 21.43 | 21.44 | 21.44 | 21.44 | 21.44 | 21.44 |
| 88 | 11.69 | 11.69 | 7.06 | 7.07 | 7.06 | 7.06 | 7.06 | 7.06 | 7.06 | 7.06 |
| 89 | 51.28 | 51.28 | 27.33 | 25.68 | 17.44 | 17.1 | 17.07 | 17.07 | 17.07 | 17.07 |
| 90 | 9.55 | 9.55 | 6.78 | 6.78 | 6.78 | 6.78 | 6.78 | 6.78 | 6.78 | 6.78 |
| 91 | 38.11 | 38.11 | 19.2 | 19.07 | 13.62 | 12.72 | 12.09 | 12.09 | 12.09 | 12.09 |
| 92 | 46.17 | 46.17 | 23.1 | 23.1 | 16.23 | 16.23 | 16.23 | 16.23 | 16.23 | 16.23 |
| 93 | 9.97 | 9.97 | 6.94 | 6.94 | 6.94 | 6.94 | 6.94 | 6.94 | 6.94 | 6.94 |
| 94 | 57.05 | 57.05 | 29.89 | 28.55 | 20.54 | 19.58 | 19.58 | 19.56 | 19.58 | 19.56 |
| 95 | 10.03 | 10.03 | 8.45 | 8.45 | 8.45 | 8.45 | 8.45 | 8.45 | 8.45 | 8.45 |
| 96 | 19.12 | 19.12 | 11.57 | 9.56 | 8.98 | 8.97 | 8.98 | 8.97 | 8.98 | 8.97 |
| 97 | 10.33 | 10.33 | 7.4 | 7.41 | 7.4 | 7.41 | 7.4 | 7.41 | 7.4 | 7.41 |
| 98 | 36.54 | 36.54 | 18.58 | 18.28 | 16.87 | 16.87 | 16.87 | 16.87 | 16.87 | 16.87 |
| 99 | 27.47 | 27.47 | 14.32 | 13.74 | 9.86 | 9.16 | 8.57 | 8.57 | 8.57 | 8.57 |
| 100 | 30.61 | 30.61 | 15.75 | 15.34 | 10.71 | 10.2 | 8.26 | 8.26 | 8.26 | 8.24 |
| i | l | a | e | w | s | d | p | q | b | x (k = 1) | x (k = 2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 12 | 0 | 0 | 12 | 22 | 10 | 4 | 1 | 0 | 1 |
| 2 | 6 | 26 | 0 | 0 | 26 | 42 | 16 | 3 | 4 | 0 | 1 |
| 3 | 6 | 29 | 4 | 0 | 25 | 39 | 14 | 4 | 10 | 1 | 0 |
| 4 | 3 | 38 | 0 | 0 | 38 | 45 | 7 | 2 | 1 | 0 | 1 |
| 5 | 4 | 39 | 0 | 0 | 39 | 52 | 13 | 2 | 6 | 1 | 0 |
| 6 | 4 | 39 | 0 | 0 | 39 | 48 | 9 | 3 | 1 | 1 | 0 |
| 7 | 4 | 45 | 0 | 0 | 45 | 56 | 11 | 3 | 7 | 0 | 1 |
| 8 | 4 | 51 | 0 | 0 | 51 | 61 | 10 | 3 | 2 | 1 | 0 |
| 9 | 5 | 70 | 0 | 0 | 70 | 79 | 9 | 4 | 11 | 0 | 1 |
| 10 | 6 | 71 | 0 | 0 | 71 | 90 | 19 | 3 | 1 | 1 | 0 |
| 11 | 4 | 76 | 0 | 0 | 76 | 88 | 12 | 2 | 7 | 1 | 0 |
| 12 | 3 | 78 | 0 | 0 | 78 | 86 | 8 | 1 | 4 | 0 | 1 |
| 13 | 5 | 82 | 0 | 0 | 82 | 92 | 10 | 3 | 11 | 0 | 1 |
| 14 | 3 | 90 | 2 | 0 | 88 | 98 | 10 | 2 | 13 | 1 | 0 |
| 15 | 7 | 96 | 3 | 0 | 93 | 112 | 19 | 4 | 6 | 0 | 1 |
| 16 | 6 | 98 | 0 | 0 | 98 | 115 | 17 | 4 | 7 | 1 | 0 |
| 17 | 4 | 112 | 0 | 0 | 112 | 119 | 7 | 3 | 1 | 0 | 1 |
| 18 | 6 | 114 | 0 | 1 | 115 | 130 | 15 | 3 | 6 | 1 | 0 |
| 19 | 5 | 115 | 0 | 0 | 115 | 130 | 15 | 2 | 1 | 1 | 0 |
| 20 | 7 | 118 | 0 | 1 | 119 | 136 | 17 | 5 | 9 | 0 | 1 |
| i | l | a | e | w | s | d | p | q | b | x (k = 1) | x (k = 2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 13 | 0 | 0 | 13 | 27 | 14 | 4 | 1 | 1 | 0 |
| 2 | 6 | 22 | 0 | 0 | 22 | 35 | 13 | 4 | 1 | 0 | 1 |
| 3 | 5 | 32 | 0 | 0 | 32 | 39 | 7 | 4 | 1 | 1 | 0 |
| 4 | 4 | 42 | 0 | 0 | 42 | 50 | 8 | 3 | 1 | 1 | 0 |
| 5 | 6 | 46 | 0 | 0 | 46 | 59 | 13 | 3 | 10 | 0 | 1 |
| 6 | 6 | 55 | 4 | 0 | 51 | 63 | 12 | 4 | 4 | 1 | 0 |
| 7 | 7 | 56 | 0 | 0 | 56 | 82 | 26 | 2 | 1 | 0 | 1 |
| 8 | 6 | 60 | 0 | 0 | 60 | 76 | 16 | 3 | 10 | 0 | 1 |
| 9 | 4 | 62 | 0 | 1 | 63 | 71 | 8 | 3 | 4 | 1 | 0 |
| 10 | 4 | 63 | 0 | 0 | 63 | 76 | 13 | 2 | 12 | 1 | 0 |
| 11 | 6 | 65 | 0 | 11 | 76 | 92 | 16 | 3 | 10 | 0 | 1 |
| 12 | 5 | 68 | 0 | 3 | 71 | 86 | 15 | 2 | 7 | 1 | 0 |
| 13 | 3 | 70 | 0 | 1 | 71 | 84 | 13 | 1 | 1 | 1 | 0 |
| 14 | 4 | 74 | 0 | 2 | 76 | 84 | 8 | 2 | 12 | 1 | 0 |
| 15 | 6 | 83 | 0 | 1 | 84 | 98 | 14 | 3 | 1 | 1 | 0 |
| 16 | 6 | 84 | 0 | 0 | 84 | 108 | 24 | 2 | 4 | 0 | 1 |
| 17 | 3 | 87 | 0 | 0 | 87 | 92 | 5 | 2 | 7 | 1 | 0 |
| 18 | 6 | 109 | 0 | 0 | 109 | 123 | 14 | 4 | 7 | 1 | 0 |
| 19 | 5 | 125 | 0 | 0 | 125 | 132 | 7 | 4 | 1 | 1 | 0 |
| 20 | 6 | 127 | 0 | 0 | 127 | 140 | 13 | 4 | 1 | 0 | 1 |
| i | l | a | e | w | s | d | p | q | b | x (k = 1) | x (k = 2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 15 | 0 | 0 | 15 | 22 | 7 | 3 | 1 | 0 | 1 |
| 2 | 5 | 23 | 0 | 0 | 23 | 35 | 12 | 3 | 11 | 1 | 0 |
| 3 | 6 | 33 | 0 | 0 | 33 | 50 | 17 | 3 | 5 | 0 | 1 |
| 4 | 5 | 51 | 0 | 0 | 51 | 62 | 11 | 4 | 1 | 0 | 1 |
| 5 | 6 | 65 | 1 | 0 | 64 | 89 | 25 | 3 | 7 | 0 | 1 |
| 6 | 3 | 70 | 0 | 0 | 70 | 76 | 6 | 2 | 1 | 1 | 0 |
| 7 | 6 | 75 | 0 | 0 | 75 | 101 | 26 | 2 | 4 | 1 | 0 |
| 8 | 3 | 77 | 2 | 0 | 75 | 82 | 7 | 2 | 13 | 0 | 1 |
| 9 | 6 | 78 | 1 | 0 | 77 | 94 | 17 | 3 | 10 | 1 | 0 |
| 10 | 3 | 82 | 0 | 0 | 82 | 89 | 7 | 2 | 1 | 0 | 1 |
| 11 | 6 | 89 | 0 | 0 | 89 | 101 | 12 | 4 | 10 | 0 | 1 |
| 12 | 6 | 91 | 0 | 3 | 94 | 110 | 16 | 3 | 10 | 1 | 0 |
| 13 | 3 | 100 | 0 | 1 | 101 | 108 | 7 | 2 | 1 | 0 | 1 |
| 14 | 7 | 100 | 0 | 1 | 101 | 121 | 20 | 3 | 9 | 0 | 1 |
| 15 | 3 | 101 | 0 | 0 | 101 | 110 | 9 | 2 | 1 | 1 | 0 |
| 16 | 4 | 116 | 0 | 0 | 116 | 125 | 9 | 3 | 12 | 1 | 0 |
| 17 | 3 | 124 | 0 | 0 | 124 | 132 | 8 | 2 | 9 | 0 | 1 |
| 18 | 5 | 129 | 0 | 0 | 129 | 146 | 17 | 3 | 1 | 1 | 0 |
| 19 | 5 | 137 | 0 | 0 | 137 | 146 | 9 | 3 | 1 | 0 | 1 |
| 20 | 5 | 147 | 0 | 0 | 147 | 155 | 8 | 4 | 1 | 0 | 1 |
| i | l | a | e | w | s | d | p | q | b | x (k = 1) | x (k = 2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 11 | 0 | 0 | 11 | 21 | 10 | 4 | 1 | 0 | 1 |
| 2 | 6 | 24 | 0 | 0 | 24 | 40 | 16 | 3 | 4 | 0 | 1 |
| 3 | 6 | 27 | 4 | 0 | 23 | 37 | 14 | 4 | 5 | 1 | 0 |
| 4 | 3 | 35 | 0 | 0 | 35 | 42 | 7 | 2 | 1 | 0 | 1 |
| 5 | 4 | 36 | 0 | 1 | 37 | 50 | 13 | 2 | 12 | 1 | 0 |
| 6 | 4 | 36 | 0 | 1 | 37 | 46 | 9 | 3 | 1 | 1 | 0 |
| 7 | 4 | 41 | 0 | 0 | 41 | 52 | 11 | 3 | 12 | 0 | 1 |
| 8 | 4 | 47 | 0 | 0 | 47 | 57 | 10 | 3 | 8 | 1 | 0 |
| 9 | 5 | 64 | 0 | 0 | 64 | 73 | 9 | 4 | 4 | 0 | 1 |
| 10 | 6 | 65 | 0 | 0 | 65 | 84 | 19 | 3 | 10 | 1 | 0 |
| 11 | 4 | 69 | 0 | 0 | 69 | 81 | 12 | 2 | 6 | 1 | 0 |
| 12 | 3 | 71 | 0 | 0 | 71 | 79 | 8 | 1 | 1 | 0 | 1 |
| 13 | 5 | 75 | 0 | 0 | 75 | 85 | 10 | 3 | 7 | 0 | 1 |
| 14 | 3 | 82 | 0 | 0 | 82 | 95 | 13 | 1 | 1 | 0 | 1 |
| 15 | 7 | 88 | 3 | 0 | 85 | 104 | 19 | 4 | 7 | 1 | 0 |
| 16 | 6 | 89 | 4 | 0 | 85 | 102 | 17 | 4 | 4 | 0 | 1 |
| 17 | 4 | 102 | 0 | 0 | 102 | 109 | 7 | 3 | 5 | 0 | 1 |
| 18 | 6 | 104 | 0 | 0 | 104 | 119 | 15 | 3 | 1 | 1 | 0 |
| 19 | 5 | 104 | 0 | 0 | 104 | 119 | 15 | 2 | 7 | 1 | 0 |
| 20 | 7 | 107 | 0 | 2 | 109 | 126 | 17 | 5 | 9 | 0 | 1 |
| i | l | a | e | w | s | d | p | q | b | x (k = 1) | x (k = 2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 22 | 0 | 0 | 22 | 36 | 14 | 4 | 1 | 0 | 1 |
| 2 | 6 | 30 | 0 | 0 | 30 | 43 | 13 | 4 | 1 | 1 | 0 |
| 3 | 5 | 39 | 0 | 0 | 39 | 46 | 7 | 4 | 5 | 0 | 1 |
| 4 | 4 | 48 | 0 | 0 | 48 | 56 | 8 | 3 | 6 | 0 | 1 |
| 5 | 6 | 52 | 0 | 0 | 52 | 65 | 13 | 3 | 1 | 1 | 0 |
| 6 | 6 | 60 | 4 | 0 | 56 | 68 | 12 | 4 | 10 | 0 | 1 |
| 7 | 7 | 61 | 0 | 0 | 61 | 87 | 26 | 2 | 9 | 1 | 0 |
| 8 | 6 | 65 | 0 | 0 | 65 | 81 | 16 | 3 | 1 | 1 | 0 |
| 9 | 4 | 67 | 0 | 1 | 68 | 76 | 8 | 3 | 5 | 0 | 1 |
| 10 | 4 | 68 | 0 | 0 | 68 | 81 | 13 | 2 | 1 | 0 | 1 |
| 11 | 6 | 70 | 0 | 11 | 81 | 97 | 16 | 3 | 1 | 1 | 0 |
| 12 | 5 | 73 | 0 | 3 | 76 | 91 | 15 | 2 | 5 | 0 | 1 |
| 13 | 3 | 75 | 0 | 1 | 76 | 89 | 13 | 1 | 10 | 0 | 1 |
| 14 | 4 | 79 | 0 | 2 | 81 | 89 | 8 | 2 | 1 | 0 | 1 |
| 15 | 6 | 87 | 0 | 2 | 89 | 103 | 14 | 3 | 10 | 0 | 1 |
| 16 | 6 | 88 | 0 | 0 | 88 | 112 | 24 | 2 | 7 | 1 | 0 |
| 17 | 3 | 91 | 0 | 0 | 91 | 96 | 5 | 2 | 2 | 0 | 1 |
| 18 | 6 | 111 | 0 | 0 | 111 | 125 | 14 | 4 | 6 | 0 | 1 |
| 19 | 5 | 126 | 0 | 0 | 126 | 133 | 7 | 4 | 1 | 0 | 1 |
| 20 | 6 | 128 | 0 | 0 | 128 | 141 | 13 | 4 | 6 | 1 | 0 |
| i | l | a | e | w | s | d | p | q | b | x (k = 1) | x (k = 2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 10 | 0 | 0 | 10 | 17 | 7 | 3 | 1 | 0 | 1 |
| 2 | 5 | 17 | 0 | 0 | 17 | 29 | 12 | 3 | 1 | 1 | 0 |
| 3 | 6 | 26 | 0 | 0 | 26 | 43 | 17 | 3 | 10 | 0 | 1 |
| 4 | 5 | 42 | 0 | 0 | 42 | 53 | 11 | 4 | 5 | 1 | 0 |
| 5 | 6 | 55 | 0 | 0 | 55 | 81 | 26 | 2 | 4 | 0 | 1 |
| 6 | 3 | 59 | 0 | 0 | 59 | 65 | 6 | 2 | 1 | 1 | 0 |
| 7 | 6 | 64 | 0 | 0 | 64 | 86 | 22 | 3 | 10 | 0 | 1 |
| 8 | 3 | 65 | 3 | 0 | 62 | 69 | 7 | 2 | 4 | 1 | 0 |
| 9 | 6 | 66 | 0 | 0 | 66 | 83 | 17 | 3 | 7 | 1 | 0 |
| 10 | 3 | 69 | 0 | 0 | 69 | 76 | 7 | 2 | 13 | 1 | 0 |
| 11 | 6 | 75 | 0 | 1 | 76 | 95 | 19 | 2 | 1 | 1 | 0 |
| 12 | 6 | 77 | 0 | 6 | 83 | 99 | 16 | 3 | 7 | 1 | 0 |
| 13 | 3 | 85 | 0 | 0 | 85 | 95 | 10 | 1 | 4 | 0 | 1 |
| 14 | 7 | 85 | 0 | 1 | 86 | 106 | 20 | 3 | 9 | 0 | 1 |
| 15 | 3 | 86 | 0 | 0 | 86 | 96 | 10 | 1 | 1 | 0 | 1 |
| 16 | 4 | 100 | 0 | 0 | 100 | 109 | 9 | 3 | 1 | 1 | 0 |
| 17 | 3 | 107 | 0 | 0 | 107 | 115 | 8 | 2 | 7 | 0 | 1 |
| 18 | 5 | 112 | 0 | 0 | 112 | 129 | 17 | 3 | 1 | 1 | 0 |
| 19 | 5 | 119 | 0 | 0 | 119 | 128 | 9 | 3 | 6 | 0 | 1 |
| 20 | 5 | 128 | 0 | 0 | 128 | 136 | 8 | 4 | 1 | 0 | 1 |
References
- Vis, I.F.A.; De Koster, R.M.B.M. Transshipment of containers at a container terminal: An overview. Eur. J. Oper. Res. 2003, 147, 1–16. [Google Scholar] [CrossRef]
- Steenken, D.; Voß, S.; Stahlbock, R. Container terminal operation and operations research—A classification and literature review. OR Spectr. 2004, 26, 3–49. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Stahlbock, R.; Voß, S. Operations research at container terminals: A literature update. OR Spectr. 2007, 30, 1–52. [Google Scholar] [CrossRef]
- Rashidi, H.; Tsang, E.P. Novel constraints satisfaction models for optimization problems in container terminals. Appl. Math. Model. 2013, 37, 3601–3634. [Google Scholar] [CrossRef]
- Murty, K.G.; Liu, J.; Wan, Y.-W.; Linn, R. A decision support system for operations in a container terminal. Decis. Support Syst. 2005, 39, 309–332. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Roodbergen, K.J. Seaside operations in container terminals: Literature overview, trends, and research directions. Flex. Serv. Manuf. J. 2013, 27, 224–262. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Papadimitriou, S. The dynamic berth allocation problem for a container port. Transp. Res. Part B Methodol. 2001, 35, 401–417. [Google Scholar] [CrossRef]
- Nishimura, E.; Imai, A.; Papadimitriou, S. Berth allocation planning in the public berth system by genetic algorithms. Eur. J. Oper. Res. 2001, 131, 282–292. [Google Scholar] [CrossRef]
- Lim, A. The berth planning problem. Oper. Res. Lett. 1998, 22, 105–110. [Google Scholar] [CrossRef]
- Kim, K.H.; Moon, K.C. Berth scheduling by simulated annealing. Transp. Res. Part B Methodol. 2003, 37, 541–560. [Google Scholar] [CrossRef]
- Guan, Y.; Cheung, R.K. The berth allocation problem: Models and solution methods. OR Spectr. 2004, 26, 75–92. [Google Scholar] [CrossRef]
- Imai, A.; Sun, X.; Nishimura, E.; Papadimitriou, S. Berth allocation in a container port: Using a continuous location space approach. Transp. Res. Part B Methodol. 2005, 39, 199–221. [Google Scholar] [CrossRef] [Green Version]
- Imai, A.; Nishimura, E.; Hattori, M.; Papadimitriou, S. Berth allocation at indented berths for mega-containerships. Eur. J. Oper. Res. 2007, 179, 579–593. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.-F.; Kang, H.-G. Study on Berth and Quay-crane Allocation under Stochastic Environments in Container Terminal. Syst. Eng. Theory Pract. 2008, 28, 161–169. [Google Scholar] [CrossRef]
- Dulebenets, M.A. Application of Evolutionary Computation for Berth Scheduling at Marine Container Terminals: Parameter Tuning Versus Parameter Control. IEEE Trans. Intell. Transp. Syst. 2017, 19, 25–37. [Google Scholar] [CrossRef]
- Yıldırım, M.S.; Aydın, M.M.; Gökkuş, Ü. Simulation optimization of the berth allocation in a container terminal with flexible vessel priority management. Marit. Policy Manag. 2020, 47, 1–16. [Google Scholar] [CrossRef]
- Corry, P.; Bierwirth, C. The Berth Allocation Problem with Channel Restrictions. Transp. Sci. 2019, 53, 708–727. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, J.; Liu, M.; Chu, C. The berth allocation optimisation with the consideration of time-varying water depths. Int. J. Prod. Res. 2018, 57, 488–516. [Google Scholar] [CrossRef]
- De, A.; Pratap, S.; Kumar, A.; Tiwari, M. A hybrid dynamic berth allocation planning problem with fuel costs considerations for container terminal port using chemical reaction optimization approach. Ann. Oper. Res. 2018, 290, 783–811. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.-M.; Kim, K.H. A scheduling method for Berth and Quay cranes. OR Spectr. 2003, 25, 1–23. [Google Scholar] [CrossRef]
- Meisel, F.; Bierwirth, C. A Framework for Integrated Berth Allocation and Crane Operations Planning in Seaport Container Terminals. Transp. Sci. 2013, 47, 131–147. [Google Scholar] [CrossRef]
- Türkoğulları, Y.B.; Taşkın, Z.C.; Aras, N.; Altınel, İ.K. Optimal berth allocation, time-variant quay crane assignment and scheduling with crane setups in container terminals. Eur. J. Oper. Res. 2016, 254, 985–1001. [Google Scholar] [CrossRef]
- Agra, A.; Oliveira, M. MIP approaches for the integrated berth allocation and quay crane assignment and scheduling problem. Eur. J. Oper. Res. 2018, 264, 138–148. [Google Scholar] [CrossRef] [Green Version]
- Xi, X.; Liu, C.; Miao, L.; Xi, X.; Liu, C.; Miao, L. Reactive strategy for discrete berth allocation and quay crane assignment problems under uncertainty. Comput. Ind. Eng. 2018, 126, 196–216. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A. Functional integration approach for the berth allocation, quay crane assignment and specific quay crane assignment problems. Comput. Ind. Eng. 2016, 102, 458–466. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Wang, K.; Zhen, L.; Wang, S.; Laporte, G. Column Generation for the Integrated Berth Allocation, Quay Crane Assignment, and Yard Assignment Problem. Transp. Sci. 2018, 52, 812–834. [Google Scholar] [CrossRef]
- Tasoglu, G.; Yildiz, G. Simulated annealing based simulation optimization method for solving integrated berth allocation and quay crane scheduling problems. Simul. Model. Pract. Theory 2019, 97, 101948. [Google Scholar] [CrossRef]
- Zheng, F.; Li, Y.; Chu, F.; Liu, M.; Xu, Y. Integrated berth allocation and quay crane assignment with maintenance activities. Int. J. Prod. Res. 2018, 57, 3478–3503. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.B.; Reinau, K.H. Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability 2020, 12, 3202. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Wang, X.; Meng, Q. Joint berth allocation and quay crane assignment under different carbon taxation policies. Transp. Res. Part B Methodol. 2018, 117, 18–36. [Google Scholar] [CrossRef]
- Wang, T.; Du, Y.; Fang, D.; Li, Z.-C. Berth Allocation and Quay Crane Assignment for the Trade-off Between Service Efficiency and Operating Cost Considering Carbon Emission Taxation. Transp. Sci. 2020, 54, 1307–1331. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Papadimitriou, S. Berthing ships at a multi-user container terminal with a limited quay capacity. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 136–151. [Google Scholar] [CrossRef] [Green Version]
- Dulebenets, M.A.; Golias, M.M.; Mishra, S. A collaborative agreement for berth allocation under excessive demand. Eng. Appl. Artif. Intell. 2018, 69, 76–92. [Google Scholar] [CrossRef]
- Hendriks, M.P.M.; Armbruster, D.; Laumanns, M.; Lefeber, E.; Udding, J.T. Strategic allocation of cyclically calling vessels for multi-terminal container operators. Flex. Serv. Manuf. J. 2012, 24, 248–273. [Google Scholar] [CrossRef] [Green Version]
- Gharehgozli, A.H.; Roy, D.; De Koster, R. Sea container terminals: New technologies and OR models. Marit. Econ. Logist. 2016, 18, 103–140. [Google Scholar] [CrossRef]
- Chen, J.H.; Lee, D.-H.; Cao, J.X. Heuristics for quay crane scheduling at indented berth. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 1005–1020. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Papadimitriou, S. Marine container terminal configurations for efficient handling of mega-containerships. Transp. Res. Part E Logist. Transp. Rev. 2013, 49, 141–158. [Google Scholar] [CrossRef]
- Frojan, P.; Correcher, J.F.; Alvarez-Valdes, R.; Koulouris, G.; Tamarit, J.M. The continuous Berth Allocation Problem in a container terminal with multiple quays. Expert Syst. Appl. 2015, 42, 7356–7366. [Google Scholar] [CrossRef]
- Correcher, J.F.; Bossche, T.V.D.; Álvarez-Valdés, R.; Berghe, G.V. The berth allocation problem in terminals with irregular layouts. Eur. J. Oper. Res. 2019, 272, 1096–1108. [Google Scholar] [CrossRef]
- Krimi, I.; Todosijević, R.; Benmansour, R.; Ratli, M.; El Cadi, A.A.; Aloullal, A. Modelling and solving the multi-quays berth allocation and crane assignment problem with availability constraints. J. Glob. Optim. 2020, 78, 349–373. [Google Scholar] [CrossRef]
- Lee, D.-H.; Jin, J.; Chen, J.H. Terminal and yard allocation problem for a container transshipment hub with multiple terminals. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 516–528. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, Z.; Li, R. A Collaborative Berth Allocation Problem with Multiple Ports Based on Genetic Algorithm. J. Coast. Res. 2015, 73, 290–297. [Google Scholar] [CrossRef]
- Ma, H.L.; Chung, S.; Chan, H.K.; Cui, L. An integrated model for berth and yard planning in container terminals with multi-continuous berth layout. Ann. Oper. Res. 2017, 273, 409–431. [Google Scholar] [CrossRef]
- Venturini, G.; Iris, Ç.; Kontovas, C.A.; Larsen, A. The multi-port berth allocation problem with speed optimization and emission considerations. Transp. Res. Part D Transp. Environ. 2017, 54, 142–159. [Google Scholar] [CrossRef] [Green Version]
- Schepler, X.; Balev, S.; Michel, S.; Sanlaville, É. Global planning in a multi-terminal and multi-modal maritime container port. Transp. Res. Part E Logist. Transp. Rev. 2017, 100, 38–62. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.H.; Park, Y.-M. A crane scheduling method for port container terminals. Eur. J. Oper. Res. 2004, 156, 752–768. [Google Scholar] [CrossRef]
- Grubišić, N.; Dundović, Č.; Žuškin, S. A split task solution for quay crane scheduling problem in mid-size container terminals. Tech. Gaz. 2016, 23, 1723–1730. [Google Scholar] [CrossRef] [Green Version]


| Vessel Class | Length [m] | Capacity [TEU] | Positions [Bays] | Size Range [m] | li | hup | Dmax |
|---|---|---|---|---|---|---|---|
| CMA Agadir | 139 | 966 | B01–B26 | 120–165 | 3 | 26 | 37 |
| CMA Africa IV | 228 | 3600 | B01–B52 | 166–230 | 4 | 52 | 69 |
| APL China | 276 | 4832 | B01–B62 | 231–276 | 5 | 62 | 77 |
| CMA Bizet | 300 | 6628 | B01–B72 | 277–330 | 6 | 72 | 92 |
| CMA Andromeda | 363 | 11400 | B01–B86 | 331–365 | 7 | 86 | 132 |
| λ | 2 | 3 | 3.2 | 3.3 | 3.5 | 4 |
|---|---|---|---|---|---|---|
| n | 720 | 1080 | 1152 | 1188 | 1260 | 1440 |
| Q [000 TEU/year] | 580 | 875.2 | 930.1 | 966.9 | 1027 | 1179.2 |
| QC | 1 | 2 | 3 | 4 | 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case/Ship | Full | Split | Full | Split | Full | Split | Full | Split | Full | Split |
| 1 | 32.5 | 32.5 | 16.66 | 16.27 | 12.47 | 10.84 | 10.12 | 10.12 | 10.12 | 10.12 |
| 2 | 42.98 | 42.98 | 21.85 | 21.5 | 16.31 | 16.32 | 16.31 | 16.32 | 16.31 | 16.32 |
| 3 | 48.64 | 48.64 | 24.4 | 24.32 | 16.99 | 16.27 | 13.65 | 13.54 | 13.65 | 13.52 |
| 4 | 8.53 | 8.53 | 6.52 | 6.54 | 6.52 | 6.53 | 6.52 | 6.53 | 6.52 | 6.53 |
| Seed = 400, λ = 3.2 | ||||||||
| Case | V | a | a(T) | TEU | Z | Solving Time (min) | Z′ | Z″ |
| 1 | 1–20 | 12–118 | 12–118 | 17,782 | 283 | 1.07 | 279 | 326 |
| 2 | 21–40 | 140–277 | 20–157 | 18,149 | 273 | 0.39 | 273 | 307 |
| 3 | 41–60 | 284–414 | 20–150 | 13,937 | 237 | 0.07 | 237 | 249 |
| 4 | 61–80 | 417–627 | 9–219 | 16,188 | 263 | 0.03 | 263 | 272 |
| 5 | 81–100 | 632–825 | 8–201 | 16,206 | 270 | 0.05 | 270 | 286 |
| Seed = 700, λ = 3.2 | ||||||||
| Case | V | a | a(T) | TEU | Z | Solving Time (min) | Z′ | Z″ |
| 6 | 1–20 | 6–151 | 6–151 | 17,782 | 267 | 0.05 | 267 | 287 |
| 7 | 21–40 | 157–271 | 13–127 | 18,149 | 311 | 19.49 | 302 | 428 |
| 8 | 41–60 | 272–398 | 8–134 | 13,937 | 236 | 0.04 | 236 | 244 |
| 9 | 61–80 | 419–638 | 11–230 | 16,188 | 267 | 0.08 | 267 | 279 |
| 10 | 81–100 | 639–771 | 15–147 | 16,206 | 281 | 0.80 | 279 | 380 |
| Seed = 400, λ = 3.5 | ||||||||
| Case | V | a | a(T) | TEU | Z | Solving Time (min) | Z′ | Z″ |
| 11 | 1–20 | 11–107 | 11–107 | 17,782 | 289 | 2.24 | 286 | 332 |
| 12 | 21–40 | 127–250 | 7–130 | 18,149 | 280 | 0.66 | 278 | 317 |
| 13 | 41–60 | 256–372 | 16–132 | 13,937 | 240 | 0.14 | 240 | 254 |
| 14 | 61–80 | 375–566 | 15–206 | 16,188 | 264 | 0.04 | 264 | 272 |
| 15 | 81–100 | 570–750 | 18–198 | 16,206 | 270 | 0.04 | 270 | 286 |
| Seed = 700, λ = 3.5 | ||||||||
| Case | V | a | a(T) | TEU | Z | Solving Time (min) | Z′ | Z″ |
| 16 | 1–20 | 6–137 | 6–137 | 17,782 | 270 | 0.12 | 270 | 292 |
| 17 | 21–40 | 142–248 | 22–128 | 18,149 | 313 | 68.6 | 303 | 442 |
| 18 | 41–60 | 249–364 | 9–124 | 13,937 | 238 | 0.08 | 237 | 248 |
| 19 | 61–80 | 384–585 | 24–225 | 16,188 | 267 | 0.07 | 267 | 281 |
| 20 | 81–100 | 586–704 | 10–128 | 16,206 | 292 | 2.68 | 289 | 416 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grubisic, N.; Krljan, T.; Maglic, L. The Optimization Process for Seaside Operations at Medium-Sized Container Terminals with a Multi-Quay Layout. J. Mar. Sci. Eng. 2020, 8, 891. https://doi.org/10.3390/jmse8110891
Grubisic N, Krljan T, Maglic L. The Optimization Process for Seaside Operations at Medium-Sized Container Terminals with a Multi-Quay Layout. Journal of Marine Science and Engineering. 2020; 8(11):891. https://doi.org/10.3390/jmse8110891
Chicago/Turabian StyleGrubisic, Neven, Tomislav Krljan, and Livia Maglic. 2020. "The Optimization Process for Seaside Operations at Medium-Sized Container Terminals with a Multi-Quay Layout" Journal of Marine Science and Engineering 8, no. 11: 891. https://doi.org/10.3390/jmse8110891
APA StyleGrubisic, N., Krljan, T., & Maglic, L. (2020). The Optimization Process for Seaside Operations at Medium-Sized Container Terminals with a Multi-Quay Layout. Journal of Marine Science and Engineering, 8(11), 891. https://doi.org/10.3390/jmse8110891







