Numerical Investigation of a Two-Element Wingsail for Ship Auxiliary Propulsion
Abstract
1. Introduction
2. Methods
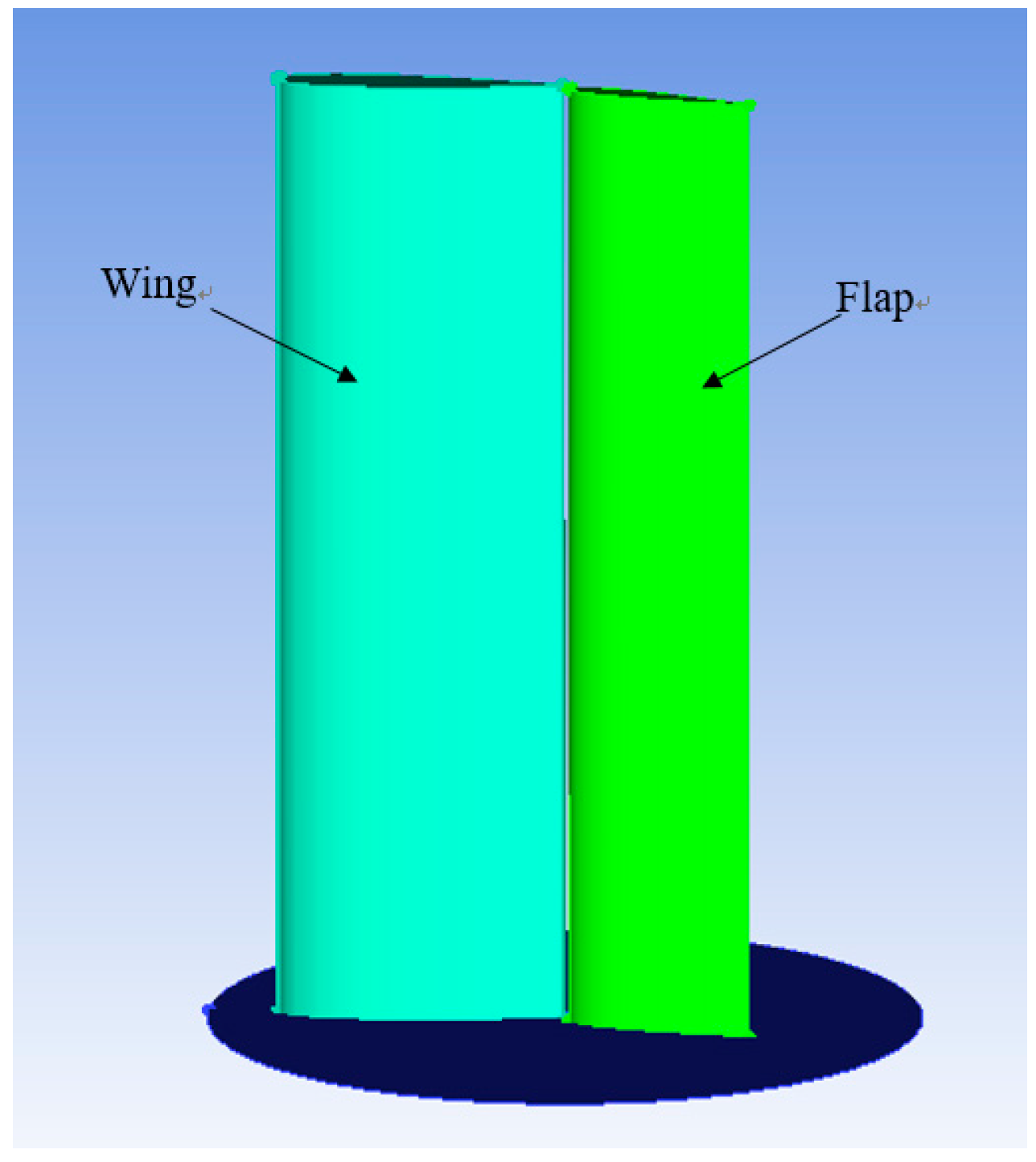
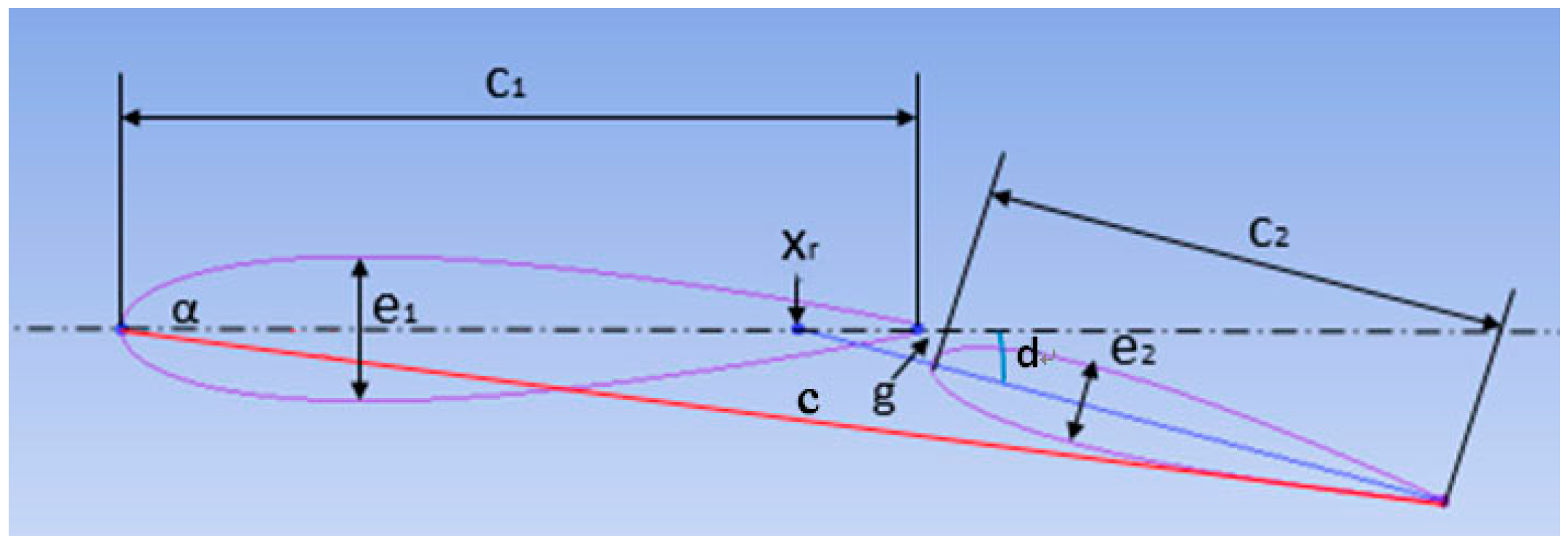
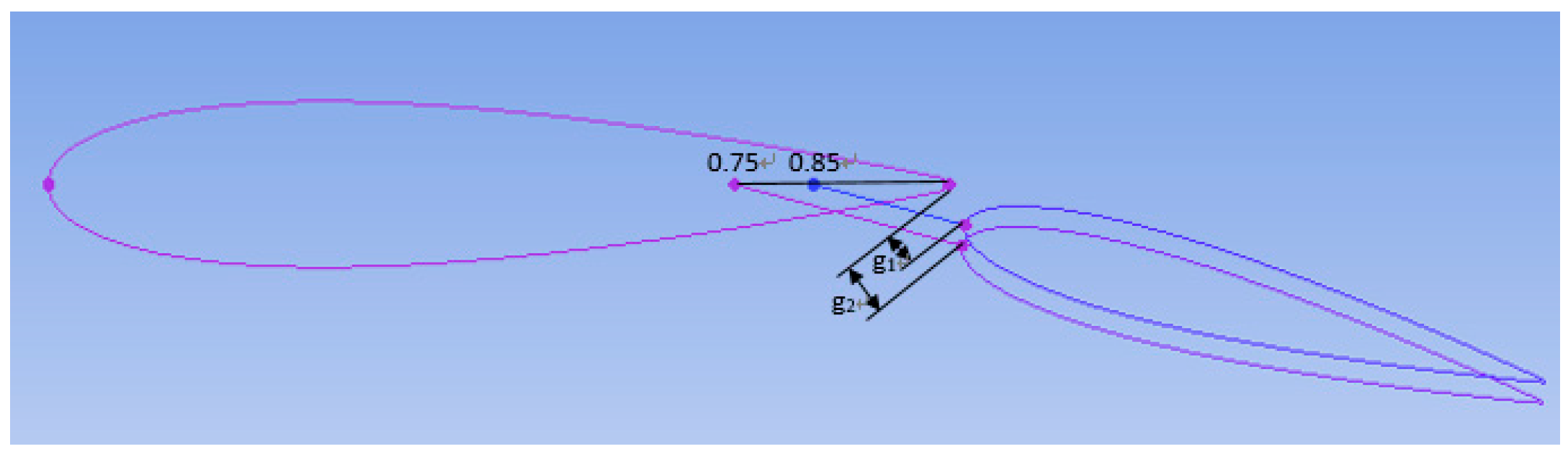
2.1. The Geometry of the Wingsail
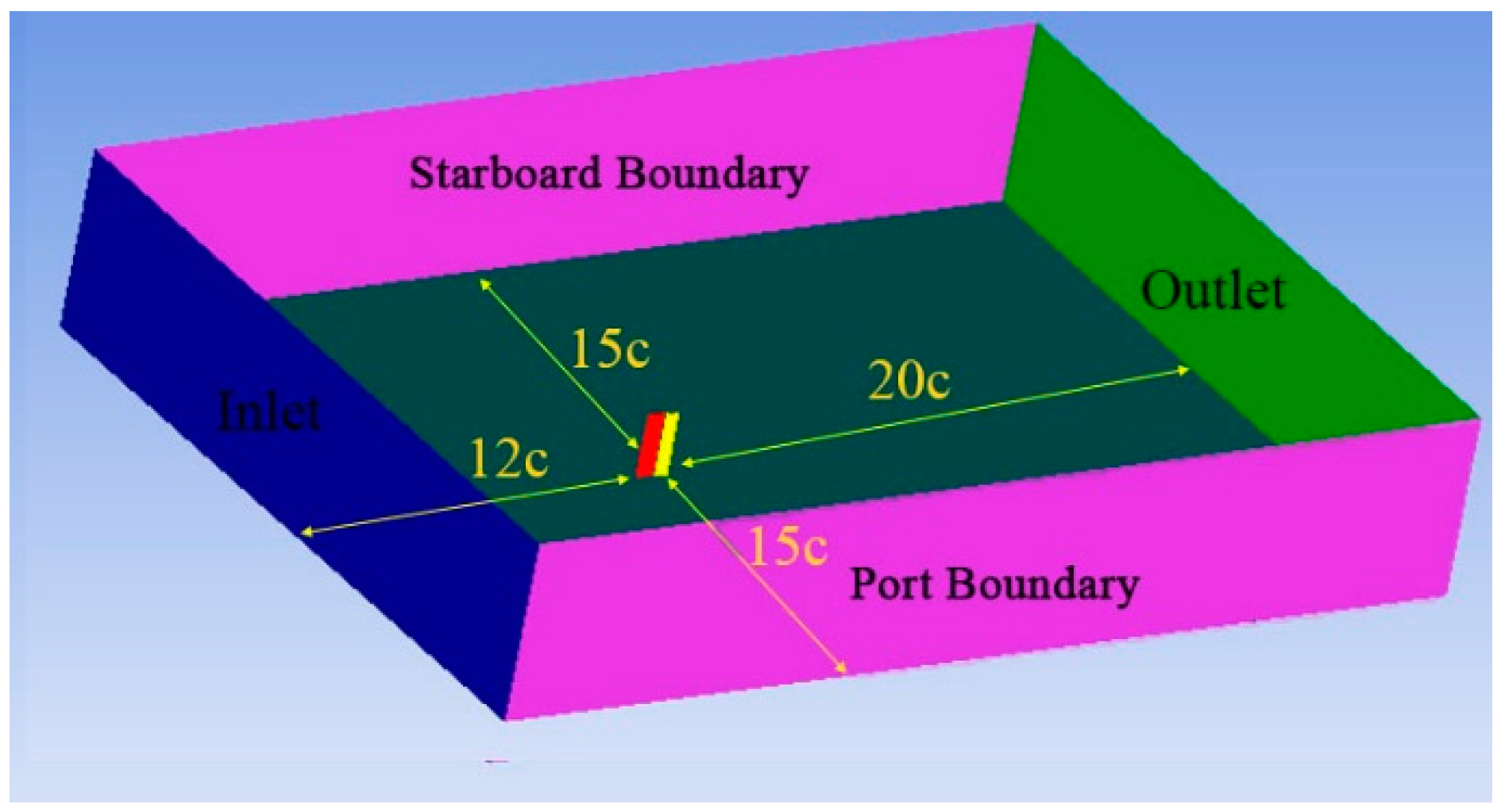
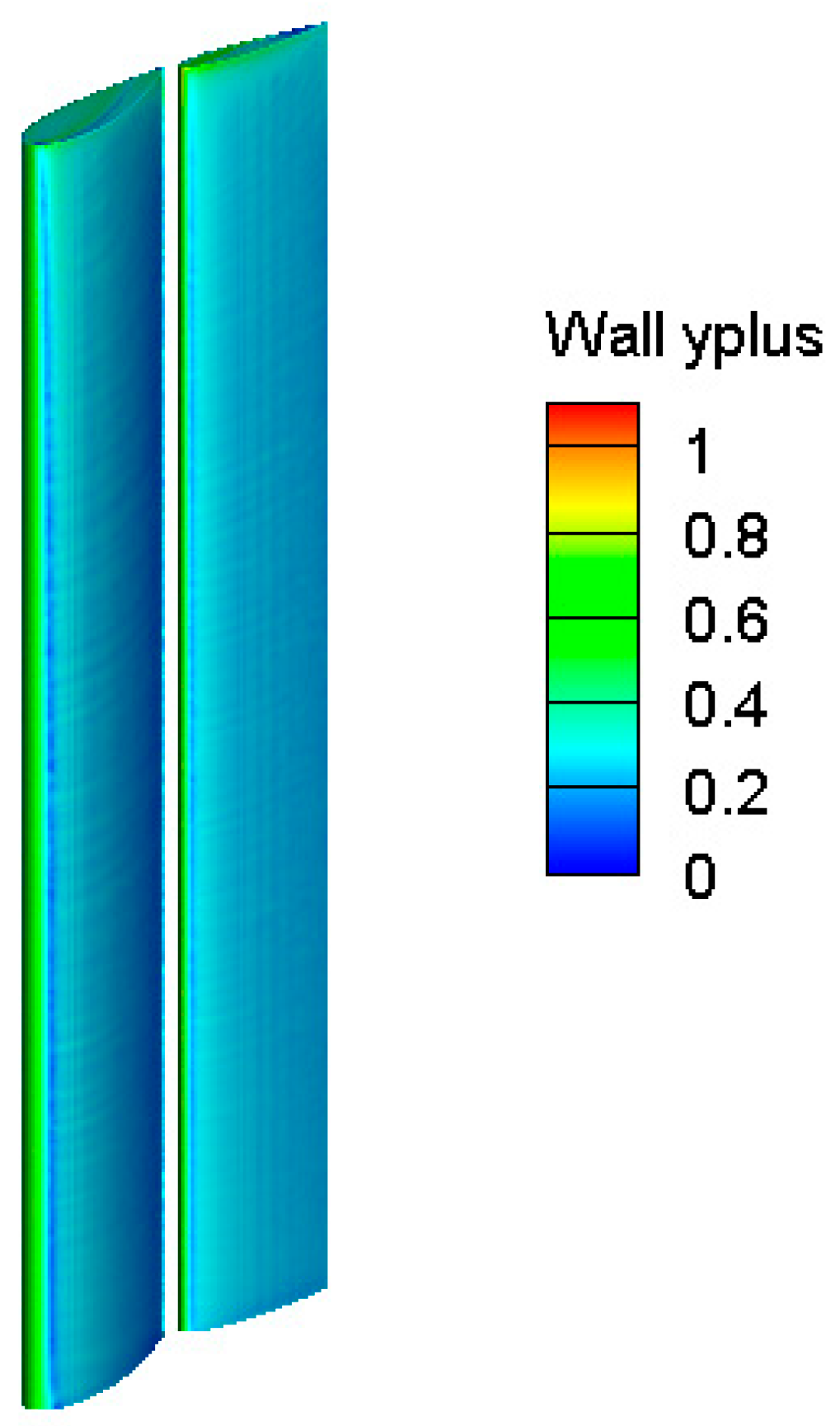
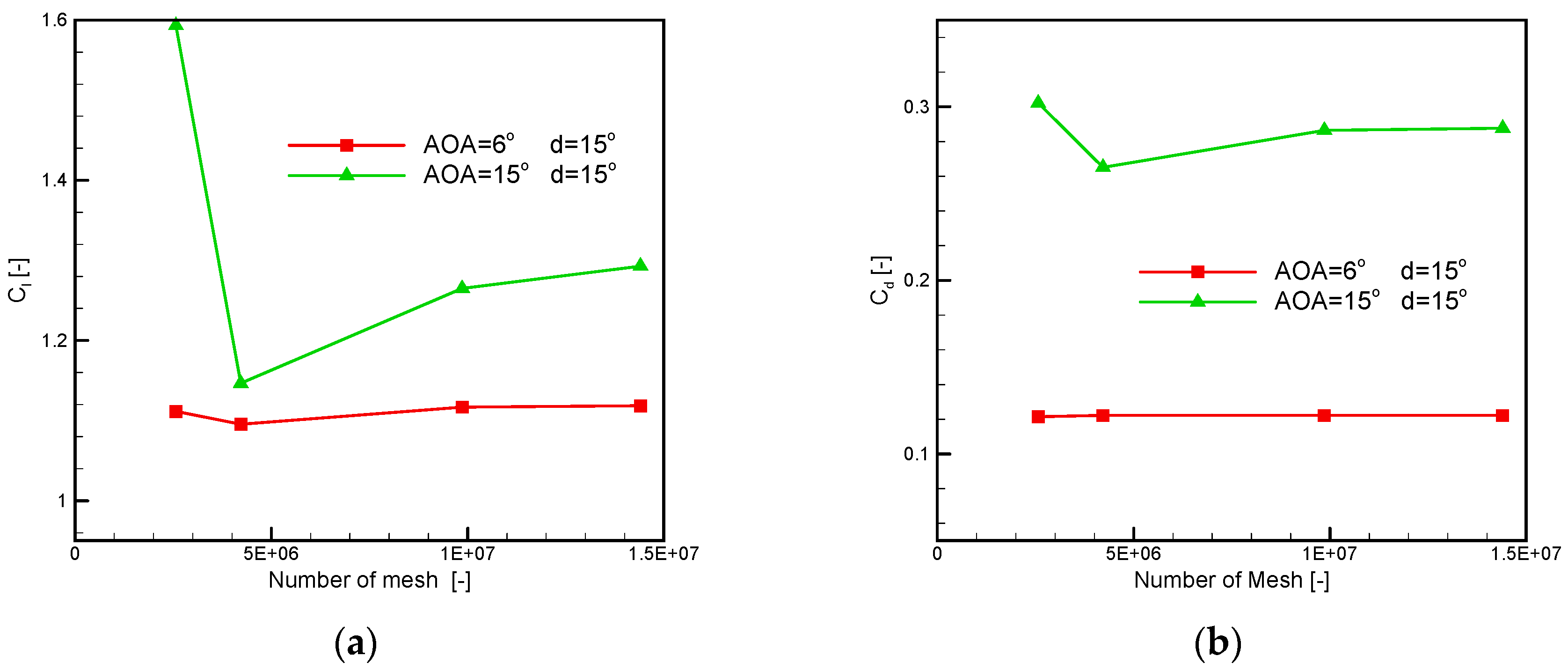
2.2. The Grid Structure
2.3. Computational Approach
3. Numerical Results
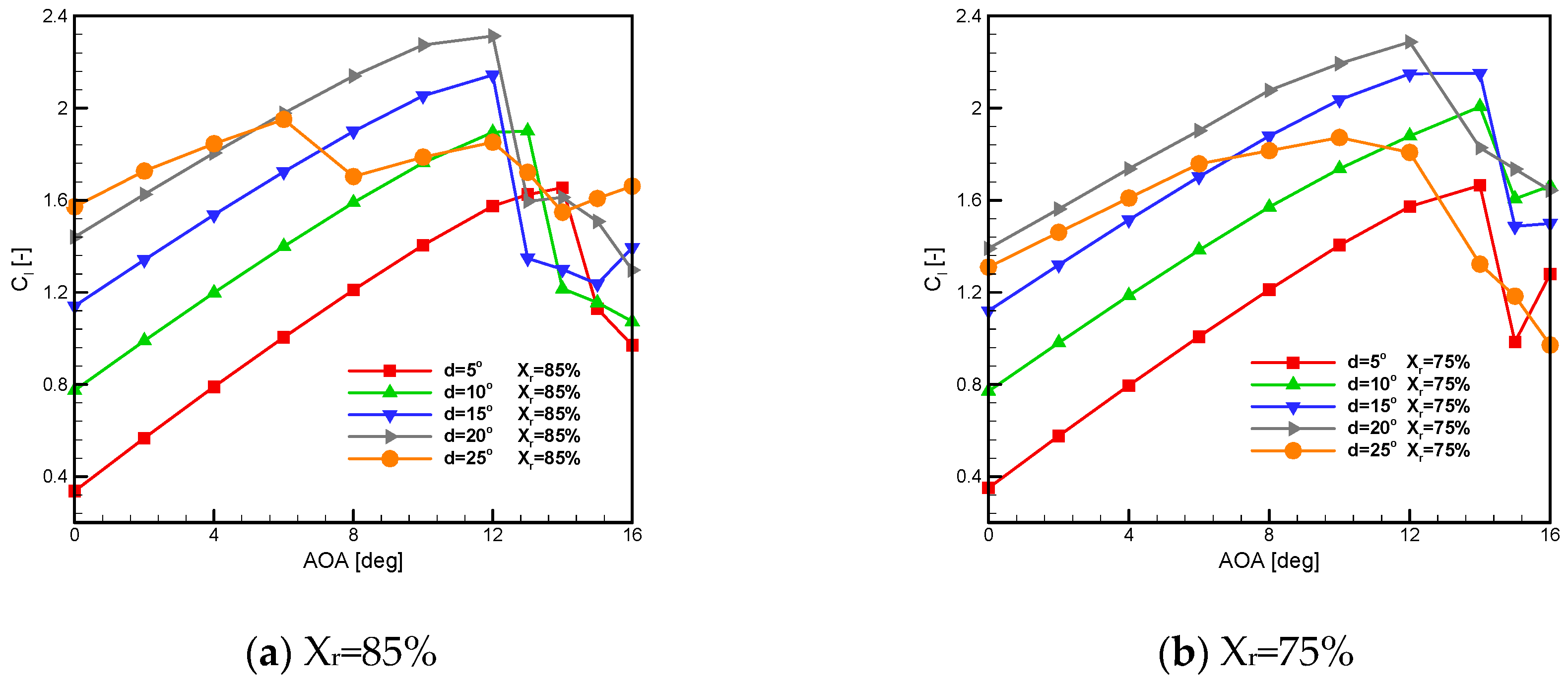
3.1. Two-Dimensional Wingsail Configurations Study
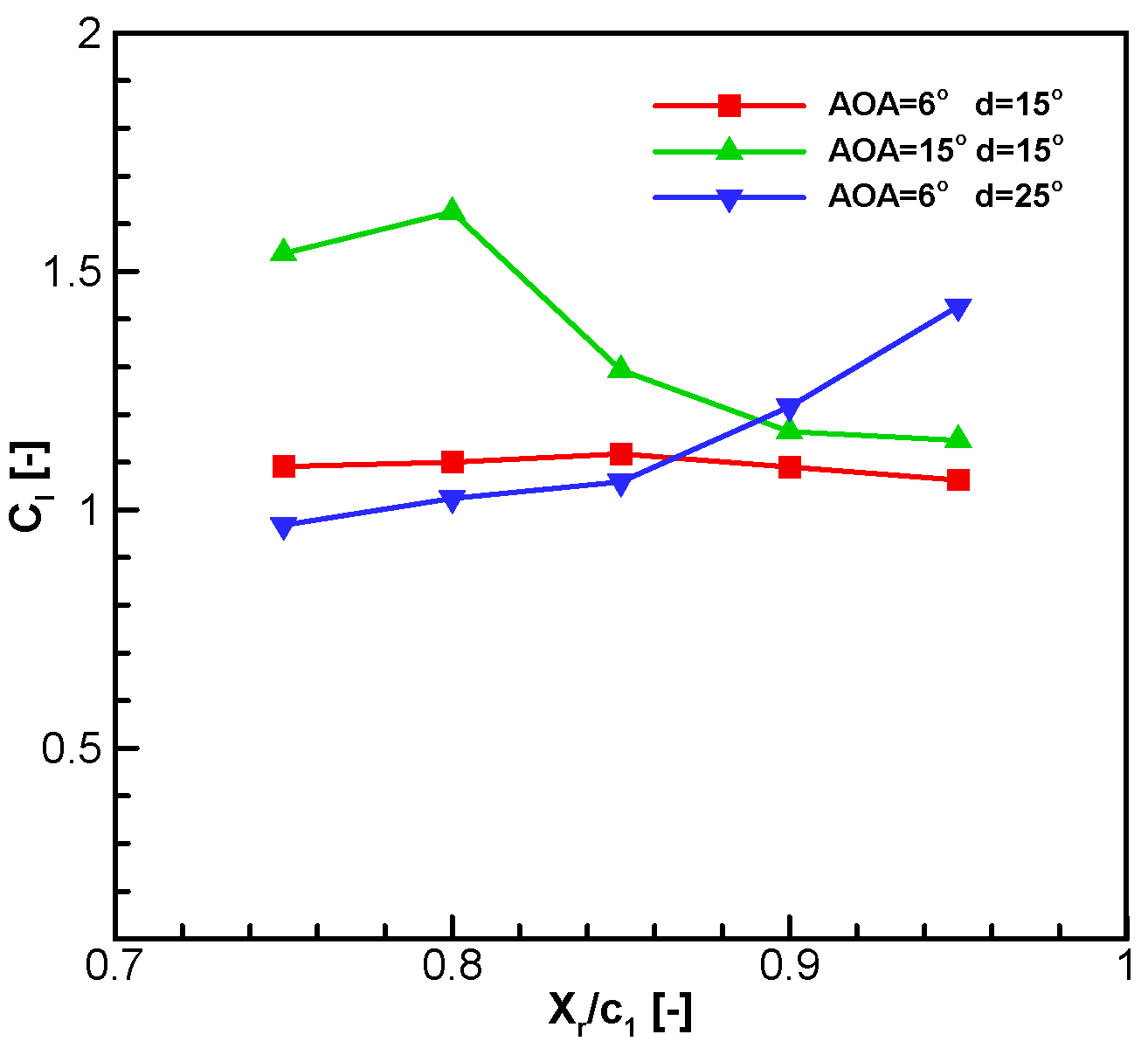
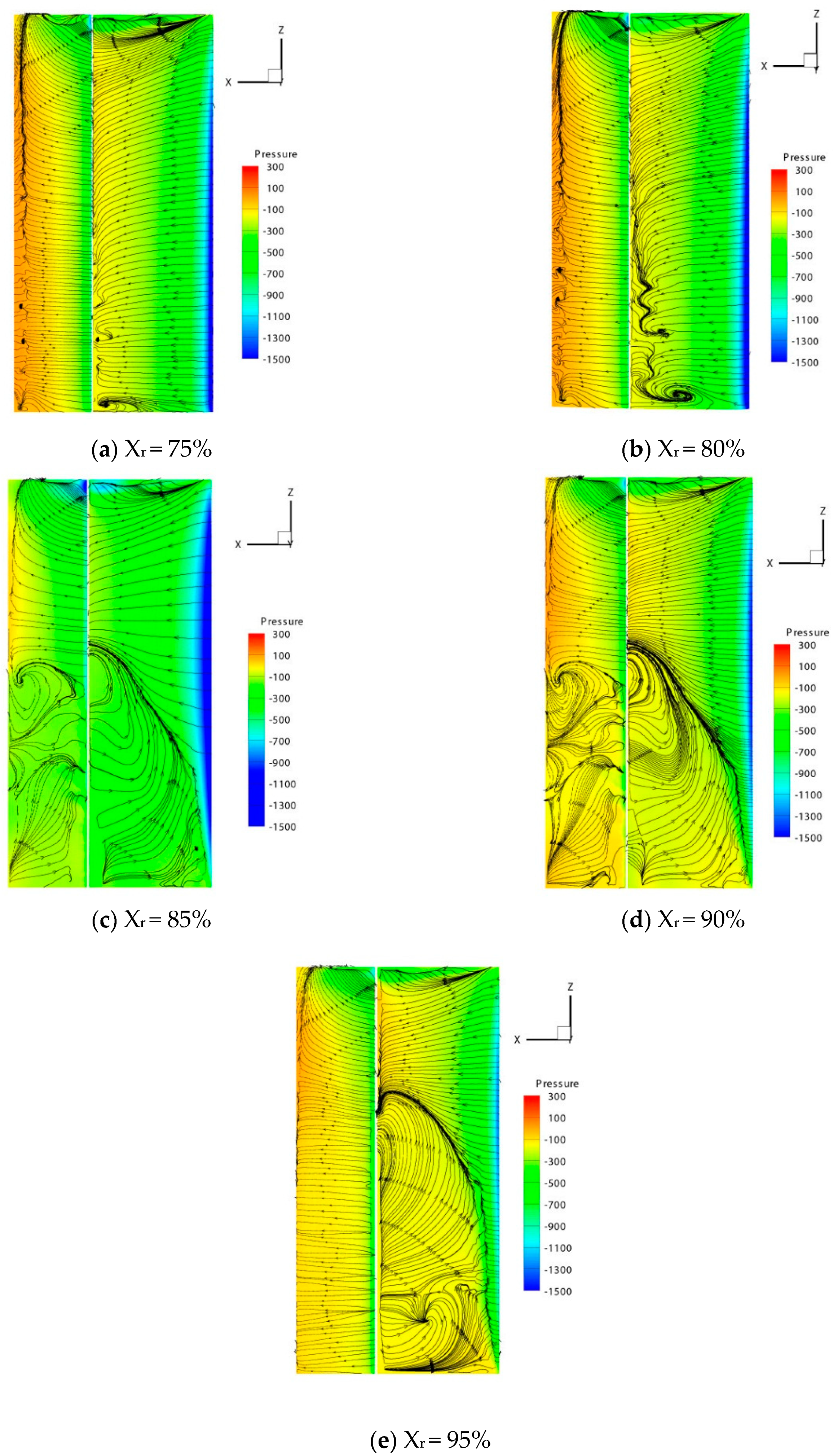
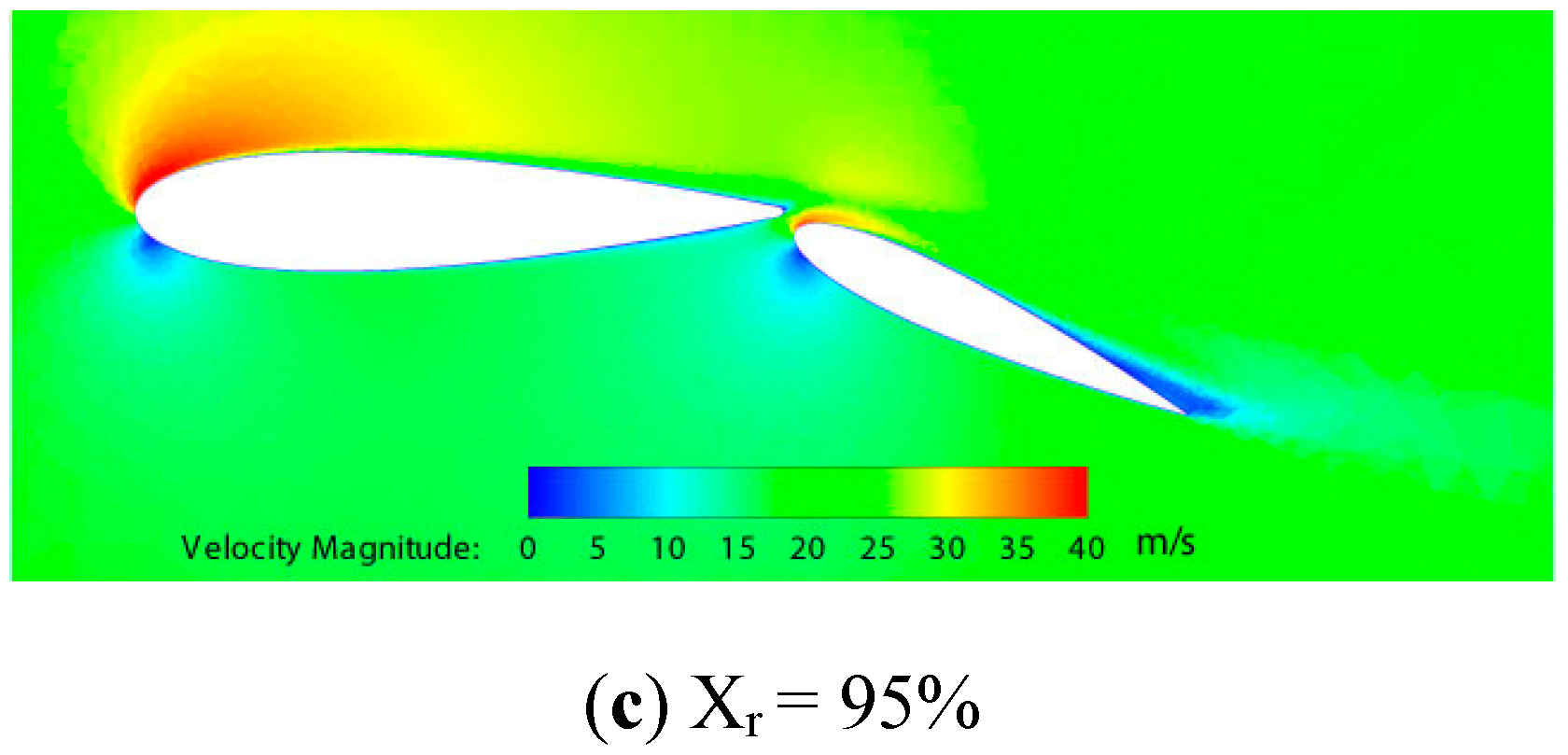
3.2. Three-Dimensional Study about Effect of Flap Rotation Axis Position
3.2.1. Aerodynamic Performance
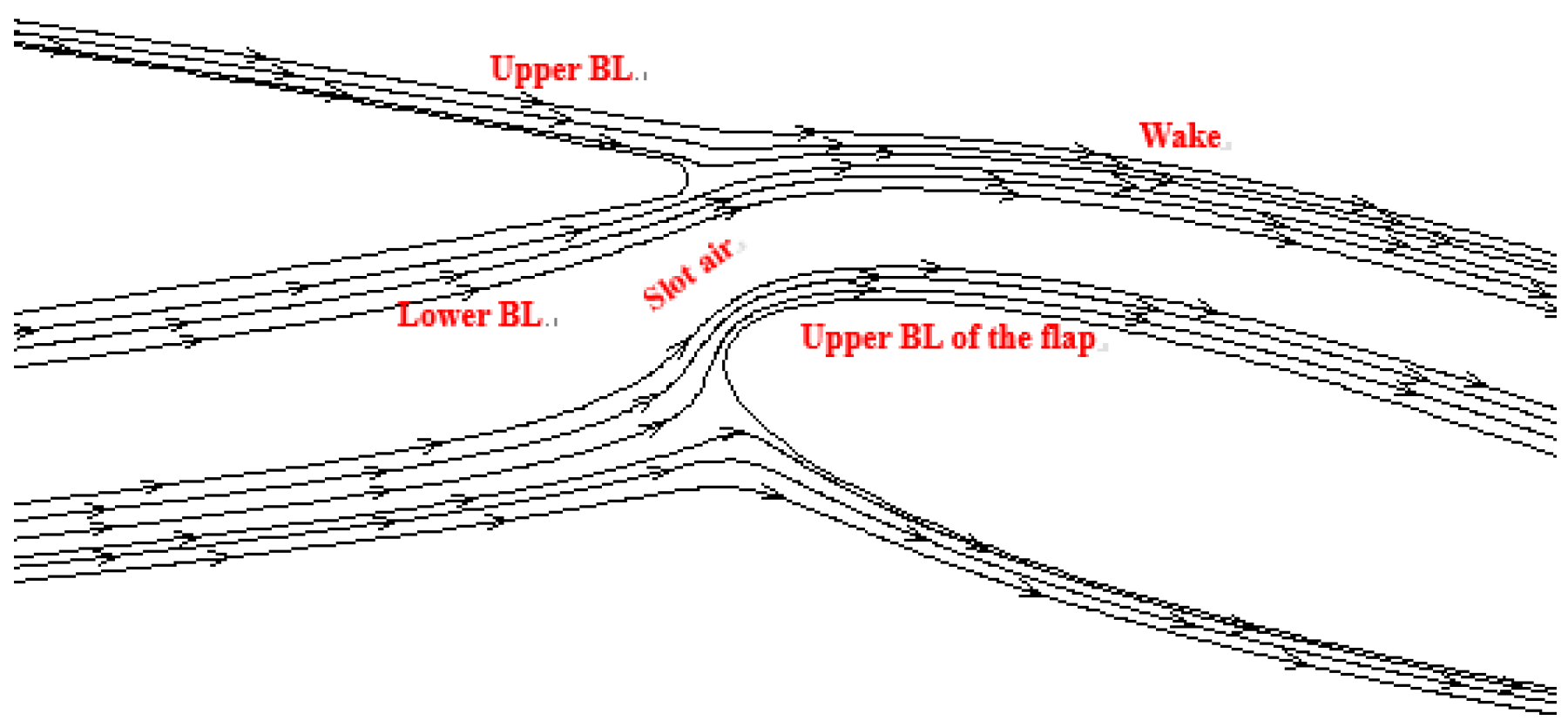
3.2.2. Streamlines
3.2.3. Velocity Magnitude Contours
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Re | Reynolds number [-] |
| α | Angle of attack of the main wing (AOA) [°] |
| c | total chord of the wingsail [m] |
| c1 | chord of the main wing [m] |
| c2 | chord of the flap [m] |
| CD | Drag coefficient [-] |
| CL | Lift coefficient [-] |
| d | Flap deflection angle [°] |
| g | non-dimensional slot width (g/c1) [-] |
| e1 | thickness of the main wing [m] |
| e2 | thickness of the flap [m] |
| AR | The aspect area of wingsail [m2] |
| y+ | Non-dimensional wall distance [-] |
| ρ | The density of the air [kg/m3] |
| z | The height of wingsail in the vertical direction [m] |
| h | Wingsail height [m] |
| L | Lift force [N] |
| D | Drag force [N] |
| v | The velocity of inflow [m/s] |
| Xr | The position of flap rotation axis in the direction of the wing chord [-] |
References
- Ishihara, M.; Watanabe, T.; Shimizu, K.; Yoshimi, K.; Namura, H. Prospect of sailequipped motor ship as assessed from experimental ship Daioh. In Proceedings of the Shipboard Energy Conservation Symposium; Society of Naval Architects and Marine Engineers: New York, NY, USA, 1980; pp. 181–198. [Google Scholar]
- Available online: http://www.sohu.com/a/275284498_100091571 (accessed on 14 November 2018).
- Blakeley, A.W.; Flay, R.G.J.; Richards, P.J. Design and Optimisation of Multi-Element Wing Sails for Multihull Yachts. In Proceedings of the 18th Australasian Fluid Mechanics Conference, Tasmania, Australia, 3–7 December 2012. [Google Scholar]
- Available online: http://k.sina.com.cn/article_6424865154_17ef3a982001001t6p.html (accessed on 20 December 2017).
- Kind, R.J. An Experimentel Investigation of a Low- Speed Circulation Controlled Airfoil. Aero. Quart. 1968, 19, 170–182. [Google Scholar] [CrossRef]
- Seifert, A.; Bachar, T.; Koss, D.; Shepshelovich, M.; Wygnanski, I. Oscillatory Blowing: A Tool to Delay Boundary-Layer Separation. AIAA J. 1993, 31, 2052–2060. [Google Scholar] [CrossRef]
- Seifert, A.; Darabi, A.; Wyganski, I. Delay of airfoil stall by periodic excitation. J. Aircr. 1996, 33, 691–698. [Google Scholar] [CrossRef]
- Kralj, D.M.; Klarin, B. Wing Sails for Hybrid Propulsion of a Ship. J. Sustain. Dev. Energy Water Environ. Syst. 2016, 4, 1–13. [Google Scholar] [CrossRef]
- Marine, B. E-ShiP1 with Sailing Rotors to Reduce Fuel Costs and to Reduce Emissions. Available online: http://www.marinebuzz.com (accessed on 28 August 2008).
- Borglund, D.; Kuttenkeuler, J. Active Wing Flutter Suppression Using A Trailing Edge Flap. J. Fluids Struct. 2002, 16, 271–294. [Google Scholar] [CrossRef]
- Daniel, W.A. The CFD Assisted Design and Experimental Testing of a Wingsail with High Lift Devices; University of Salford: Salford, UK, 1996. [Google Scholar]
- Carr, L.W.; McAlister, K.W. The effect of a leading-edge slat on the dynamic stall of an oscillating airfoil. AIAA Pap. 1983, 83, 2533. [Google Scholar]
- Available online: http://cookeassociates.com/sports/commercial,php (accessed on 6 August 2015).
- Li, Q.; Nihei, Y.; Nakashima, T.; Iked, Y. A study on the performance of cascade hard sails and sail-equipped vessels. Ocean Eng. 2015, 98, 23–31. [Google Scholar] [CrossRef]
- Fish, F.E.; Battle, J.M. Hydrodynamic design of the humpback whale flipper. J. Morphol. 1995, 225, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Toshifumi, F.; Koichi, H.; Michio, U.; Nimura, T. On aerodynamic characteristics of a hybrid-sail with square soft sail. In Proceedings of the International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, Honolulu, HI, USA, 25–30 May 2003; pp. 2576–2583. [Google Scholar]
- Fujiwara, T.; Hirata, K.; Ueno, M.; Nimura, T. On the development of high-performance sails for an ocean-going sailing ship. In Proceedings of the International Conference on Marine Simulation and Ship Manoeuvrability, MARSIM’03, Kanazawa, Kanazawa, Japan, 25–28 August 2003. RC-23-1–9. [Google Scholar]
- Chapin, V.; Gourdain, N.; Verdin, N. Aerodynamic Study of a Two-elements Wingsail for High Performance Multihull Yachts. In Proceedings of the 5th High Performance Yacht Design Conference Auckland, Auckland, New Zealand, 10–12 March 2015. [Google Scholar]
- Fiumara, A.; Gourdain, N.; Chapin, V.; Senter, J.; Bury, Y. Numerical and experimental analysis of the flow around a two-element wingsail at Reynolds number 0.53 × 106. Int. J. Heat Fluid Flow 2016, 62, 538–551. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Hassan, G.E.; Hassan, A.; Youssef, M.E. Numerical Investigation of Medium Range Re Number Aerodynamics Characteristics for NACA0018 Airfoil. CFD Lett. 2014, 6, 175–187. [Google Scholar]
- Malan, P.; Suluksna, K.; Juntasaro, E. Calibrating the γ-Reθ Transition Model for Commercial CFD. In Proceedings of the 47th AIAA Aerospace Science Meeting, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Douvi, C.E.; Tsavalos, I.A.; Margaris, P.D. Evaluation of the Turbulence Models for the Simulation of the Flow Over a National Advisory Committee for Aeronautics (NACA) 0012 Airfoil. Mech. Eng. Res. 2012, 4, 100–111. [Google Scholar]
- Rhee, S.H.; Kim, H. A suggestion of gap flow control devices for the suppression of rudder cavitation. J. Mar. Sci. Technol. 2008, 13, 356–370. [Google Scholar] [CrossRef]
- Gentry, A. The Aerodynamic of Sail Interaction. In Proceedings of the 3th AIAA Symposium on the Aero/Hydronautics of Sailing, Redondo Beach, CA, USA, 20 November 1971. [Google Scholar]
- Smith, A.M.O. High-Lift Aerodynamics. J. Aircr. 1975, 12, 501–530. [Google Scholar] [CrossRef]
- Biber, K.; Zumwalt, G. Experimental studies of a two-element airfoil with large separation. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]








| c | 0.35 m |
| h | 0.7 m |
| Re | 5 × 105 |
| d | 0–25° |
| α | 0–20° |
| g | 2.4% |
| Xr | 75%–95% |
| Configurations | e2/c2 | d | CL | CD | L/D |
|---|---|---|---|---|---|
| r1.51815x0.85g2.4α6d5 | 15% | 5° | 1.005 | 0.0213 | 47.16 |
| r1.51815x0.85g2.4α6d15 | 15% | 15° | 1.724 | 0.0338 | 50.94 |
| r1.51815x0.85g2.4α6d25 | 15% | 25° | 1.951 | 0.06 | 32.53 |
| r1.51812x0.85g2.4α6d5 | 12% | 5° | 1.002 | 0.0207 | 48.5 |
| r1.51812x0.85g2.4α6d15 | 12% | 15° | 1.73 | 0.0336 | 51.47 |
| r1.51812x0.85g2.4α6d25 | 12% | 25° | 1.606 | 0.1628 | 9.87 |
| r1.51810x0.85g2.4α6d5 | 10% | 5° | 1.002 | 0.0208 | 48.22 |
| r1.51810x0.85g2.4α6d15 | 10% | 15° | 1.74 | 0.0337 | 51.59 |
| r1.51810x0.85g2.4α6d25 | 10% | 25° | 1.649 | 0.1649 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, H.; Sun, P. Numerical Investigation of a Two-Element Wingsail for Ship Auxiliary Propulsion. J. Mar. Sci. Eng. 2020, 8, 333. https://doi.org/10.3390/jmse8050333
Li C, Wang H, Sun P. Numerical Investigation of a Two-Element Wingsail for Ship Auxiliary Propulsion. Journal of Marine Science and Engineering. 2020; 8(5):333. https://doi.org/10.3390/jmse8050333
Chicago/Turabian StyleLi, Chen, Hongming Wang, and Peiting Sun. 2020. "Numerical Investigation of a Two-Element Wingsail for Ship Auxiliary Propulsion" Journal of Marine Science and Engineering 8, no. 5: 333. https://doi.org/10.3390/jmse8050333
APA StyleLi, C., Wang, H., & Sun, P. (2020). Numerical Investigation of a Two-Element Wingsail for Ship Auxiliary Propulsion. Journal of Marine Science and Engineering, 8(5), 333. https://doi.org/10.3390/jmse8050333





