Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea
Abstract
:1. Introduction
2. Study Area, Data, and Data Processing Methods
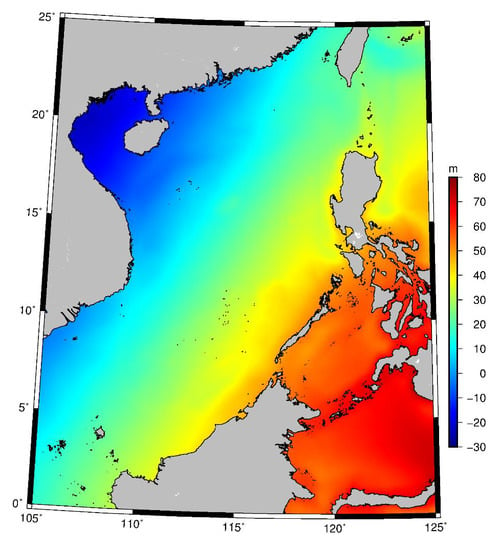
2.1. Study Area and Data
2.2. Data Processing Methods
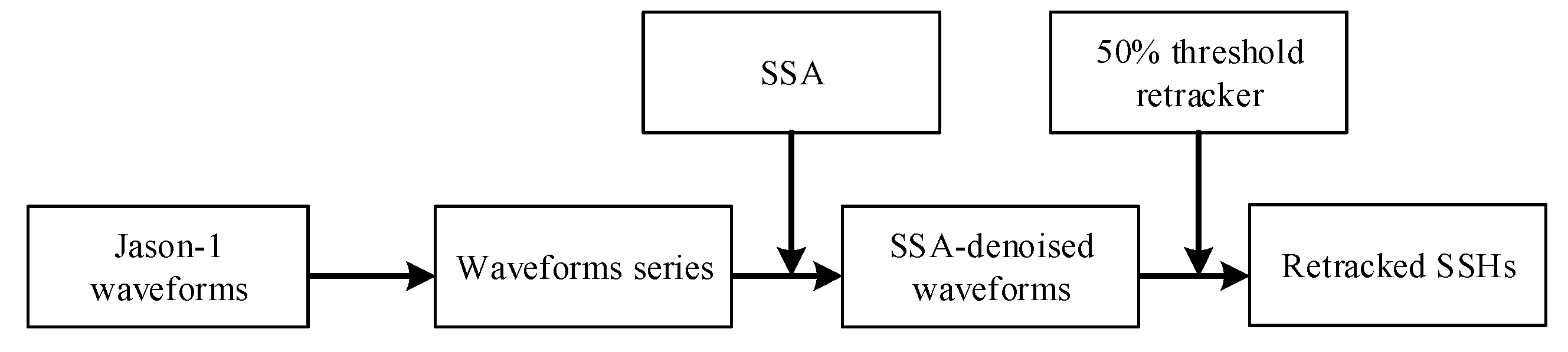
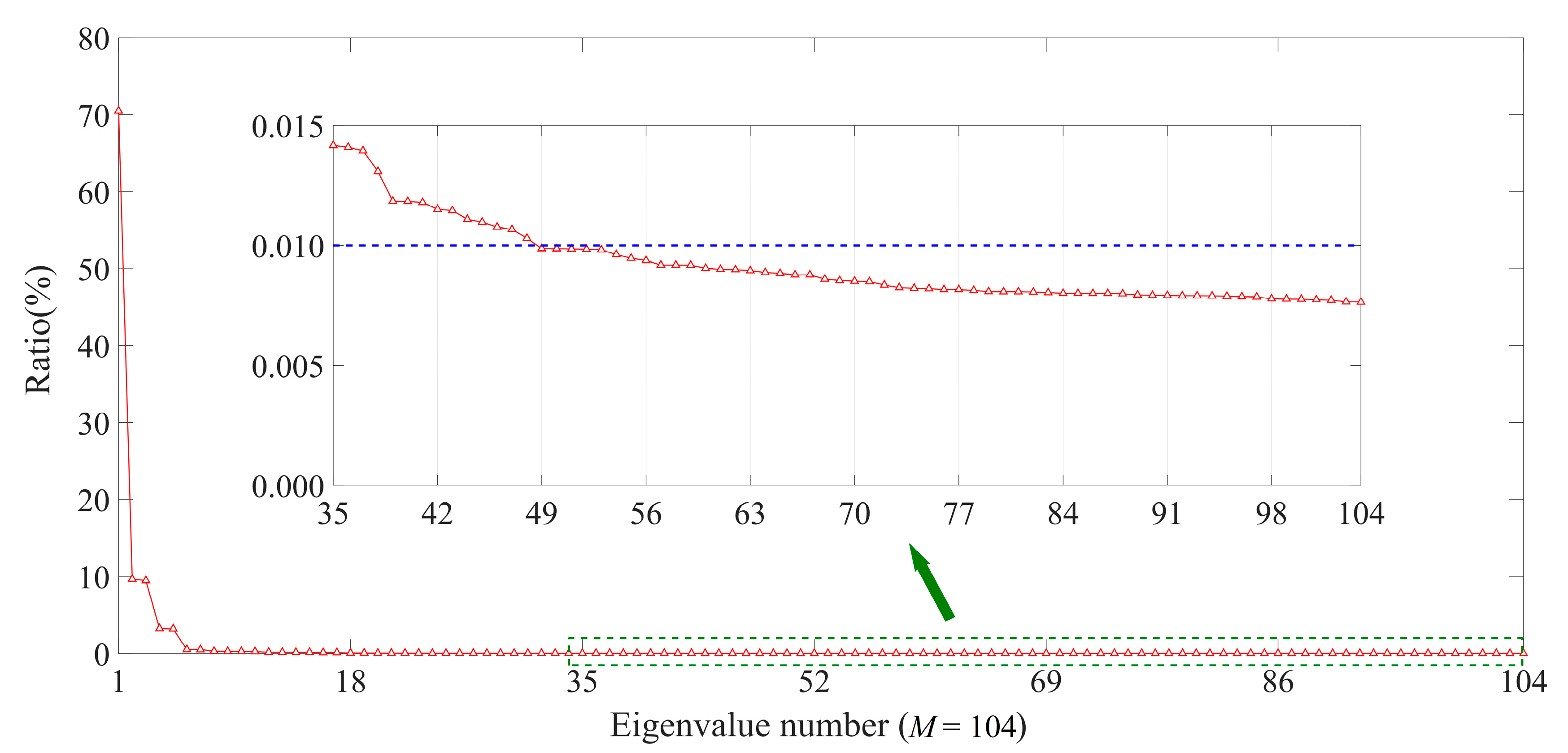
2.2.1. Singular Spectrum Analysis (SSA) Applied to Altimeter Waveforms
2.2.2. Waveform Retracking Method
2.2.3. Estimating Sea Surface Height
3. Results
3.1. SSA-Denoised Waveform Series
3.2. Comparison of Retracked SSHs
3.3. Comparison of Retracked SSHs Discrepancies at Crossover Points
4. MSSH Model and Validation
4.1. MSSH Model from SSA-Denoised Waveform Retracked SSHs
4.2. Validations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quartly, G.; Chen, G. Introduction to the Special Issue on “Satellite Altimetry: New Sensors and New Applications”. Sensors 2006, 6, 616–619. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Gao, Y.; Hwang, C.; Sun, J. A multi-subwaveform parametric retracker of the radar satellite altimetric waveform and recovery of gravity anomalies over coastal oceans. Sci. China Earth Sci. 2010, 53, 610–616. [Google Scholar] [CrossRef]
- Hernandez, F.; Schaeffer, P. The CLS01 Mean Sea Surface: A Validation with the GSFC00.1 Surface; CLS: Ramonville St Agne, France, 2001. [Google Scholar]
- Hwang, C.; Hsu, H.-Y.; Jang, R. Global mean sea surface and marine gravity anomaly from multi-satellite altimetry: Applications of deflection-geoid and inverse Vening Meinesz formulae. J. Geodesy 2002, 76, 407–418. [Google Scholar] [CrossRef]
- Fu, L.L.; Cazenave, A. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Deng, X. Improvement of Geodetic Parameter Estimation in Coastal Regions from Satellite Radar Altimetry. Ph.D. Thesis, Curtin University of Technology, Perth, Australia, 2003. [Google Scholar]
- Deng, X.; Featherstone, W.E. A coastal retracking system for satellite radar altimeter waveforms: Application to ERS-2 around Australia. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Gommenginger, C.; Thibaut, P.; Fenodlio-Marc, L.; Quartly, G.; Deng, X.; Gomez-Enri, J.; Challenor, P.; Gao, Y. Retracking Altimeter Waveforms Near the Coasts. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–102. [Google Scholar]
- Deng, X.; Featherstone, W.E.; Hwang, C.; Berry, P.A.M. Estimation of Contamination of ERS-2 and POSEIDON Satellite Radar Altimetry Close to the Coasts of Australia. Mar. Geod. 2002, 25, 249–271. [Google Scholar] [CrossRef]
- Yang, L.; Lin, M.; Pan, D. Retracking Jason1 Altimeter Waveform Over Chinacoastal Zone. In Proceedings of the SPIE-Microwave Remote Sensing of the Atmosphere and Environment VI, Noumea, New Caledonia, 19 November 2008; Volume 7154. [Google Scholar]
- Idris, N.H.; Deng, X. The Retracking Technique on Multi-Peak and Quasi-Specular Waveforms for Jason-1 and Jason-2 Missions near the Coast. Mar. Geod. 2012, 35, 217–237. [Google Scholar] [CrossRef] [Green Version]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Physica D 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: New York, NY, USA, 2013. [Google Scholar]
- Shen, Y.; Guo, J.; Liu, X.; Kong, Q.; Guo, L.; Li, W. Long-term prediction of polar motion using a combined SSA and ARMA model. J. Geodesy 2018, 92, 333–343. [Google Scholar] [CrossRef]
- Guo, J.; Shi, K.; Liu, X.; Sun, Y.; Li, W.; Kong, Q. Singular spectrum analysis of ionospheric anomalies preceding great earthquakes: Case studies of Kaikoura and Fukushima earthquakes. J. Geodyn. 2019, 124, 1–13. [Google Scholar] [CrossRef]
- CNES. Jason-1 Products Handbook; SALP-MU-M5-OP-13184-CN; Issue: 5 Rev 1; CNES: Paris, France, 2016. [Google Scholar]
- Yang, L.; Lin, M.; Liu, Q.; Pan, D. A coastal altimetry retracking strategy based on waveform classification and sub-waveform extraction. Int. J. Remote Sens. 2012, 33, 7806–7819. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.; Deng, X.; Hsu, H.-Y.; Liu, Y. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data. J. Geodesy 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Guo, J.; Hwang, C.; Chang, X.; Liu, Y. Improved threshold retracker for satellite altimeter waveform retracking over coastal sea. Prog. Nat. Sci. 2006, 16, 732–738. [Google Scholar]
- Ganguly, D.; Chander, S.; Desai, S.; Chauhan, P. A Subwaveform-Based Retracker for Multipeak Waveforms: A Case Study over Ukai Dam/Reservoir. Mar. Geod. 2015, 38, 581–596. [Google Scholar] [CrossRef]
- Davis, C.H. Growth of the Greenland ice sheet: A performance assessment of altimeter retracking algorithms. IEEE Trans. Geosci. Remote 1995, 33, 1108–1116. [Google Scholar] [CrossRef]
- Davis, C.H. A robust threshold retracking algorithm for measuring ice-sheet surface elevation change from satellite radar altimeter. IEEE Trans. Geosci. Remote 1997, 35, 974–979. [Google Scholar] [CrossRef]
- Uebbing, B.; Kusche, J.; Forootan, E. Waveform retracking for improving level estimations from topex/poseidon, Jason-1, and Jason-2 altimetry observations over african lakes. IEEE Trans. Geosci. Remote 2015, 53, 2211–2224. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, B04406. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Guo, J.; Liu, X.; Zhu, C.; Niu, Y.; Li, Z.; Ji, B.; Ouyang, Y. Mean sea surface model over China seas and its adjacent ocean established with the 19-year moving average method from multi-satellite altimeter data. Cont. Shelf Res. 2020, 192, 104009. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Schaeffer, P.; Faugère, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the improvement of recent mean sea surface models: A new approach for identifying and quantifying their errors. J. Geophys. Res. Oceans 2018, 123, 5889–5911. [Google Scholar] [CrossRef]
- Andersen, O.; Knudsen, P.; Stenseng, L. A New DTU18 MSS Mean Sea Surface—Improvement from SAR Altimetry. In Proceedings of the 25 Years of Progress in Radar Altimetry Symposium, Portugal, Duration, 24–29 September 2018. [Google Scholar]
- Guo, J.; Wang, J.; Hu, Z.; Hwang, C.; Chen, C.; Gao, Y. Temporal-spatial variations of sea level over Chinese seas derived from altimeter data of TOPEX/Poseidon, Jason-1 and Jason-2 from 1993 to 2012. Chin. J. Geophys. 2015, 58, 3103–3120. [Google Scholar]
- Guo, J.; Hu, Z.; Wang, J.; Chang, X.; Li, G. Sea level change of China seas and neighboring ocean based on satellite altimetry missions from 1993 to 2012. J. Coast. Res. 2015, 73, 17–21. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H.; Luo, Z.; Shum, C.K.; Tseng, K.-H.; Zhong, B. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms. Remote Sens. 2017, 9, 1077. [Google Scholar] [CrossRef]
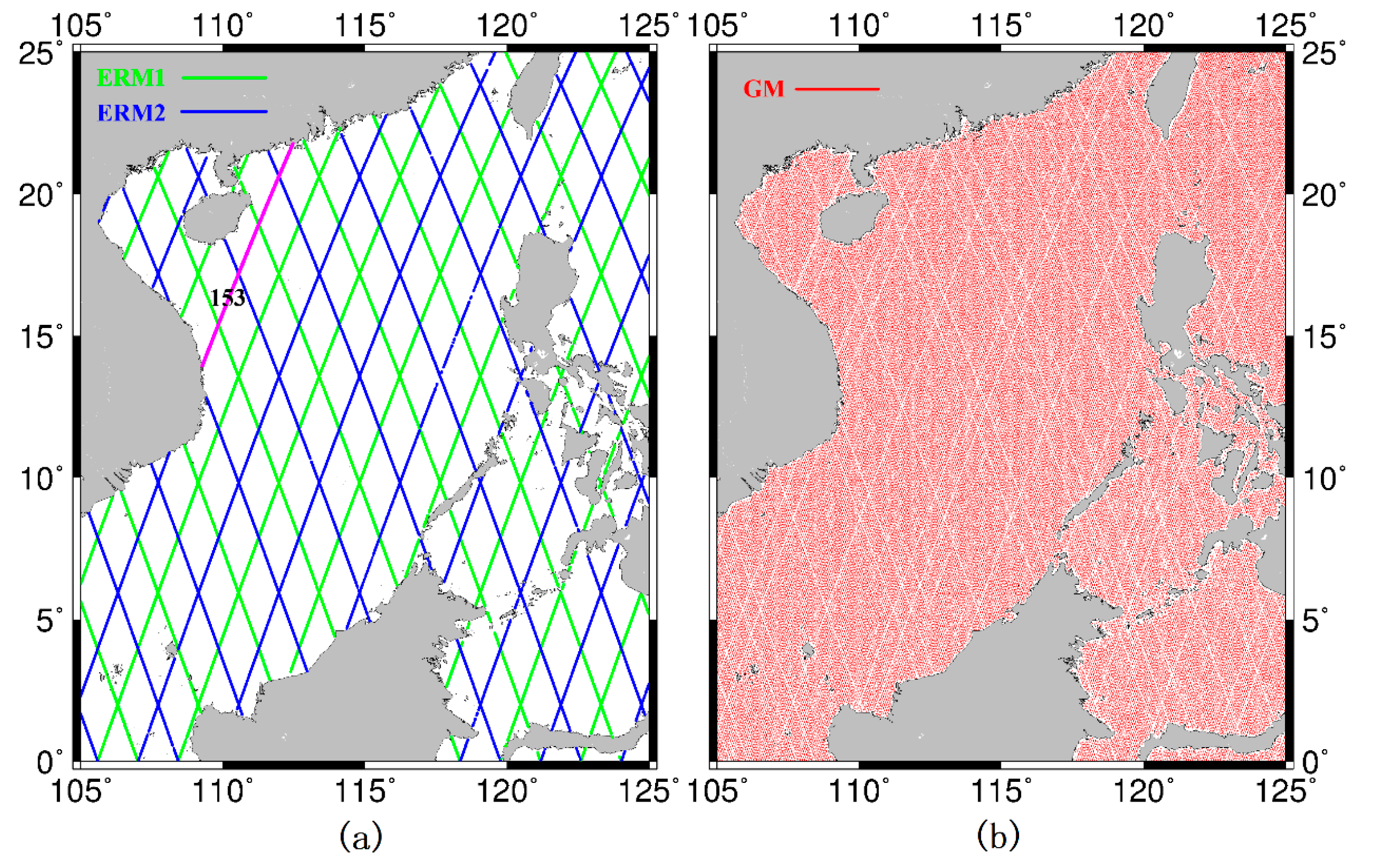

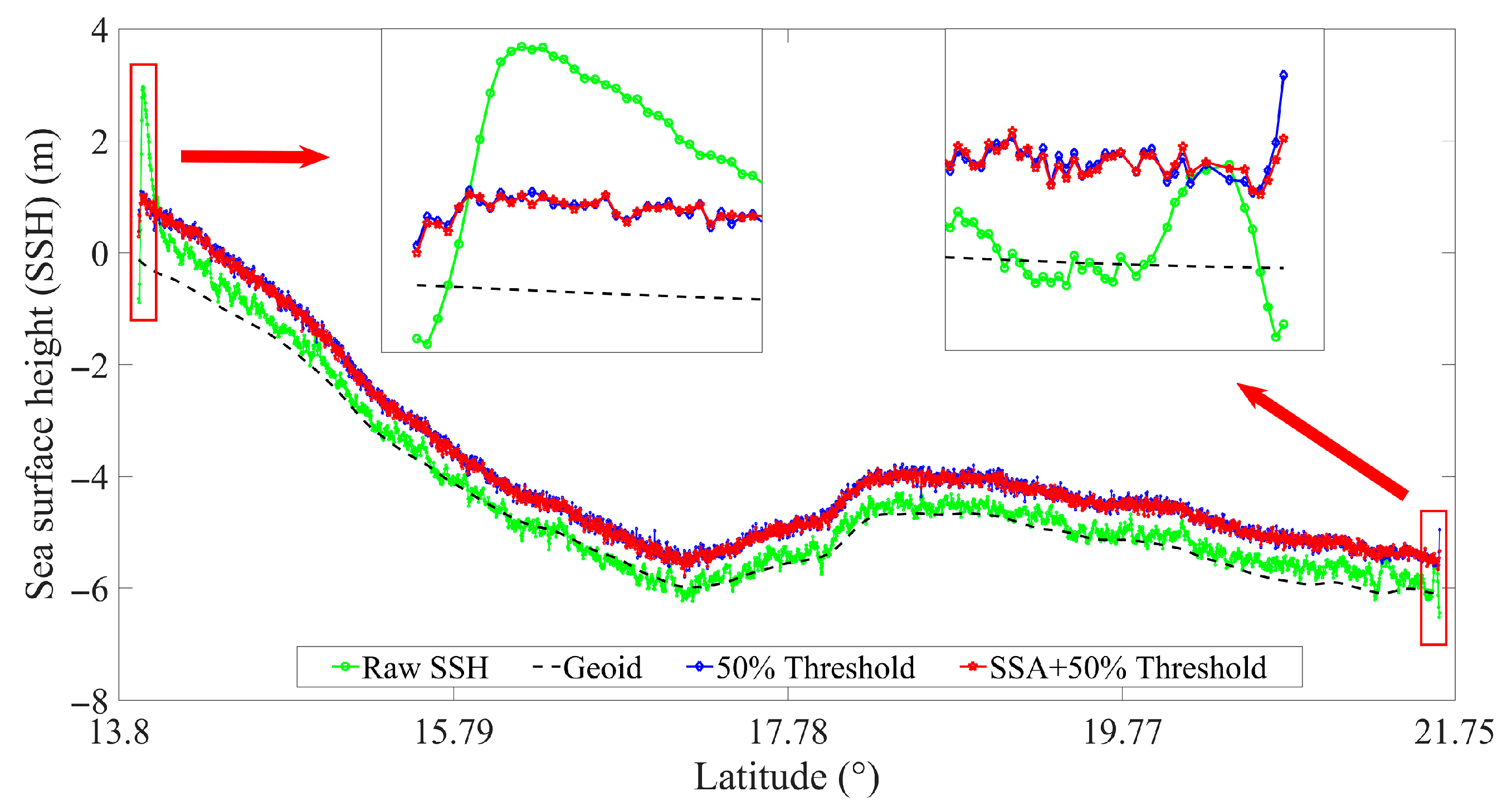
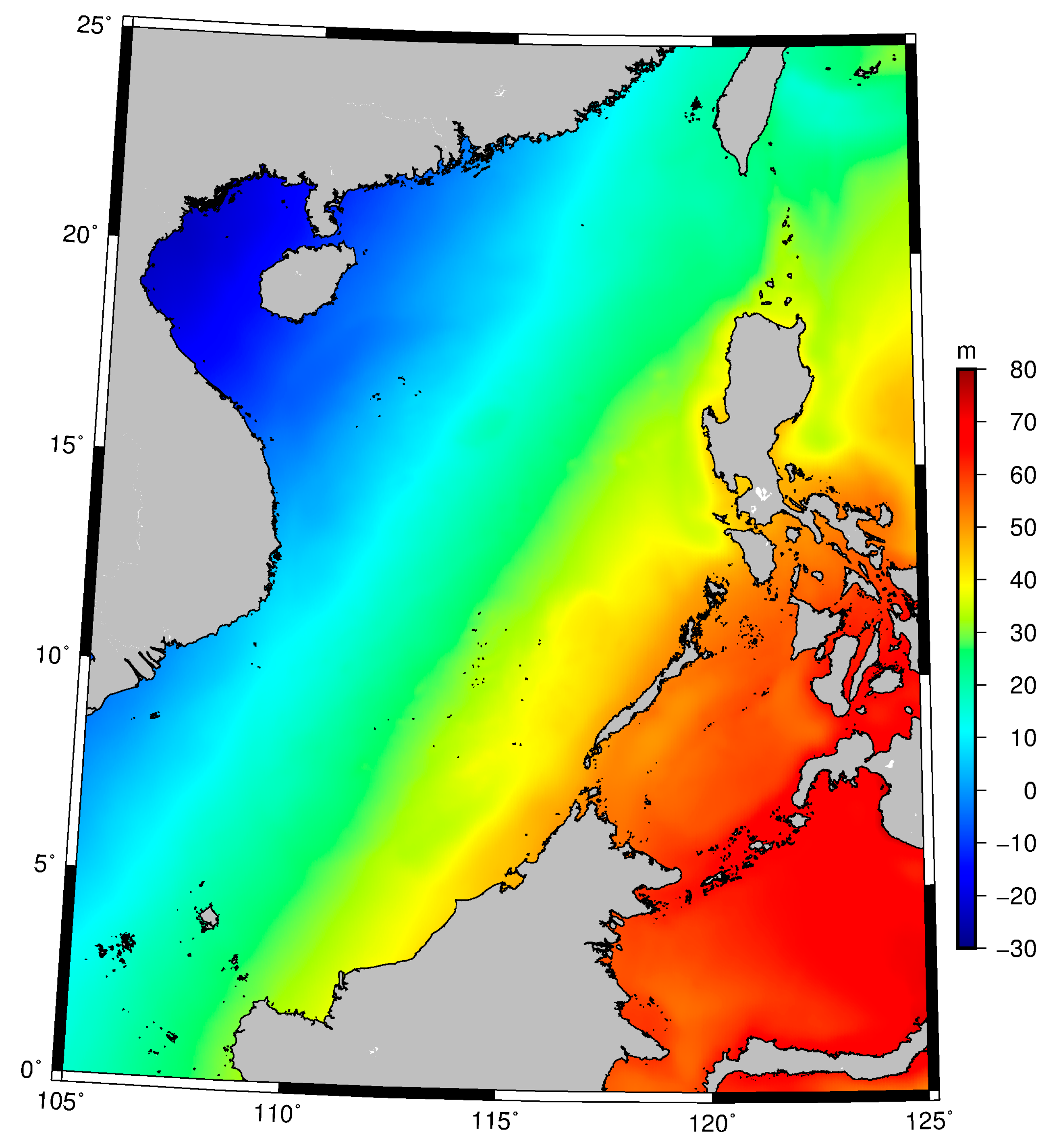
| Missions | Data Duration | Cycle Number | Orbit Altitude (km) | Mean Track Separation at the Equator (km) |
|---|---|---|---|---|
| ERM1 | 2002/01/15–2009/01/26 | 001-259 | 1336 | 315 |
| ERM2 | 2009/02/10–2012/03/03 | 262-374 | 1336 | 315 |
| GM | 2012/05/07–2013/06/21 | 500-537 | 1324 | 7 |
| The c340-p153 Track | Retracker | δraw (m) | δretracked (m) | IMP (%) |
|---|---|---|---|---|
| Entire track | 50% threshold | 0.2954 | 0.1587 | 46.27 |
| SSA + 50% threshold | 0.2954 | 0.1519 | 48.57 | |
| Land to Ocean (Distance < 10 km) | 50% threshold | 0.8813 | 0.1170 | 86.73 |
| SSA + 50% threshold | 0.8813 | 0.1164 | 86.80 | |
| Ocean to Land (Distance < 10 km) | 50% threshold | 0.1681 | 0.0900 | 46.47 |
| SSA + 50% threshold | 0.1681 | 0.0690 | 58.99 |
| Distance | Retracker | Mean (m) | STD (m) | RMS (m) |
|---|---|---|---|---|
| d ≤ 10 km (2526) | 50% threshold | 0.0125 | 0.5052 | 0.5053 |
| SSA + 50% threshold | 0.0059 | 0.4467 | 0.4466 | |
| d > 10 km (48,407) | 50%threshold | −0.0007 | 0.2664 | 0.2664 |
| SSA + 50%threshold | −0.0002 | 0.2529 | 0.2529 |
| Model Discrepancy | M1-C | M2-C | M1-D | M2-D | M1-M2 | C-D |
|---|---|---|---|---|---|---|
| Max | 2.2095 | 2.1881 | 4.3607 | 4.3481 | 0.3909 | 4.5890 |
| Min | −1.2853 | −1.3391 | −0.6792 | −0.7294 | −0.3536 | −1.5820 |
| Mean | 0.1414 | 0.1281 | 0.1607 | 0.1474 | 0.0133 | 0.0193 |
| STD | 0.0698 | 0.0709 | 0.1179 | 0.1188 | 0.0141 | 0.1090 |
| RMS | 0.1577 | 0.1464 | 0.1993 | 0.1893 | 0.0194 | 0.1107 |
| Number of points | 325,951 | 325,951 | 325,951 | 325,951 | 325,951 | 325,951 |
| Model Discrepancy | M1-C | M2-C | M1-D | M2-D | M1-M2 | C-D | |
|---|---|---|---|---|---|---|---|
| Coastal region | Max | 1.8059 | 1.7862 | 4.3607 | 4.3481 | 0.3909 | 4.0920 |
| Min | −1.2853 | −1.3391 | −0.6792 | −0.7294 | −0.3536 | −1.5820 | |
| Mean | 0.1173 | 0.1033 | 0.2125 | 0.1985 | 0.0140 | 0.0951 | |
| STD | 0.1521 | 0.1543 | 0.3215 | 0.3230 | 0.0262 | 0.3120 | |
| RMS | 0.1921 | 0.1857 | 0.3853 | 0.3791 | 0.0297 | 0.3262 | |
| Number of points | 31,257 | 31,257 | 31,257 | 31,257 | 31,257 | 31,257 | |
| Open ocean | Max | 2.2095 | 2.1881 | 3.3181 | 3.3000 | 0.1403 | 4.5890 |
| Min | −1.2709 | −1.2890 | −0.3862 | −0.4003 | −0.3463 | −1.4930 | |
| Mean | 0.1439 | 0.1308 | 0.1552 | 0.1420 | 0.0132 | 0.0112 | |
| STD | 0.0535 | 0.0545 | 0.0641 | 0.0651 | 0.0121 | 0.0461 | |
| RMS | 0.1536 | 0.1416 | 0.1679 | 0.1562 | 0.0179 | 0.0475 | |
| Number of points | 294,694 | 294,694 | 294,694 | 294,694 | 294,694 | 294,694 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Guo, J.; Niu, Y.; Zhu, C.; Li, Z.; Liu, X. Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea. J. Mar. Sci. Eng. 2020, 8, 426. https://doi.org/10.3390/jmse8060426
Yuan J, Guo J, Niu Y, Zhu C, Li Z, Liu X. Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea. Journal of Marine Science and Engineering. 2020; 8(6):426. https://doi.org/10.3390/jmse8060426
Chicago/Turabian StyleYuan, Jiajia, Jinyun Guo, Yupeng Niu, Chengcheng Zhu, Zhen Li, and Xin Liu. 2020. "Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea" Journal of Marine Science and Engineering 8, no. 6: 426. https://doi.org/10.3390/jmse8060426
APA StyleYuan, J., Guo, J., Niu, Y., Zhu, C., Li, Z., & Liu, X. (2020). Denoising Effect of Jason-1 Altimeter Waveforms with Singular Spectrum Analysis: A Case Study of Modelling Mean Sea Surface Height over South China Sea. Journal of Marine Science and Engineering, 8(6), 426. https://doi.org/10.3390/jmse8060426