Hydrodynamics of Biomimetic Marine Propulsion and Trends in Computational Simulations
Abstract
:1. Introduction
2. Fish Swimming Modes and Biomimetic Marine Propulsors
2.1. Swimming Locomotion
2.1.1. BCF Swimming Modes
2.1.2. MPF Swimming Modes
2.2. Non-Swimming Locomotion
3. Numerical Models
3.1. Hydrodynamics
3.2. Non-Dimensional Parameters
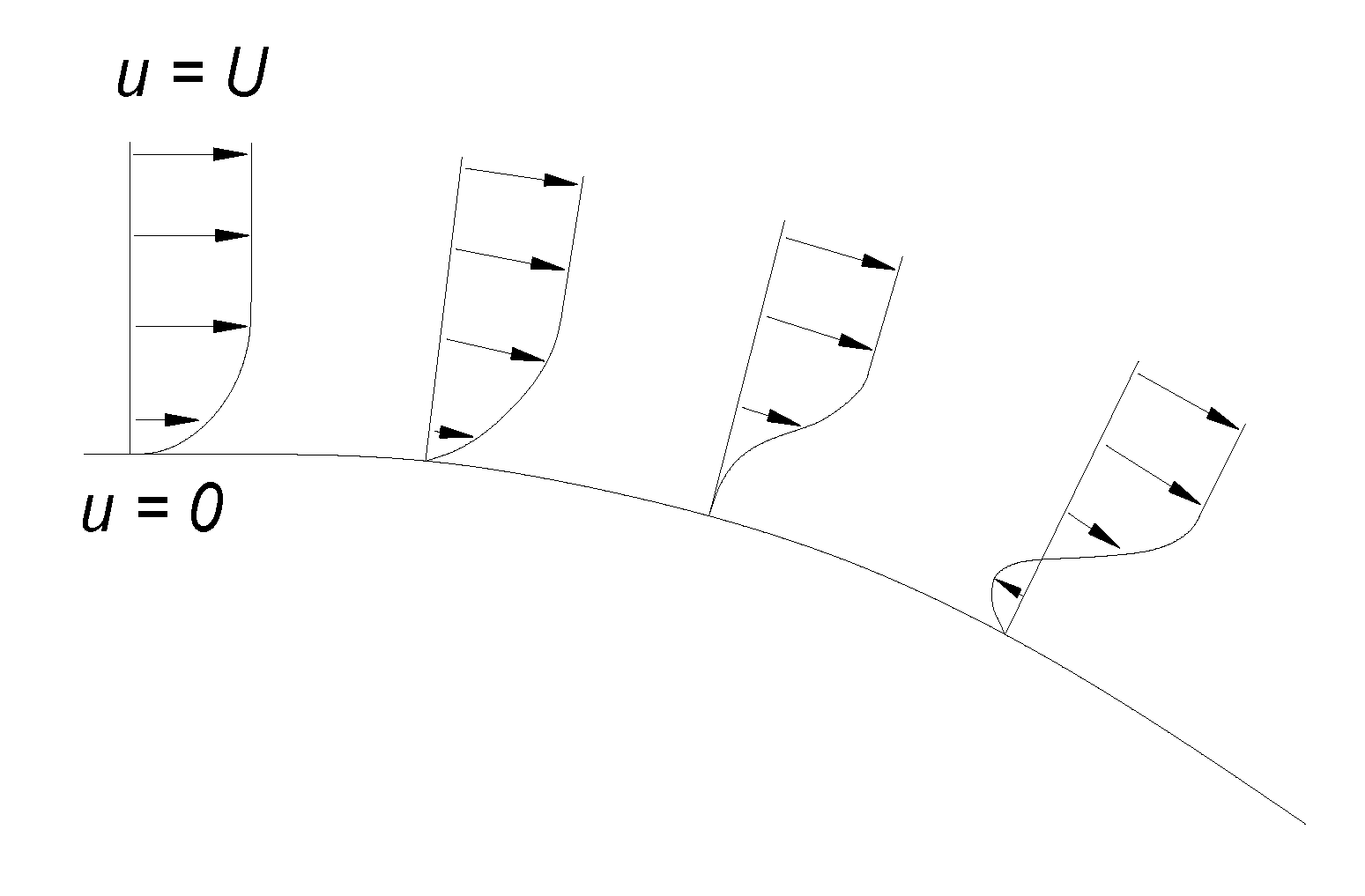
3.3. Turbulence
3.4. Grid Strategies
4. Experimental Validations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gray, J. Studies in animal locomotion: VI. The propulsive powers of dolphin. J. Exp. Biol. 1936, 13, 192–199. [Google Scholar]
- Gawn, R.W.L. Aspects of the locomotion of whales. Nature 1948, 161, 44–46. [Google Scholar] [CrossRef]
- Parry, D.A. The swimming of whales and a discussion of Gray’s paradox. J. Exp. Biol. 1949, 26, 24–34. [Google Scholar] [PubMed]
- Gero, D.R. The hydrodynamic aspects of fish propulsion. Am. Mus. Novit. 1952, 1601, 1–32. [Google Scholar]
- Kramer, M.O. Boundary layer stabilization by distributed damping. J. Am. Soc. Nav. Eng. 1960, 72, 25–33. [Google Scholar] [CrossRef]
- Webb, P.W. Hydrodynamics and Energetics of Fish Propulsion; Department of the Environment Fisheries and Marine Service: Ottawa, ON, Canada, 1975; pp. 1–158.
- Aleyev, Y.G. Hydrodynamic resistance and speed of movement of nekters. Zool. Zhurnal 1974, 53, 493–507. [Google Scholar]
- Van Oossanen, P.; Oosterveld, M.W.C. Hydrodynamic resistance characteristics of humans, dolphins, and ship forms. Schiffstechnik 1989, 36, 31–48. [Google Scholar]
- Fish, F.E.; Hui, C.A. Dolphin swimming—A review. Mammal Rev. 1991, 21, 181–195. [Google Scholar] [CrossRef]
- Gopalkrishnan, R.; Triantafyllou, M.S.; Triantafyllou, G.S.; Barrett, D. Active vorticity control in a shear flow using a flapping foil. J. Fluid Mech. 1994, 274, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Barrett, D.S. Propulsive Efficiency of a Flexible Hull Underwater Vehicle. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- Anderson, J.M. Vorticity Control for Efficient Propulsion. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- Streitlien, K.; Triantafyllou, G.S.; Triantafyllou, M.S. Efficient foil propulsion through vortex control. Am. Inst. Aeronaut. Astronaut. J. 1996, 34, 2315–2319. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Triantafyllou, G.S. An efficient swimming machine. Sci. Am. 1995, 272, 64–70. [Google Scholar] [CrossRef]
- Sfakiotakis, M.; Lane, D.M.; Davies, J.B.C. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.Y.; Chahine, G.L. Computational hydrodynamics of animal swimming: Boundary element method and three dimensional vortex wake structure. Comp. Biochem. Physiol. Part A 2001, 131, 51–60. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Techet, A.; Hover, F.S. Review of experimental work in biomimetic foils. IEEE J. Ocean. Eng. 2004, 29, 585–594. [Google Scholar] [CrossRef] [Green Version]
- Colgate, J.E. Mechanics and control of swimming: A review. IEEE J. Ocean. Eng. 2004, 29, 660–673. [Google Scholar] [CrossRef]
- Mittal, R. Computational modelling in bio-hydrodynamics: Trends, challenges and recent advances. IEEE J. Ocean. Eng. 2004, 29, 595–604. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.R. Trends in biorobotic autonomous undersea vehicles. IEEE J. Ocean. Eng. 2005, 30, 109–139. [Google Scholar] [CrossRef]
- Kato, N. Median and paired fin controllers for biomimetic marine vehicles. Appl. Mech. Rev. 2005, 58, 238–252. [Google Scholar] [CrossRef]
- Chu, W.S.; Lee, K.T.; Song, S.H.; Han, M.W.; Lee, J.Y.; Kim, H.S.; Kim, M.S.; Park, Y.J.; Cho, K.J.; Ahn, S.H. Review of biomimetic underwater robots using smart actuators. Int. J. Precis. Eng. Manuf. 2012, 13, 1281–1292. [Google Scholar] [CrossRef]
- Raj, A.; Thakur, A. Fish-inspired robots: Design, sensing, actuation, and autonomy—A review of research. Bioinspir. Biomim. 2016, 11. [Google Scholar] [CrossRef]
- Rozhdestvensky, K.; Ryzhov, V. Aerodynamics of flapping-wing propulsors. Prog. Aerosp. Sci. 2003, 39, 585–633. [Google Scholar] [CrossRef]
- Naito, S.; Isshiki, H. Effect of bow wings on ship propulsion and motions. Appl. Mech. Rev. 2005, 58, 253–268. [Google Scholar] [CrossRef]
- Shyy, W.; Aono, H.; Chimakurthi, S.K.; Trizilia, P.; Kang, C.K.; Cesnik, H.L.C.E.S. Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2010, 46, 284–327. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhu, Q. A review on flow energy harvesters based on flapping foils. J. Fluids Struct. 2014, 46, 174–191. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean. Eng. 2019, 195, 106712. [Google Scholar] [CrossRef]
- Breder, C.M. The locomotion of fishes. Zoologica 1926, 4, 159–297. [Google Scholar]
- Lindsey, C.C. Form, function and locomotory habits in fish. Fish Physiol. 1978, 7, 1–100. [Google Scholar] [CrossRef]
- Metin, S.; Menciassi, A.; Low, K.H.; Kim, S. Survey and introduction to the focused section on bio-inspired mechatronics. IEEE/ASME Trans. Mechatron. 2013, 18, 409–418. [Google Scholar] [CrossRef] [Green Version]
- Cohen, A.H.; Colmes, P.J.; Rand, R.H. The nature of the coupling between segmental oscillators of the lamprey spinal generator for locomotion: A mathematical model. J. Math. Biol. 1982, 13, 345–369. [Google Scholar] [CrossRef]
- Grillner, S.; Deliagina, T.; Ekeberg, A.; Manira, R.H.; Lansner, H.A.; Orlovsky, G.N.; Wallen, P. Neural networks that coordinate locomotion and body orientation in the lamprey. Trends Neurosci. 1995, 18, 270–279. [Google Scholar] [CrossRef]
- Grillner, S.; Matsushima, T. The neural network underlying locomotion in lamprey—Synaptic and cellular mechanisms. Neuron 1991, 7, 1–15. [Google Scholar] [CrossRef]
- Ayers, J.; Wilbur, C.; Olcott, C. Lamprey robots. In Proceedings of the 1st International Symposium of Aqua Bio-Mechanisms, ISABMEC 2000, Tokai University Pacific Center, Honolulu, HI, USA, 27–30 August 2000. [Google Scholar]
- Ayers, J.; Rulkov, N.; Knudsen, D.; Kim, Y.B.; Volkovskii, A.; Selverston, A. Controlling underwater robots with electronic nervous systems. Appl. Bionics Biomech. 2010, 7, 57–67. [Google Scholar] [CrossRef] [Green Version]
- Ayers, J.; Westphal, A.; Blustein, D. A conserved neural circuit-based architecture for ambulatory and undulatory biomimetic robots. Mar. Technol. Soc. J. 2011, 45, 147–152. [Google Scholar] [CrossRef]
- Wilbur, C.; Vorus, W.; Cao, Y.; Currie, S.N. A lamprey-based undulatory vehicle. In Neurotechnology for Biomimetic Robots; MIT Press: Cambridge, MA, USA, 2002; pp. 285–296. [Google Scholar]
- Westphal, A.; Rulkov, N.F.; Ayers, J.; Brady, D.; Hunt, M. Controlling a lamprey-based robot with an electronic nervous system. Smart Struct. Syst. 2011, 8, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Li, F.; Stefanini, C.; Chena, D.; Dario, P. Biomimetic flexible/compliant sensors for a soft-body lamprey-like robot. Robot. Auton. Syst. 2010, 58, 1138–1148. [Google Scholar] [CrossRef]
- Xu, J.X.; Niu, X.L.; Ren, Q.Y. Modeling and control design of an anguilliform robotic fish. Int. J. Model. Simul. Sci. Comput. 2012, 3, 1250018. [Google Scholar] [CrossRef]
- Crespi, A.; Badertscher, A.; Guignard, A.; Ijspeert, A.J. AmphiBot I: An amphibious snake-like robot. Robot. Auton. Syst. 2005, 50, 163–175. [Google Scholar] [CrossRef] [Green Version]
- Ijspeert, J.A. A connectionist central pattern generator for the aquatic and terrestrial gaits of a simulated salamander. Biol. Cybern. 2001, 84, 331–348. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Crespi, A.; Cabelguen, J.M. Simulation and robotics studies of salamander locomotion: Applying neurobiological principles to the control of locomotion in robots. Neuroinformatics 2005, 3, 171–195. [Google Scholar] [CrossRef] [Green Version]
- Crespi, A.; Karakasiliotis, K.; Guignard, A.; Ijspeert, A.J. Salamandra Robotica II: An amphibious robot to study salamander-like swimming and walking gaits. IEEE Trans. Robot. 2013, 29, 308–320. [Google Scholar] [CrossRef] [Green Version]
- McIsaac, K.P.; Ostrowski, J.P. Experiments in closed-loop control for an underwater eel-like robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 750–755. [Google Scholar] [CrossRef]
- McIsaac, K.P.; Ostrowski, J.P. Experimental verification of open-loop control for an underwater eel-like robot. Int. J. Robot. Res. 2002, 21, 849–859. [Google Scholar] [CrossRef]
- McIsaac, K.P.; Ostrowski, J.P. Motion planning for anguilliform locomotion. IEEE Trans. Robot. Autom. 2003, 19, 637–652. [Google Scholar] [CrossRef]
- Lamas, M.I.; Rodríguez, J.D.; Rodríguez, C.G.; González, P.B. Design aspects and two-dimensional CFD simulation of a marine propulsor based on a biologically-inspired undulating movement. J. Marit. Res. 2020, 7, 73–88. [Google Scholar]
- Lamas, M.I.; Rodríguez, J.D.; Rodríguez, C.G. CFD analysis of biologically-inspired marine propulsors. Brodogradnja 2012, 63, 125–133. [Google Scholar]
- Lamas, M.I.; Rodríguez, J.D.; Rodríguez, C.G.; González, P.B. Three-dimensional CFD analysis to study the thrust and efficiency of a biologically-inspired marine propulsor. Pol. Marit. Res. 2011, 18, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Kumph, J.M. Maneuvering of a Robotic Pike. Mater’s Thesis, Department of Ocean Engineering, Massachussets Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Watts, C.M. A Comparison Study of Biologically Inspired Propulsion Systems for an Autonomous Underwater Vehicle. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2009. [Google Scholar]
- Watts, C.; McGookin, E.; Macauley, M. Biomimetic propulsion systems for mini-autonomous underwater vehicles. In Proceedings of the IEEE Conference OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007. [Google Scholar] [CrossRef]
- Watts, C.; McGookin, E. Modeling and simulation of a biomimetic underwater vehicle. In Proceedings of the Grand Challenges in Modeling and Simulation symposium, Edinburgh, UK, 16–19 June 2008; pp. 402–408. [Google Scholar]
- Hirata, K.; Takimoto, T.; Tamura, K. Study on turning performance of a fish robot. In Proceedings of the 1st International Symposium of Aqua Bio-Mechanisms, ISABMEC 2000, Tokai University Pacific Center, Honolulu, HI, USA, 27–30 August 2000. [Google Scholar]
- Heo, S.; Wiguna, T.; Park, H.C.; Goo, N.S. Effect of an artificial caudal fin on the performance of a biomimetic fish robot propelled by piezoelectric actuators. J. Bionic Eng. 2007, 4, 151–158. [Google Scholar] [CrossRef]
- Li, W.; Tianmiao, W.; Guanhao, W.; Jianhong, L. Hybrid undulatory kinematics of a robotic Mackerel (Scomber scombrus): Theoretical modeling and experimental investigation. Sci. China Technol. Sci. 2012, 55, 2941–2952. [Google Scholar] [CrossRef]
- Barrett, D.S.; Triantafyllou, M.S.; Yue, D.K.P. Drag reduction in fish-like locomotion. J. Fluid Mech. 1999, 392, 183–212. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.M.; Chabra, N.K. Maneuvering and stability performance of a robotic tuna. Integr. Comp. Biol. 2002, 42, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Wen, L.; Guo, Y. Experimental design and performance of underwater vehicle based on capacity of voyage. In Proceedings of the IEEE International Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 587–591. [Google Scholar] [CrossRef]
- Liang, J.; Zheng, W.; Wen, L.; Wang, T.; Xie, C. Propulsive and maneuvering performance of two joints biorobotic autonomous undersea vehicle. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Guilin, China, 19–23 December 2009; pp. 314–320. [Google Scholar] [CrossRef]
- Liang, J.; Wang, T.; Wen, L. Development of a two-joint robotic fish for real-world exploration. J. Field Robot. 2011, 28, 70–79. [Google Scholar] [CrossRef]
- Wang, T.; Wen, L.; Liang, J.; Wu, G. Fuzzy vorticity control of a biomimetic robotic fish using a flapping lunate tail. J. Bionic Eng. 2010, 7, 56–65. [Google Scholar] [CrossRef]
- Liu, Y.X.; Chen, W.S.; Liu, J.K. Research on the swing of the body of two-joint robot fish. J. Bionic Eng. 2008, 5, 159–165. [Google Scholar] [CrossRef]
- Suleman, A.; Crawford, C. Design and testing of a biomimetic tuna using shape memory alloy induced propulsion. Comput. Struct. 2008, 86, 491–499. [Google Scholar] [CrossRef]
- Kruusmaa, M.; Fiorini, P.; Megill, W.; de Vittorio, M.; Akanyeti, O.; Visentin, F.; Chambers, L.; El Daou, H.; Fiazza, M.C.; Ježov, J.; et al. FILOSE for svenning: A flow sensing bioinspired robot. IEEE Robot. Autom. Mag. 2014, 21, 51–62. [Google Scholar] [CrossRef]
- Nakashima, M.; Tokuo, K.; Kaminaga, K.; Ono, K. Experimental study of a self-propelled two-joint dolphin robot. In Proceedings of the Ninth International Offshore and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. [Google Scholar]
- Nakashima, M.; Ono, K. Development and experiment of two-joint dolphin robot. In Neurotechnology for Biomimetic Robots; MIT Press: Cambrige, MA, USA, 2002; pp. 309–324. [Google Scholar]
- Nakashima, M.; Takashi, Y.; Ono, K. Three dimensional manoeuverability of the dolphin robot. In Bio-Mechanisms of Swimming and Flying; Springer: Tokio, Japan, 2004; pp. 79–92. [Google Scholar] [CrossRef]
- Nakashima, M.; Tsubaki, T.; Ono, K. Three-dimensional movement in water of the dolphin robot—Control between two positions by roll and pitch combination. J. Robot. Mechatron. 2006, 18, 347–355. [Google Scholar] [CrossRef]
- Yu, J.; Hu, Y.; Fan, R.; Wang, L.; Kuzucu, A. Mechanical design and motion control of biomimetic robotic dolphin. Adv. Robot. 2007, 21, 499–513. [Google Scholar] [CrossRef]
- Yu, J.; Hu, Y.; Huo, J.; Wang, L. An adjustable Scotch Yoke mechanism for robotic dolphin. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Sanya, China, 15–28 December 2007; pp. 513–518. [Google Scholar] [CrossRef]
- Yu, J.; Hu, Y.; Huo, J.; Wang, L. Dolphin-like propulsive mechanism based on an adjustable Scotch yoke. Mech. Mach. Theory 2009, 44, 603–614. [Google Scholar] [CrossRef]
- Shen, F.; Wei, C.; Cao, Z.; Xu, D.; Yu, J.; Zhou, C. Implementation of a multi-link robotic dolphin with two 3-DOF flippers. J. Comput. Inf. Syst. 2011, 7, 2601–2607. [Google Scholar]
- Shen, F.; Cao, Z.Q.; Xu, D.; Zhou, C. A dynamic model of robotic dolphin based on Kane method and its speed optimization method. Acta Autom. Sin. 2012, 38, 1247–1256. [Google Scholar] [CrossRef]
- Liu, P.; He, K.; Ou, X.; Du, R. Mechanical design, kinematic modeling and simulation of a robotic dolphin. In Proceedings of the IEEE International Conference on Information and Automation, Shenzhen, China, 6–8 June 2011. [Google Scholar] [CrossRef]
- Dogangil, G.; Ozcicek, E.; Kuzucu, A. Design, construction, and control of a robotic dolphin. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Shatin, China, 5–9 July 2005; pp. 51–56. [Google Scholar] [CrossRef]
- Dogangil, G.; Ozcicek, E.; Kuzucu, A. Modeling, simulation, and development of a robotic dolphin prototype. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; pp. 952–957. [Google Scholar] [CrossRef]
- Ho, T.; Lee, S. Design of a multi-locomotion underwater robot. Adv. Mater. Res. 2012, 488, 1732–1736. [Google Scholar] [CrossRef]
- Aghbali, B.; Yousefi-Koma, A. Design and fuzzy control of the shark robot-fish dorsal fin using SMA. In Proceedings of the 10th Biennial Conference on Engineering Systems Design and Analysis, Istanbul, Turkey, 12–14 July 2010. [Google Scholar] [CrossRef]
- Long, J.H., Jr.; Koob, T.; Schaefer, J.; Summers, A.; Bantilan, K.; Grotmol, S.; Porter, M. Inspired by sharks: A biomimetic skeleton for the flapping, propulsive tail of an aquatic robot. Mar. Technol. Soc. J. 2011, 45, 119–129. [Google Scholar] [CrossRef]
- Kodati, P.; Hinkle, J.; Deng, X. Micro autonomous robotic ostraciiform (MARCO): Design and fabrication. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 14–15 April 2007. [Google Scholar] [CrossRef]
- Kodati, P.; Hinkle, J.; Winn, A.; Deng, X. Microautonomous robotic ostraciiform (MARCO): Hydrodynamics, design, and fabrication. IEEE Trans. Robot. 2008, 24, 105–111. [Google Scholar] [CrossRef]
- Gordon, M.; Hove, J.; Webb, P.; Weihs, D. Boxfishes as unusually well-controlled autonomous underwater vehicles. Physiol. Biochem. Zool. 2000, 74, 663–671. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhao, W.; Xie, G.; Wang, L. Development and target following of vision-based autonomous robotic fish. Robotica 2009, 27, 1075–1089. [Google Scholar] [CrossRef]
- Anderson, J.M.; Streitlien, K.; Barrett, D.S.; Triantafyllou, M.S. Oscillating foils of high propulsive efficiency. J. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef] [Green Version]
- Read, D.A.; Hover, F.S.; Triantafyllou, M.S. Forces on oscillating foils for propulsion and maneuvering. J. Fluids Struct. 2003, 17, 163–183. [Google Scholar] [CrossRef]
- Yamamoto, I.; Terada, Y.; Nagamatu, T.; Imaizumi, Y. Propulsion system with flexible/rigid oscillating fin. IEEE J. Ocean. Eng. 1995, 20. [Google Scholar] [CrossRef]
- Streitlien, K.; Triantafyllou, G.S. On thrust estimates for flapping foils. J. Fluids Struct. 1998, 12, 47–55. [Google Scholar] [CrossRef]
- Paterson, E.G.; Stern, F. Computation of unsteady viscous marine-propulsor blade flows—Part 1: Validation and analysis. J. Fluids Eng. Trans. ASME 1997, 119, 145–154. [Google Scholar] [CrossRef]
- Paterson, E.G.; Stern, F. Computation of unsteady viscous marine-propulsor blade flows—Part 2: Parametric study. J. Fluids Eng. Trans. ASME 1999, 121, 139–147. [Google Scholar] [CrossRef]
- Karpouzian, G.; Spedding, G.; Cheng, H.K. Lunate-tail swimming propulsion. Part 2. Performance analysis. J. Fluid Mech. 1990, 210, 329–351. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Bose, N. Oscillating foils for marine propulsion. In Proceedings of the 4th International Offshore and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994; Volume 3, pp. 539–544. [Google Scholar]
- Saimek, S.; Li, P.Y. Motion planning and control of a swimming machine. In Proceedings of the American Control Conference, Arlington, VA, USA, 25–27 June 2001; pp. 125–130. [Google Scholar] [CrossRef] [Green Version]
- Herr, H.; Dennis, B. A swimming robot actuated by living muscle tissue. J. Neuroeng. Rehabil. 2004, 1, 6–9. [Google Scholar] [CrossRef] [Green Version]
- Guo, S. A new type of fish-like underwater microrobot. IEEE/ASME Trans. Mechatron. 2003, 8, 136–141. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Politis, G.K. Hydrodynamic performance of flapping wings for augmenting ship propulsion in waves. Ocean. Eng. 2013, 72, 227–240. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Filippas, E.S. Ship propulsion in waves by actively controlled flapping foils. Appl. Ocean. Res. 2015, 52, 1–11. [Google Scholar] [CrossRef]
- Filippas, E.; Gerostathis, G.; Belibassakis, K.A. Semi-activated oscillating hydrofoil as a nearshore biomimetic energy device system in waves and currents. Ocean. Eng. 2018, 154, 396–415. [Google Scholar] [CrossRef]
- Koutsogiannakis, P.E.; Filippas, E.S.; Belibassakis, K.A. A study of multi-component oscillating-foil hydrokinetic turbines with a GPU-accelerated boundary element method. J. Mar. Sci. Eng. 2019, 7, 424. [Google Scholar] [CrossRef] [Green Version]
- Kato, N. Control performance in the horizontal plane of a fish robot with mechanical pectoral fins. IEEE J. Ocean. Eng. 2000, 25, 121–129. [Google Scholar] [CrossRef]
- Kato, N. Swimming and walking of an amphibious robot with fin actuators. Mar. Technol. Soc. J. 2011, 45, 181–197. [Google Scholar] [CrossRef]
- Licht, S.; Polidoro, V.; Flores, M.; Hover, F.S.; Triantafyllou, M.S. Design and projected performance of a flapping foil AUV. IEEE J. Ocean. Eng. 2004, 29, 786–794. [Google Scholar] [CrossRef]
- Licht, S.C.; Wibawa, M.S.; Hover, F.S.; Triantafyllou, M.S. In-line motion causes high thrust and efficiency in flapping foils that use power downstroke. J. Exp. Biol. 2010, 213, 63–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H.J.; Song, S.H.; Ahn, S.H. A turtle-like swimming robot using a smart soft composite (SSC) structure. Smart Mater. Struct. 2013, 22, 014007. [Google Scholar] [CrossRef]
- Salumae, T.; Raag, R.; Rebane, J.; Ernits, A.; Toming, G.; Ratas, M.; Kruusmaa, M. Design principle of a biomimetic underwater robot U-CAT. In Proceedings of the 2014 Oceans, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Bozkurttas, M.; Mittal, R.; Dong, H.; Lauder, G.V.; Madden, P. Low-dimensional models and performance scaling of a highly deformable fish pectoral fin. J. Fluid Mech. 2009, 631, 311–342. [Google Scholar] [CrossRef] [Green Version]
- Bozkurttas, M.; Tangorra, J.; Lauder, G.; Mittal, R. Understanding the hydrodynamics of swimming: From fish fins to flexible propulsors for autonomous underwater vehicles. Adv. Sci. Technol. 2008, 58, 193–202. [Google Scholar] [CrossRef]
- Georgiades, C.; Nahon, M.; Buehler, M. Simulation of an underwater hexapod robot. Ocean. Eng. 2009, 36, 39–47. [Google Scholar] [CrossRef]
- Long, J.H., Jr.; Schumacher, J.; Livingston, N.; Kemp, M. Four flippers or two? Tetrapodal swimming with an aquatic robot. Bioinspiration Biomim. 2006, 1, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Sitorus, P.E.; Nazaruddin, Y.Y.; Leksono, E.; Budiyono, A. Design and implementation of paired pectoral fins locomotion of labriform fish applied to a fish robot. J. Bionic Eng. 2009, 6, 37–45. [Google Scholar] [CrossRef]
- Cai, Y.; Bi, S.; Zheng, L. Design and experiments of a robotic fish imitating cow-nosed ray. J. Bionic Eng. 2010, 7, 120–126. [Google Scholar] [CrossRef]
- Punning, A.; Anton, M.; Kruusmaa, M.; Aabloo, A. A biologically inspired ray-like underwater robot with electroactive polymer pectoral fins. In Proceedings of the IEEE Conference on Mechatronics and Robotics, Aachen, Germany, 13–15 September 2004; pp. 241–245. [Google Scholar]
- Chen, Z.; Um, T.I.; Bart-Smith, H. Ionic polymer-metal composite enabled robotic manta ray. Electroact. Polym. Actuators Devices (EAPAD) 2011, 7976, 797637. [Google Scholar] [CrossRef]
- Clarck, R.P.; Smits, A.J. Thrust production and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 2006, 562, 415–429. [Google Scholar] [CrossRef] [Green Version]
- Low, K.H. Locomotion simulation and system integration of robotic fish with modular undulating fin. Int. J. Simul. 2008, 7, 64–77. [Google Scholar]
- Zhang, Y.H.; Song, Y.; Yang, J.; Low, K.H. Numerical and experimental research on modular oscillating fin. J. Bionic Eng. 2008, 5, 13–23. [Google Scholar] [CrossRef]
- Zhang, Y.H.; He, J.H. Research on influence on fin ray motion pattern on the propulsion of bionic undulating fins. Chin. J. Eng. Des. 2017, 24, 89–99. [Google Scholar] [CrossRef]
- Low, K.H.; Willy, A. Biomimetic motion planning of an undulating robotic fish fin. JVC/J. Vib. Control 2006, 12, 1337–1359. [Google Scholar] [CrossRef]
- Low, K.H. Design, development and locomotion control of bio-fish robot with undulating anal fins. Int. J. Robot. Autom. 2007, 22, 88–99. [Google Scholar] [CrossRef]
- Low, K.H. Maneuvering of biomimetic fish by integrating a buoyancy body with modular undulating fins. Int. J. Hum. Robot. 2007, 4, 671–695. [Google Scholar] [CrossRef]
- Hu, T.; Shen, L.; Low, K.H. Bionic asymmetry: From amiiform fish to undulating robotic fins. Chin. Sci. Bull. 2009, 54, 562–568. [Google Scholar] [CrossRef]
- Low, K.H. Modelling and parametric study of modular undulating fin rays for fish robots. Mech. Mach. Theory 2009, 44, 615–632. [Google Scholar] [CrossRef]
- Epstein, M.; Colgate, J.E.; Maciver, M.A. Generating thrust with a biologically-inspired robotic ribbon fin. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2412–2417. [Google Scholar] [CrossRef]
- MacIver, M.A.; Sharabash, N.M.; Nelson, M.E. Prey-capture behavior in gymnotid electric fish: Motion analysis and effects of water conductivity. J. Exp. Biol. 2001, 204, 543–557. [Google Scholar]
- MacIver, M.A.; Fontaine, E.; Burdick, J.W. Designing future underwater vehicles: Principles and mechanisms of the weakly electric fish. IEEE J. Ocean. Eng. 2004, 29, 651–659. [Google Scholar] [CrossRef]
- Siahmansouri, M.; Ghanbari, S.; Fakhrabadi, M.M.S. Design, implementation and control of a fish robot with undulating fins. Int. J. Adv. Robot. Syst. 2011, 8, 61–69. [Google Scholar] [CrossRef]
- Conte, J.; Modarres-Sadeghi, Y.; Watts, M.N.; Hover, F.S.; Triantafyllou, M.S. A fast-starting mechanical fish that accelerates at 40 m s−2. Bioinspiration Biomim. 2020, 5, 035004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Epps, B.P.; Techet, A.H. Impulse generated during unsteady maneuvering of swimming fish. Exp. Fluids 2007, 43, 691–700. [Google Scholar] [CrossRef]
- Dabiri, J.O. Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 2009, 41, 17–33. [Google Scholar] [CrossRef] [Green Version]
- Gharib, M.; Rambod, E.; Shariff, K. A universal time scale for vortex ring formation. J. Fluid Mech. 1998, 360, 121–140. [Google Scholar] [CrossRef] [Green Version]
- Krueger, P.S.; Gharib, M. The significance of vortex ring formation to the impulse and thrust of a starting jet. Phys. Fluids 2003, 15, 1271–1281. [Google Scholar] [CrossRef] [Green Version]
- Krueger, P.S. An over-pressure correction to the slug model for vortex ring circulation. J. Fluid Mech. 2005, 545, 427–443. [Google Scholar] [CrossRef]
- Krueger, P.S. Measurement of propulsive power and evaluation of propulsive performance from the wake of a self-propelled vehicle. Bioinspiration Biomim. 2006, 1, S49. [Google Scholar] [CrossRef]
- Ruiz, L.A.; Whittlesey, R.W.; Dabiri, J.O. Vortex-enhanced propulsion. J. Fluid Mech. 2011, 668, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Shi, L.; Ye, X.; Li, L. A new jellyfish type of underwater microrobot. In Proceedings of the International Conference on Mechatronics and Automation (ICMA 2007), Harbin, China, 5–8 August 2007; pp. 509–514. [Google Scholar] [CrossRef]
- Yang, Y.; Ye, X.; Guo, S. A new type of jellyfish-like microrobot. In Proceedings of the IEEE International Conference on Integration Technology (ICIT’07), Shenzhen, China, 20–24 March 2007; pp. 673–678. [Google Scholar] [CrossRef]
- Shi, L.; Guo, S.; Asaka, K. A novel jellyfish-like biomimetic microrobot. In Proceedings of the IEEE/ICME International Conference on Complex Medical Engineering (CME), Gold Coast, Australia, 13–15 July 2010; pp. 277–281. [Google Scholar] [CrossRef]
- Yeom, S.W.; Oh, I.K. A biomimetic jellyfish robot based on ionic polymer metal composite actuators. Smart Mater. Struct. 2009, 18, 085002. [Google Scholar] [CrossRef]
- Villanueva, A.; Smith, C.; Priya, S. A biomimetic robotic jellyfish (Robojelly) actuated by shape memory alloy composite actuators. Bioinspiration Biomim. 2011, 6, 036004. [Google Scholar] [CrossRef] [PubMed]
- Najem, J.; Sarles, S.A.; Akle, B.; Leo, D.J. Biomimetic jellyfish-inspired underwater vehicle actuated by ionic polymer metal composite actuators. Smart Mater. Struct. 2012, 21, 094026. [Google Scholar] [CrossRef] [Green Version]
- Krieg, M.; Mohseni, K. Thrust characterization of a bioinspired vortex ring thruster for locomotion of underwater robots. IEEE J. Ocean. Eng. 2008, 33, 123–132. [Google Scholar] [CrossRef] [Green Version]
- Krieg, M.; Mohseni, K. Dynamic modeling and control of biologically inspired vortex ring thrusters for underwater robot locomotion. IEEE Trans. Robot. 2010, 26, 542–554. [Google Scholar] [CrossRef]
- Serchi, F.G.; Arienti, A.; Laschi, C. A biomimetic, swimming soft robot inspired by the Octopus vulgaris. Lect. Notes Comput. Sci. 2012, 7375, 349–351. [Google Scholar] [CrossRef] [Green Version]
- Serchi, F.G.; Arienti, A.; Laschi, C. Biomimetic Vortex Propulsion: Toward the New Paradigm of Soft Unmanned Underwater Vehicles. IEEE/ASME Trans. Mechatron. 2013, 18, 484–493. [Google Scholar] [CrossRef]
- Van Buren, T.; Floryan, D.; Brunner, D.; Senturk, U.; Smits, A.J. Impact of trailing edge shape on the wake and propulsive performance of pitching panels. Phys. Rev. Fluids 2017, 2, 014702. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, X.; Yue, D.K.P. Turbulent flow over a flexible wall undergoing a streamwise travelling wave motion. J. Fluid Mech. 2003, 484, 197–221. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Kawachi, K. A numerical study of undulatory swimming. J. Comput. Phys. 1999, 155, 223–247. [Google Scholar] [CrossRef]
- Huera-Huarte, F.J. Propulsión acuática bio-inspirada basada en aleteo: Revisión y últimos avances. DYNA Ingeniería e Industria 2016, 91, 560–563. [Google Scholar] [CrossRef] [Green Version]
- Gazzola, M.; Argentina, M.; Mahadevan, L. Scaling macroscopic aquatic locomotion. Nat. Phys. 2014, 10, 758–761. [Google Scholar] [CrossRef] [Green Version]
- Taylor, G.K.; Nuds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Rohr, J.; Fish, F. Strouhal numbers and optimization of swimming by odontocete cetaceans. J. Exp. Biol. 2004, 207, 1633–1642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Triantafyllou, G.S.; Triantafyllou, M.S.; Grosengaugh, M.A. Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Floch, F.; Phoemsatphawee, S.; Laurens, J.M.; Leroux, J.B. Porpoising foil as a propulsion system. Ocean. Eng. 2012, 39, 53–61. [Google Scholar] [CrossRef]
- Katz, J.; Weihs, D. Hydrodynamic propulsion by large amplitude oscillations of an airfoil with chordwise flexibility. J. Fluid Mech. 1978, 88, 485–497. [Google Scholar] [CrossRef]
- Jones, K.D.; Lai, J.C.S.; Tuncer, I.H.; Platzer, M.F. Computational and experimental investigation of flapping-foil propulsion. In Proceedings of the 1st International Symposium on Aqua Bio-Mechanisms/International Seminar on Aqua Bio-Mechanisms, Tokai University Pacific Center, Honolulu, HI, USA, 27–30 August 2000. [Google Scholar]
- Lan, C.E. The unsteady quasi-vortex-lattice method with applications to animal propulsion. J. Fluid Mech. 1979, 93, 747–765. [Google Scholar] [CrossRef]
- Isogai, K.; Shinmoto, Y.; Watanabe, Y. Effects of dynamic stall on propulsive efficiency and thrust of flapping airfoil. AIAA J. 1999, 37, 1145–1151. [Google Scholar] [CrossRef]
- Triantalyllou, M.S.; Triantafillou, G.S.; Yue, D.K.P. Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Lu, X.Y.; Yin, Z.X. Propulsive performance of a fish-like travelling wavy wall. Acta Mech. 2005, 175, 197–215. [Google Scholar] [CrossRef]
- Blake, R.W. The mechanics of labriform locomotion II. An analysis of the recovery stroke and the overall fin-beat cycle propulsive efficiency in the alglefish. J. Exp. Biol. 1980, 85, 337–342. [Google Scholar]
- Mattheijssens, J.; Marcel, J.P.; Bosschaerts, W.; Lefeber, D. Oscillating foils for ship propulsion. In Proceedings of the 9th National Congress on Theoretical and Applied Mechanics, Brussels, Belgium, 9–11 May 2012. [Google Scholar]
- Kim, J.Y.; Ghajar, A.J.; Tang, C.; Fouth, G.L. Comparison of near-wall treatment methods for high Reynolds number backward-facing step flow. Int. J. Comput. Fluid Dyn. 2005, 19, 493–500. [Google Scholar] [CrossRef]
- Tytell, E.D.; Hsu, C.Y.; Williams, T.L.; Cohen, A.H.; Fauci, L.J. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc. Natl. Acad. Sci. USA 2010, 107, 19832–19837. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Borazjani, I.; Sotiropoulos, F.; Baker, T.V.; Anderson, E.J.; Lauder, G.V. Disentangling the functional roles of morphology and motion in the swimming of fish. Integr. Comp. Biol. 2010, 50, 1140–1154. [Google Scholar] [CrossRef] [Green Version]
- Bhalla, A.P.S.; Griffith, B.E.; Patankar, N.A. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 2013, 9, e1003097. [Google Scholar] [CrossRef] [Green Version]
- Cherukat, P.; Na, Y.; Hanratty, T.J.; McLaughlin, J.B. Direct numerical simulation of a fully developed turbulent flow over a wavy wall. Theor. Comput. Fluid Dyn. 1998, 11, 109–134. [Google Scholar] [CrossRef]
- Maass, C.; Schumann, U. Numerical Simulation of Turbulent Flow over a Wavy Boundary; Fluid Mechanics and Its Applications: Dordrecht, The Netherlands, 1994; pp. 287–297. [Google Scholar]
- You, D.; Wang, M.; Mittal, R.; Moin, P. Large-Eddy simulations of longitudinal vortices embedded in a turbulent boundary layer. AIAA J. 2006, 44, 3032–3039. [Google Scholar] [CrossRef]
- Hasse, C.; Sohm, V.; Wetzel, M. Hybrid URANS/LES turbulence simulation of vortex shedding behind a triangular flameholder. Flow Turbul. Combust. 2009, 83, 1–20. [Google Scholar] [CrossRef]
- Balaras, E. Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations. Comput. Fluids 2004, 33, 375–404. [Google Scholar] [CrossRef]
- Fauci, L.; Peskin, C.S. A computational model of aquatic animal locomotion. J. Comput. Phys. 1988, 77, 85–108. [Google Scholar] [CrossRef]
- Van Rees, W.M.; Gazzola, M.; Koumoutsakos, P. Optimal shapes for anguilliform swimmers at intermediate Reynolds numbers. J. Fluid Mech. 2013, 722, R3. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Leftwich, M.C.; Hsu, C.Y.; Griffith, B.E.; Cohen, A.H.; Smits, A.J.; Hamlet, C.; Fauci, L.J. Role of body stiffness in undulatory swimming: Insights from robotic and computational models. Phys. Rev. Fluids 2016, 1, 073202. [Google Scholar] [CrossRef]
- Griffith, B.E.; Hornung, R.D.; McQueen, D.M.; Peskin, C.S. An adaptive, formally second order accurate version of the immersed boundary method. J. Comput. Phys. 2017, 223, 10–49. [Google Scholar] [CrossRef]
- Griffith, B.E. An accurate and efficient method for the incompressible Navier–Stokes equations using the projection method as a preconditioner. J. Comput. Phys. 2009, 228, 7565–7595. [Google Scholar] [CrossRef]
- Akhtar, I.; Mittal, R.; Lauder, G.V.; Drucker, E. Hydrodynamics of a biologically inspired tandem flapping foil configuration. Theor. Comput. Fluid Dyn. 2007, 21, 155–170. [Google Scholar] [CrossRef]
- Gazzola, M.; Chatelain, P.; van Rees, W.M.; Koumoutsakos, P. Simulations of single and multiple swimmers with non-divergence free deforming geometries. J. Comput. Phys. 2011, 230, 7093–7114. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [Green Version]
- Dong, H.; Bozkurttas, M.; Mittal, R.; Madden, P.; Lauder, G.V. Computational modelling and analysis of the hydrodynamics of a highly deformable fish pectoral fin. J. Fluid Mech. 2010, 645, 345–373. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F.; Tytell, E.D.; Lauder, G.V. Hydrodynamics of the bluegill sunfish c-start escape response: Three-dimensional simulations and comparison with experimental data. J. Exp. Biol. 2012, 215, 671–684. [Google Scholar] [CrossRef] [Green Version]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef] [Green Version]
- Eldredge, J.D. Numerical simulatons of undulatory swimming at moderate Reynolds number. Bioinspir. Biomim. 2006, 1, S19–S24. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Yuming, L.; Yue, D.K.P. Dynamics of a three-dimensional oscillating foil near the free surface. AIAA J. 2006, 44, 2997–3009. [Google Scholar] [CrossRef]
- De Silva, L.W.A.; Yamaguchi, H. Numerical study on active wave devouring propulsion. J. Mar. Sci. Technol. 2012, 17, 261–275. [Google Scholar] [CrossRef] [Green Version]
- Filippas, E.S.; Belibassakis, K.A. Hydrodynamic analysis of flapping-foil thrusters operating beneath the free surface and in waves. Eng. Anal. Bound. Elem. 2014, 41, 47–59. [Google Scholar] [CrossRef]
- Filippas, E.S.; Papadakis, G.P.; Belibassakis, K.A. Free-surface effects on the performance of flapping-foil thruster for augmenting ship propulsion in waves. J. Mar. Sci. Eng. 2020, 8, 357. [Google Scholar] [CrossRef]
- Lauder, G.V.; Tytell, E.D. Hydrodynamics of undulatory propulsion. Fish Biomech. 2006, 23, 425–468. [Google Scholar] [CrossRef]
- Babu, M.N.P.; Krishnankutty, P.; Mallikarjuna, J.M. Experimental study of flapping foil propulsion system for ships and underwater vehicles and PIV study of caudal fin propulsors. In Proceedings of the IEEE/OES Autonomous Underwater Vehicles, Oxford, MS, USA, 6–9 October 2014. [Google Scholar] [CrossRef]
- Drucker, E.G.; Lauder, G.V. Locomotor forces on a swimming fish: Three-dimensional vortex wake dynamics quantified using digital particle image velocimetry. J. Exp. Biol. 1999, 202, 2393–2412. [Google Scholar] [PubMed]
- Drucker, E.G.; Lauder, G.V. A hydrodynamic analysis of fish swimming speed: Wake structure and locomotor force in slow and fast labriform swimmers. J. Exp. Biol. 2000, 203, 2379–2393. [Google Scholar]
- Drucker, E.G.; Lauder, G.V. Locomotor function of the dorsal fin in teleost fishes: Experimental analysis of wake forces in sunfish. J. Exp. Biol. 2001, 204, 2943–2958. [Google Scholar]
- Videler, J.J.; Muller, U.K.; Stamhuis, E.J. Aquatic vertebrate locomotion: Wakes from body waves. J. Exp. Biol. 1999, 202, 2430–3423. [Google Scholar]
- Videler, J.J.; Stamhuis, E.J.; Maijller, U.K.; van Duren, L.A. The scaling and structure of aquatic animal wakes. Integr. Comp. Biol. 2002, 42, 988–996. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muller, U.K.; Stamhuis, E.J.; Videler, J.J. Hydrodynamics of unsteady fish swimming and the effects of body size: Comparing the flow fields of fish larvae and adults. J. Exp. Biol. 2000, 203, 193–206. [Google Scholar] [PubMed]
- Stamhuis, E.J.; Videler, J.J. Quantitative flow analysis around aquatic animals using laser sheet particle image velocimetry. J. Exp. Biol. 1995, 198, 283–294. [Google Scholar] [PubMed]
- Wen, L.; Wang, T.M.; Wu, G.H.; Liang, J. Quantitative thrust efficiency of a self-propulsive robotic fish: Experimental method and hydrodynamic investigation. IEEE/ASME Trans. Mechatron. 2013, 18, 1027–1038. [Google Scholar] [CrossRef]
- Wen, L.; Wang, T.M.; Wu, G.H.; Liang, J. Hydrodynamic investigation of a self-propulsive robotic fish based on a force-feedback control method. Bioinspir. Biomim. 2012, 7, 036012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, E.J.; McGillis, W.R.; Grosengaugh, M.A. The boundary layer of swimming fish. J. Exp. Biol. 2001, 204, 81–102. [Google Scholar]
- Buckles, J.; Hanratty, T.J.; Adrian, R.J. Turbulent flow over a large-amplitude wavy surface. J. Fluid Mech. 1984, 140, 27–44. [Google Scholar] [CrossRef]
- Kuzan, J.D.; Hanratty, T.J.; Adrian, R.J. Turbulent flows with incipient separation over solid waves. Exp. Fluids 1989, 7, 88–98. [Google Scholar] [CrossRef]
- Hudson, J.D. The Effect of a Wavy Boundary on Turbulent Flow. Ph.D. Thesis, University of Illinoids Urbana, Champaign, IL, USA, 1993. [Google Scholar]
- Hudson, J.D.; Dykhno, L.; Hanratty, T.J. Turbulence production in flow over a wavy wall. Exp. Fluids 1996, 20, 257–265. [Google Scholar] [CrossRef]








| Author | Institution | Propulsion Mode | Source of Inspiration |
|---|---|---|---|
| Cohen [32] | Cornell University, USA | Anguilliform | Lamprey |
| Grillner and Matsushima [33]; Grillner et al. [34] | Karolinska Institute, Sweden | Anguilliform | Lamprey |
| Ayers et al. [35,36,37]; Wilbur et al. [38]; Westphal et al. [39] | Northeastern University, USA | Anguilliform | Lamprey |
| Liu et al. [40] | Zhejiang University, China | Anguilliform | Lamprey |
| Xu et al. [41] | National University of Singapore, Singapore | Anguilliform | Eel/lamprey |
| Crespi et al. [42] | Swiss Federal Institute of Technology, Switzerland | Anguilliform | Sea snake |
| Ijspeert et al. [43]; Ijspeert et al. [44]; Crespi et al. [45] | Swiss Federal Institute of Technology, Switzerland | Anguilliform | Salamander |
| McIsaac and Ostrowski [46,47,48] | University of Western Ontario, Canada | Anguilliform | Eel |
| Lamas et al. [49,50,51] | University of A Coruña, Spain | Anguilliform | Eel |
| Kumph [52] | Massachussets Institute of Technology, USA | Caranguiform | Pike |
| Watts et al. [53,54,55] | University of Glasgow, United Kingdom | Caranguiform | Salmon |
| Hirata et al. [56] | Ship Research Institute Shinkawa, Japan | Caranguiform | Sea bream |
| Heo et al. [57] Li et al. [58] | Konkuk University, Korea Beihang University, China | Caranguiform Hybrid | Mackerel Mackerel |
| Barrett [11]; Barrett et al. [59]; Anderson and Chabra [60] | Massachussets Institute of Technology, USA | Thunniform | Tuna |
| Liang et al. [61]; Liang et al. [62]; Liang et al. [63]; Wang et al. [64]; Liu et al. [65] | Beihang University, China | Thunniform | Tuna |
| Suleman and Crawford [66] Kruusmaa et al. [67] | University of Victoria, Canada Tallinn University of Technology, Estonia | Thunniform Thunniform | Tuna Tuna |
| Nakashima et al. [68]; Nakashima et al. [69]; Nakashima et al. [70]; Nakashima et al. [71] | Tokyo Institute of Technology, Japan | Thunniform | Dolphin |
| Yu et al. [72]; Yu et al. [73]; Yu et al. [74]; Shen et al. [75]; Shen et al. [76]; Liu et al. [77] | Chinese Academy of Sciences, China | Thunniform | Dolphin |
| Dogangil et al. [78]; Dogangil et al. [79] | Istanbul Technical University, Turkey | Thunniform | Dolphin |
| Ho and Lee [80] | Konkuk University, South Korea | Thunniform | Dolphin |
| Aghbali et al. [81] | College of Engineering, Iran | Thunniform | Shark |
| Long et al. [82] | Vassar College, USA | Thunniform | Shark |
| Kodati et al. [83]; Kodati et al. [84] | University of Delaware, USA | Ostraciiform | Boxfish |
| Gordon et al. [85] | University of California, USA | Ostraciiform | Boxfish |
| Hu et al. [86] | Peking University, China | Ostraciiform | Boxfish |
| Anderson et al. [87] | Massachussets Institute of Technology, USA | Ostraciiform | Flapping foil |
| Read et al. [88] | Massachussets Institute of Technology, USA | Ostraciiform | Flapping foil |
| Yamamoto et al. [89] | Mitsubishi Heavy Industries, Japan | Ostraciiform | Flapping foil |
| Streitlien and Triantafyllou [90] | City College of New York, USA | Ostraciiform | Flapping foil |
| Paterson and Stern [91,92] | University of Lowa, USA | Ostraciiform | Flapping foil |
| Karpouzian et al. [93] | Univ of Southern California, USA | Ostraciiform | Flapping foil |
| Yamaguchi and Bose [94] | University of Tokyo, Japan | Ostraciiform | Flapping foil |
| Saimek and Li [95] | University of Minnesota, USA | Ostraciiform | Flapping foil |
| Herr and Dennis [96] | MA Institute of Technology, USA | Ostraciiform | Flapping foil |
| Guo [97] | Kagawa University, Japan | Ostraciiform | Flapping foil |
| Belibassakis and Politis [98]; Belibassakis and Filippas [99]; Filippas et al. [100]; Koutsogiannakis et al. [101] | National Technical University of Athens, Greece | Ostraciiform | Flapping foil |
| Author | Institution | Propulsion Mode | Source of Inspiration |
|---|---|---|---|
| Kato et al. [102] | Tokai University, Japan | Labriform | Black bass |
| Kato et al. [103] | Tokai University, Japan | Labriform | Sea turtle |
| Litch et al. [104,105] | Massachussets Institute of Technology, USA | Labriform | Sea turtle |
| Kim et al. [106] Salumae et al. [107] | Seoul National University, South Korea Tallinn University of Technology, Estonia | Labriform Labriform | Sea turtle Sea turtle |
| Bozkurttas et al. [108,109] | Franklin W. Olin College of Engineering, USA | Labriform | Sunfish |
| Georgiades et al. [110] | McGill University, Canada | Labriform | Flapping foil |
| Long et al. [111] | Vassar College, USA | Labriform | Flapping foil |
| Sitorus et al. [112] | Bandung Institute of Technology, Indonesia | Labriform | Flapping foil |
| Cai et al. [113] | Beihang University, China | Rajiform | Ray |
| Punning et al. [114] | Tartu Univeristy, Estonia | Rajiform | Ray |
| Chen et al. [115] | University of Virginia, USA | Rajiform | Ray |
| Clark and Smiths [116] | Princeton University, USA | Rajiform | Ray |
| Low, K.H. [117]; Zhang et al. [118,119] | Nanyang Technological University, Singapore | Rajiform | Ray |
| Low and Willy [120] | Nanyang Technological University, Singapore | Rajiform/gymnotiform | Ray/knifefish |
| Low [121]; Low [122]; Hu et al. [123]; Low [124] | Nanyang Technological University, Singapore | Gymnotiform | Knifefish |
| Epstein et al. [125] | Northwestern University, USA | Gymnotiform | Knifefish |
| McIver et al. [126,127] | Northwestern University, USA | Gymnotiform | Knifefish |
| Siahmansouri et al. [128] | University of Tabriz, Iran | Gymnotiform | Knifefish |
| Author | Institution | Propulsion Mode | Source of Inspiration |
|---|---|---|---|
| Gharib et al. [132]; Krueger and Gharib [133]; Krueger [134], Krueger [135], Ruiz et al. [136] | California Institute of Technology, USA | Jet | Piston-cylinder |
| Guo et al. [137]; Yang et al. [138]; Shi et al. [139] | Kagawa University, Japan | Jet | Jellyfish |
| Yeom and Oh [140] | Chonnam National University, South Korea | Jet | Jellyfish |
| Villanueva et al. [141]; Najem et al. [142] | Virginia Tech, USA | Jet | Jellyfish |
| Krieg and Mohseni [143]; Krieg and Mohseni [144] | University of Colorado, USA | Jet | Squid |
| Serchi et al. [145]; Serchi et al. [146] | Scuola Superiore Sant’Anna, Italy | Jet | Octopus |
| Dimension | Reference Parameter | Non-Dimensional Parameter |
|---|---|---|
| Length | ||
| Velocity | ||
| Pressure | ||
| Time | ||
| Gravity |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamas, M.I.; Rodriguez, C.G. Hydrodynamics of Biomimetic Marine Propulsion and Trends in Computational Simulations. J. Mar. Sci. Eng. 2020, 8, 479. https://doi.org/10.3390/jmse8070479
Lamas MI, Rodriguez CG. Hydrodynamics of Biomimetic Marine Propulsion and Trends in Computational Simulations. Journal of Marine Science and Engineering. 2020; 8(7):479. https://doi.org/10.3390/jmse8070479
Chicago/Turabian StyleLamas, M. I., and C. G. Rodriguez. 2020. "Hydrodynamics of Biomimetic Marine Propulsion and Trends in Computational Simulations" Journal of Marine Science and Engineering 8, no. 7: 479. https://doi.org/10.3390/jmse8070479
APA StyleLamas, M. I., & Rodriguez, C. G. (2020). Hydrodynamics of Biomimetic Marine Propulsion and Trends in Computational Simulations. Journal of Marine Science and Engineering, 8(7), 479. https://doi.org/10.3390/jmse8070479






