1. Introduction
The marine ramjet (MRJ) is the nautical equivalent of the aeronautical ramjet, using water instead of air as the main working fluid. In both cases, the incoming ambient fluid enters the propulsor due to the motion of the vehicle, without using means such as pumps or compressors. The flow is first dynamically pressurized due to slowing down in the inlet, then additional energy is introduced, after which the flow is expanded and accelerated in a nozzle, generating thrust. Different concepts for marine ramjet propulsion are summarized by Gany [
1]. In the case of the marine ramjet type investigated in this research, energy is added not in the form of fuel combustion or chemical reaction but by introducing a secondary gaseous fluid, reducing the mean density of the flow, making it compressible, and adding its expansion work. While the main fluid is water (mass flow rate,
), the secondary fluid is traditionally compressed air (mass flow rate
). The present study focuses on the replacement of the compressed air with an on-board pressure liquefied gas (LG, flow rate,
), boiling at superheat conditions and generating gas bubbles upon injection into the water. The use of LG is a means of a compact storage of gas when ambient air is not readily available (particularly for underwater vehicles with no access to air). Schematic illustration of the two-phase marine ramjet is depicted in
Figure 1.
The two-phase marine ramjet concept received some attention already in the 1940s (Tangren et al. [
2]). It was studied more extensively in the 1960s and 1970s (Schell and Ornof [
3], Muench and Garrett [
4], Mottard and Shoemaker [
5], Witte [
6], Grainer [
7], Amos et al. [
8], and Chernyy [
9]). Comprehensive research on MRJ was conducted at the Technion—Israel Institute of Technology in the 1990s and 2000s. It included static tests and dynamic experiments in a specially constructed 10 m diameter pool (Albagli [
10] and Koren [
11]), and patents by Varshay and Gany [
12,
13]. Sea trials with a 4 m boat were conducted as well (Valensy [
14]). Application of the concept for waterjet boosting was studied by Gany and Gofer [
15]. Fundamental theoretical considerations of the thermodynamic cycle of the MRJ were presented by Gany [
16]. Albagli and Gany [
17] and Mor and Gany [
18] conducted analyses of homogenous quasi-one-dimensional two-phase compressible flow related to the MRJ. The models included wall friction, relative velocities, and heat and mass transfer between phases, leading to a system of nine ordinary differential equations (ODEs). The numerical solution of this equation system has been incorporated into a simulator, used for performance evaluation in the present study. More recently research has been conducted by Chahine and collaborators at Dynaflow [
19,
20,
21], by Gowing et al. [
22], and by researchers in China [
23,
24]. Other works on marine ramjet have focused on water reactive chemicals such as lithium, triethyl aluminum [
25], thermite fuel [
26], and metallized fuels containing, e.g., magnesium or aluminum [
27,
28,
29,
30]. The present research deals with a non-reactive operation.
The operating principle of the marine ramjet as illustrated by
Figure 1, is as follows: water at ambient conditions enters the MRJ inlet due to the vessel motion. The water velocity reduces and its pressure increases within the diffuser (inlet) due to the enlargement of the flow cross section. This process is typical to ramjets, in general. A secondary compressible fluid (gas), with significantly lower density, is injected at the mixing chamber into the mainstream flow. Expansion of the secondary fluid from the mixing chamber pressure to the exhaust pressure (typically the ambient pressure) while moving as a multiphase mixture along the nozzle, provides expansion work, which, by a proper design of the nozzle, is converted into an increase in the kinetic energy (i.e., velocity) of the exhaust multiphase jet, hence producing thrust. Similarly to the aeronautical jet engine, the thrust developed by the MRJ is equal to the difference between the outgoing and incoming momentum flow rate. With a proper design of the nozzle (exit pressure equal to the ambient pressure) and accounting for the fact that the mass fraction of the gas component in the flow is very low (typically, less than 1%) compared to the water flow rate, the thrust equation is approximated as follows:
where
F is the thrust and
and
are the exit jet and incoming flow velocities, respectively.
2. Thermodynamic Cycle
When the gas component is air or any non-condensable and non-soluble gas, the expansion process can be assumed to be isothermal, due to the rapid heat transfer between the small bubbles and surrounding water, and accounting for the relatively small mass fraction of air and the very large overall heat capacity of the water (see Gany [
16] and Albagli and Gany [
17]).
Figure 2 presents the ideal thermodynamic power cycle per unit mass of air; it assumes adiabatic compression of air from the ambient pressure
Pa and temperature
Ta (point a) to the mixing chamber pressure
Pmix (point comp), followed by isobaric cooling (path comp to mix), and isothermal expansion of bubbles due to dropping from the mixing chamber pressure (point mix) to the exit pressure (point a, assuming that the exit pressure is equal to the ambient pressure), while flowing through the nozzle. The ideal specific expansion work (per unit mass of air or gas), is given in Equation (2):
In Equation (2) R is the specific gas constant, Ta is the ambient temperature, Pmix the pressure in the mixing chamber, and Pa is the ambient pressure.
From this mechanistic explanation, assuming a similar characteristic bubble size for all gases examined, it is implied that the thrust generated is proportional to the volume of injected gas rather than to its mass. For this reason, when employing a gas or LG other than air, its mass flow rate is first converted to a volume-equivalent air mass flow rate (its mass flow rate divided by its molecular weight and multiplied by that of air), allowing comparison between different operating gases on an equal scale. The gas to the water mass ratio is then given as the air (or air-equivalent) mass flow rate divided by the water mass flow rate (hereafter, a/w = ).
As mentioned before, for submerged marine vessels employing MRJ propulsion, there is a need for an onboard compact gas source due to the lack of access to ambient air.
Pressure liquefied gas (LG) can be compactly stored as a liquid in a self-contained unit by pressurizing it to its vapor pressure and above at the room (storing) temperature; thereby it can serve as a source of gas instead of compressed air, enabling the MRJ submerged operation. Upon injection as small droplets into the flowing water within the mixing chamber, it boils (being in superheat conditions), forming bubbles, which both grow due to phase change and expand due to the pressure gradient while the multiphase mixture is flowing through the exhaust nozzle.
Figure 3 presents the ideal simplified thermodynamic cycle of the LG for the boiling-expansion driven MRJ. The liquefied gas reduces in pressure as it is injected (
Figure 3, A to B, at constant enthalpy); boils in the mixing chamber (B to C, constant pressure/temperature); then heats up in the mixing chamber to the water (ambient) temperature at constant pressure (C to D), and finally expands isothermally from the mixing chamber pressure to the ambient pressure, while moving along the nozzle (D to E). The closure of the cycle, namely, the liquefaction process of the gas, storing it as a liquid at a higher pressure (E to D to F and back to A), is conducted externally at the liquefaction plant. The maximal work that can be done by the gas on the fluid flowing through the propulsor in such an ideal cycle, consists of two processes: first is an increase in volume due to phase change, when the LG is boiling, namely, turning into vapors (path ABCD). Since the initial size of a droplet is some two orders of magnitude smaller than the resulting bubble, the potential work done by the growing bubble (per unit mass) at constant pressure can be approximated by
Pmixv =
RTa, and denoted as “Potential work due to phase change” in
Figure 3. The other process, denoted as “Expansion work” in
Figure 3 (path DE), is the work due to expansion of bubbles because of the pressure drop from
Pmix to
Pa while moving in the nozzle. The work done on the fluid during the latter process is formulated in Equation (2). The ideal work per unit mass of the LG, combining the two contributions, is approximated by Equation (3).
The process of the phase change (boiling) of a superheated pressure liquefied gas (propane) when injected into a host liquid (water) was studied by Haustein et al. [
31], revealing 200-folds volume growth within 30 ms (
Figure 4). It is noted that in the turbulent flow and convection regime due to the velocity difference between the phases within the propulsor, boiling is expected to be faster than in quiescent or natural floating conditions characteristic to laboratory experiments.
Realizing the potential additional work associated with the phase change of an LG compared to compressed air may not be straightforward because of the non-equilibrium (transient) phase change process. In this study, a certain thrust advantage has been indicated with a boiling liquefied gas at high velocities, in comparison to compressed air propulsion. However, this method is not devoid of disadvantages. The main disadvantage is that, as a self-contained unit carrying its own “fuel”, operation time/range is rather limited. Additionally, in underwater operation the entire unit’s surface is subject to drag.
In general, both the air and LG propelled MRJs have a moderate thrust margin compared to the vessel drag, making them feasible for operation at medium/high but not at very high cruise speed range. See discussion in Gany [
1]. In addition, similarly to the aeronautical ramjet, the MRJ has to be brought to an optimal work range (velocity) that varies with operating and ambient conditions (working fluids, ambient temperature, and depth). This aspect of acceleration of the MRJ to a working velocity is not dealt with in this study, though different methods exist (e.g., the use of rocket boosters or compressed air for launching).
3. Experimental Setup
The tow pool setup employed in this experimental investigation was originally designed and constructed by Varshay [
32]; it was modified by Koren [
11] for controlled MRJ operation with compressed air (up to 50 g/s of air) at low/medium velocities (up to 13 m/s, about 25 knots). Additional modifications were made in the present investigation to adapt the system for LG storage, supply, and operation, as well as to increase its velocity up to 18 m/s (about 35 knots). The 10 m diameter pool is presented in
Figure 5.
Figure 6 shows a cross-sectional schematic illustration of the system: a computer-controlled 7.5 kW central electric motor rotates an arm supporting the test MRJ propulsor submerged within the circular water-channel at a preset velocity. The path of rotation was 30 m long (diameter of rotation 9.55 m), the depth of the pool was about 0.8 m, and the width varied between a minimum of 1 m and a maximum of 2 m because of the hexagonal structure of the walls. This results in a blockage ratio of 0.5% and less. Baffles located in the pool about 2.5 m apart were aimed at reducing the water circulation due to the MRJ propulsor rotation. With the minimum free path between baffles at a cross-section (0.45 m wide), the blockage ratio was about 1%.
The propulsor’s supporting arm also functioned to accommodate both the compressed air and LG supply pipes. As mentioned, a computer controlled central electric motor was a priori set to rotate the supporting arm to yield the determined preset speed of the propulsor in the water. The angular velocity of the arm, moment, and power consumption of the motor were instantaneously recorded, enabling determination of the resistance force (drag). The air supply was measured by a choked-flow orifice meter, whereas the LG average flow rate was measured by the LG mass loss during a test divided by the test duration. Pressure was measured during operation with calibrated transducers at different locations along the MRJ propulsor, as depicted in
Figure 7. The entire data were transferred through an optical encoder, located at the center axis of the rotating arm, to a computer, where they were recorded by a custom Labview program. This data transfer method limited the sampling rate to 1.25 Hz, so results were later time-averaged to reduce noise-induced errors.
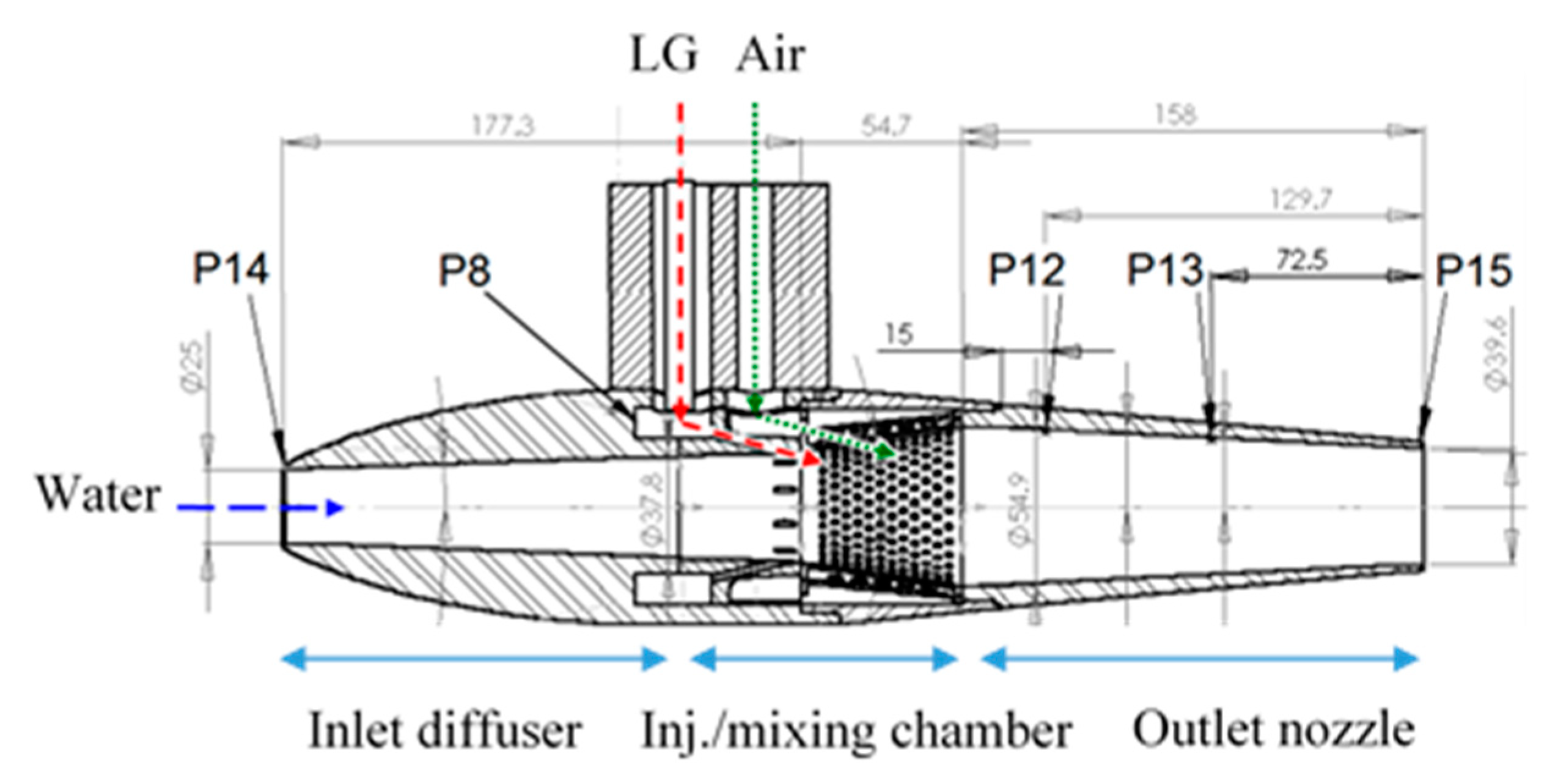
The overall dimensions of the MRJ propulsor in our experiments are: the maximum outer diameter 80 mm, overall length 390 mm, of which the mixing chamber takes up 55 mm, and the nozzle 158 mm. The inlet diameter was 25 mm, the nozzle exit diameter was either 39.6 mm or 32 mm, and the other internal dimensions can be seen in
Figure 7. Pressure measurements in the MRJ propulsor were as follows: P14 at the inlet (for estimating the effective capture cross-section); P12, P13, and P15 along the nozzle; P8 was taken within the LG preinjection chamber (for verification that the LG is in liquid form, i.e., above saturation pressure, before injection).
3.1. Test Procedure
The MRJ can operate at low speed but has a significant advantage at the medium/high speeds. Hence, the central electric motor was adjusted to yield speeds of up to 18 m/s (about 35 knots) by optimizing the transmission.
Liquefied gas was delivered to the MRJ propulsor from a high-pressure tank, fixed to the central axis, as shown in
Figure 6. The tank was periodically repressurized with nitrogen (inert gas) to maintain a roughly constant flow rate and avoid boiling prior to injection, thereby delivering the LG into the primary water flow as a liquid. As shown in
Figure 6 and
Figure 7, either LG or compressed air could be introduced into the water flow within the mixing chamber. The duration of the liquefied gas injection was determined by a remotely controlled pneumatic valve, whereas when conducting tests with compressed air, it was remotely controlled by a pressure regulator and a valve on the main supply line. The liquefied gas was injected into the water at an angle of 20 degrees from the downstream direction, through an injection ring with up to ten 0.8 mm jets, thereby enabling the presetting of the radial distribution and an air-equivalent mass flow rate from 3 to 30 g/s. The liquefied gas stream would then break up and boil in the primary water flow. In the following chapter, all experiments were conducted with 5 injection jets, maintaining good distribution and an adequate LG flow rate. When using air, it was injected through a fine mesh (1 mm holes) at the inner walls, distributing the incoming bubbles along the mixing chamber. The difference in the injection way between liquefied gas and air resulted from the different densities of these two fluids and the way the bubbles were formed. For the liquefied gas, a relatively small injection area was sufficient. In addition, the gas bubbles volume increased gradually along the chamber while the LG was boiling. Air required a larger injection area and spreading to avoid an abrupt increase in volume and back pressure.
For our laboratory investigation, characterization of the process, and concept demonstration, two types of readily available liquefied gases, butane and R134a (synthetic refrigerant gas), were used in the experiments. In practical applications, non-polluting LGs such as liquid air may be employed. The physical properties of the LGs used are presented in the following sections. Injection pressures of the LGs were above saturation in the preinjection chamber (P8 label in
Figure 7), around 7–8 atm for R134a and 3 atm for butane, whereas the mixing chamber pressure was typically about 1.5 atm (absolute), depending on inlet flow and injection conditions. Compressed air source pressure was typically around 5 atm (i.e., above twice the mixing chamber pressure) to allow flow rate measuring via a choked-flow orifice.
The LG flow rate was measured by weighing the liquefied gas tank before and after every experiment and dividing by the injection duration (retrieved from the pressure readings). The uncertainty associated with this averaged flow-rate measurement is discussed in the next subsection.
Each experiment was conducted as follows: water temperature was measured at several locations in the pool, and the LG tank (for liquefied gas runs) was weighed. The MRJ propulsor was then accelerated by the central electric motor until it reached the desired velocity; after a short duration at constant velocity, liquefied gas (or compressed air) was injected for 13–16 s (equivalent to at least 6 complete rotations around the tow pool). After which the MRJ propulsor was slowed down to a standstill, and the LG tank was weighed again. All data were recorded, plotted, and saved in preparation for the next run. The liquefied gas experiments were immediately followed (or preceded) by an experiment with compressed air, for comparison under similar conditions (water level in the pool, water temperature, velocity, and flow rate).
3.2. Uncertainty of Results
As explained in the previous section, the data collected included pressure readings, drag readings, airflow rate (in compressed air experiments), or LG tank weight measurements (in LG experiments).
Injection time was 13 s or above and a reading was taken every 0.8 s, leading to a 6% uncertainty in average mass flow-rate. In the LG tests, all experiments were within a 15% average flow rate. For comparison of different experiments, the results were interpolated to the average value.
Calibration of the pressure readings led to a bias-error up to 0.05 atm (5 kPa). Drag measurements were accompanied by a high level of noise and therefore averaging over a minimum of 11 data points was used, leading to an error of less than 1 N in the average value. Generally, lower errors were associated with higher velocities, as the signal-to-noise ratio increased with the increase in drag.
5. Conclusions
This study is one of a few attempts to adapt the marine ramjet principle to underwater operation, and the only one known to use the method of phase transfer. Storing of a pressure liquefied gas (LG) at a superheat condition can serve as a compact onboard source of bubbles for a submerged propulsion unit, resulting from the boiling of the LG droplets injected into the water stream within the propulsor. Thermodynamic analysis of the power cycle reveals a potential for additional expansion work because of the growing bubbles due to phase change and, hence, more thrust compared to air at similar air-equivalent flow rates
Experiments employing two liquefied gases, a refrigerant gas R134a and butane, were conducted in a 10-m diameter tow pool with a submerged propulsor moving at a range of velocities from about 7 to 18 m/s (14–35 knots). A comparison to the use of air revealed comparable results with a somewhat lower performance of the LG at the low speed range. However, at velocities exceeding about 15 m/s, the liquefied gases demonstrated a thrust advantage over air, reaching a peak increase of up to 19% for R134a and 40% for butane. This additional thrust may be attributed to the phase change process, as shown in the thermodynamic analysis. Two outlet nozzles were tested (39.6 and 32 mm diameter), revealing better performance for the larger nozzle. This is one of the parameters, which shows that efficient operation of the multiphase marine ramjet, in general, and realization of the phase-change expansion work of LG, in particular, need a careful design. It should minimize the blockage effect and highly non-equilibrium situations and ensure complete boiling of the LG within the propulsor before expulsion through the outlet nozzle.