On Power-Absorption Degrees of Freedom for Point Absorber Wave Energy Converters
Abstract
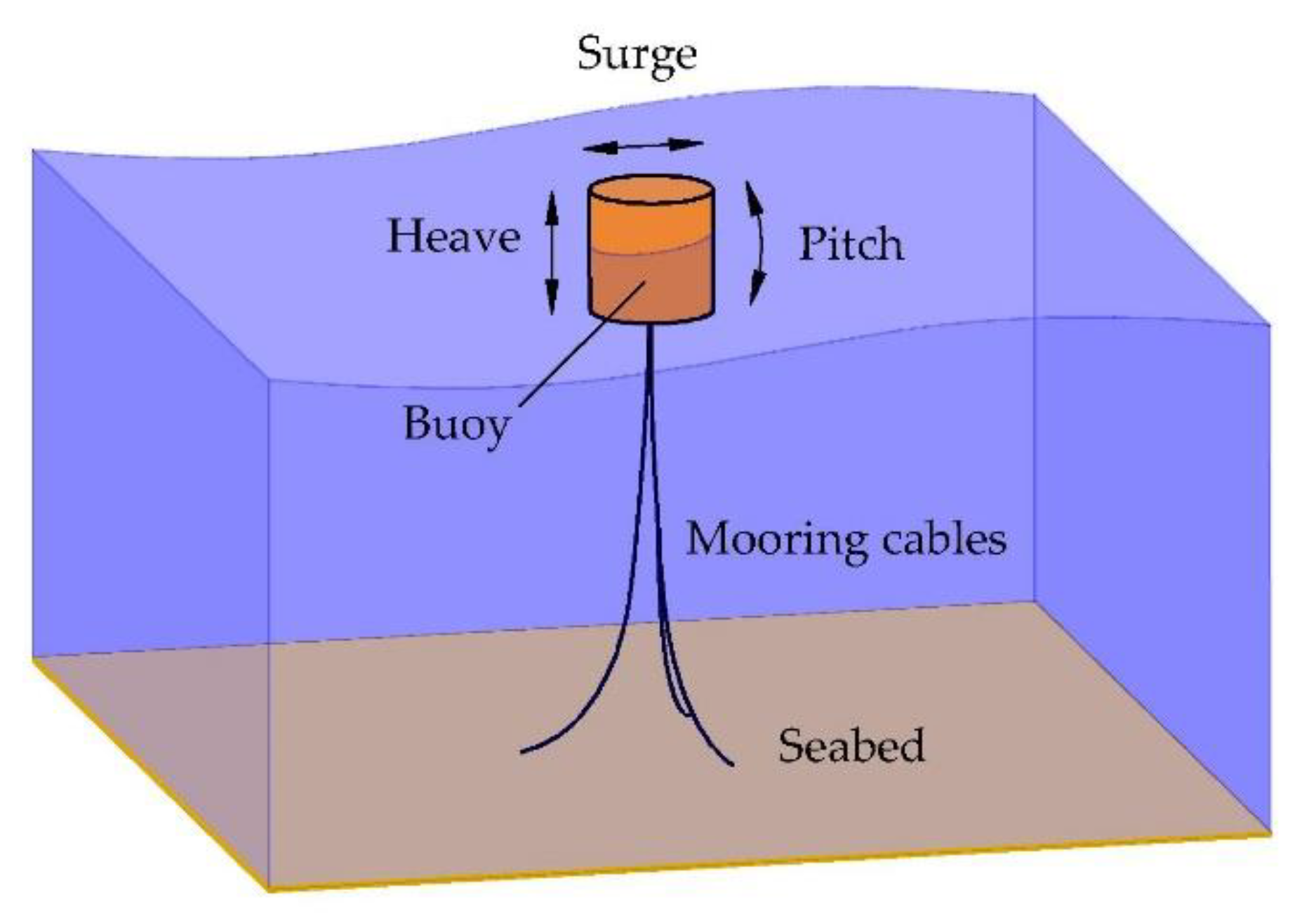
:1. Introduction
2. Methods
2.1. Power Absorption in Surge
2.2. Power Absorption in Pitch
2.3. Power Absorption in Heave
2.4. Absorbed Power
2.5. Setting of the Analysis Process
3. Results
3.1. Maximum Power Absorption in Surge
3.2. Maximum Power Absorption in Pitch
3.3. Maximum Power Absorption in Heave
3.4. Comparison of Power Absorption between Different Power-Absorption Degrees of Freedom
4. Conclusions
Funding
Conflicts of Interest
Nomenclature
| a5 | Non-dimensional rotational inertia of the buoy in pitch. |
| aij (j = 1, 3, 5) | Non-dimensional mass of the internal mass. |
| b | Non-dimensional depth of the center of mass. |
| C | Damping coefficient matrix. |
| cri | Radiation damping coefficient. |
| cu, ku | Damping coefficient and spring stiffness of the PTO system. |
| CWR | Capture width ratio. |
| dg | Depth of center of mass of the buoy. |
| F | Excitation force column. |
| F0 | Excitation force column per unit wave amplitude. |
| Fej (j = 1, 3) | Excitation force in surge and heave, respectively. |
| Frj (j = 1, 3) | Radiation force in surge and heave, respectively. |
| Fu | Control force applied on the buoy by the PTO system. |
| g | Gravitational acceleration. |
| Hs | Significant wave height. |
| I5max | Maximum rotational inertia in pitch. |
| Ii5 | Rotational inertia of the internal mass in pitch. |
| It5 | Total rotational inertia of the buoy and the internal mass. |
| K | Stiffness matrix. |
| ks3, τs5 | Hydrostatic restoring stiffness in heave and pitch. |
| m | Mass of the buoy. |
| M | Mass matrix. |
| m0 | Zero-order moment of the motion-amplitude spectrum. |
| mij (j = 1, 3) | Mass the internal mass in surge and heave, respectively. |
| Me5, Mr5 | Excitation and radiation moment in pitch. |
| mlp, zlp | Concentrated mass and z coordinate of the p-th point on the leftmost edge. |
| mrij | Added mass. |
| mrq, zrq | Concentrated mass and z coordinate of the q-th point on the rightmost edge. |
| mt | Total mass of the buoy and the internal mass. |
| P | Time-averaged absorbed power. |
| Pin | Energy flux per unit wave crest. |
| Pn | Time averaged absorbed power at the n-th discretized wave frequency. |
| r, d | Radius and draft of the buoy. |
| Sh | Wave spectrum. |
| Sm | Motion-amplitude spectrum. |
| Te | Energy period. |
| V | Displaced volume. |
| W | Width of buoy. |
| x | Displacement column. |
| xcb | x coordinate of the center of buoyancy in the fixed coordinate system G-xyz. |
| xicb, yicb, zicb | Coordinate of the center of buoyancy in the body-fitted coordinate system G-xiyizi. |
| xij (j = 1, 3) | Displacement of the internal mass in surge and heave, respectively. |
| xj (j = 1, 3) | Displacement of the buoy in surge and heave, respectively. |
| xr1, xr3 | Relative displacement amplitude between the internal mass and the buoy. |
| xs | Significant motion amplitude. |
| zl, zr | z coordinate of the center of mass containing all mass points in the leftmost and rightmost edges. |
| Δω | Sampling interval of the discretized frequency. |
| θ5, θi5 | Angular displacement of the buoy and the internal mass in pitch. |
| ρ | Water density. |
| ω | Wave frequency. |
| ωn, An | Frequency and amplitude of the n-th discretized regular-wave component. |
References
- Miquel, A.M.; Lamberti, A.; Antonini, A.; Archetti, R. The MoonWEC, a new technology for wave energy conversion in the Mediterranean sea. Ocean Eng. 2020, 217, 107958. [Google Scholar] [CrossRef]
- Davidson, J.; Genest, R.; Ringwood, J.V. Adaptive Control of a Wave Energy Converter. IEEE Trans. Sustain. Energy 2018, 9, 1588–1595. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://www.emec.org.uk/marine-energy/wave-developers/ (accessed on 8 September 2020).
- López, M.; Ramos, V.; Rosa-Santos, P.; Taveira-Pinto, F. Effects of the PTO inclination on the performance of the CECO wave energy converter. Mar. Struct. 2018, 61, 452–466. [Google Scholar] [CrossRef]
- Lejerskog, E.; Boström, C.; Hai, L.; Waters, R.; Leijon, M. Experimental results on power absorption from a wave energy converter at the Lysekil wave energy research site. Renew. Energy 2015, 77, 9–14. [Google Scholar] [CrossRef]
- Liang, C.; Zuo, L. On the dynamics and design of a two-body wave energy converter. Renew. Energy 2017, 101, 265–274. [Google Scholar] [CrossRef]
- Cordonnier, J.; Gorintin, F.; De Cagny, A.; Clément, A.H.; Babarit, A. SEAREV: Case study of the development of a wave energy converter. Renew. Energy 2015, 80, 40–52. [Google Scholar] [CrossRef]
- Korde, U.A. Systems of reactively loaded coupled oscillating bodies in wave energy conversion. Appl. Ocean Res. 2003, 25, 79–91. [Google Scholar] [CrossRef]
- Brekken, T.K.A.; Hapke, H.M.; Stillinger, C.; Zrudell, J. Machines and drives comparison for low-power renewable energy and oscillating applications. IEEE Trans. Energy Conver. 2010, 25, 1162–1170. [Google Scholar] [CrossRef]
- French, M.J.; Bracewell, R. The reduction of structural costs in obtaining energy from sea-waves. In Proceedings of the Fourth International Offshore Mechanics & Arctic Engineering Symposium Conference, ASME, Dallas, TX, USA, 17 February 1985. [Google Scholar]
- Budar, K.; Falnes, J. A resonant point absorber of ocean-wave power. Nature 1975, 256, 478–479. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Zou, S.; Robinett, R.D.; Bacelli, G.; Wilson, D.G.; Coe, R.; Korde, U. Multiresonant feedback control of a three-degree-of-freedom wave energy converter. IEEE Trans. Sustain. Energy 2017, 8, 1518–1527. [Google Scholar] [CrossRef]
- Newman, J.N. The interaction of stationary vessels with regular waves. In Proceedings of the 11th Symposium on Naval Hydrodynamics, London, UK, 28 March–2 April 1976; pp. 491–501. [Google Scholar]
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Mei, C.C. Power extraction from water waves. J. Ship Res. 1976, 20, 63–66. [Google Scholar]
- Falnes, J. Wave-energy conversion through relative motion between two single-mode oscillating bodies. J. Offshore Mech. Arct. 1999, 121, 32–38. [Google Scholar] [CrossRef]
- Grilli, A.R.; Merrill, J.; Grilli, S.T.; Spaulding, M.L.; Cheung, J.T. Experimental and numerical study of spar buoy-magnet/spring oscillators used as wave energy. In Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Davis, E.; Ertekin, R.C.; Riggs, H. Buoy Based WEC Device to provide low power to sensors. In Proceedings of the ASME 28th International Conference on Ocean, Offshore, and Artic Engineering, Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar]
- Ocean Power Technologies. PowerBuoy. Available online: http://www.oceanpowertechnologies.com (accessed on 9 August 2020).
- Symonds, D.; Davis, E.; Ertekin, R.C. Low-power autonomous wave energy capture device for remote sensing and communications applications. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010. [Google Scholar]
- Pizer, D. Numerical Modeling of Wave Energy Absorbers; University of Edinburgh: Edinburgh, UK, 1994. [Google Scholar]
- Gemme, D.A.; Greene, H.R.; Tucker, T.A.; Sepe, R.B.; Bastien, S.P. Hybrid Resonant Wave Energy Harvesting Buoy for Sensor Applications. In 2013 OCEANS-San Diego; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Chai, H.; Guan, W.; Wan, X.; Li, X.; Zhao, Q.; Liu, S. A wave power device with pendulum based on ocean monitoring buoy. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 052013. [Google Scholar] [CrossRef]
- Tarrant, K.R. Numerical Modelling of Parametric Resonance of a Heaving Point Absorber Wave Energy Converter. Ph.D. Thesis, Department of Mechanical and Manufacturing Engineering, Trinity College, Dublin, Ireland, 2015. [Google Scholar]
- Yavuz, H. On control of a pitching and surging wave energy converter. Int. J. Green Energy 2011, 8, 555–584. [Google Scholar] [CrossRef]
- Oetinger, D.; Magaña, M.E.; Sawodny, O. Centralised model predictive controller design for wave energy converter arrays. IET Renew. Power Gen. 2015, 9, 142–153. [Google Scholar] [CrossRef]
- Genest, R.; Ringwood, J.V. A critical comparison of model-predictive and pseudospectral control for wave energy devices. J. Ocean Eng. Mar. Energy 2016, 2, 485–499. [Google Scholar] [CrossRef] [Green Version]
- Henriques, J.C.C.; Lopes, M.F.P.; Gomes, R.P.F.; Gato, L.M.C.; Falcão, A.F.O. On the annual wave energy absorption by two-body heaving WECs with latching control. Renew. Energy 2012, 45, 31–40. [Google Scholar] [CrossRef]
- Falnes, J. Ocean. Waves and Oscillating Systems: Linear Interaction Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Wu, J.; Yao, Y.; Zhou, L.; Göteman, M. Real-time latching control strategies for the solo Duck wave energy converter in irregular waves. Appl. Energy 2018, 222, 717–728. [Google Scholar] [CrossRef]
- Wu, J.; Ni, Z. On the design of an integrated system for wave energy conversion purpose with the reaction mass on board. Sustainability 2020, 12, 2865. [Google Scholar] [CrossRef] [Green Version]
- Parks, P.C. Wedges, Plates and Waves—Some Simple Mathematical Models of Wave Power Machines. In Power from Waves; Academic Press: Cambridge, MA, USA, 1980; pp. 251–285. [Google Scholar]
- Falnes, J.; Hals, J. Heaving buoys, point absorbers and arrays. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 246–277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
















© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J. On Power-Absorption Degrees of Freedom for Point Absorber Wave Energy Converters. J. Mar. Sci. Eng. 2020, 8, 711. https://doi.org/10.3390/jmse8090711
Wu J. On Power-Absorption Degrees of Freedom for Point Absorber Wave Energy Converters. Journal of Marine Science and Engineering. 2020; 8(9):711. https://doi.org/10.3390/jmse8090711
Chicago/Turabian StyleWu, Jinming. 2020. "On Power-Absorption Degrees of Freedom for Point Absorber Wave Energy Converters" Journal of Marine Science and Engineering 8, no. 9: 711. https://doi.org/10.3390/jmse8090711
APA StyleWu, J. (2020). On Power-Absorption Degrees of Freedom for Point Absorber Wave Energy Converters. Journal of Marine Science and Engineering, 8(9), 711. https://doi.org/10.3390/jmse8090711



