Meshless Model for Wave-Induced Oscillatory Seabed Response around a Submerged Breakwater Due to Regular and Irregular Wave Loading
Abstract
:1. Introduction
2. Theoretical Model
2.1. Wave Model
2.2. Seabed Model
2.3. Mesh-Free Model for a Porous Seabed
3. Regular Wave-Induced Soil Response around a Submerged Breakwater
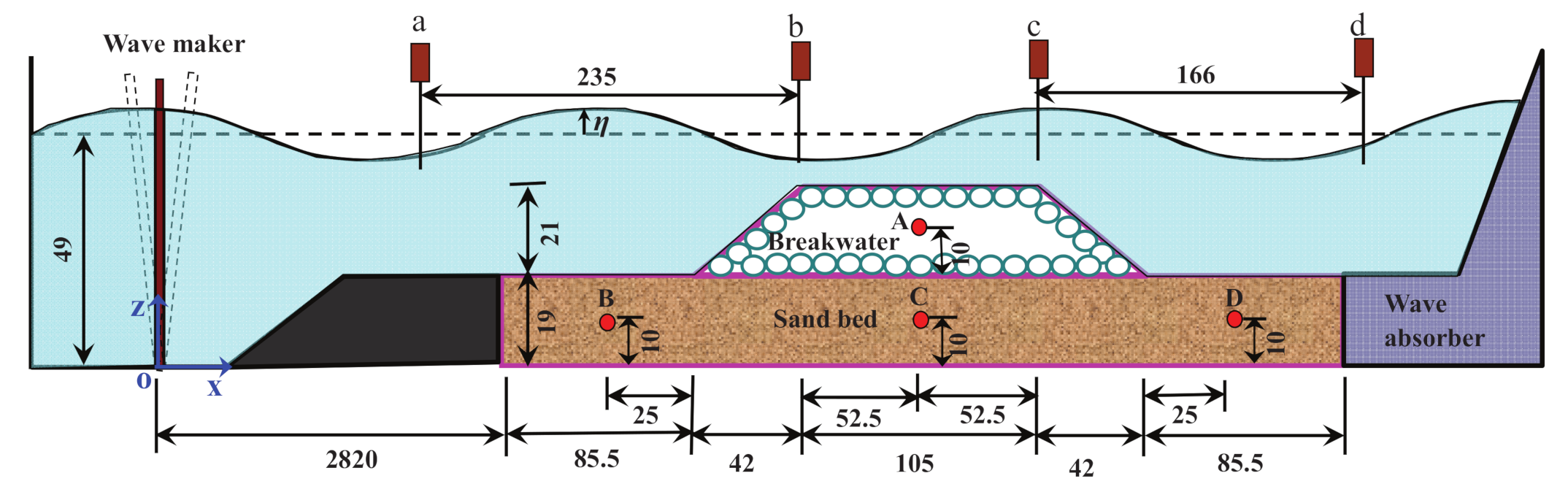
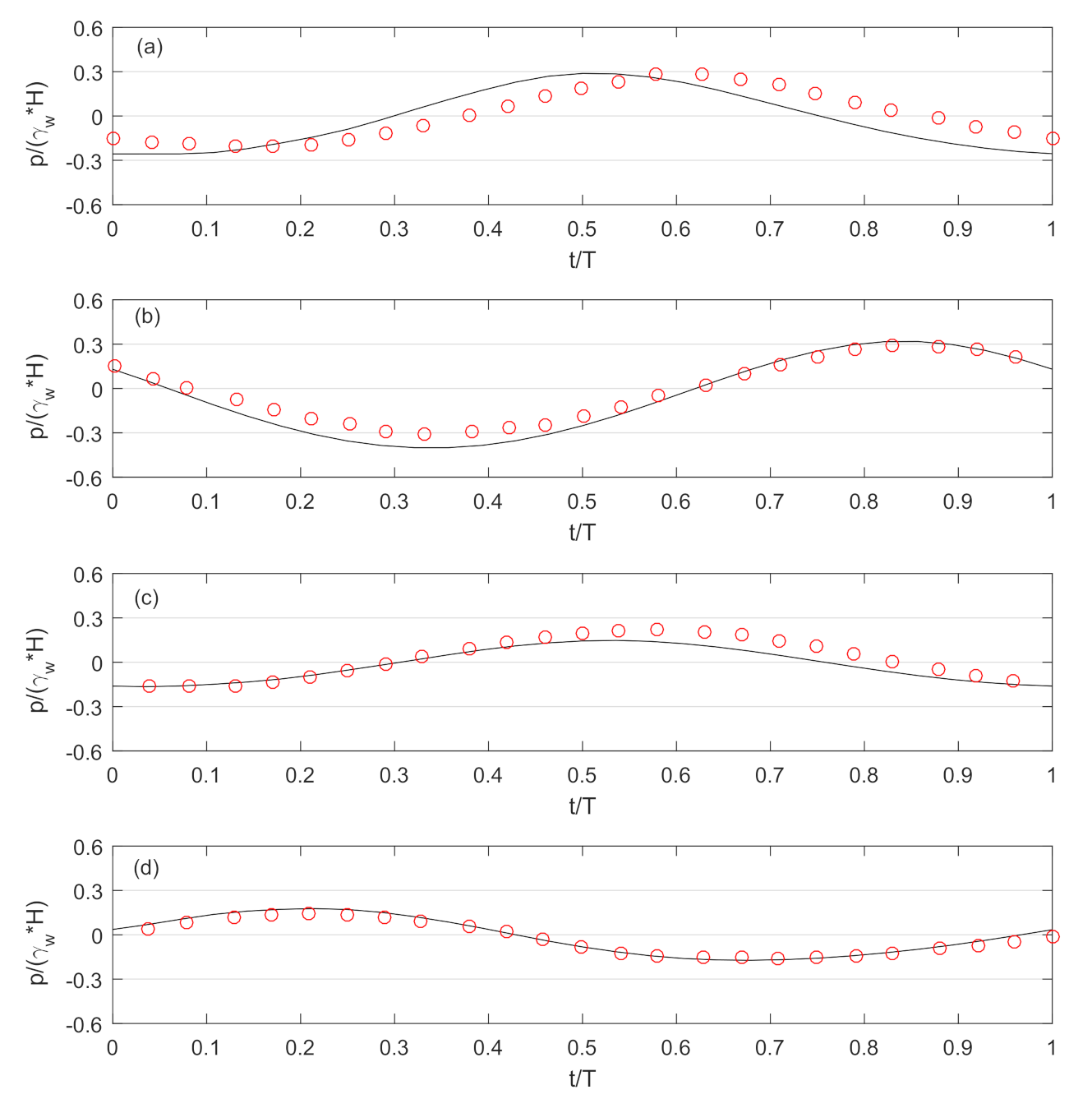
3.1. Validation of the Present Model with Regular Wave Loading
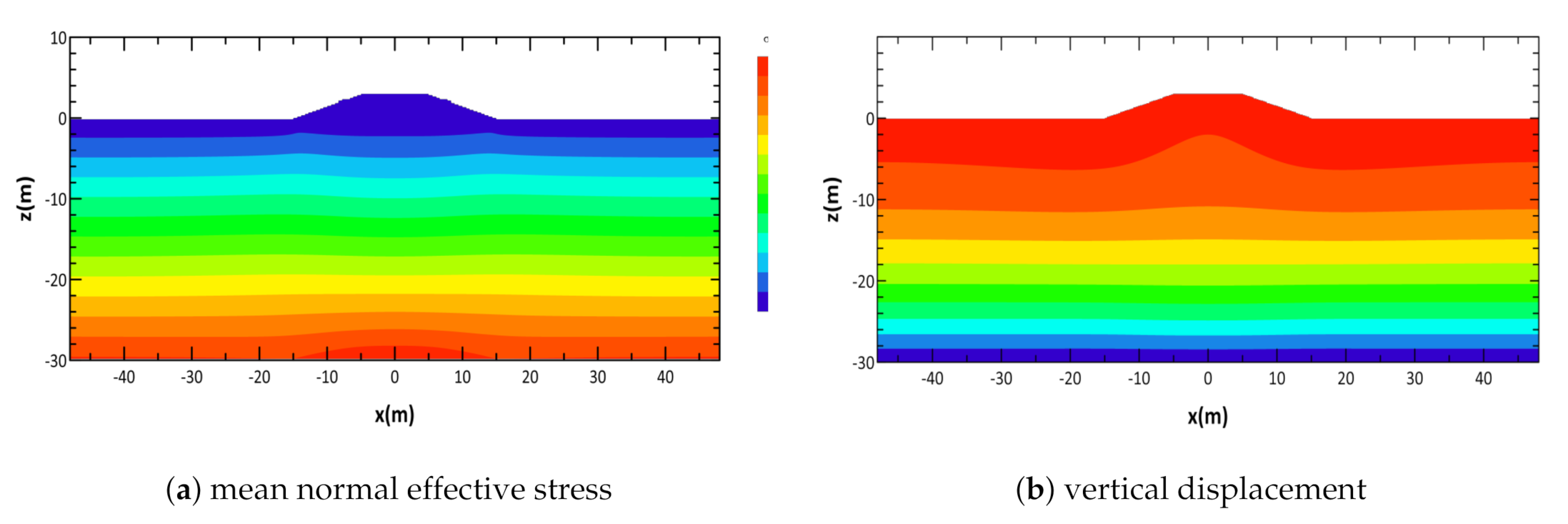
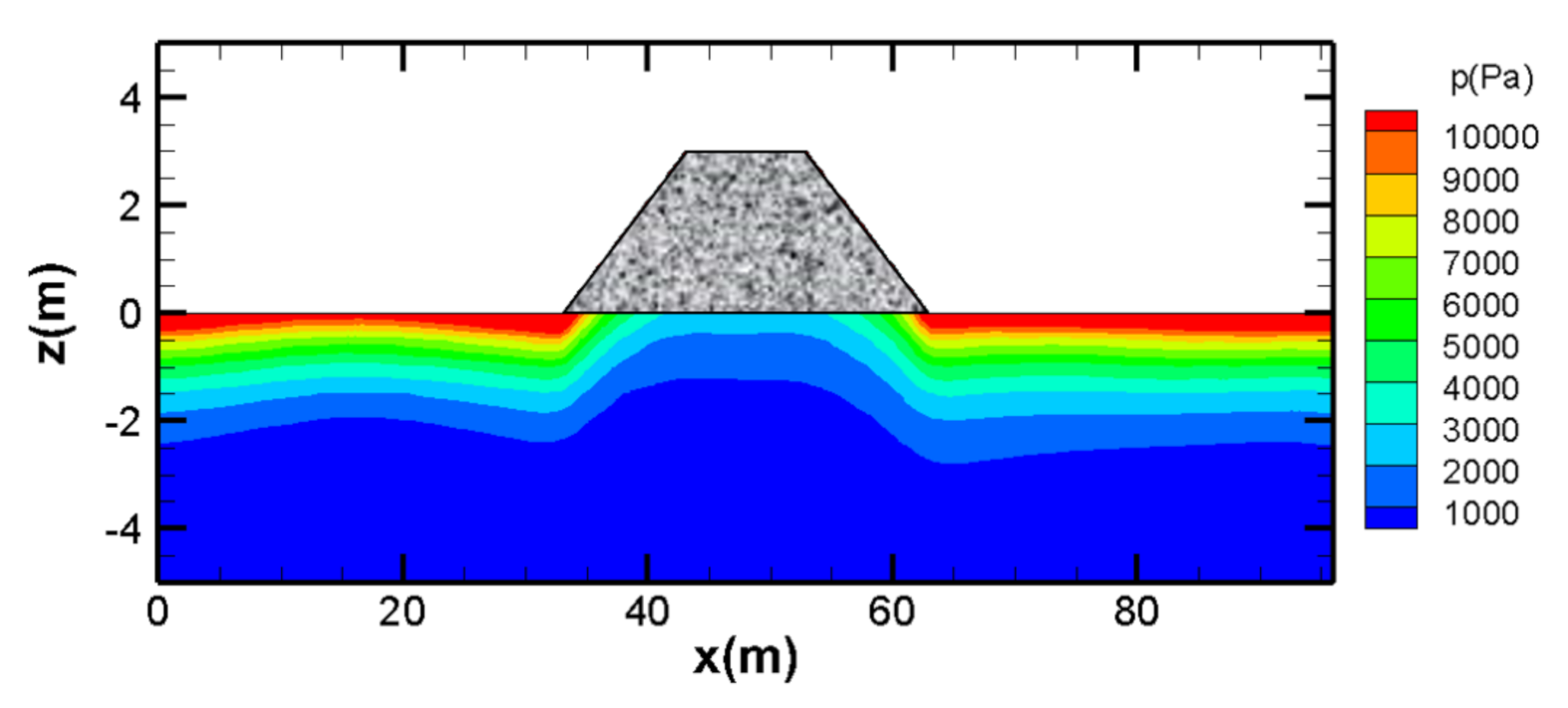
3.2. Consolidation Process of Seabed under a Submerged Breakwater
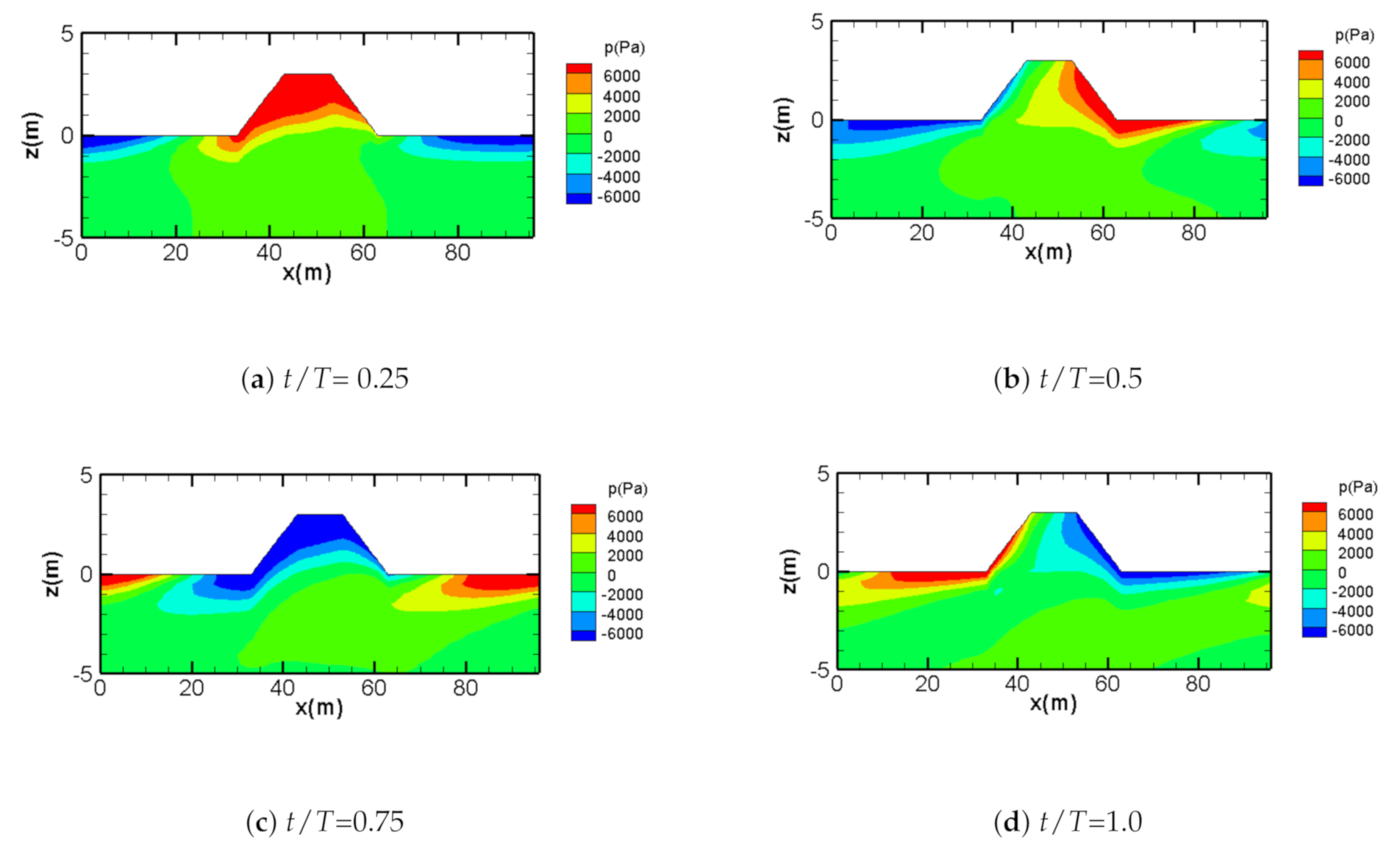
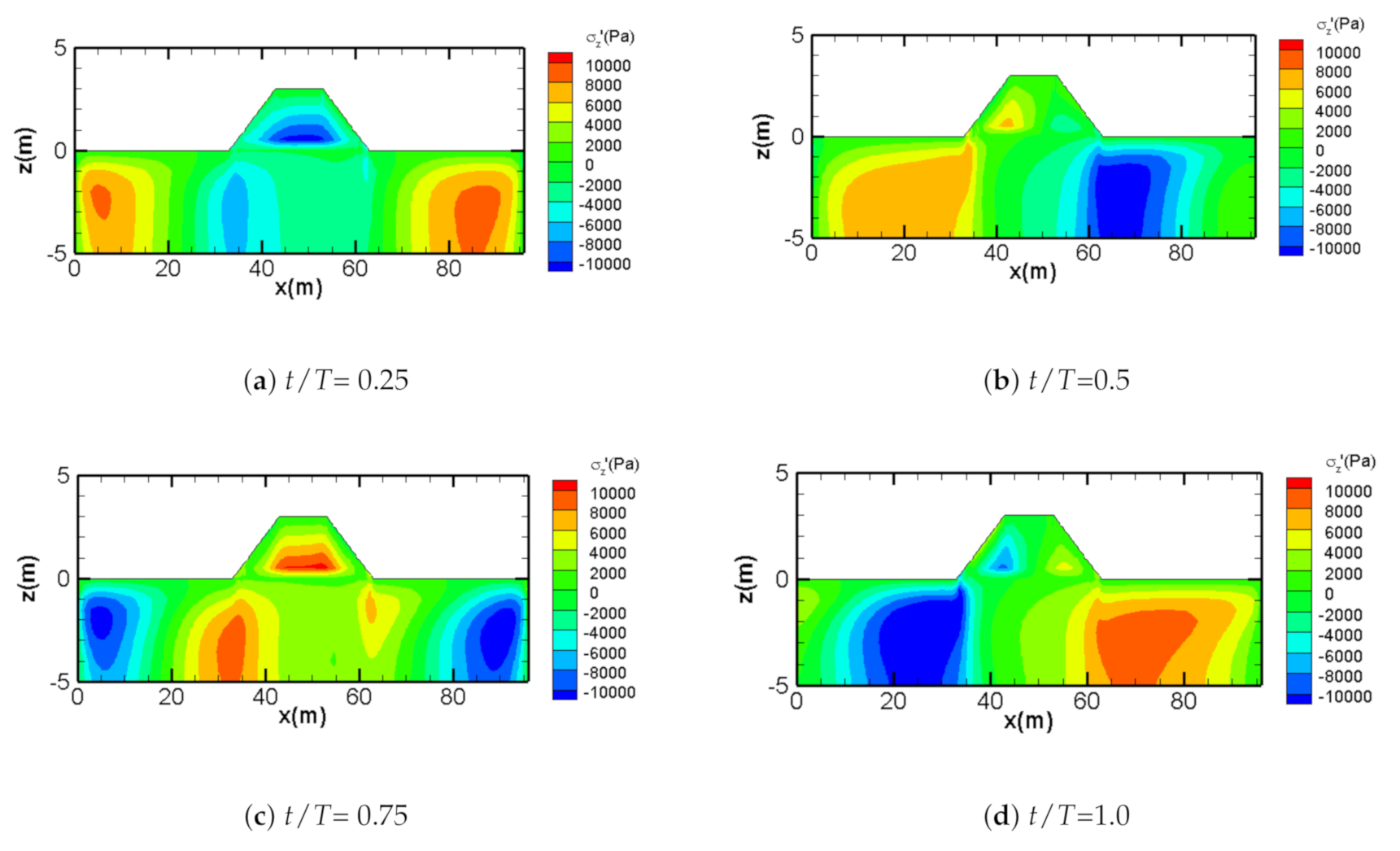
3.3. Dynamic Analysis of Wave-Breakwater-Seabed Interactions
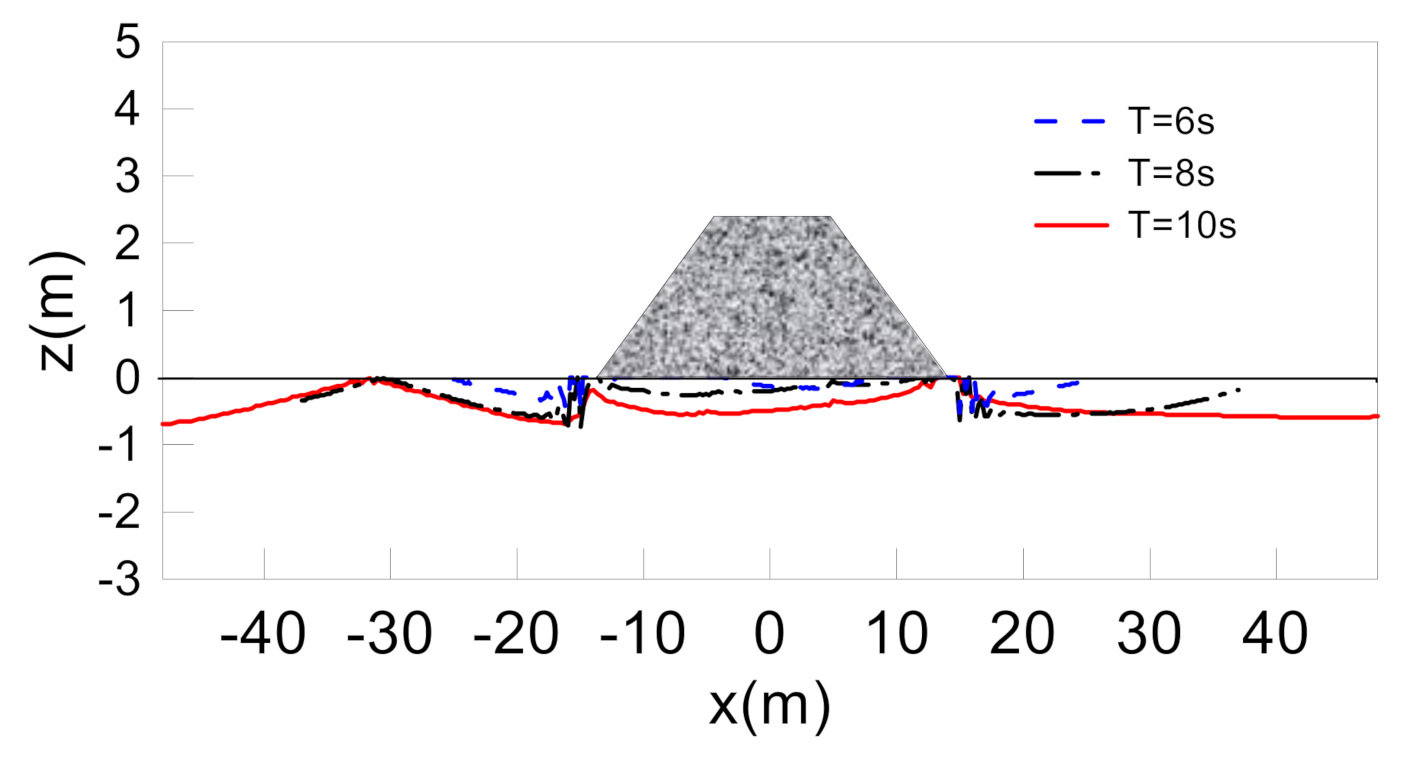
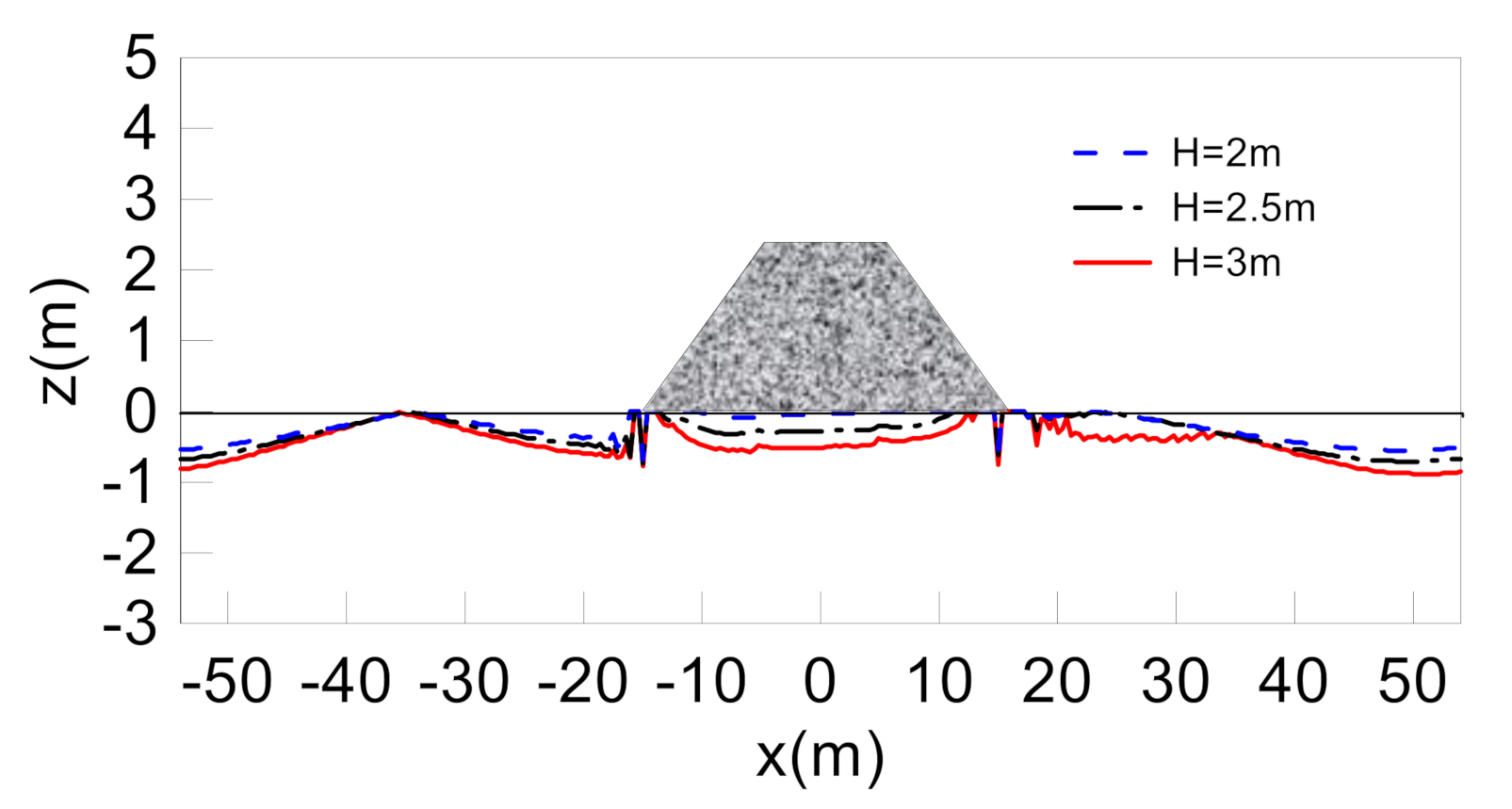
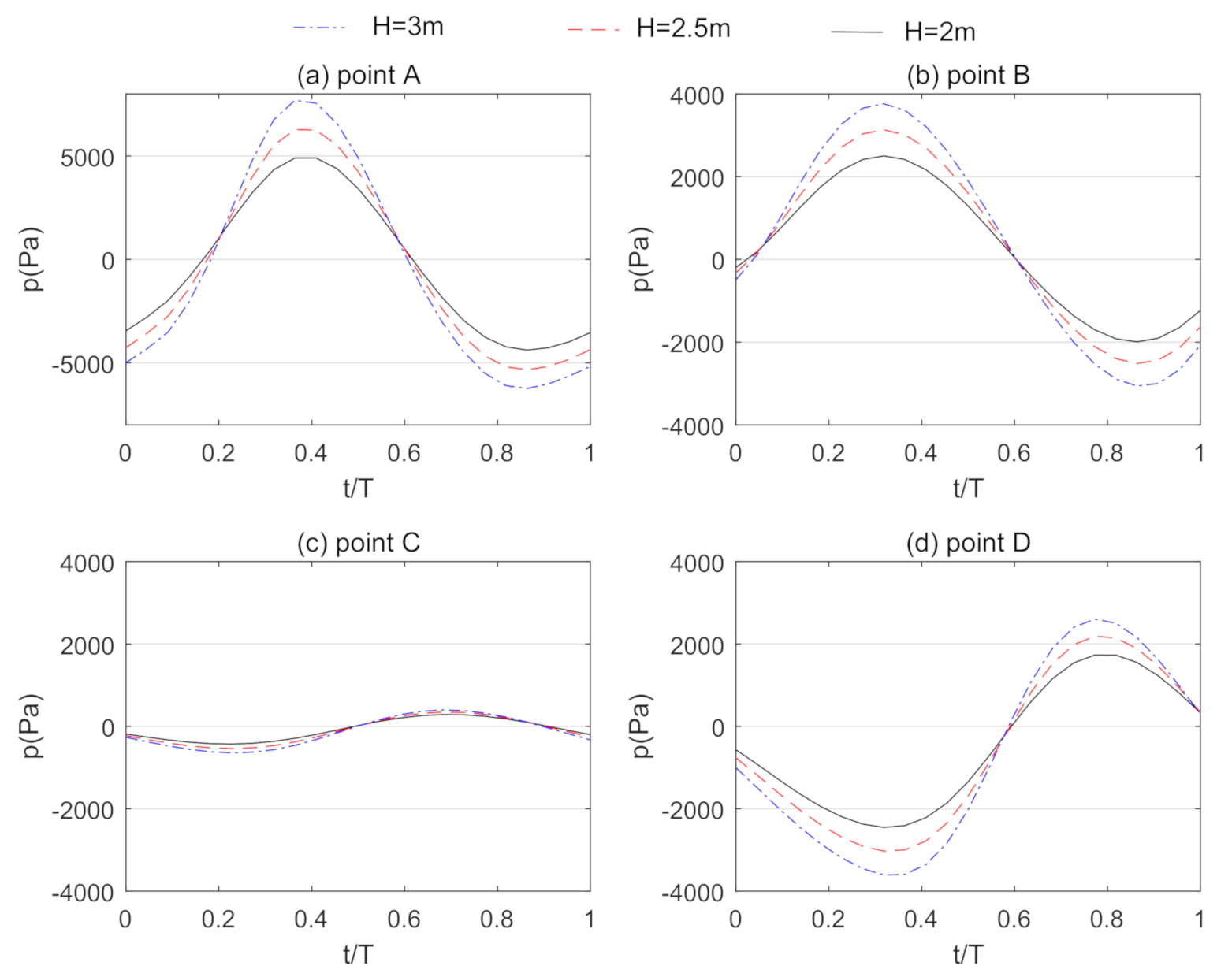
3.4. Effects of Wave Characteristics
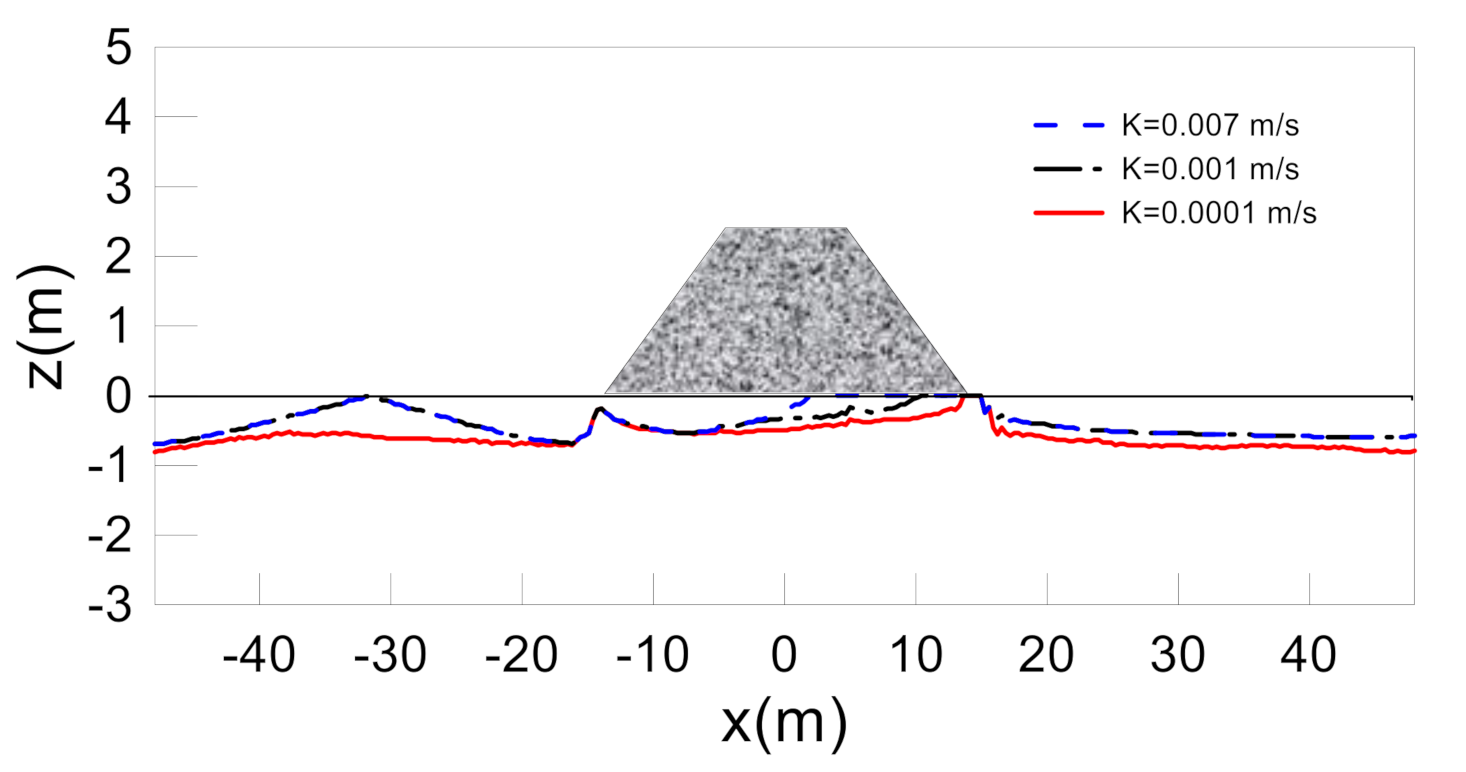
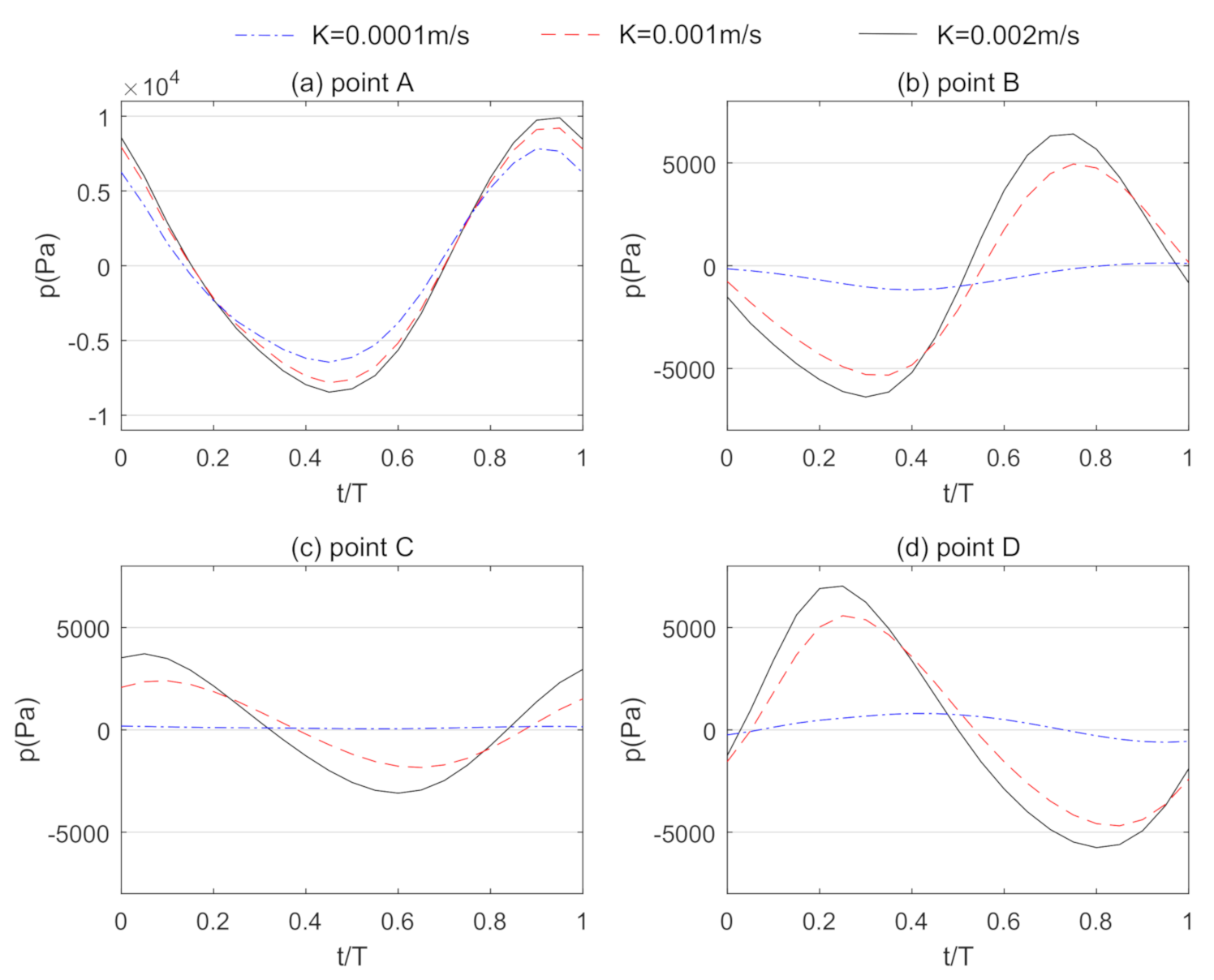
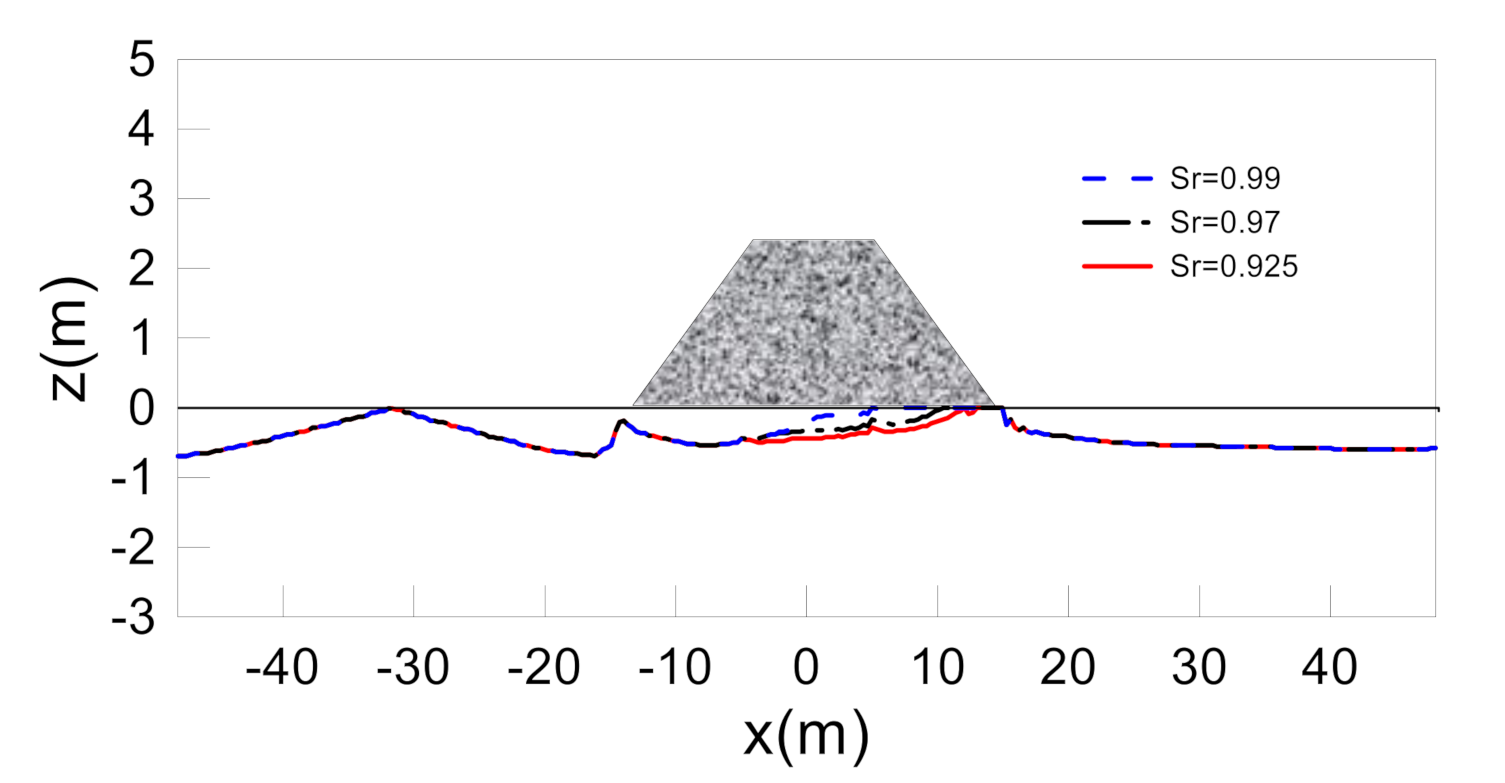
3.5. Effects of Soil Characteristics
4. Irregular Wave-Induced Soil Response around a Submerged Breakwater
4.1. Irregular Wave Model: JONSWAP Spectrum and B-M Spectrum
- B-M spectrum:with and being the highest one-third wave height and the relevant wave period, significantly, which are recognized as significant wave height and wave period, respectively.
- JONSWAP spectrum:withwhere means the peak period correlate with the frequency at the spectrum peak (). The JONSWAP spectrum is characterized by the peak enhancement factor , which controls the sharpness of the spectral peak [56]. In the present study, the mean value of is used.
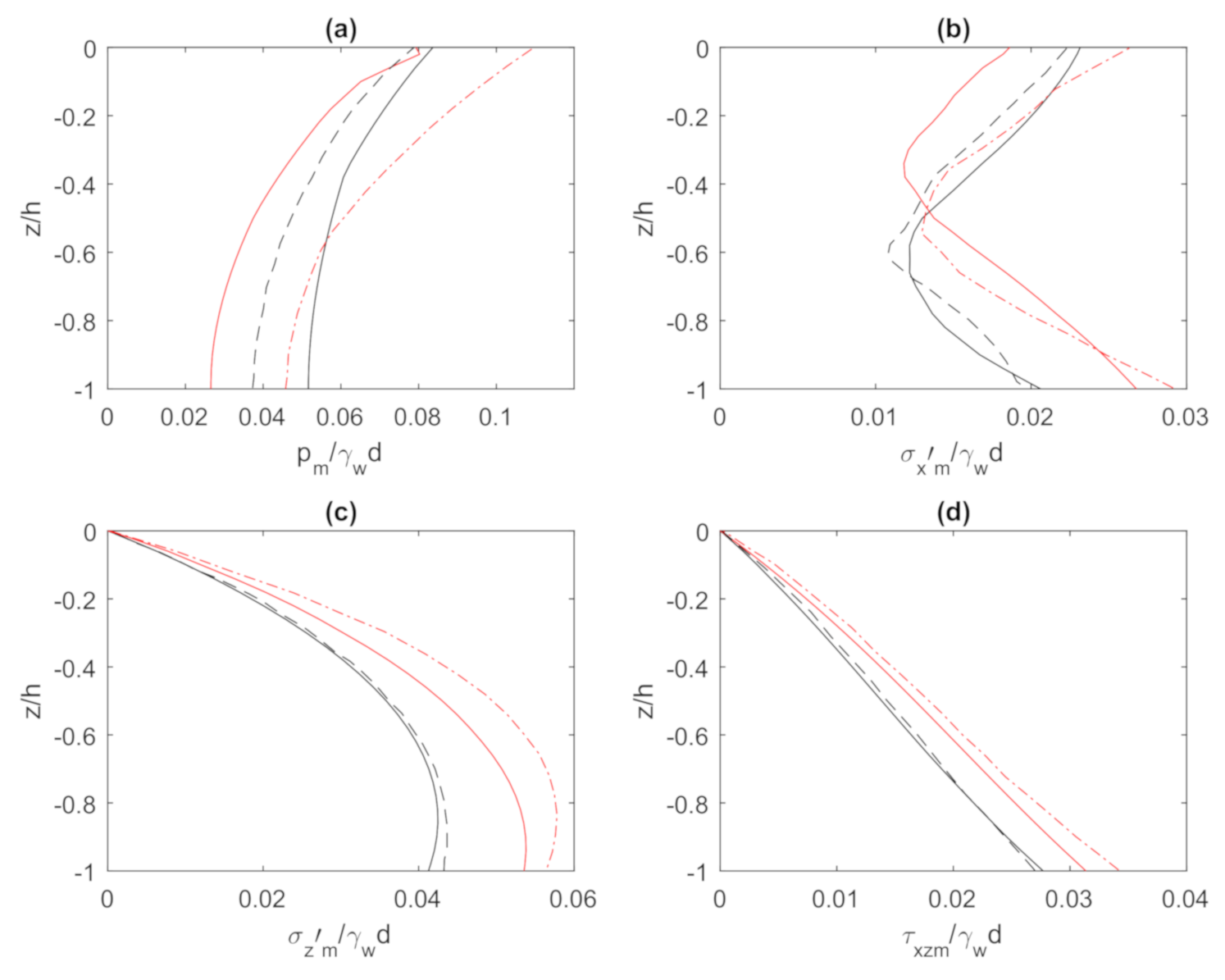
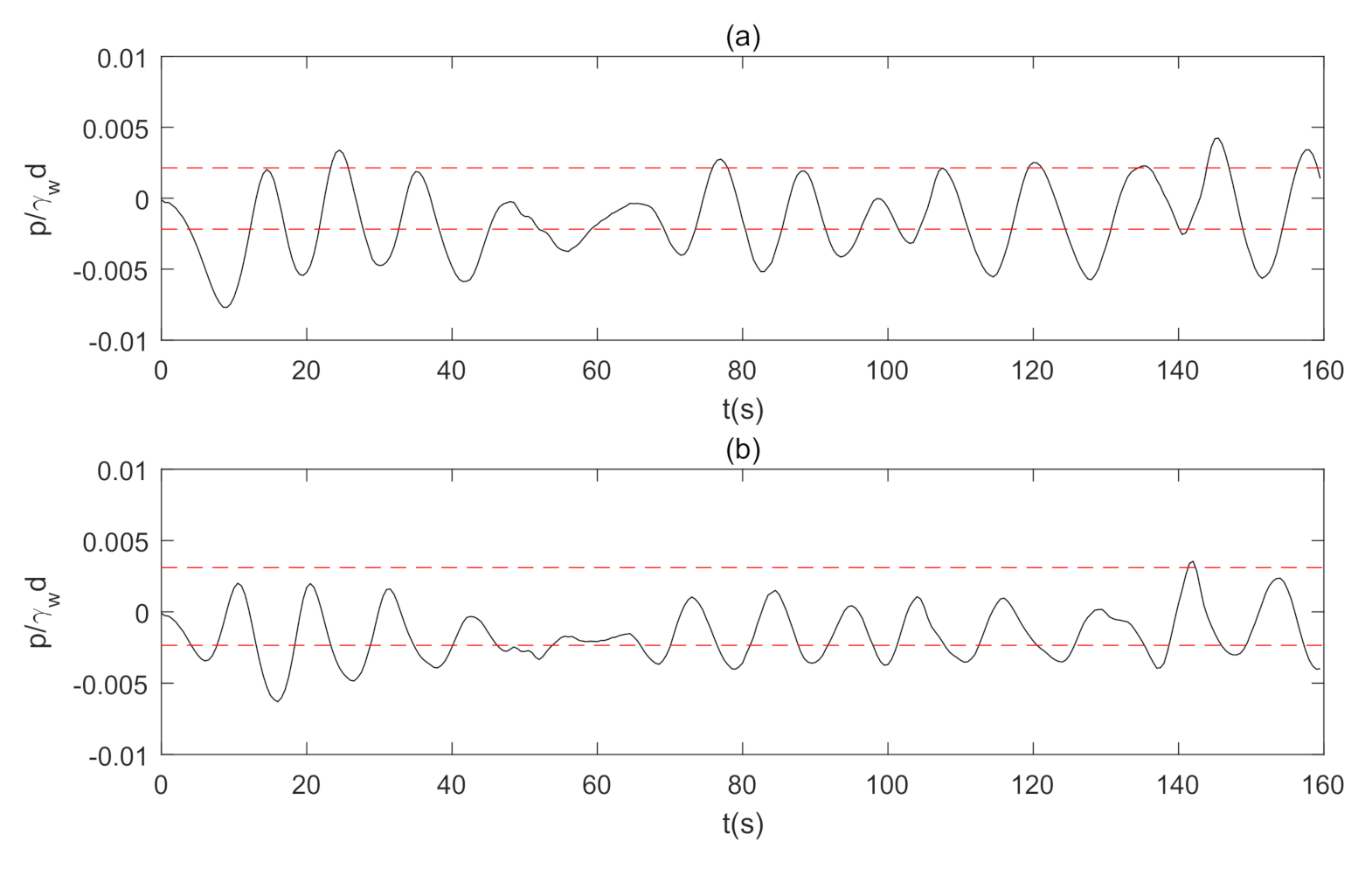
4.2. Comparison with the Previous Solution with Irregular Wave Loading
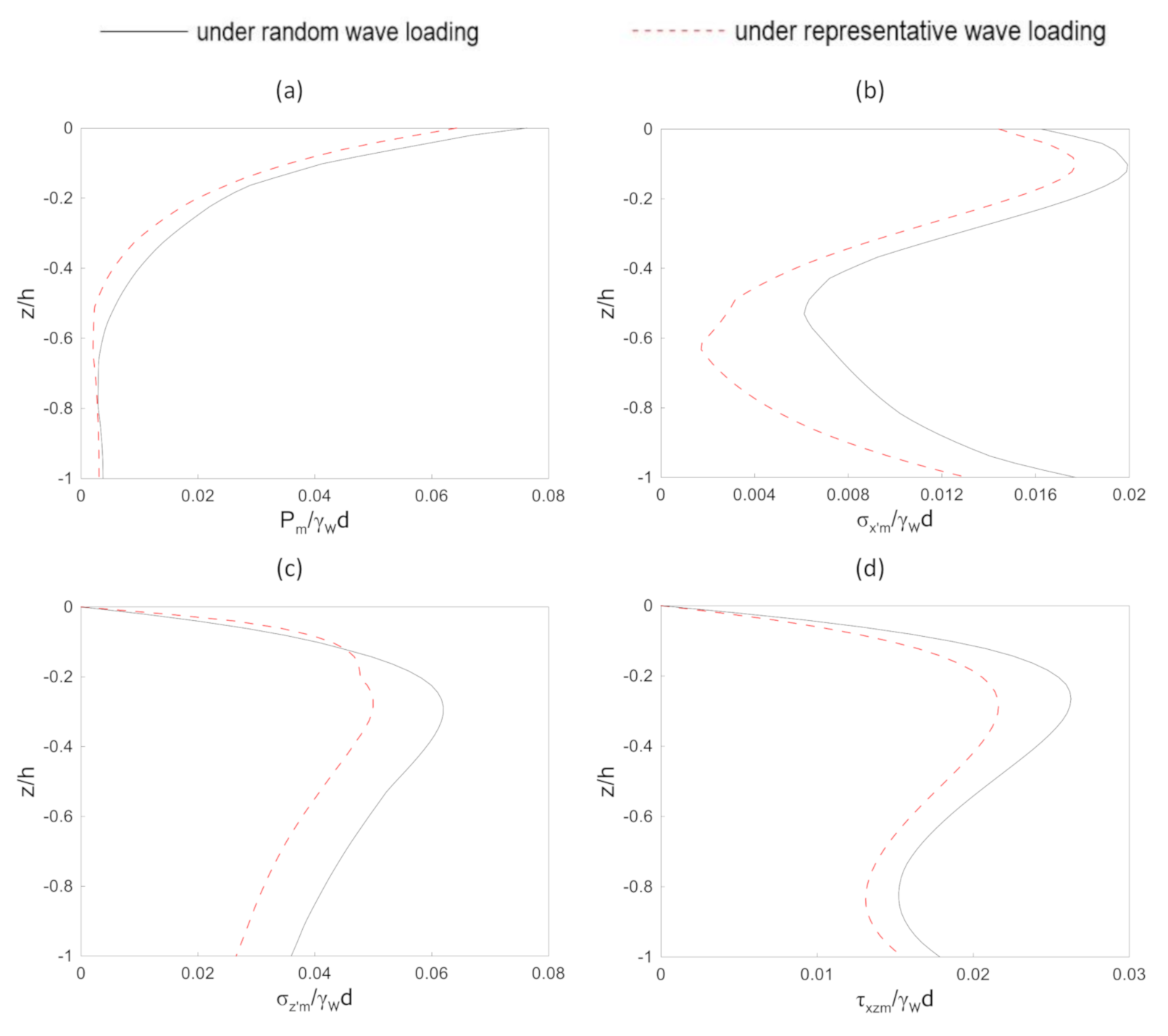
4.3. Soil Response around a Submerged Breakwater with Irregular Wave Loading
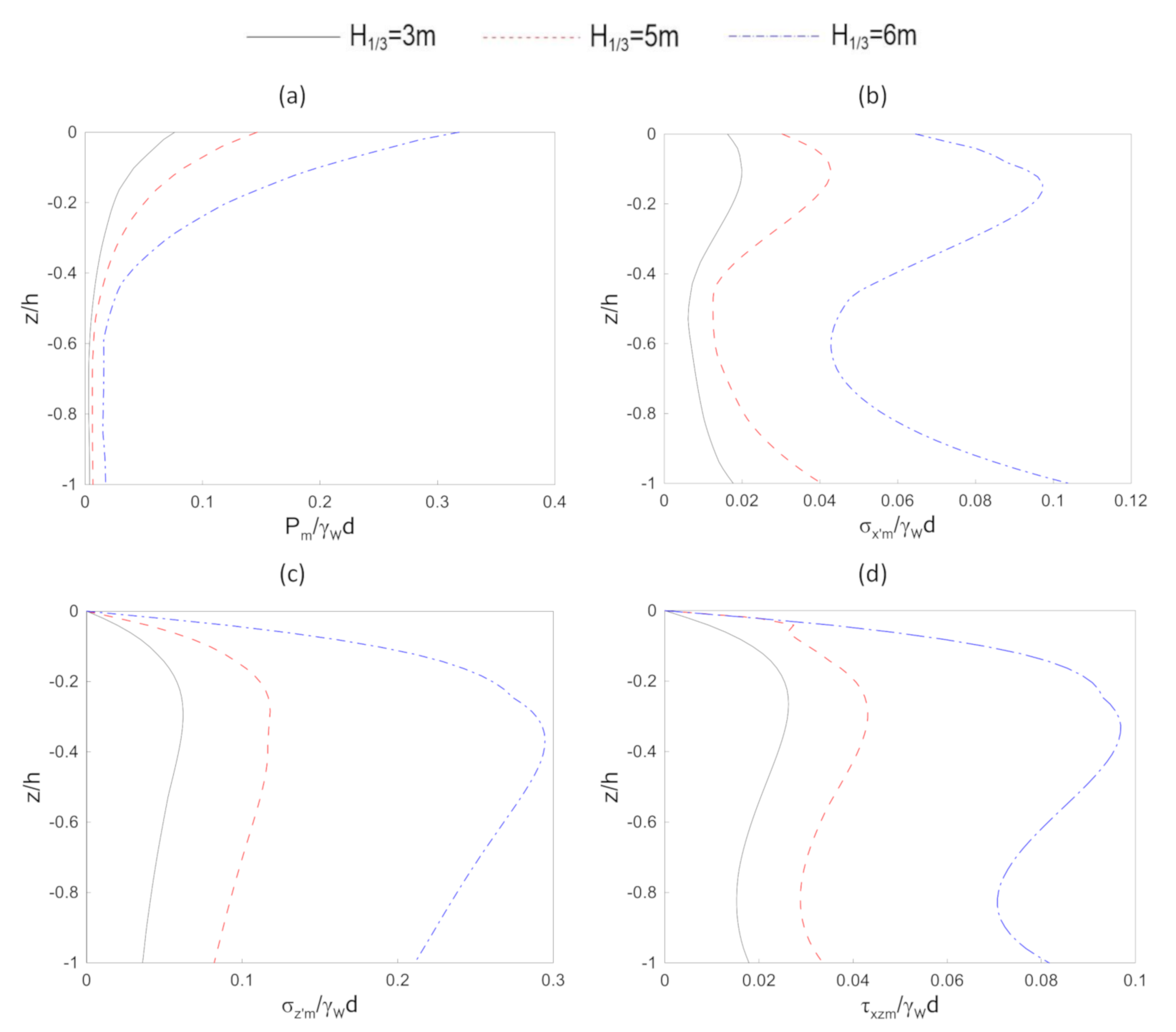
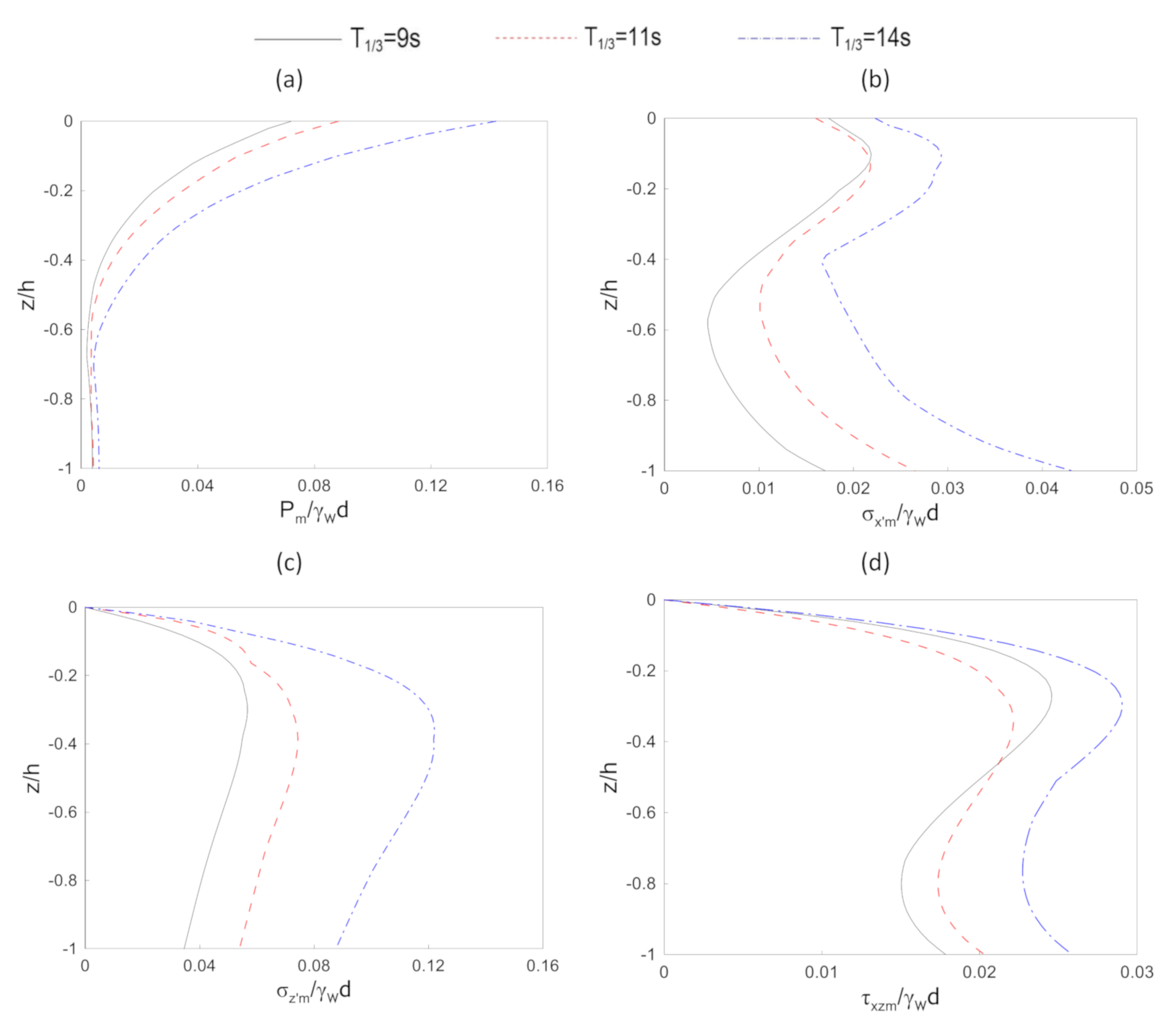
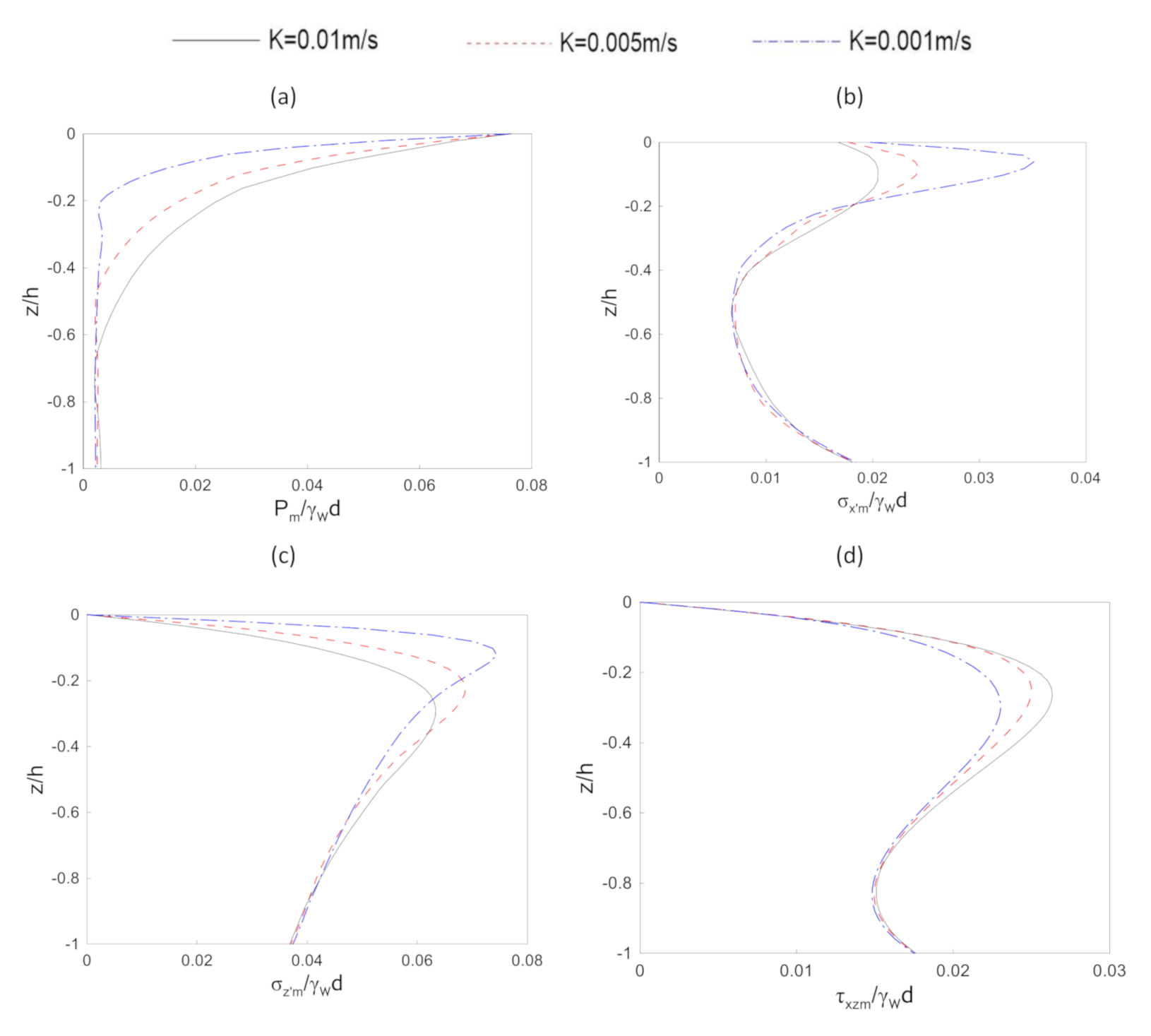
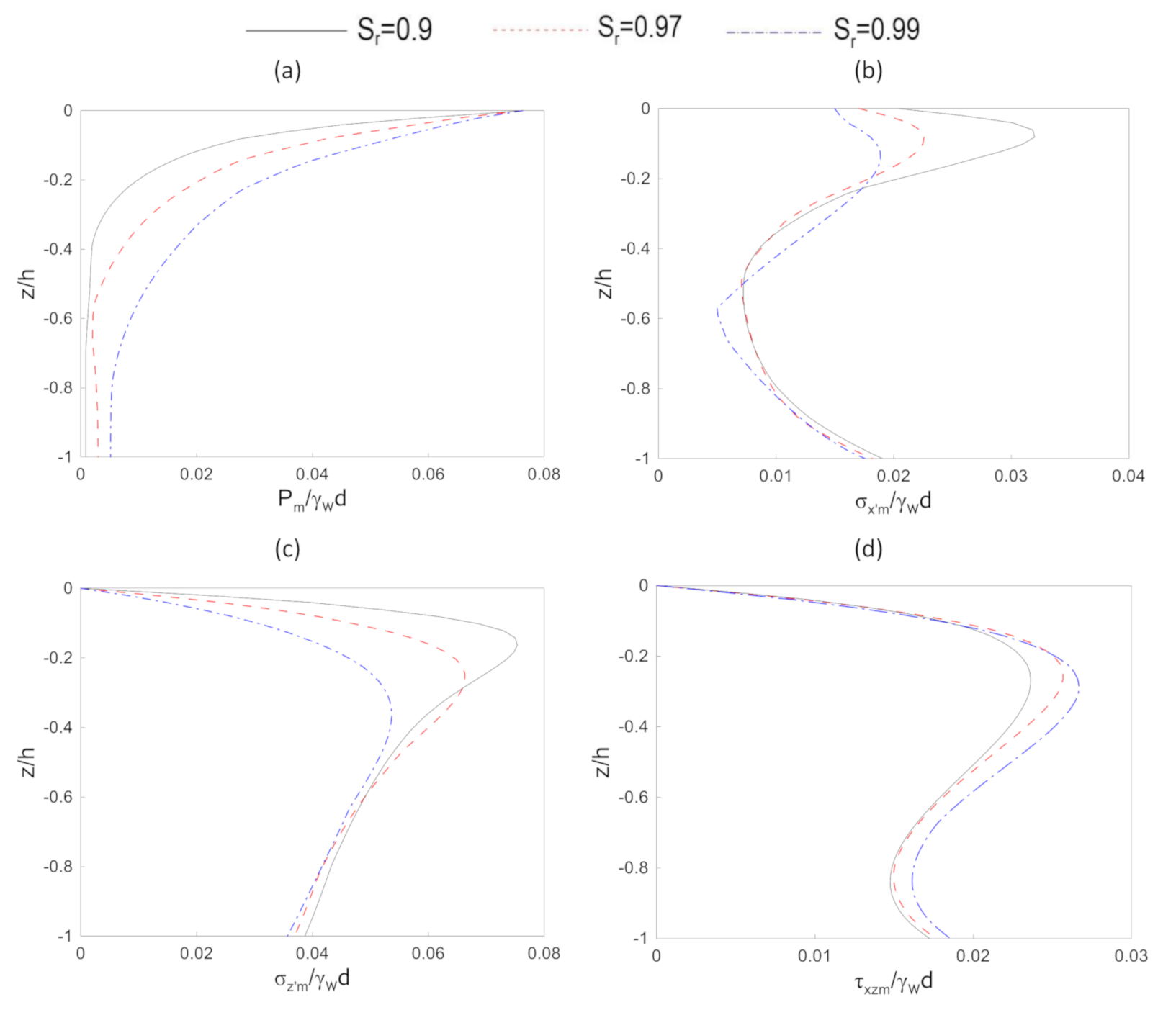
4.4. Parametric Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Woth, K.; Weisse, R.; von Storch, H. Climate change and North Sea storm surge extremes: An ensemble study of storm surge extremes expected in a changed climate projected by four different regional climate models. Ocean Dyn. 2006, 56, 3–15. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Chang. 2016, 134, 387–401. [Google Scholar] [CrossRef] [Green Version]
- Mel, R.; Sterl, A.; Lionello, P. High resolution climate projection of storm surge at the Venetian coast. Nat. Hazards Earth Syst. Sci. 2013, 13, 1135–1142. [Google Scholar] [CrossRef] [Green Version]
- Mel, R.; Lionello, P. Storm Surge Ensemble Prediction for the City of Venice. Weather Forecast. 2014, 29, 1044–1057. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; Vriend, H.J.D. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Resio, D.; Irish, J.; Cialone, M. A surge response function approach to coastal hazard assessment-Part 1: Basic concepts. Nat. Hazards 2009, 51, 163–182. [Google Scholar] [CrossRef]
- Dean, R. Beach Nourishment: Theory and Practice; World Scientific: Singapore, 2002. [Google Scholar]
- Silvester, R.; Hsu, J.R.C. Coastal Stabilization; PTR Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Maiolo, M.; Mel, R.A.; Sinopoli, S. A Stepwise Approach to Beach Restoration at Calabaia Beach. Water 2020, 12, 2677. [Google Scholar] [CrossRef]
- Coelho, C.; Narra, P.; Marinho, B.; Lima, M. Coastal Management Software to Support the Decision-Makers to Mitigate Coastal Erosion. J. Mar. Sci. Eng. 2020, 8, 37. [Google Scholar] [CrossRef] [Green Version]
- Silvester, R. Coastal Engineering; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Kamphuis, J.W. Introduction to Coastal Engineering and Management; World Scientific: Singapore, 2000. [Google Scholar]
- Martins, G.M.; Amaral, A.F.; Wallenstein, F.M.; Neto, A.I. Influence of a breakwater on nearby rocky intertidal community structure. Mar. Environ. Res. 2009, 67, 237–245. [Google Scholar] [CrossRef] [Green Version]
- Maiolo, M.; Mel, R.A.; Sinopoli, S. A Simplified Method for an Evaluation of the Effect of Submerged Breakwaters on Wave Damping: The Case Study of Calabaia Beach. J. Mar. Sci. Eng. 2020, 8, 510. [Google Scholar] [CrossRef]
- Heaps, N.S. Storm surges 1967-1982. Geophys. J. Int. 1983, 74, 331–376. [Google Scholar] [CrossRef] [Green Version]
- Vousdoukas, M.I.; Almeida, L.P.; Ferreira, O. Beach erosion and recovery during consecutive storms at a steep-sloping, meso-tidal beach. Earth Surf. Process. Landf. 2012, 37, 583–593. [Google Scholar] [CrossRef]
- Vousdouka, M.I. Observations of wave run-up and groundwater seepage line motions on a reflective-tointermediate, meso-tidal beach. Mar. Geol. 2014, 350, 52–70. [Google Scholar] [CrossRef]
- Ji, T.; Li, G. Contemporary monitoring of storm surge activity. Prog. Phys. Geogr. Earth Environ. 2019, 44, 299–314. [Google Scholar] [CrossRef]
- Sumer, B.M. Liquefaction around Mainre Structures; World Scientific: Singapore, 2014. [Google Scholar]
- Jeng, D.S. Mechanics of Wave-Seabed-Structure Interactions: Modelling, Processes and Applications; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Tsai, Y.T.; McDougal, W.G.; Sollitt, C.K. Response of finite depth seabed to waves and caisson motion. J. Waterw. Port Coast. Ocean Eng. ASCE 1990, 116, 1–20. [Google Scholar] [CrossRef]
- Mei, C.C.; Foda, M.A. Wave-induced response in a fluid-filled poro-elastic solid with a free surface-a boundary layer theory. Geophys. J. R. Astron. Soc. 1981, 66, 597–631. [Google Scholar] [CrossRef]
- Mase, H.; Sakai, T.; Sakamoto, M. Wave-induced porewater pressure and effective stresses around breakwater. Ocean Eng. 1994, 21, 361–379. [Google Scholar] [CrossRef]
- Mostafa, A.M.; Mizutani, N.; Iwata, K. Nonlinear wave, composite breakwater and seabed dynamic interaction. J. Waterw. Port Coastal Ocean Eng. ASCE 1999, 125, 88–97. [Google Scholar] [CrossRef]
- Jeng, D.S.; Cha, D.H.; Lin, Y.S.; Hu, P.S. Analysis on pore pressure in an anisotropic seabed in the vicinity of a caisson. Appl. Ocean Res. 2000, 22, 317–329. [Google Scholar] [CrossRef]
- Jeng, D.S.; Ye, J.H.; Zhang, J.S.; Liu, P.L.F. An integrated model for the wave-induced seabed response around marine structures: Model verifications and applications. Coast. Eng. 2013, 72, 1–19. [Google Scholar] [CrossRef]
- Karim, M.R.; Nogami, T.; Wang, J.G. Analysis of transient response of saturated porous elastic soil under cyclic loading using element-free Galerkin method. Int. J. Solids Struct. 2002, 39, 6011–6033. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, G.; Lin, P. Numerical analysis of biot’s consolidation process by radial point interpolation method. Int. J. Solids Struct. 2002, 39, 1557–1573. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhang, B.; Nogami, T. Wave-induced seabed response analysis by radial point interpolation meshless method. Ocean Eng. 2004, 31, 21–42. [Google Scholar] [CrossRef]
- Wang, X.X.; Jeng, D.S.; Tsai, C.C. Meshfree model for wave-seabed interactions around offshore pipelines. J. Mar. Sci. Eng. 2019, 7, 87. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Jeng, D.S.; Tsai, C.C. Response of a porous seabed around an immersed tunnel under wave loading: Meshfree model. J. Mar. Sci. Eng. 1988, 7, 369. [Google Scholar] [CrossRef] [Green Version]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorption for Navier-Stokes models: Application to OpenFOAM. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Mel, R.; Viero, D.P.; Carniello, L.; D’Alpaos, L. Optimal floodgate operation for river flood management: The case study of Padova (Italy). J. Hydrol. Reg. Stud. 2020, 30, 100702. [Google Scholar] [CrossRef]
- Higuera, P. Enhancing active wave absorption in RANS models. Appl. Ocean Res. 2020, 94, 102000. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 26, 155–164. [Google Scholar] [CrossRef]
- Verruijt, A. Flow Through Porous Media; Chapter Elastic Storage of Aquifers; Academic Press: London, UK, 1969; pp. 331–376. [Google Scholar]
- Yamamoto, T.; Koning, H.; Sellmeijer, H.; Hijum, E.V. On the response of a poro-elastic bed to water waves. J. Fluid Mech. 1978, 87, 193–206. [Google Scholar] [CrossRef]
- Šarler, B.; Vertnik, R. Meshfree explicit local radial basis function collocation method for diffusion problems. Comput. Math. Appl. 2006, 51, 1269–1282. [Google Scholar] [CrossRef] [Green Version]
- Kosec, G.; Sarler, B. Local RBF collocation method for Darcy flow. Comput. Model. Eng. Sci. 2008, 25, 197–208. [Google Scholar]
- Tsai, C.C.; Lin, Z.H.; Hsu, T.W. Using a local radial basis function collocation method to approximate radiation boundary conditions. Ocean Eng. 2015, 105, 231–241. [Google Scholar] [CrossRef]
- Kosec, G.; Založnik, M.; Šarler, B.; Combeau, H. A meshless approach towards solution of macrosegregation phenomena. Comput. Mater. Contin. 2011, 22, 169–195. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searchings. Commun. ACM 19752, 18, 509–517. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Lee, C.K.; Liu, X.; Fan, S.C. Local multiquadric approximation for solving boundary value problems. Comput. Mech. 2003, 30, 396–409. [Google Scholar] [CrossRef]
- Liu, X.; Liu, G.; Tai, K.; Lam, K. Radial point interpolation collocation method (rpicm) for partial differential equations. Comput. Math. Appl. 2005, 50, 1425–1442. [Google Scholar] [CrossRef] [Green Version]
- Li, X.S. An overview of SuperLU: Algorithms, implementation, and user interface. ACM Trans. Math. Softw. (TOMS) 2005, 31, 302–325. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 431, 50–67. [Google Scholar] [CrossRef]
- Mizutani, N.; Mostafa, A.M. Nonlinear wave-induced seabed instability around coastal structures. Coast. Eng. J. 1998, 40, 131–160. [Google Scholar] [CrossRef]
- Ye, J.; Jeng, D.S. Response of seabed to natural loading-waves and currents. J. Eng. Mech. ASCE 2012, 138, 601–613. [Google Scholar] [CrossRef]
- Jeng, D.S.; Zhao, H.Y. Two-dimensional model for pore pressure accumulations in marine sediments. J. Waterw. Port, Coast. Ocean Eng. ASCE 2015, 141, 04014042. [Google Scholar] [CrossRef] [Green Version]
- Jeng, D.S.; Lin, Y.S. Non-linear wave-induced response of porous seabed: A finite element analysis. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 15–42. [Google Scholar] [CrossRef]
- Luan, M.; Qu, P.; Jeng, D.S.; Guo, Y.; Yang, Q. Dynamic response of a porous seabed-pipeline interaction under wave loading: Soil-pipe contact effects and inertial effects. Comput. Geotech. 2008, 35, 173–186. [Google Scholar] [CrossRef]
- Zhao, H.; Jeng, D.S.; Guo, Z.; Zhang, J.S. Two-dimensional model for pore pressure accumulations in the vicinity of a buried pipeline. J. Offshore Mech. Arct. Eng. ASME 2014, 136, 042001. [Google Scholar] [CrossRef]
- Lin, Z.; Guo, Y.K.; Jeng, D.S.; Liao, C.C.; Rey, N. An integrated numerical model for wave–soil–pipeline interaction. Coast. Eng. 2016, 108, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Goda, Y. Random Seas and Design of Marine Structures; World Scientific Press: Singapore, 2000. [Google Scholar]
- Liu, H.; Jeng, D.S. A semi-analytical solution for random wave-induced soil response in marine sediments. Ocean Eng. 2007, 34, 1211–1224. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Ross, A.W. Inherent benchmark or not? Comparing NashSutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef] [Green Version]
- Schaefli, B.; Gupta, H.V. Do Nash values have value. Hydrol. Process. 2007, 21, 2075–2080. [Google Scholar] [CrossRef] [Green Version]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the KlingGupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. Evaluating model performance: Towards a non-parametric variant of the KlingGupta efficiency. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, N.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Wagener, T.; Liu, Y. Reconciling theory with observations? Elements of a diagnostic approach to model evaluation. Hydrol. Process. 2008, 22, 3802–3813. [Google Scholar] [CrossRef]
- Mathevet, T.; Gupta, H.; Perrin, C.; Andreassian, V.; Moine, N.L. Assessing the performance and robustness of two conceptual rainfall-runoff models on a worldwide sample of watersheds. J. Hydrol. 2020, 585, 124698. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Jeng, D.S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness. Int. J. Numer. Anal. Methods Geomech. 1994, 18, 785–807. [Google Scholar] [CrossRef]
- Xu, H.X.; Dong, P. A probabilistic analysis of random wave-induced liquefaction. Ocean Eng. 2011, 38, 860–867. [Google Scholar] [CrossRef]





| Wave Characteristics | |
|---|---|
| Water depth | 0.3 m |
| Wave height | 0.03 m |
| Wave period | 1.4 s |
| Soil characteristics | |
| Thickness of seabed | 0.19 m |
| Poisson’s ratio | 0.33 |
| Soil porosity | 0.3 |
| Soil permeability | 0.0022 m/s |
| Degree of saturation | 0.99 |
| Shear modulus | 5 N/m |
| Breakwater parameters | |
| Breakwater height | 0.21 m |
| Crown Length | 1.05 m |
| Slope length | 0.42 m |
| Poisson’s ration | 0.33 |
| Porosity | 0.26 |
| Permeability | 0.0018 m/s |
| Shear modulus | N/m |
| Wave Conditions | |
|---|---|
| Water depth () | 11 m |
| Wave height () | 2 m, 2.5 m, 3 m |
| Wave period () | 6 s, 8 s, 10 s |
| Soil characteristics | |
| Thickness of seabed () | 30 m |
| Poisson’s ratio () | 0.33 |
| Soil porosity () | 0.3 |
| Soil permeability ( or K) | 0.0001 m/s, 0.001 m/s, 0.002 m/s, 0.007 m/s |
| Degree of saturation () | 0.925, 0.97, 0.99 |
| Shear modulus () | N/m |
| Breakwater conditions | |
| Breakwater height () | 3 m |
| Crown Length () | 10 m |
| Slope length () | 10 m |
| Poisson’s ration () | 0.24 |
| Porosity () | 0.3 |
| Permeability () | 0.01 m/s |
| Degree of saturation | 0.975 |
| Shear modulus () | N/m |
| Wave Conditions | |
|---|---|
| Water depth d | 11 m |
| Significant wave height | 3 m, 5 m, 6 m |
| Significant wave period | 9 s, 11 s, 14 s |
| Soil characteristics | |
| Thickness of seabed h | 30 m |
| Poisson’s ratio | 0.33 |
| Soil porosity n | 0.3 |
| Soil permeability or K | 0.001 m/s, 0.005 m/s, 0.007 m/s, 0.01 m/s |
| Degree of saturation | 0.9, 0.97, 0.98, 0.99 |
| Shear modulus G | N/m |
| Breakwater conditions | |
| Breakwater height | 3 m |
| Crown Length | 10 m |
| Slope length | 10 m |
| Poisson’s ration | 0.24 |
| Porosity | 0.3 |
| Permeability | 0.01 m/s |
| Shear modulus | N/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, D.-S.; Wang, X.; Tsai, C.-C. Meshless Model for Wave-Induced Oscillatory Seabed Response around a Submerged Breakwater Due to Regular and Irregular Wave Loading. J. Mar. Sci. Eng. 2021, 9, 15. https://doi.org/10.3390/jmse9010015
Jeng D-S, Wang X, Tsai C-C. Meshless Model for Wave-Induced Oscillatory Seabed Response around a Submerged Breakwater Due to Regular and Irregular Wave Loading. Journal of Marine Science and Engineering. 2021; 9(1):15. https://doi.org/10.3390/jmse9010015
Chicago/Turabian StyleJeng, Dong-Sheng, Xiaoxiao Wang, and Chia-Cheng Tsai. 2021. "Meshless Model for Wave-Induced Oscillatory Seabed Response around a Submerged Breakwater Due to Regular and Irregular Wave Loading" Journal of Marine Science and Engineering 9, no. 1: 15. https://doi.org/10.3390/jmse9010015
APA StyleJeng, D.-S., Wang, X., & Tsai, C.-C. (2021). Meshless Model for Wave-Induced Oscillatory Seabed Response around a Submerged Breakwater Due to Regular and Irregular Wave Loading. Journal of Marine Science and Engineering, 9(1), 15. https://doi.org/10.3390/jmse9010015







