Development of a Comparison Framework for Evaluating Environmental Contours of Extreme Sea States

Abstract

Environmental contours of extreme sea states are often utilized for the purposes of reliability-based offshore design. Many methods have been proposed to estimate environmental contours of extreme sea states, including, but not limited to, the traditional inverse first-order reliability method (I-FORM) and subsequent modifications, copula methods, and Monte Carlo methods. These methods differ in terms of both the methodology selected for defining the joint distribution of sea state parameters and in the method used to construct the environmental contour from the joint distribution. It is often difficult to compare the results of proposed methods to determine which method should be used for a particular application or geographical region. The comparison of the predictions from various contour methods at a single site and across many sites is important to making environmental contours of extreme sea states useful in practice. The goal of this paper is to develop a comparison framework for evaluating methods for developing environmental contours of extreme sea states. This paper develops generalized metrics for comparing the performance of contour methods to one another across a collection of study sites, and applies these metrics and methods to develop conclusions about trends in the wave resource across geographic locations, as demonstrated for a pilot dataset. These proposed metrics and methods are intended to judge the environmental contours themselves relative to other contour methods, and are thus agnostic to a specific device, structure, or field of application. The metrics developed and applied in this paper include measures of predictive accuracy, physical validity, and aggregated temporal performance that can be used to both assess contour methods and provide recommendations for the use of certain methods in various geographical regions. The application and aggregation of the metrics proposed in this paper outline a comparison framework for environmental contour methods that can be applied to support design analysis workflows for offshore structures. This comparison framework could be extended in future work to include additional metrics of interest, potentially including those to address issues pertinent to a specific application area or analysis discipline, such as metrics related to structural response across contour methods or additional physics-based metrics based on wave dynamics.

1. Introduction

Environmental contours of extreme conditions utilize existing historical data to predict expected behavior for a given return period of interest (e.g., 25 years). This return period is commonly linked to a design life for which an engineering system is expected to survive with a certain probability. The environmental contours define combinations of environmental conditions that can be used to predict the most extreme design loads for this design life. As the period of record of historical data can often be on the same order as the design life, the construction of environmental contours generally requires the extrapolation of a finite data set to estimate the possible values of additional observations. This projection utilizes the principles of probability and statistics to develop a prediction of future environmental behavior.

Environmental contours of extreme sea states are used to predict extreme conditions experienced by systems deployed in marine environments. This practice is employed for ships [1], offshore oil and gas structures [2,3], offshore wind turbines [4,5,6], and wave energy converters (WECs) [7,8,9,10]. Often, the use of an environmental contour within a design load analysis is either recommended or even specified by a design guideline or standard (see, e.g., [11,12,13,14]). While it can also be useful to make predictions over some large area (e.g., the North Pacific), it is generally more desirable for engineering applications to make predictions for a specific site (e.g., the prospective location for an offshore wind farm). The ocean environment is particularly difficult to predict, as trends and methods that appear to work at a single site often fail when applied to sites with different physical and environmental characteristics. Additionally, long-term periodic variations, such as the El Niño/La Niña, can extend the requirements for periods of record. Sea states, short term descriptions of the wave field at a specific site, are often characterized by significant wave height ($H_s$) and wave period, where wave period may be described by zero-crossing period ($T_z$), mean period ($\overline{T}$), energy period ($T_e$), and peak period ($T_p$)1, depending on the application and industry preferences. See [15] for precise definitions of these different spectral periods. These sea state metrics are calculated using spectral measurements of ocean waves and describe the behavior of the marine environment at a given location over a time period of interest (e.g., 1 h). Environmental contours of extreme sea states generated using $H_s$ and $T_e$ can be used to provide inputs for both numerical simulations or physical model testing to analyze the design response of offshore structures (see e.g., [9]).

Many methods have been proposed to generate environmental contours of extreme sea states. These methods differ in terms of both the methodology selected for defining the joint distribution of sea state parameters and in the method used to construct the environmental contour from the joint distribution. The first and most commonly applied of these methods, the inverse first-order reliability method (I-FORM), was pioneered by Haver and Winterstein [16,17]. An alternative to the I-FORM approach is to simulate sea states based on a joint probability model, until a sufficient number of extremes have been observed to define higher percentile returns (e.g., 50-year waves) [18]. This style of method is often referred to as a Monte Carlo approach and was further studied and compared to I-FORM contours in [19]. A useful comparison of the I-FORM and Monte Carlo analyses was performed by [20]. Copula methods have also been proposed in conjunction with the I-FORM method to characterize the relationship between the marginal distributions of sea state variables for the production of environmental contours [21,22]. The use of kernel density estimation (KDE) was introduced as a method for generating environmental contours by [23] and has been further explored in other studies [24,25]. A method for deriving environmental contours to enclose the highest density region of a probability density, termed the highest density contour (HDC), is proposed in [26]. Moreover, Manuel et al. [27] considered the performance of both parametric and nonparametric environmental methods using the I-FORM contour construction approach in terms of uncertainty and dependency on the amount of data available. The I-FORM method is compared to a method developed using inverse second order reliability method (I-SORM) for generating environmental contours of extreme sea states in [28]. Additionally, contour construction methods are rigorously described and compared in [29]. A useful survey of methods, including a detailed explanation of the theoretical basis for different contour methods and practical guidance, was performed by Ross et al. [30].

Although many methods have been proposed to generate environmental contours of extreme sea states, it is often difficult to compare these methods, as results are presented for a limited number of sites. In addition, contour examples throughout the literature are often presented without the underlying sea state data used to generate them. This makes it difficult to assess the performance of a proposed contour method in comparison to contour methods that are already available. It is also not straightforward to quantify the performance of a contour; while it is intuitively understood that the contour should neither fit the empirical data too closely or too loosely, this does not provide an obvious quantitative metric for assessment. Furthermore, the many design specifications and guidelines use return periods on the order of 50–100 years [11,12,13], meaning that a great deal of data must be collected prior to assessing whether this predicted contour has provided an accurate representation of the most extreme sea states. Even if enough data are available to validate a contour, a single comparison of a predicted contour to sea state data may not be sufficient to assess a method’s performance. A contour method’s performance might change across time or be sensitive to small changes in the underlying data.

A recent study by Vanem et al. [31] considered the affects of various sampling and fitting approaches on the uncertainty in environmental contours. The study employed both synthetic datasets (drawn from known distributions) as well as hindcast datasets, where the wave conditions were simulated based on wave data. Similarly, a study presented by Hiles et al. [32] reviewed methods for analyzing extreme metocean data including environmental contour methods, and applied these methods to a case study of the Canadian Pacific coast to produce a spatial analysis of extreme wave conditions. Another ongoing effort is a cooperative benchmarking exercise in which researchers have come together to present their environmental contour methods [33].2 This effort employs wave datasets from three National Data Buoy Center (NDBC) buoys operated by the U.S. National Oceanic and Atmospheric Administration (NOAA), along with three wind and wave datasets from the coastDat-2 hindcast [34]. A set of common comparison methods for this benchmarking exercise, including qualitative approaches as well as quantitative approaches, was proposed in [33].

The goal of this paper is to develop a comparison framework for evaluating environmental contours of extreme sea states. This paper develops generalized metrics for comparing the performance of contour methods to one another across a collection of study sites, and applies these metrics and methods to develop conclusions about trends in the wave resource across geographic locations, as demonstrated for a pilot dataset. The metrics developed in this work are targeted at providing a relative means of judging environmental contour methods. The application and aggregation of the metrics proposed in this paper outline a comparison framework for environmental contour methods that can be applied to support design analysis workflows for offshore structures. This paper is organized as follows. Section 2 lists the contour methods selected for study, with mathematical details provided in order to specify which variations of contour method categories are utilized. Section 3 describes the metrics developed to compare the predictive accuracy, physical validity, and aggregated temporal performance of contour methods at a single site and across many sites. Section 4 presents the data source and the method for selecting the study sites of interest analyzed in this paper. Section 5 gives the results of the comparison study, including the overall behavior of contour methods, local comparisons, and generalizable trends. Section 6 provides concluding remarks and areas of future study.

2. Selected Contour Methods

A subset of extreme sea state contour methods was selected for study to pilot the comparison metrics developed and presented in this paper. This subset of methods can be divided into two groups; parametric contour methods and non-parametric contour methods. The parametric contour methods all use the I-FORM approach to ultimately estimate the contours; however, they differ in how they define the joint distribution of $H_s$ and $T_e$. Several methods for defining the joint distribution were considered, including the traditional I-FORM method [35], the modified I-FORM using principal component analysis (PCA) [36], and the Gumbel and Clayton copula methods [22,27]. Each of these methods use parametric probability distribution fits to determine the joint distribution of sea state variables and are described in Section 2.1. Non-parametric contour methods, limited in this study to a method using kernel density estimation (KDE), do not require parameterized probability distributions to model this joint distribution. These methods also do not require the use of the I-FORM to generate contours; instead, they estimate contours directly from the joint probability distribution. This is described in Section 2.2.

In addition to the separation of the contour methods based on the method for defining the joint distribution, this separation also respects the difference in terms of the method used for constructing the environmental contour from the joint distribution. Various contour construction methods are discussed and compared in [29]. As is mentioned above, the parametric contour methods under study in the current work use the I-FORM contour construction approach. The non-parametric contour method under study uses the HDC method for contour construction. As is discussed in [29], the use of these differing contour construction methods leads to a difference in the interpretation of the contours themselves. The implications of these interpretive differences are not examined in the current work, as contours utilizing various construction methods are regularly compared directly for use in regular engineering practice. However, including this difference more rigorously in the comparison of contour methods remains an important area of future work that is noted for this study.

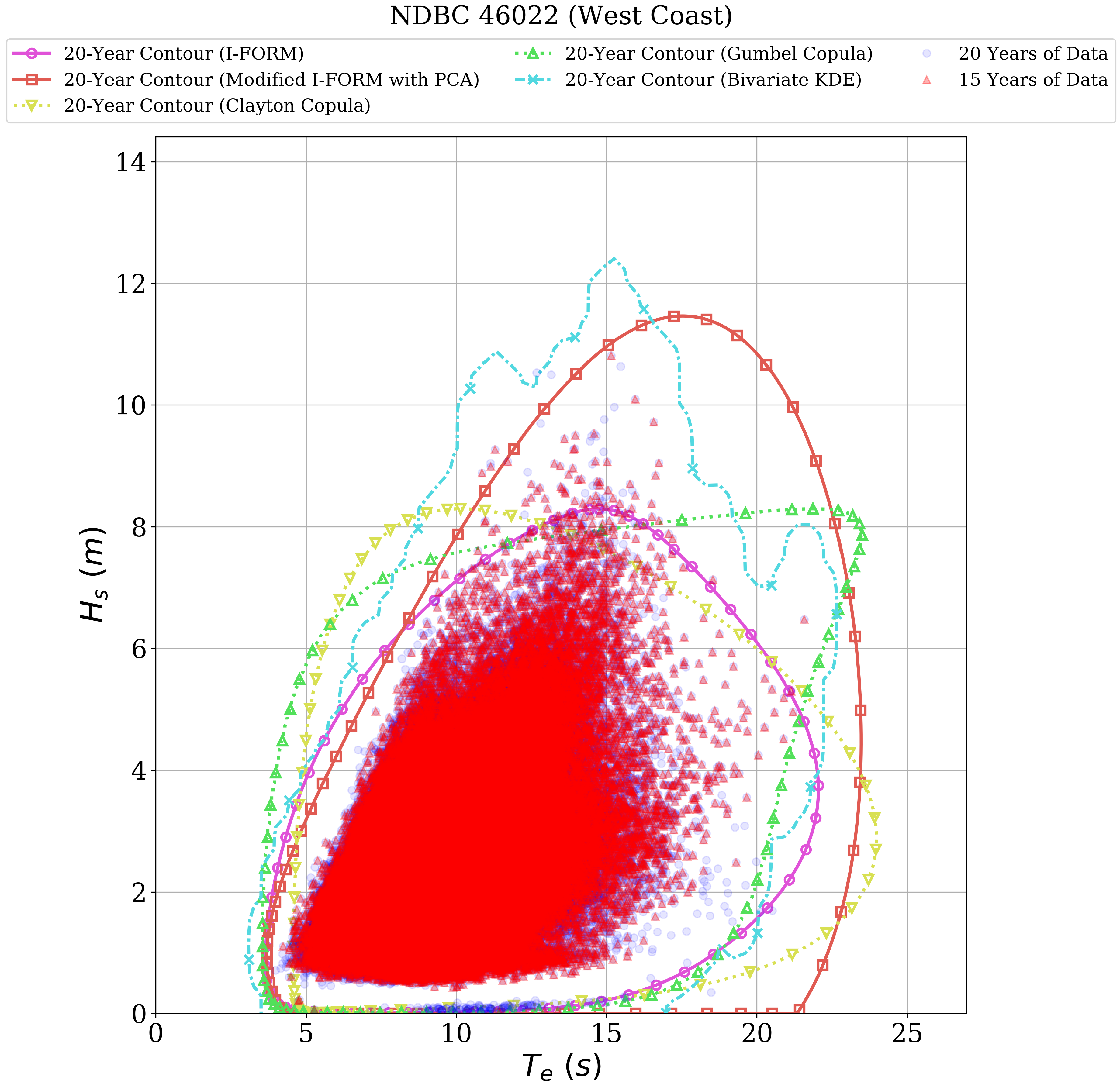
Environmental contours resulting from calculations using all five methods under consideration at a single study site are shown as an example in Figure 1.

2.1. Parametric Contour Methods

Four commonly used parametric contour methods were chosen for comparison in this study: the traditional I-FORM method, the modified I-FORM using PCA [36], the Gumbel copula method, and the Clayton copula method. These contour methods have all been implemented in the open-source WEC Design Response Toolbox (WDRT) [37].3 While all four methods use the I-FORM approach to generate environmental contours, they differ in the assumptions that are required to generate a joint distribution for $H_s$ and $T_e$. An overview of the assumptions for each method is provided below.

2.1.1. Traditional I-FORM Method

The traditional I-FORM method for generating extreme sea state contours was first proposed and then refined by Haver and Winterstein [16,17]. The implementation of the traditional I-FORM method in the WDRT uses similar steps for the construction of the joint distribution of $H_s$ and $T_e$, as given in [14,39]. This implementation differs slightly from these formulations in the functions that are used to fit the parameters of the lognormal distribution as a function of $H_s$ as a part of the construction of the conditional distribution. A two-parameter Weibull distribution (Equation (1)) is first fit to $H_s$ using maximum likelihood estimation:

$$f_{H_s}\left(h\right)=\frac{\delta }{\alpha }{\left(\frac{h}{\alpha }\right)}^{\delta -1}exp\left(-{\left(\frac{h}{\alpha }\right)}^{\delta }\right)$$

(1)

where $\alpha$ and $\delta$ are the scale and shape parameters of the distribution, respectively.

The $T_e$ values are then binned based on their corresponding $H_s$ values, and a conditional distribution of $T_e$ given $H_s$ is fit to a lognormal distribution with parameters $\mu$ and $\sigma$ estimated through a least squares procedure for the following fitting functions, where a and b are least square regression coefficients:

$$f_{\mu }\left(H_s\right)=a_1+a_2{H}_s+a_3{H}_s^2$$

(2)

$$f_{\sigma }\left(H_s\right)=b_1+b_2{H}_s+b_3{H}_s^2$$

(3)

The formulation for the distribution coefficients above was explored and presented in [27] and, as described above, differs from the formulation given in [14,39].

The conditional distribution of $T_e$ given $H_s$ is then given by:

$$f_{T_e|H_s}\left(t\right|h)=\frac{1}{\sqrt{2\pi }{f}_{\sigma }\left(h\right)t}exp\left(-\frac{1}{2}{\left(\frac{lnt-f_{\mu }\left(h\right)}{f_{\sigma }\left(h\right)}\right)}^2\right)$$

(4)

The marginal distribution of $H_s$ and the conditional distribution of $T_e$ given $H_s$ are used in the I-FORM process to calculate an environmental contour.

2.1.2. Modified I-FORM with PCA

The modified I-FORM with PCA, as detailed in [36], uses PCA to rotate the pairs of $H_s$ and $T_e$ into a new orthogonal basis in which two new variables, $C_1$ and $C_2$, are uncorrelated. An inverse Gaussian distribution (Equation (5)) is first fit to $C_1$, with parameters estimated through maximum likelihood estimation:

$$f_{C_1}\left(x\right)={\left(\frac{\lambda }{2\pi x^3}\right)}^{1/2}exp\left(\frac{-\lambda {(x-\mu )}^2}{2{\mu }^{2}x}\right)$$

(5)

where $\mu$ and $\lambda$ can be interpreted as representing the location and scale of the inverse Gaussian distribution.

$C_2$ values are then binned based on their corresponding $C_1$ values, and a conditional distribution of $C_2$ given $C_1$ is fit to a normal distribution with parameters estimated through a least squares procedure for the following fitting functions, where $\beta$ and $\gamma$ are least squares regression coefficients:

$$f_{\mu }\left(C_1\right)={\beta }_0+{\beta }_1{C}_1$$

(6)

$$f_{\sigma }\left(C_1\right)={\gamma }_0+{\gamma }_1{C}_1+{\gamma }_2{C}_1^2$$

(7)

The marginal distribution of $C_1$ and the conditional distribution of $C_2$ given $C_1$ are used in the I-FORM process to calculate a contour, and the points along the contour are then back-transformed into the original data space.

2.1.3. Gumbel and Clayton Copulas

Copula methods [22] create a joint distribution for $H_s$ and $T_e$ by fitting a marginal distribution for $H_s$, and then fitting a conditional distribution of $T_e$ given $H_s$ using a dependence structure that is based on the choice of copula. The Gumbel copula uses the following form for the conditional distribution:

$$C_{T_e|H_s}\left(t\right|h)=C(t,h)\frac{{[{(-lnh)}^{\theta }+{(-lnt)}^{\theta }]}^{-1+\frac{1}{\theta }}{(-lnh)}^{\theta -1}}{h}$$

(8)

where $\theta$ is a parameter related to Kendall’s Tau correlation measure, and $C(t,h)$ is the joint distribution of the Clayton copula, as defined in [22]. The Clayton copula uses a conditional distribution of the form:

$$C_{T_e|H_s}\left(t\right|h)=h^{-1(1+\theta )}{(h^{-\theta }+t^{-\theta }-1)}^{1+\frac{1}{\theta }}$$

(9)

where, again, $\theta$ is a parameter related to Kendall’s Tau correlation measure, and $C(t,h)$ is the joint distribution of the Clayton copula, as defined in [27].

Similar to the traditional I-FORM and PCA methods, the marginal and conditional distributions are then used in the I-FORM process to generate the environmental contour. While there are many copula methods that can be used to specify the conditional distribution, the Gumbel and Clayton copulas were chosen as illustrative examples. Recently, Vanem [40] showed that traditional copula methods can perform poorly when applied to sea state data because the copula methods assume that the data is radially symmetric. Rodriguez [41] provides a useful summary of copula methods, including those applied here, with a particular focus on their differing tail dependence. As such, relatively poor copula performance was seen in this study (see Section 5). While there are methods to adjust the copulas to deal with asymmetric data, the goal of this study was to develop metrics for comparing environmental contours; thus, it was beneficial to include methods with varying levels of performance.

2.2. Nonparametric Contour Methods

The contour methods described above require a parametric probability distribution to be fit to the marginal or conditional data. It can be difficult to find a parametric approach that is flexible enough to adequately model the sea states at a wide variety of sites, because the underlying structure of the data across multiple sites can vary drastically (in, e.g., period of record, data fidelity, local weather patterns, local bathymetry). Consequently, it is of interest to consider nonparametric methods to model extreme sea state contours for a variety of locations. The contour construction method utilized for the contour method using a nonparametric joint distribution is the HDC method.

2.2.1. Kernel Density Estimation

A commonly used nonparametric approach for defining the probability distribution of data is kernel density estimation (KDE) [42,43]. A KDE can be thought of as a smoothed histogram, where kernel functions are used in the place of histogram bins. Kernel functions are evaluated across the domain of the data, X, creating a small density curve around each data point. The resulting density curves are then summed to obtain an overall estimate of the density of the data. A kernel function $K\left(x\right)$ is a function such that:

$${\int }_{-\infty }^{\infty }K\left(x\right)dx=1.$$

(10)

The univariate kernel density estimator can then be defined as:

$$\widehat{f}\left(x\right)=\frac{1}{nh}\sum _{i=1}^{n}K\left(\frac{x-x_i}{h}\right),$$

(11)

where h is the bandwidth that serves as a smoothing parameter for the kernel estimate and $x_1,x_2,...,x_n$ are the n data points. The extension to the bivariate case is straightforward, as shown in Equation (12), and can be extended into higher dimensions. KDE allows the joint distribution of $H_s$ and $T_e$ to be estimated directly from the data, without parametric assumptions and without the need for specifying marginal and conditional distributions.

$$\widehat{f}(x_1,x_2)=\frac{1}{n}\sum _{i=1}^n{K}_1\left(\frac{x_1-x_{1i}}{h_1}\right)K_2\left(\frac{x_2-x_{2i}}{h_2}\right)$$

(12)

2.2.2. Kernel and Bandwidth Selection

It has been shown that the KDE is not sensitive to the choice of kernel [44]. Because of this, the commonly used Gaussian kernel was chosen, as defined by:

$$K\left(x\right)=\frac{1}{\sqrt{2\pi }}exp(-x^2/2)$$

(13)

Kernel methods often utilize the same kernel across the domain of interest with an optimal kernel selected by fitting the sample data. This means that while the kernel-like does a good job of representing high density areas, representation of the tails of the distribution may not be as appropriate. This may be problematic relative to the field of environmental contour construction as this relies on extrapolation in extreme regions to generate a contour. While it is beyond the scope of the current study, future work could examine the performance of kernels at the boundaries of the data to improve contour development.

While the KDE is not particularly sensitive to the kernel, it is sensitive to the choice of bandwidth. The bandwidth serves as a smoothing parameter as it controls the width of the density curves around each data point. As the value of the bandwidth increases, so does the smoothness of the KDE. It is also important to note that the behavior in the tails of the distribution can change with bandwidth. In the case of the oversmoothed KDE, non-zero probability is given to a wider range of X values than the undersmoothed KDE. With larger samples, this difference may not be as pronounced, but it emphasizes that the choice of bandwidth can affect the resulting environmental contour.

Since the density of the sea state data generally varies across the range of $H_s$ and $T_e$ values, it can be difficult to find a bandwidth that provides a reasonable amount of smoothing. A method for calculating environmental contours of extreme sea states using KDE with adaptive bandwidth selection was proposed in [23]. The use of KDE to generate environmental contours of $H_s$ and wind speed was further explored in [24], which determined that a KDE with a constant bandwidth rather than an adaptive bandwidth estimate could achieve good contour results when compared to traditional methods. Further exploration of the methods suggested in [23] with a larger number of study sites led to the same conclusion regarding a constant bandwidth KDE, as presented in [24]. Thus, a constant bandwidth was selected for use in the KDE contours presented in this study. A rule of thumb bandwidth suggested by [42] was used for this study, and is given by:

$$h_i={\left(\frac{4}{d+2}\right)}^{\frac{1}{d+4}}{n}^{\frac{-1}{d+4}}{\sigma }_i$$

(14)

where d is the number of dimensions, n is the number of data points, and ${\sigma }_i$ is the standard deviation of the ith variable. While a fixed bandwidth was used, the metrics defined in this paper can be used to assess contour performance relative to the choice of bandwidth.

3. Comparison Metrics

The five contour methods described in Section 2 were chosen to exercise the comparison metrics that are discussed in the following sections. These metrics focus on assessing three key aspects of environmental contours: predictive accuracy, physical validity, and aggregated temporal performance. Given that a definition for a perfect contour is elusive, these metrics are targeted at providing relative, not absolute, means of judging environmental contours. The metrics and methods proposed in this paper are intended to be agnostic to the device, structure, or application field of interest and are thus not directly tied to any specific device response. This allows the contour methods to be compared directly in a structured comparison framework prior to their use as inputs in a structural design workflow.

3.1. Predictive Accuracy

The purpose of environmental contours of extreme sea states is to predict future sea state behavior. Thus, the usefulness of a particular contour method should be measured by providing a quantitative estimate of this predictive accuracy. Predictive accuracy can be estimated by calculating an environmental contour using a subset of historical data and then comparing this calculated contour to the true behavior, as measured in the remainder of the data set.

The predictive accuracy metric is estimated by comparing the closeness with which the n-year contour captures n years of data and it can be approximated by calculating the overlapping area shared by the contour and the data. Empirical contours of the data were approximated by a polygon estimated using the outermost points of the data set using the shapely package in Python. This approach for constructing empirical contours is akin to an HDC method, where the contour is constructed to contain the full data density without overinflation. A binning approach is used to enforce this by allowing the contour to follow the data, even in regions of concavity in which a convex contour representation would misrepresent the data density. Although the method for finding the empirical contour of the data has some sensitivity to tuning parameters, the contour is a reliable estimate of the area covered by the n-year data set. It is important to note that this method of contour construction also differs from the various underlying contour construction methods described for each of the contour methods under study (see, e.g., [29] for an excellent discussion on the exceedance probabilities of differing contour construction methods).

Following the definition of the empirical contour of the n-year data set, the overlapping area of the n-year environmental contour can be determined. This area is defined by the intersection between the empirical contour of the data and the predicted environmental contour. The area of this polygon can be calculated using principles of geometry. The shapely package was applied to both find the intersection of the two contours and to calculate the area of this intersection.

A notional example of the comparison of an empirical contour and a predicted environmental contour, along with their overlapping area, is shown in  Figure 2. This notional comparison of the empirical data contour and the calculated environmental contour must now be transformed into a quantitative metric for comparison. The goal of this study is to both develop metrics for assessing the predictive accuracy of methods for calculating environmental contours of extreme states and to compare the results of this assessment across many sites. The comparison of the overlapping area of the n-year environmental contour with the empirical contour of n years of data across many sites requires a normalized metric that is not skewed by the magnitude of the sea states observed at a given site. This normalized metric is calculated using the sum of two ratios: the ratio of the overlapping contour area with the empirical data-based contour, and the ratio of the overlapping contour area with the predicted contour. This metric, hereafter referred to as the overlapping ratio, or $OR$, is defined as:

$$OR=\frac{1}{2}\left[\frac{OverlappingContourArea}{AreaofEmpiricalContour}+\frac{OverlappingContourArea}{AreaofPredictedContour}\right]$$

(15)

If a contour has good predictive accuracy, both ratios in the $OR$ sum should be close to 1. Therefore, an $OR$ value close to 1 represents a contour that has high predictive accuracy. Conversely, if the $OR$ value is close to 0, the contour has low predictive accuracy.

3.2. Physical Validity

Environmental contours of extreme sea states are often scrutinized for inaccurate representation of the possible wave environment that could be observed in the future. Many environmental contours cover areas of the $H_s$-$T_e$ space that are not physically possible due to the breaking steepness (defined as the ratio of height to wavelength: $S=H/L$) of ocean waves. Waves with a large steepness (i.e., large amplitude and short period), will quickly become unstable and break (see, e.g., [45]). Employing the deep water dispersion relation to relate wave period and wavelength, the breaking steepness can be expressed in terms of wave height and period: $S=2\pi \frac{H}{g{T}^2}$. While the precise steepness at which wave breaking occurs varies, depending on currents, winds, and other factors, empirical observations show breaking steepnesses of $1/25<S<1/10$ when defining S for a sea state (see, e.g., [14,45]). However, since contour methods are generally statistical in nature, contours can often be inflated in this non-physical wave breaking space. This non-physicality of many contour methods weakens their use as inputs to simulations assessing the stability of marine structures. As noted by Mackay and Jonathan [46], one potential solution to this issue is a transformation of the variables so that the contour can be defined based on, e.g., $H_s$ and S.

The overlapping area of the environmental contour and the estimated breaking steepness curve (here, we use $S>0.07$ to signify breaking), serves as a quantitative estimate of this non-physical contour behavior. Similar to the calculation presented in Section 3.1, the overlapping area of the environmental contour with the steepness curve is defined by the intersection of these two curves. The area of this intersection is also calculated using the polygon features available in the shapely Python package. A notional example of the overlapping area of the environmental contour and the breaking steepness curve is also shown in  Figure 2.

Once again, the overlapping area of the environmental contour and steepness curves is normalized by the area of the contour to allow for comparison of this metric across study sites. This metric, hereafter referred to as $OSP$, is calculated as:

$$OSP=1-\frac{OverlappingSteepnessArea}{AreaofPredictedContour}$$

(16)

If a contour has good physical validity, the overlap of the breaking steepness curve with the environmental contour will be small, meaning that the $OSP$ will be closer to 1, as given in the formulation above. Conversely, the smaller the value for the $OSP$, the greater the overlap of the breaking steepness curve with the environmental contour, indicating a lack of physical validity.

3.3. Temporal Aggregation

One important consideration for the aforementioned comparison metrics is that they can vary over time for a single site. Therefore, this paper uses a validation set approach [47] to aggregate the performance of contour methods across time as described by the predictive accuracy and physical validity metrics given in the preceding sections. In this approach, the first step is to divide the data into training and validation sets. The training set is used to fit the model (in this case, the environmental contour method) and the validation set is used to assess the performance of the model. The data are broken up into several training and validation sets and the model is assessed multiple times. The results are then combined to get an overall estimate of a method’s performance. The typical validation set approach requires randomly dividing the data into training and validation sets. However, as environmental sea state data are collected across time, the time series nature of the data is used to define the sets.

Figure 3 provides a visual representation of the time-dependent training and validation sets and the steps for the process are given as follows. Consider a buoy that has collected 20 years of historical sea state data. Using the first year of data as a training set, an environmental contour of extreme sea states is calculated with a return period of 5 years. This predicted environmental contour is then compared to the entire 5-year historical data set (the validation set). A comparison metric (i.e., the $OR$ or the $OSP$), denoted in Figure 3 as $p_1$, is estimated.

Next, the first 5 years of data are used as a training set to estimate an environmental contour with a return period of 10 years. A second comparison metric, $p_2$, is calculated by comparing to a validation set of the 10-year historical data. This process is repeated twice more, once with using 10 years of data to predict a 15-year contour and finally using 15 years of data to predict a 20-year contour. The estimated metrics ($p_i,i=1,...,4$) are then averaged to give an overall comparison metric for the contour method at that site. This calculation can be extended to any site at which enough historical observations have been collected to provide a subset of data that can be used to calculate an n-year contour for comparison to n years of data. This method for aggregating assessment metrics across time could further be extended to include additional metrics beyond the measures of predictive accuracy and physical validity proposed in this paper.

An alternative approach to characterizing temporal sensitivity could utilize the bootstrap method. This approach has been used in the EC Benchmark study [33] and in other previous contour studies; see, e.g., [23,27,31,40]. However, the forward chaining approach has been proposed in this work as a novel method of making comparisons temporally across various training and test sets with potentially fewer and faster calculations than might be required under the bootstrap method.

4. Data Collection and Study Sites

The sites selected for study in this paper are buoys deployed and maintained by the National Data Buoy Center (NDBC). NDBC buoys are located in coastal regions and in large bodies of water around and throughout the United States. Hourly spectral energy density observations (from which $H_s$ and $T_e$ may be calculated) are available for many NDBC buoys. A subset of these sites was selected for analysis. This subset includes sites with a long enough deployment such that enough observations are available for the predictive accuracy calculations described in Section 3.1. For the purposes of this study, sites with at least 20 years of data were selected.

The application of this work is intended to focus on coastal sites. Because of this focus, the subset of 39 NDBC sites selected for analysis includes coastal regions only. While NDBC buoys with sufficient data are available in, e.g., the Great Lakes, these were not included in the present study.

In addition to being geographically diverse, the behavior of waves across the sites selected for this study varies dramatically. This variation serves as a test for contour methods that have previously been developed using only single or a few sites of interest. The buoys selected for this study are shown in Figure 4. In addition to showing the locations of the buoys utilized in this study, Figure 4 distinguishes the region of each buoy (Gulf of Mexico, Alaska, the U.S. East Coast and the U.S. West Coast).

5. Aggregation of Results into a Comparison Framework

The following sections describe and present conclusions regarding the resulting comparison metrics calculated for the selected study sites. Section 5.1 presents the mean and standard deviation of the calculated predictive accuracy and physical validity metrics for each of the five contour methods. Section 5.2 gives overall comparisons for the contour methods across all study sites. Section 5.3 compares results for each method across the studied geographical regions, including the Gulf of Mexico, Alaska, the U.S. East Coast and the U.S. West Coast. This aggregation of results and accompanying comparative analysis outlines a comparison framework that could be applied for additional contour methods or augmented to include additional metrics of interest.

5.1. Contour Calculations

Environmental contours of extreme sea states were calculated using the five contour methods of interest discussed in Section 2 for all study sites. The predictive accuracy and physical validity metrics discussed in Section 3 were calculated for each of these contour methods at each site. These metrics were aggregated using the training and validation sets of data described in

Table 1. Contour Comparison Training and Validation Sets.

Training Set (Years)	Validation Set (Years)
1	5
5	10
10	15
15	20

, in order to assess the performance of contour methods across time.

Note that it may be of interest to assess contour methods for a particular training and test set in order to meet design requirements describing an expected period of performance (e.g., 15 years of data used to predict a 25 year contour). In this case, the proposed assessment metrics could be calculated for the training and test set of interest without aggregation, using the method described in Section 3.3. For the purposes of the current work, the results that follow include only the aggregated metrics, as the goal of this study is to present a complete end-to-end workflow for assessment.

Table 2. Predictive Accuracy and Physical Validity Metrics for Contour Methods.

Method	OR Metric		OSP Metric		Average (OR, OSP)
	Mean	SD	Mean	SD	Mean	SD
Traditional I-FORM	0.77	0.06	0.97	0.02	0.87	0.03
PCA/I-FORM	0.77	0.05	0.96	0.04	0.87	0.04
Clayton	0.72	0.06	0.89	0.06	0.81	0.05
Gumbel	0.72	0.07	0.90	0.05	0.81	0.05
KDE	0.81	0.04	0.95	0.02	0.88	0.03

provides the mean and standard deviation for each of the assessment metrics. The mean gives an overall indication of a method’s performance in relation to the assessment metric, while the standard deviation provides an estimate of the spread of results. A mean that is close to 1 indicates that the contour method has respectively high predictive accuracy ($OR$) or high physical validity ($OSP$). A large standard deviation would imply that the performance of that particular method greatly varies across different sites or across time.

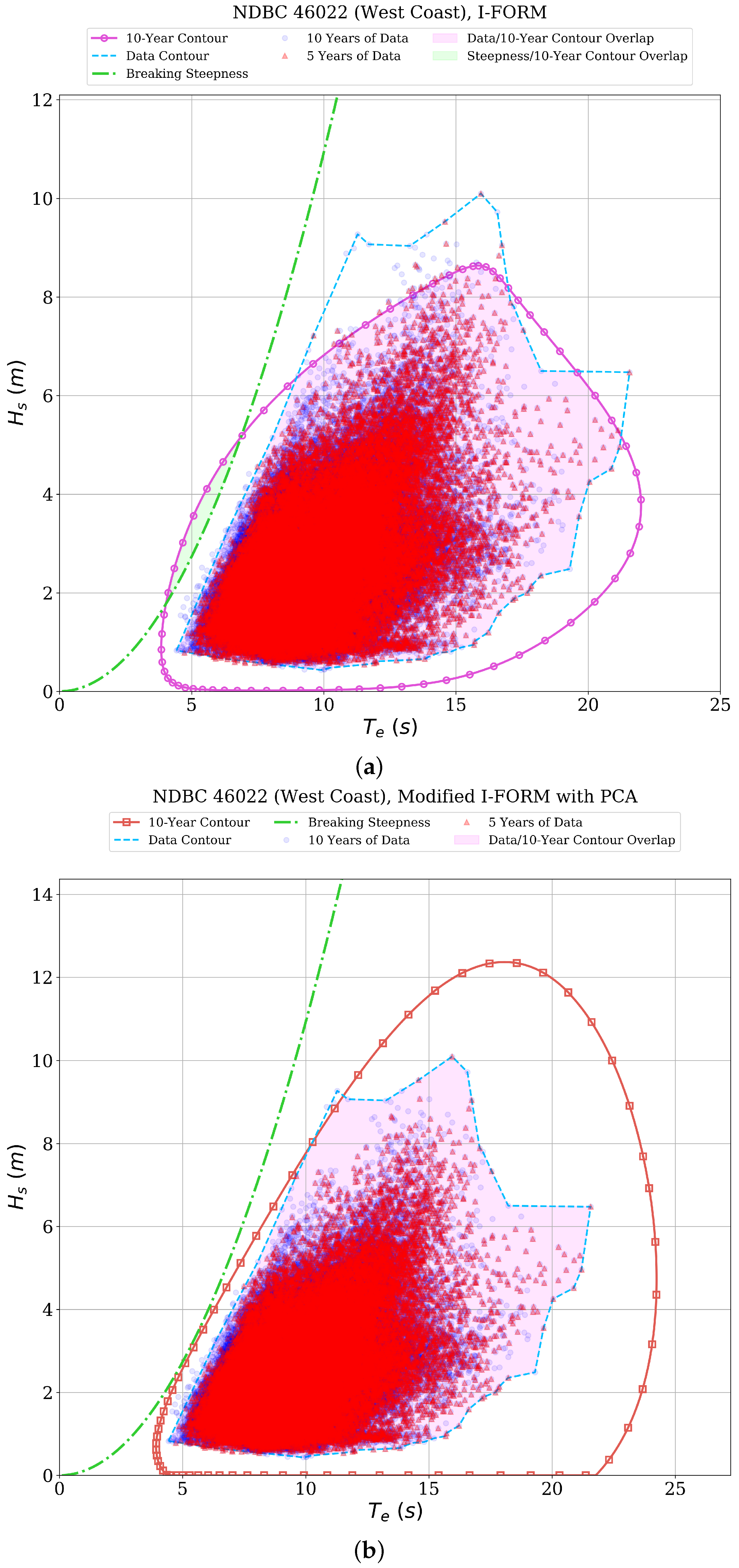
An example of the complete set of contours calculated at a single site and their corresponding graphical representations of the predictive accuracy and physical validity metrics is shown in Figure 5, Figure 6 and Figure 7. These examples show the 10-year environmental contour predicted using 5 years of data at NDBC buoy 46022.

The following sections present and review the comparison metric results in two modes. First, the overall results (across all sites) are compared for the different contour methods. Second, a region-by-region comparison is performed.

The comparison metric results are presented using boxplots. Boxplots provide a visual representation of the center and spread of the metric values. The solid line in the center of the box is the median metric value and the lower and upper edges of the box represent the 25th and 75th percentiles, respectively. The “whiskers” show the effective minimum and maximum metric values and any points that fall outside of the “whiskers” are considered outliers.

It is important to note that the metrics and methods proposed in this paper present a broad assessment of contour methods across many sites. It is still critical that engineering judgement be applied to assess the validity of a contour method prior to use at a specific site of interest. The comparison framework presented in this paper is not intended to replace this engineering judgement, but is instead intended to support and augment the design analysis process in an objective fashion that could be automated across many sites to provide a comprehensive dataset to support the decision-making process.

5.2. Overall Comparisons

The overlapping ratio ($OR$) (Equation (15)) for each contour method can be seen in Figure 8. Recall that an $OR$ value close to 1 implies that a contour has high predictive accuracy. The results presented in Figure 8 show that the KDE method has the highest median $OR$ value, as well as the smallest amount of variability in the results across sites. The Clayton and Gumbel copula methods have the lowest median $OR$ values, while the PCA and traditional I-FORM perform similarly, with less variability in the PCA contour results. These results are demonstrated in the examples of each contour method shown for NDBC 46022. For this site, the KDE method is the closest to the empirical data contour, as shown in Figure 7. The remaining methods do not match the shape of the empirical data contour and/or under- or overestimate the empirical data contour significantly in this example.

Figure 9 shows the overlapping steepness area to the predicted contour metric ($OSP$) (Equation (16)) for each contour method. Recall that an $OSP$ value close to 1 would imply that the contour method is accurately representing the physical boundary of the wave environment. Overall, all but the copula methods have median values that are close to 1, though the PCA method again has more variation in results. The copula methods show a smaller ratio, which is likely caused by the relatively inflexible parametric structure of the copula, which allows a larger area of the resulting contours to overlap the breaking steepness line. These results are again demonstrated in the examples of each contour method shown for NDBC 46022. The I-FORM, PCA, and KDE contours follow the breaking steepness line more closely when compared to the copula contours (Figure 5, Figure 6 and Figure 7).

The average of the $OR$ and $OSP$ metrics for each contour method is shown in Figure 10. Both the $OR$ and $OSP$ metrics vary between 0 and 1, with 1 indicating good accuracy for both metrics. Thus, the average of these metrics can be taken to describe the overall performance of each contour method in both predictive accuracy and physical validity. If one of these metrics is of greater importance for a given application, a weighted average could be computed. However, for the purposes of this study, both the $OR$ and $OSP$ metrics are given equal weight. The results shown in Figure 10 demonstrate that the copula methods have the lowest median value for this average metric, with slightly greater variability in the Clayton contour method results. The I-FORM and PCA methods perform similarly, with median values closer to 1 than the copula methods and with similar variability. Finally, the KDE method has the highest median value for the average metric and has the least variability across all sites, although there are some outlying sites with lower values.

The comparisons provided above could impact design analysis workflows for offshore structures and the development of contour methods in several ways. First, the overall comparisons could be used to assist in the selection of contour methods for consideration in a design analysis. It may not be feasible for an analysis to consider any number of contour methods as a first step; the down-selection of methods for consideration could be a valuable first step in this process, particularly if more than the five methods presented in this paper were available for use. Second, the results presented above could be used to drive the development of additional contour methods or variations on the methods presented herein. For instance, the performance of the copula methods in terms of the $OSP$ metric indicates that the expression of the joint distribution of $H_s$ and $T_e$ for these methods may miss some of the dependency of these parameters that encodes the physical constraint of the breaking steepness curve. Thus, the development of similar methods could focus on capturing this physical constraint as a part of the development of an expression of the joint distribution of the sea state parameters. Finally, the overall comparison framework presented could be utilized to assess newly proposed contour metrics against the methods that have previously been proposed. This would allow analysts to understand at a high level whether newer methods should be considered for deployment in design analysis workflows.

5.3. Comparisons by Geographic Region

The predictive accuracy and physical validity metrics were also calculated for each method by geographic region. Geographic regions were identified as the Gulf of Mexico, Alaska, the U.S. East Coast, and the U.S. West Coast, as depicted in Figure 4.

The $OR$ metric is shown for all five contour methods at each geographic region in Figure 11. The results in this figure show that the traditional KDE has the highest $OR$ values, on average, across all regions. The Gulf of Mexico has the lowest average $OR$ values across most methods; the KDE method performs relatively well in this region though there is more variability in the results across the gulf sites. The lowest average $OR$ values in the Gulf of Mexico are those calculated for the Clayton and Gumbel copula methods. Alaska shows relatively low variability in the results per method, with the highest average metric values calculated for the I-FORM and KDE methods. The East Coast and West Coast regions perform similarly, with the copula methods performing worse on average than the other methods.

The $OSP$ metric for each region is shown in Figure 12. The West Coast region shows the tightest grouping of overlapping steepness performances and also the best performance for most of the contour methods (i.e., values of the $OSP$ metric close to 1). Conversely, the results presented for the Gulf of Mexico show the poorest $OSP$ performance for most methods and show the highest level of variability of overlapping steepness performance amongst the regions of interest. The average performance and variability of the PCA method in terms of the $OSP$ metric differs significantly between the regions. The PCA method clearly performs best in terms of the $OSP$ metric in West Coast locations, both on average and in terms of variability, but shows a great deal of variability for sites along the East Coast. The Clayton and Gumbel copula methods have lower $OSP$ metric values on average than all of the other methods across all regions of interest.

The average of the $OR$ and $OSP$ metrics across the methods and regions of interest is shown in Figure 13. As expected, this average metric generally follows the observations presented for the $OR$ and $OSP$ metrics separately. The West Coast region has the best overall performance for all contour methods, while the Gulf of Mexico has the poorest performance overall.

The comparative conclusions across geographical regions drawn using these metrics could impact design analysis workflows for offshore structures in several ways. First, the differences in performance across regions indicate that geographical variations in the wave resource should be considered as a part of any generalized design analysis. For instance, based on these results, a methodology for developing environmental contours of extreme sea states that is applied for an analysis of a site on the West Coast should not be applied directly to an analysis performed for a site in the Gulf of Mexico withought careful consideration and review. Second, the aggregated results presented could be used to recommend contour methods for consideration at various sites of interest as a first step in developing a workflow for design analysis. This could be a first step in down-selecting a contour method to be used to predict extreme sea states for design purposes; this contour method could be further refined depending on the requirements of the design analysis. This supports an objective analysis of contour methods that could be automated to support a faster design analysis workflow.

6. Conclusions

This paper presented a comparison framework for evaluating methods for developing environmental contours of extreme sea states. Five environmental contour methods were selected as candidate methods for evaluation under this comparison framework. Each of these methods was used to calculate environmental contours of extreme sea states for 39 ocean locations, with sites from all U.S. coastal regions. In order to quantitatively evaluate the relative performance of these contours, a series of metrics investigating predictive accuracy, physical validity, and aggregated temporal performance were developed and utilized in a proposed comparison framework.

By evaluating the contour methods via these metrics, both across the bulk set of sites and within specific geographic regions, this study has provided general performance ratings for each method. These performance ratings could be used to compare and select the best contour method to predict extreme sea states at a specific site or within a given region for use in many application fields of interest. In addition, these performance metrics could be used to evaluate the performance of newly proposed contour methods against the methods that have previously been presented both in the literature and/or in the standard of practice.

Future work could improve upon this study in a number of ways. With the metrics developed here, a number of factors beyond geographic region which may affect contour performance could be considered. For example, locations could be classified in terms of local weather patterns (e.g., whether or not strong seasonal storms are present) or local bathymetry (e.g., is the water sufficiently shallow to affect wave propagation). In addition, this work could be extended to a wider set of contour methods and sites and could be used to evaluate new methods for calculating environmental contours of extreme sea states. The contour methods that are studied in this work utilize differing contour construction methods, which may impact the approach that should be taken for evaluating the contours against one another. This remains an important area of future work that is beyond the scope of the current study.

Furthermore, additional metrics beyond those detailed in this work could be included in the proposed comparison framework to provide greater insight into the performance of environmental contours of extreme sea states. These additional metrics could include those to address issues pertinent to a specific application area or analysis discipline, such as metrics related to structural response across contour methods or additional physics-based metrics based on wave dynamics.