DEA-Bootstrapping Analysis for Different Models of Spanish Port Governance
Abstract
:1. Introduction
2. Materials and Methods
3. Methodology
3.1. Definition of the Inputs/Outputs
3.2. Scenarios of the Port System
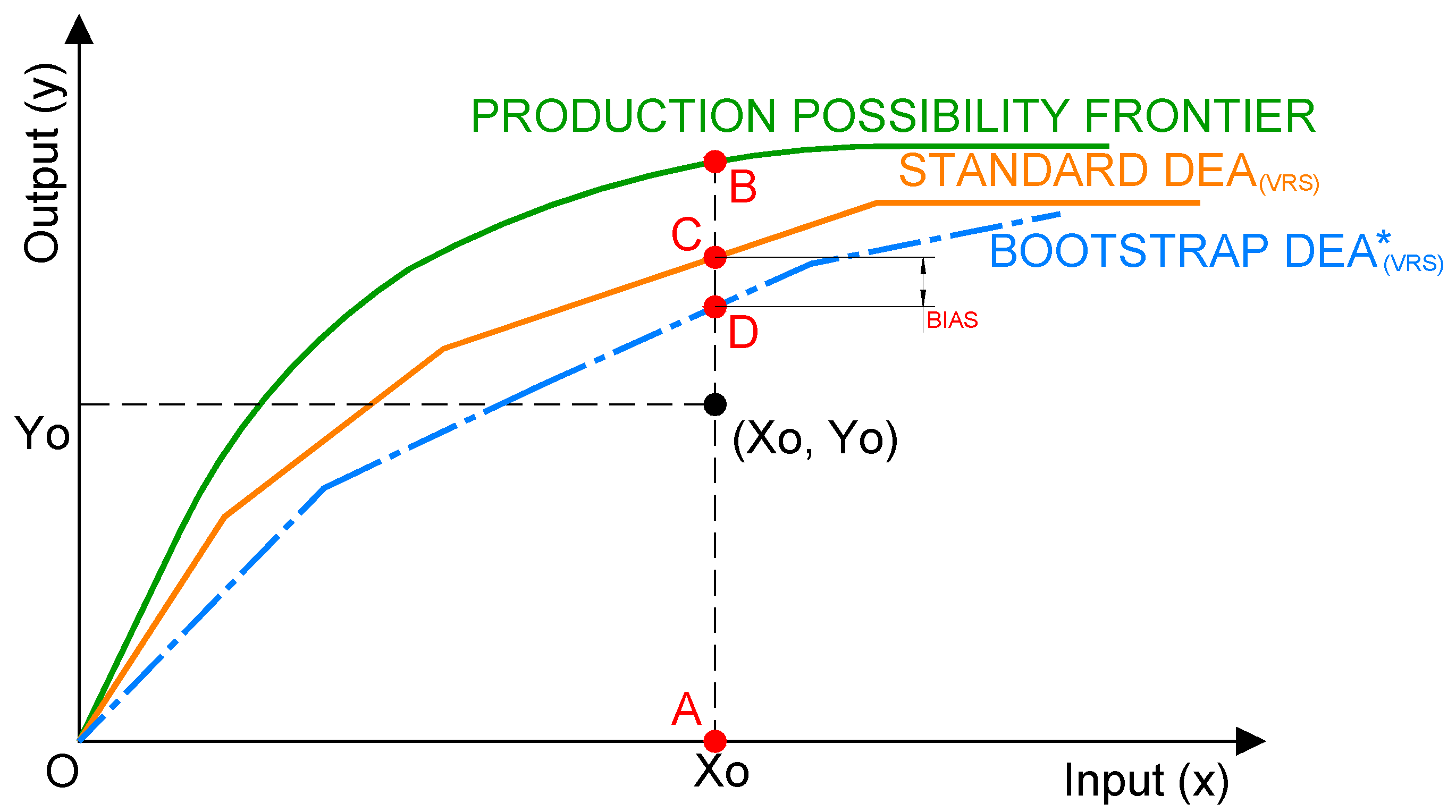
3.3. Visualisation of Data
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- González, A.R.; González-Cancelas, N.; Serrano, B.M.; Orive, A.C. Preparation of a smart port indicator and calculation of a ranking for the spanish port system. Logistics 2020, 4, 9. [Google Scholar] [CrossRef]
- González-Cancelas, M.; Flores, F.S.; Orive, A.C. Modelo de eficiencia de las terminales de contenedores del sistema portuario español. Rect@ Rev. Electrónica Comun. Trab. Asepuma 2013, 14, 49–67. [Google Scholar]
- Bonilla, M.; Medal, A.; Casaus, T.; Sala, R.; Sala, T.C.R. The traffic in Spanish ports: An efficiency analysis. Int. J. Transp. Econ. /Riv. Internazionale Econ. Trasp. 2002, 2, 215–230. [Google Scholar]
- Coto-Millan, P.; Banos-Pino, J.; Rodriguez-Alvarez, A. Economic efficiency in Spanish ports: Some empirical evidence. Marit. Policy Manag. 2000, 27, 169–174. [Google Scholar] [CrossRef]
- Bartual, A.M.; Garrido, R.S. Análisis de la eficiencia y liderazgo de los puertos españoles por áreas geográficas. Revista Estud. Reg. 2011, 91, 161–182. [Google Scholar]
- Tongzon, J.L. Port choice and freight forwarders. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 186–195. [Google Scholar] [CrossRef]
- Parra, F. Análisis de Eficiencia y Productividad. 2007. Available online: http://econometria.files.wordpress.com (accessed on 20 October 2020).
- Todaro, M.P. Economic Development, 6th ed.; Longam: London, UK, 1997; pp. 549–550. [Google Scholar]
- Serrano, B.M.; González-Cancelas, N.; Soler-Flores, F.; Camarero-Orive, A. Classification and prediction of port variables using Bayesian Networks. Transp. Policy 2018, 67, 57–66. [Google Scholar] [CrossRef]
- Bartual, A.M. Perspectivas sobre la eficiencia del sistema portuario español. Rect@ Rev. Electrónica Comun. Trab. Asepuma 2011, 12, 1–20. [Google Scholar]
- Orive, A.C.; Mayora, J.M.P.; González-Cancelas, M.N. Determinación de indicadores de calidad en terminales portuarias de contenedores. Estud. Construcción Transp. 2005, 102, 161–172. [Google Scholar]
- Coelli, T.J. Recent developments in frontier modelling and efficiency measurement. Aust. J. Agric. Econ. 1995, 39, 219–245. [Google Scholar] [CrossRef] [Green Version]
- Samuelson, P.A.; Nordhaus, W.D. Economics, 19th ed; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Almawsheki, E.S.; Shah, M.Z. Technical efficiency analysis of container terminals in the middle eastern region. Asian J. Shipp. Logist. 2015, 31. [Google Scholar] [CrossRef] [Green Version]
- Kutin, N.; Nguyen, T.T.; Vallee, T. Relative efficiencies of ASEAN container ports based on data envelopment analysis. Asian J. Shipp. Logist. 2017, 33. [Google Scholar] [CrossRef]
- Cullinane, K.; Song, D.W.; Gray, R. A stochastic frontier model of the efficiency of major container terminals in Asia: Assessing the influence of administrative and ownership structures. Transp. Res. Part A Policy Pract. 2002, 36, 743–762. [Google Scholar] [CrossRef]
- Serrano, M.M.G.; Trujillo, L. La medición de la Eficiencia en el Sector Portuario: Revisión de la Evidencia Empírica; Universidad de Las Palmas de G.C., Departamento de Análisis Económico Aplicado. Documento de Trabajo: Las Palmas, Spain, 2005. [Google Scholar]
- Charłampowicz, J.; Mańkowski, C. Economic efficiency evaluation system of maritime container terminals. Ekon. I Prawo. Econ. Law 2020, 19, 21–32. [Google Scholar] [CrossRef] [Green Version]
- González-Cancelas, N.; Orive, A.C. Caracterización de parámetros físicos de las terminales de contenedores del sistema portuario español. Ing. Y Cienc. 2009, 5, 49–74. [Google Scholar]
- Wen, M.; Guo, L.H.; Kang, R.; Yang, Y. Data envelopment analysis with uncertain inputs and outputs. J. Appl. Math. 2014, 2014, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Pham, T.Q.M.; Kim, H.Y.; Lee, C.H. A study on the analysis of container port’s efficiency using uncertainty DEA model. J. Korea Port Econ.Assoc. 2016, 32, 165–178. [Google Scholar]
- Lio, W.; Liu, B. Uncertain data envelopment analysis with imprecisely observed inputs and outputs. Fuzzy Optim. Decis. Mak. 2017, 17, 357–373. [Google Scholar] [CrossRef]
- Pham, T.Q.M.; Park, G.K.; Choi, K.H. The efficiency analysis of world top container ports using two-stage uncertainty DEA model and FCM. Marit. Bus. Rev. 2020. [CrossRef]
- Gil-Ropero, A.; Dominguez, I.T.; Jiménez, M.D.M.C. Bootstrapped operating efficiency in container ports: A case study in Spain and Portugal. Ind. Manag. Data Syst. 2019, 119, 924–928. [Google Scholar] [CrossRef]
- Zhu, C. Analysis of operation efficiency for railway intermediary stations based on Cross-efficiency DEA. J. Railw. Sci. Eng. 2010, 6, 95–98. [Google Scholar]
- Teng, Y.; Feng, F.L.; Zhang, J. Assessment of china railway logistics performance based on DEA. J. Railw. Sci. Eng. 2010, 5, 23–34. [Google Scholar]
- Huang, C.F.; Shen, Y.P.; Chen, Y.W. Research on re-evaluating DEA efficient DMU based on production frontier. Oper. Res. Manag. Sci. 2008, 2, 48–52. [Google Scholar]
- Martinez-Budria, E.; Diaz-Armas, R.; Navarro-Ibanez, M.; Ravelo-Mesa, T. A study of the efficiency of Spanish port authorities using data envelopment analysis. Int. J. Transp. Econ./Riv. Internazionale Econ. Trasp. 1999, 237–253. [Google Scholar]
- Valentine, V.F.; Gray, R. The measurement of port efficiency using data envelopment analysis. In Proceedings of the 9th World Conference on Transport Research, Seoul, South Korea, 22–27 July 2001; Volume 22, p. 27. [Google Scholar]
- Wang, T.F.; Song, D.W.; Cullinane, K. Container port production efficiency: A comparative study of DEA and FDH approaches. J. East. Asia Soc. Transp. Stud. 2003, 5, 698–713. [Google Scholar]
- Barros, C.P. The measurement of efficiency of Portuguese sea port authorities with DEA. Int. J. Transp. Econ./Riv. Internazionale Econ. Trasp. 2003, 30, 335–354. [Google Scholar]
- Lin, L.C.; Tseng, L.A. Application of DEA and SFA on the measurement of operating efficiencies for 27 international container ports. East. Asia Soc. Transp. Stud. 2005, 5, 592–607. [Google Scholar]
- Cullinane, K.P.; Wang, T.F. The efficiency of European container ports: A cross-sectional data envelopment analysis. Int. J. Logist. Res. Appl. 2006, 9, 19–31. [Google Scholar] [CrossRef]
- Chiu, Y.H.; Huang, C.W.; Ma, C.M. Assessment of China transit and economic efficiencies in a modified value-chains DEA model. Eur. J. Oper. Res. 2011, 209, 95–103. [Google Scholar] [CrossRef]
- Barros, C.P.; Athanassiou, M. Efficiency in European seaports with DEA: Evidence from Greece and Portugal. In Port Management; Palgrave Macmillan: London, UK, 2015; pp. 293–313. [Google Scholar]
- Ropero, A.G. Eficiencia Operativa de Terminales de Contenedores. Análisis del Puerto Bahía de Algeciras y su Relación con los Puertos de la Península Ibérica. Ph.D. Thesis, Universidad de Cádiz, Cádiz, Spain, 2016. [Google Scholar]
- Gil-Ropero, A.; Turias, I.J.; Cerban, M. efficiency evolution of largest iberian peninsula container ports: An application of malmquist productivity index. Int. J. Transp. Econ. 2018, 45, 53–81. [Google Scholar]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Thanassoulis, E. Introduction to the Theory and Application of Data Envelopment Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- García, J.E.; Serrano, V.C. Competitividad y eficiencia. Estud. De Econ. Apl. 2003, 21, 423–450. [Google Scholar]
- Roll, Y.; Hayuth, Y. Port performance comparison applying data envelopment analysis (DEA). Marit. Policy Manag. 1993, 20, 153–161. [Google Scholar] [CrossRef]
- López Bermúdez, B. Eficiencia Portuaria y Modelos de Gobernanza. Ph.D. Thesis, Universidad de Acoruña, La Coruna, Spain, January 2018. [Google Scholar]
- Simar, L.; Wilson, P.W. Sensitivity analysis of efficiency scores: How to bootstrap in nonparametric frontier models. Manag. Sci. 1998, 44, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Orive, A.C.; Jiménez, M.D.M.C.; Domínguez, I.J.T.; Cancelas, N.G.; Orive, A.C. Metodología para la clasificación de los puertos mediante indicadores de explotación utilizando análisis de conglomerados. Inge Cuc 2016, 12, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Villaverde, J.; Maza, A. El hinterland de las fachadas marítimas españolas. Pap. De Econ. Española 2012, 131, 180–199. [Google Scholar]
- Villaverde Castro, J.; Maza Fernández, A.J. Competencia y Competividad Portuarias: Una Aplicación a las Fachadas Marítimas Españolas; Revista de Evaluación de Programas y Políticas Públicas: Madrid, Spain, 2015. [Google Scholar] [CrossRef] [Green Version]

| Year | Author | Scope of Study | Input | Output | Model |
|---|---|---|---|---|---|
| 1999 | Martínez-Budría, E. et al. | 26 spanish ports 1993–1997 |
|
| DEA-BCC (1) |
| 2001 | Valentine, J.S. y Gray, H.B. | 21 container ports in the world’s top 100 |
|
| DEA-CCR (2) |
| 2003 | Wang, T., Song, D.W. y Cullinane, K. | 28 ports in the TOP 30 (2001) world and 57 terminals |
|
| DEA-CCR-I DEA-BCC-I Stochastic function of Cobb-Douglas |
| 2003 | Barros, C.P. | 5 Portuguese ports 1999–2000 | Technical Efficiency
|
| DEA |
| 2005 | Lin, L. y Tseng, L. | 27 International Container Ports 1999–2002 |
|
| SFA (3) DEA-CCR DEA-BCC |
| 2006 | Cullinane, K. y Wang, T. | 69 Container terminals in 24 European countries 2002 |
|
| DEA-CCR DEA-BCC |
| 2011 | Chiu, Y., Huang, Ch. y Ma, Ch. | 30 Regions in China (Coastal, Central, and West) |
|
| DEA |
| 2015 | Barros, C.P. y Athanassiou, M. | 4 Portuguese ports and 2 Greeks 1998–2000 |
|
| DEA-BCC DEA-CCR |
| 2016 | Gil Ropero, A. | Port of Algeciras and the rest of the Port Authorities |
|
| DEA-CCR DEA-BCC |
| 2018 | Gil Ropero, A., Turias Domínguez, I. y Cerbán Jiménez, M.M. | 28 Spanish Port Authorities and 7 Portuguese Port Authorities |
|
| DEA-CCR DEA-Bootstrapping |
| 2020 | Thi Quynh Mai Pham y Gyei Kark Park and Kyoung-Hoon Choi | Top container ports |
|
| DEA-CCR DEA-BCC |
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| Financial | Financial | ||||
| Port Authorities | Turnover (€) | Investment (€) | Traffic (T) | EBITDA (€) | |
| SCENARIO 0 | A Coruña | 31,762,114.53 | 4,527,000.00 | 15,703,803.00 | 19,432,000.00 |
| Alicante | 12,067,584.45 | 2,201,000.00 | 3,191,163.00 | 5,942,000.00 | |
| Almería | 16,021,150.81 | 1,691,000.00 | 7,060,555.00 | 7,356,000.00 | |
| Avilés | 16,376,000.00 | 6,269,000.00 | 5,024,863.00 | 8,621,000.00 | |
| Bahía de Algeciras | 82,824,044.61 | 18,259,000.00 | 107,361,029.00 | 39,121,000.00 | |
| Bahía de Cádiz | 19,563,761.86 | 4,256,000.00 | 3,955,515.00 | 8,898,000.00 | |
| Baleares | 78,576,783.37 | 21,965,000.00 | 16,453,613.00 | 41,193,000.00 | |
| Barcelona | 173,527,000.00 | 49,285,000.00 | 67,756,258.00 | 102,397,000.00 | |
| Bilbao | 70,594,000.00 | 49,198,000.00 | 35,695,401.00 | 37,502,000.00 | |
| Cartagena | 45,935,000.00 | 23,127,000.00 | 33,941,690.00 | 30,091,000.00 | |
| Castellón | 31,334,907.92 | 4,140,000.00 | 21,137,627.00 | 20,929,000.00 | |
| Ceuta | 15,506,045.63 | 2,759,000.00 | 2,448,438.00 | 2,816,000.00 | |
| Ferrol-San Cibrao | 20,311,671.53 | 9,207,000.00 | 13,707,823.00 | 12,542,000.00 | |
| Gijón | 42,189,250.00 | 6,514,000.00 | 19,699,445.00 | 27,746,000.00 | |
| Huelva | 45,291,596.62 | 39,386,000.00 | 32,966,864.00 | 17,505,000.00 | |
| Las Palmas | 77,659,710.00 | 14,497,000.00 | 26,974,184.00 | 54,078,000.00 | |
| Málaga | 18,627,805.96 | 1,113,000.00 | 3,320,198.00 | 7,328,000.00 | |
| Marín-Ría de Pontevedra | 9,745,604.03 | 2,757,000.00 | 2,541,733.00 | 5,940,000.00 | |
| Melilla | 9,758,678.76 | 3,134,000.00 | 873,528.00 | 3,841,000.00 | |
| Motril | 7,714,000.00 | 1,262,000.00 | 2,852,896.00 | 3,091,000.00 | |
| Pasaia | 12,244,000.00 | 2,426,000.00 | 3,138,321.00 | 3,875,000.00 | |
| Santa Cruz deTenerife | 46,516,319.33 | 24,633,000.00 | 13,051,755.00 | 27,627,000.00 | |
| Santander | 22,852,000.00 | 8,304,000.00 | 5,984,392.00 | 12,172,000.00 | |
| Sevilla | 20,177,000.00 | 8,499,000.00 | 4,436,320.00 | 11,276,000.00 | |
| Tarragona | 57,220,018.34 | 18,660,000.00 | 32,084,325.00 | 30,236,000.00 | |
| Valencia | 138,048,000.00 | 19,543,000.00 | 76,621,101.00 | 81,525,000.00 | |
| Vigo | 31,241,366.12 | 8,650,000.00 | 4,362,465.00 | 17,475,000.00 | |
| Vilagarcía | 5,056,758.71 | 843,000.00 | 1,211,306.00 | 2,604,000.00 | |
| SCENARIO 1 | Bilbao and Pasajes | 82,838,000.00 | 51,624,000.00 | 38,833,722.00 | 41,377,000.00 |
| Gijón, Avilés and Santander | 81,417,250.00 | 21,087,000.00 | 30,708,700.00 | 48,539,000.00 | |
| A Coruña and Ferrol-San Cibrao | 52,073,786.06 | 13,734,000.00 | 29,411,626.00 | 31,974,000.00 | |
| Vigo, Marín-Ría de Pontevedra and Vilagarcía | 46,043,728.86 | 12,250,000.00 | 8,115,504.00 | 26,019,000.00 | |
| Huelva, Sevilla and Bahía de Cádiz | 85,032,358.48 | 52,141,000.00 | 41,358,699.00 | 37,679,000.00 | |
| Valencia and Castellón | 169,382,907.92 | 23,683,000.00 | 97,758,728.00 | 102,454,000.00 | |
| Barcelona and Tarragona | 230,747,018.34 | 67,945,000.00 | 99,840,583.00 | 132,633,000.00 | |
| Ceuta and Bahía de Algeciras | 98,330,090.24 | 21,018,000.00 | 109,809,467.00 | 41,937,000.00 | |
| Málaga, Motril, Almería and Melilla | 52,121,635.53 | 7,200,000.00 | 14,107,177.00 | 21,616,000.00 | |
| Baleares | 78,576,783.37 | 21,965,000.00 | 16,453,613.00 | 41,193,000.00 | |
| Santa Cruz de Tenerife and Las Palmas | 124,176,029.33 | 39,130,000.00 | 40,025,939.00 | 81,705,000.00 | |
| Alicante and Cartagena | 58,002,584.45 | 25,328,000.00 | 37,132,853.00 | 36,033,000.00 | |
| SCENARIO 2 | Bilbao, Pasajes, Santader, Gijón and Avilés | 164,255,250.00 | 72,711,000.00 | 69,542,422.00 | 89,916,000.00 |
| A Coruña, Ferrol-San Cibrao, Vigo, Marín-Ría de Pontevedra and Vilagarcía | 98,117,514.92 | 25,984,000.00 | 37,527,130.00 | 57,993,000.00 | |
| Huelva, Sevilla and Bahía de Cádiz | 85,032,358.48 | 52,141,000.00 | 41,358,699.00 | 37,679,000.00 | |
| Bahía de Algeciras, Málaga, Motril and Almería | 125,187,001.38 | 22,325,000.00 | 120,594,678.00 | 56,896,000.00 | |
| Baleares | 78,576,783.37 | 21,965,000.00 | 16,453,613.00 | 41,193,000.00 | |
| Alicante, Cartagena, Valencia, Castellón, Tarragona and Barcelona | 320,084,510.71 | 97,413,000.00 | 158,111,063.00 | 271,120,000.00 | |
| Santa Cruz de Tenerife and Las Palmas | 124,176,029.33 | 39,130,000.00 | 40,025,939.00 | 81,705,000.00 | |
| Ceuta and Melilla | 25,264,724.39 | 5,893,000.00 | 3,321,966.00 | 6,657,000.00 | |
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| Operational | Operational | ||||
| Port Authorities | Storage Area (m2) | Trackline with draughts > 4 m (m) | Traffic (T) | Ships (nº) | |
| SCENARIO 0 | A Coruña | 467,421.18 | 12,242.30 | 15,703,803.00 | 1221 |
| Alicante | 198,052.00 | 6411.92 | 3,191,163.00 | 732 | |
| Almería | 532,561.00 | 5359.30 | 7,060,555.00 | 1972 | |
| Avilés | 546,376.64 | 4841.50 | 5,024,863.00 | 823 | |
| Bahía de Algeciras | 3,760,321.71 | 21,075.00 | 107,361,029.00 | 28,913 | |
| Bahía de Cádiz | 3,078,851.36 | 9712.00 | 3,955,515.00 | 1197 | |
| Baleares | 525,497.00 | 25,517.39 | 16,453,613.00 | 50,366 | |
| Barcelona | 5,023,964.14 | 22,890.00 | 67,756,258.00 | 9038 | |
| Bilbao | 3,139,476.00 | 22,510.00 | 35,695,401.00 | 2925 | |
| Cartagena | 602,880.00 | 12,696.00 | 33,941,690.00 | 2203 | |
| Castellón | 805,777.00 | 8750.00 | 21,137,627.00 | 1856 | |
| Ceuta | 131,091.27 | 3453.00 | 2,448,438.00 | 11,147 | |
| Ferrol-San Cibrao | 873,594.00 | 12,330.00 | 13,707,823.00 | 1130 | |
| Gijón | 2,594,533.55 | 11,719.00 | 19,699,445.00 | 1229 | |
| Huelva | 655,144.00 | 10,132.00 | 32,966,864.00 | 2396 | |
| Las Palmas | 3,139,026.00 | 22,174.44 | 26,974,184.00 | 12,283 | |
| Málaga | 494,331.00 | 7306.00 | 3,320,198.00 | 1764 | |
| Marín y Ría de Pontevedra | 183,195.00 | 4261.00 | 2,541,733.00 | 500 | |
| Melilla | 11,354.00 | 2004.34 | 873,528.00 | 1776 | |
| Motril | 759,785.00 | 3127.00 | 2,852,896.00 | 1357 | |
| Pasaia | 481,117.00 | 5383.00 | 3,138,321.00 | 911 | |
| Santa Cruz deTenerife | 1,010,082.00 | 13,725.50 | 13,051,755.00 | 16,400 | |
| Santander | 943,445.00 | 7427.30 | 5,984,392.00 | 1626 | |
| Sevilla | 1,067,915.00 | 5283.00 | 4,436,320.00 | 1016 | |
| Tarragona | 2,479,522.00 | 15,095.00 | 32,084,325.00 | 2554 | |
| Valencia | 4,783,331.00 | 28,909.29 | 76,621,101.00 | 7722 | |
| Vigo | 745,177.00 | 12,190.00 | 4,362,465.00 | 1726 | |
| Vilagarcía | 242,561.00 | 2665.00 | 1,211,306.00 | 336 | |
| SCENARIO 1 | Bilbao and Pasajes | 3,620,593.00 | 27,893.00 | 38,833,722.00 | 3836 |
| Gijón, Avilés and Santander | 4,084,355.19 | 23,987.80 | 30,708,700.00 | 3678 | |
| A Coruña and Ferrol + San Cibrao | 1,341,015.18 | 24,572.30 | 29,411,626.00 | 2351 | |
| Vigo, Marín - Ría de Pontevedra and Vilagarcía | 1,170,933.00 | 19,116.00 | 8,115,504.00 | 2562 | |
| Huelva, Sevilla and Bahía de Cádiz | 4,801,910.36 | 25,127.00 | 41,358,699.00 | 4609 | |
| Valencia and Castellón | 5,589,108.00 | 37,659.29 | 97,758,728.00 | 9578 | |
| Barcelona and Tarragona | 7,503,486.14 | 37,985.00 | 99,840,583.00 | 11,592 | |
| Ceuta and Bahía de Algeciras | 3,891,412.98 | 24,528.00 | 109,809,467.00 | 40,060 | |
| Málaga, Motril, Almería and Melilla | 1,798,031.00 | 17,796.64 | 14,107,177.00 | 6869 | |
| Baleares | 525,497.00 | 25,517.39 | 16,453,613.00 | 50,366 | |
| Santa Cruz de Tenerife and Las Palmas | 4,149,108.00 | 35,899.94 | 40,025,939.00 | 28,683 | |
| Alicante and Cartagena | 800,932.00 | 19,107.92 | 37,132,853.00 | 2935 | |
| SCENARIO 2 | Bilbao, Pasajes, Santader, Gijón and Avilés | 7,704,948.19 | 51,880.80 | 69,542,422.00 | 7514 |
| A Coruña, Ferrol - San Cibrao, Vigo, Marín - Ría de Pontevedra and Vilagarcía | 2,511,948.18 | 43,688.30 | 37,527,130.00 | 4913 | |
| Huelva, Sevilla and Bahía de Cádiz | 4,801,910.36 | 25,127.00 | 41,358,699.00 | 4609 | |
| Bahía de Algeciras, Málaga, Motril and Almería | 5,546,998.71 | 36,867.30 | 120,594,678.00 | 34,006 | |
| Baleares | 525,497.00 | 25,517.39 | 16,453,613.00 | 50,366 | |
| Alicante, Cartagena, Valencia, Castellón, Tarragona and Barcelona | 9,110,195.14 | 65,842.92 | 158,111,063.00 | 24,105 | |
| Santa Cruz de Tenerife and Las Palmas | 4,149,108.00 | 35,899.94 | 40,025,939.00 | 28,683 | |
| Ceuta and Melilla | 142,445.27 | 5457.34 | 3,321,966.00 | 12,923 | |
| Turnover (€) | Investment (€) | Traffic (T) | EBITDA (€) | ||
|---|---|---|---|---|---|
| Average | Scenario 0 | 41,383,649.02 | 12,753,750.00 | 20,127,021.82 | 22,969,964.29 |
| Scenario 1 | 96,561,847.72 | 29,758,750.00 | 46,963,050.92 | 53,596,583.33 | |
| Scenario 2 | 127,586,771.57 | 42,195,250.00 | 60,866,938.75 | 80,394,875.00 | |
| Maximum value | Scenario 0 | 173,527,000.00 | 49,285,000.00 | 107,361,029.00 | 102,397,000.00 |
| Scenario 1 | 230,747,018.34 | 67,945,000.00 | 109,809,467.00 | 132,633,000.00 | |
| Scenario 2 | 320,084,510.71 | 97,413,000.00 | 158,111,063.00 | 271,120,000.00 | |
| Minimum value | Scenario 0 | 5,056,758.71 | 843,000.00 | 873,528.00 | 2,604,000.00 |
| Scenario 1 | 46,043,728.86 | 7,200,000.00 | 8,115,504.00 | 21,616,000.00 | |
| Scenario 2 | 25,264,724.39 | 5,893,000.00 | 3,321,966.00 | 6,657,000.00 | |
| Standard Deviation | Scenario 0 | 39,915,755.49 | 13,910,418.17 | 25,708,484.08 | 23,971,447.99 |
| Scenario 1 | 54,723,560.02 | 18,747,603.99 | 35,239,285.77 | 33,980,266.17 | |
| Scenario 2 | 87,805,340.21 | 30,409,755.12 | 53,107,329.73 | 81,346,867.42 |
| Storage Area (m2) | Track-Line with Draughts > 4 m (m) | Traffic (T) | Ships (nº) | ||
|---|---|---|---|---|---|
| Average | Scenario 0 | 1,402,727.92 | 11,399.65 | 20,127,021.82 | 5969 |
| Scenario 1 | 3,273,031.82 | 26,599.19 | 46,963,050.92 | 13,927 | |
| Scenario 2 | 4,311,631.36 | 36,285.12 | 60,866,938.75 | 20,890 | |
| Maximum Value | Scenario 0 | 5,023,964.14 | 28,909.29 | 107,361,029.00 | 50,366 |
| Scenario 1 | 7,503,486.14 | 37,985.00 | 109,809,467.00 | 50,366 | |
| Scenario 2 | 9,110,195.14 | 65,842.92 | 158,111,063.00 | 50,366 | |
| Minimum Value | Scenario 0 | 11,354.00 | 2004.34 | 873,528.00 | 336 |
| Scenario 1 | 525,497.00 | 17,796.64 | 8,115,504.00 | 2351 | |
| Scenario 2 | 142,445.27 | 5,457.34 | 3,321,966.00 | 4609 | |
| Standard Deviation | Scenario 0 | 1,495,594.13 | 8,383.07 | 25,843,314.02 | 5508.07 |
| Scenario 1 | 2,164,060.40 | 7,060.12 | 35,239,285.77 | 16,460.26 | |
| Scenario 2 | 3,191,272.00 | 18,373.05 | 53,107,329.73 | 1636.84 |
| Operational | Financial | ||||
|---|---|---|---|---|---|
| DMU No. | DMU Name | DEA VRS Efficiency | BOOT Efficiency | BOOT Efficiency | DEA VRS Efficiency |
| 1 | A Coruña | 0.59554 | 0.50776 | 0.8686 | 0.91278 |
| 2 | Alicante | 0.28659 | 0.24684 | 0.76767 | 0.78554 |
| 3 | Almería | 0.39935 | 0.36371 | 0.92469 | 1.00000 |
| 4 | Avilés | 0.30641 | 0.28241 | 0.80584 | 0.81304 |
| 5 | Bahía de Algeciras | 1.00000 | 0.74661 | 0.8716 | 1.00000 |
| 6 | Bahía de Cádiz | 0.09087 | 0.07632 | 0.68081 | 0.68993 |
| 7 | Baleares | 1.00000 | 0.67493 | 0.71746 | 0.75528 |
| 8 | Barcelona | 0.63111 | 0.52065 | 0.88689 | 1.00000 |
| 9 | Bilbao | 0.38413 | 0.32634 | 0.80152 | 0.82697 |
| 10 | Cartagena | 1.00000 | 0.83254 | 0.95996 | 1.00000 |
| 11 | Castellón | 0.67894 | 0.61534 | 0.89388 | 1.00000 |
| 12 | Ceuta | 1.00000 | 0.67732 | 0.27573 | 0.28426 |
| 13 | Ferrol-San Cibrao | 0.34829 | 0.30412 | 0.95686 | 0.98053 |
| 14 | Gijón | 0.35740 | 0.31984 | 0.92362 | 0.97022 |
| 15 | Huelva | 1.00000 | 0.85293 | 0.66431 | 0.70194 |
| 16 | Las Palmas | 0.34808 | 0.26535 | 0.91511 | 1.00000 |
| 17 | Málaga | 0.17835 | 0.15205 | 0.87333 | 1.00000 |
| 18 | Marín y Ría de Pontevedra | 0.26652 | 0.22988 | 0.97883 | 1.00000 |
| 19 | Melilla | 1.00000 | 0.66117 | 0.63454 | 0.64563 |
| 20 | Motril | 0.40027 | 0.33935 | 0.70278 | 0.75394 |
| 21 | Pasaia | 0.18689 | 0.17024 | 0.49467 | 0.50784 |
| 22 | Santa Cruz deTenerife | 0.59563 | 0.45507 | 0.84652 | 0.86325 |
| 23 | Santander | 0.20433 | 0.17973 | 0.79206 | 0.79956 |
| 24 | Sevilla | 0.23129 | 0.21407 | 0.83911 | 0.84567 |
| 25 | Tarragona | 0.44252 | 0.37922 | 0.79215 | 0.82321 |
| 26 | Valencia | 0.71368 | 0.60715 | 0.88024 | 1.00000 |
| 27 | Vigo | 0.14159 | 0.12011 | 0.81468 | 0.82521 |
| 28 | Vilagarcía | 0.26549 | 0.24047 | 0.86799 | 1.00000 |
| Arithmetic mean | 0.50190 | 0.40576 | 0.80112 | 0.84945 |
| Geometric mean | 0.41163 | 0.34331 | 0.78136 | 0.82561 |
| Standard deviation | 0.30271 | 0.22098 | 0.14860 | 0.17062 |
| Average deviation | 0,26385 | 0.19200 | 0.10636 | 0.13102 |
| Variance | 0.09163 | 0.04883 | 0.02208 | 0.02911 |
| Operational | Financial | ||||
|---|---|---|---|---|---|
| DMU No. | DMU Name | DEA VRS Efficiency | BOOT Efficiency | BOOT Efficiency | DEA VRS Efficiency |
| 1 | Bilbao-Pasajes | 0.37542 | 0.34877 | 0.75420 | 0.80640 |
| 2 | Gijón-Avilés-Santander | 0.29940 | 0.27557 | 0.93189 | 0.94763 |
| 3 | A Coruña-Ferrol + San Cibrao | 0.59020 | 0.53210 | 0.93880 | 1.00000 |
| 4 | Vigo-Marín + Ría de Pontevedra-Vilagarcía | 0.30695 | 0.25846 | 0.94004 | 1.00000 |
| 5 | Huelva-Sevilla-Bahía de Cádiz | 0.37664 | 0.34992 | 0.73144 | 0.74222 |
| 6 | Valencia-Castellón | 0.89026 | 0.86093 | 0.94099 | 1.00000 |
| 7 | Barcelona-Tarragona | 0.90922 | 0.88019 | 0.94158 | 1.00000 |
| 8 | Ceuta-Bahía de Algeciras | 1.00000 | 0.80368 | 0.94048 | 1.00000 |
| 9 | Málaga-Motril-Almería-Melilla | 1.00000 | 0.76868 | 0.93854 | 1.00000 |
| 10 | Baleares | 1.00000 | 0.76516 | 0.81472 | 0.82573 |
| 11 | Santa Cruz de Tenerife-Las Palmas | 0.63435 | 0.56253 | 0.96662 | 1.00000 |
| 12 | Alicante-Cartagena | 1.00000 | 0.76411 | 0.96717 | 1.00000 |
| Arithmetic mean | 0.69853 | 0.59750 | 0.90397 | 0.94349 |
| Geometric mean | 0.63038 | 0.54665 | 0.90068 | 0.93874 |
| Standard deviation | 0.28594 | 0.22807 | 0.07418 | 0.09070 |
| Average deviation | 0.26804 | 0.20961 | 0.0617 | 0.07602 |
| Variance | 0.08176 | 0.05202 | 0.0055 | 0.00822 |
| Operational | Financial | ||||
|---|---|---|---|---|---|
| DMU No. | DMU Name | DEA VRS Efficiency | BOOT Efficiency | BOOT Efficiency | DEA VRS Efficiency |
| 1 | Bilbao–Pasajes-Santader-Gijón-Avilés | 0.49661 | 0.45855 | 0.69902 | 0.74383 |
| 2 | A Coruña-Ferrol + San Cibrao-Vigo-Marín + Ría de Pontevedra-Vilagarcía | 0.65094 | 0.60925 | 0.8485 | 0.88959 |
| 3 | Huelva-Sevilla-Bahía de Cádiz | 0.53880 | 0.49961 | 0.73063 | 0.77207 |
| 4 | Bahía de Algeciras-Málaga-Motril-Almería | 1.00000 | 0.85286 | 0.88816 | 1.00000 |
| 5 | Baleares | 1.00000 | 0.82499 | 0.7382 | 0.77445 |
| 6 | Alicante-Cartagena-Valencia-Castellón-Tarragona-Barcelona | 1.00000 | 0.88084 | 0.89108 | 1.00000 |
| 7 | Santa Cruz de Tenerife-Las Palmas | 0.66044 | 0.60224 | 0.80962 | 0.85659 |
| 8 | Ceuta-Melilla | 1.00000 | 0.82675 | 0.88586 | 1.00000 |
| Arithmetic mean | 0.79334 | 0.69438 | 0.81138 | 0.87956 |
| Geometric mean | 0.76313 | 0.67495 | 0.80794 | 0.87349 |
| Standard deviation | 0.21260 | 0.15959 | 0.07388 | 0.10318 |
| Average deviation | 0.20665 | 0.15197 | 0.06701 | 0.09283 |
| Variance | 0.04520 | 0.02546 | 0.00545 | 0.01064 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra Santiago, J.I.; Camarero Orive, A.; González Cancelas, N. DEA-Bootstrapping Analysis for Different Models of Spanish Port Governance. J. Mar. Sci. Eng. 2021, 9, 30. https://doi.org/10.3390/jmse9010030
Parra Santiago JI, Camarero Orive A, González Cancelas N. DEA-Bootstrapping Analysis for Different Models of Spanish Port Governance. Journal of Marine Science and Engineering. 2021; 9(1):30. https://doi.org/10.3390/jmse9010030
Chicago/Turabian StyleParra Santiago, Jose Ignacio, Alberto Camarero Orive, and Nicoletta González Cancelas. 2021. "DEA-Bootstrapping Analysis for Different Models of Spanish Port Governance" Journal of Marine Science and Engineering 9, no. 1: 30. https://doi.org/10.3390/jmse9010030
APA StyleParra Santiago, J. I., Camarero Orive, A., & González Cancelas, N. (2021). DEA-Bootstrapping Analysis for Different Models of Spanish Port Governance. Journal of Marine Science and Engineering, 9(1), 30. https://doi.org/10.3390/jmse9010030







