Influence of the Shape of Gear Wheel Bodies in Marine Engines on the Gearing Deformation and Meshing Stiffness
Abstract
:1. Introduction
2. Materials and Methods
2.1. Body Shape of Forged Spur Gears
2.2. Construction of Cast Spur Gears
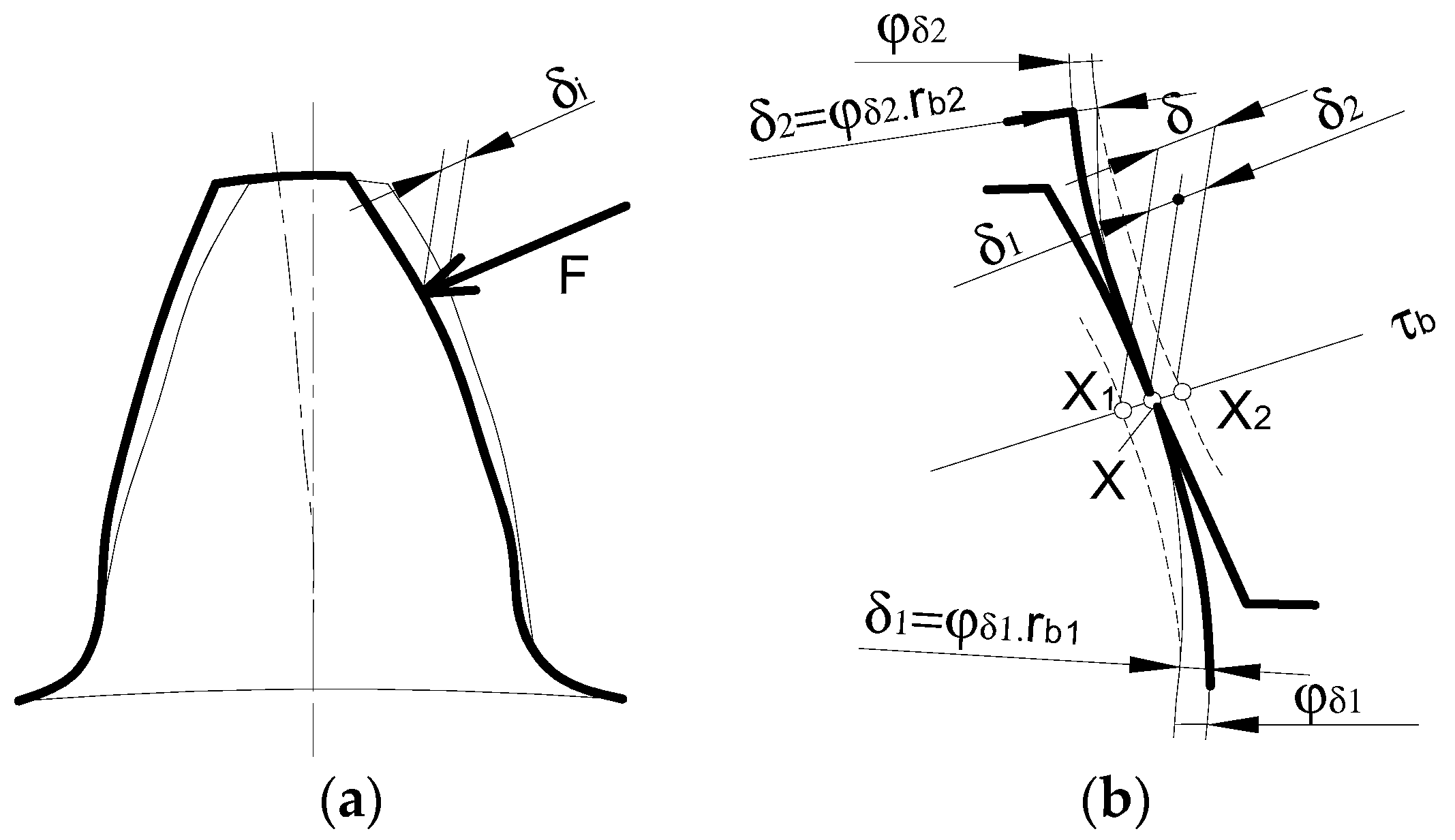
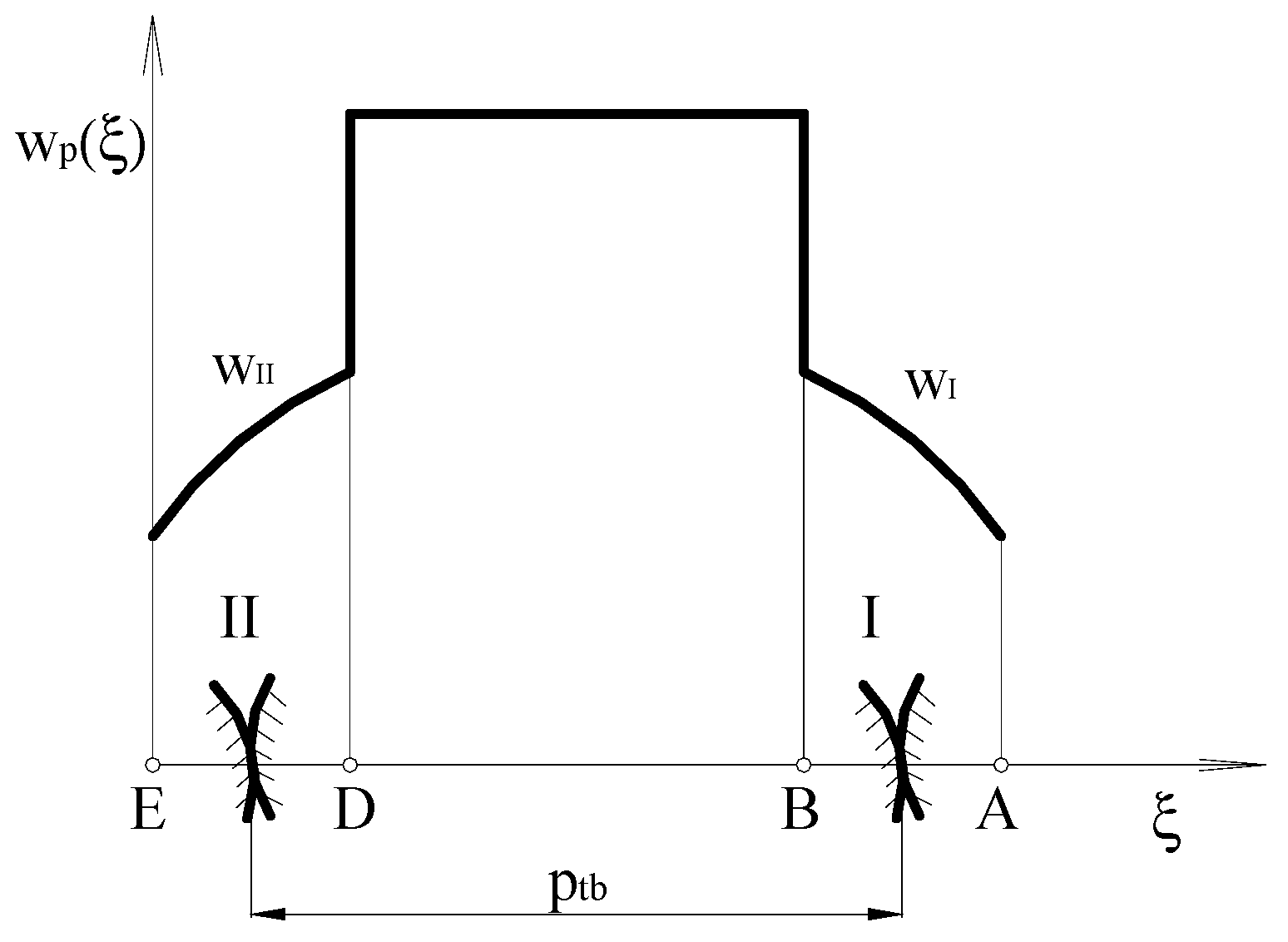
2.3. Gear Deformation and Meshing Stiffness
3. Results and Discussion
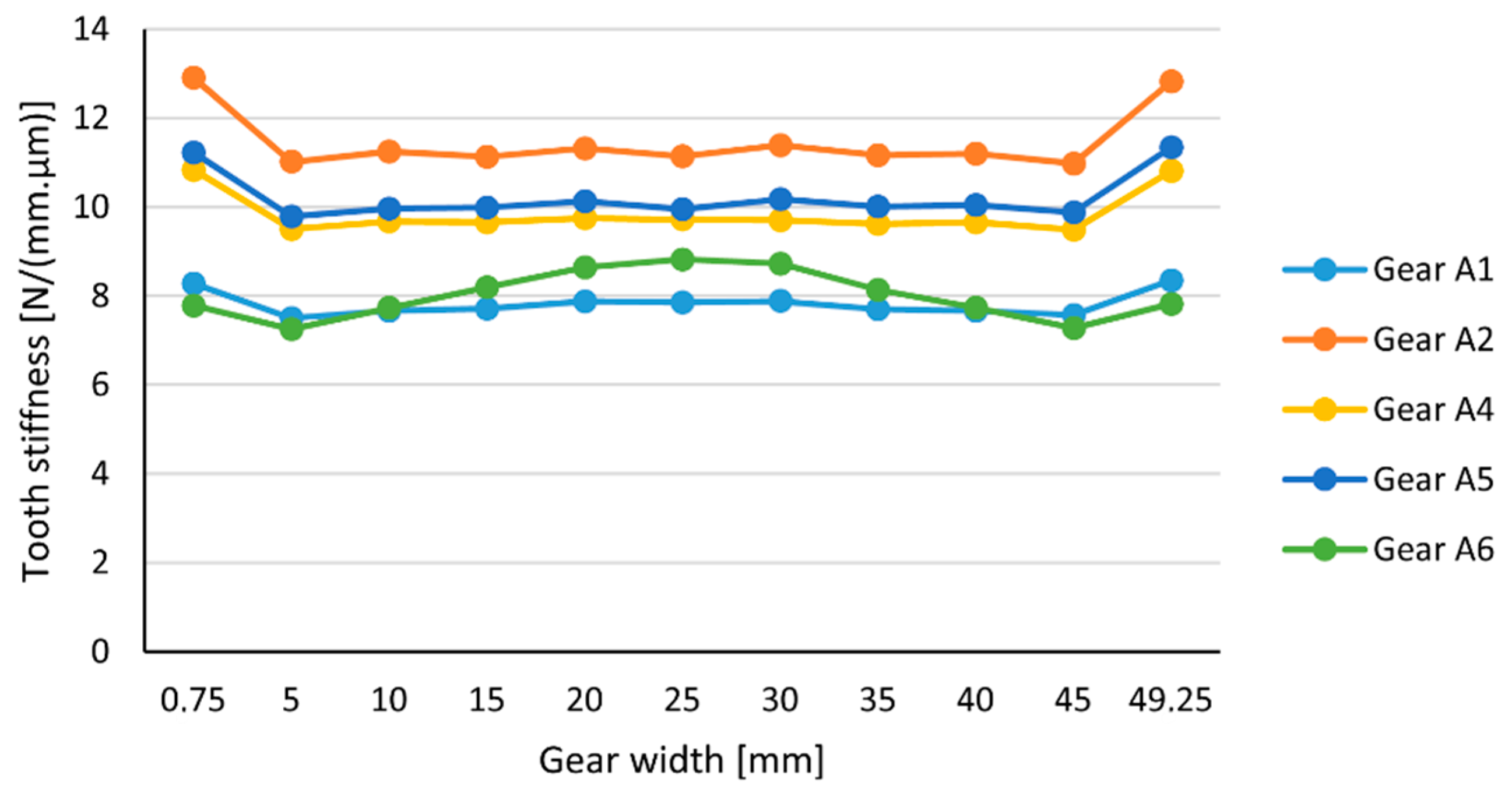
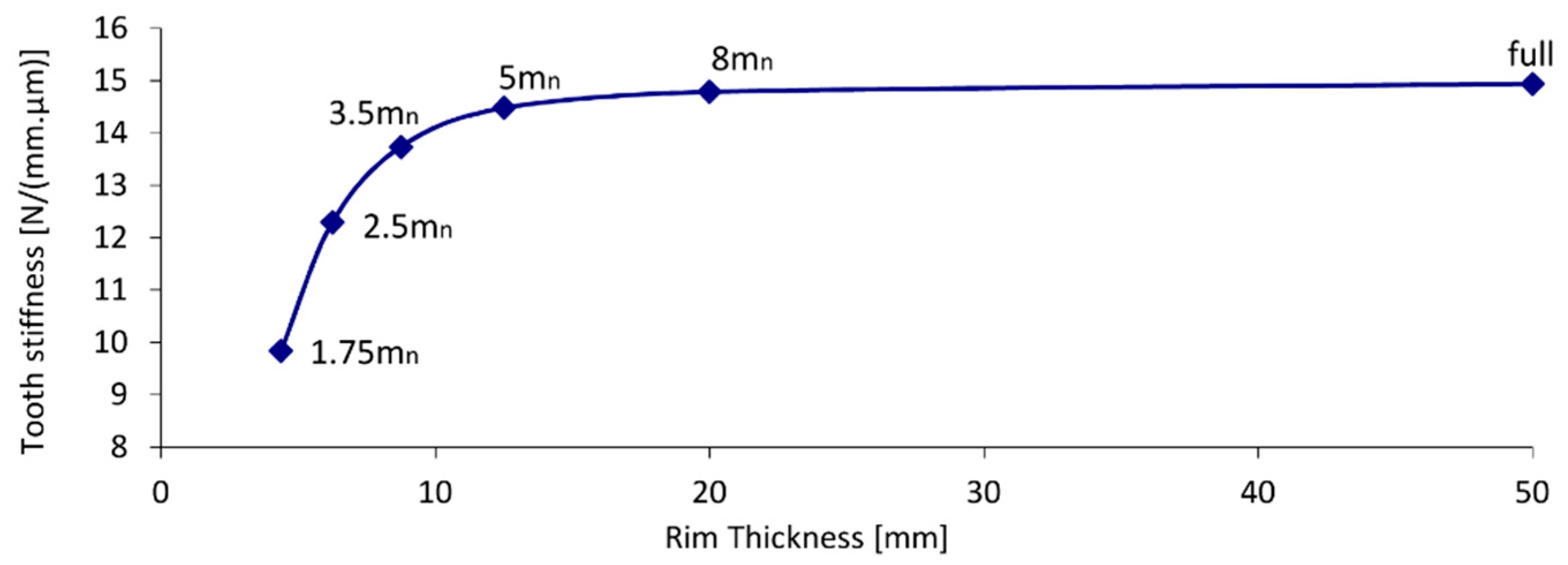
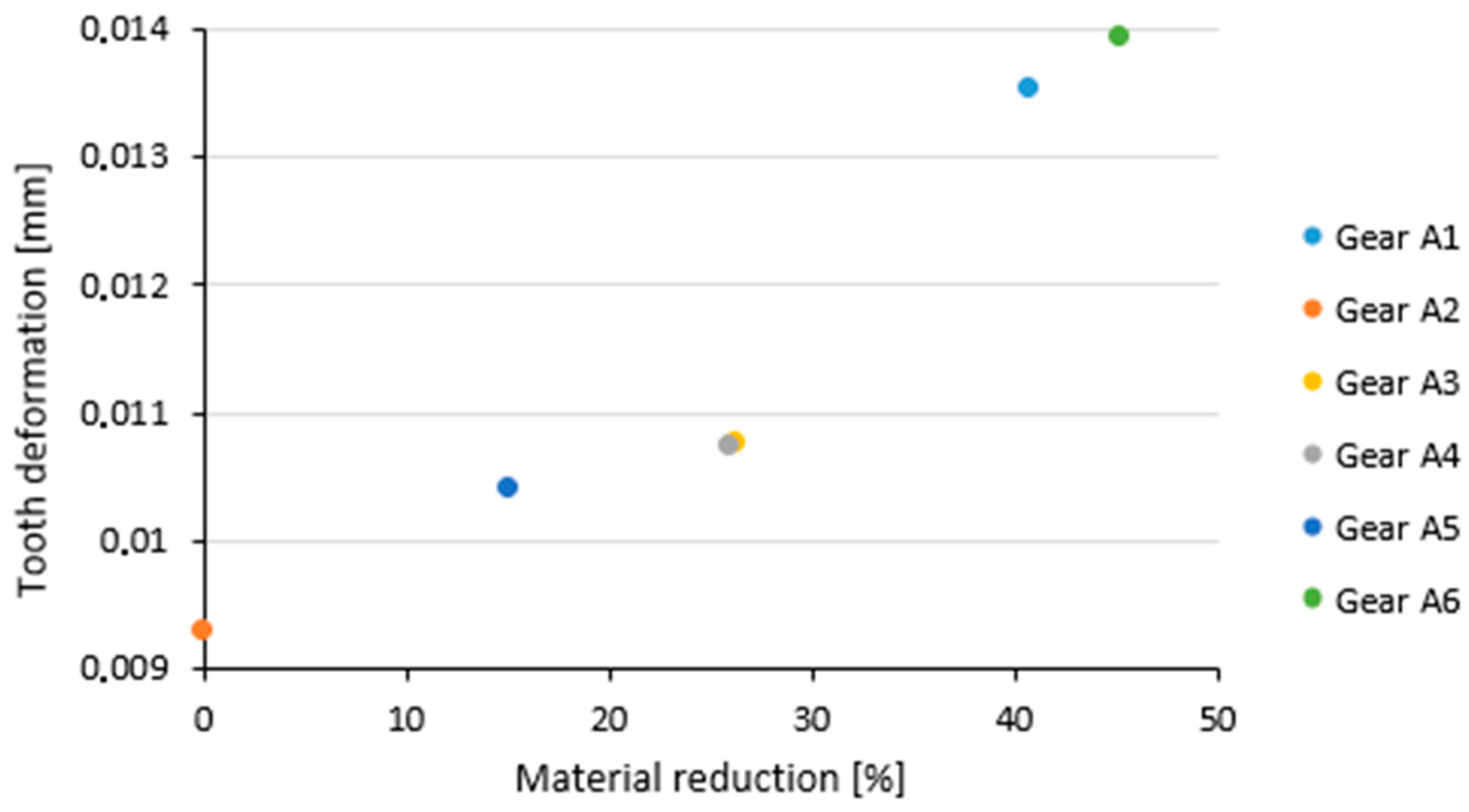
3.1. The Deformation and Gear Stiffness of Forged Gear Wheels
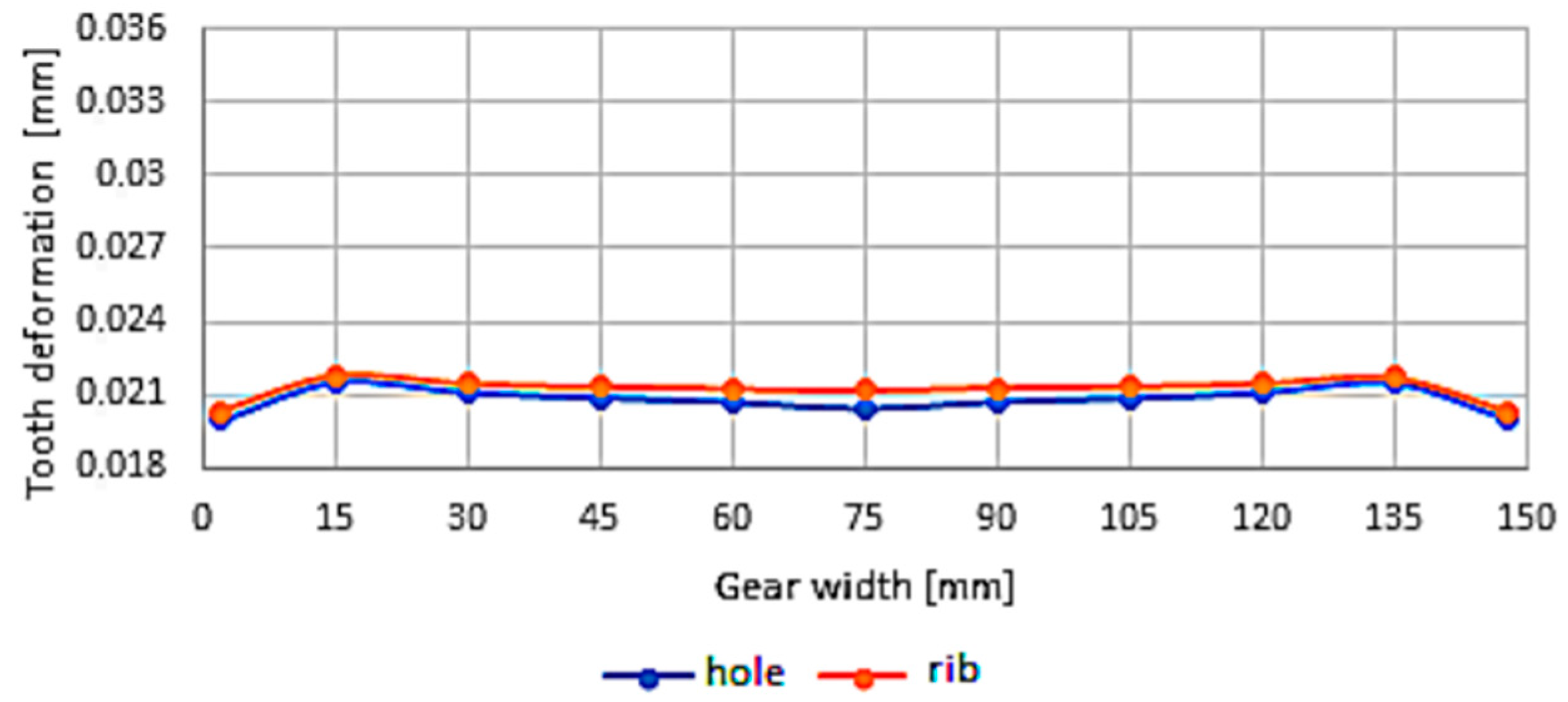
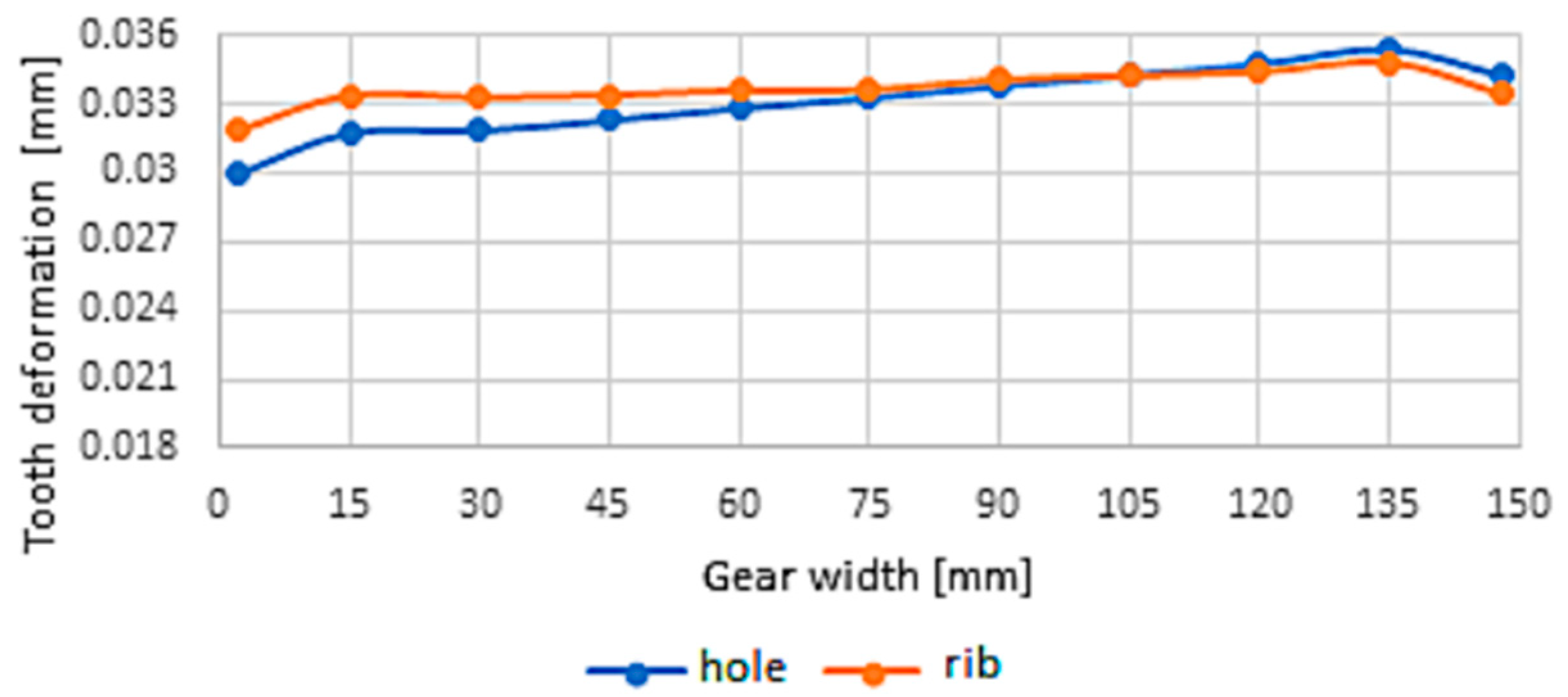
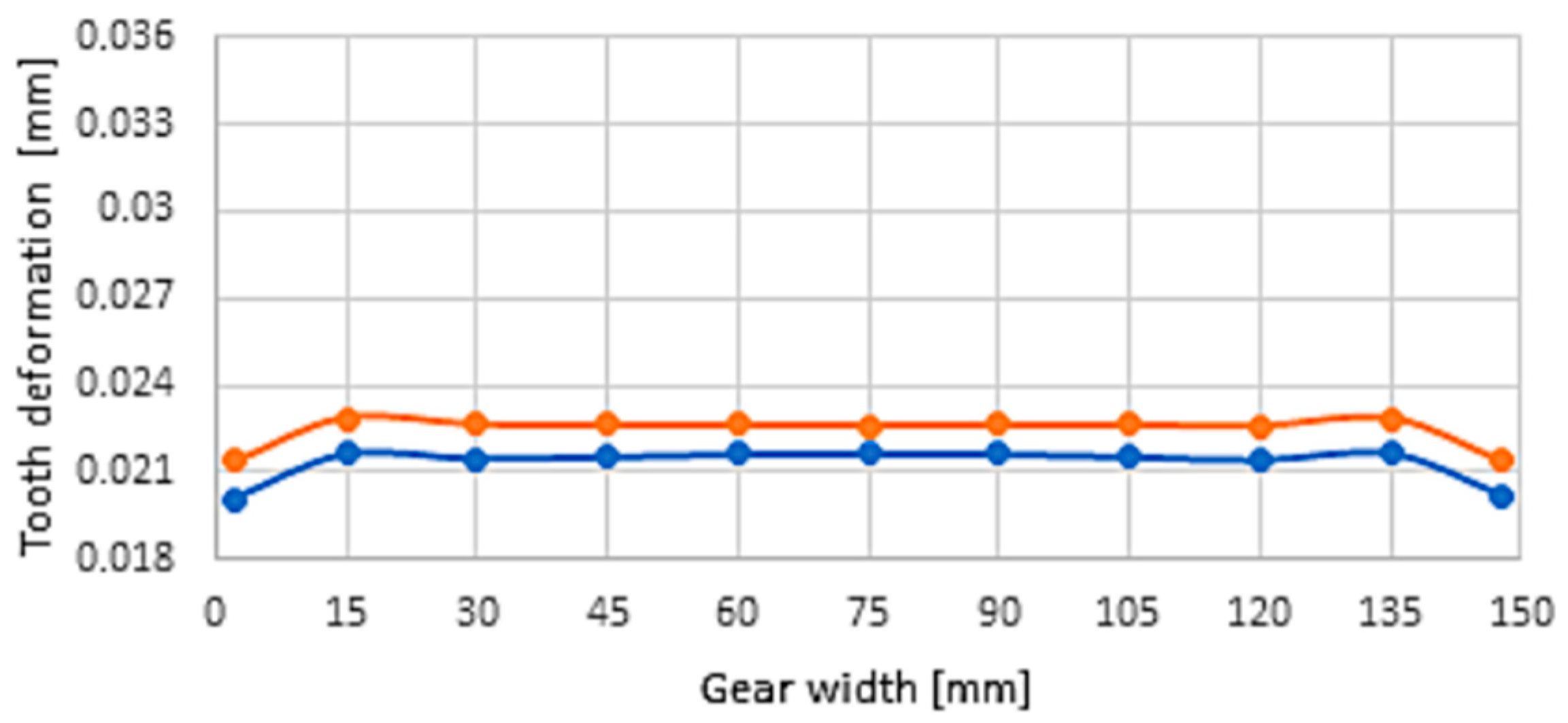
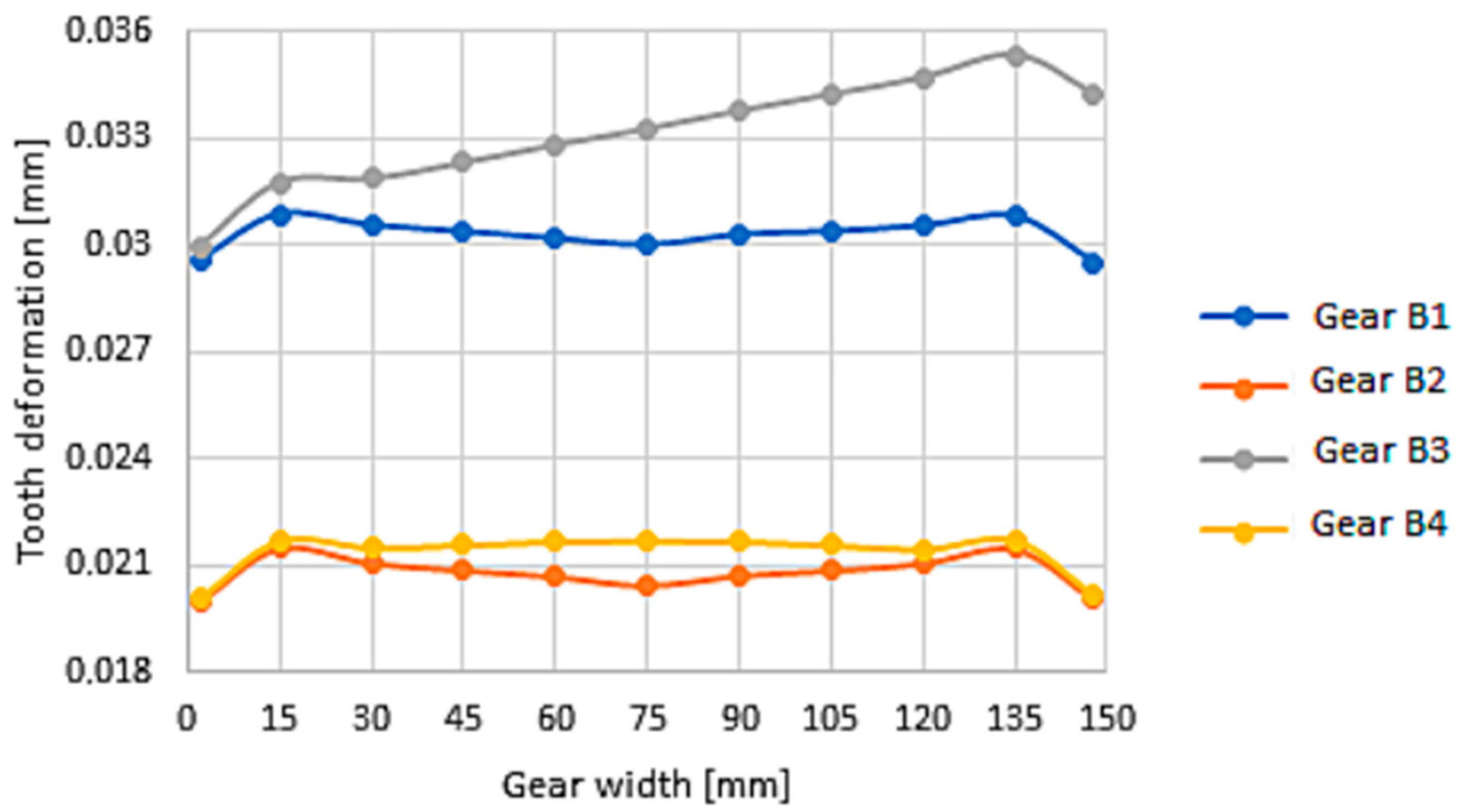
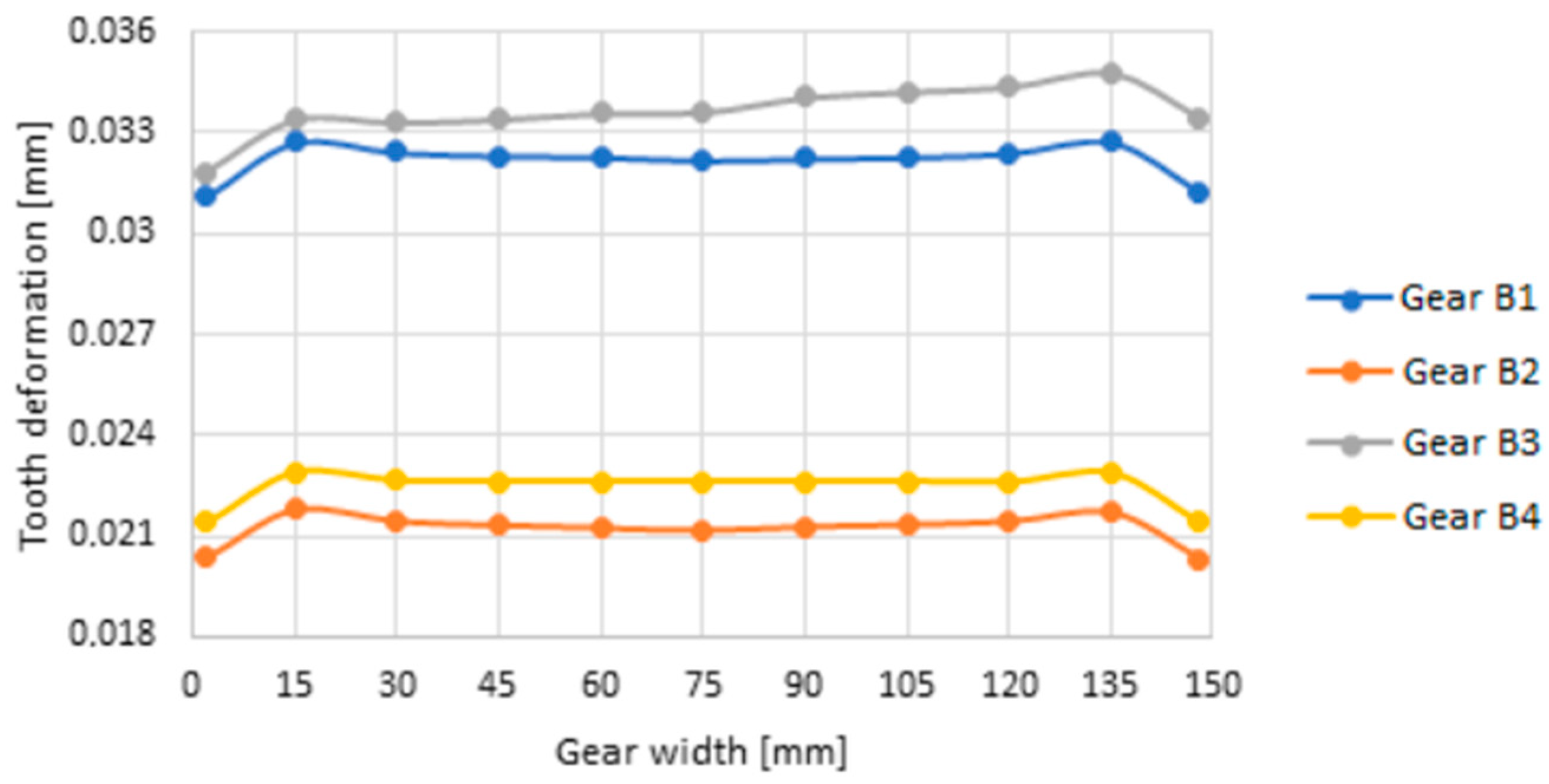
3.2. Deformation and Stiffness of Gearing of Cast Gears
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.M.; Govindaraj, E.; Balamurugan, D.; Daniel, F. Design analysis and fabrication of automotive transmission gearbox using hollow gears for weight reduction. Mater. Today Proc. 2021, 45, 6822–6832. [Google Scholar] [CrossRef]
- Stroh, J.; Sediako, D. Residual Stress Characterization for Marine Gear Cases in As-Cast and T5 Heat Treated Conditions with Application of Neutron Diffraction. Light Met. 2019, 2019, 395–399. [Google Scholar]
- Henriksson, M. Analysis of gear noise and dynamic transmission error measurements. ASME Int. Mech. Eng. Congr. Expo. 2004, 47020, 229–237. [Google Scholar]
- Park, S.; Kim, S.; Choi, J.H. Gear fault diagnosis using transmission error and ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2018, 10, 262–275. [Google Scholar] [CrossRef]
- Dong, J.W.; Pei, W.C.; Long, H.Y.; Chu, J.; Ji, H.C. Solution of spur gear meshing stiffness and analysis of degradation characteristics. Mechanika 2020, 26, 153–160. [Google Scholar]
- Malakova, S.; Puskar, M.; Frankovsky, P.; Sivak, S.; Palko, M.; Palko, M. Meshing Stiffness—A Parameter Affecting the Emission of Gearboxes. Appl. Sci. 2020, 10, 8678. [Google Scholar] [CrossRef]
- Jakubovičová, L.; Ftorek, B.; Baniari, V.; Sapietová, A.; Potoček, T.; Vaško, M. Engineering Design of a Test Device. Procedia Eng. 2017, 177, 520–525. [Google Scholar] [CrossRef]
- Wang, C. High power density design for planetary gear transmission system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5647–5658. [Google Scholar] [CrossRef]
- Monkova, K.; Monka, P.; Tkac, J.; Hricova, R.; Mandulak, D. Effect of the Weight reduction of a Gear Wheel on Modal Characteristics. MATEC Web Conf. 2019, 299, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Wang, C.X. Small Module Design of Ball Mill Main Drive Gear with Φ2.4 × 10m. Adv. Mater. Res. 2013, 787, 490–494. [Google Scholar] [CrossRef]
- Marunić, G. Rim Stress Analysis of Thin-Rimmed Gear. Key Eng. Mater. 2007, 348–349, 141–144. [Google Scholar] [CrossRef]
- Naveen, P.N.E.; Sujith Kumar, B.; Goriparthi, B.K.; Hota, R.S.; Chaitanya Mayee, M.; Gopala Raju, S.S.S.V. Design and analysis of thin wall gear structure with Tio2/GF reinforced Nylon66 composites. Mater. Today Proc. 2021, 46, 382–389. [Google Scholar] [CrossRef]
- Zhao, N.; Sun, L.L.; Fu, B.B.; Li, H.F.; Wang, Q.B. Web Structural Optimization of the Big Aviation Herringbone Gear Based on APDL Language. Appl. Mech. Mater. 2014, 487, 692–698. [Google Scholar] [CrossRef]
- Medvecká-Beňová, S. Influence of the face width and length of contact on teeth deformation and stiffness. Sci. J. Sil. Univ. Technol. Ser. Transp. 2016, 91, 99–106. [Google Scholar] [CrossRef]
- Patel, A.; Shakya, P. Spur gear crack modelling and analysis under variable speed conditions using variational mode decomposition. Mech. Mach. Theory 2021, 164, 104357. [Google Scholar] [CrossRef]
- Pleguezuelos, M.; Sánchez, M.B.; Pedrero, J.I. Analytical model for meshing stiffness, load sharing, and transmission error for spur gears with profile modification under non-nominal load conditions. Appl. Math. Model. 2021, 97, 344–365. [Google Scholar] [CrossRef]
- Flek, J.; Dub, M.; Kolar, J.; Lopot, F.; Petr, K. Determination of Mesh Stiffness of Gear—Analytical Approach vs. FEM Analysis. Appl. Sci. 2021, 11, 4960. [Google Scholar] [CrossRef]
- Xiong, Y.S.; Huang, K.; Xu, F.W.; Yi, Y.; Sang, M.; Zhai, H. Research on the Influence of Backlash on Mesh Stiffness and the Nonlinear Dynamics of Spur Gears. Appl. Sci. 2019, 9, 1029. [Google Scholar] [CrossRef] [Green Version]
- Gkimisis, L.; Vasileiou, G.; Sakaridis, E.; Spitas, C.; Spitas, V. A fast, non-implicit SDOF model for spur gear dynamics. Mech. Mach. Theory 2021, 160, 104279. [Google Scholar] [CrossRef]
- Marques, P.M.T.; Marafona, J.D.M.; Martins, R.C.; Seabra, J.H.O. A continuous analytical solution for the load sharing and friction torque of involute spur and helical gears considering a non-uniform line stiffness and line load. Mech. Mach. Theory 2021, 161, 104320. [Google Scholar] [CrossRef]
- Shen, J.; Hu, N.Q.; Zhang, L.; Luo, P. Dynamic Analysis of Planetary Gear with Root Crack in Sun Gear Based on Improved Time-Varying Mesh Stiffness. Appl. Sci. 2020, 10, 8379. [Google Scholar] [CrossRef]
- Císar, M.; Kuric, I.; Čuboňová, N.; Kandera, M. Design of the clamping system for the CNC machine tool. MATEC Web Conf. 2017, 137, 01003. Available online: https://www.researchgate.net/publication/321215438_Design_of_the_clamping_system_for_the_CNC_machine_tool (accessed on 20 September 2021). [CrossRef] [Green Version]
- Hudak, R.; Polacek, I.; Klein, P.; Sabol, R.; Varga, R.; Zivcak, J.; Vazquez, M. Nanocrystalline Magnetic Glass-Coated Microwires Using the Effect of Superparamagnetism Are Usable as Temperature Sensors in Biomedical Applications. IEEE Trans. Magn. 2017, 53, 1–5. Available online: https://ieeexplore.ieee.org/abstract/document/7814333 (accessed on 20 September 2021). [CrossRef]
- Jiang, H.; Sitoci-Ficici, K.; Reinshagen, C.; Molcanyi, M.; Zivcak, J.; Hudak, R.; Laube, T.; Schnabelrauch, M.; Weisser, J.; Schäfer, U.; et al. Adjustable Polyurethane Foam as Filling Material for a Novel Spondyloplasty: Biomechanics and Biocompatibility. World Neurosurg. 2018, 112, e848–e858. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1878875018302171 (accessed on 20 September 2021). [CrossRef]
- Koutecký, T.; Zikmund, T.; Glittová, D.; Paloušek, D.; Živčák, J.; Kaiser, J. X-ray micro-CT measurement of large parts at very low temperature. Rev. Sci. Instrum. 2017, 88, 033707. Available online: https://aip.scitation.org/doi/abs/10.1063/1.4979077 (accessed on 20 September 2021). [CrossRef]
- Murčinková, Z.; Živčák, J.; Zajac, J. Experimental study of parameters influencing the damping of particulate, fibre-reinforced, hybrid, and sandwich composites. Int. J. Mater. Res. 2020, 111, 688–697. Available online: https://www.degruyter.com/document/doi/10.3139/146.111933/pdf (accessed on 20 September 2021). [CrossRef]
- Pistek, V.; Klimes, L.; Mauder, T.; Kucera, P. Optimal design of structure in rheological models: An automotive application to dampers with high viscosity silicone fluids. J. Vibroengineering 2017, 19, 4459–4470. Available online: https://www.jvejournals.com/article/18348 (accessed on 20 September 2021). [CrossRef]
- Puškár, M.; Jahnátek, A.; Kuric, I.; Kádárová, J.; Kopas, M.; Šoltésová, M. Complex analysis focused on influence of biodiesel and its mixture on regulated and unregulated emissions of motor vehicles with the aim to protect air quality and environment. Air Qual. Atmos. Health 2019, 12, 855–864. Available online: https://link.springer.com/article/10.1007/s11869-019-00704-w (accessed on 20 September 2021). [CrossRef]
- Píštěk, V.; Kučera, P.; Fomin, O.; Lovska, A. Effective Mistuning Identification Method of Integrated Bladed Discs of Marine Engine Turbochargers. J. Mar. Sci. Eng. 2020, 8, 379. Available online: https://www.mdpi.com/2077-1312/8/5/379 (accessed on 20 September 2021).
- Sabol, R.; Klein, P.; Ryba, T.; Hvizdos, L.; Varga, R.; Rovnak, M.; Sulla, I.; Mudronova, D.; Galik, J.; Polacek, I.; et al. Novel Applications of Bistable Magnetic Microwires. Acta Phys. Pol. A 2017, 131, 1150–1152. [Google Scholar] [CrossRef]
- Sága, M.; Bulej, V.; Čuboňova, N.; Kuric, I.; Virgala, I.; Eberth, M. Case study: Performance analysis and development of robotized screwing application with integrated vision sensing system for automotive industry. Int. J. Adv. Robot. Syst. 2020, 17, 172988142092399. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=184m0r70kg0f0a00bs7s0vq0g8225814&site=xueshu_se&hitarticle=1 (accessed on 20 September 2021). [CrossRef]
- Toth, T.; Hudak, R.; Zivcak, J. Dimensional verification and quality control of implants produced by additive manufacturing. Qual. Innov. Prosper. 2015, 19, 9–21. Available online: https://www.qip-journal.eu/index.php/QIP/article/view/393 (accessed on 20 September 2021). [CrossRef] [Green Version]
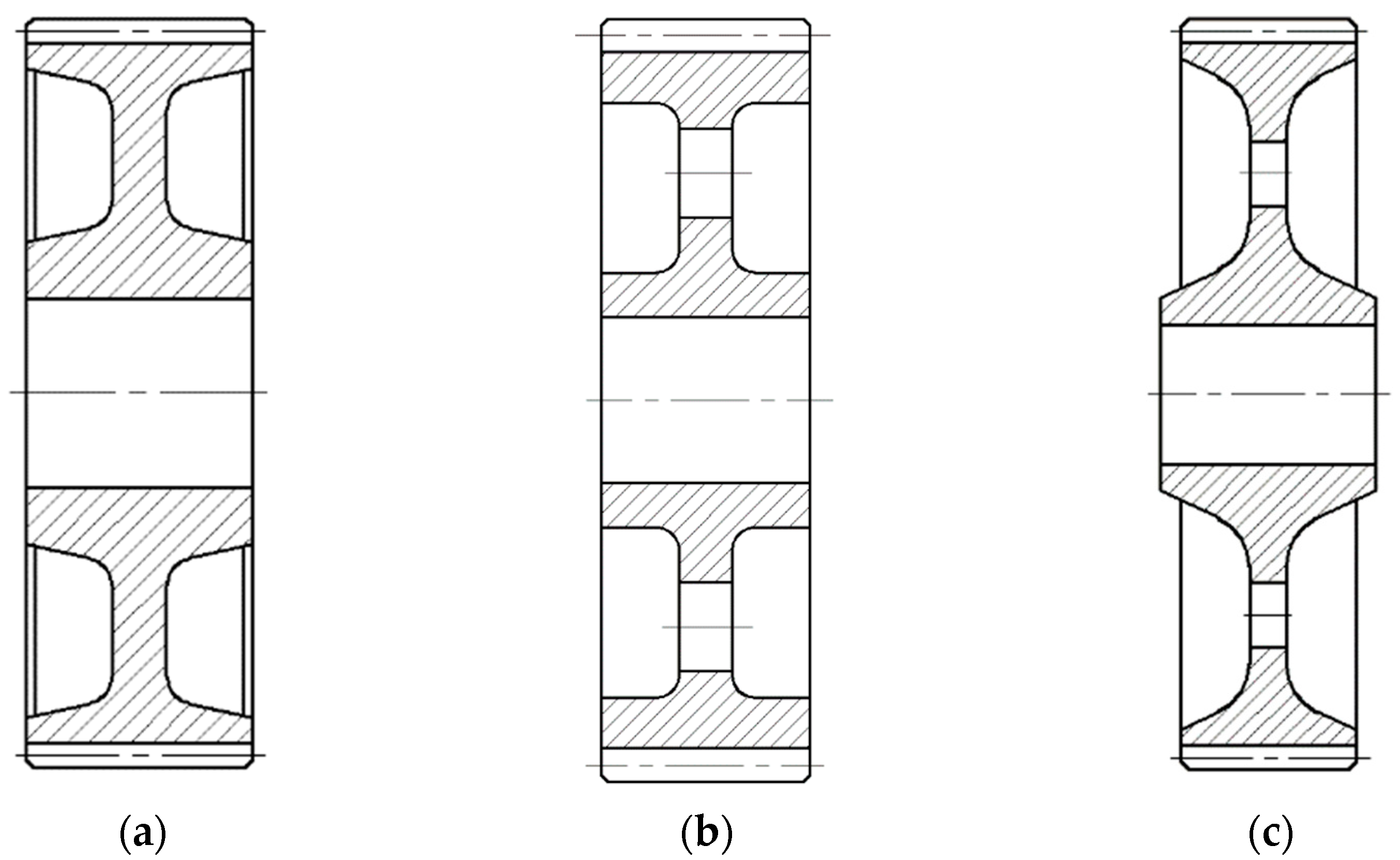







| Forged Spur Gear | Gear Parameters |
|---|---|
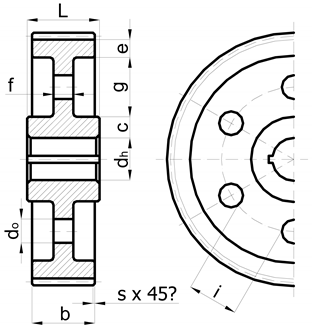 | mn—modulus [mm] h—height of key [mm] b—width of gear wheel [mm] dh—diameter of the hole for the shaft [mm] g—calculated using parameters e, c, dh and df (root diameter) chamfer s = 0.3 mn e = (3 to 4) mn c = (1.2 to 1.8 )h do = (0.4 to 0.7) g f = 0.3b i = (0.4 to 0.7) do L = (1.0 to 1.25) b bs = 0.3 mn |
| Variant | Wheel Size | 3D Model |
|---|---|---|
| A1 |  |  |
| A2 | 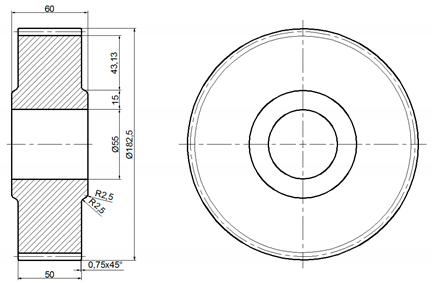 |  |
| A3 |  |  |
| A4 | 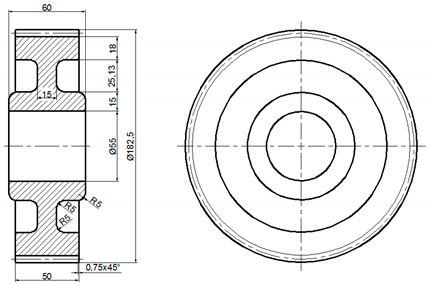 |  |
| A5 | 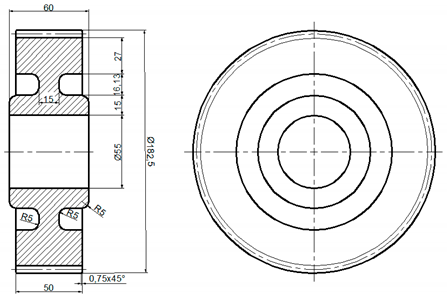 |  |
| A6 | 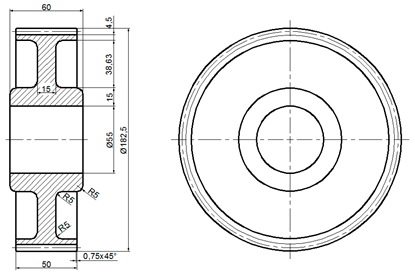 |  |
| Cast Medium-Sized Gear Wheel | Wheel Parameters |
|---|---|
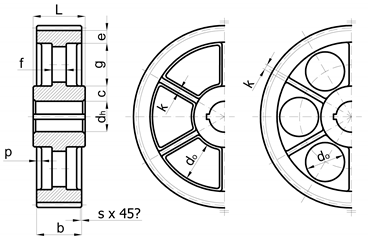 | mn—modulus [mm] h—height of key [mm] b—width of wheel [mm] e = (4 to 5) mn c = (1.8 to 2.2) h f = (0.2 to 0.3) b do = (0.6 to 0.7) g k = (0.4 to 0.6) f p = (0.2 to 0.5) k s = 0.3 mn L = (1.0 to 1.25) b |
| Large Casted Spur Gear | Wheel Parameters |
|---|---|
 | mn—modulus [mm] h—height of key [mm] b—width of wheel [mm] dh—diameter of the hole for the shaft [mm] e = (1.6 to 2.0) mn g = 2.0 mn f = (1.4 to 1.7) mn k = (1.1 to 1.3) mn L = (1.0 to 1.25) dh l1= 0.5 dh H = (8.0 to 10.0) mn h = (6.0 to 8.0) mn l1= 0.5 dh 1 c = 0.4dh + (5 to 10 [mm]) |
| Variant | Wheel Size | 3D Model |
|---|---|---|
| B1 | 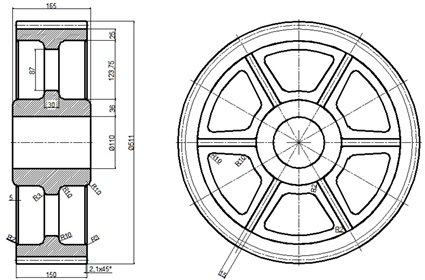 |  |
| B2 | 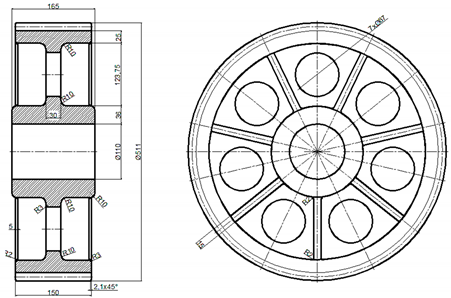 |  |
| B3 | 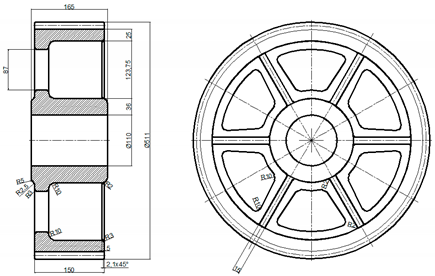 |  |
| B4 | 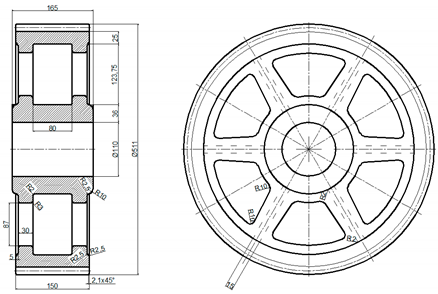 |  |
| Variant | 3D Model | Maximum Deformation [mm] | Illustration of Deformation | Cut Section |
|---|---|---|---|---|
| A1 |  | 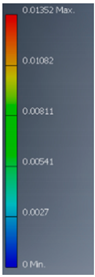 | 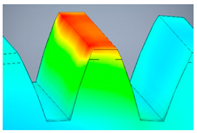 | 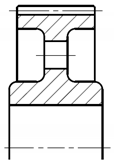 |
| A2 |  | 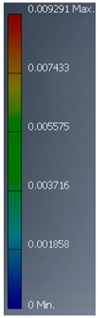 | 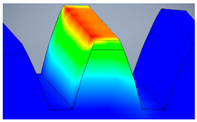 | 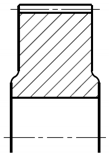 |
| A3 |  | 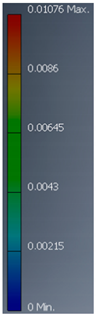 | 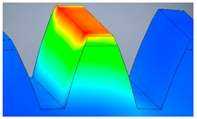 | 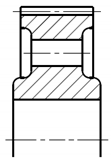 |
| A4 |  |  | 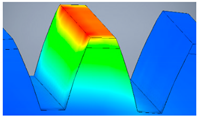 | 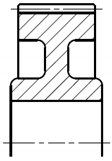 |
| A5 |  | 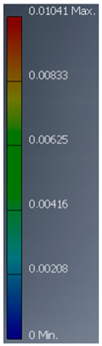 | 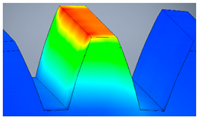 | 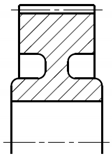 |
| A6 |  | 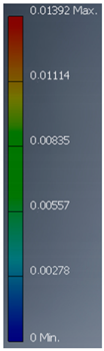 | 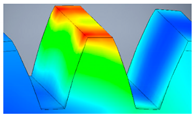 | 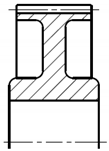 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maláková, S.; Puškár, M.; Frankovský, P.; Sivák, S.; Harachová, D. Influence of the Shape of Gear Wheel Bodies in Marine Engines on the Gearing Deformation and Meshing Stiffness. J. Mar. Sci. Eng. 2021, 9, 1060. https://doi.org/10.3390/jmse9101060
Maláková S, Puškár M, Frankovský P, Sivák S, Harachová D. Influence of the Shape of Gear Wheel Bodies in Marine Engines on the Gearing Deformation and Meshing Stiffness. Journal of Marine Science and Engineering. 2021; 9(10):1060. https://doi.org/10.3390/jmse9101060
Chicago/Turabian StyleMaláková, Silvia, Michal Puškár, Peter Frankovský, Samuel Sivák, and Daniela Harachová. 2021. "Influence of the Shape of Gear Wheel Bodies in Marine Engines on the Gearing Deformation and Meshing Stiffness" Journal of Marine Science and Engineering 9, no. 10: 1060. https://doi.org/10.3390/jmse9101060
APA StyleMaláková, S., Puškár, M., Frankovský, P., Sivák, S., & Harachová, D. (2021). Influence of the Shape of Gear Wheel Bodies in Marine Engines on the Gearing Deformation and Meshing Stiffness. Journal of Marine Science and Engineering, 9(10), 1060. https://doi.org/10.3390/jmse9101060







