Dynamic Responses for WindFloat Floating Offshore Wind Turbine at Intermediate Water Depth Based on Local Conditions in China
Abstract
:1. Introduction
2. Theory Background
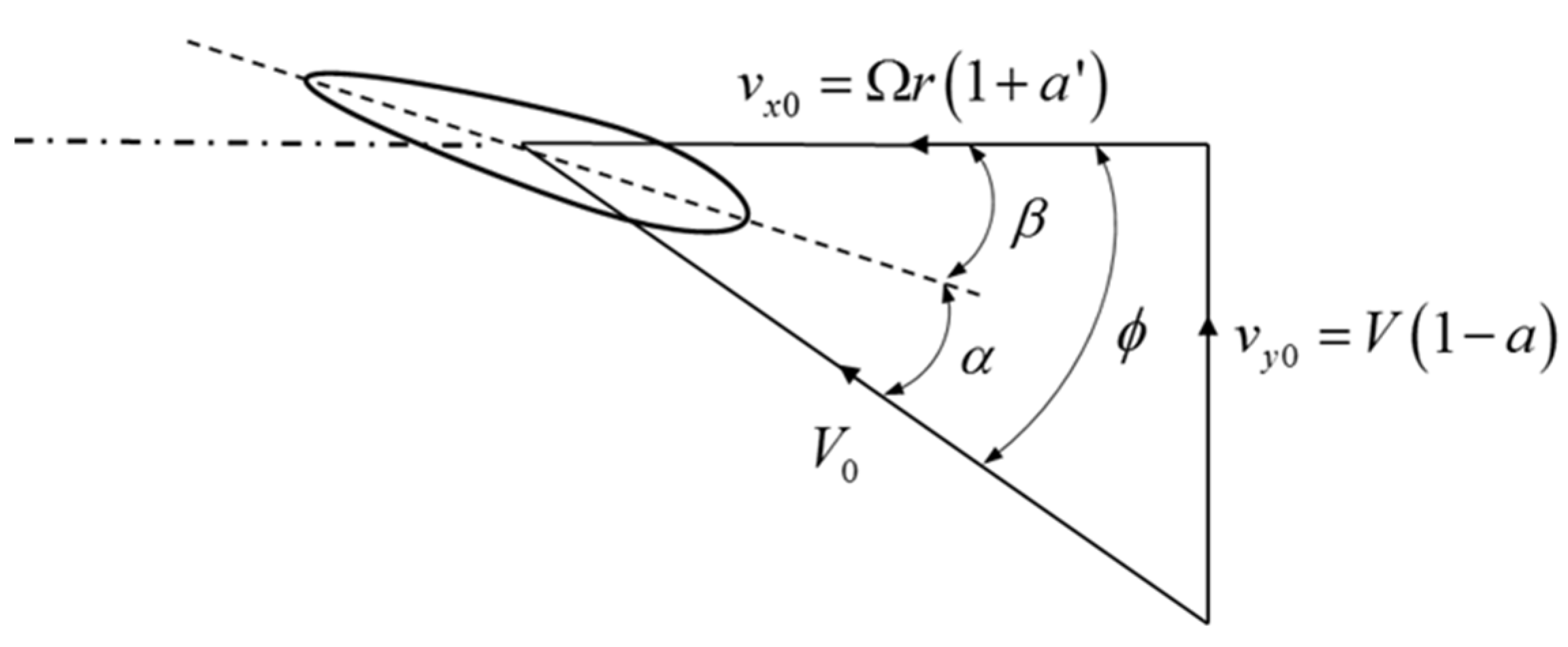
2.1. Aerodynamic Load
2.1.1. Blade Element Momentum Theory
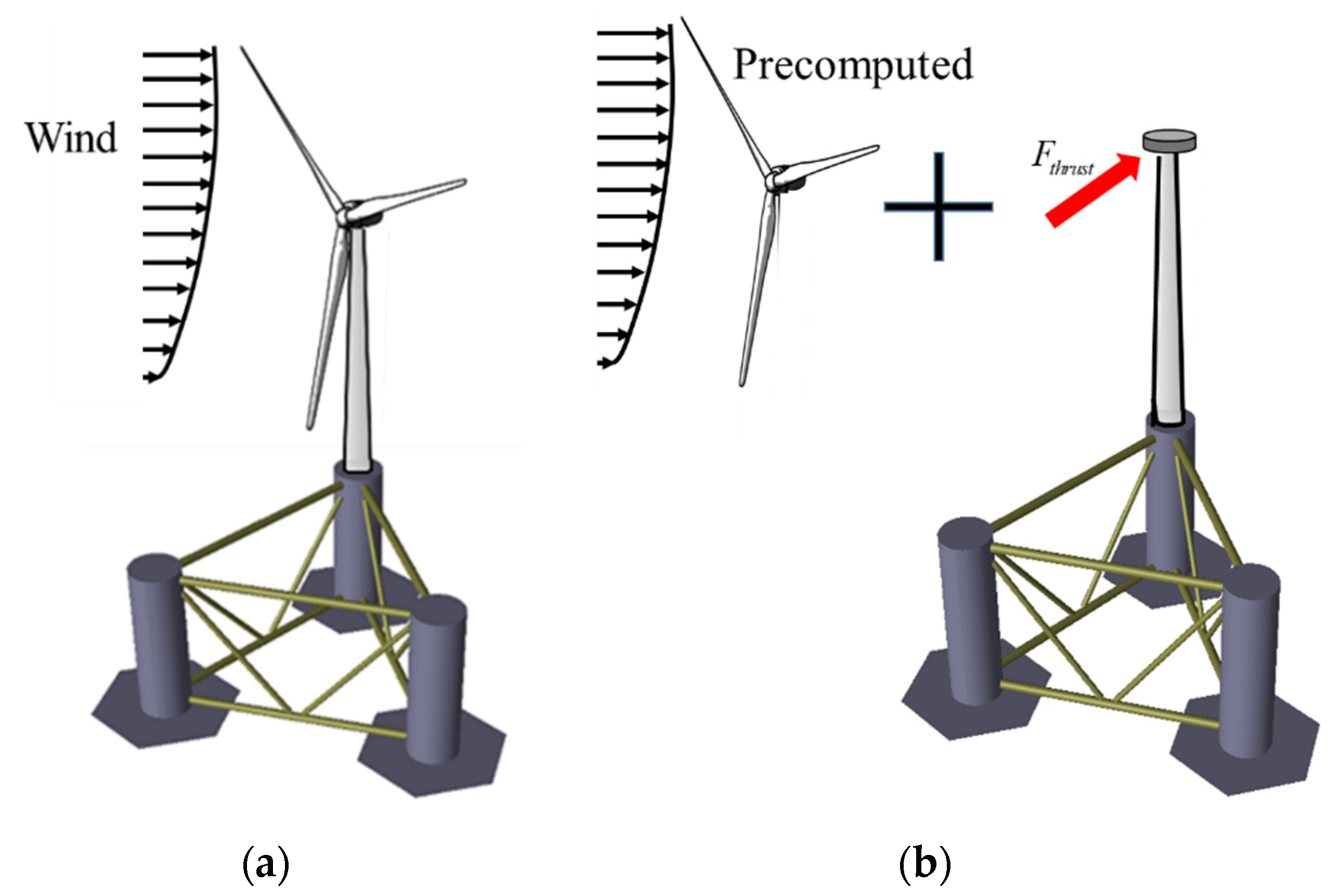
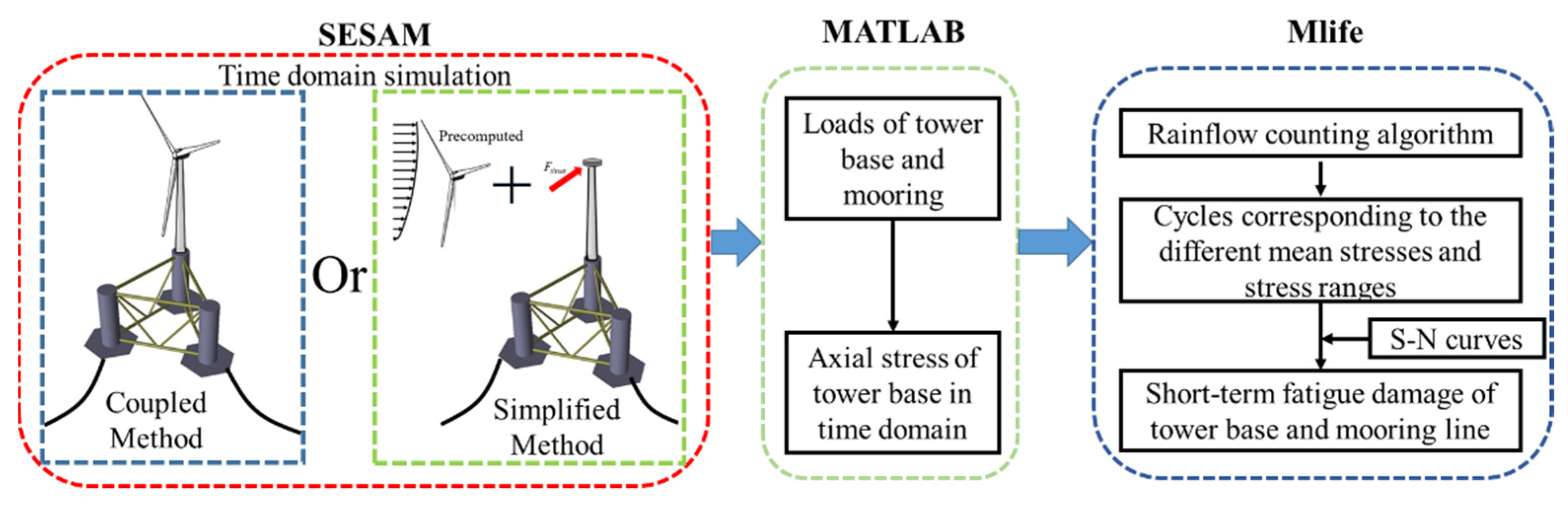
2.1.2. Aerodynamic Calculation by Coupled Method and Simplified Method
2.2. Hydrodynamic Theory
2.2.1. Morison Equation
2.2.2. Potential Flow Theory
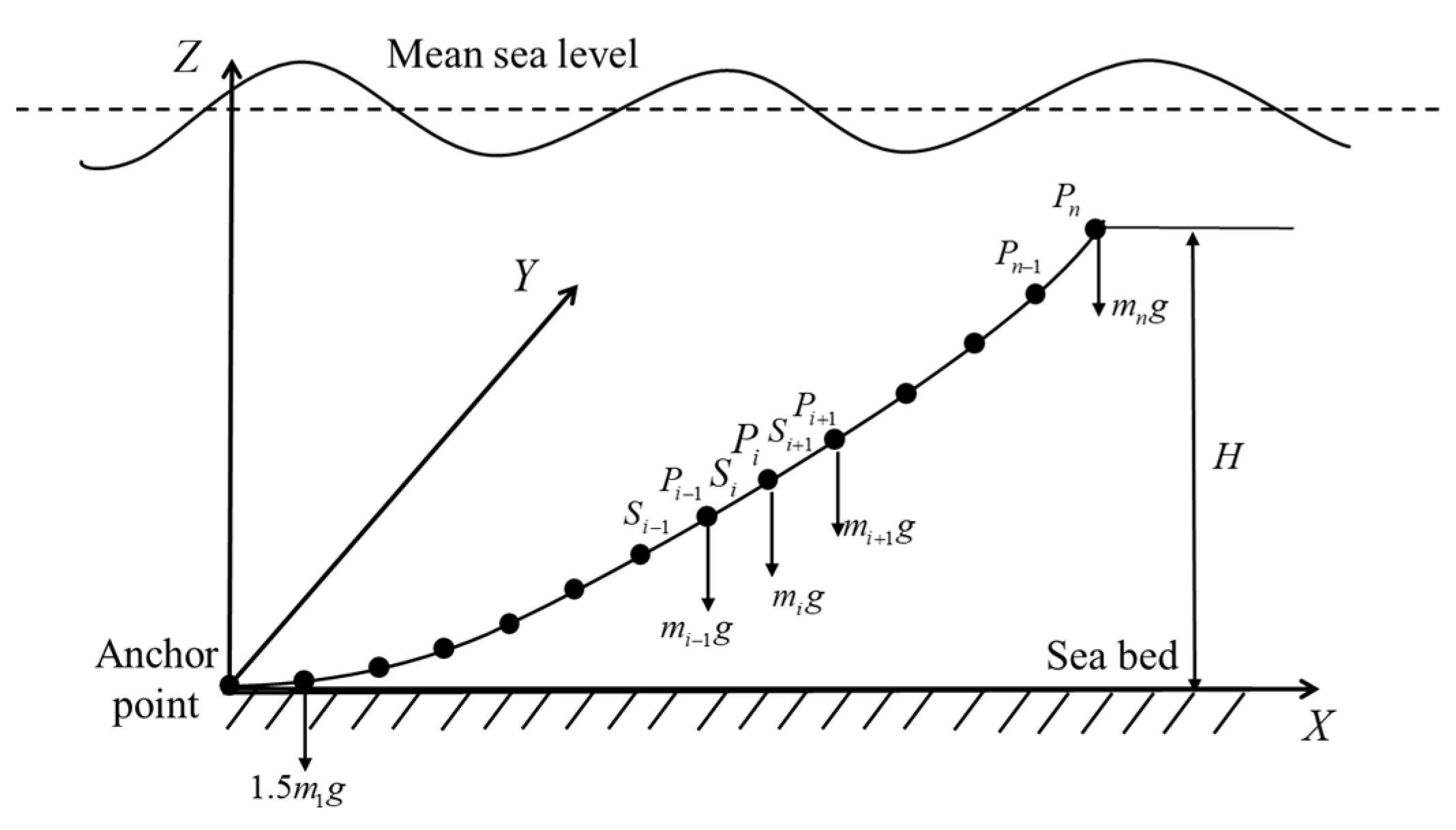
2.3. Mooring System Theory
2.4. Fatigue Damage Calculation
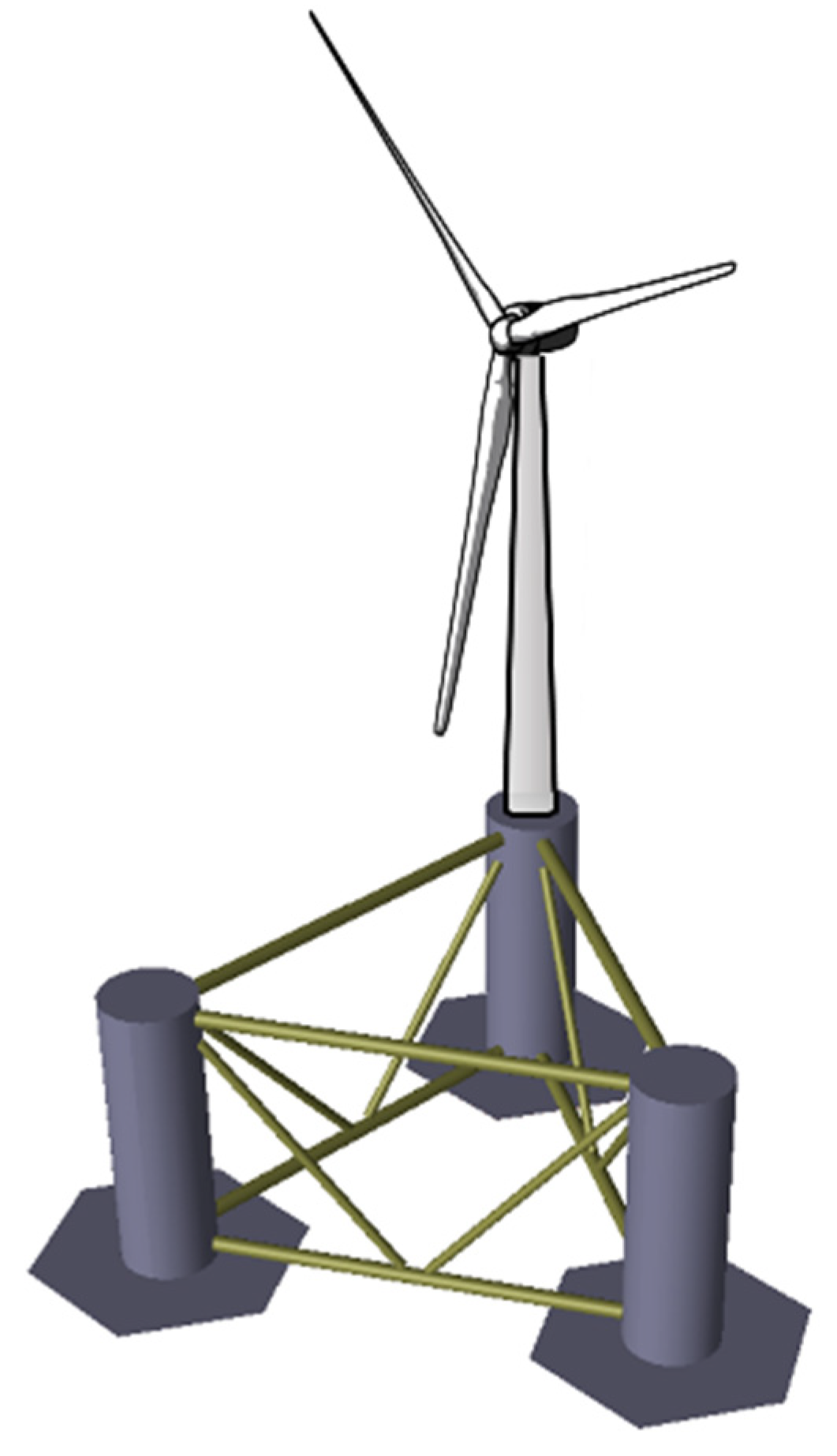
3. Model Description
3.1. Wind Turbine Model
3.2. WindFloat Floating Platform Properties
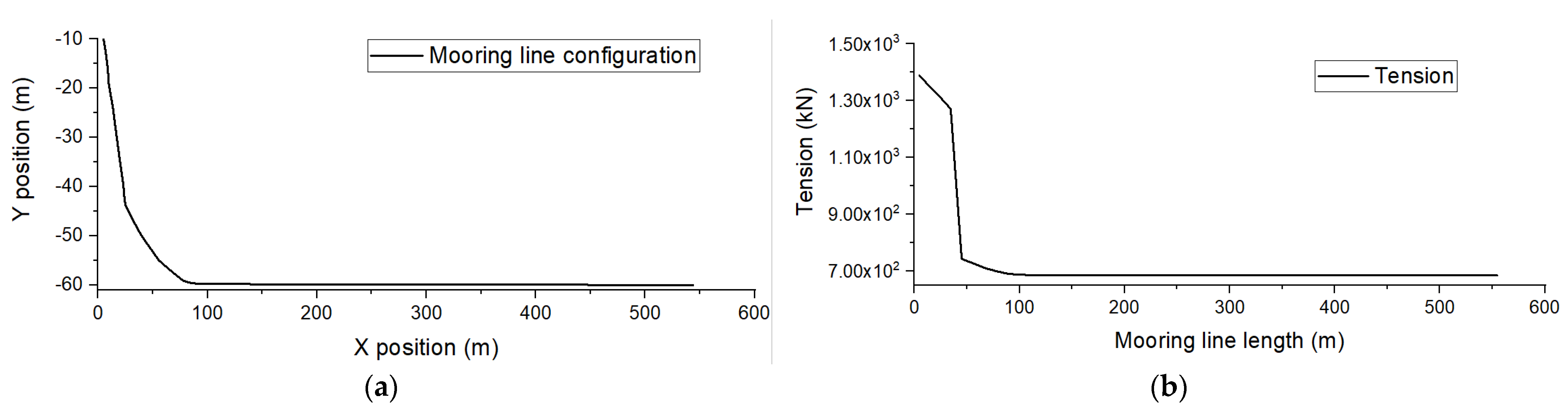
3.3. Mooring System Design
4. Result and Discussion
4.1. Load Case Definition
4.2. Natural frequencies of WindFloat SFOWT
4.3. Comparison of Dynamic Responses Using Coupled and Simplified Method
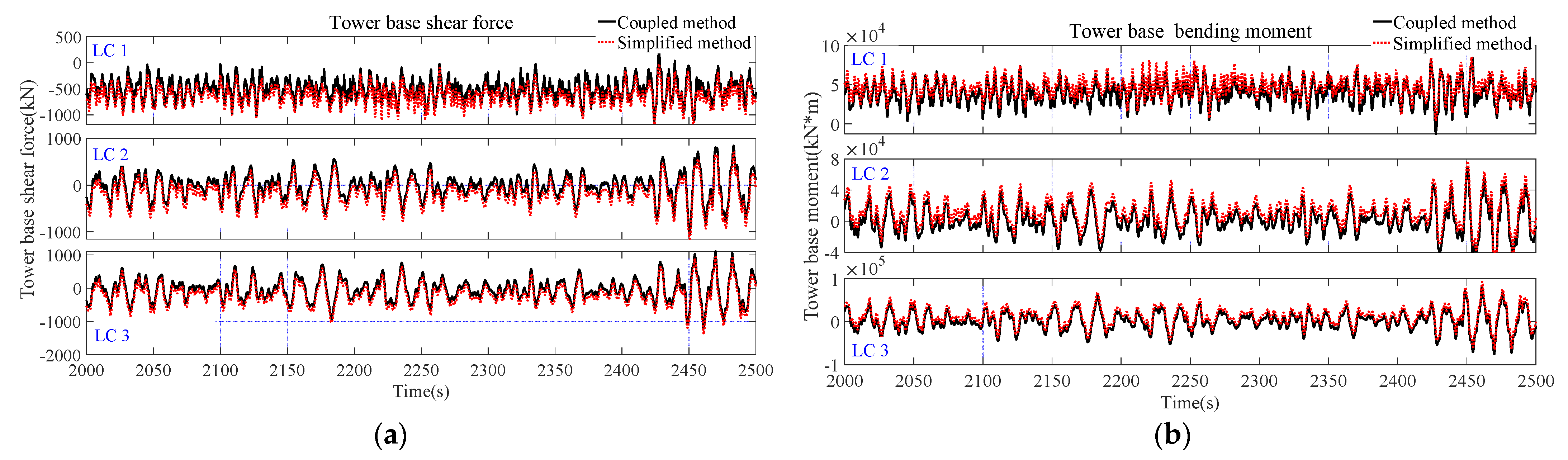
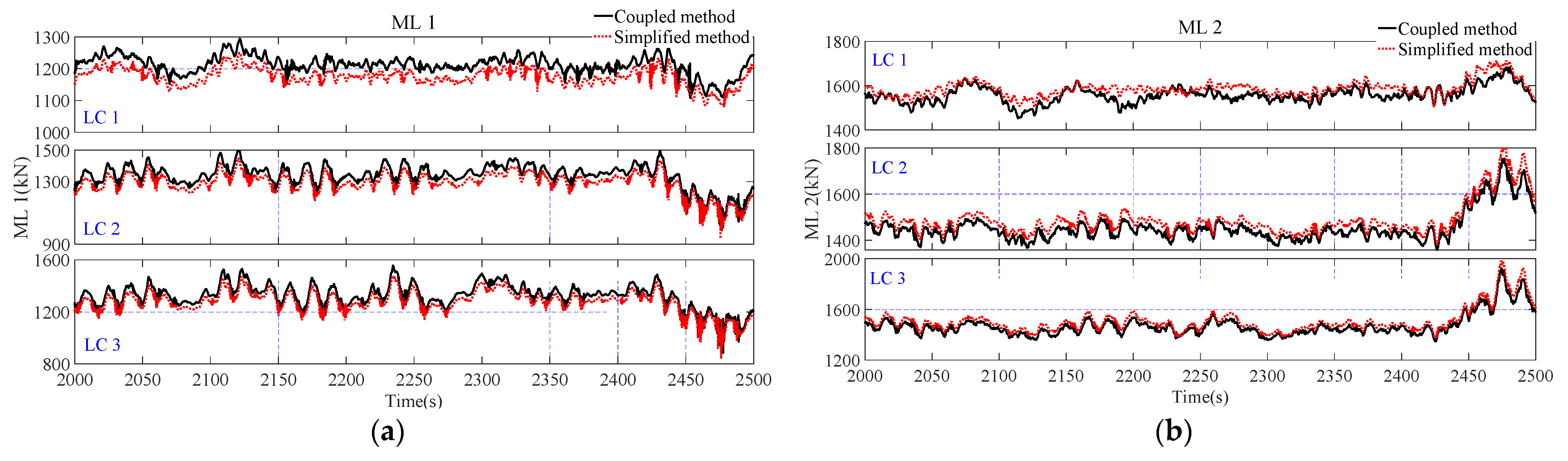
4.3.1. Comparison of Time-Domain Response
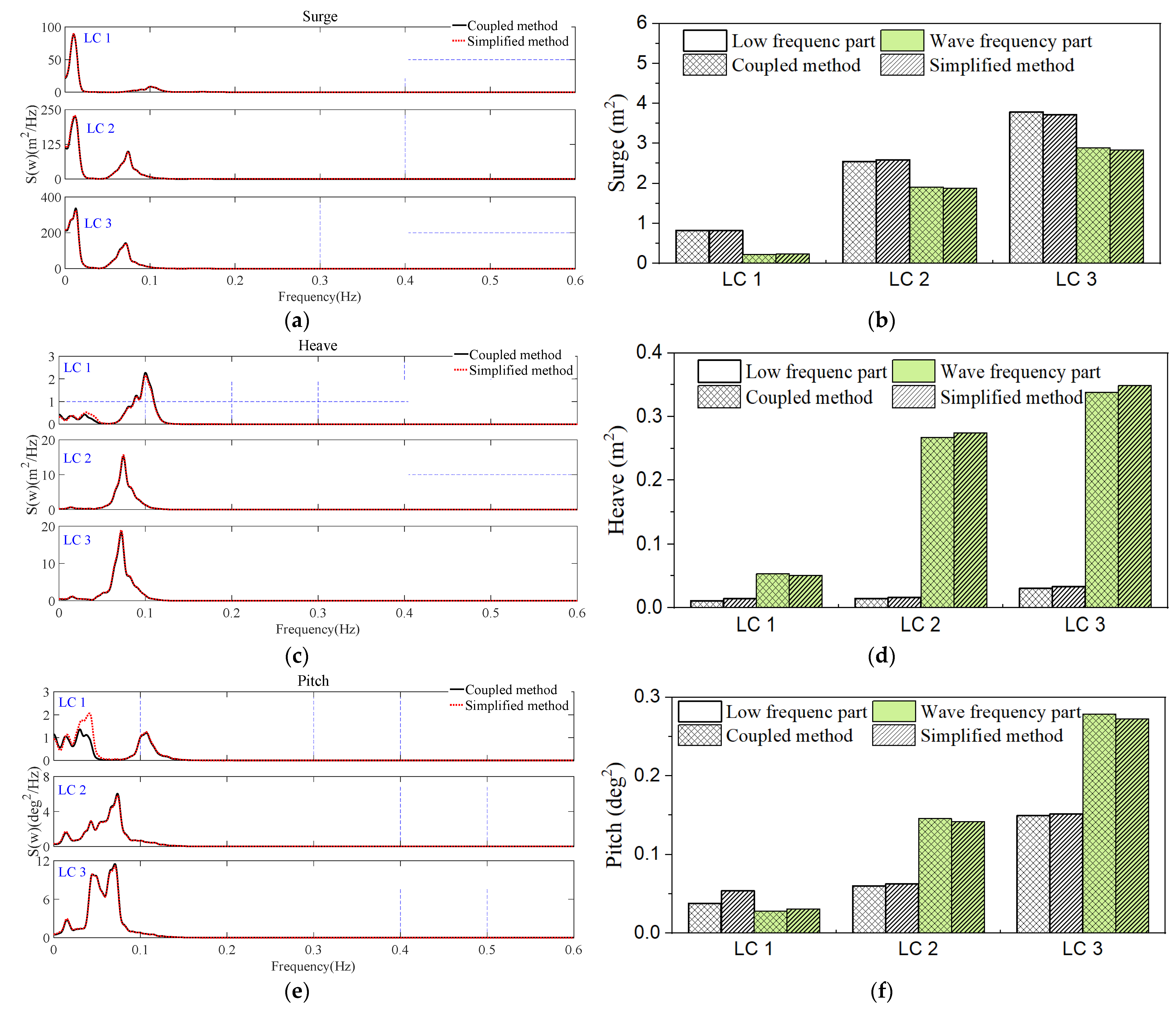
4.3.2. Comparison of Frequency-Domain Response
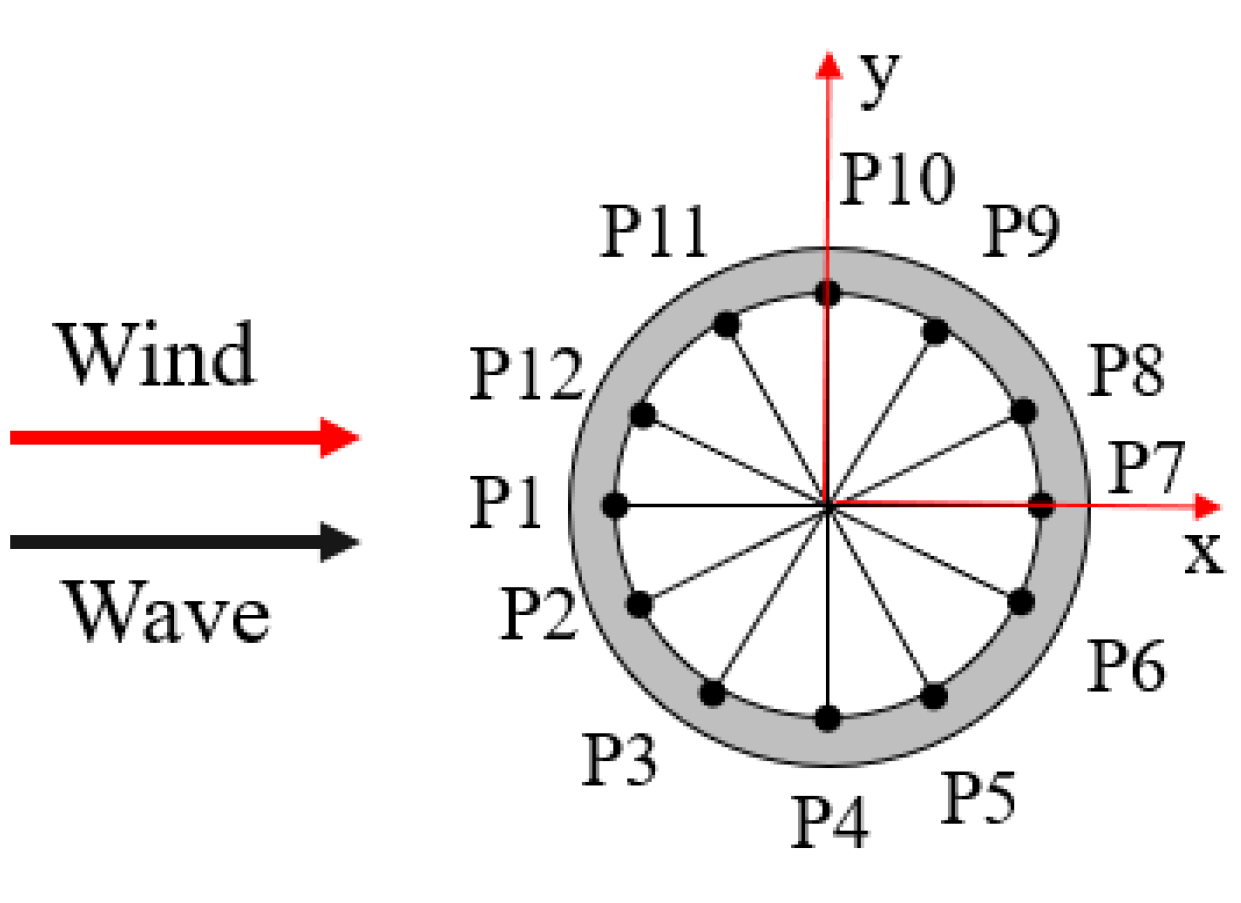
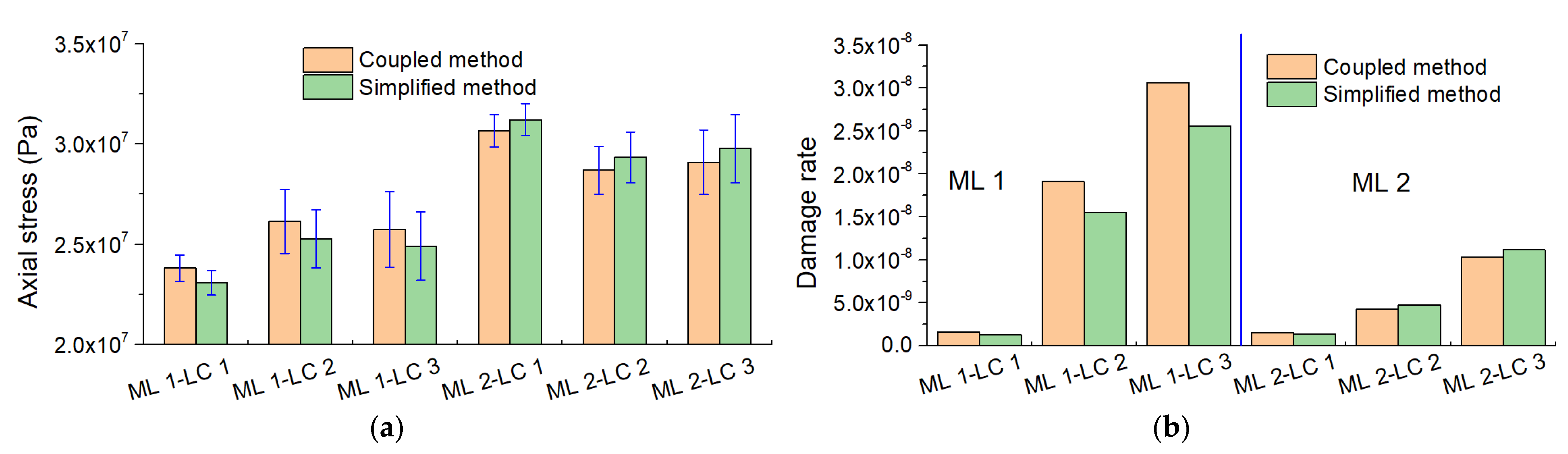
4.3.3. Comparison of Fatigue Damage
5. Conclusions
- (1)
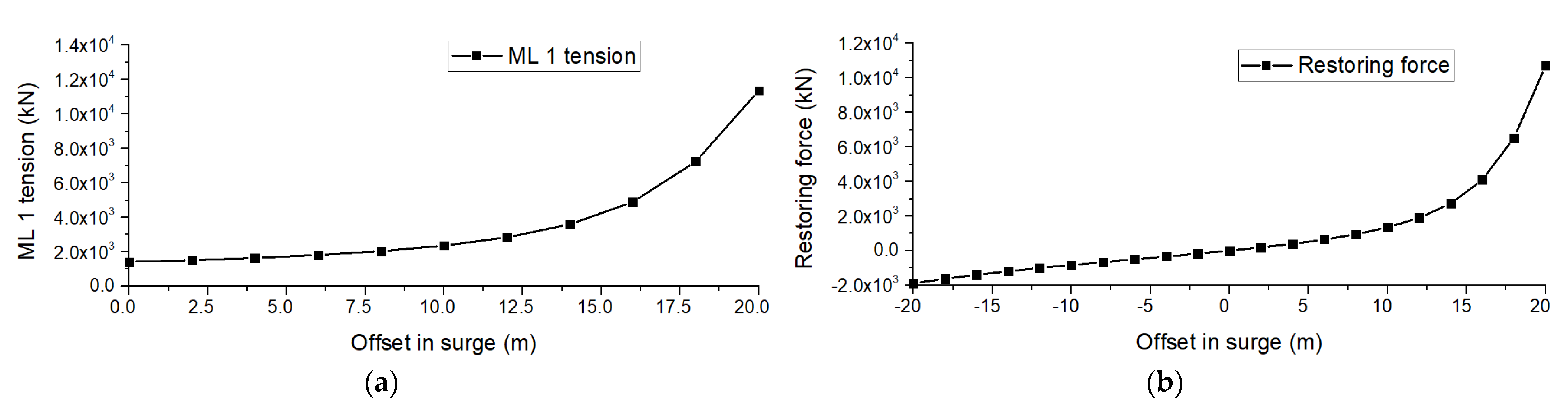
- The WindFloat SFOWT motions and force responses are quite reasonable at a moderate water depth, showing the possibility of semisubmersible floating wind turbines installing at moderate depths. The amplitude of the surge motion response is 9.07 m under a normal operating condition. For the extreme conditions, the amplitude of the surge motion response is approximately 20 m. The maximum pitch motion for all load cases is below 5°. For the mooring line tension responses, the maximum value for ML 1 and ML 2 are 1337.7 kN and 1791.6 kN, respectively, under normal operating conditions. The PSD analysis of the WindFloat SFOWT under different load cases shows that the low frequency responses are the main part of the surge motion response for all load cases, while the heave and pitch motion are mainly dominated by the wave excitation force. The fatigue damage results indicate that the points on the leeward side experience greater fatigue damage than those points on the heading wave side, to which should be paid more attention. For the mooring line tension fatigue, the fatigue damage on ML 1 is larger than that of ML 2 for all load cases.
- (2)
- A comparison between the coupled and simplified methods shows that the simplified method overestimates the maximum motion responses of the WindFloat SFOWT, while the STD value does not change a lot. The simplified method predicts a close PSD response in surge motion. The response spectra in the low frequency region of the heave and pitch motion are larger when using the simplified method. For the mooring line tension responses, the calculated response spectra of the simplified method are underestimated under different load cases for both the low frequency and wave frequency parts, while the response spectra of ML 2 are the opposite. Under normal operating conditions, the difference between the coupled method and simplified method is larger, while it is close under extreme sea conditions because the wave excitation force dominates the tower base responses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- DeCastro, M.; Salvador, S.; Gómez-Gesteira, M.; Costoya, X.; Carvalho, D.; Sanz-Larruga, F.J.; Gimeno, L. Europe, China and the United States: Three different approaches to the development of offshore wind energy. Renew. Sustain. Energy Rev. 2019, 109, 55–70. [Google Scholar] [CrossRef]
- Dong, F.G.; Shi, L.; Ding, X.H.; Li, Y.; Shi, Y.P. Study on China’s renewable energy policy reform and improved design of renewable portfolio standard. Energies 2019, 12, 2147. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Park, H.; Chung, C.; Kim, Y. Comparison of dynamic response of monopile, tripod and jacket foundation system for a 5-MW wind turbine. In Proceedings of the Twenty-first International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Global Wind Report. 2021. Available online: https://gwec.net/global-wind-report-2021/ (accessed on 25 March 2021).
- Karimirad, M.; Michailides, C. Fault condition effects on the dynamic response of V-shaped offshore wind turbine. J. Mar. Sci. Technol. 2019, 24, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Karimirad, M.; Michailides, C. Dynamic Analysis of a Braceless Semisubmersible Offshore Wind Turbine in Operational Conditions. Energy Procedia 2015, 80, 21–29. [Google Scholar] [CrossRef] [Green Version]
- Oguz, E.; Clelland, D.; Day, A.H.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and numerical analysis of a TLP floating offshore wind turbine. Ocean. Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhao, Y.; He, Y.; Shao, Y.; Mao, W.; Han, Z.; Huang, C.; Gu, X.; Jiang, Z. Transient response of a TLP-type floating offshore wind turbine under tendon failure conditions. Ocean Eng. 2021, 220, 108486. [Google Scholar] [CrossRef]
- Antonutti, R.; Peyrard, C.; Johanning, L.; Incecik, A.; Ingram, D. An investigation of the effects of wind-induced inclination on floating wind turbine dynamics: Heave plate excursion. Ocean Eng. 2014, 91, 208–217. [Google Scholar] [CrossRef] [Green Version]
- Tao, L.; Cai, S. Heave motion suppression of a Spar with a heave plate. Ocean Eng. 2004, 31, 669–692. [Google Scholar] [CrossRef] [Green Version]
- Karimirad, M.; Michailides, C. V-shaped semisubmersible offshore wind turbine: An alternative concept for offshore wind technology. Renew. Energy 2015, 83, 126–143. [Google Scholar] [CrossRef] [Green Version]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Moreno, J.; Thiagarajan K, P.; Cameron, M. Hydrodynamic Coefficients of Hexagonal Heave Plates for Floating Offshore Wind Turbine Platforms. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Luan, C.; Gao, Z.; Moan, T. Design and Analysis of a Braceless Steel 5-Mw Semi-Submersible Wind Turbine. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Xu, K.; Gao, Z.; Moan, T. Effect of hydrodynamic load modelling on the response of floating wind turbines and its mooring system in small water depths. J. Phys. Conf. Ser. 2018, 1104, 12006. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Bayati, I.; Gueydon, S.; Belloli, M. Study of the effect of water depth on potential flow solution of the OC4 semisubmersible floating offshore wind turbine. Energy Procedia 2015, 80, 168–176. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Tang, Y.; Hu, J.; Ruan, S.; Chen, C. Dynamic response in frequency and time domains of a floating foundation for offshore wind turbines. Ocean Eng. 2013, 60, 115–123. [Google Scholar] [CrossRef]
- Ingram, G. Wind Turbine Blade Analysis Using the Blade Element Momentum Method; Version 1.1; Durham University: Durham, UK, 2011. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Zhang, M.; Xu, F.; Zhang, Z.; Ying, X. Energy budget analysis and engineering modeling of post-flutter limit cycle oscillation of a bridge deck. J. Wind. Eng. Ind. Aerod. 2019, 188, 410–420. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Han, Y. Assessment of wind-induced nonlinear post-critical performance of bridge decks. J. Wind. Eng. Ind. Aerod. 2020, 203, 104251. [Google Scholar] [CrossRef]
- Schafhirt, S.; Muskulus, M. Decoupled simulations of offshore wind turbines with reduced rotor loads and aerodynamic damping. Wind Energy Sci. 2018, 3, 25–41. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, T.; Zhang, S. Prediction of dynamic response of semi-submersible floating offshore wind turbine using augmented Morison’s equation with frequency dependent hydrodynamic coefficients. Renew. Energy 2019, 131, 1186–1207. [Google Scholar] [CrossRef]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge university press: Cambridge, UK, 1993. [Google Scholar]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef] [Green Version]
- Hayman, G. MLife Theory Mannual for Version 1.00; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Li, H.; Hu, Z.; Wang, J.; Meng, X. Short-term fatigue analysis for tower base of a spar-type wind turbine under stochastic wind-wave loads. Int J. Nav Arch. Ocean. 2018, 10, 9–20. [Google Scholar] [CrossRef]
- Thies, P.R.; Johanning, L.; Harnois, V.; Smith, H.C.; Parish, D.N. Mooring line fatigue damage evaluation for floating marine energy converters: Field measurements and prediction. Renew. Energy 2014, 63, 133–144. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Value |
|---|---|
| Rated power/MW | 5 |
| Rotor Orientation | Upwind |
| Rotor, Hub diameter/m | 126, 3 |
| Hub height/m | 90 |
| Cut-in, Rated, Cut-Out Wind speed/m/s | 3, 11.4, 25 |
| Cut-in, Rated, Rated Rotor Speed/rpm | 6.9, 12.1 |
| Overhang, Shaft tilt, Precone | 5 m, 5°, 2.5° |
| Rotor, Nacelle, Tower mass/ton | 110, 240, 347.46 |
| Tower top, diameter, wall thickness/m | 3.87, 0.019 |
| Parameter | Value |
|---|---|
| Column diameter/m | 10.7 |
| Distance of column to column/m | 56.4 |
| Brace diameter/m | 28 |
| Cross brace diameter/m | 2.0 |
| Diagonal brace diameter/m | 2.2 |
| Column height/m | 33.6 |
| Draft/m | 22.9 |
| COG (x, y, z)/m | (−32.6, 0, −13.1) |
| Mass of the platform/m | 2.02 × 106 |
| Radius of gyration—rx/m | 25.8 |
| Radius of gyration—ry/m | 25.8 |
| Radius of gyration—rz/m | 32.3 |
| Parameter | Value |
|---|---|
| Water depth/m | 60 |
| Mooring line length/m | 560 |
| Mass per unit length/(kg/m) | 648 |
| Diameter of mooring line/m | 0.180 |
| Axial stiffness/kN | 2.92 × 109 |
| Fairlead for ML 1 (x, y, z) /m | (5.35, 0, −10) |
| Fairlead for ML 2 (x, y, z) /m | (−51.52, 32.83, −10) |
| Fairlead for ML 3 (x, y, z) /m | (−51.52, −32.83, −10) |
| Anchor point of ML 1 (x, y, z) /m | (543.84, 0, −60) |
| Anchor point of ML 2 (x, y, z) /m | (−320.76, 499.18, −60) |
| Anchor point of ML 3 (x, y, z) /m | (−320.76, −499.18, −60) |
| Pretension/ kN | 1400 kN |
| Clump mass/kg | 75,000 |
| Load Case | Hs/m | Tp/s | Uw/(m/s) | TI |
|---|---|---|---|---|
| Load case 1 (LC 1) | 5.4 | 9.7 | 18.7 | 0.12 |
| Load case 2 (LC 2) | 9.4 | 13.5 | 30.1 | 0.12 |
| Load case 3 (LC 3) | 11.0 | 14.3 | 33.7 | 0.12 |
| Mode | Natural Period/s | Natural Frequency/Hz |
|---|---|---|
| Surge | 75.8 | 0.013 |
| Heave | 20.4 | 0.049 |
| Pitch | 31.2 | 0.032 |
| Mode | Load Case | Maximum | Minimum | Average | Standard Deviation | ||||
|---|---|---|---|---|---|---|---|---|---|
| Coupled Method | Simplified Method | Coupled Method | Simplified Method | Coupled Method | Simplified Method | Coupled Method | Simplified Method | ||
| Surge/m | LC 1 | 10.06 | 11.18 | 0.99 | 2.16 | 4.38 | 5.55 | 1.09 | 1.10 |
| LC 2 | 11.96 | 13.05 | −5.67 | −4.51 | 1.80 | 2.77 | 2.25 | 2.25 | |
| LC 3 | 14.81 | 15.70 | −6.05 | −4.86 | 2.39 | 3.34 | 2.79 | 2.77 | |
| Heave/m | LC 1 | −0.21 | −0.32 | −1.86 | −1.99 | −0.90 | −1.05 | 0.26 | 0.26 |
| LC 2 | 1.28 | 1.01 | −1.53 | −1.90 | 0.03 | −0.26 | 0.53 | 0.54 | |
| LC 3 | 1.45 | 1.16 | −1.79 | −2.15 | 0.01 | −0.30 | 0.61 | 0.62 | |
| Pitch/° | LC 1 | 2.61 | 3.03 | 0.75 | 1.07 | 1.59 | 1.86 | 0.27 | 0.30 |
| LC 2 | 1.60 | 2.14 | −1.49 | −1.02 | 0.00 | 0.47 | 0.46 | 0.45 | |
| LC 3 | 2.08 | 2.58 | −1.90 | −1.46 | 0.03 | 0.52 | 0.66 | 0.65 | |
| Mode | Load Case | Maximum | Minimum | Average | Standard deviation | ||||
|---|---|---|---|---|---|---|---|---|---|
| Coupled Method | Simplified Method | Coupled Method | Simplified Method | Coupled Method | Simplified Method | Coupled Method | Simplified Method | ||
| Tower base Fx/kN | LC 1 | 1335.8 | 1304.0 | −447.1 | −220.9 | 501.5 | 627.2 | 219.7 | 194.6 |
| LC 2 | 1189.2 | 1316.2 | −1228.4 | −1118.4 | 33.0 | 167.5 | 297.5 | 296.3 | |
| LC 3 | 1421.4 | 1537.5 | −1246.0 | −1089.3 | 44.6 | 178.9 | 353.8 | 352.4 | |
| Tower base My/kN*m | LC 1 | 97,092.0 | 93,171.0 | −26,980.0 | −12,934.0 | 38,788.7 | 46,348.7 | 15,462.2 | 13,521.1 |
| LC 2 | 79,377.0 | 88,518.0 | −83,887.0 | −75,899.0 | 1764.2 | 11,350.9 | 19,802.2 | 19,644.9 | |
| LC 3 | 95,648.0 | 103,000.0 | −84,430.0 | −73,843.0 | 2804.6 | 12,196.0 | 23,593.2 | 23,392.4 | |
| ML 1/kN | LC 1 | 1337.7 | 1286.0 | 993.8 | 975.2 | 1212.2 | 1174.5 | 33.5 | 31.2 |
| LC 2 | 1721.4 | 1618.9 | 995.6 | 936.1 | 1330.7 | 1285.7 | 81.2 | 73.9 | |
| LC 3 | 1747.2 | 1641.0 | 885.6 | 838.8 | 1310.8 | 1267.9 | 96.0 | 86.7 | |
| ML 2/kN | LC 1 | 1791.6 | 1835.4 | 1442.2 | 1463.9 | 1560.4 | 1588.6 | 40.9 | 40.5 |
| LC 2 | 1815.6 | 1860.4 | 1313.5 | 1350.7 | 1460.2 | 1493.2 | 60.7 | 64.5 | |
| LC 3 | 1960.9 | 1998.0 | 1299.6 | 1323.6 | 1480.8 | 1515.1 | 81.9 | 85.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Zhang, L.; Shi, W.; Wang, B.; Li, X. Dynamic Responses for WindFloat Floating Offshore Wind Turbine at Intermediate Water Depth Based on Local Conditions in China. J. Mar. Sci. Eng. 2021, 9, 1093. https://doi.org/10.3390/jmse9101093
Gao S, Zhang L, Shi W, Wang B, Li X. Dynamic Responses for WindFloat Floating Offshore Wind Turbine at Intermediate Water Depth Based on Local Conditions in China. Journal of Marine Science and Engineering. 2021; 9(10):1093. https://doi.org/10.3390/jmse9101093
Chicago/Turabian StyleGao, Shan, Lixian Zhang, Wei Shi, Bin Wang, and Xin Li. 2021. "Dynamic Responses for WindFloat Floating Offshore Wind Turbine at Intermediate Water Depth Based on Local Conditions in China" Journal of Marine Science and Engineering 9, no. 10: 1093. https://doi.org/10.3390/jmse9101093
APA StyleGao, S., Zhang, L., Shi, W., Wang, B., & Li, X. (2021). Dynamic Responses for WindFloat Floating Offshore Wind Turbine at Intermediate Water Depth Based on Local Conditions in China. Journal of Marine Science and Engineering, 9(10), 1093. https://doi.org/10.3390/jmse9101093







