Exploring the Spatial Variations of Stressors Impacting Platform Removal in the Northern Gulf of Mexico
Abstract
:1. Introduction
2. Literature Review
2.1. Factors Affecting Platform Integrity
2.1.1. Platform Design and Production
2.1.2. Metocean
2.1.3. Geohazards
2.1.4. Incidents
2.2. Existing Methods of Integrity Evaluation
3. Materials and Methods
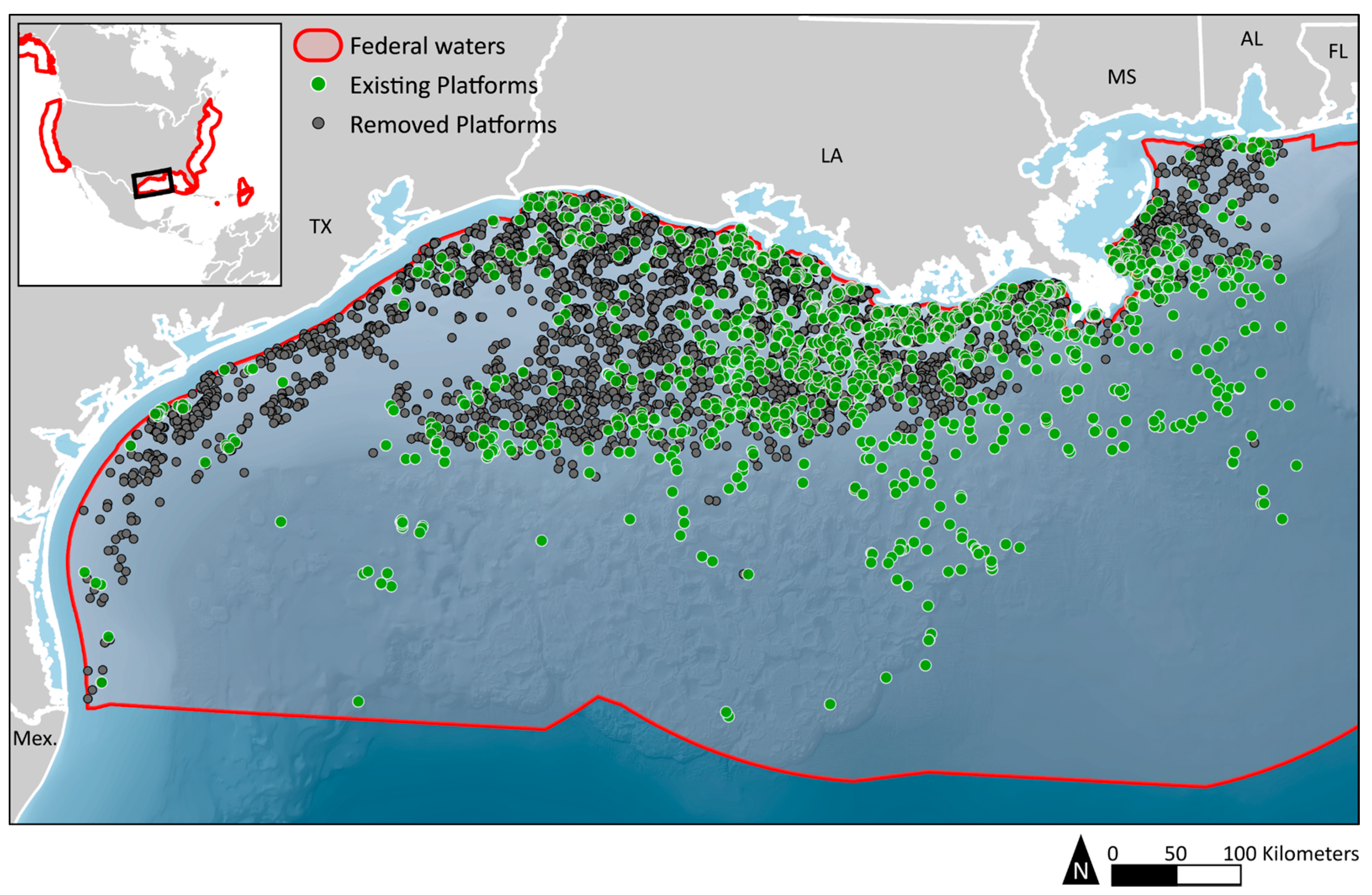
3.1. Data
3.2. Dependent Variable
3.3. Independent Variable Selection—Singular Value Decomposition
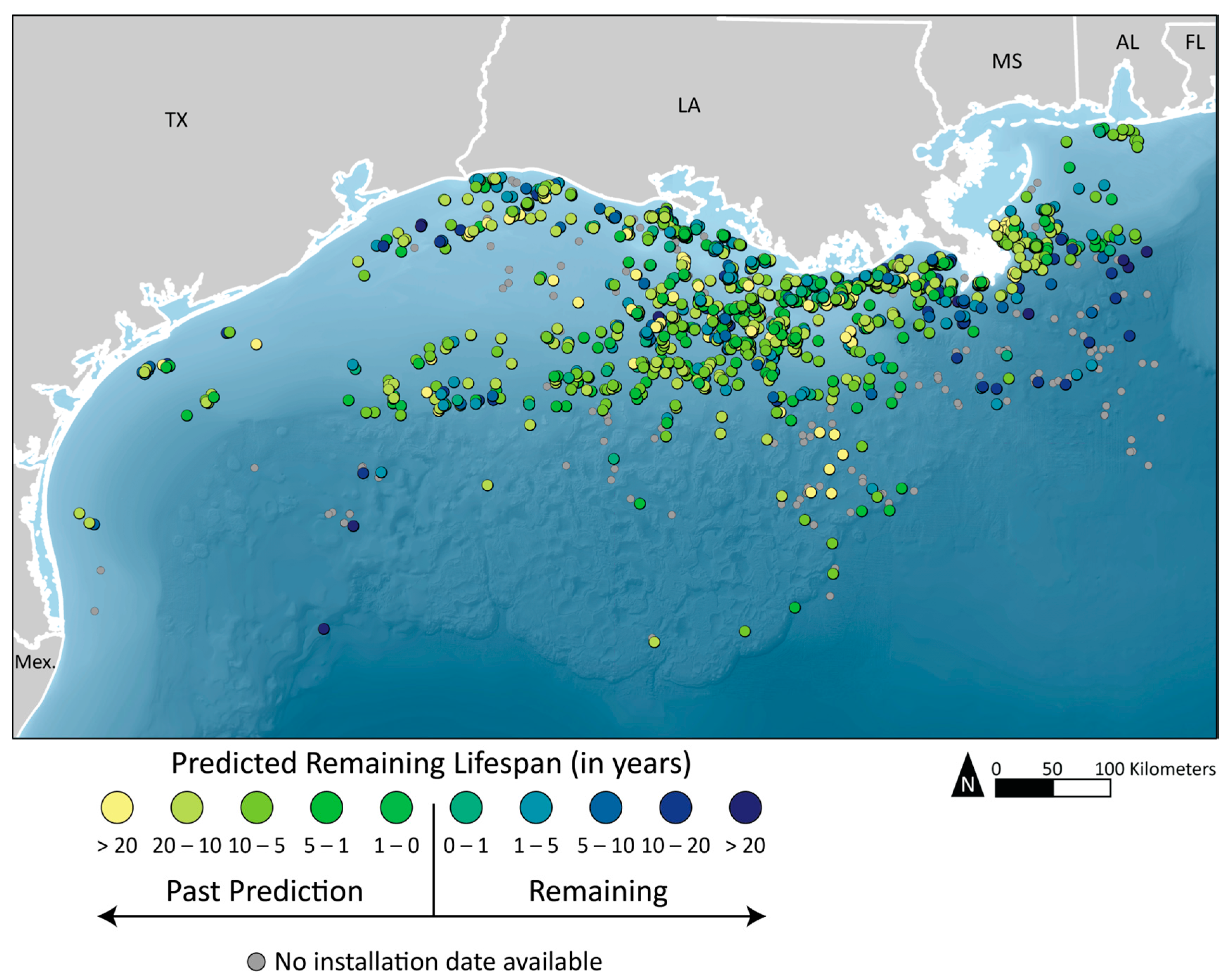
3.4. Geostatistical Analysis and Prediction
4. Results
4.1. Singular Value Decomposition
4.2. Geographically Weighted Regression
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable Name | Definition | Source(s) |
|---|---|---|
| Incident Sum | Total incident severity per OCS lease block. | BSEE. Offshore Incident Statistics. Bureau of Safety and Environmental Enforcement, 2019a. https://www.bsee.gov/stats-facts/offshore-incident-statistics (accessed on 21 February 2020). Mary J. Hoover (2002) Incidents Associated with Oil and Gas Operations: Outer Continental Shelf 2000, U.S. Department of the Interior: Minerals Management Service Engineering and Operations Division. Kristen Stanley, Cheryl Anderson, L. John Chadwell, Karen Sagall (2001) Incidents Associated with Oil and Gas Operations: Outer Continental Shelf 1999, U.S. Department of the Interior: Minerals Management Service Engineering and Operations Division. L. John Chadwell, Cheryl Blundon, Cheryl Anderson, Mariella Cacho (2000) Incidents Associated with Oil and Gas Operations: Outer Continental Shelf 1998, U.S. Department of the Interior: Minerals Management Service. L. John Chadwell, Cheryl Blundon, Cheryl Anderson (n.d.) Incidents Associated with Oil and Gas Operations: Outer Continental Shelf 1997, U.S. Department of the Interior: Minerals Management Service L. John Chadwell, Melinda Mayes, Cheryl Anderson (1998) Incidents Associated with Oil and Gas Operations: Outer Continental Shelf 1995–1996, U.S. Department of the Interior: Minerals Management Service. Ulysses Cotton (1995) Accidents Associated with Oil and Gas Operations: Outer Continental Shelf 1991–1994, U.S. Department of the Interior: Minerals Management Service. Mineral Management Service (1992) Accidents Associated with Oil and Gas Operations: Outer Continental Shelf 1956–1990, U.S. Department of the Interior |
| Phosphorus | Mean surface phosphorus measured in (μmol/kg). | Garcia, H. E.; Locarnini, R. A.; Boyer, T. P.; Antonov, J. I.; Baranova, O. K.; Zweng, M. M.; Levitus, S. World Ocean Atlas 2019, Dissolved Inorganic Nutrients (phosphate, nitrate and nitrate+nitrite, silicate); Mishonov, A., Technical Ed.; NOAA Atlas NESDIS, 2019; Vol 4, p. 35. |
| Salinity | Mean surface salinity (unitless). | Zweng, M. M.; Reagan, J. R.; Antonov, J. I.; Locarnini, R. A.; Mishonov, A. V.; Boyer, T. P. Seidov, D. World Ocean Atlas 2019; Mishonov, A., Technical Ed.; NOAA Atlas NESDIS 2019; p. 50. Vol 2. |
| Slot Drill Count | Total number of drilling slots that have been used at a location. | Bureau of Safety and Environmental Enforcement. Platform/Rig Information. Bureau of Safety and Environmental Enforcement, 2020. https://www.data.bsee.gov/Main/Platform.aspx (accessed on 15 January 2021) |
| Surface Magnitude | Surface water velocity magnitude maximum (m/s). | Bleck, R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Modell. 37, 55–88 (2002). |
| MRWG | Maximum Reported Wind Gust maximum (kt). | Knapp, K. R., M. C. Kruk, D. H. Levinson, H. J. Diamond, and C. J. Neumann, 2010: The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone best track data. Bulletin of the American Meteorological Society, 91, 363–376. non-government domain doi:10.1175/2009BAMS2755.1 Knapp, K. R., H. J. Diamond, J. P. Kossin, M. C. Kruk, C. J. Schreck, 2018: International Best Track Archive for Climate Stewardship (IBTrACS) Project, Version 4. [indicate subset used]. NOAA National Centers for Environmental Information. non-government domain https://doi.org/10.25921/82ty-9e19 (accessed on 15 November 2020) |
| C5 Yearly | Annual average Category 5 hurricane occurrences. | Knapp, K. R., M. C. Kruk, D. H. Levinson, H. J. Diamond, and C. J. Neumann, 2010: The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone best track data. Bulletin of the American Meteorological Society, 91, 363–376. non-government domain doi:10.1175/2009BAMS2755.1 |
| Knapp, K. R., H. J. Diamond, J. P. Kossin, M. C. Kruk, C. J. Schreck, 2018: International Best Track Archive for Climate Stewardship (IBTrACS) Project, Version 4. [indicate subset used]. NOAA National Centers for Environmental Information. non-government domain https://doi.org/10.25921/82ty-9e19 (accessed on 5 November 2021) | ||
| Water Depth | Bathymetric depth at platform location (m). | Bureau of Safety and Environmental Enforcement. Platform/Rig Information. Bureau of Safety and Environmental Enforcement, 2020. https://www.data.bsee.gov/Main/Platform.aspx (accessed on 3 January 2021) |
Appendix B
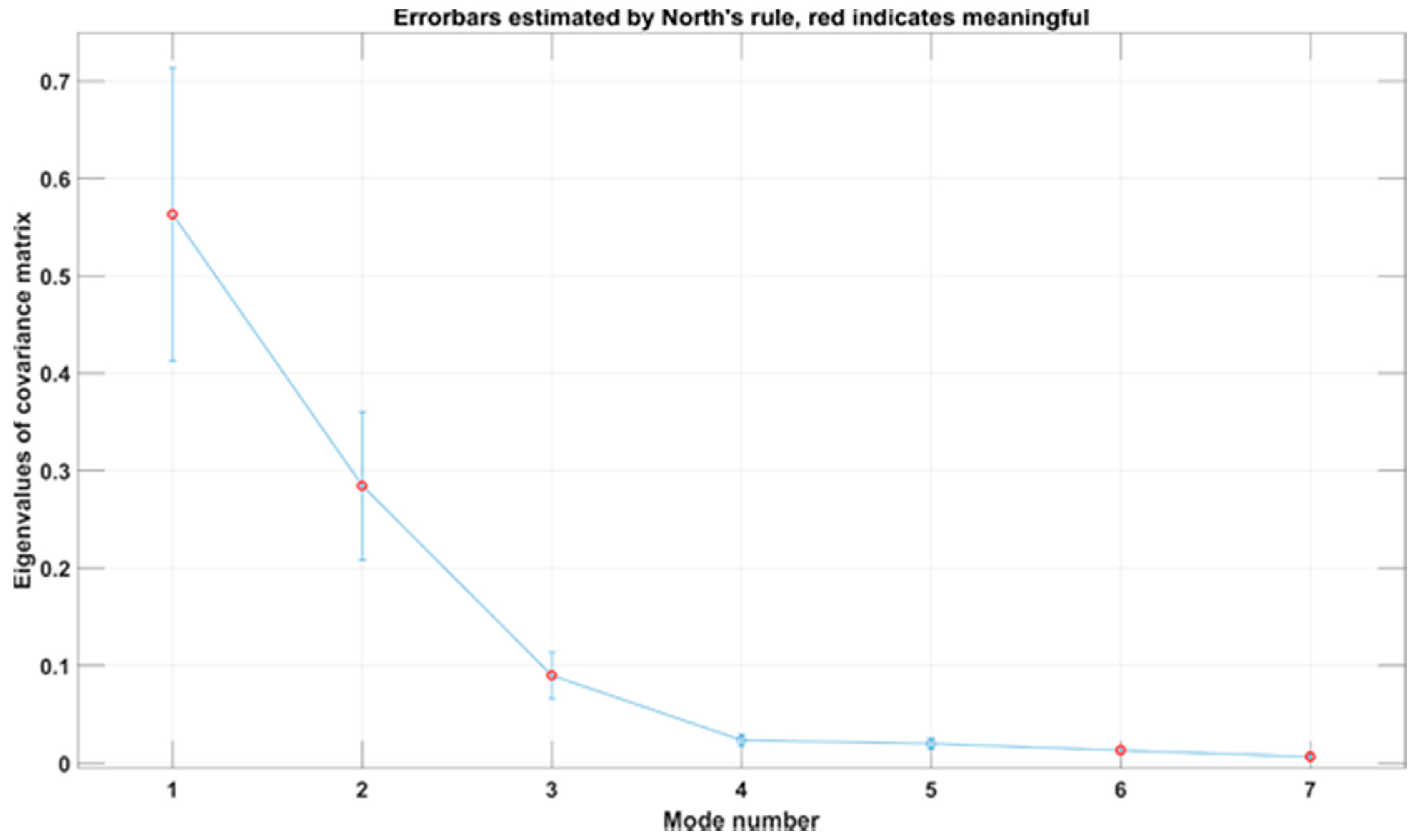
Appendix C

References
- BSEE Platform/Rig Information. Available online: https://www.data.bsee.gov/Main/Platform.aspx (accessed on 5 May 2020).
- Stacey, A.; Birkinshaw, M.; Sharp, J.V. Life Extension Issues for Ageing Offshore Installations. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 48227, pp. 199–215. [Google Scholar]
- Ersdal, G. Assessment of Existing Offshore Structures for Life Extension; University of Stavanger: Stavanger, Norway, 2005. [Google Scholar]
- Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F.; Vanem, E.; Carvalho, H.; Correia, J. Advanced research on offshore structures and foundation design: Part 1. Proc. Inst. Civ. Eng. Marit. Eng. 2019, 172, 118–123. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F.; Pavlou, D.; Gao, F.-P.; Carvalho, H.; Oliveira-Pinto, S. Advanced Research on Offshore Structures and Foundation Design: Part 2. Proc. Inst. Civ. Eng. Marit. Eng. 2020, 173, 96–99. [Google Scholar] [CrossRef]
- Deepwater Horizon Study Group. Final Report on the Investigation of the Macondo Well Blowout; University of California: Berkley, CA, USA, 2011. [Google Scholar]
- Halim, S.Z.; Yu, M.; Escobar, H.; Quddus, N. Towards a causal model from pipeline incident data analysis. Process Saf. Environ. Prot. 2020, 143, 348–360. [Google Scholar] [CrossRef]
- Halim, S.Z.; Janardanan, S.; Flechas, T.; Mannan, M.S. In search of causes behind offshore incidents: Fire in offshore oil and gas facilities. J. Loss Prev. Process Ind. 2018, 54, 254–265. [Google Scholar] [CrossRef]
- Moan, T. Life cycle structural integrity management of offshore structures. Struct. Infrastruct. Eng. 2018, 14, 911–927. [Google Scholar] [CrossRef] [Green Version]
- Soom, E.M.; Husain, M.K.A.; Zaki, N.I.M.; Nor, M.N.K.M.; Najafian, G. Lifetime Extension of Ageing Offshore Structures by Global Ultimate Strength Assessment (GUSA). Malays. J. Civ. Eng. 2018, 30, 152–171. [Google Scholar]
- O’Connor, P.E.; Bucknell, J.R.; DeFrance, S.J.; Westlake, H.S.; Westlake, F.J. Structural Integrity Management (SIM) of Offshore Facilities. Offshore Technol. Conf. 2005, 11, 1–11. [Google Scholar]
- ISO Petroleum and Natural Gas Industries—Fixed Steel Offshore Structures, Internatonal Standards Organization: ISO 19902:2020. 2020, Volume 622. Available online: https://www.iso.org/standard/65688.html (accessed on 8 January 2021).
- Mourão, A.; Correia, J.A.F.O.; Ávila, B.V.; de Oliveira, C.C.; Ferradosa, T.; Carvalho, H.; Castro, J.M.; De Jesus, A.M.P. A fatigue damage evaluation using local damage parameters for an offshore structure. Proc. Inst. Civ. Eng. Marit. Eng. 2020, 173, 43–57. [Google Scholar] [CrossRef]
- Sharp, J.; Ersdal, G.; Galbraith, D. Meaningful and Leading Structural Integrity KPIs. In Proceedings of the SPE Offshore Europe Conference and Exhibition; Society of Petroleum Engineers, Aberdeen, UK, 8–11 September 2015. [Google Scholar]
- Berek, E.P.; Cooper, C.K.; Driver, D.B.; Heideman, J.C.; Mitchell, D.A.; Stear, J.D.; Vogel, M.J. Development of Revised Gulf of Mexico Metocean Hurricane Conditions for Reference by API Recommended Practices. Offshore Technol. Conf. 2007, 13, 1–11. [Google Scholar]
- Matsushima, I. Carbon steel—Corrosion by seawater. In Uhlig’s Corrosion Handbook; Revie, R., Ed.; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Melchers, R.E. Principles of marine corrosion. In Springer Handbook of Ocean Engineering; Dhanak, M.R., Xiros, N.I., Eds.; Springer: Cham, Switzerland, 2016; pp. 111–126. ISBN 978-3-319-16648-3. [Google Scholar]
- Mcleod, D.; Jacobson, J.R.; Tangirala, S. Autonomous inspection of subsea facilities-Gulf of Mexico trials. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012. [Google Scholar]
- Quinn, R.; Kavanagh, K.; Power, J.; Thompson, H. Integrated Approach to Subsea Integrity Management: Benefits of Early Field Integrity Management Planning for Chevron’s Tahiti Field. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2007. [Google Scholar]
- Matthews, S.A.; Yang, T.-C. Mapping the results of local statistics: Using geographically weighted regression. Demogr. Res. 2012, 26, 151–166. [Google Scholar] [CrossRef] [Green Version]
- Worden, K.; Rogers, T.; Cross, E.J. Identification of Nonlinear Wave Forces Using Gaussian Process NARX Models BT—Nonlinear Dynamics; Kerschen, G., Ed.; Springer: Cham, Switzerland, 2017; Volume 1, pp. 203–221. [Google Scholar]
- Almedallah, M.K.; Walsh, S.D.C. A numerical method to optimize use of existing assets in offshore natural gas and oil field developments. J. Nat. Gas Sci. Eng. 2019, 67, 43–55. [Google Scholar] [CrossRef]
- Aoghs.org Editors Offshore Petroleum Exploration History. Available online: https://aoghs.org/offshore-history/offshore-oil-history (accessed on 15 June 2021).
- BSEE Offshore Incident Statistics. Available online: https://www.bsee.gov/stats-facts/offshore-incident-statistics (accessed on 21 February 2020).
- Deyab, S.M.; Taleb-berrouane, M.; Khan, F.; Yang, M. Failure analysis of the offshore process component considering causation dependence. Process Saf. Environ. Prot. 2018, 113, 220–232. [Google Scholar] [CrossRef]
- BOEM. Offshore Oil and Gas Economic Contributions; Department of the Interior: Washington, DC, USA, 2016. [Google Scholar]
- Ersdal, G.; Sharp, J.V.; Stacey, A. Ageing and Life Extension of Offshore Structures: The Challenge of Managing Structural Integrity; John Wiley & Sons: Hoboken, NJ, USA, 2019; ISBN 1119284392. [Google Scholar]
- Holmes, R. The fatigue behaviour of welded joints under North Sea environmental and random loading conditions. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 1980. [Google Scholar]
- Bhandari, J.; Abbassi, R.; Garaniya, V.; Khan, F. Risk analysis of deepwater drilling operations using Bayesian network. J. Loss Prev. Process Ind. 2015, 38, 11–23. [Google Scholar] [CrossRef]
- Nelson, J.; Dyer, A.; Romeo, L.; Wenzlick, M.; Zaengle, D.; Duran, R.; Sabbatino, M.; Wingo, P.; Barkhurst, A.; Rose, K.; et al. Evaluating Offshore Infrastructure Integrity; Department of Energy: Albany, OR, USA, 2021. [Google Scholar]
- ISO General Principles on Reliability for Structures, International Standards Organization ISO 2394:2015. 2015, Volume 111. Available online: https://www.iso.org/standard/58036.html (accessed on 9 January 2021).
- Nabavian, N.; Morshed, A. Extending Life of Fixed Offshore Installations by Integrity Management: A Structural Overview; Abu Dhabi International Petroleum Exhibition and Conference: Abu Dhabi, United Arab Emirates, 2010. [Google Scholar]
- Sharma, R. An introduction to offshore platforms. In Proceedings of the International Symposium on Marine Design and Construction, Vizag, India, 2–6 December 2019. [Google Scholar]
- Smyth, L. Using an Offshore Platform Beyond Its Expected Lifespan. Available online: https://www.engineerlive.com/content/using-offshore-platform-beyond-its-expected-lifespan (accessed on 15 June 2021).
- Ersdal, G.; Selnes, P. Life extension of ageing petroleum facilities offshore. In Society of Petroleum Engineers International Conference, 5–8 May 2010; Society of Petroleum Engineers: Florence, Italy, 2010. [Google Scholar]
- Solland, G.; Sigurdsson, G.; Ghosal, A. Life extension and assessment of existing offshore structures. In Proceedings of the SPE Project and Facilities Challenges Conference at METS, Doha, Qatar, 13–16 February 2011; Society of Petroleum Engineers: Florence, Italy, 2011. [Google Scholar]
- Aeran, A.; Siriwardane, S.C.; Mikkelsen, O.; Langen, I. A framework to assess structural integrity of ageing offshore jacket structures for life extension. Mar. Struct. 2017, 56, 237–259. [Google Scholar] [CrossRef]
- Muehlenbachs, L.; Cohen, M.A.; Gerarden, T. The impact of water depth on safety and environmental performance in offshore oil and gas production. Energy Policy 2013, 55, 699–705. [Google Scholar] [CrossRef]
- BOEM. 2016 Update of Occurrence Rates for Offshore Oil Spills. 2016; p. 17. Available online: https://www.bsee.gov/sites/bsee.gov/files/osrr-oil-spill-response-research/1086aa.pdf (accessed on 3 January 2021).
- Rim-Rukeh, A. Oil spill management in Nigeria: SWOT analysis of the joint investigation visit (JIV) process. J. Environ. Prot. 2015, 6, 259. [Google Scholar] [CrossRef] [Green Version]
- Pulsipher, A.G.; Iledare, O.O.; Mesyanzhinov, D.V.; Dupont, A.; Zhu, Q.L. Forecasting the number of offshore platforms on the Gulf of Mexico OCS to the year 2023. In Prepared by the Center for Energy Studies, Louisiana State University, Baton Rouge, La. OCS Study MMS; Louisiana State University: Baton Rouge, LA, USA, 2001; Volume 13, pp. 1–52. [Google Scholar]
- Wen, Y.K.; Banon, H. Development of environmental combination design criteria for fixed platforms in the Gulf of Mexico. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1991. [Google Scholar]
- Dhanak, M.R.; Xiros, N.I. Springer Handbook of Ocean Engineering; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 3319166492. [Google Scholar]
- Zhang, S. When a Hurricane Hits an Offshore Oil Platform; The Atlantic: Boston, MA, USA, 2017; p. 1. [Google Scholar]
- MMS. MMS Completes Assessment of Destroyed and Damaged Facilities from Hurricanes Gustav and Ike; Department of the Interior: Washington, DC, USA, 2008. [Google Scholar]
- EIA Hurricane Laura Shut in More Gulf of Mexico Crude Oil Production than Any Storm Since 2008. Available online: https://www.eia.gov/todayinenergy/detail.php?id=45376 (accessed on 15 June 2021).
- Appendini, C.M.; Pedrozo-Acuña, A.; Meza-Padilla, R.; Torres-Freyermuth, A.; Cerezo-Mota, R.; López-González, J.; Ruiz-Salcines, P. On the Role of Climate Change on Wind Waves Generated by Tropical Cyclones in the Gulf of Mexico. Coast. Eng. J. 2017, 59, 1740001–1740032. [Google Scholar] [CrossRef]
- Appendini, C.M.; Ruiz-Salcines, P.; Duran, R. Tropical Cyclone Wind Waves in the Gulf of Mexico under a Changing Climate. Geophys. Res. Lett. 2021. [Google Scholar] [CrossRef]
- Nunez, M. Prevention of Metal Corrosion: New Research; Nova Publishers: Hauppauge, NY, USA, 2007; ISBN 1594545006. [Google Scholar]
- Guedes Soares, C.; Garbatov, Y.; Zayed, A. Effect of environmental factors on steel plate corrosion under marine immersion conditions. Corros. Eng. Sci. Technol. 2011, 46, 524–541. [Google Scholar] [CrossRef]
- Melchers, R.E. The effect of corrosion on the structural reliability of steel offshore structures. Corros. Sci. 2005, 47, 2391–2410. [Google Scholar] [CrossRef]
- Shultz, J.R.; Fischbeck, P. Predicting Risks Associated with Offshore Production Facilities: Neural Network, Statistical, and Expert Opinion Models. In Proceedings of the SPE/EPA Exploration and Production Environmental Conference, Society of Petroleum Engineers, Austin, TX, USA, 13–17 March 1999. [Google Scholar]
- Kaiser, M.J.; Pulsipher, A.G. Loss categories, hazard types in marine operations describe. Oil Gas J. 2007, 105, 39–44. [Google Scholar]
- Nezamian, A.; Nicolson, R.J.; Iosif, D. State of Art in Life Extension of Existing Offshore Structures. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; Volume 44892, pp. 165–174. [Google Scholar]
- Sharp, J.V.; Ersdal, G.; Galbraith, D. Development of key performance indicators for offshore structural integrity. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 48227, pp. 123–130. [Google Scholar]
- Shaughnessy, J.M.; Romo, L.A.; Soza, R.L. Problems of ultra-deep high-temperature, high-pressure drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers, Denver, Colorado, 5–8 October 2003. [Google Scholar]
- Suzanne, L.; Farrokh, N.; Maarten, V.; Jean-Sébastien, L.; Fredrik, F.C.; Kvalstad, T.J. Case Studies of Offshore Slope Stability. In Proceedings of the Geo-Congress 2013: Stability and Performance of Slopes and Embankments III, San Diego, CA, USA, 3–7 March 2013; pp. 2369–2408. [Google Scholar]
- Graham, B.; Reilly, W.K.; Beinecke, F.; Boesch, D.F.; Garcia, T.D.; Murray, C.A.; Ulmer, F. Deep Water: The Gulf Oil Disaster and the Future of Offshore Drilling: Report to the President; Department of the Interior: Washington, DC, USA, 2012. [Google Scholar]
- Guédé, F. Risk-based structural integrity management for offshore jacket platforms. Mar. Struct. 2019, 63, 444–461. [Google Scholar] [CrossRef]
- Rogers, T.J.; Worden, K.; Fuentes, R.; Dervilis, N.; Tygesen, U.T.; Cross, E.J. A Bayesian non-parametric clustering approach for semi-supervised Structural Health Monitoring. Mech. Syst. Signal Process. 2019, 119, 100–119. [Google Scholar] [CrossRef]
- Yang, D.Y.; Frangopol, D.M. Evidence-based framework for real-time life-cycle management of fatigue-critical details of structures. Struct. Infrastruct. Eng. 2018, 14, 509–522. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, C.; Sun, C.; Zhan, W.; Sun, S.; Xu, B.; Dong, Y. Assessment of offshore oil/gas platform status in the northern Gulf of Mexico using multi-source satellite time-series images. Remote Sens. Environ. 2018, 208, 63–81. [Google Scholar] [CrossRef]
- García, D.M.; Lee, J.; Keck, J.; Yang, P.; Guzzetta, R. Hot Spot Analysis of Water Main Failures in California. J. AWWA 2018, 110, E39–E49. [Google Scholar] [CrossRef]
- Cao, Q.; Rui, G.; Liang, Y. Study on PM2. 5 pollution and the mortality due to lung cancer in China based on geographic weighted regression model. BMC Public Health 2018, 18, 925. [Google Scholar] [CrossRef]
- Nelson, J.R.; Grubesic, T.H.; Miller, J.A.; Chamberlain, A.W. The equity of tree distribution in the most ruthlessly hot city in the United States: Phoenix, Arizona. Urban For. Urban Green. 2021, 59, 127016. [Google Scholar] [CrossRef]
- Olawole, M.O.; Olapoju, O.M. Understanding the spatial patterns of tanker accidents in Nigeria using geographically weighted regression. Int. J. Veh. Saf. 2018, 10, 58–77. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 0470855258. [Google Scholar]
- Oshan, T.M.; Li, Z.; Kang, W.; Wolf, L.J.; Fotheringham, A.S. mgwr: A Python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale. ISPRS Int. J. Geo-Inf. 2019, 8, 269. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Romeo, L.; Dyer, A.; Wenzlick, M.; Duran, R.; Nelson, J.; Sabbatino, M.; Wingo, P.; Rose, K.; Bauer, J. Comprehensive GOM Federal Waters Platform, Incident, Metocean, and Geohazard Dataset. 2021. Available online: https://doi.org/10.18141/1779221 (accessed on 26 April 2021).
- Hsieh, W.W. Machine Learning Methods in the Environmental Sciences: Neural Networks and Kernels; Cambridge University Press: Cambridge, UK, 2009; ISBN 0521791928. [Google Scholar]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography; Newnes: Boston, MA, USA, 2014; ISBN 0123877830. [Google Scholar]
- Triguero, I.; García-Gil, D.; Maillo, J.; Luengo, J.; García, S.; Herrera, F. Transforming big data into smart data: An insight on the use of the k-nearest neighbors algorithm to obtain quality data. WIREs Data Min. Knowl. Discov. 2019, 9, e1289. [Google Scholar] [CrossRef]
- ESRI ArcGIS Desktop Software. 2020. Available online: https://www.esri.com/en-us/arcgis/products (accessed on 9 October 2020).
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Kolian, S.R.; Godec, M.; Sammarco, P.W. Alternate uses of retired oil and gas platforms in the Gulf of Mexico. Ocean Coast. Manag. 2019, 167, 52–59. [Google Scholar] [CrossRef]
- Leporini, M.; Marchetti, B.; Corvaro, F.; Polonara, F. Reconversion of offshore oil and gas platforms into renewable energy ites production: Assessment of different scenarios. Renew. Energy 2019, 135, 1121–1132. [Google Scholar] [CrossRef]
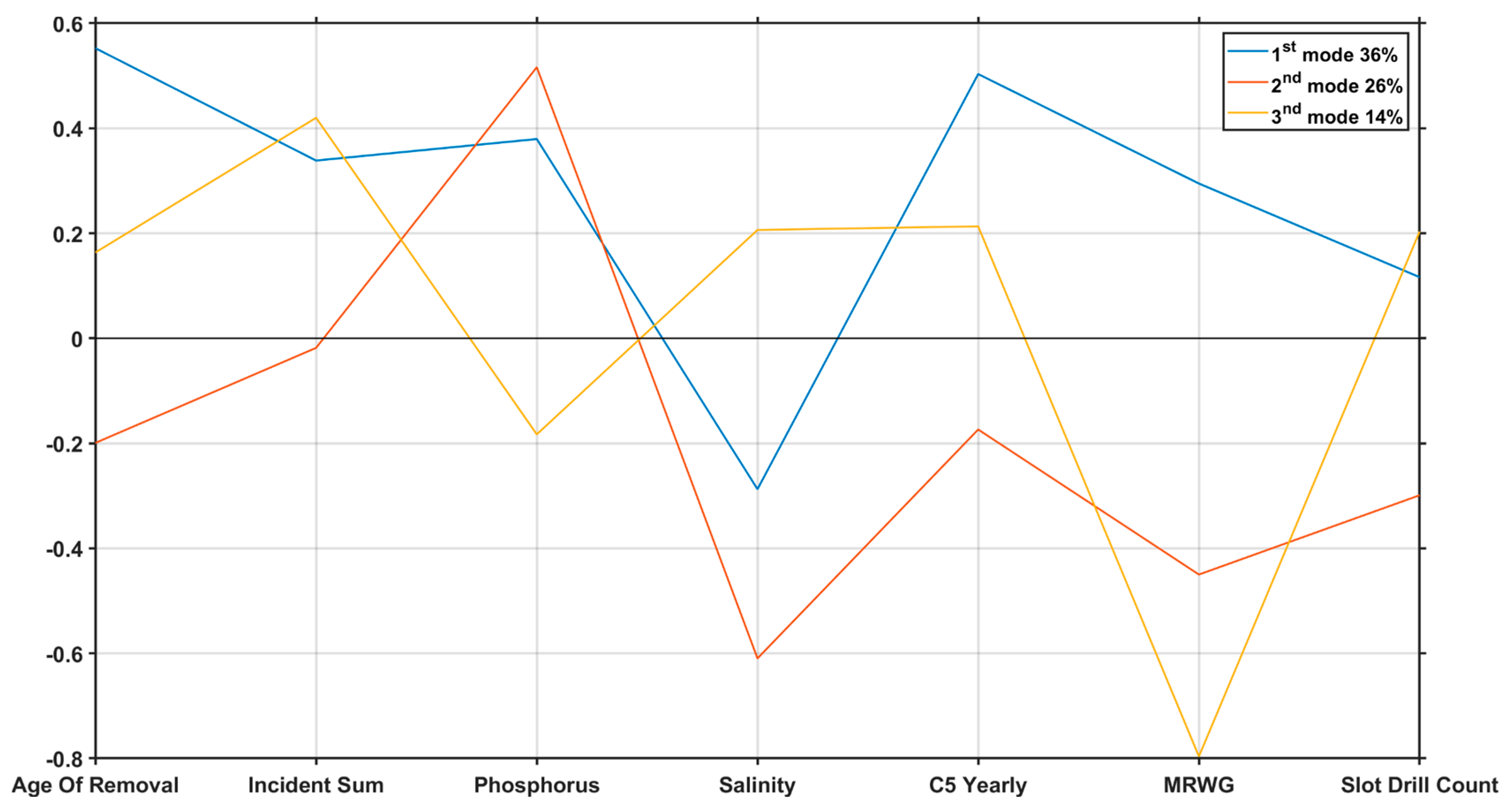
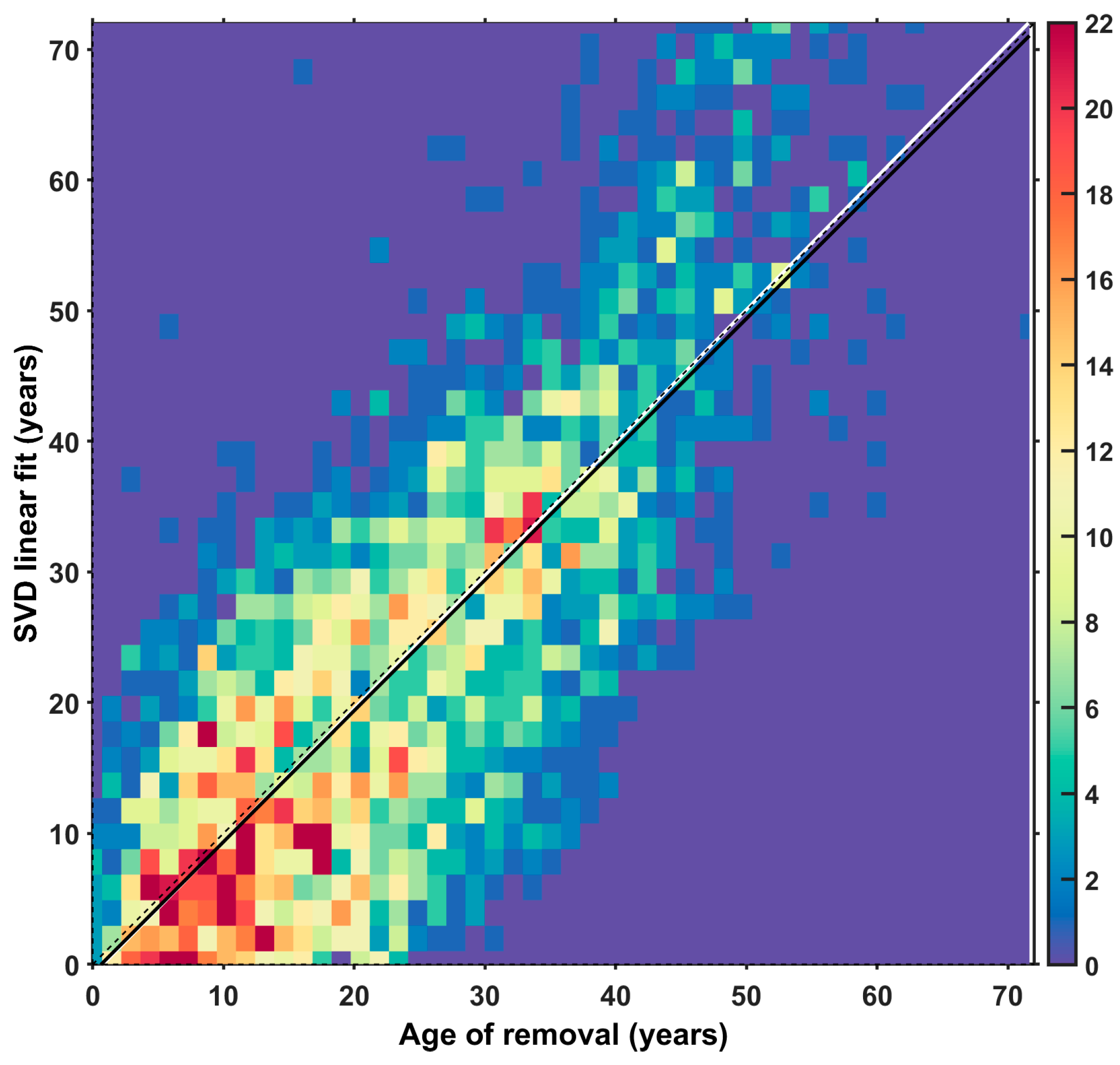
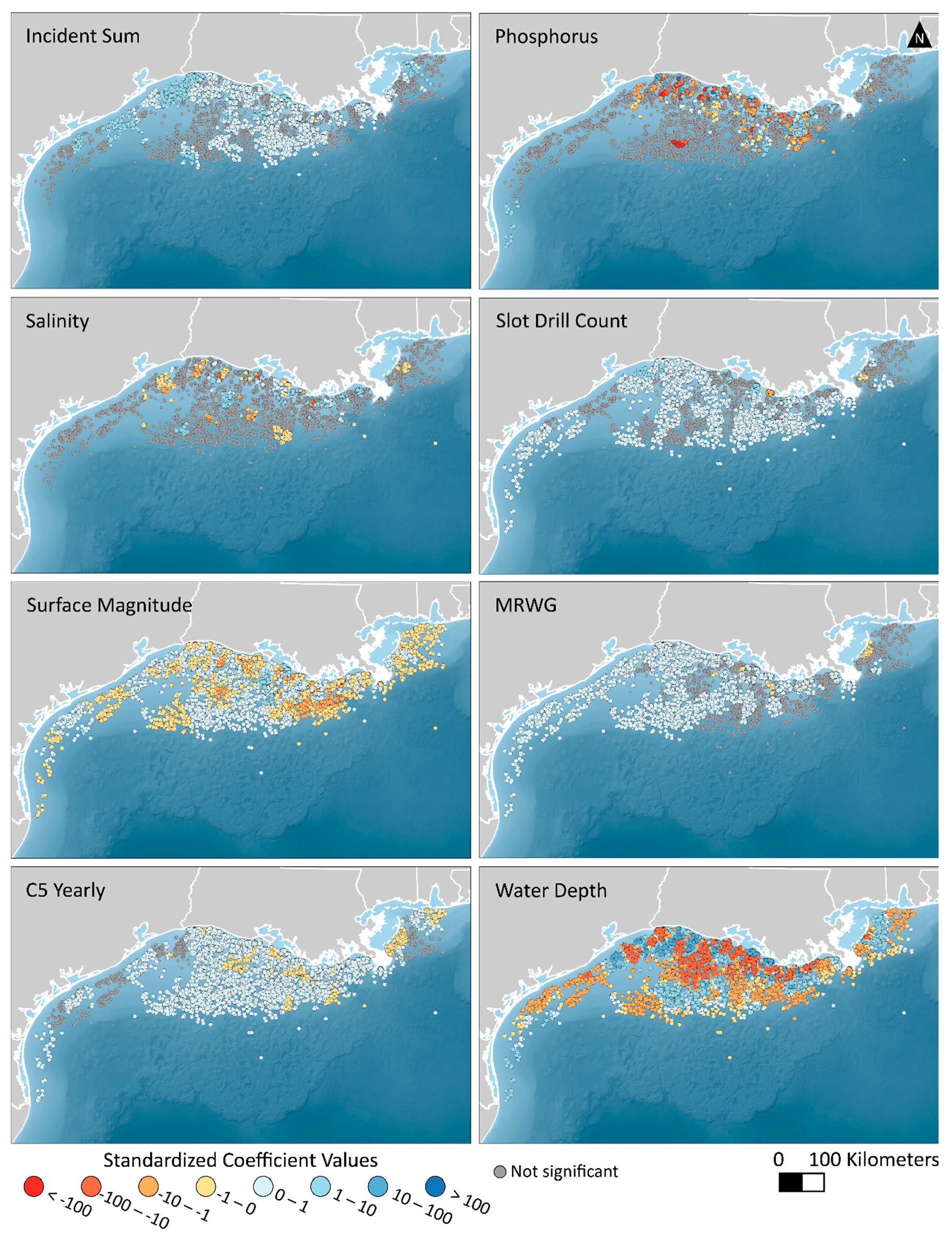
| Variable | Unit | Mean | Min | Max |
|---|---|---|---|---|
| Incident sum | Sum of severity | 5.01 | 0 | 109.0 |
| Phosphorus | μmol/kg | 0.45 | 0.03 | 0.76 |
| Salinity | Unitless | 30.10 | 21.54 | 36.0 |
| Slot drill count | Count | 2.57 | 0 | 49.0 |
| Surface magnitude | m/s | 1.54 | 0.60 | 3.80 |
| MRWG | kt | 80.80 | 0 | 185.0 |
| C5 Yearly | C5 occurrences/year | 0.004 | 0 | 0.02 |
| Water depth | m | 25.55 | 1 | 2425.0 |
| Variable | OLS Regression Coefficients (Standardized) | GWR Coefficient Statistics (Standardized) | |||
|---|---|---|---|---|---|
| Mean | Min | Median | Max | ||
| Incident sum | 0.17 ** (0.013) | 0.496 | −0.901 | 0.304 | 3.413 |
| Phosphorus | −0.066 ** (0.015) | −0.863 | −4113.03 | −0.036 | 2688.39 |
| Salinity | −0.154 ** (0.015) | −0.319 | −2662.63 | 0.02 | 190.981 |
| Slot drill count | 0.206 ** (0.015) | 0.329 | −1.73 | 0.307 | 2.815 |
| Surface magnitude | −0.035 * (0.012) | −0.084 | −6.257 | −0.031 | 2.881 |
| MRWG | 0.191 ** (0.010) | 0.209 | −0.438 | 0.205 | 0.704 |
| C5 Yearly | 0.546 ** (0.013) | 0.759 | −15.641 | 0.711 | 4.583 |
| Water depth | −0.286 ** (0.053) | −4.983 | −110.722 | −2.303 | 98.159 |
| R2 | 0.511 | ||||
| AIC | 11,317.09 | 9110.07 | |||
| Mean Absolute Error (MAE) | Mean Squared Error (MSE) | Root Mean Square Error (RMSE) | Pearson’s Correlation Coefficient (r) |
|---|---|---|---|
| 6.16 | 65.80 | 8.11 | 0.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nelson, J.R.; Romeo, L.; Duran, R. Exploring the Spatial Variations of Stressors Impacting Platform Removal in the Northern Gulf of Mexico. J. Mar. Sci. Eng. 2021, 9, 1223. https://doi.org/10.3390/jmse9111223
Nelson JR, Romeo L, Duran R. Exploring the Spatial Variations of Stressors Impacting Platform Removal in the Northern Gulf of Mexico. Journal of Marine Science and Engineering. 2021; 9(11):1223. https://doi.org/10.3390/jmse9111223
Chicago/Turabian StyleNelson, Jake R., Lucy Romeo, and Rodrigo Duran. 2021. "Exploring the Spatial Variations of Stressors Impacting Platform Removal in the Northern Gulf of Mexico" Journal of Marine Science and Engineering 9, no. 11: 1223. https://doi.org/10.3390/jmse9111223
APA StyleNelson, J. R., Romeo, L., & Duran, R. (2021). Exploring the Spatial Variations of Stressors Impacting Platform Removal in the Northern Gulf of Mexico. Journal of Marine Science and Engineering, 9(11), 1223. https://doi.org/10.3390/jmse9111223






