Station-Keeping Control of Autonomous and Remotely-Operated Vehicles for Free Floating Manipulation
Abstract
:1. Introduction
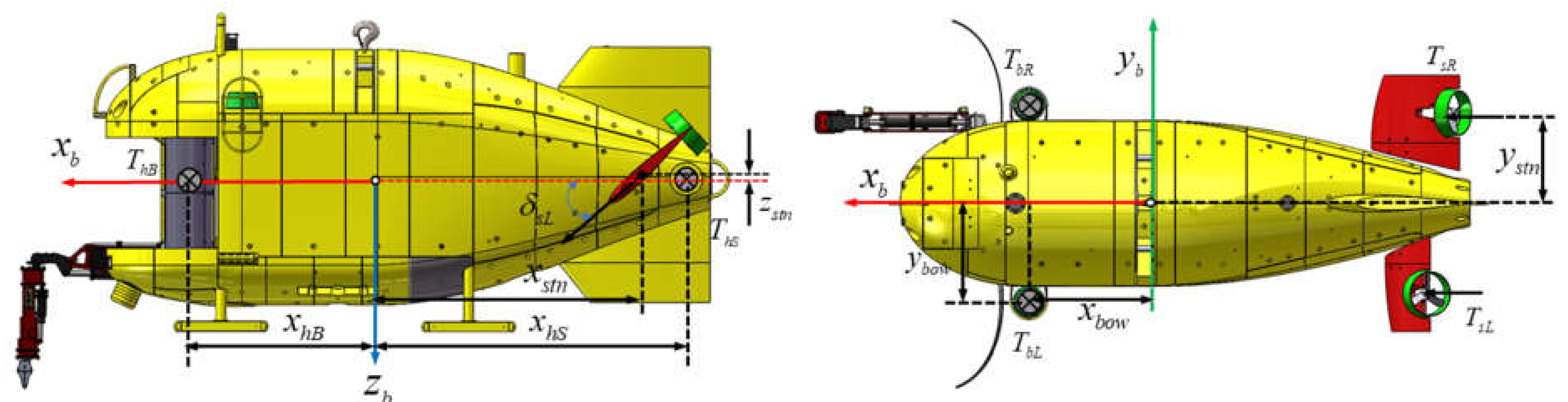
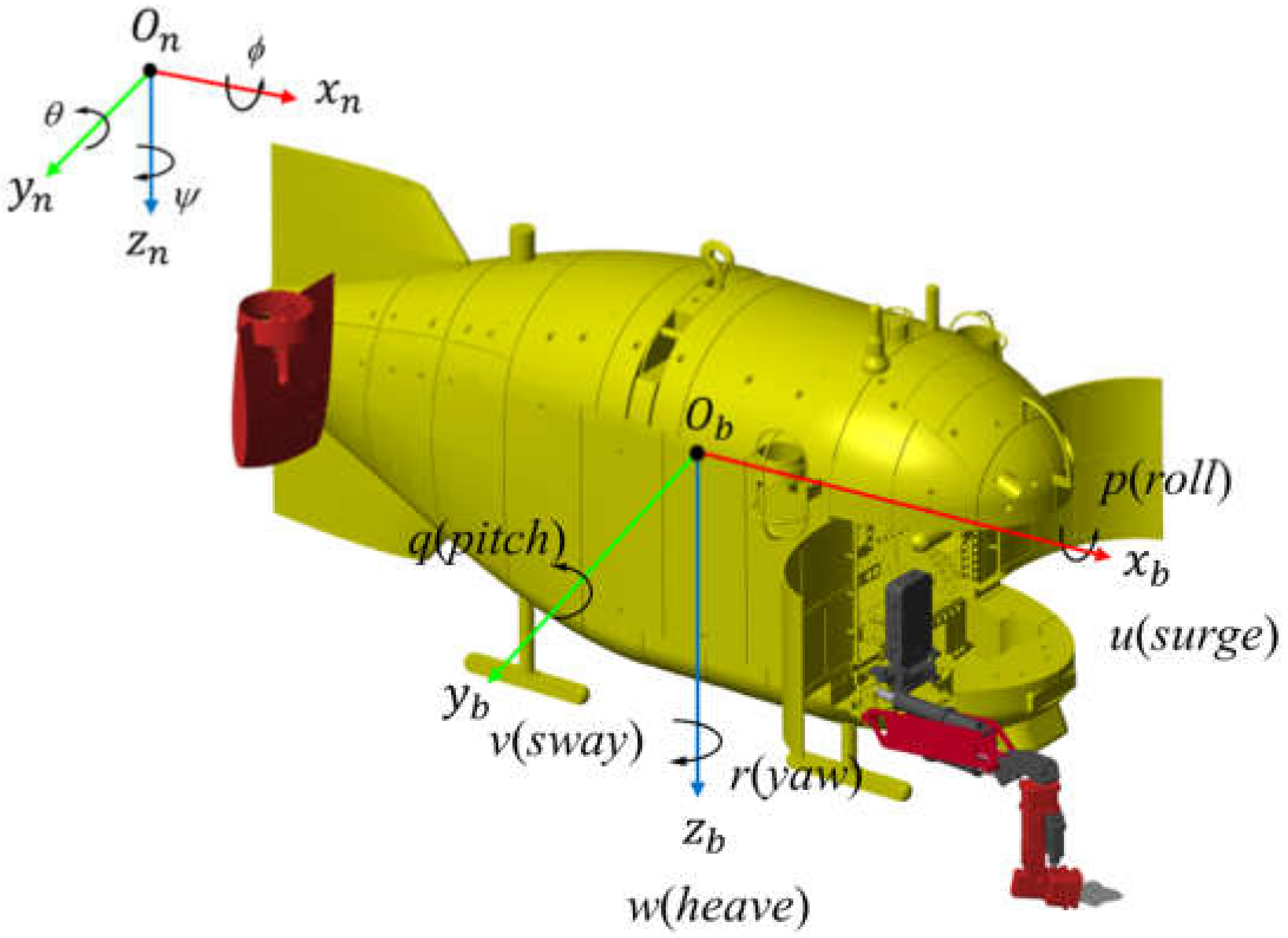
2. Model Dynamics
2.1. Vehicle Dynamics
2.2. Manipulator Dynamics
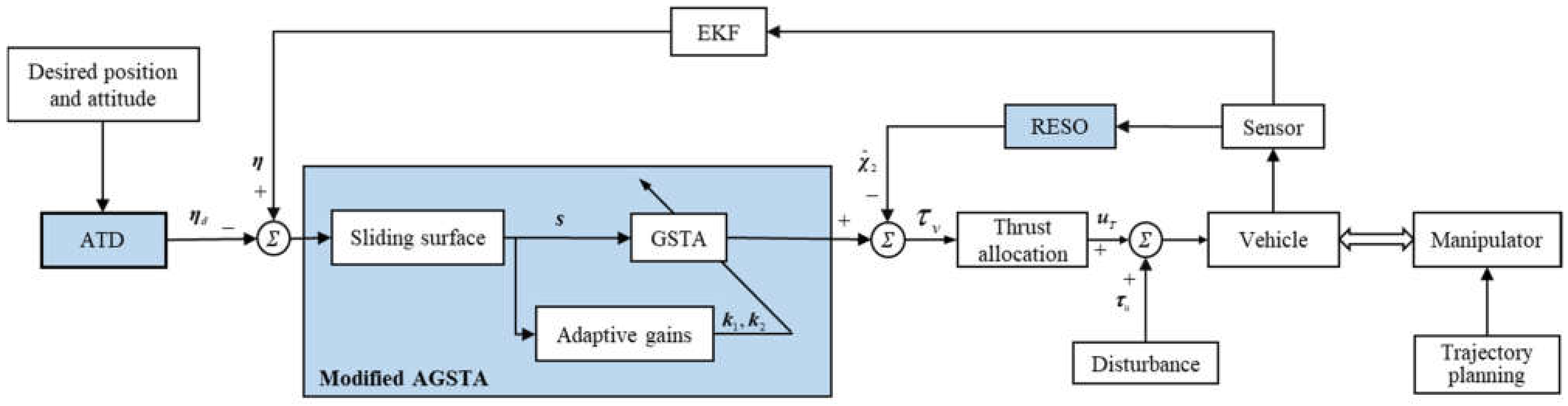
3. Controller Design
3.1. Adaptive Tracking Differentiator
3.2. Reduced-Order Extended State Observer
3.3. Modified AGSTA Design
3.4. Stability Analysis
4. Simulation Results
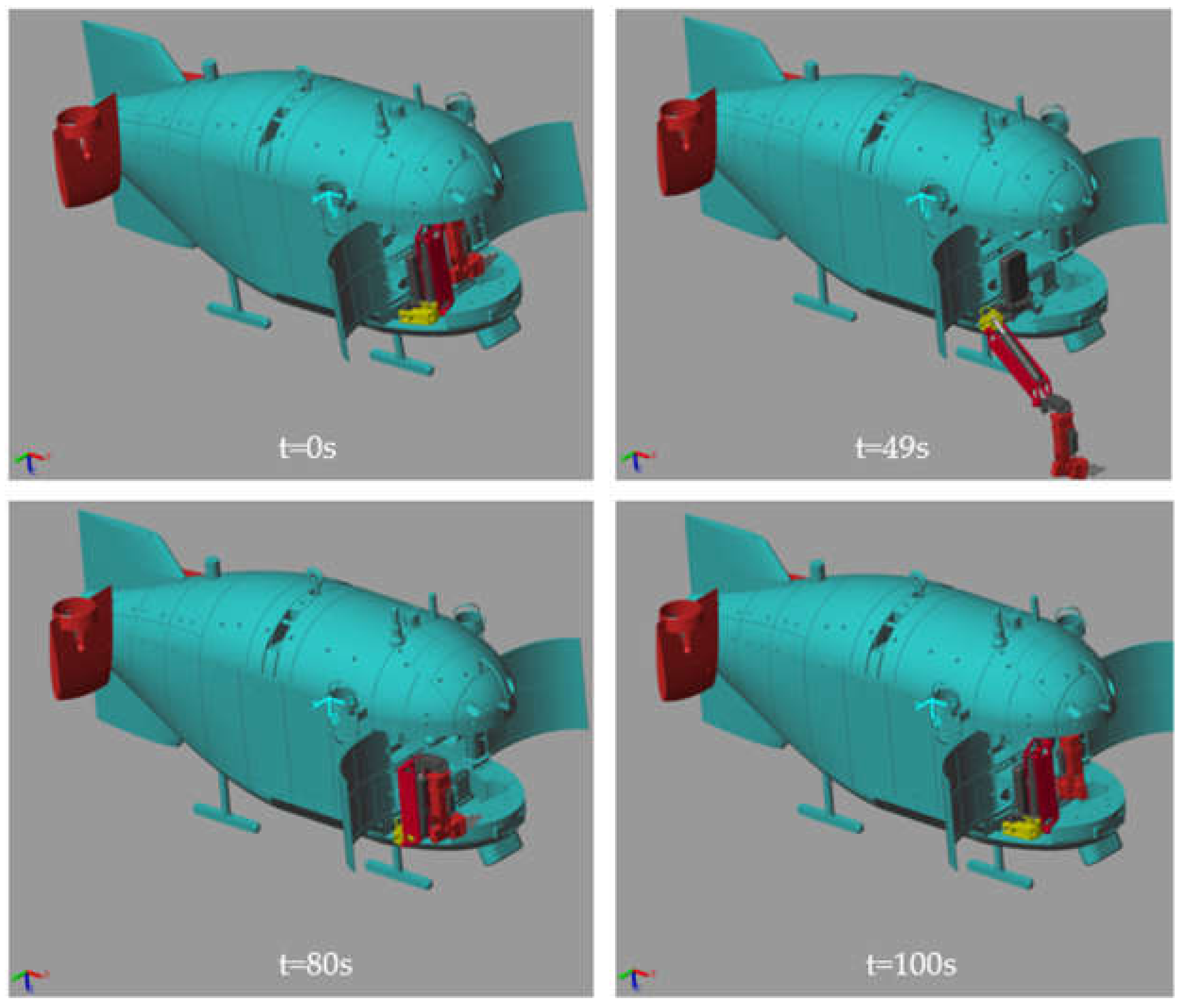
4.1. Description of the Simulation System
4.2. Description of the Task
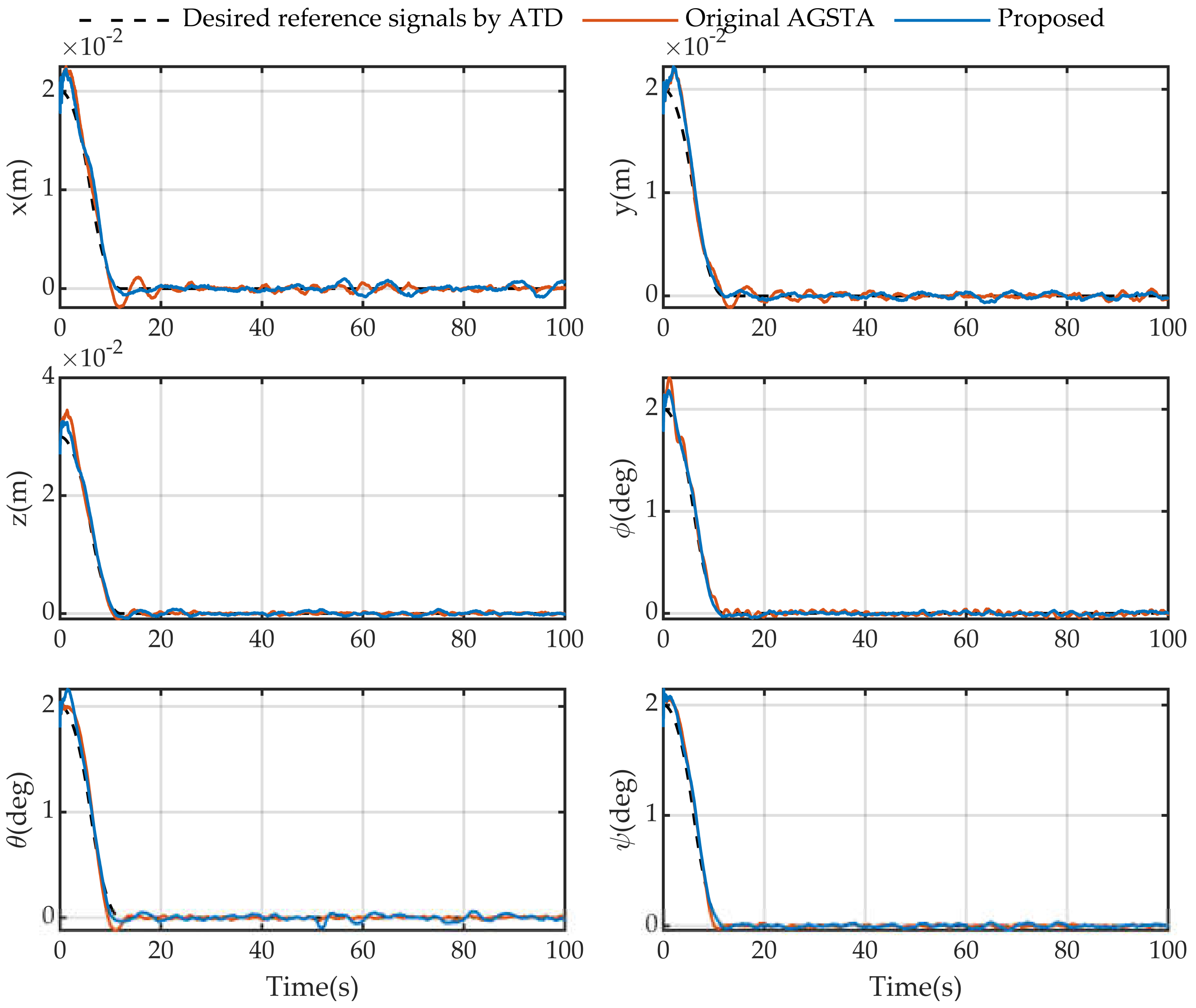
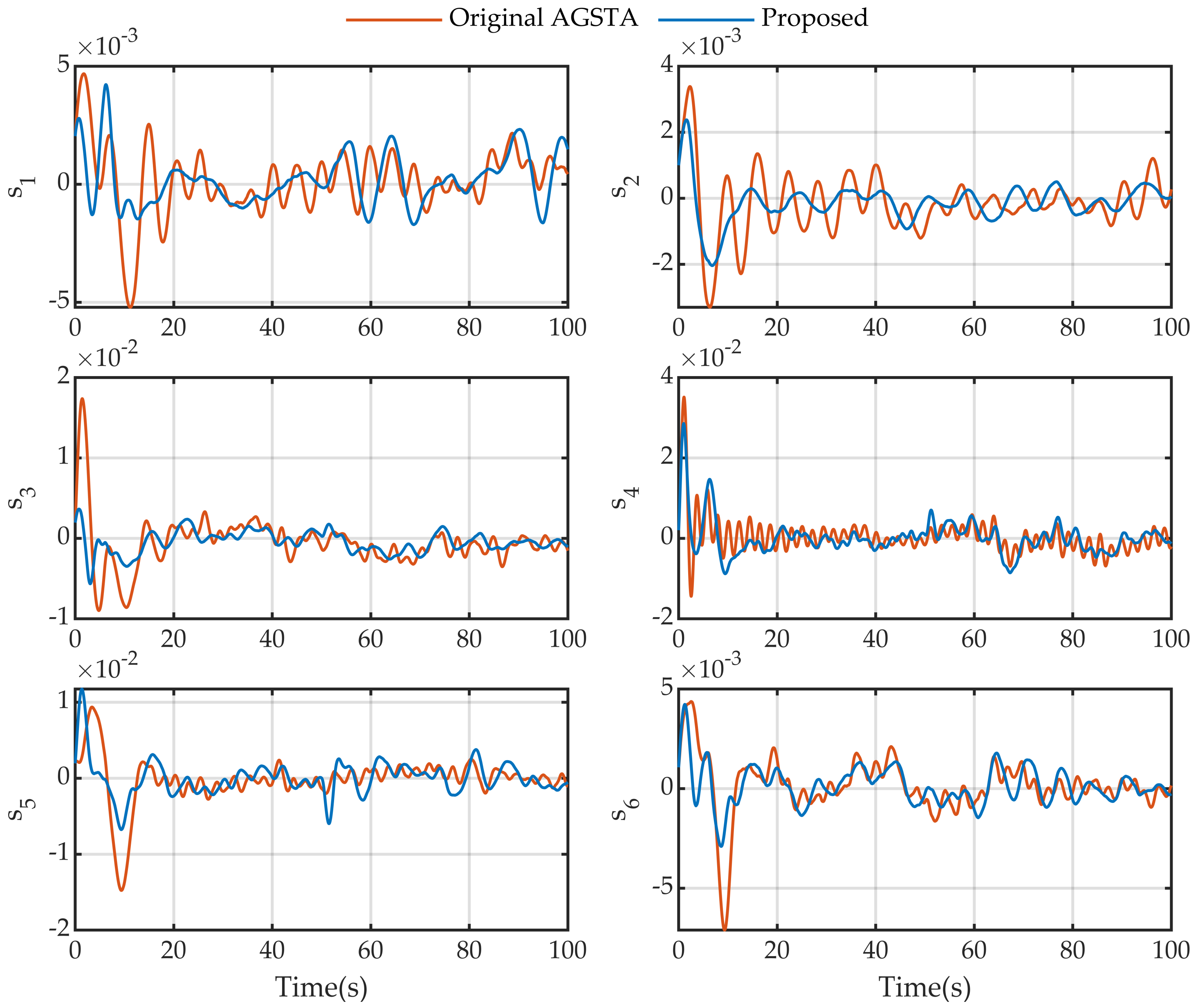
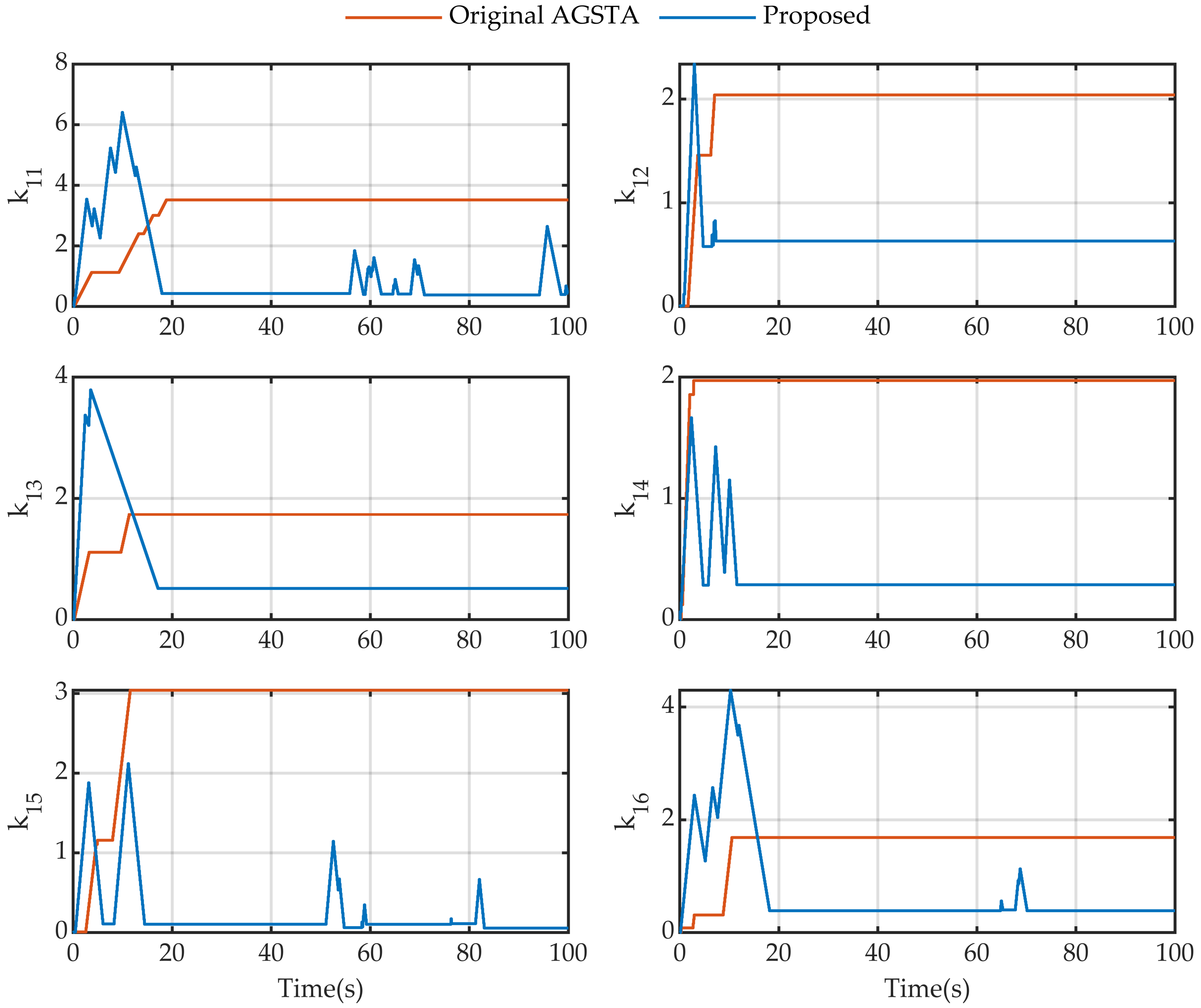
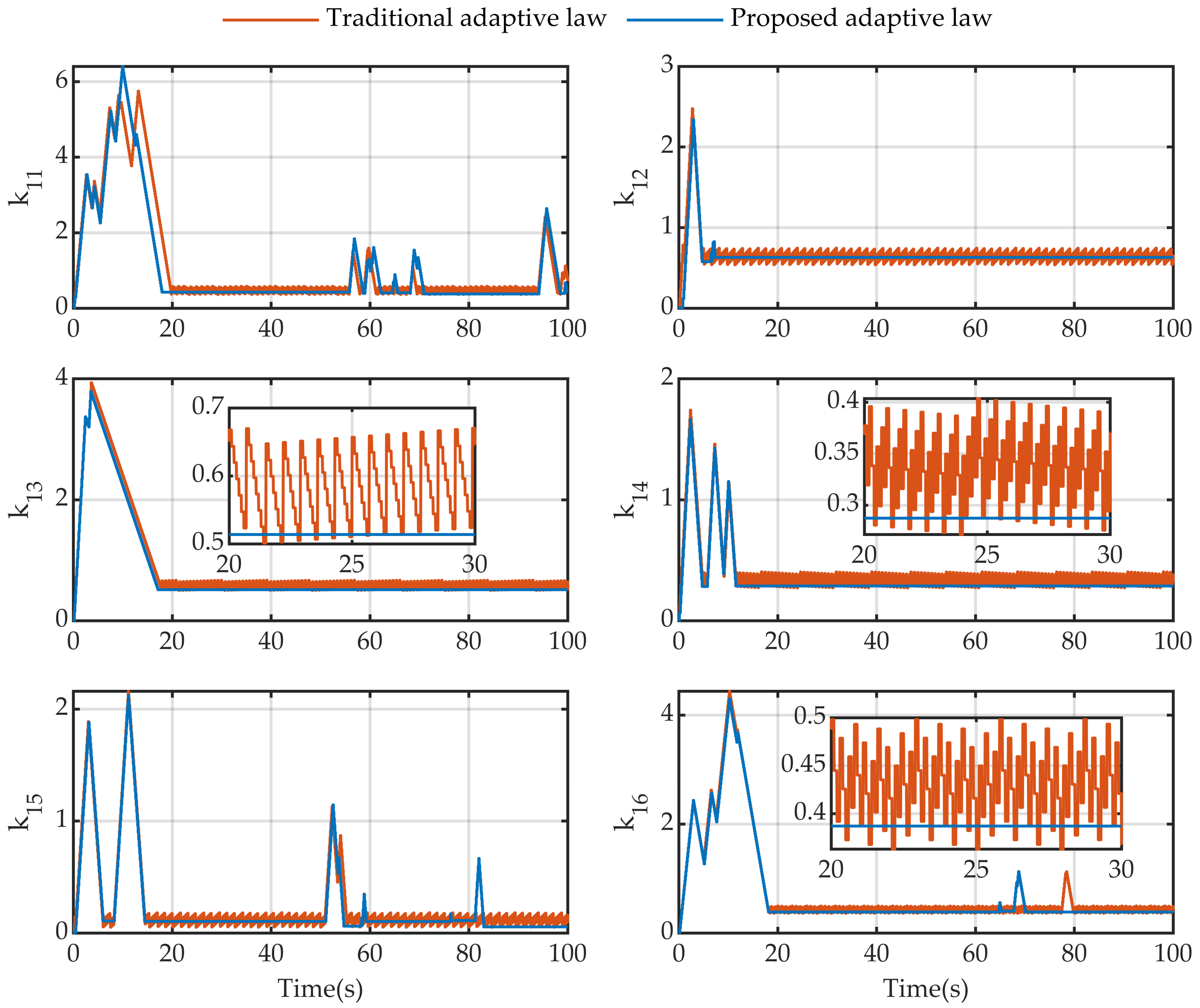
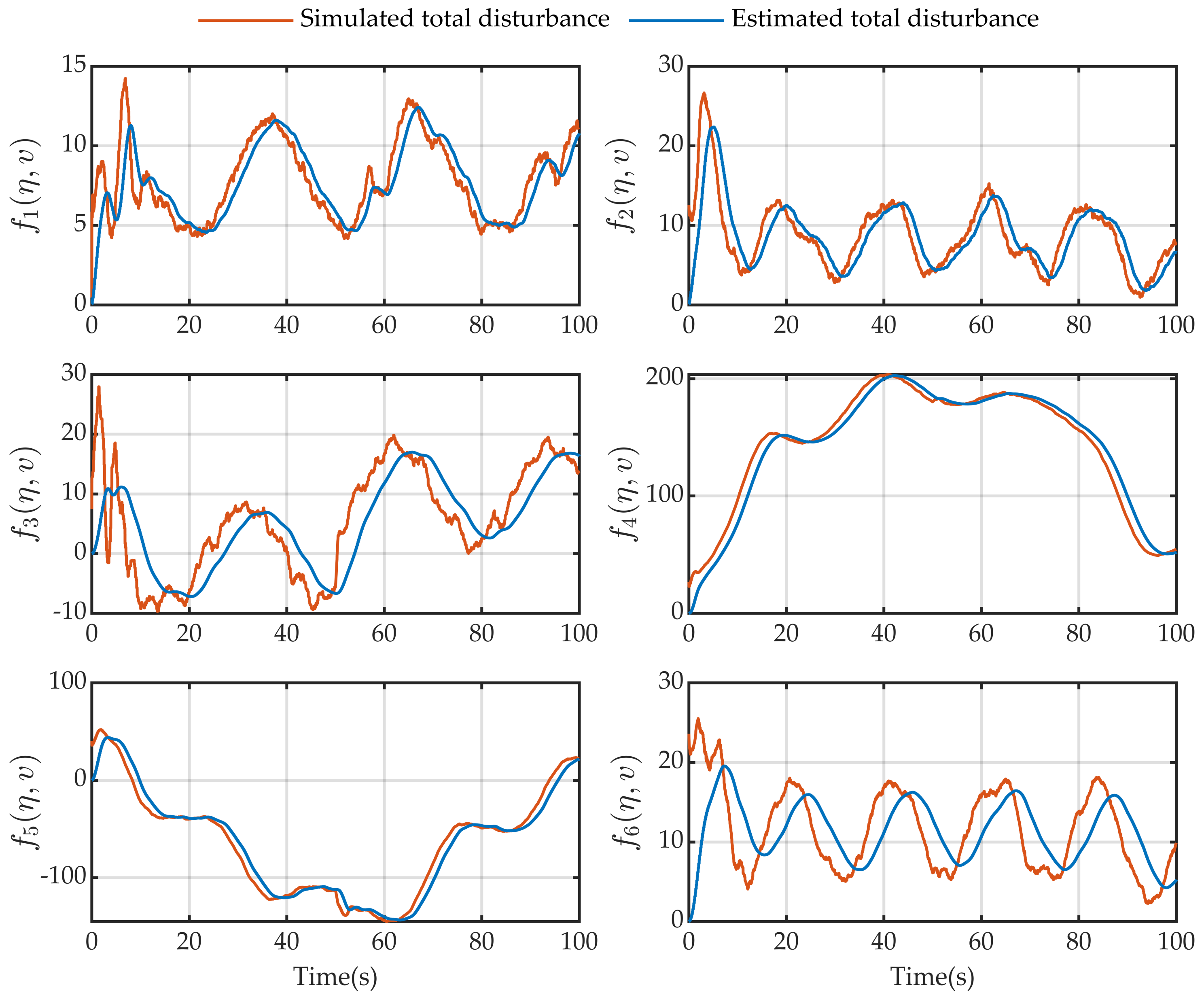
4.3. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Coefficient | Value | coefficient | Value | Coefficient | Value | Coefficient | Value |
|---|---|---|---|---|---|---|---|
| −0.601 | 0.115 | 0.031 | −0.345 | ||||
| 0.008 | −1.419 | 0.051 | 0.063 | ||||
| 0.165 | 0.073 | −2.564 | −0.194 | ||||
| 1.148 | 0.044 | −4.199 | 0.753 | ||||
| −0.117 | −12.006 | 1.361 | 7.257 | ||||
| −0.352 | −0.617 | 0.231 | −0.029 | ||||
| −3.085 | −1.174 | −0.343 | −0.967 | ||||
| −0.307 | −0.114 | 0.179 | 0.048 | ||||
| 0.030 | −0.347 | −0.271 | 0.006 | ||||
| 0.0002 | −0.774 | −0.061 | 0.428 | ||||
| −1.930 | 1.271 | −0.150 | −1.775 | ||||
| −0.051 | 0.006 | 1.318 | −2.12 | ||||
| 0.004 | 2.549 | −5.087 | −0.599 | ||||
| m | 4325.925 kg | 1027.77 kg/m3 | 999 kg·m2 | 4036 kg·m2 | |||
| 3703 kg·m2 | 0 kg·m2 | 0 kg·m2 | 38 kg·m2 | ||||
| 0 m | 0 m | 0 m | 0 m | ||||
| 0 m | 0.05 m | g | 9.8 m/s2 | B | (m+2)*g |
Appendix B
References
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: Chichester, UK/New York, NY, USA, 1994; ISBN 978-0-471-94113-2. [Google Scholar]
- Heshmati-Alamdari, S.; Bechlioulis, C.P.; Karras, G.C.; Nikou, A.; Dimarogonas, D.V.; Kyriakopoulos, K.J. A Robust Interaction Control Approach for Underwater Vehicle Manipulator Systems. Annu. Rev. Control 2018, 46, 315–325. [Google Scholar] [CrossRef]
- Brignone, L.; Raugel, E.; Opderbecke, J.; Rigaud, V.; Piasco, R.; Ragot, S. First Sea Trials of HROV the New Hybrid Vehicle Developed by IFREMER. In Proceedings of the OCEANS 2015—Genova, Genova, Italy, 18–21 May 2015; IEEE: Genova, Italy, 2015; pp. 1–7. [Google Scholar]
- Side, Z.; Yuh, J. Experimental Study on Advanced Underwater Robot Control. IEEE Trans. Robot. 2005, 21, 695–703. [Google Scholar] [CrossRef]
- Mohan, S.; Kim, J. Coordinated Motion Control in Task Space of an Autonomous Underwater Vehicle–Manipulator System. Ocean Eng. 2015, 104, 155–167. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, S. Design of an Indirect Adaptive Controller for the Trajectory Tracking of UVMS. Ocean Eng. 2018, 151, 234–245. [Google Scholar] [CrossRef]
- Londhe, P.S.; Santhakumar, M.; Patre, B.M.; Waghmare, L.M. Task Space Control of an Autonomous Underwater Vehicle Manipulator System by Robust Single-Input Fuzzy Logic Control Scheme. IEEE J. Ocean. Eng. 2016, 1–16. [Google Scholar] [CrossRef]
- Barbalata, C.; Dunnigan, M.; Petillot, Y. Coupled and Decoupled Force/Motion Controllers for an Underwater Vehicle-Manipulator System. J. Mar. Sci. Eng. 2018, 6, 96. [Google Scholar] [CrossRef] [Green Version]
- Koval, E.V. Automatic Stabilization System of Underwater Manipulation Robot. In “Oceans Engineering for Today’s Technology and Tomorrow’s Preservation” Proceedings of the OCEANS ’94, Brest, France, 13–16 September 1994; IEEE: Piscataway, NJ, USA.
- Mclain, T.W.; Rock, S.M.; Lee, M.J. Experiments in the Coordinated Control of an Underwater Arm/Vehicle System. Auton. Robots 1996, 3, 213–232. [Google Scholar] [CrossRef]
- Antonelli, G.; Cataldi, E. Recursive Adaptive Control for an Underwater Vehicle Carrying a Manipulator. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 847–852. [Google Scholar]
- Lynch, B.; Ellery, A. Efficient Control of an AUV-Manipulator System: An Application for the Exploration of Europa. IEEE J. Ocean. Eng. 2014, 39, 552–570. [Google Scholar] [CrossRef]
- Huang, H.; Tang, Q.; Li, H.; Liang, L.; Li, W.; Pang, Y. Vehicle-Manipulator System Dynamic Modeling and Control for Underwater Autonomous Manipulation. Multibody Syst. Dyn. 2017, 41, 125–147. [Google Scholar] [CrossRef]
- Huang, H.; Li, J.; Zhang, G.; Tang, Q.; Wan, L. Adaptive Recurrent Neural Network Motion Control for Observation Class Remotely Operated Vehicle Manipulator System with Modeling Uncertainty. Adv. Mech. Eng. 2018, 10, 168781401880409. [Google Scholar] [CrossRef]
- Dannigan, M.W.; Russell, G.T. Evaluation and Reduction of the Dynamic Coupling between a Manipulator and an Underwater Vehicle. IEEE J. Ocean. Eng. 1998, 23, 260–273. [Google Scholar] [CrossRef]
- Cai, M.; Wang, S.; Wang, Y.; Wang, R.; Tan, M. Coordinated Control of Underwater Biomimetic Vehicle-Manipulator System for Free Floating Autonomous Manipulation. IEEE Trans. Syst. Man Cybern. Syst. 2019, 1–11. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Thanh, H.L.N.N.; Vu, M.T.; Mung, N.X.; Nguyen, N.P.; Phuong, N.T. Perturbation Observer-Based Robust Control Using a Multiple Sliding Surfaces for Nonlinear Systems with Influences of Matched and Unmatched Uncertainties. Mathematics 2020, 8, 1371. [Google Scholar] [CrossRef]
- Vu, M.T.; Le, T.-H.; Thanh, H.L.N.N.; Huynh, T.-T.; Van, M.; Hoang, Q.-D.; Do, T.D. Robust Position Control of an Over-Actuated Underwater Vehicle under Model Uncertainties and Ocean Current Effects Using Dynamic Sliding Mode Surface and Optimal Allocation Control. Sensors 2021, 21, 747. [Google Scholar] [CrossRef] [PubMed]
- Lima, G.S.; Trimpe, S.; Bessa, W.M. Sliding Mode Control with Gaussian Process Regression for Underwater Robots. J. Intell. Robot. Syst. 2020, 99, 487–498. [Google Scholar] [CrossRef]
- Sun, C.; Gong, G.; Yang, H. Sliding Mode Control with Adaptive Fuzzy Immune Feedback Reaching Law. Int. J. Control Autom. Syst. 2020, 18, 363–373. [Google Scholar] [CrossRef]
- Wang, G.; Wu, J.; Zeng, B.; Xu, Z.; Ma, X. A Chattering-Free Sliding Mode Control Strategy for Modular High-Temperature Gas-Cooled Reactors. Ann. Nucl. Energy 2019, 133, 688–695. [Google Scholar] [CrossRef]
- Shi, X.; Cheng, Y. Fuzzy Adaptive Sliding Mode Control for Unmanned Quadrotor. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; IEEE: Boston, MA, USA, 2020; pp. 1654–1658. [Google Scholar]
- Qiao, L.; Zhang, W. Trajectory Tracking Control of AUVs via Adaptive Fast Nonsingular Integral Terminal Sliding Mode Control. IEEE Trans. Ind. Inform. 2020, 16, 1248–1258. [Google Scholar] [CrossRef]
- Wu, X.; Jin, P.; Zou, T.; Qi, Z.; Xiao, H.; Lou, P. Backstepping Trajectory Tracking Based on Fuzzy Sliding Mode Control for Differential Mobile Robots. J. Intell Robot Syst. 2019, 96, 109–121. [Google Scholar] [CrossRef]
- Vahidi-Moghaddam, A. Disturbance-Observer-Based Fuzzy Terminal Sliding Mode Control for MIMO Uncertain Nonlinear Systems. Appl. Math. Model. 2019, 70, 109–127. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity Approach to High-Order Sliding Mode Design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Guo, J. A Novel High Order Sliding Mode Control Method. ISA Trans. 2021, 111, 1–7. [Google Scholar] [CrossRef]
- González-García, J.; Narcizo-Nuci, N.A.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Gómez-Espinosa, A.; Cuan-Urquizo, E.; Cabello, J.A.E. Model-Free High Order Sliding Mode Control with Finite-Time Tracking for Unmanned Underwater Vehicles. Appl. Sci. 2021, 11, 1836. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Control Engineering; Springer: New York, NY, USA, 2014; ISBN 978-0-8176-4892-3. [Google Scholar]
- Pérez-Ventura, U.; Fridman, L. When Is It Reasonable to Implement the Discontinuous Sliding-Mode Controllers Instead of the Continuous Ones? Frequency Domain Criteria. Int. J. Robust Nonlinear Control 2019, 29, 810–828. [Google Scholar] [CrossRef]
- Moreno, J.A. A Linear Framework for the Robust Stability Analysis of a Generalized Super-Twisting Algorithm. In Proceedings of the International Conference on Electrical Engineering, Toluca, Mexico, 10–13 January 2009. [Google Scholar]
- Castillo, I.; Fridman, L.; Moreno, J.A. Super-Twisting Algorithm in Presence of Time and State Dependent Perturbations. Int. J. Control 2018, 91, 2535–2548. [Google Scholar] [CrossRef]
- Guerrero, J.; Torres, J.; Creuze, V.; Chemori, A. Trajectory Tracking for Autonomous Underwater Vehicle: An Adaptive Approach. Ocean Eng. 2019, 172, 511–522. [Google Scholar] [CrossRef] [Green Version]
- SNAME, T. Nomenclature for Treating the Motion of a Submerged Body through a Fluid. Soc. Nav. Archit. Mar. Eng. Tech. Res. Bull. 1950, 1–5. [Google Scholar]
- Fischer, N.; Hughes, D.; Walters, P.; Schwartz, E.M.; Dixon, W.E. Nonlinear RISE-Based Control of an Autonomous Underwater Vehicle. IEEE Trans. Robot. 2014, 30, 845–852. [Google Scholar] [CrossRef] [Green Version]
- Spicer, R.L.; Black, J. Simulating the Dynamics and Control of a Free-Flying Small Satellite with a Robotic Manipulator for 3D Printing. In Proceedings of the AIAA Scitech 2020 Forum; American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 6 January 2020. [Google Scholar]
- McMillan, S.; Orin, D.E.; McGhee, R.B. Efficient Dynamic Simulation of an Underwater Vehicle with a Robotic Manipulator. IEEE Trans. Syst. Man Cybern. 1995, 25, 1194–1206. [Google Scholar] [CrossRef] [Green Version]
- Yuguang, Z.; Fan, Y. Dynamic Modeling and Adaptive Fuzzy Sliding Mode Control for Multi-Link Underwater Manipulators. Ocean Eng. 2019, 187, 106202. [Google Scholar] [CrossRef]
- Ren, C.; Ding, Y.; Ma, S. A Structure-Improved Extended State Observer Based Control with Application to an Omnidirectional Mobile Robot. ISA Trans. 2020, 101, 335–345. [Google Scholar] [CrossRef]
- Long, Y.; Du, Z.; Cong, L.; Wang, W.; Zhang, Z.; Dong, W. Active Disturbance Rejection Control Based Human Gait Tracking for Lower Extremity Rehabilitation Exoskeleton. Isa Trans 2017, 67, 389–397. [Google Scholar] [CrossRef]
- Zhang, M.; Guan, Y.; Zhao, W. Adaptive Super-Twisting Sliding Mode Control for Stabilization Platform of Laser Seeker Based on Extended State Observer. Optik 2019, 199, 163337. [Google Scholar] [CrossRef]
- Lee, S.-D.; Hong Phuc, B.D.; Xu, X.; You, S.-S. Roll Suppression of Marine Vessels Using Adaptive Super-Twisting Sliding Mode Control Synthesis. Ocean Eng. 2020, 195, 106724. [Google Scholar] [CrossRef]
- Rangel, M.A.G.; Manzanilla, A.; Suarez, A.E.Z.; Muñoz, F.; Salazar, S.; Lozano, R. Adaptive Non-Singular Terminal Sliding Mode Control for an Unmanned Underwater Vehicle: Real-Time Experiments. Int. J. Control Autom. Syst. 2020, 18, 615–628. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 5. [Google Scholar] [CrossRef] [Green Version]
- Filippov, A.F. Differential Equations with Discontinuous Righthand Sides: Control Systems; Springer Science & Business Media: Berlin, Germany, 2013; Volume 18. [Google Scholar]
- Shtessel, Y.; Taleb, M. A Novel Adaptive-Gain Supertwisting Sliding Mode Controller: Methodology and Application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]
- Wang, B.; Brogliato, B.; Acary, V.; Boubakir, A.; Plestan, F. Experimental Comparisons between Implicit and Explicit Implementations of Discrete-Time Sliding Mode Controllers: Towards Chattering Suppression in Output and Input Signals. In Proceedings of the 2014 13th International Workshop on Variable Structure Systems (VSS), Nantes, France, 29 June–2 July 2014; IEEE: Nantes, France, 2014; pp. 1–6. [Google Scholar]
- Wang, Y.; Zhu, K.; Yan, F.; Chen, B. Adaptive Super-Twisting Nonsingular Fast Terminal Sliding Mode Control for Cable-Driven Manipulators Using Time-Delay Estimation. Adv. Eng. Softw. 2019, 128, 113–124. [Google Scholar] [CrossRef]
- Brogliato, B.; Polyakov, A. Digital Implementation of Sliding-mode Control via the Implicit Method: A Tutorial. Int. J. Robust Nonlinear Control 2020, rnc.5121. [Google Scholar] [CrossRef]
- Koch, S.; Reichhartinger, M. Discrete-Time Equivalents of the Super-Twisting Algorithm. Automatica 2019, 107, 190–199. [Google Scholar] [CrossRef]
- Brogliato, B.; Polyakov, A.; Efimov, D. The Implicit Discretization of the Supertwisting Sliding-Mode Control Algorithm. IEEE Trans. Autom. Control 2020, 65, 3707–3713. [Google Scholar] [CrossRef] [Green Version]



| Joint i | (mm) | (mm) | (deg) | Joint Limit (deg) |
|---|---|---|---|---|
| 1 | 0 | 0 | 90 | −30~90 |
| 2 | 130.4 | 138.22 | 90 | −30~90 |
| 3 | 641.8 | 0 | 0 | −90~30 |
| 4 | 220.2 | 442.64 | 90 | −90~90 |
| 5 | 21.5 | 0 | −90 | 0~90 |
| 6 | −48.1 | 239.60 | 90 | −180~180 |
| AGSTA | |
| [2.5500, 0.0021, 0.0690, 0.3192, 3.1620, 1.2692, 0.0049, 0.0020] | |
| [1.5830, 0.0023, 0.1189, 0.7272, 2.1222, 2.5352, 0.0040, 0.0028] | |
| [5.1820, 0.0031, 0.1628, 0.3680, 1.8180, 1.2795, 0.0063, 0.0066] | |
| [5.7932, 0.0032, 0.2474, 1.1557, 2.0171, 0.9480, 0.0066, 0.0155] | |
| [4.0165, 0.0030, 0.0609, 0.5230, 3.9955, 3.2493, 0.0080, 0.0079] | |
| [2.8460, 0.0020, 0.2053, 0.7632, 1.4879, 0.6179, 0.0065, 0.0055] | |
| Proposed | |
| [2.0576, 0.0023, 0.1315, 1.4140, 0.8028, 0.0045, 0.4425, 1.1732, 2.1554, 0.0017, 1.0792] | |
| [1.0407, 0.0029, 0.2787, 1.1101, 0.9778, 0.0066, 0.6360, 0.6514, 0.7757, 0.0019, 1.1541] | |
| [3.1099, 0.0065, 0.2468, 1.4638, 0.2408, 0.0050, 0.5251, 0.6666, 1.5306, 0.0031, 0.5379] | |
| [8.1867, 0.0068, 0.1687, 0.7613, 0.5755, 0.0658, 0.3288, 1.9506, 2.5442, 0.0077, 1.0778] | |
| [3.1722, 0.0269, 0.1682, 0.6937, 0.6108, 0.0068, 0.1132, 0.2298, 1.4234, 0.0032, 1.1901] | |
| [2.3681, 0.0026, 0.1639, 0.8678, 0.5303, 0.0061, 0.4155, 1.6172, 2.6475, 0.0015, 0.5143] |
| State Variables | CHAT | RMSE | ||
|---|---|---|---|---|
| AGSTA | Proposed | AGSTA | Proposed | |
| 0.0363 | 0.0285 | 6.1005 × 10−4 | 5.9895 × 10−4 | |
| 0.0749 | 0.0462 | 6.0119 × 10−4 | 5.8173 × 10−4 | |
| 0.1045 | 0.0672 | 7.5175 × 10−4 | 5.1327 × 10−4 | |
| 0.0903 | 0.0538 | 7.5865 × 10−4 | 5.3599 × 10−4 | |
| 0.1173 | 0.0887 | 7.7607 × 10−4 | 7.5049 × 10−4 | |
| 0.1006 | 0.0662 | 5.6136 × 10−4 | 5.5314 × 10−4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, N.; Tang, Y.; Jiang, Z.; Bai, Y.; Liang, S. Station-Keeping Control of Autonomous and Remotely-Operated Vehicles for Free Floating Manipulation. J. Mar. Sci. Eng. 2021, 9, 1305. https://doi.org/10.3390/jmse9111305
Ding N, Tang Y, Jiang Z, Bai Y, Liang S. Station-Keeping Control of Autonomous and Remotely-Operated Vehicles for Free Floating Manipulation. Journal of Marine Science and Engineering. 2021; 9(11):1305. https://doi.org/10.3390/jmse9111305
Chicago/Turabian StyleDing, Ningning, Yuangui Tang, Zhibin Jiang, Yunfei Bai, and Shixun Liang. 2021. "Station-Keeping Control of Autonomous and Remotely-Operated Vehicles for Free Floating Manipulation" Journal of Marine Science and Engineering 9, no. 11: 1305. https://doi.org/10.3390/jmse9111305
APA StyleDing, N., Tang, Y., Jiang, Z., Bai, Y., & Liang, S. (2021). Station-Keeping Control of Autonomous and Remotely-Operated Vehicles for Free Floating Manipulation. Journal of Marine Science and Engineering, 9(11), 1305. https://doi.org/10.3390/jmse9111305






