Study of the Sound Escape with the Use of an Air Bubble Curtain in Offshore Pile Driving
Abstract
:1. Introduction
2. Model Description and Mathematical Statement
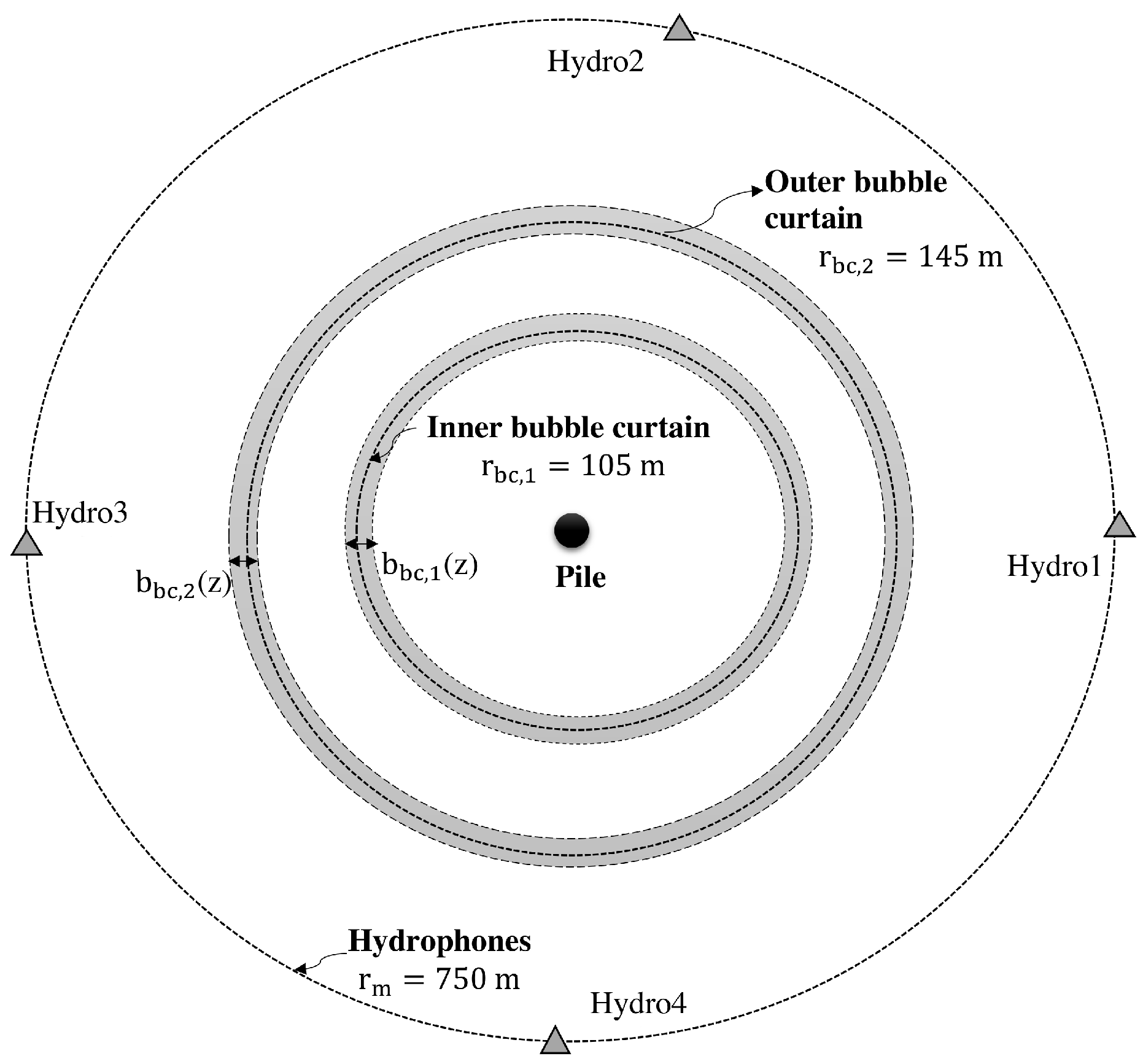
2.1. Description of the Model
2.2. Governing Equations
3. Noise Predictions of Non-Mitigated Field
4. Modeling the Air Bubble Curtain
4.1. Local Effective Wavenumber in a Bubble Curtain
4.2. Local Transmission Coefficients of a Bubble Curtain
5. Validation Study of the Effective Wavenumber Model
6. Validation Study of the Complete Model Including the Air Bubble Curtain
6.1. Maximum Noise Reduction Level
- scenario 1—noise prediction without the presence of air bubble curtain (base case);
- scenario 2—elimination of the waterborne path at the position of the air bubble curtain leaving the propagation of the waves through the soil unaffected; and
- scenario 3—same as scenario 2 but with an additional 1 m gap at the lowest part of the seawater column in which the noise presumably leaks.
6.2. Validation of the Noise Reduction with the Model of the Air Bubble Curtain
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bailey, H.; Senior, B.; Simmons, D.; Rusin, J.; Picken, G.; Thompson, P.M. Assessing underwater noise levels during pile-driving at an offshore windfarm and its potential effects on marine mammals. Mar. Pollut. Bull. 2010, 60, 888–897. [Google Scholar] [CrossRef]
- Bundesamt fur Seeschifffahrt und Hydrographie (BSH). Standard Investigation of the Impacts of Offshore Wind Turbines on the Marine Environment (StUK4); Technical Report 7003; German Federal Maritime and Hydrographic Agency: Hamburg, Germany, 2013.
- Office of Protected Resources, National Marine Fisheries Service. Technical Guidance for Assessing the Effects of Anthropogenic Sound on Marine Mammal Hearing: Underwater Acoustic Thresholds for Onset of Permanent and Temporary Threshold Shifts; Technical Report; NOAA Technical Memorandum NMFS-OPR-55; U.S. Department of Commerce, National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2016.
- Stöber, U.; Thomsen, F. Effect of impact pile driving noise on marine mammals: A comparison of different noise exposure criteria. J. Acoust. Soc. Am. 2019, 145, 3252. [Google Scholar] [CrossRef] [PubMed]
- Tsouvalas, A. Underwater Noise Emission Due to Offshore Pile Installation: A Review. Energies 2020, 13, 3037. [Google Scholar] [CrossRef]
- Reinhall, P.G.; Dahl, P.H. Underwater Mach wave radiation from impact pile driving: Theory and observation. J. Acoust. Soc. Am. 2011, 130, 1209–1216. [Google Scholar] [CrossRef] [PubMed]
- MacGillivray, A.O. Finite difference computational modeling of marine impact pile driving. J. Acoust. Soc. Am. 2014, 136, 2206. [Google Scholar] [CrossRef] [Green Version]
- Wilkes, D.R.; Gourlay, T.P.; Gavrilov, A.N. Numerical Modeling of Radiated Sound for Impact Pile Driving in Offshore Environments. IEEE J. Ocean. Eng. 2016, 41, 1072–1078. [Google Scholar] [CrossRef]
- Wilkes, D.R.; Gavrilov, A.N. Sound radiation from impact-driven raked piles. J. Acoust. Soc. Am. 2017, 142, 1. [Google Scholar] [CrossRef] [PubMed]
- Lippert, T.; Lippert, S. Modeling of pile driving noise by means of wavenumber integration. Acoust. Aust. 2012, 40, 178–182. [Google Scholar]
- Kim, H.; Potty, G.R.; Miller, J.H.; Smith, K.B.; Dossot, G. Long range propagation modeling of offshore wind turbine noise using finite element and parabolic equation models. J. Acoust. Soc. Am. 2012, 131, 3392. [Google Scholar] [CrossRef]
- Zampolli, M.; Nijhof, M.J.; de Jong, C.A.; Ainslie, M.A.; Jansen, E.H.; Quesson, B.A. Validation of finite element computations for the quantitative prediction of underwater noise from impact pile driving. J. Acoust. Soc. Am. 2013, 133, 72–81. [Google Scholar] [CrossRef]
- Lippert, T.; von Estorff, O. The significance of parameter uncertainties for the prediction of offshore pile driving noise. J. Acoust. Soc. Am. 2014, 136, 2463–2471. [Google Scholar] [CrossRef] [PubMed]
- Dahl, P.H.; Dall’Osto, D.R. On the underwater sound field from impact pile driving: Arrival structure, precursor arrivals, and energy streamlines. J. Acoust. Soc. Am. 2017, 142, 1141. [Google Scholar] [CrossRef] [PubMed]
- Fricke, M.B.; Rolfes, R. Towards a complete physically based forecast model for underwater noise related to impact pile driving. J. Acoust. Soc. Am. 2015. [Google Scholar] [CrossRef] [PubMed]
- Tsouvalas, A.; Metrikine, A.V. A semi-analytical model for the prediction of underwater noise from offshore pile driving. J. Sound Vib. 2013, 332, 3232–3257. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Metrikine, A.V. A three-dimensional vibroacoustic model for the prediction of underwater noise from offshore pile driving. J. Sound Vib. 2014, 333, 2283–2311. [Google Scholar] [CrossRef]
- Deng, Q.; Jiang, W.; Tan, M.; Xing, J. Modeling of offshore pile driving noise using a semi-analytical variational formulation. Appl. Acoust. 2016, 104, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Deng, Q.; Jiang, W.; Zhang, W. Theoretical investigation of the effects of the cushion on reducing underwater noise from offshore pile driving. J. Acoust. Soc. Am. 2016, 140, 2780. [Google Scholar] [CrossRef]
- von Pein, J.; Klages, E.; Lippert, S.; von Estorff, O. A hybrid model for the 3D computation of pile driving noise. In Proceedings of the OCEANS 2019—Marseille, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Metrikine, A.V. Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage. J. Mar. Sci. Eng. 2016, 4, 44. [Google Scholar] [CrossRef]
- Hazelwood, R.A.; Macey, P.C. Modeling Water Motion near Seismic Waves Propagating across a Graded Seabed, as Generated by Man-Made Impacts. J. Mar. Sci. Eng. 2016, 4, 47. [Google Scholar] [CrossRef]
- Hazelwood, R.A.; Macey, P.C.; Robinson, S.P.; Wang, L.S. Optimal Transmission of Interface Vibration Wavelets—A Simulation of Seabed Seismic Responses. J. Mar. Sci. Eng. 2018, 4, 61. [Google Scholar] [CrossRef] [Green Version]
- Tsouvalas, A.; Metrikine, A.V. Noise reduction by the application of an air-bubble curtain in offshore pile driving. J. Sound Vib. 2016, 371, 150–170. [Google Scholar] [CrossRef]
- Lippert, S.; Huisman, M.; Ruhnau, M.; Estorff, O.; van Zandwijk, K. Prognosis of underwater pile driving noise for submerged skirt piles of jacket structures. In Proceedings of the UACE 2017 4th Underwater Acoustics Conference and Exhibition, Skiathos, Greece, 2–8 September 2017. [Google Scholar]
- Bohne, T.; Grießmann, T.; Rolfes, R. Modeling the noise mitigation of a bubble curtain. J. Acoust. Soc. Am. 2019, 146, 2212. [Google Scholar] [CrossRef]
- Bohne, T.; Grießmann, T.; Rolfes, R. Development of an efficient buoyant jet integral model of a bubble plume coupled with a population dynamics model for bubble breakup and coalescence to predict the transmission loss of a bubble curtain. Int. J. Multiph. Flow 2020, 132. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Peng, Y.; Metrikine, A.V. A Pile-Soil-Water Vibroacoustic Model Based On A Mode Matching Method. In Proceedings of the 5th Underwater Acoustics Conference and Exhibition 2019 (UACE2019), Hersonissos, Greece, 30 June–5 July 2019; pp. 667–674. [Google Scholar]
- Peng, Y.; Tsouvalas, A.; Metrikine, A.V. A coupled modelling approach for the fast computation of underwater radiation from offshore pile driving. In Proceedings of the EURODYN 2020 XI International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020. [Google Scholar] [CrossRef]
- Kaplunov, J.; Kossovich, L.Y.; Nolde, E. Dynamics of Thin Walled Elastic Bodies; Academic Press: San Diego, CA, USA, 1998; pp. 129–134. [Google Scholar]
- Tsouvalas, A. Underwater Noise Generated by Offshore Pile Driving. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Ewing, W.M.; Jardetzky, W.S.; Press, F. Elastic Waves in Layered Media; Lamont Geological Observatory Contribution No. 189; McGraw-Hill: New York, NY, USA, 1957. [Google Scholar]
- Achenbach, J.D. Wave Propagation in Elastic Solids; North-Holland Series in Applied Mathematics and Mechanics, v. 16; North-Holland Pub. Co.: Amsterdam, The Netherlands; American Elsevier Pub. Co.: New York, NY, USA, 1973. [Google Scholar]
- Beskos, D.E. Boundary Element Methods in Dynamic Analysis. Appl. Mech. Rev. 1987, 40, 1–23. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Commander, K.W.; Prosperetti, A. Linear pressure waves in bubbly liquids: Comparison between theory and experiments. J. Acoust. Soc. Am. 1989, 85, 732–746. [Google Scholar] [CrossRef]
- Lehr, F.; Millies, M.; Mewes, D. Bubble-Size distributions and flow fields in bubble columns. AIChE J. 2002, 48, 2426–2443. [Google Scholar] [CrossRef]
- Milgram, J.H. Mean flow in round bubble plumes. J. Fluid Mech. 1983, 133, 345–376. [Google Scholar] [CrossRef]
- Walters, J.K.; Davidson, J.F. The initial motion of a gas bubble formed in an inviscid liquid. J. Fluid Mech. 1963, 17, 321. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Voit, H.; Zeppenfeld, R.; Mersmann, A. Calculation of primary bubble volume in gravitational and centrifugal fields. Chem. Eng. Technol. 1987, 10, 99–103. [Google Scholar] [CrossRef]
- Rustemeier, J. Optimierung von Blasenschleiern zur Minderung von Unterwasser-Rammschall (Optimization of Bubble Curtains to Reduce Underwater Pile-Driving Noise). Ph.D. Thesis, Institut für Statik und Dynamik, Hannover, Germany, 2016. [Google Scholar]
- Lippert, S.; Nijhof, M.; Lippert, T.; Wilkes, D.; Gavrilov, A.; Heitmann, K.; Ruhnau, M.; von Estorff, O.; Schäfke, A.; Schäfer, I.; et al. COMPILE—A Generic Benchmark Case for Predictions of Marine Pile-Driving Noise. IEEE J. Ocean. Eng. 2016, 41, 1061–1071. [Google Scholar] [CrossRef]











| Parameter | Air Bubble Curtain |
|---|---|
| Water depth [m] | 50 |
| Density of the fluid [kg/m] | 1000 |
| Nozzle diameter [mm] | 50 |
| Air flow rate [m/s] | 0.024, 0.283 and 0.590 |
| Spreading coefficient [m] | 0.6 |
| Amplification factor [-] | 1 |
| Entrainment coefficient [-] | 0.18 |
| Parameter | Pile | Parameter | Fluid | Marine Sediment | Bottom Soil |
|---|---|---|---|---|---|
| Length [m] | 75 | Depth [m] | 40.1 | 1.5 | ∞ |
| Density [kg/m] | 7850 | Density [kg/m] | 1000 | 1621.5 | 1937.74 |
| Outer diameter [m] | 8 | [m/s] | 1500 | 1603 | 1852 |
| Wall thickness [mm] | 90 | [m/s] | - | 82 | 362 |
| The penetration depth [m] | 30.5 | [] | - | 0.91 | 0.88 |
| Maximum Blow Energy [kJ] | 2150 | [] | - | 1.86 | 2.77 |
| Levels | Measured | Modeled | Modeled | Modeled | |||
|---|---|---|---|---|---|---|---|
| with DBBC | Scenario 1 | Scenario 2 | Scenario 3 | ||||
| SEL | 165∼168 (167) | 12∼15 (13) | 180 | 150 | 158.8 | 30.0 | 20.9 |
| 184∼187 (186) | 12∼15 (13) | 199 | 165 | 177.6 | 35.0 | 21.4 |
| Parameter | Air Bubble Curtain |
|---|---|
| location of the inner bubble curtain [m] | 105 |
| location of the outer bubble curtain [m] | 145 |
| Nozzle diameter [mm] | 1.5 |
| Nozzle spacing [m] | 0.30 |
| Air flow rate [m/s/m] | 0.0087 |
| Spreading coefficient [-] | 0.1 |
| Entrainment coefficient [-] | 0.18 |
| Noise Reduction Levels | ||
|---|---|---|
| Measurement | 12 ∼15 (13 ) | 12 ∼15 (13 ) |
| Maximum noise reduction | 30 | 35 |
| Estimation of noise reduction | 21 | 21 |
| Computed noise reduction | 20 | 21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Tsouvalas, A.; Stampoultzoglou, T.; Metrikine, A. Study of the Sound Escape with the Use of an Air Bubble Curtain in Offshore Pile Driving. J. Mar. Sci. Eng. 2021, 9, 232. https://doi.org/10.3390/jmse9020232
Peng Y, Tsouvalas A, Stampoultzoglou T, Metrikine A. Study of the Sound Escape with the Use of an Air Bubble Curtain in Offshore Pile Driving. Journal of Marine Science and Engineering. 2021; 9(2):232. https://doi.org/10.3390/jmse9020232
Chicago/Turabian StylePeng, Yaxi, Apostolos Tsouvalas, Tasos Stampoultzoglou, and Andrei Metrikine. 2021. "Study of the Sound Escape with the Use of an Air Bubble Curtain in Offshore Pile Driving" Journal of Marine Science and Engineering 9, no. 2: 232. https://doi.org/10.3390/jmse9020232
APA StylePeng, Y., Tsouvalas, A., Stampoultzoglou, T., & Metrikine, A. (2021). Study of the Sound Escape with the Use of an Air Bubble Curtain in Offshore Pile Driving. Journal of Marine Science and Engineering, 9(2), 232. https://doi.org/10.3390/jmse9020232







