A Coupled Hydrodynamic-Equilibrium Type Beach Profile Evolution Model
Abstract
:1. Introduction
2. Materials and Methods
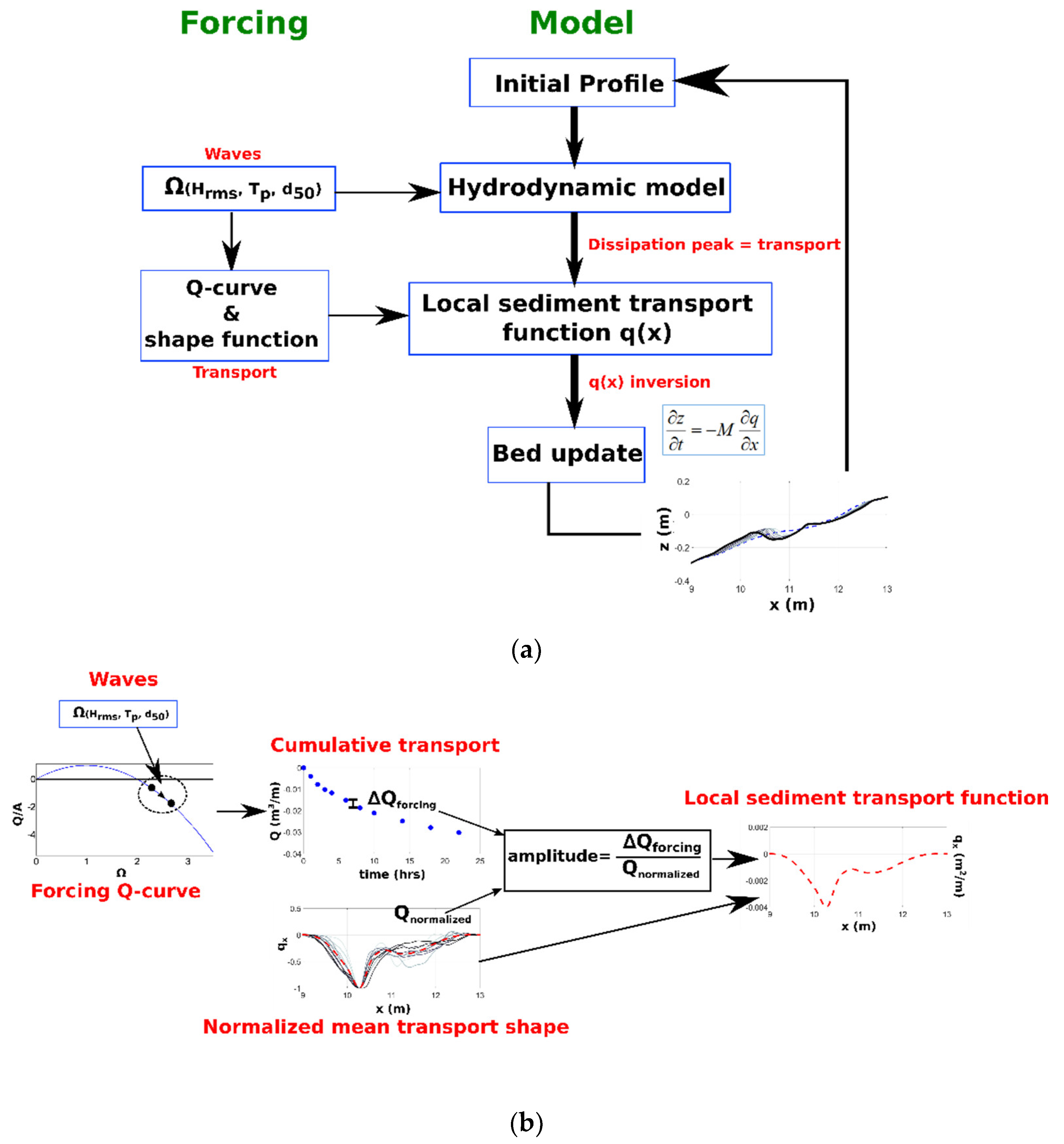
2.1. Model Concepts
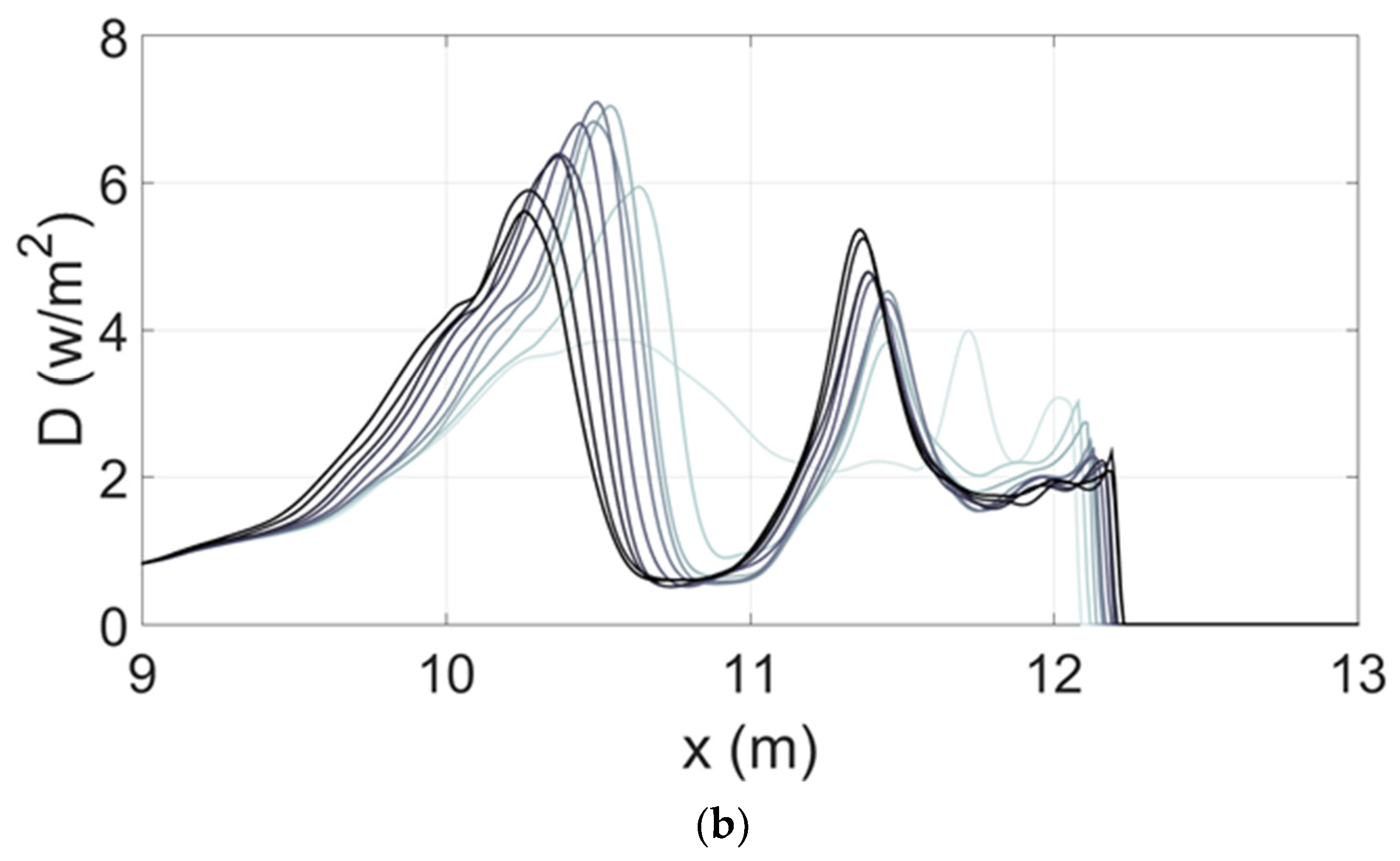
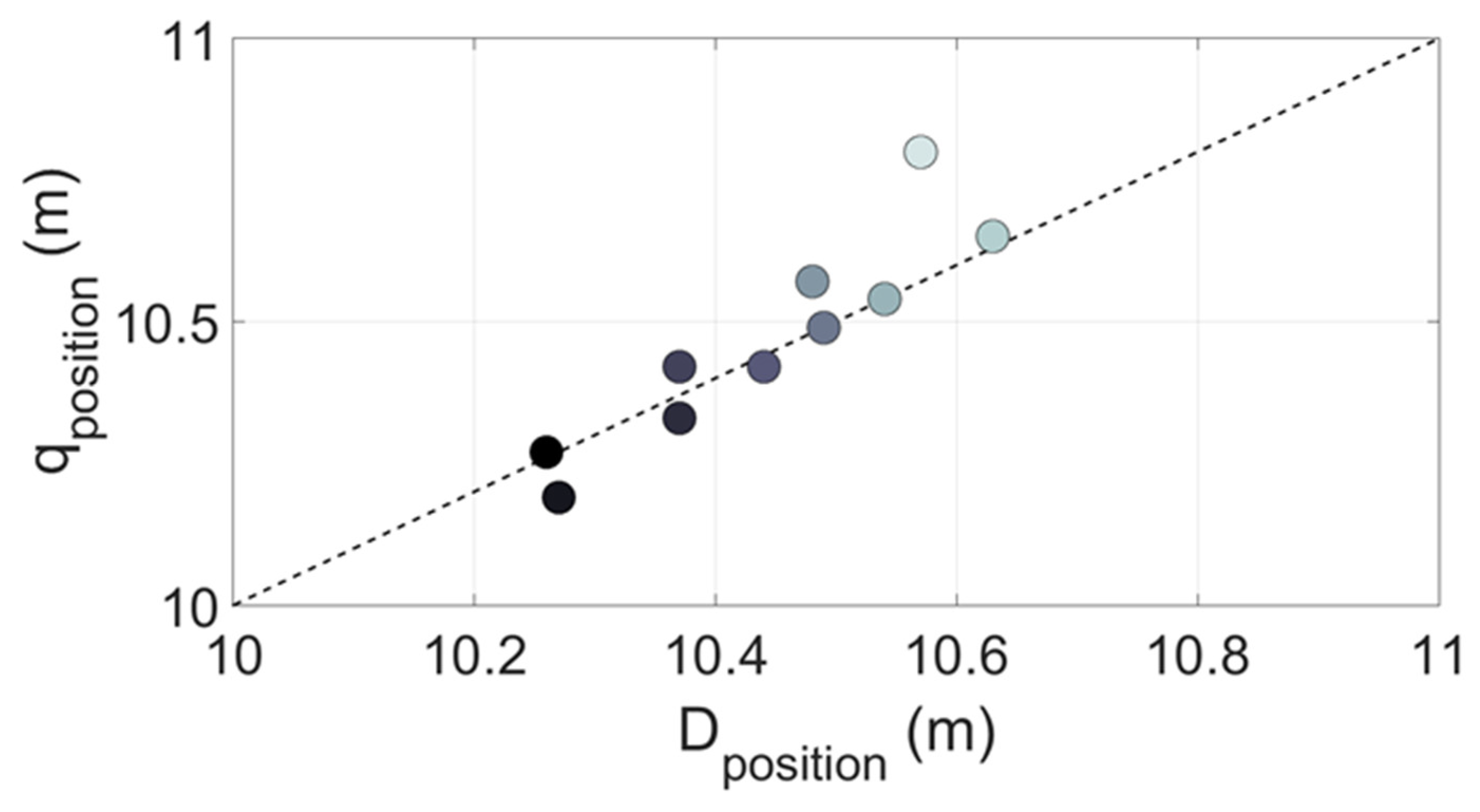
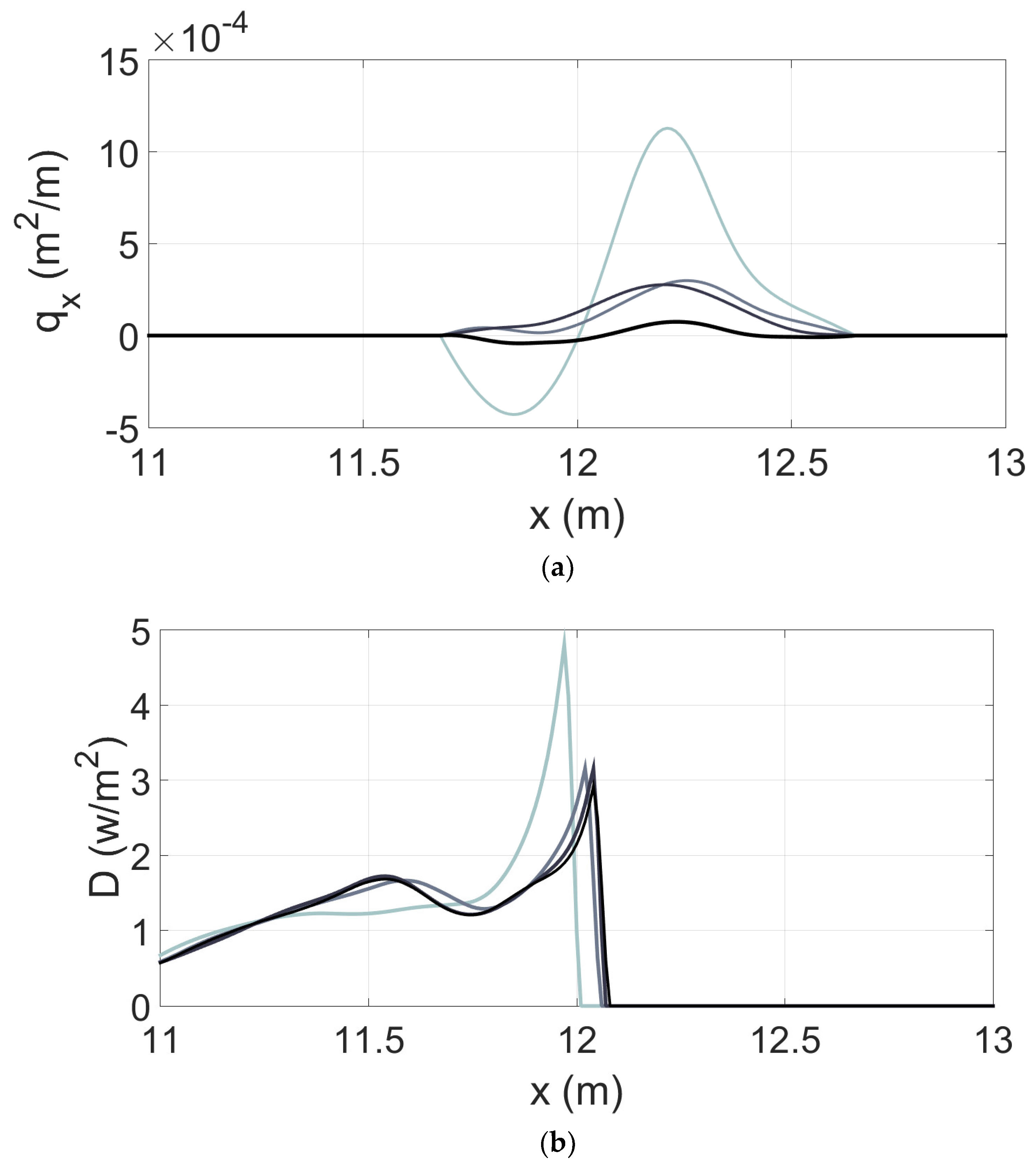
- Given an initial profile and incident wave conditions, a parametric wave hydrodynamic model (here Alsina and Baldock [10]) provides the wave dissipation, D, across the profile, with Qeq defined by (1). Other wave models could be adopted instead. D is defined in equation (9) of Alsina and Baldock [10]).
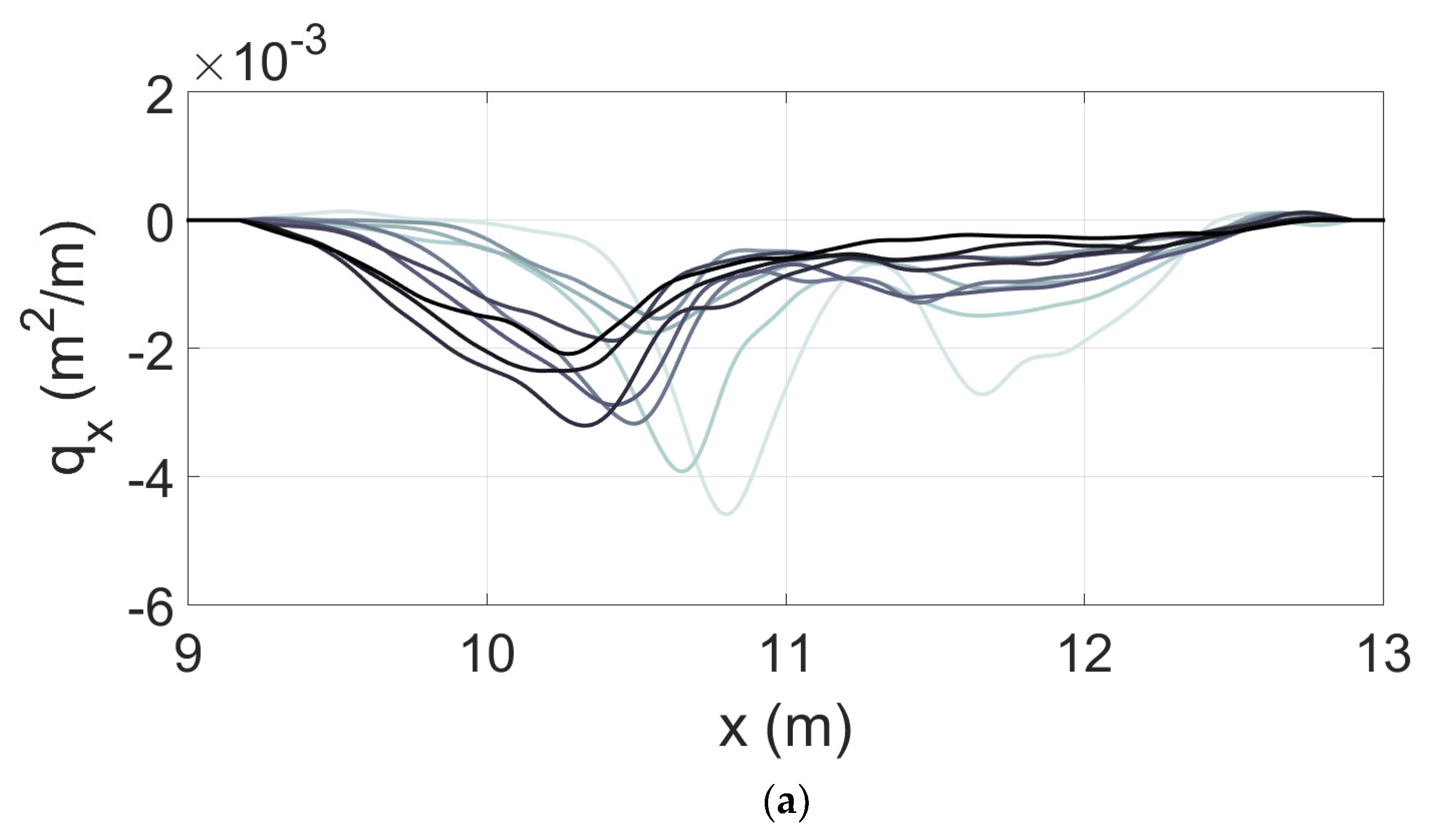
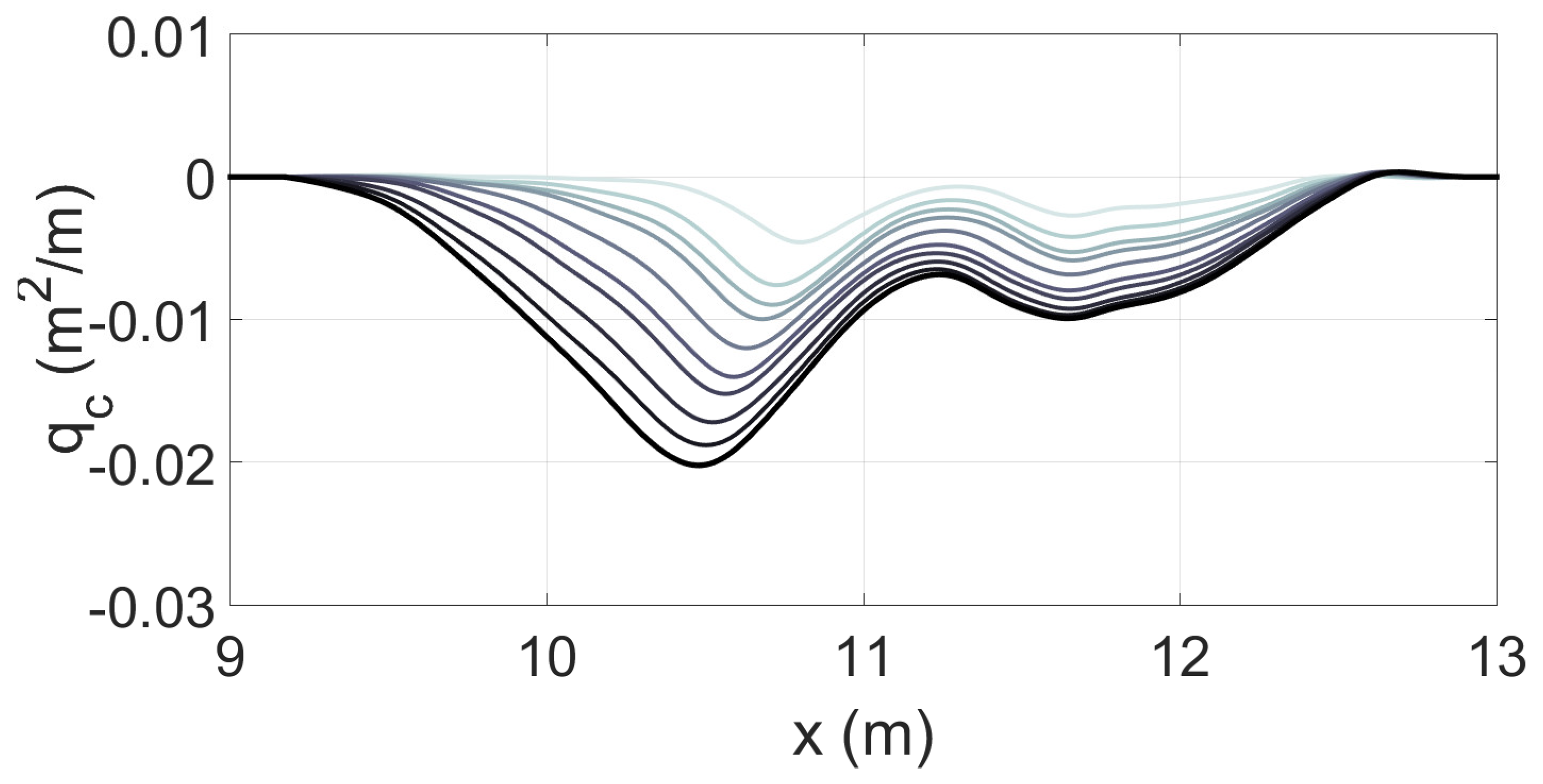
- Predefined normalised dynamic local sediment transport functions define the transport rate at any location. The sediment transport functions are constrained to match the maxima (minima for erosion) of transport with the location of the maxima in the dissipation obtained from the parametric wave model. The transport rates are then non-normalized according to the Q(t) curve and the time discretization to provide the required dimensional local sediment transport rates.
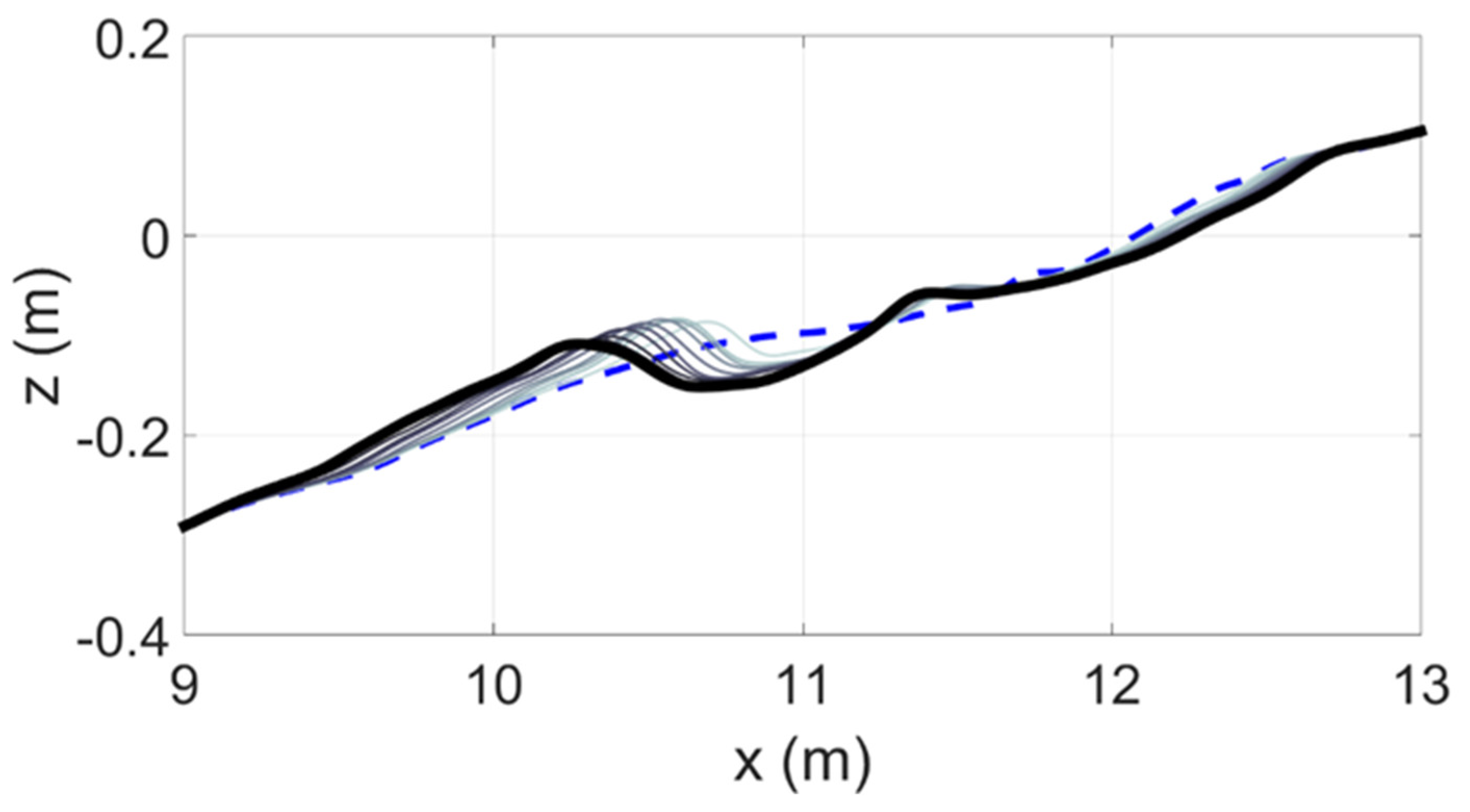
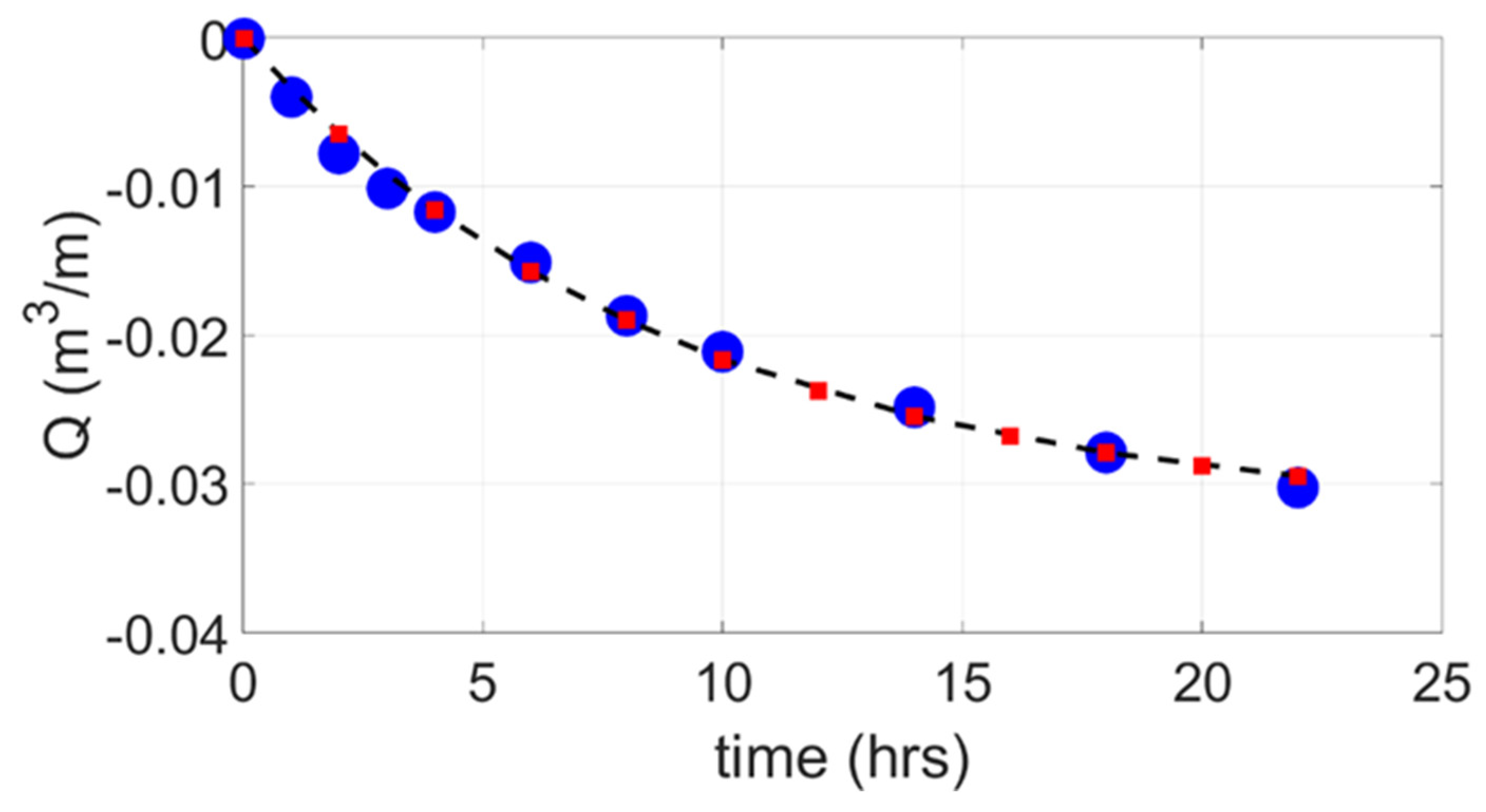
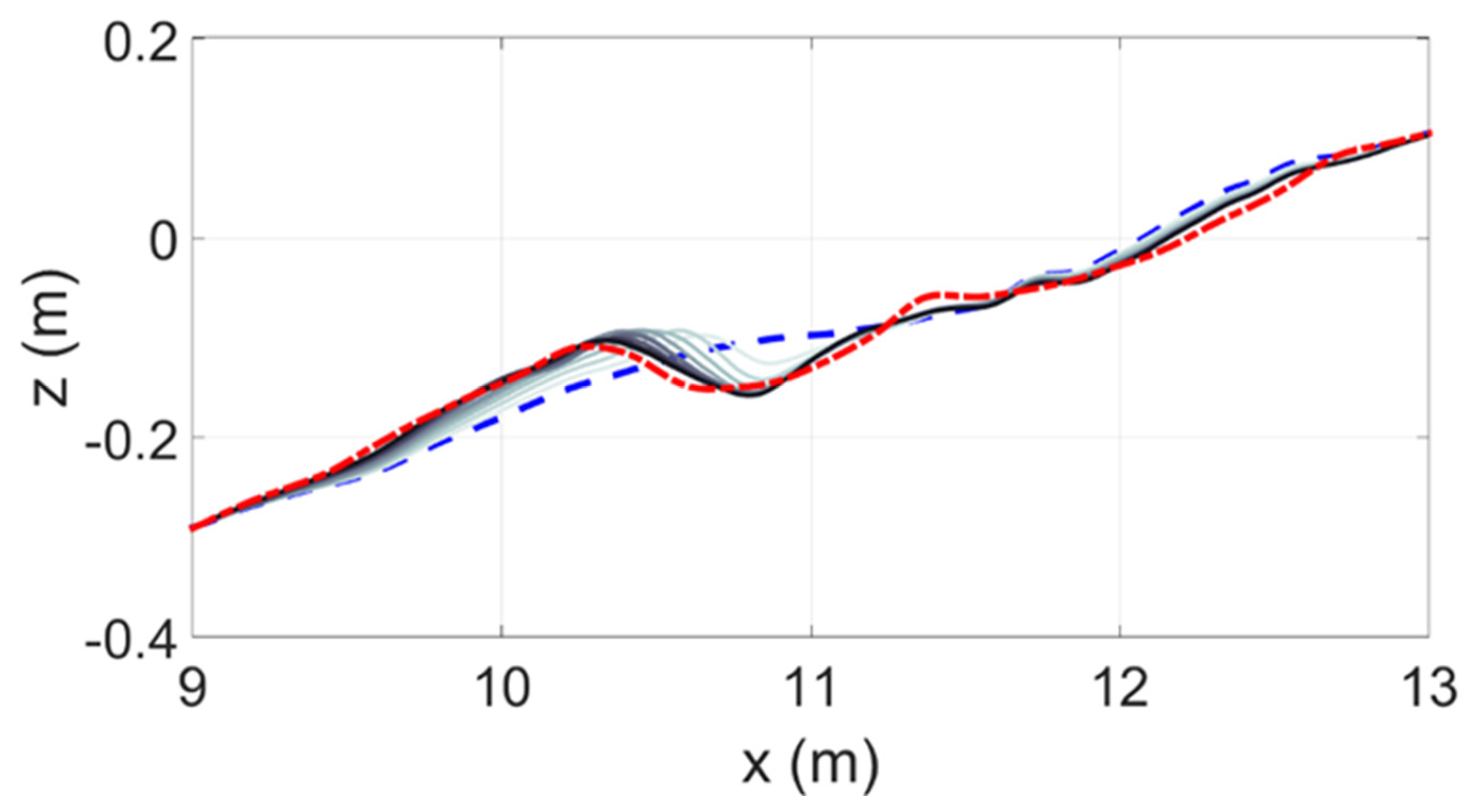
- The beach profile is then updated in the usual manner by using the sediment continuity equation to obtain the bed elevation change from the dimensional local sediment transport function, q(x).
2.2. Experimental Setup
2.3. Model Development
3. Results
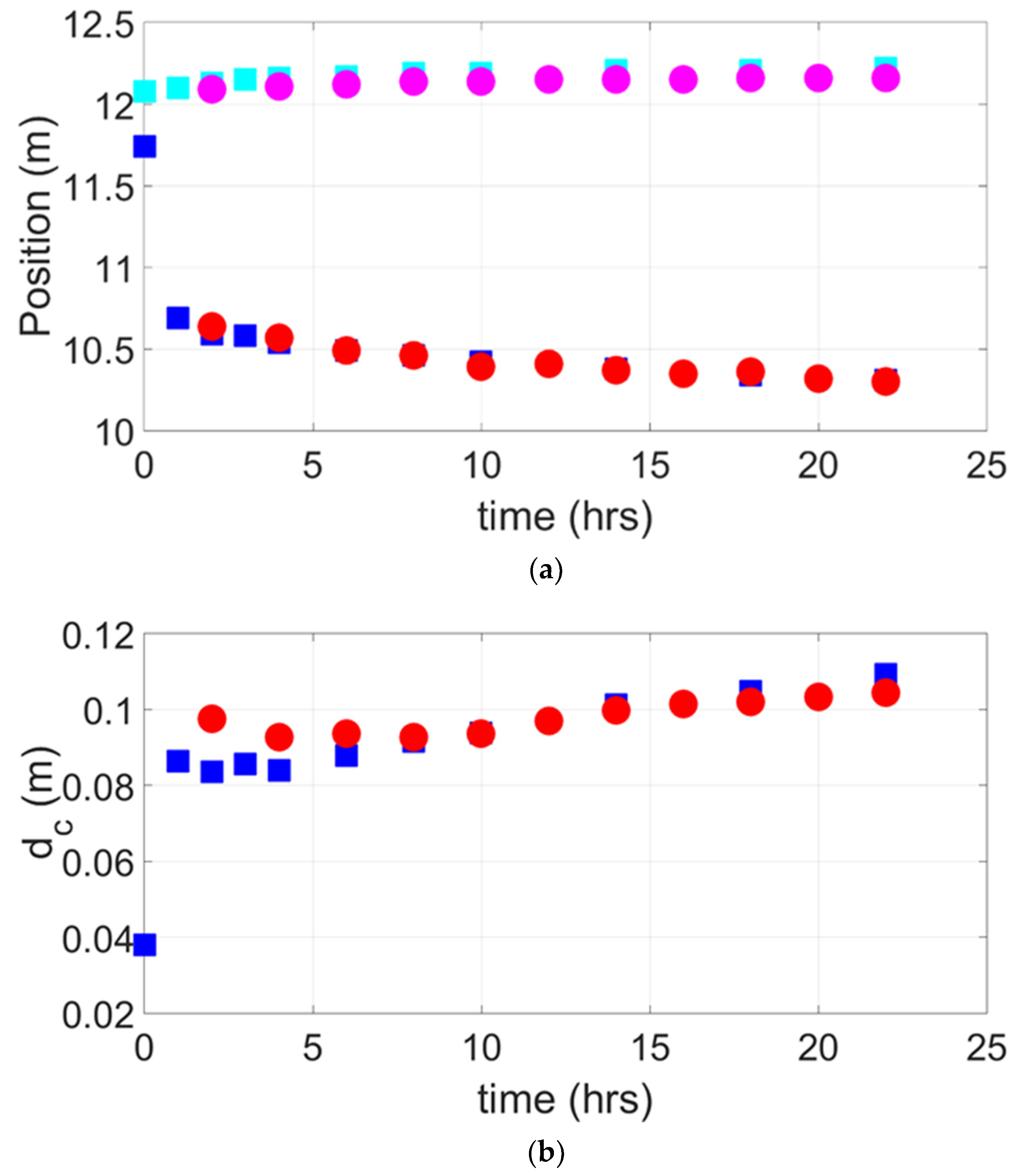
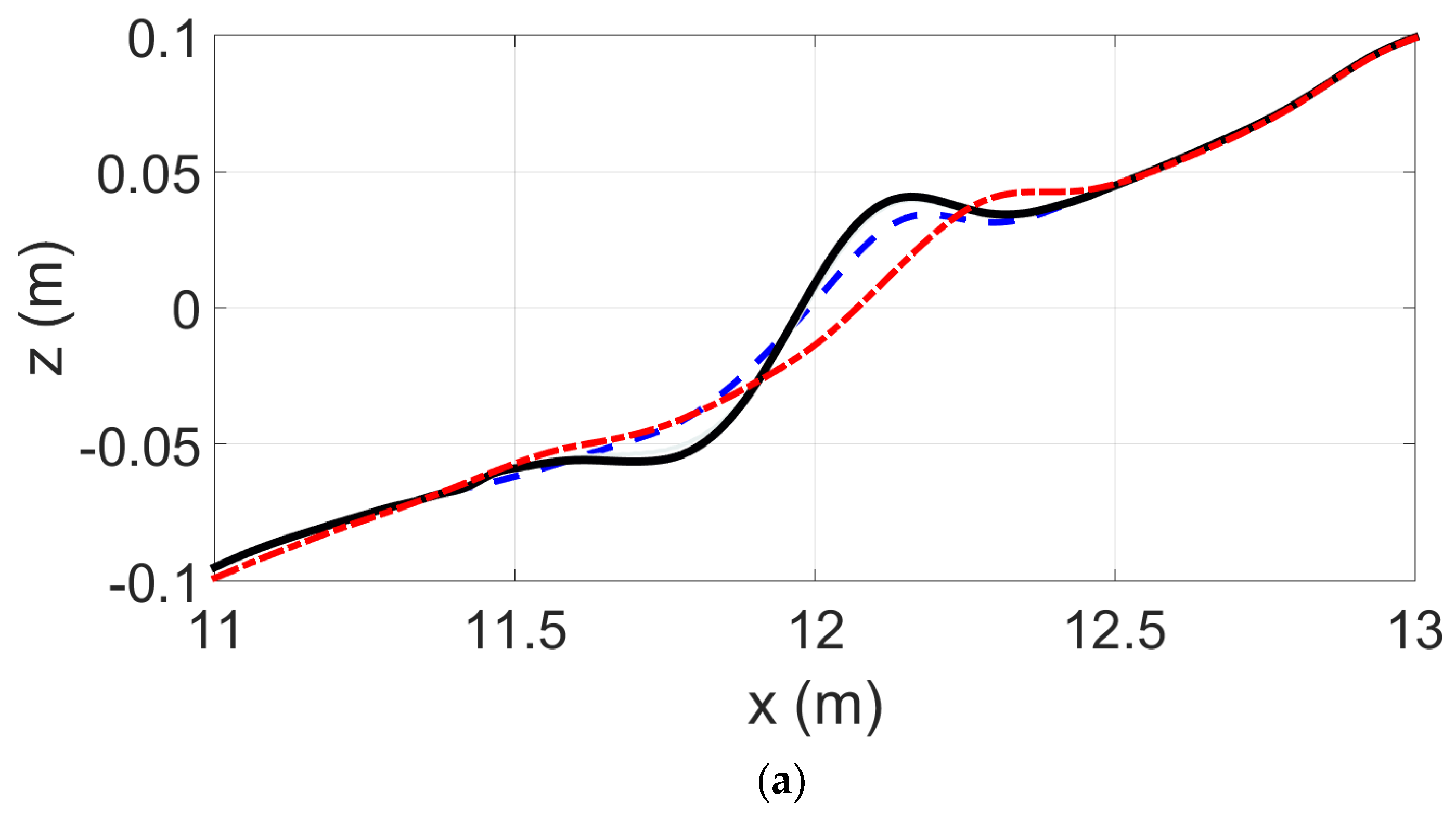
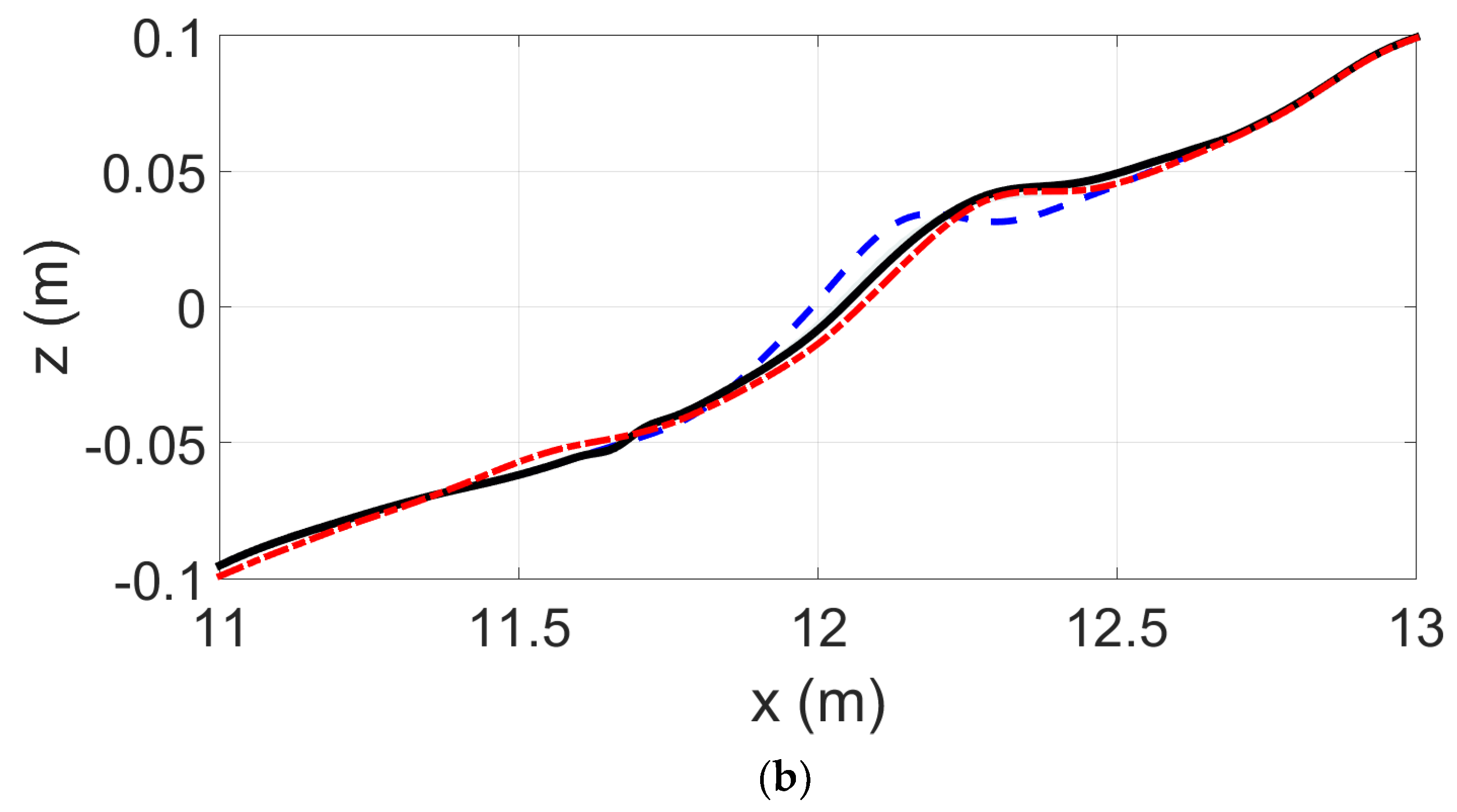
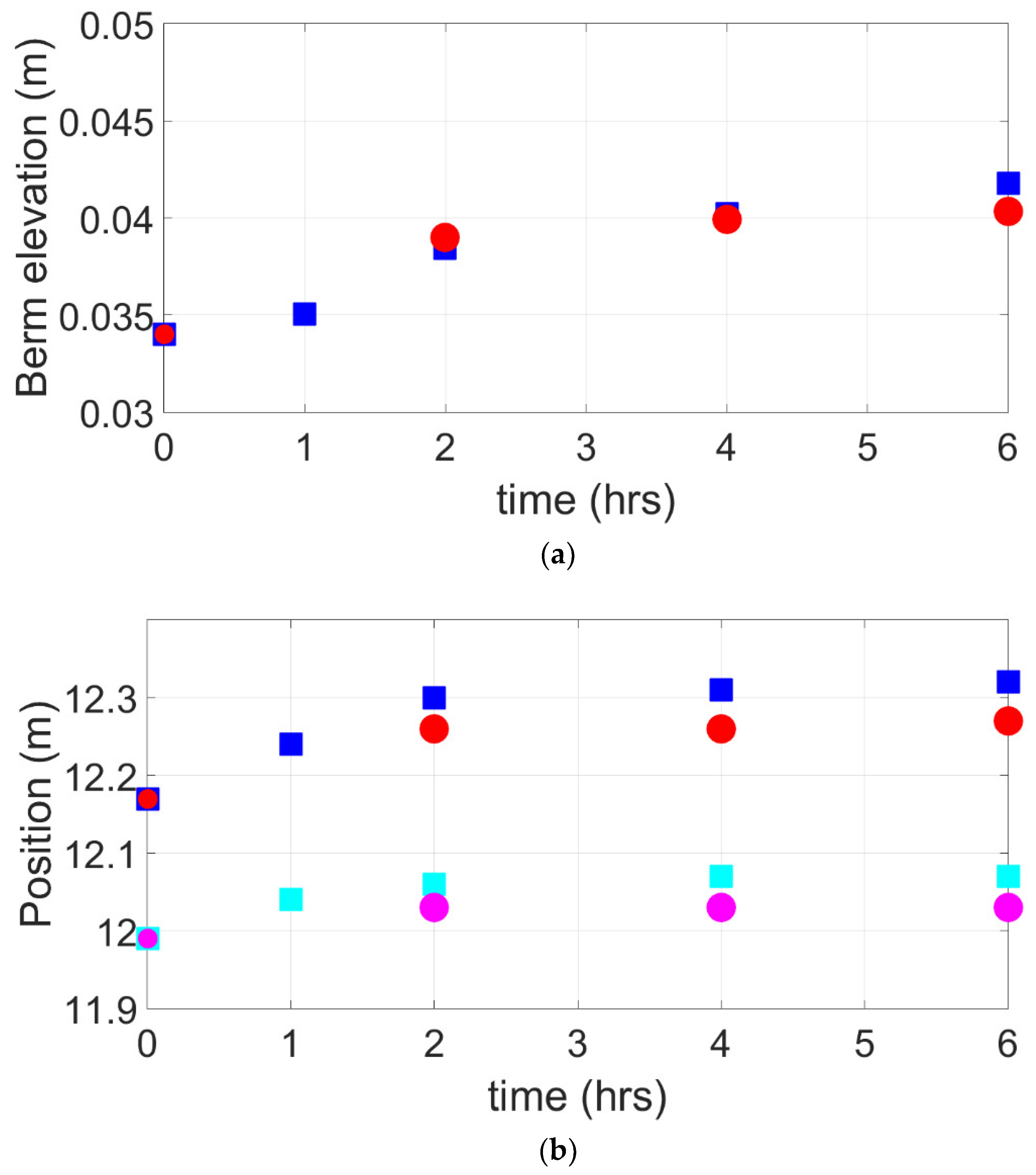
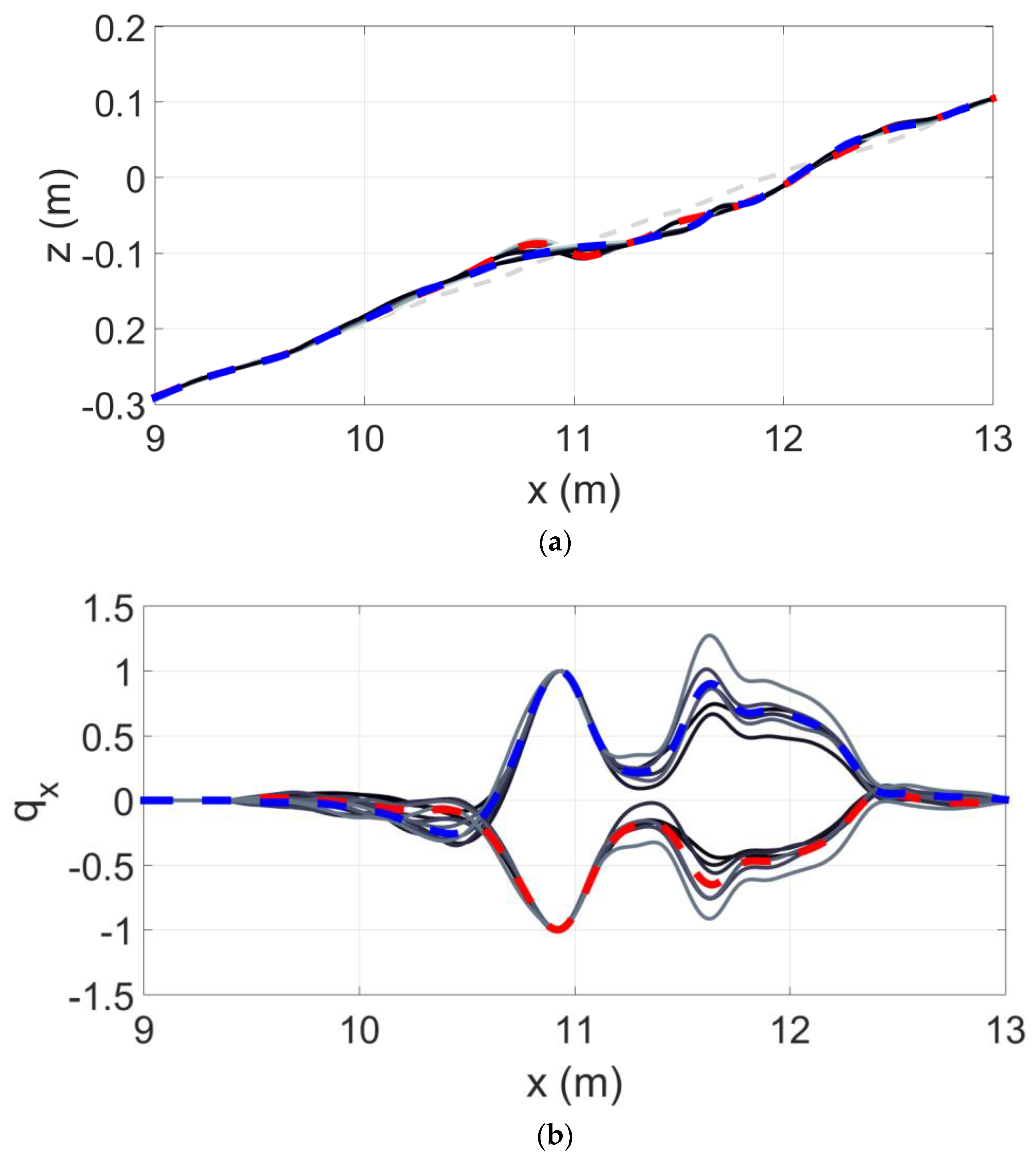
3.1. Erosive Conditions, Case A
3.2. Accretive Conditions, Case B
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruessink, B.G.; Coco, G.; Ranasinghe, R.; Turner, I.L. Coupled and noncoupled behavior of three-dimensional morphological patterns in a double sandbar system. J. Geophys. Res. Space Phys. 2007, 112, 7. [Google Scholar] [CrossRef]
- Yates, M.L.; Guza, R.T.; O’Reilly, W.C. Equilibrium shoreline response: Observations and modeling. J. Geophys. Res. Space Phys. 2009, 114, 16. [Google Scholar] [CrossRef] [Green Version]
- Van Der Meulen, T.; Gourlay, M.R. Beach and Dune Erosion Tests; American Society of Civil Engineers (ASCE): New York, NY, USA, 1969. [Google Scholar]
- Wright, L.; Short, A.; Green, M. Short-term changes in the morphodynamic states of beaches and surf zones: An empirical predictive model. Mar. Geol. 1985, 62, 339–364. [Google Scholar] [CrossRef]
- Davidson, M.A.; Turner, I.L.; Guza, R. The effect of temporal wave averaging on the performance of an empirical shoreline evolution model. Coast. Eng. 2011, 58, 802–805. [Google Scholar] [CrossRef] [Green Version]
- Splinter, K.D.; Turner, I.L.; Davidson, M.A.; Barnard, P.L.; Castelle, B.; Oltman-Shay, J. A generalized equilibrium model for predicting daily to interannual shoreline response. J. Geophys. Res. Earth Surf. 2014, 119, 1936–1958. [Google Scholar] [CrossRef] [Green Version]
- Davidson, M.A.; Turner, I.L. A behavioral template beach profile model for predicting seasonal to interannual shoreline evolution. J. Geophys. Res. Space Phys. 2009, 114, 1. [Google Scholar] [CrossRef]
- Birrien, F.; Atkinson, A.; Shimamoto, T.; Baldock, T. Hysteresis in the evolution of beach profile parameters under sequences of wave climates—Part 2; Modelling. Coast. Eng. 2018, 133, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Janssen, T.; Battjes, J. A note on wave energy dissipation over steep beaches. Coast. Eng. 2007, 54, 711–716. [Google Scholar] [CrossRef]
- Alsina, J.; Baldock, T. Improved representation of breaking wave energy dissipation in parametric wave transformation models. Coast. Eng. 2007, 54, 765–769. [Google Scholar] [CrossRef]
- Baldock, T.; Birrien, F.; Atkinson, A.; Shimamoto, T.; Wu, S.; Callaghan, D.; Nielsen, P. Morphological hysteresis in the evolution of beach profiles under sequences of wave climates—Part 1; observations. Coast. Eng. 2017, 128, 92–105. [Google Scholar] [CrossRef] [Green Version]
- Baldock, T.; Alsina, J.; Caceres, I.; Vicinanza, D.; Contestabile, P.; Power, H.; Sanchezarcilla, A. Large-scale experiments on beach profile evolution and surf and swash zone sediment transport induced by long waves, wave groups and random waves. Coast. Eng. 2011, 58, 214–227. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fredsoe, J. Formation and development of a breaker bar under regular waves. Part 2: Sediment transport and morphology. Coast. Eng. 2014, 88, 55–68. [Google Scholar] [CrossRef]
- Bayle, P.M.; Beuzen, T.; Blenkinsopp, C.E.; Baldock, T.E.; Turner, I.L. A new approach for scaling beach profile evolution and sediment transport rates in distorted laboratory models. Coast. Eng. 2021, 163, 103794. [Google Scholar] [CrossRef]
- Patterson, D.C. Modelling as an Aid to Understand the Evolution of Australia’s Central East Coast in Response to Late Pleistocene-Holocene and Future Sea Level Change. Ph.D. Thesis, The University of Queensland, St Lucia, QLD, Australia, 2013. [Google Scholar]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather. Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Weir, F.M.; Hughes, M.G.; Baldock, T.E. Beach face and berm morphodynamics fronting a coastal lagoon. Geomorphology 2006, 82, 331–346. [Google Scholar] [CrossRef]
- Atkinson, A.L.; Baldock, T.E.; Birrien, F.; Callaghan, D.P.; Nielsen, P.; Beuzen, T.; Turner, I.L.; Blenkinsopp, C.E.; Ranasinghe, R. Laboratory investigation of the Bruun Rule and beach response to sea level rise. Coast. Eng. 2018, 136, 183–202. [Google Scholar] [CrossRef]
- Baldock, T.E.; Son, P.K.; Manoonvoravong, P.; Barnes, M.P.; Alsina, J.M. Probabilistic-Deterministic Modelling of Swash Zone Morphology. Coast. Sediments ‘07 2007, 272–285. [Google Scholar] [CrossRef]



| Case | Wave Height, Hrms (m) | Wave Period, Tp (s) |
|---|---|---|
| Case A, erosive | 0.1 | 1 |
| Case B, accretive | 0.04 | 1 |
| Case C, cyclic | 0.04, 0.1 | 1 |
| Compared Feature | RMSE (cm) |
|---|---|
| Modelled vs. observed profiles | 0.75 |
| Observed (initial vs. final) profiles | 2.21 |
| Shoreline position | 5.16 |
| Sandbar position | 2.4 |
| Sandbar depth to crest | 0.69 |
| Compared Feature | RMSE (cm) |
|---|---|
| Modelled vs. observed profiles | 0.46 |
| Observed (initial vs. final) profiles | 0.75 |
| Shoreline position | 3.7 |
| Sandbar position | 4.69 |
| Sandbar depth to crest | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Birrien, F.; Baldock, T. A Coupled Hydrodynamic-Equilibrium Type Beach Profile Evolution Model. J. Mar. Sci. Eng. 2021, 9, 353. https://doi.org/10.3390/jmse9040353
Birrien F, Baldock T. A Coupled Hydrodynamic-Equilibrium Type Beach Profile Evolution Model. Journal of Marine Science and Engineering. 2021; 9(4):353. https://doi.org/10.3390/jmse9040353
Chicago/Turabian StyleBirrien, Florent, and Tom Baldock. 2021. "A Coupled Hydrodynamic-Equilibrium Type Beach Profile Evolution Model" Journal of Marine Science and Engineering 9, no. 4: 353. https://doi.org/10.3390/jmse9040353
APA StyleBirrien, F., & Baldock, T. (2021). A Coupled Hydrodynamic-Equilibrium Type Beach Profile Evolution Model. Journal of Marine Science and Engineering, 9(4), 353. https://doi.org/10.3390/jmse9040353






