Small-Scale Morpho-Sedimentary Dynamics in the Swash Zone of a Megatidal Mixed Sand–Gravel Beach
Abstract
:1. Introduction
2. Methods
2.1. Site Description
2.2. Experiment Overview
2.2.1. Range Sensor and Camera Array
2.2.2. Overhead Camera
2.3. Data Processing
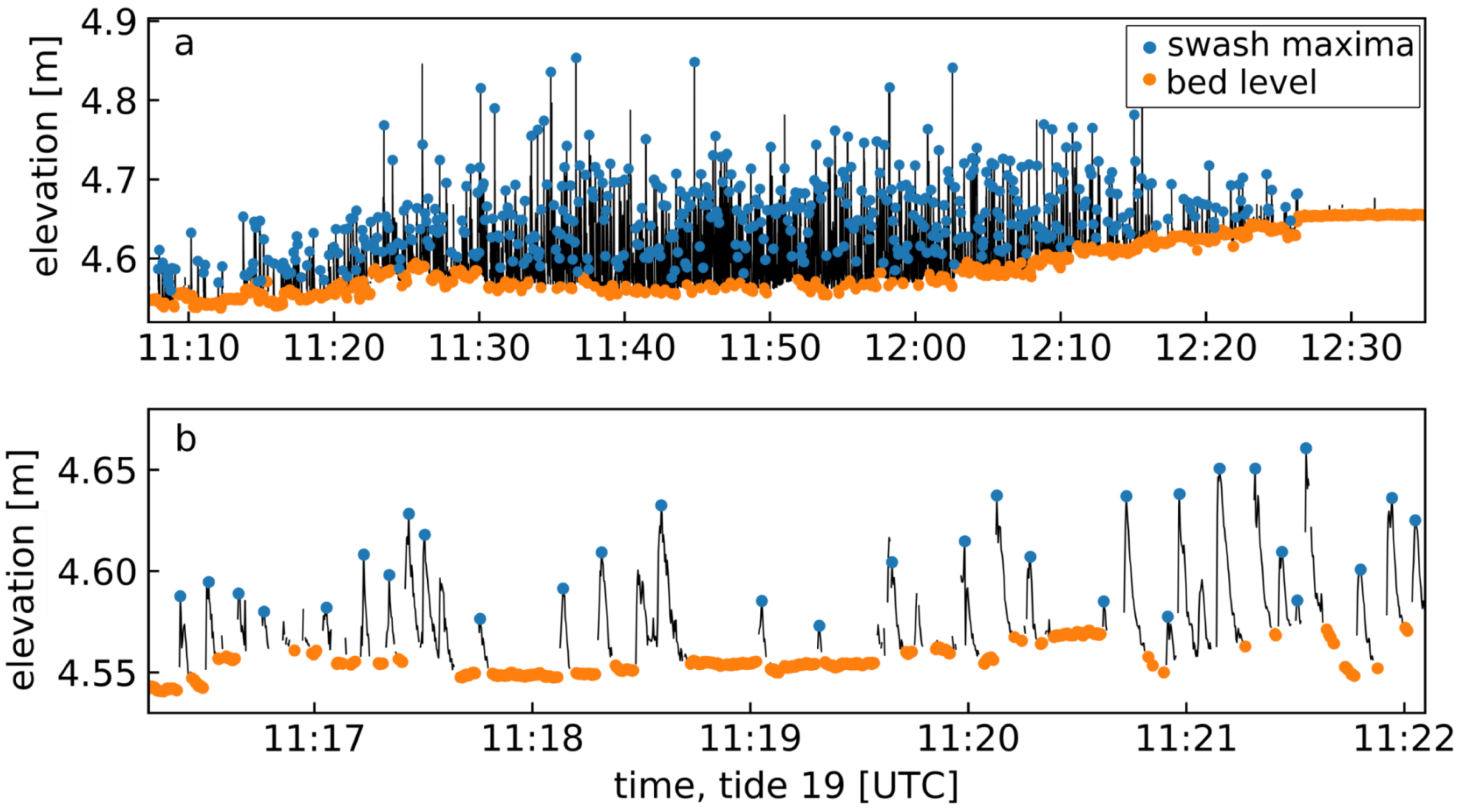
2.3.1. Range Data: Bed Level and Swash Height
2.3.2. Array Cameras: Digital Grain Sizing
2.3.3. Cobble Tracking
3. Results
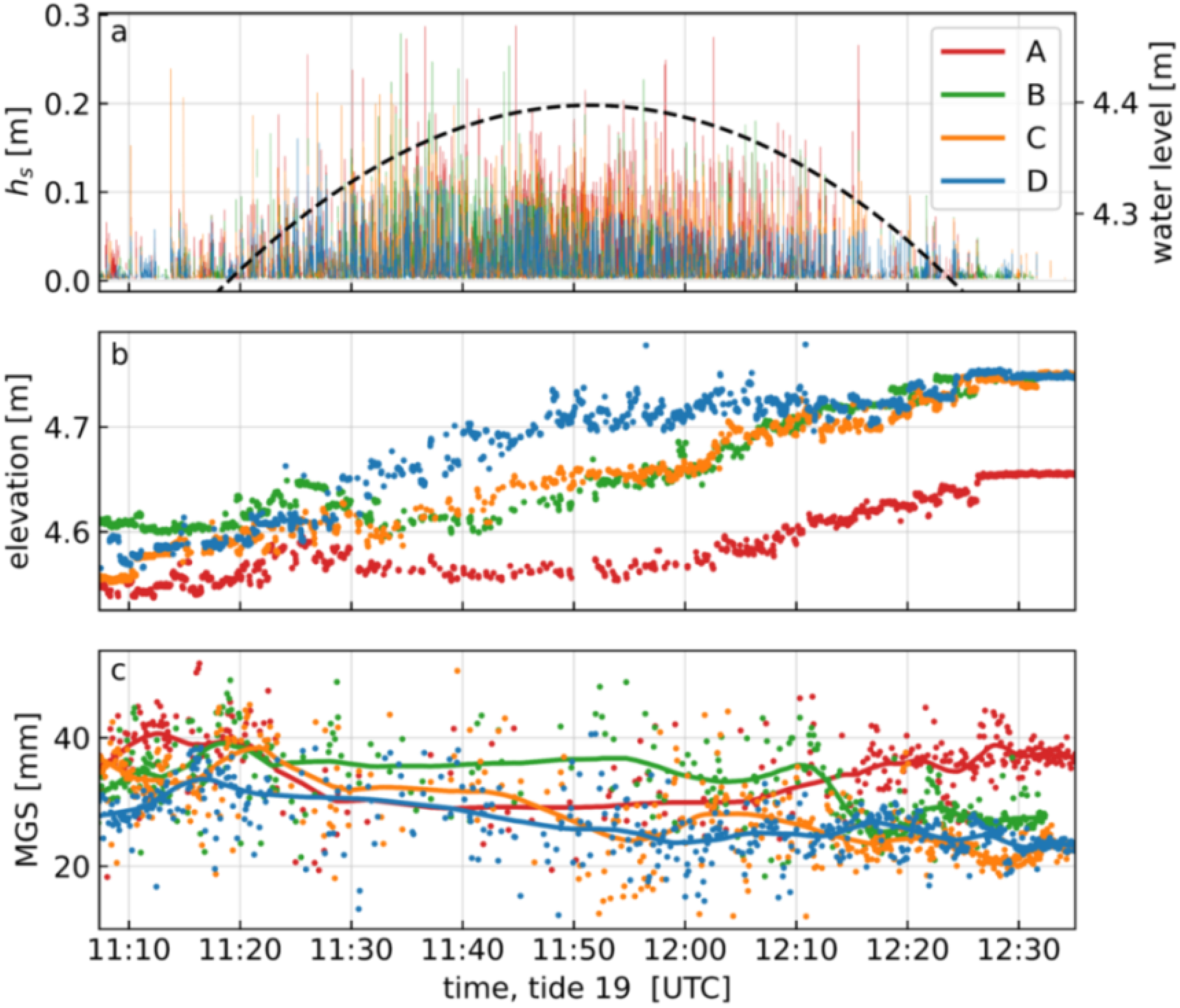
3.1. Coevolution of Bed Level and Mean Grain Size
3.2. Cobble Dynamics
- Station 1 (S1): at high tide, when the shoreline position was nearest to the HWL. Here, the tracer cobbles were deployed atop the coarse berm material. The camera’s cross-shore field of view spanned 3.5 to 7 m in local cross-shore coordinates, and contained almost entirely coarse berm material. Note that this is the station associated with the images in Figure 4.
- Station 2 (S2): 45 min after high tide. The shoreline and swash zone coincided with the region immediately seaward of the coarse berm. Coarse berm material was present in the landward one third of the camera’s field of view, which spanned from 8.5 to 12 m (i.e., 5 m seaward of S1). The cobbles were deployed in the mid-swash, over a combination of the coarse seaward face of the berm and the finer material farther seaward.
- Station 3 (S3): 75 min after high tide. The swash zone no longer coincided with any coarse-grained berm material, and the substrate was predominantly fine-grained and uniform. The cobbles were deployed near mid-swash and mid-camera field of view: i.e., 12.5 to 16 m across-shore (9 m seaward of S1).
- Station 4 (S4): 85 min after high tide, with the bed conditions and the cobble deployment being similar to those described for S3. The cross-shore field of view of the camera in this location was 15.5 to 19 m (12 m seaward of S1).
4. Discussion
5. Conclusions
- In general, increases in bed level correspond to increases in mean surficial grain size.
- The largest mean grain sizes occur at the leading edge of the swash front, during both the flooding and ebbing tide. The smallest mean grain sizes are associated with the mid-swash zone.
- The magnitude of inter-swash-event bed level change is largest near the leading edge of the swash zone.
- Bed level change and swash height are uncorrelated at inter-swash timescales.
- The cumulative transport of cobbles in the swash is greater where the substrate consists of finer material. Cumulative transport is lower where the surficial material is coarser (i.e., of similar size to the cobble being trasported).
- Cobble transport tends to diverge shoreward or seaward from the mid-swash.
- The divergence of cobble transport from the mid-swash results in a deposit of coarse-grained material that migrates with the leading edge of the swash. The coarse-grained depoist is stranded near the high water line, becoming a nascent berm. Accumulation of coarse-grained material is also likely to occur at the beach step.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Digital Grain Sizing Validation

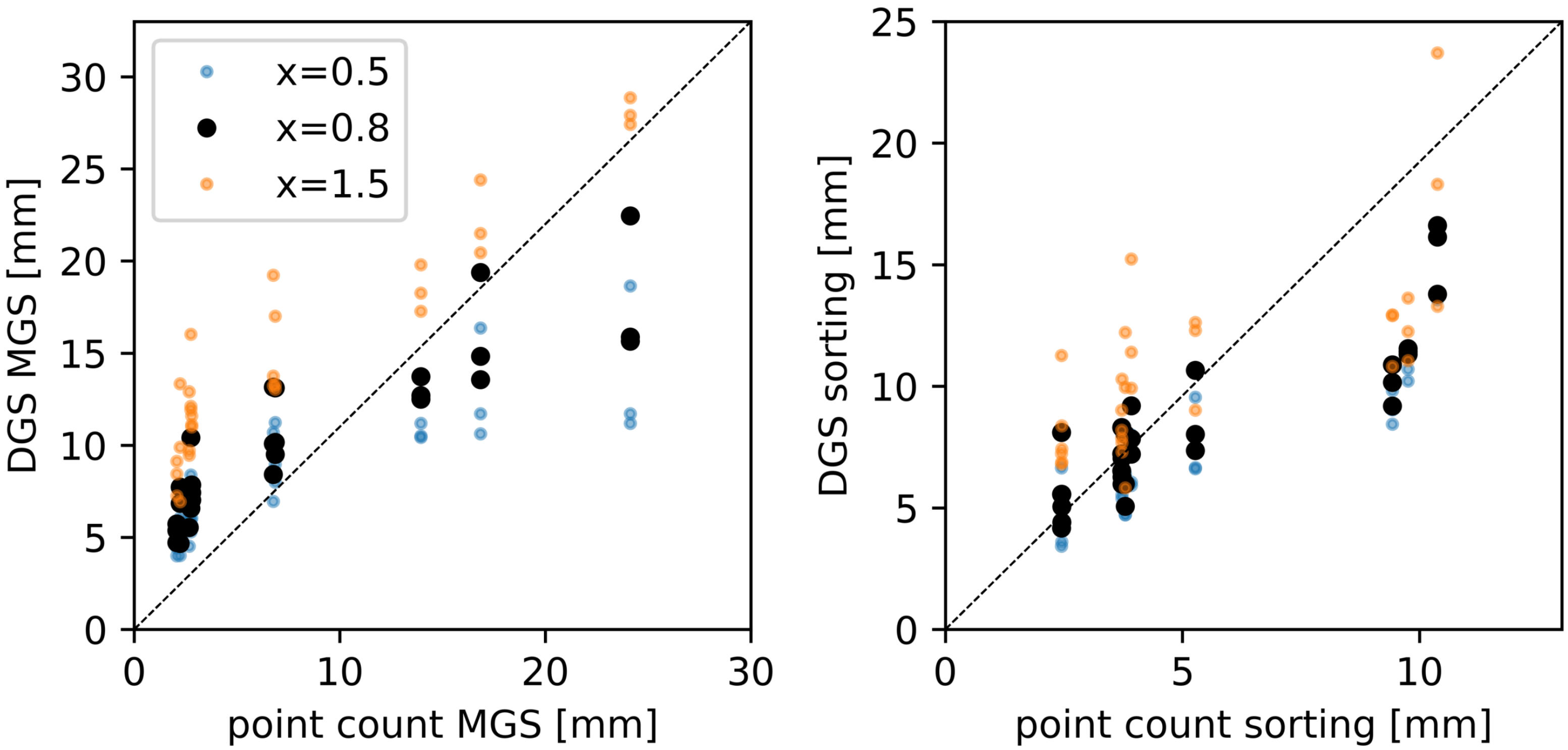
| x | DGS-Sieve RMSE (mm) | DGS-Point Count RMSE (mm) |
|---|---|---|
| 0.5 | 4.11 | 4.63 |
| 0.7 | 3.43 | 4.36 |
| 0.8 | 3.35 | 4.39 |
| 0.9 | 3.48 | 4.55 |
| 1.0 | 3.81 | 4.83 |
| 1.2 | 4.90 | 5.71 |
| 1.3 | 5.71 | 6.27 |
| 1.5 | 7.08 | 7.56 |
References
- Puleo, J.A.; Blenkinsopp, C.; Conley, D.; Masselink, G.; Turner, I.L.; Russell, P.; Buscombe, D.; Howe, D.; Lanckriet, T.; McCall, R.; et al. Comprehensive field study of swash-zone processes. I: Experimental design with examples of hydrodynamic and sediment transport measurements. J. Waterw. Port Coast. Ocean Eng. 2013, 140, 14–28. [Google Scholar] [CrossRef] [Green Version]
- Lanckriet, T.; Puleo, J.A.; Masselink, G.; Turner, I.L.; Conley, D.; Blenkinsopp, C.; Russell, P. Comprehensive field study of swash-zone processes. II: Sheet flow sediment concentrations during quasi-steady backwash. J. Waterw. Port Coast. Ocean Eng. 2013, 140, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Turner, I.L.; Russell, P.E.; Butt, T. Measurement of wave-by-wave bed-levels in the swash zone. Coast. Eng. 2008, 55, 1237–1242. [Google Scholar] [CrossRef]
- Rubin, D.M. A simple autocorrelation algorithm for determining grain size from digital images of sediment. J. Sediment. Res. 2004, 74, 160–165. [Google Scholar] [CrossRef] [Green Version]
- Buscombe, D. Transferable wavelet method for grain-size distribution from images of sediment surfaces and thin sections, and other natural granular patterns. Sedimentology 2013, 60, 1709–1732. [Google Scholar] [CrossRef]
- Dean, R.G. Equilibrium beach profiles: Characteristics and applications. J. Coast. Res. 1991, 7, 53–84. [Google Scholar]
- Horn, D.P.; Walton, S.M. Sediment-level oscillations in the swash zone of a mixed sand and gravel beach. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; World Scientific Publishing Co.: Singapore, 2004; Volume 3, pp. 2390–2402. [Google Scholar]
- Masselink, G.; Russell, P.; Turner, I.; Blenkinsopp, C. Net sediment transport and morphological change in the swash zone of a high-energy sandy beach from swash event to tidal cycle time scales. Mar. Geol. 2009, 267, 18–35. [Google Scholar] [CrossRef]
- Russell, P.; Masselink, G.; Blenkinsopp, C.; Turner, I. A comparison of berm accretion in the swash zone on sand and gravel beaches at the timescale of individual waves. J. Coast. Res. 2009, SI 56, 1791–1795. [Google Scholar]
- Blenkinsopp, C.; Turner, I.; Masselink, G.; Russell, P. Swash zone sediment fluxes: Field observations. Coast. Eng. 2011, 58, 28–44. [Google Scholar] [CrossRef]
- Kulkarni, C.D.; Levoy, F.; Monfort, O.; Miles, J. Morphological variations of a mixed sediment beachface (Teignmouth, UK). Cont. Shelf Res. 2004, 24, 1203–1218. [Google Scholar] [CrossRef]
- Buscombe, D.; Rubin, D.; Warrick, J. A universal approximation of grain size from images of noncohesive sediment. J. Geophys. Res. Earth Surf. 2010, 115, F02015. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.J.; Chung, C.H. Estimation of riverbed grain-size distribution using image-processing techniques. J. Hydrol. 2012, 440, 102–112. [Google Scholar] [CrossRef]
- Warrick, J.A.; Rubin, D.M.; Ruggiero, P.; Harney, J.N.; Draut, A.E.; Buscombe, D. Cobble Cam: Grain-size measurements of sand to boulder from digital photographs and autocorrelation analyses. Earth Surf. Process. Landforms J. Br. Geomorphol. Res. Group 2009, 34, 1811–1821. [Google Scholar] [CrossRef]
- Austin, M.J.; Buscombe, D. Morphological change and sediment dynamics of the beach step on a macrotidal gravel beach. Mar. Geol. 2008, 249, 167–183. [Google Scholar] [CrossRef]
- Nordstrom, K.F.; Jackson, N.L. Distribution of surface pebbles with changes in wave energy on a sandy estuarine beach. J. Sediment. Res. 1993, 63, 1152–1159. [Google Scholar]
- Ciavola, P.; Castiglione, E. Sediment dynamics of mixed sand and gravel beaches at short time-scales. J. Coast. Res. 2009, II, 1751–1755. [Google Scholar]
- Stark, N.; Hay, A.E. Pebble and cobble transport on a steep, mega-tidal, mixed sand and gravel beach. Mar. Geol. 2016, 382, 210–223. [Google Scholar] [CrossRef]
- Osborne, P.E. Transport of gravel and cobble on a mixed-sediment inner bank shoreline of a large inlet, Grays Harbor, Washington. Mar. Geol. 2005, 224, 145–156. [Google Scholar] [CrossRef]
- Allan, J.C.; Hart, R.; Tranquili, J.V. The use of Passive Integrated Transponder (PIT) tags to trace cobble transport in a mixed sand-and-gravel beach on the high-energy Oregon coast, USA. Mar. Geol. 2006, 232, 63–86. [Google Scholar] [CrossRef]
- Curtiss, G.M.; Osborne, P.D.; Horner-Devine, A.R. Seasonal patterns of coarse sediment transport on a mixed sand and gravel beach due to vessel wakes, wind waves, and tidal currents. Mar. Geol. 2009, 259, 73–85. [Google Scholar] [CrossRef]
- Dickson, M.E.; Kench, P.S.; Kantor, M.S. Longshore transport of cobbles on a mixed sand and gravel beach, southern Hawke Bay, New Zealand. Mar. Geol. 2011, 287, 31–42. [Google Scholar] [CrossRef]
- Miller, I.M.; Warrick, J.A.; Morgan, C. Observations of coarse sediment movements on the mixed beach of the Elwha Delta, Washington. Mar. Geol. 2011, 282, 201–214. [Google Scholar] [CrossRef]
- Miller, I.M.; Warrick, J.A. Measuring sediment transport and bed disturbance with tracers on a mixed beach. Mar. Geol. 2012, 299, 1–17. [Google Scholar] [CrossRef]
- Bertoni, D.; Sarti, G.; Benelli, G.; Pozzebon, A.; Raguseo, G. Transport trajectories of “smart” pebbles on an artificial coarse-grained beach at Marina di Pisa (Italy): Implications for beach morphodynamics. Mar. Geol. 2012, 291, 227–235. [Google Scholar] [CrossRef]
- Grottoli, E.; Bertoni, D.; Ciavola, P.; Pozzebon, A. Short term displacements of marked pebbles in the swash zone: Focus on particle shape and size. Mar. Geol. 2015, 367, 143–158. [Google Scholar] [CrossRef]
- Grottoli, E.; Bertoni, D.; Pozzebon, A.; Ciavola, P. Influence of particle shape on pebble transport in a mixed sand and gravel beach during low energy conditions: Implications for nourishment projects. Ocean Coast. Manag. 2019, 169, 171–181. [Google Scholar] [CrossRef]
- Levoy, F.; Anthony, E.J.; Monfort, O.; Larsonneur, C. The morphodynamics of megatidal beaches in Normandy, France. Mar. Geol. 2000, 171, 39–59. [Google Scholar] [CrossRef]
- Taylor, R.B.; Wittman, S.L.; Milne, M.J.; Kober, S.M. Beach Morphology and Coastal Changes at Selected Sites, Mainland Nova Scotia; Technical Report; Geological Survey of Canada: Ottawa, ON, Canada, 1985. [Google Scholar]
- Hay, A.E.; Zedel, L.; Stark, N. Sediment dynamics on a steep, megatidal, mixed sand-gravel-cobble beach. Earth Surf. Dyn. 2014, 2, 117–152. [Google Scholar] [CrossRef] [Green Version]
- Guest, T.B. Morpho-Sedimentary Dynamics of a Megatidal, Mixed Sand-Gravel Beach. Ph.D. Thesis, Dalhousie University, Halifax, NS, Canada, 2020. [Google Scholar]
- Barnard, P.L.; Rubin, D.M.; Harney, J.; Mustain, N. Field test comparison of an autocorrelation technique for determining grain size using a digital beachball camera versus traditional methods. Sediment. Geol. 2007, 201, 180–195. [Google Scholar] [CrossRef]
- Duncan, J.R., Jr. The effects of water table and tide cycle on swash-backwash sediment distribution and beach profile development. Mar. Geol. 1964, 2, 186–197. [Google Scholar] [CrossRef]
- Pontee, N.I.; Pye, K.; Blott, S.J. Morphodynamic behaviour and sedimentary variation of mixed sand and gravel beaches, Suffolk, UK. J. Coast. Res. 2004, 20, 256–276. [Google Scholar] [CrossRef]
- Austin, M.J.; Masselink, G. Observations of morphological change and sediment transport on a steep gravel beach. Mar. Geol. 2006, 229, 59–77. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Kenworthy, S.T.; Crowe, J.C. Experimental study of the transport of mixed sand and gravel. Water Resour. Res. 2001, 37, 3349–3358. [Google Scholar] [CrossRef] [Green Version]
- Cuttler, M.V.; Lowe, R.J.; Falter, J.L.; Buscombe, D. Estimating the settling velocity of bioclastic sediment using common grain-size analysis techniques. Sedimentology 2017, 64, 987–1004. [Google Scholar] [CrossRef]
- Ingram, R.L. Sieve Analysis. In Procedures in Sedimentary Petrology; Carver, R.E., Ed.; Wiley Interscience: New York, NY, USA, 1971; pp. 49–67. [Google Scholar]
- Kellerhals, R.; Bray, D.I. Sampling procedures for coarse fluvial sediments. J. Hydraul. Div. 1971, 97, 1165–1180. [Google Scholar] [CrossRef]
- Church, M.A.; McLean, D.; Wolcott, J. River Bed Gravels: Sampling and Analysis, Sediment Transport in Gravel-Bed Rivers; Thorne, C.R., Bathurst, J.C., Hey, R.D., Eds.; John Wiley: New York, NY, USA, 1987; pp. 43–88. [Google Scholar]
- Diplas, P.; Sutherland, A.J. Sampling techniques for gravel sized sediments. J. Hydraul. Eng. 1988, 114, 484–501. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guest, T.B.; Hay, A.E. Small-Scale Morpho-Sedimentary Dynamics in the Swash Zone of a Megatidal Mixed Sand–Gravel Beach. J. Mar. Sci. Eng. 2021, 9, 413. https://doi.org/10.3390/jmse9040413
Guest TB, Hay AE. Small-Scale Morpho-Sedimentary Dynamics in the Swash Zone of a Megatidal Mixed Sand–Gravel Beach. Journal of Marine Science and Engineering. 2021; 9(4):413. https://doi.org/10.3390/jmse9040413
Chicago/Turabian StyleGuest, Tristan B., and Alex E. Hay. 2021. "Small-Scale Morpho-Sedimentary Dynamics in the Swash Zone of a Megatidal Mixed Sand–Gravel Beach" Journal of Marine Science and Engineering 9, no. 4: 413. https://doi.org/10.3390/jmse9040413
APA StyleGuest, T. B., & Hay, A. E. (2021). Small-Scale Morpho-Sedimentary Dynamics in the Swash Zone of a Megatidal Mixed Sand–Gravel Beach. Journal of Marine Science and Engineering, 9(4), 413. https://doi.org/10.3390/jmse9040413






