A Buckling Analysis and Optimization Method for a Variable Stiffness Cylindrical Pressure Shell of AUV
Abstract
:1. Introduction
2. Problem Formulation
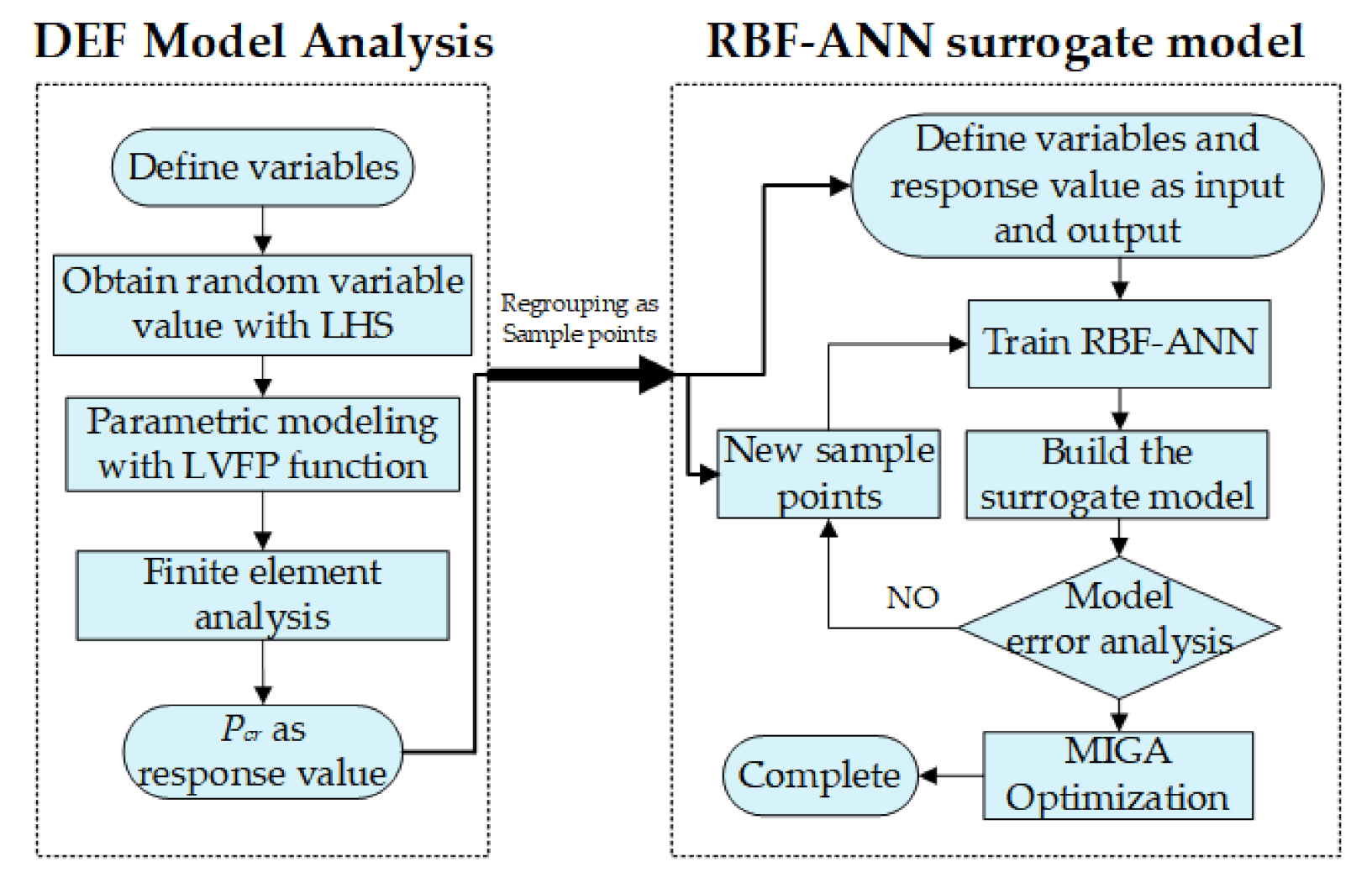
3. A Buckling Analysis and Optimization Method for VS Cylinder
- Define variables (fiber angles radius and L/D ratio);
- Obtain random value through Latin Hypercube Sample method;
- Build the DFE simulation model with the obtained variables;
- Carry out FE analysis to acquire the critical buckling pressure Pcr and group the variable as a sample point;
- Define the input and output and build the initial surrogate model with RBF method;
- Calculate and acquire new sample points from DFE model analysis module to evaluate and reduce the error between surrogate model and the real label value (Pcr obtained from FE analysis based on DFE method);
- If the error criteria meet the requirement, then stop and complete building the surrogate model, but if not, then go back to step 6 to continue training the surrogate model;
- When the RBF surrogate model is built, the MIGA is used as the optimization tool to find the optimum Pcr with the corresponding variables.
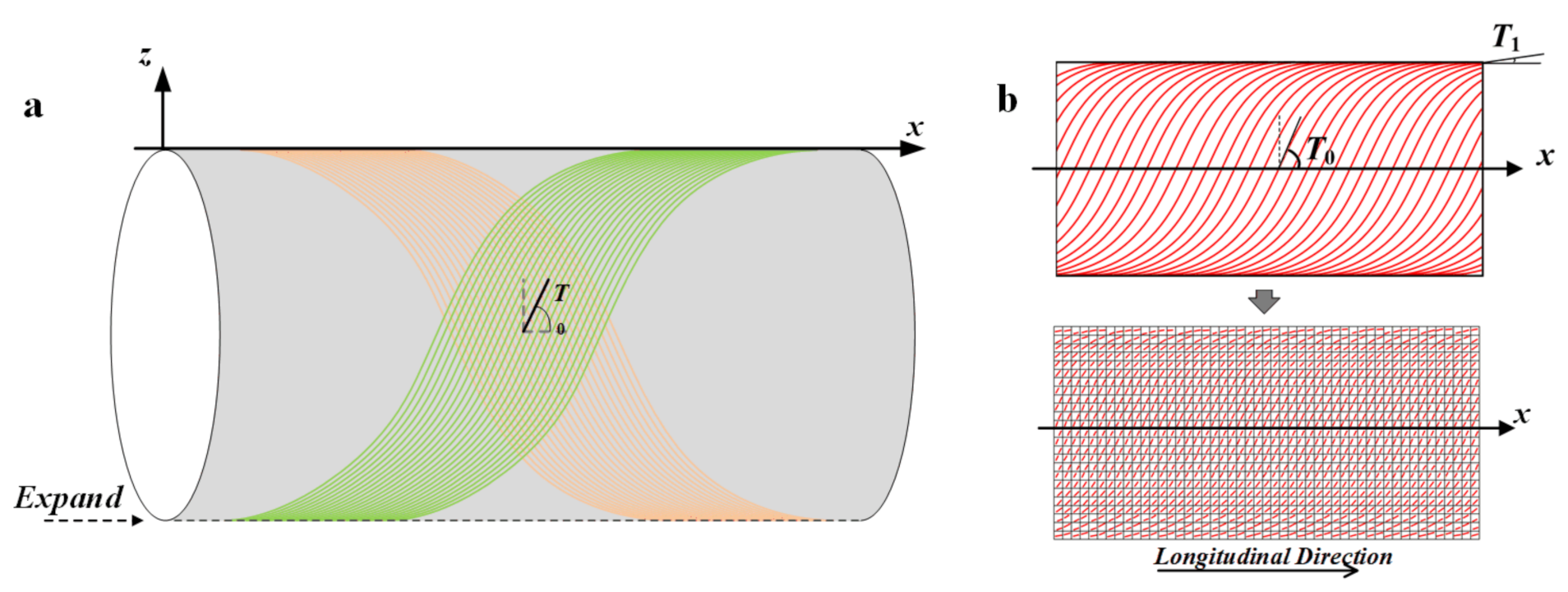
3.1. The DFE Method Based on the Fiber Path Function
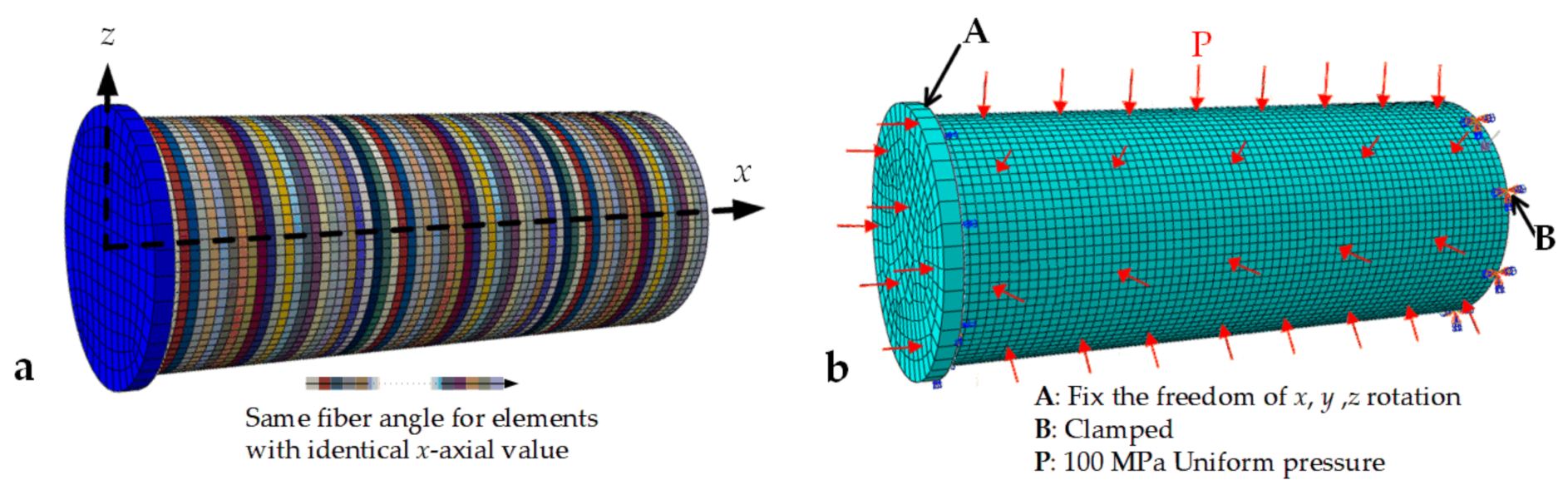
3.2. The DFE Simulation Model with Defects
3.3. The RBF Surrogate Model
4. Model Validation
4.1. The Validation of DFE Simulation Model
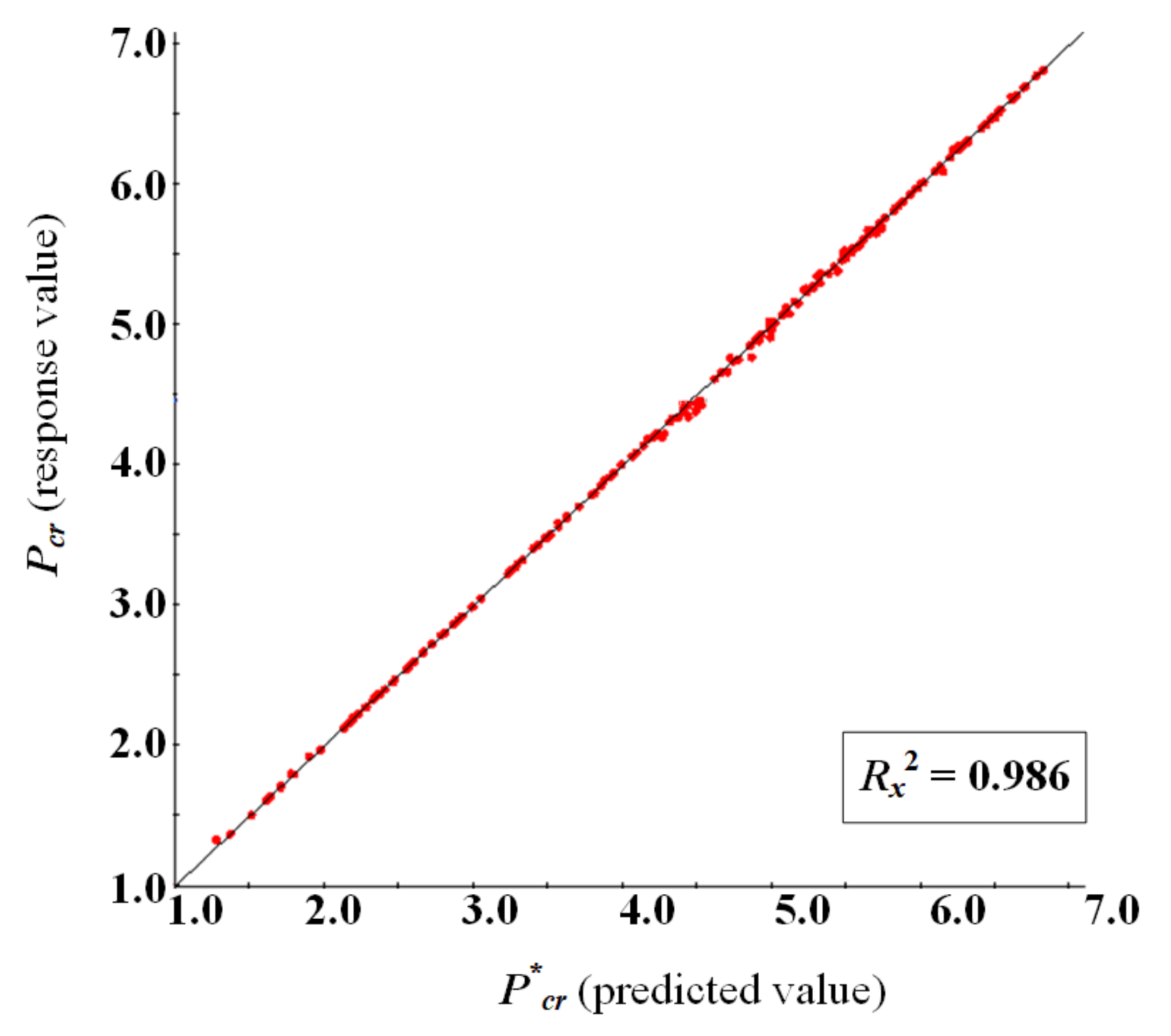
4.2. Surrogate Model Error Analysis
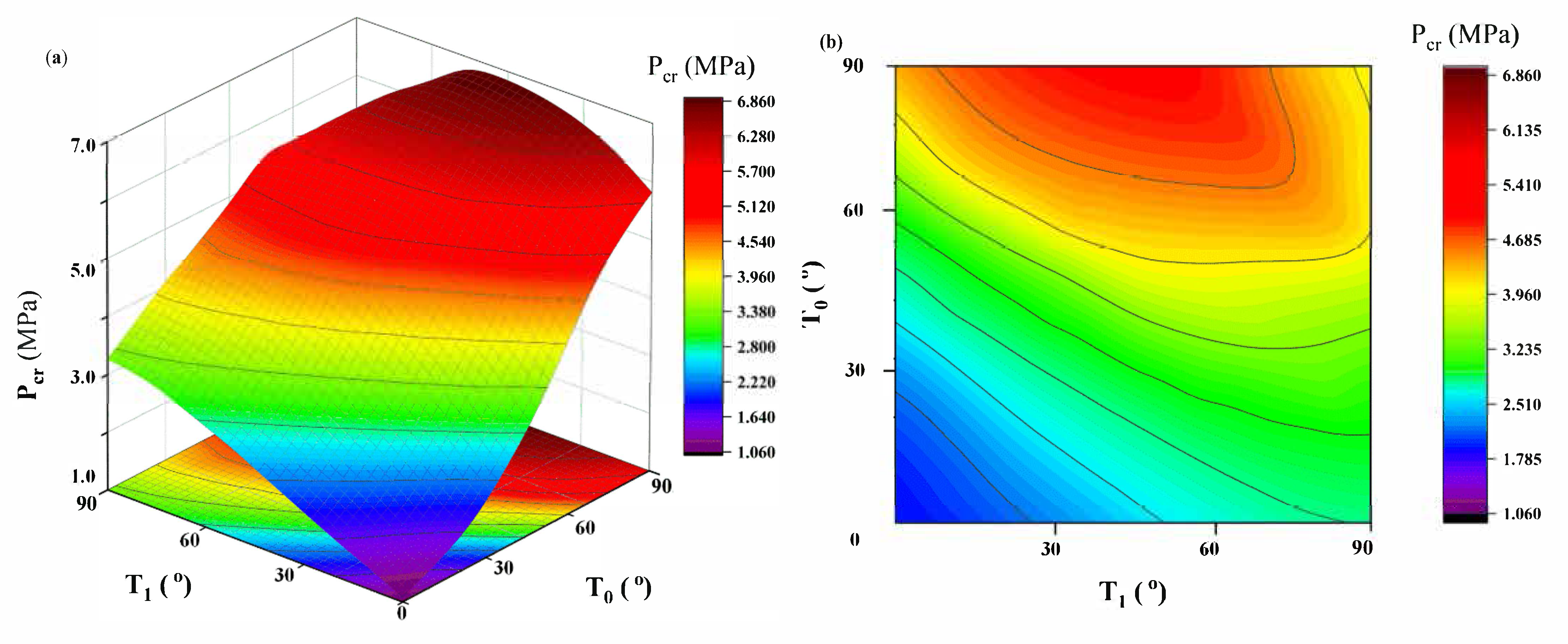
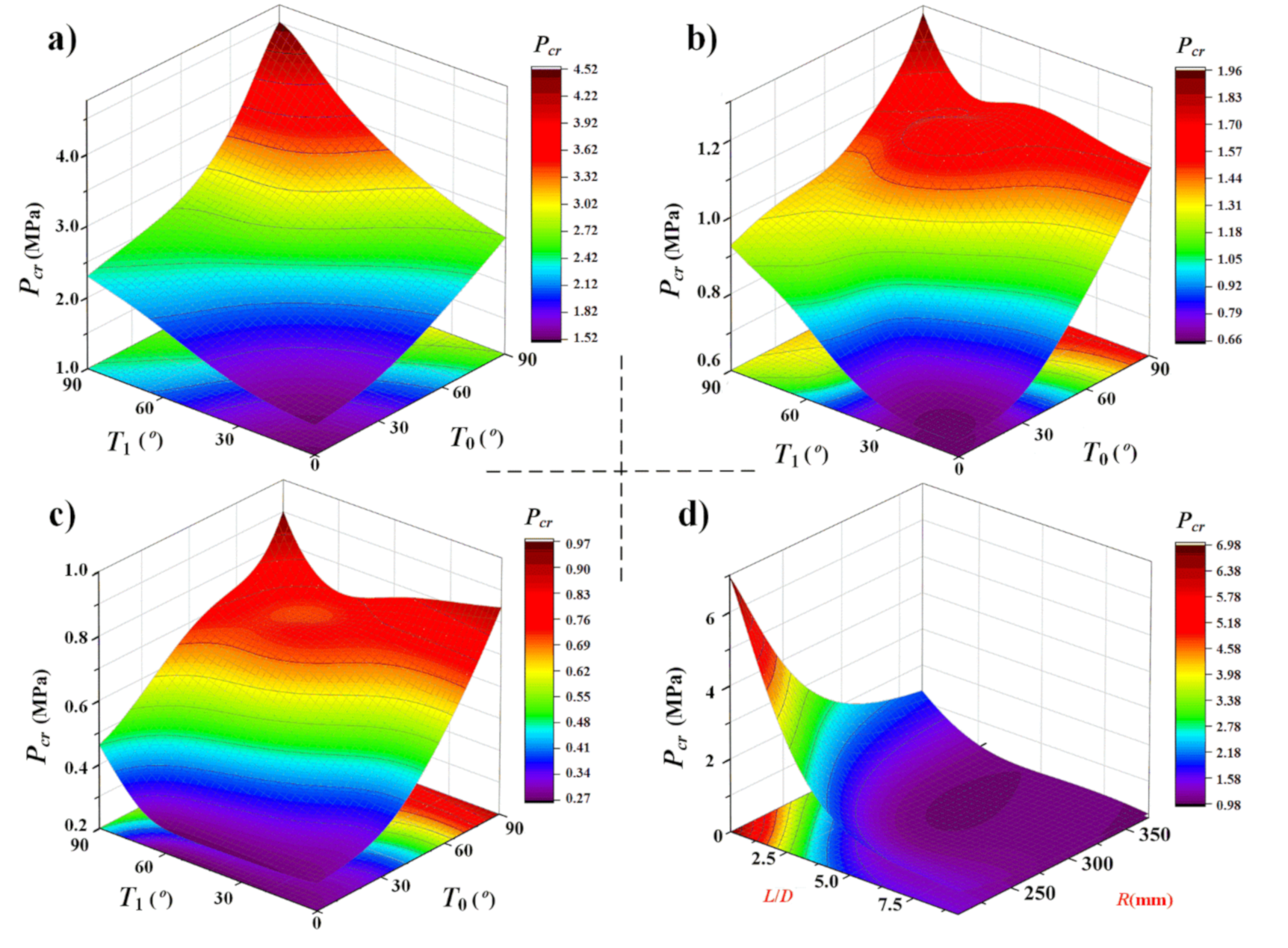
5. Results and Discussions
6. Conclusions
- The VS simulation model based on the DFE with the LVFP function can accurately describe the critical buckling pressure for the VS cylindrical shell with the defects under the combination compression.
- The proposed design and optimization method has higher efficiency for the critical buckling pressure analysis for the VS cylindrical shell than that for the FEA.
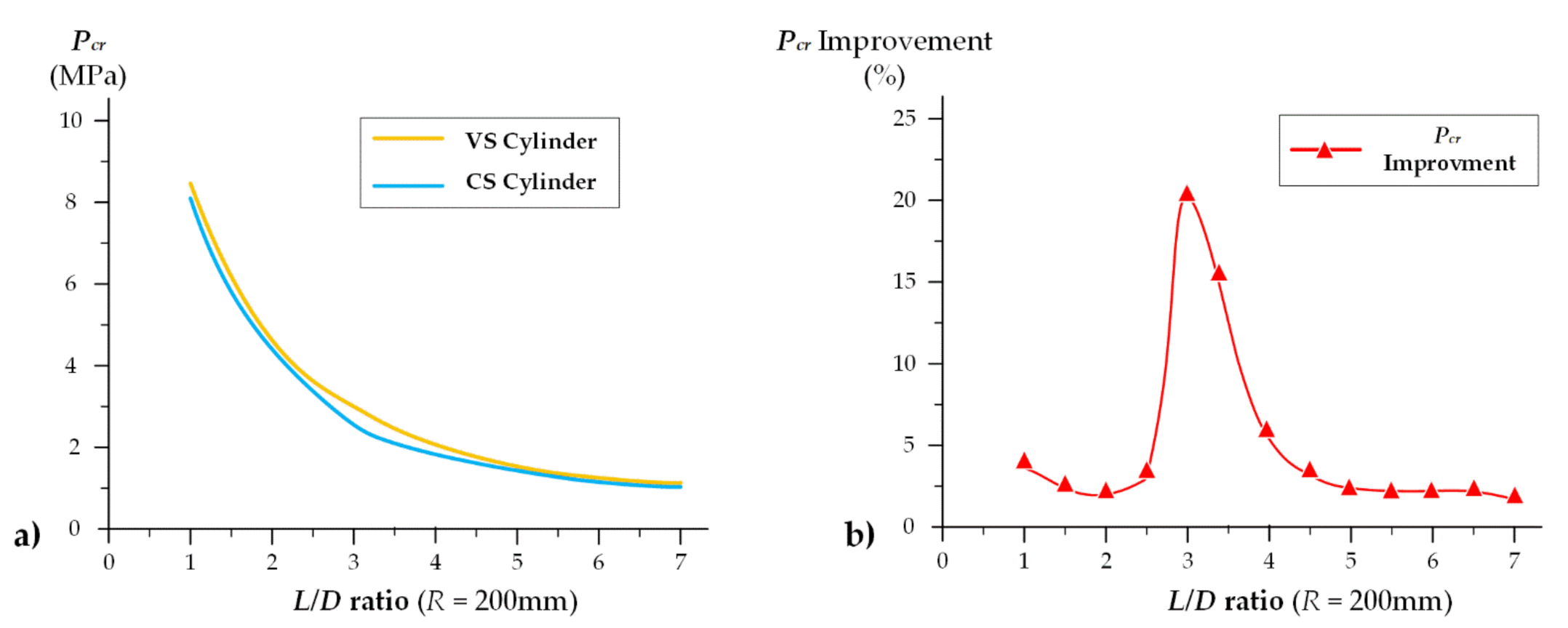
- The optimum Pcr for the VS cylindrical shell can be improved by 21.1% compared with that of the CS cylindrical shell under the same geometry, material properties, and boundary condition. In addition, the maximum improvement of Pcr will occur when the midpoint fiber angle is close to 90° and the L/D ratio is around 3.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hur, S.-H.; Son, H.-J.; Kweon, J.-H.; Choi, J.-H. Postbuckling of composite cylinders under external hydrostatic pressure. Compos. Struct. 2008, 86, 114–124. [Google Scholar] [CrossRef]
- Khani, A.; Abdalla, M.; Gurdal, Z. Optimum tailoring of fibre-steered longitudinally stiffened cylinders. Compos. Struct. 2015, 122, 343–351. [Google Scholar] [CrossRef]
- Prasanna, A.B.; Raju, K.S.; Ramji, K.; Satish, P. Free Vibration, Buckling and Design Optimisation of Composite Pressure Hulls. Mater. Today Proc. 2017, 4, 7381–7387. [Google Scholar] [CrossRef]
- Craven, R.; Graham, D.; Dalzel-Job, J. Conceptual design of a composite pressure hull. Ocean Eng. 2016, 128, 153–162. [Google Scholar] [CrossRef]
- Li, B.; Pang, Y.; Zhu, X.; Cheng, Y. 6σ Optimization Design of Ring-stiffened Composite Pressure Hull of Underwater Vehicle. Acta Armamentarii 2018, 39, 1172–1177. [Google Scholar]
- A. Luersen, M.; A. Steeves, C.; Nair, P.B. Curved fiber paths optimization of a composite cylindrical shell via Kriging-based approach. J. Compos. Mater. 2015, 49, 3583–3597. [Google Scholar] [CrossRef]
- Chen, X.; Wu, Z.; Nie, G.; Weaver, P. Buckling analysis of variable angle tow composite plates with a through-the-width or an embedded rectangular delamination. Int. J. Solids Struct. 2018, 138, 166–180. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Pang, Y.; Yang, Z. Research on Composite Material Pressure Hulls Based on Approximation. Ship Eng. 2015, 37, 74–78. [Google Scholar]
- Huang, G.; Wang, H.; Li, G. An efficient reanalysis assisted optimization for variable-stiffness composite design by using path functions. Compos. Struct. 2016, 153, 409–420. [Google Scholar] [CrossRef]
- Almeida, J.H.S.; Bittrich, L.; Jansen, E.; Tita, V.; Spickenheuer, A. Buckling optimization of composite cylinders for axial compression: A design methodology considering a variable-axial fiber layout. Compos. Struct. 2019, 222, 110928. [Google Scholar] [CrossRef]
- Peeters, D.M.; Hesse, S.; Abdalla, M.M. Stacking sequence optimisation of variable stiffness laminates with manufacturing constraints. Compos. Struct. 2015, 125, 596–604. [Google Scholar] [CrossRef]
- Peeters, D.; Abdalla, M. Design Guidelines in Nonconventional Composite Laminate Optimization. J. Aircr. 2017, 54, 1454–1464. [Google Scholar] [CrossRef] [Green Version]
- Liang, C.-C.; Chen, H.-W.; Jen, C.-Y. Optimum design of filament-wound multilayer-sandwich submersible pressure hulls. Ocean Eng. 2003, 30, 1941–1967. [Google Scholar] [CrossRef]
- Lee, G.-C.; Kweon, J.-H.; Choi, J.-H. Optimization of composite sandwich cylinders for underwater vehicle application. Compos. Struct. 2013, 96, 691–697. [Google Scholar] [CrossRef]
- Blom, A.W.; Stickler, P.B.; Gürdal, Z. Optimization of a composite cylinder under bending by tailoring stiffness properties in circumferential direction. Compos. Part B Eng. 2010, 41, 157–165. [Google Scholar] [CrossRef]
- Almeida, J.H.S.; Ribeiro, M.L.; Tita, V.; Amico, S. Damage and failure in carbon/epoxy filament wound composite tubes under external pressure: Experimental and numerical approaches. Mater. Des. 2016, 96, 431–438. [Google Scholar] [CrossRef]
- Almeida, J.H.S.; Tonatto, M.L.; Ribeiro, M.L.; Tita, V.; Amico, S. Buckling and post-buckling of filament wound composite tubes under axial compression: Linear, nonlinear, damage and experimental analyses. Compos. Part B Eng. 2018, 149, 227–239. [Google Scholar] [CrossRef]
- Tyazhel’Nikov, V.V.; Semenkov, V.E.; Ryabkov, V.A.; Stambul’Chik, M.A.; Bogorodskii, A.A. Improving the quality of wheel-tire steel by optimizing the addition of complex titanium-bearing deoxidizers. Compos. Struct. 1988, 32, 270–271. [Google Scholar] [CrossRef]
- Hu, J.; Sundararaman, S.; Menta, V.G.K.; Chandrashekhara, K.; Chernicoff, W. Failure Pressure Prediction of Composite Cylinders for Hydrogen Storage Using Thermo-mechanical Analysis and Neural Network. Adv. Compos. Mater. 2009, 18, 233–249. [Google Scholar] [CrossRef]
- Nik, M.A.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Surrogate-based multi-objective optimization of a composite laminate with curvilinear fibers. Compos. Struct. 2012, 94, 2306–2313. [Google Scholar] [CrossRef] [Green Version]
- Almeida, J.H.S.; Ribeiro, M.L.; Tita, V.; Amico, S. Stacking sequence optimization in composite tubes under internal pressure based on genetic algorithm accounting for progressive damage. Compos. Struct. 2017, 178, 20–26. [Google Scholar] [CrossRef]
- Hao, P.; Wang, B.; Li, G. Surrogate-Based Optimum Design for Stiffened Shells with Adaptive Sampling. AIAA J. 2012, 50, 2389–2407. [Google Scholar] [CrossRef]
- Hao, P.; Wang, B.; Li, G.; Tian, K.; Du, K.; Wang, X.; Tang, X. Surrogate-based optimization of stiffened shells including load-carrying capacity and imperfection sensitivity. Thin Walled Struct. 2013, 72, 164–174. [Google Scholar] [CrossRef]
- Rouhi, M.; Ghayoor, H.; Fortin-Simpson, J.; Zacchia, T.T.; Hoa, S.V.; Hojjati, M. Design, manufacturing, and testing of a variable stiffness composite cylinder. Compos. Struct. 2018, 184, 146–152. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Almeida, J.H.S., Jr.; St-Pierre, L.; Wang, Z.; Castro, S.G. Reliability-based buckling optimization with an accelerated Kriging metamodel for filament-wound variable angle tow composite cylinders. Compos. Struct. 2020, 254, 112821. [Google Scholar] [CrossRef]
- Labans, E.; Bisagni, C. Buckling and free vibration study of variable and constant-stiffness cylindrical shells. Compos. Struct. 2019, 210, 446–457. [Google Scholar] [CrossRef]
- Shen, K.; Pan, G.; Shi, Y. Optimization of Composites Shell Subjected to Hydrostatic Pressure to Maximize Design Pressure Factor. J. Ship Mech. 2017, 21, 1552–1563. [Google Scholar] [CrossRef]
- Wei, R.; Pan, G.; Jiang, J.; Shen, K.; Lyu, D. An efficient approach for stacking sequence optimization of symmetrical laminated composite cylindrical shells based on a genetic algorithm. Thin Walled Struct. 2019, 142, 160–170. [Google Scholar] [CrossRef]
- Chun, S.K.; Guang, P. Optimizing the buckling strength of filament winding composite cylinders under hydrostatic pressure. J. Reinf. Plast. Compos. 2018, 37, 892–904. [Google Scholar] [CrossRef]
- László, P.K.; George, S.S. Mechanics of Composite Structures; Cambridge University Press: Cambridge, UK, 2003; pp. 68–83. [Google Scholar]
- Gürdal, Z.; Tatting, B.; Wu, C. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Honda, S.; Narita, Y. Vibration design of laminated fibrous composite plates with local anisotropy induced by short fibers and curvilinear fibers. Compos. Struct. 2011, 93, 902–910. [Google Scholar] [CrossRef] [Green Version]
- Blom, A.W.; Tatting, B.F.; Hol, J.M.; Gürdal, Z. Fiber path definitions for elastically tailored conical shells. Compos. Part B Eng. 2009, 40, 77–84. [Google Scholar] [CrossRef]
- Brampton, C.J.; Wu, K.C.; Kim, H.A. New optimization method for steered fiber composites using the level set method. Struct. Multidiscip. Optim. 2015, 52, 493–505. [Google Scholar] [CrossRef]
- Wang, H.; Li, Q.; Li, G. Review on Structure Design and Uncertainty Analysis of Variables Stiffness Composites. Chin. J. Mech. Eng. 2019, 55, 46–55. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.Q.; Zhang, S.J.; XU, Z.Y. The Buckling of Variable-Stiffness Composite Panels with Curvilinear Fiber Format. J. Reinf. Plast. Compos. 2009, 5, 31–35. [Google Scholar] [CrossRef]
- Nopour, H.; Ataabadi, A.K.; Shokrieh, M.M. Correction to: Fiber Path Optimization in a Variable-Stifness Cylinder to Maximize Its Buckling Load Under External Hydrostatic Pressure. Mech. Compos. Mater. 2019, 55, 139. [Google Scholar] [CrossRef] [Green Version]
- Song, B.; Lyu, D.; Jiang, J. Optimization of composite ring stiffened cylindrical hulls for unmanned underwater vehicles using multi-island genetic algorithm. J. Reinf. Plast. Compos. 2018, 37, 668–684. [Google Scholar] [CrossRef]




| (a) Axial Compression | |||||||||
| Material Properties | Elastic Modulus | Shear Modulus | Poisson Ratio | Tensile Strength | Compress Strength | Shear Strength | |||
| Symbol | E11 | E12 | G12 | μ12 | Xt | Yt | Xc | Yc | S |
| Value | 141 | 10.3 | 4.5 | 0.3 | 1701 | 95.4 | 1163 | 244 | 116.5 |
| Unit | GPa | GPa | GPa | - | MPa | MPa | MPa | MPa | MPa |
| Geometric Parameters | Radius | Length | Layer Thickness | Stacking Sequence | |||||
| Value | 300 | 790 | 0.181 | [± 45°/± <15°/60°>]s | |||||
| Unit | mm | mm | mm | degree | |||||
| (b) Lateral Compression | |||||||||
| Material Properties | Elastic Modulus | Shear Modulus | Poisson Ratio | Tensile Strength | Compress Strength | Shear Strength | |||
| Symbol | E11 | E12 | G12 | μ12 | Xt | Yt | Xc | Yc | S |
| Value | 147 | 9 | 5 | 0.3 | 2004 | 53 | 1197 | 204 | 137 |
| Unit | GPa | GPa | GPa | - | MPa | MPa | MPa | MPa | MPa |
| Geometric Parameters | Radius | Length | Layer Thickness | Stacking Sequence | |||||
| Value | 250 | 1250 | 0.146 | [± <90°/75°>]12s | |||||
| Unit | mm | mm | mm | degree | |||||
| L/D | Pcr (MPa) | ||||
|---|---|---|---|---|---|
| R = 200 mm | R = 250 mm | R = 300 mm | Defect Consideration, R = 350 mm | ||
| With Overlap Only | With Overlap and Geometric Defect | ||||
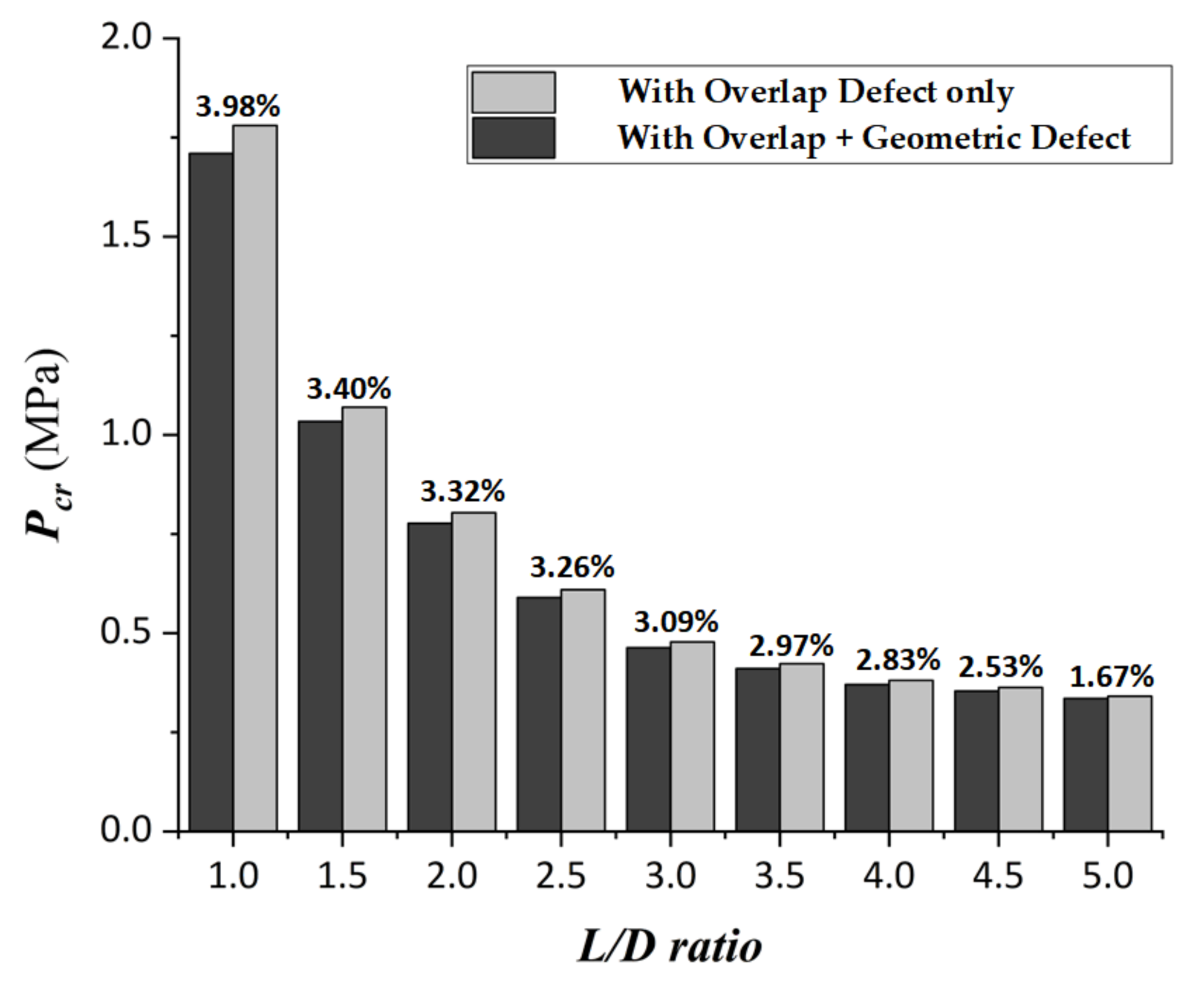
| 1.0 | 7.3317 | 3.7901 | 2.3885 | 1.7808 | 1.7098 |
| 1.5 | 4.4271 | 2.4903 | 1.5328 | 1.0703 | 1.0339 |
| 2.0 | 3.0784 | 1.8858 | 1.2837 | 0.8037 | 0.7770 |
| 2.5 | 2.3511 | 1.2987 | 0.8378 | 0.6097 | 0.5898 |
| 3.0 | 2.0716 | 1.1194 | 0.6952 | 0.4781 | 0.4633 |
| 3.5 | 1.9117 | 1.0234 | 0.6261 | 0.4231 | 0.4105 |
| 4.0 | 1.4803 | 0.9486 | 0.5745 | 0.3811 | 0.3703 |
| 4.5 | 1.1914 | 0.7433 | 0.5328 | 0.3632 | 0.3540 |
| 5.0 | 1.0519 | 0.5714 | 0.4561 | 0.3413 | 0.3356 |
| L/D | VS Cylindrical Shell | CS Cylindrical Shell | Pcr Improvement (%) | ||
|---|---|---|---|---|---|
| Optimum Fiber Angle (Degree) | Optimum Pcr (MPa) | Optimum Fiber Angle (Degree) | Optimum Pcr (MPa) | ||
| 1.0 | ± <89/48>12s | 8.5362 | ± [80]12s | 8.1901 | 4.2 |
| 1.5 | ± <89/27>12s | 5.7778 | ± [79]12s | 5.4011 | 6.9 |
| 2.0 | ± <86/79>12s | 4.5174 | ± [89]12s | 4.4265 | 2.1 |
| 2.5 | ± <80/75>12s | 3.9861 | ± [73]12s | 3.7510 | 6.3 |
| 3.0 | ± <87/31>12s | 3.1214 | ± [78]12s | 2.5786 | 21.1 |
| 3.5 | ± <88/45>12s | 2.4590 | ± [84]12s | 2.1138 | 16.3 |
| 4.0 | ± <89/51>12s | 2.0091 | ± [89]12s | 1.9009 | 5.7 |
| 4.5 | ± <89/85>12s | 1.8358 | ± [89]12s | 1.7833 | 2.9 |
| 5.0 | ± <89/87>12s | 1.7595 | ± [89]12s | 1.7126 | 2.3 |
| 5.5 | ± <89/87>12s | 1.7067 | ± [89]12s | 1.6683 | 2.3 |
| 6.0 | ± <89/86>12s | 1.6791 | ± [89]12s | 1.6388 | 2.5 |
| 6.5 | ± <88/82>12s | 1.6451 | ± [89]12s | 1.6167 | 1.8 |
| 7.0 | ± <88/82>12s | 1.6223 | ± [89]12s | 1.6026 | 1.2 |
| L/D (R = 200 mm) | Calculation Time (s) | Pcr Value (MPa) | |||
|---|---|---|---|---|---|
| FE | RBF | FE | RBF | Pcr Error (%) | |
| 2.0 | 13.1 | 0.9 | 3.2923 | 3.0869 | 6.2 |
| 2.5 | 13.2 | 0.9 | 2.1350 | 2.2449 | 5.1 |
| 3.0 | 13.6 | 0.8 | 1.8861 | 1.9031 | 0.9 |
| 3.5 | 14.7 | 0.9 | 1.6500 | 1.7151 | 3.9 |
| 4.0 | 17.8 | 1.0 | 1.6235 | 1.5547 | 4.2 |
| 4.5 | 19.1 | 1.0 | 1.4115 | 1.4019 | 0.7 |
| 5.0 | 21.7 | 0.9 | 1.1626 | 1.1347 | 2.4 |
| 5.5 | 22.0 | 0.8 | 0.9148 | 0.9707 | 6.1 |
| 6.0 | 24.1 | 1.0 | 0.8363 | 0.7869 | 5.9 |
| 6.5 | 24.9 | 0.9 | 0.7611 | 0.7153 | 6.0 |
| 7.0 | 26.0 | 0.8 | 0.7265 | 0.6877 | 5.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Cao, Y.; Liu, J. A Buckling Analysis and Optimization Method for a Variable Stiffness Cylindrical Pressure Shell of AUV. J. Mar. Sci. Eng. 2021, 9, 637. https://doi.org/10.3390/jmse9060637
Yang Z, Cao Y, Liu J. A Buckling Analysis and Optimization Method for a Variable Stiffness Cylindrical Pressure Shell of AUV. Journal of Marine Science and Engineering. 2021; 9(6):637. https://doi.org/10.3390/jmse9060637
Chicago/Turabian StyleYang, Zhaoqi, Yonghui Cao, and Jing Liu. 2021. "A Buckling Analysis and Optimization Method for a Variable Stiffness Cylindrical Pressure Shell of AUV" Journal of Marine Science and Engineering 9, no. 6: 637. https://doi.org/10.3390/jmse9060637
APA StyleYang, Z., Cao, Y., & Liu, J. (2021). A Buckling Analysis and Optimization Method for a Variable Stiffness Cylindrical Pressure Shell of AUV. Journal of Marine Science and Engineering, 9(6), 637. https://doi.org/10.3390/jmse9060637






