The Impact of Fortnightly Stratification Variability on the Generation of Baroclinic Tides in the Luzon Strait
Abstract
:1. Introduction
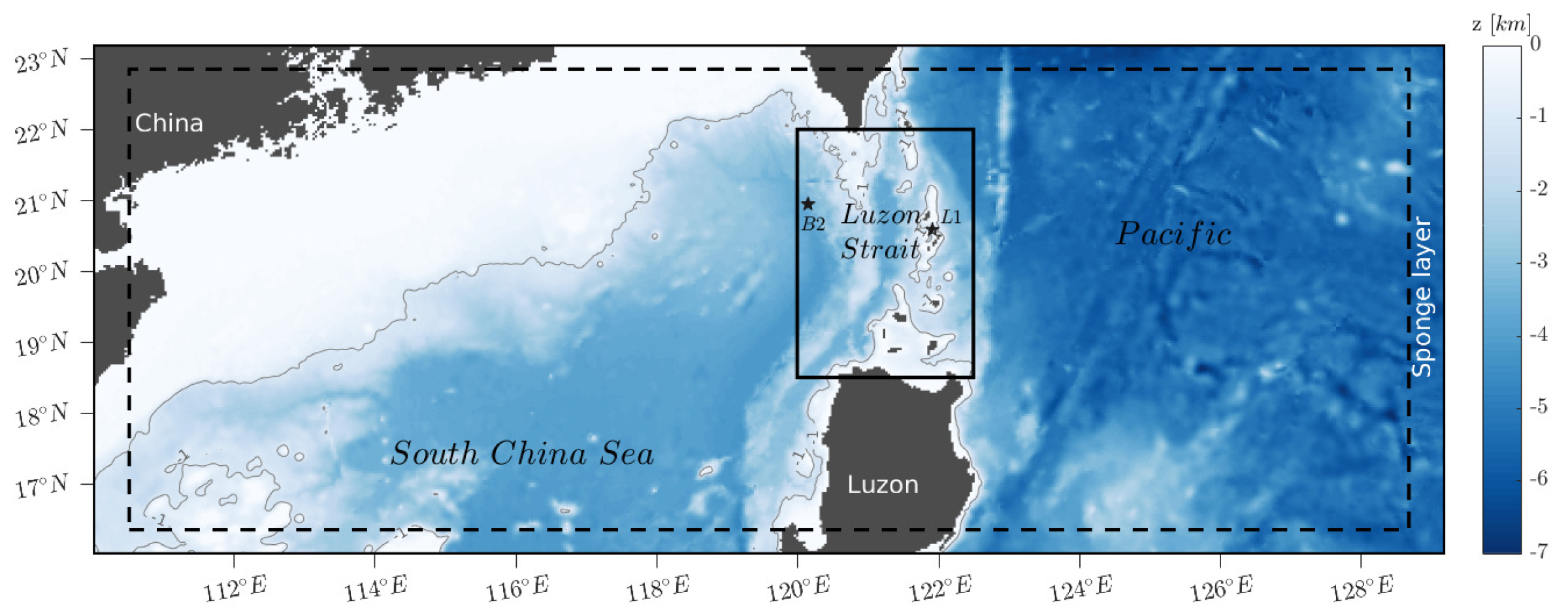
2. Materials and Methods
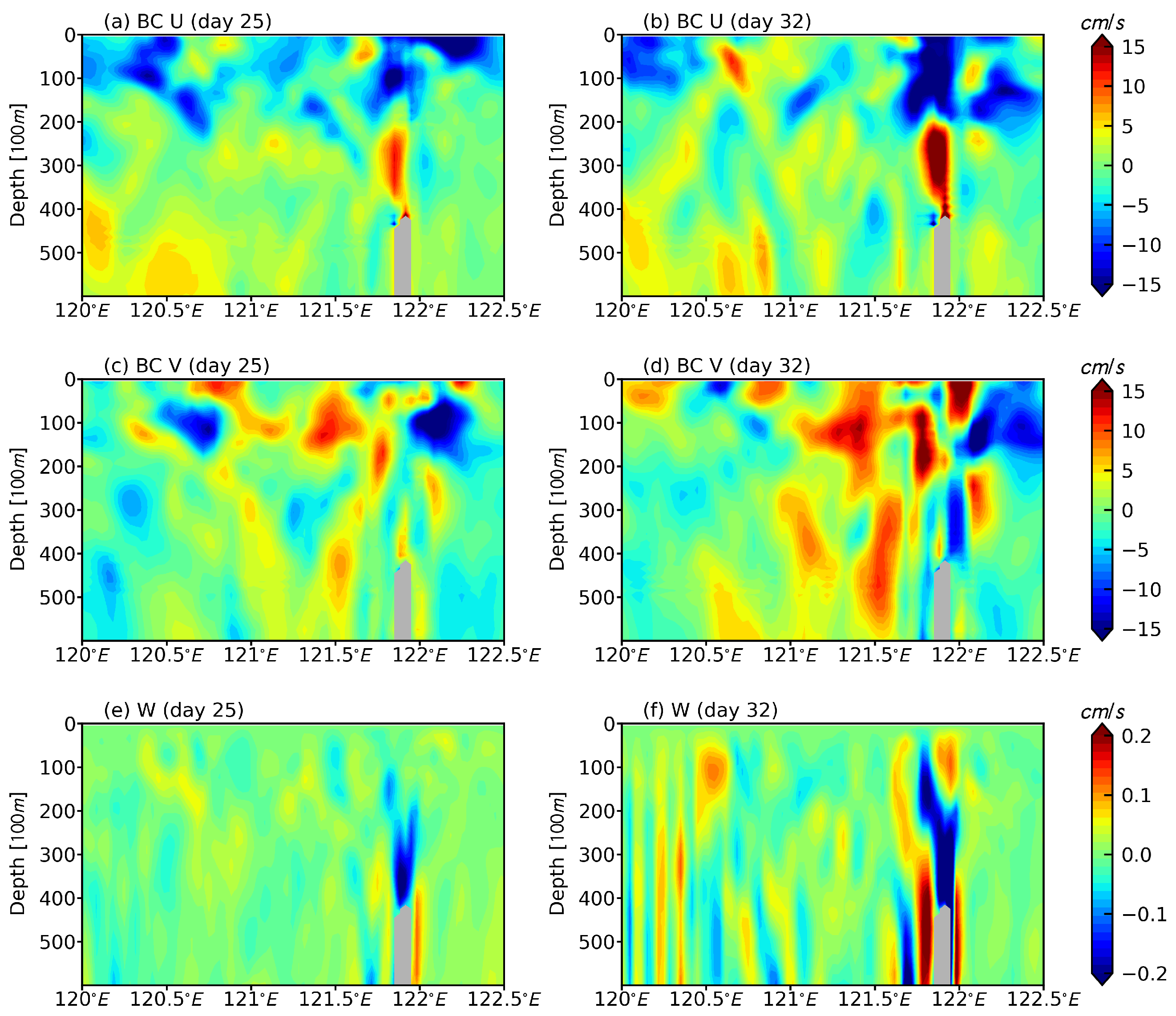
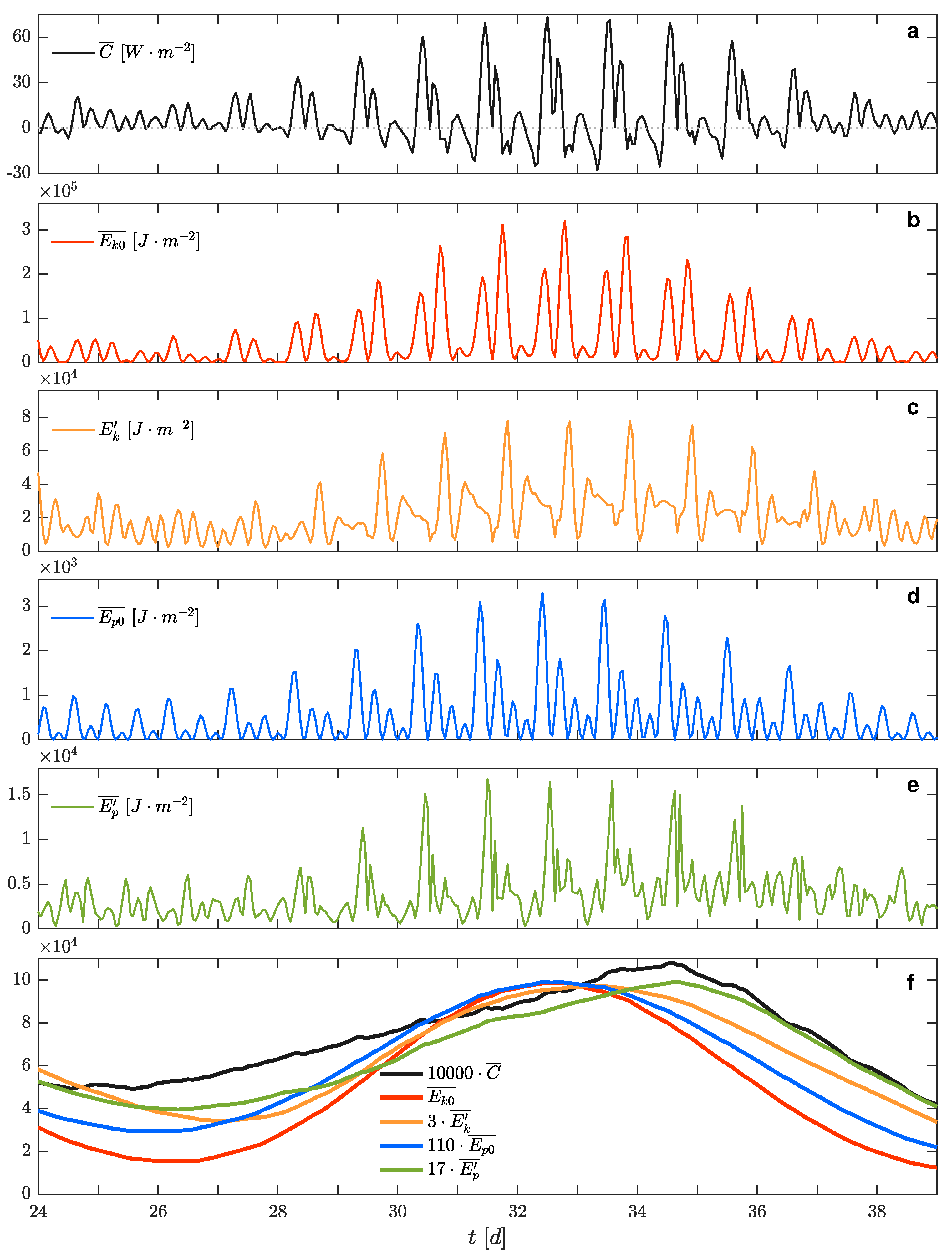
3. Results
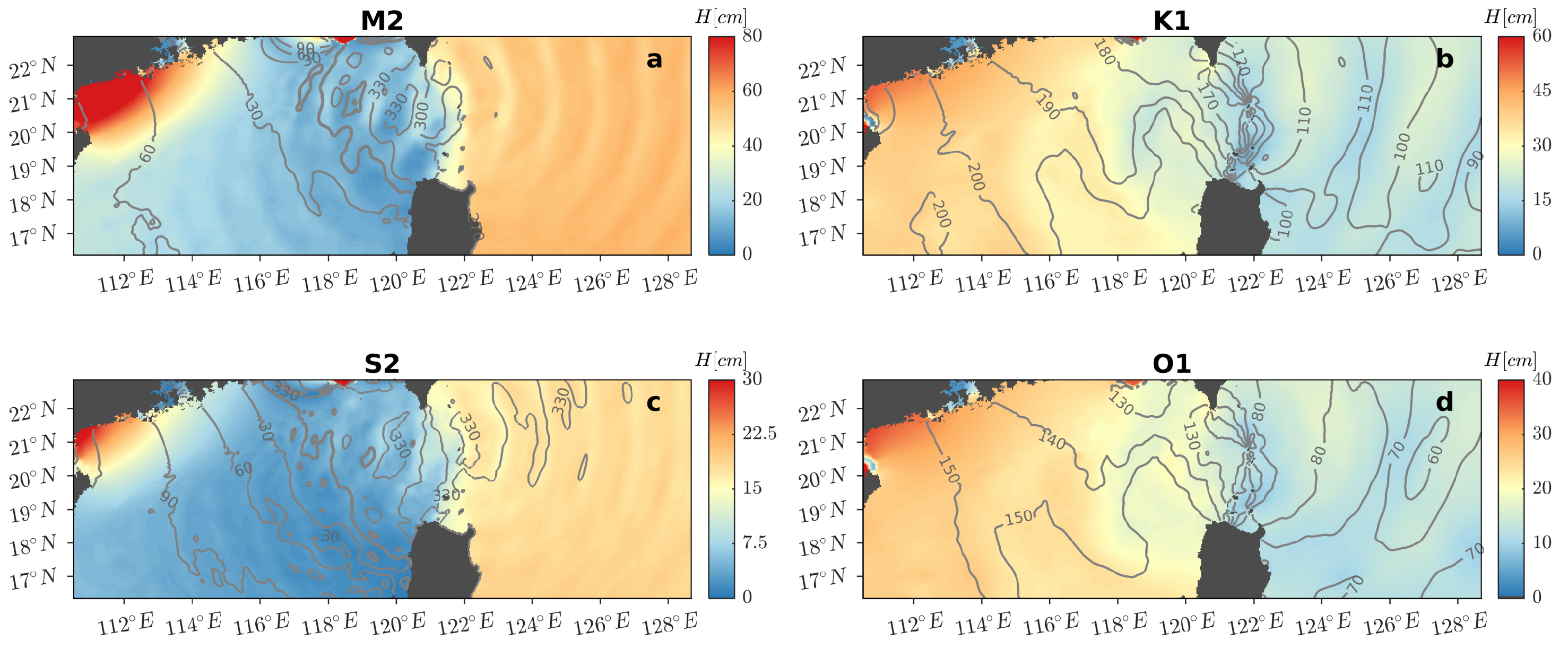
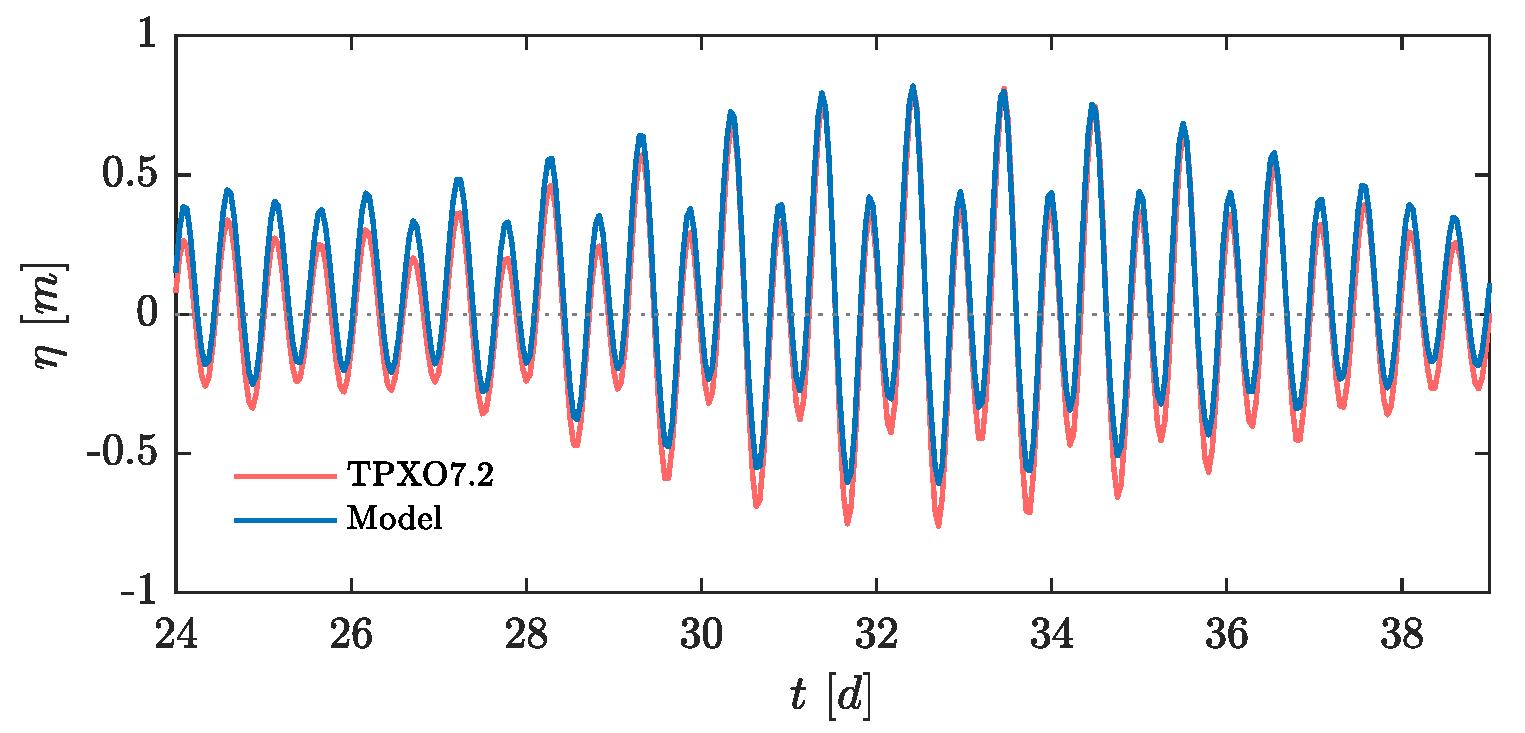
3.1. Model Validation
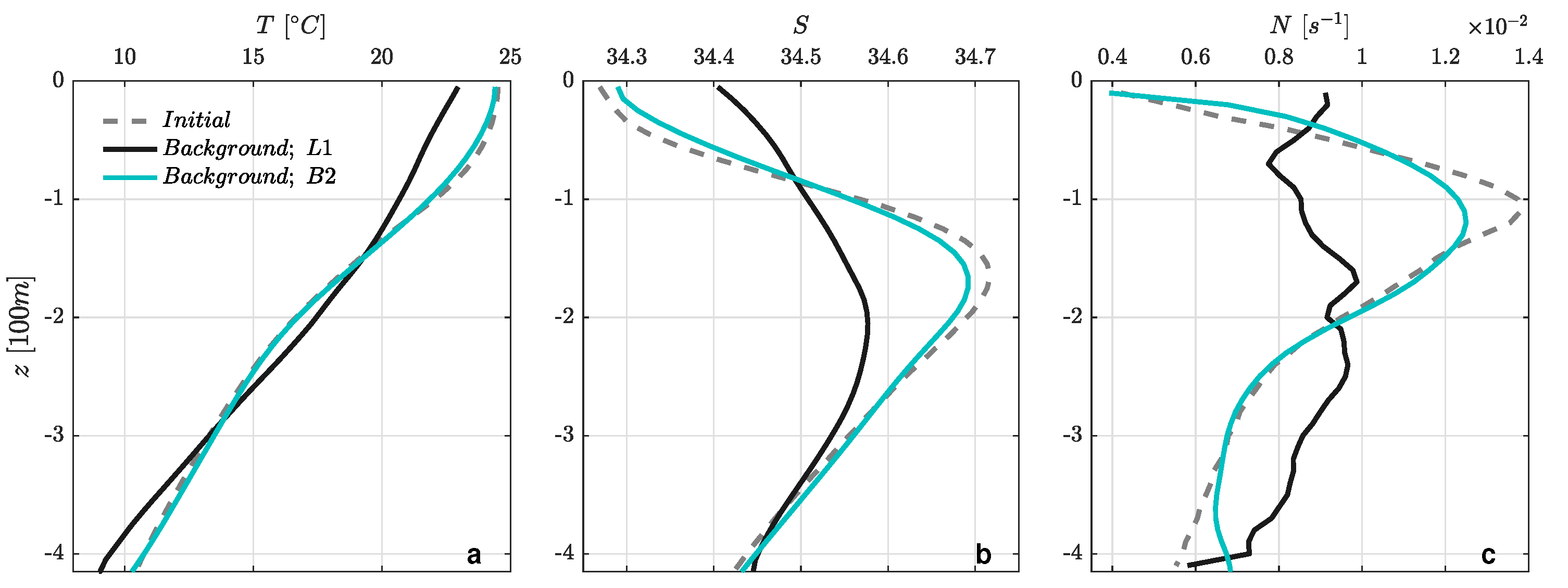
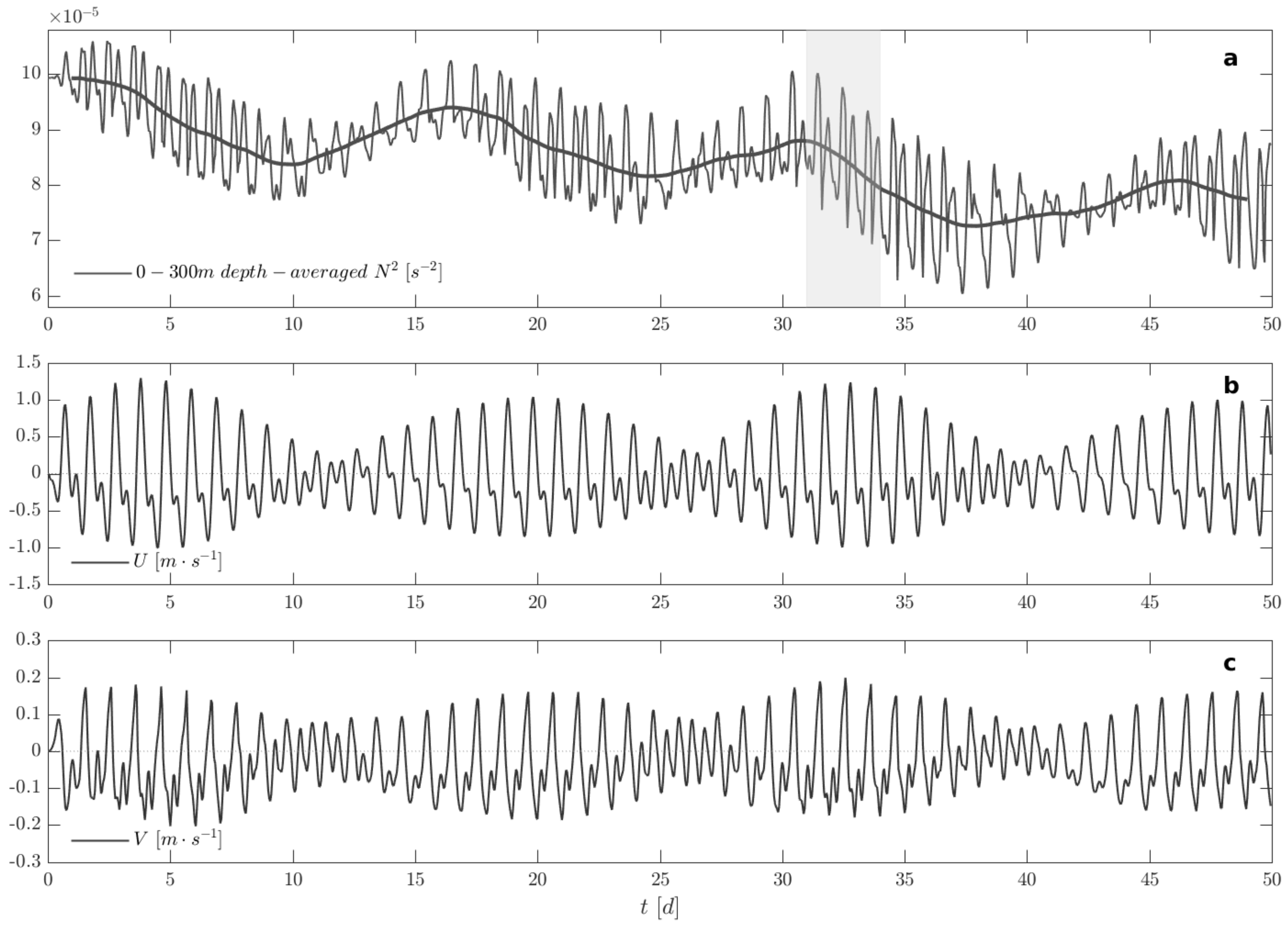
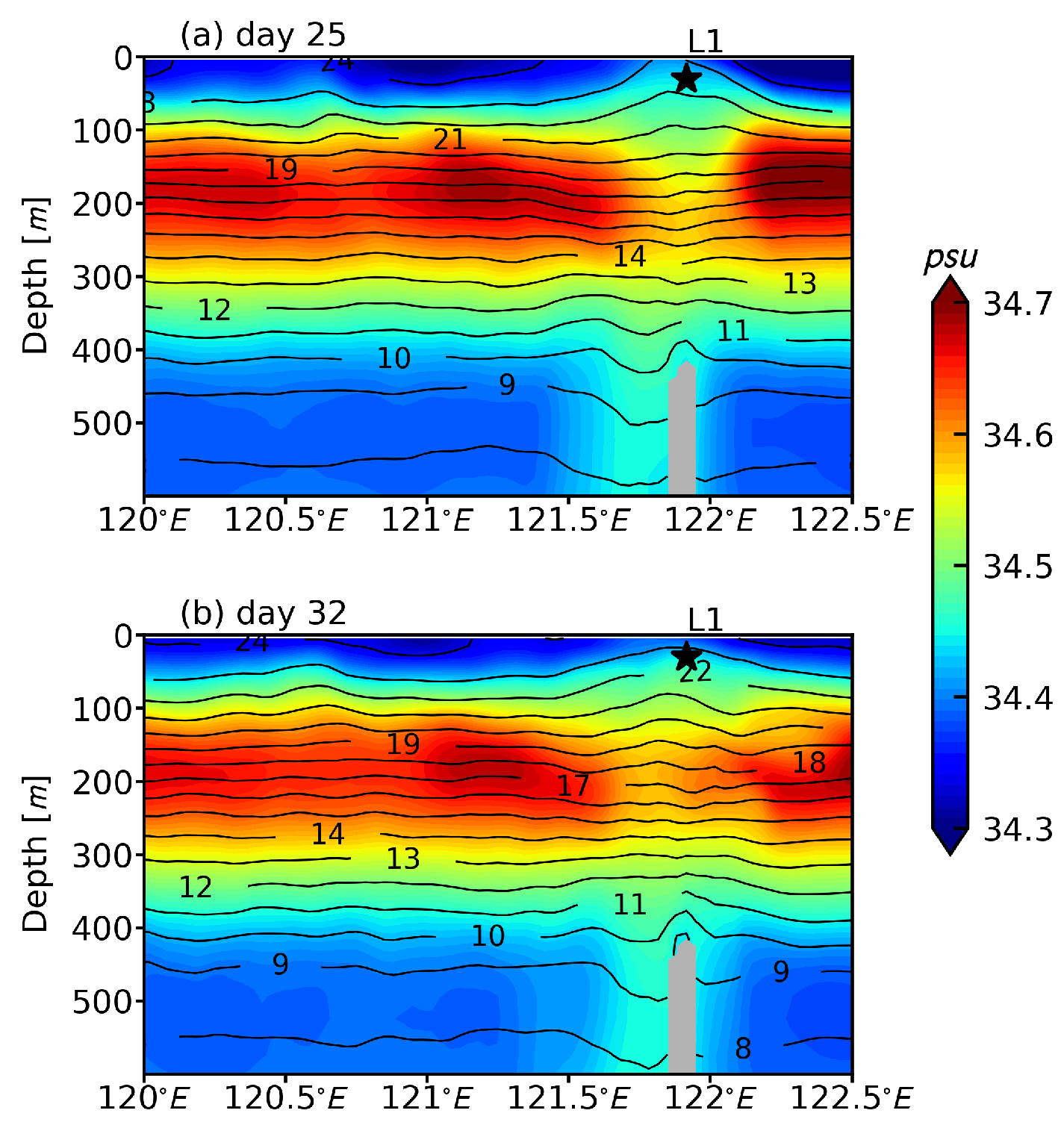
3.2. Stratification Variability
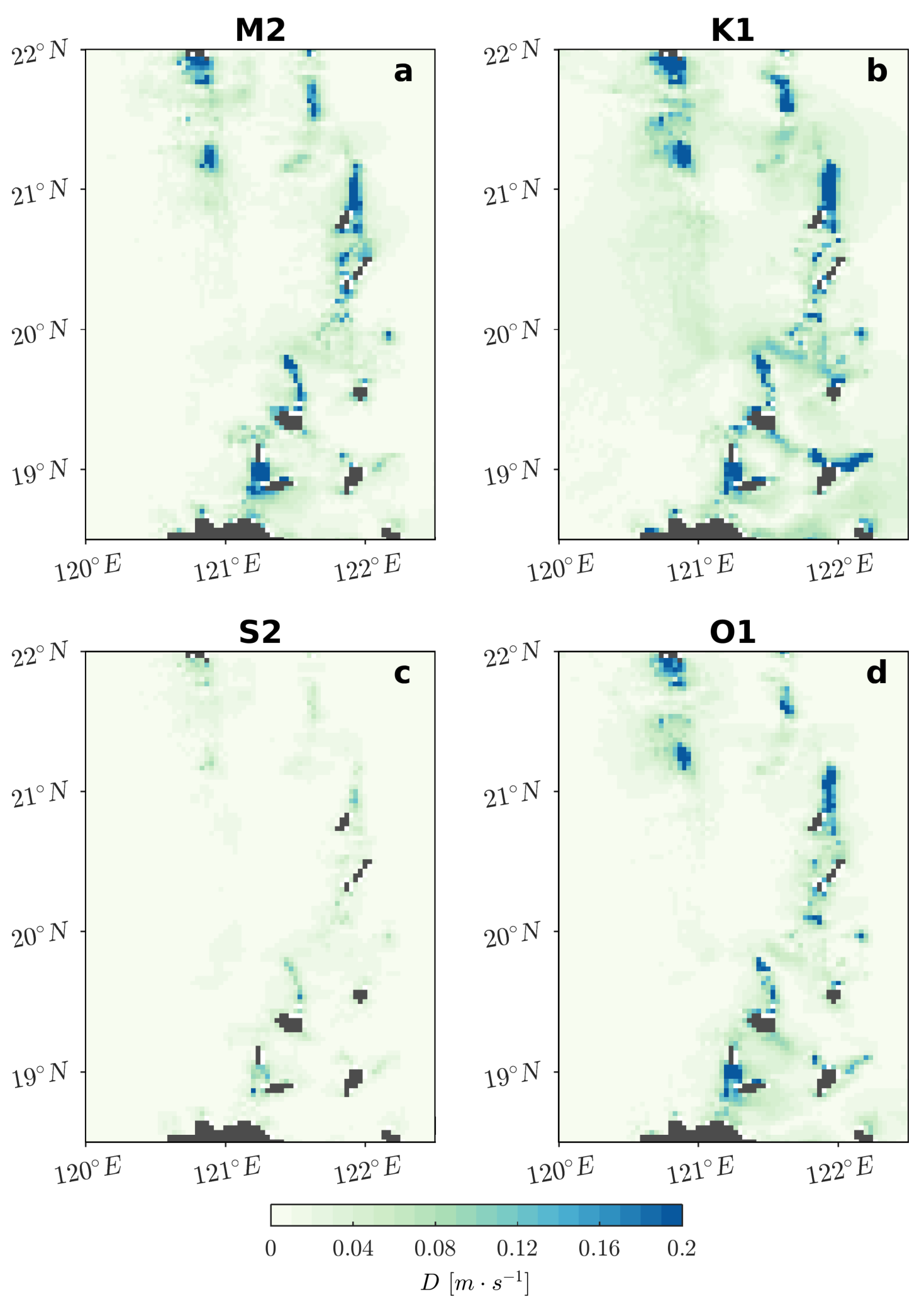
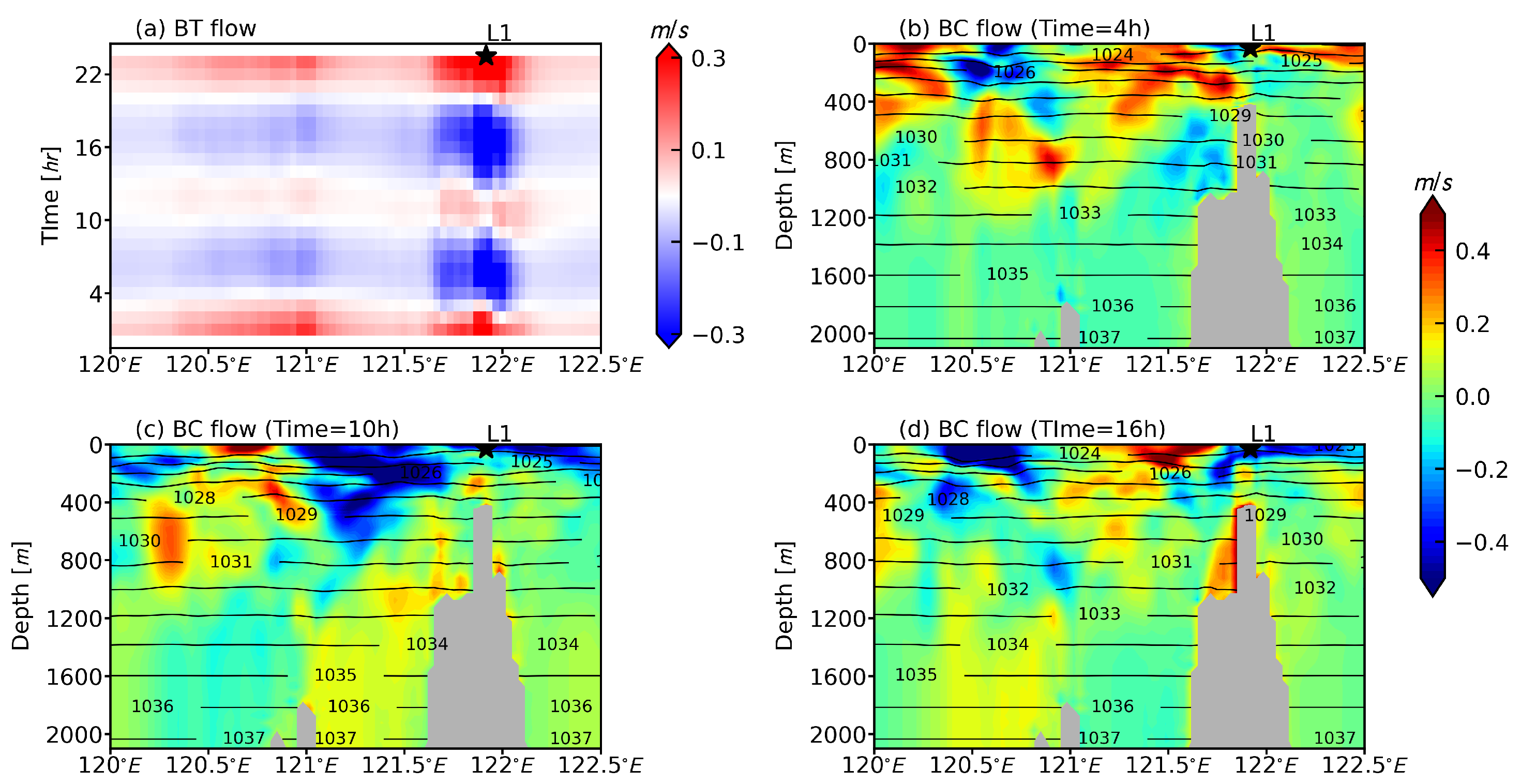
3.3. Energy Transfer
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Egbert, G.D.; Ray, R.D. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 2000, 405, 775–778. [Google Scholar] [CrossRef]
- Laurent, L.S.; Garrett, C. The role of internal tides in mixing the deep ocean. J. Phys. Oceanogr. 2002, 32, 2882–2899. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.H. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 2003, 423, 159–162. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Stephenson, G.; Ansong, J.; Arbic, B.; Green, J.; Richman, J.; Shriver, J.; Vic, C.; Wallcraft, A.; Zhao, Z. On the interplay between horizontal resolution and wave drag and their effect on tidal baroclinic mode waves in realistic global ocean simulations. Ocean Model. 2020, 152, 101656. [Google Scholar] [CrossRef]
- Klymak, J.M.; Pinkel, R.; Liu, C.-T.; Liu, A.K.; David, L. Prototypical solitons in the south china sea. Geophys. Res. Lett. 2006, 33, l11607. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Chen, Z.; Zhao, W.; Zhang, Z.; Zhou, C.; Yang, Q.; Tian, J. An extreme internal solitary wave event observed in the northern south china sea. Sci. Rep. 2016, 6, 30041. [Google Scholar] [CrossRef] [Green Version]
- Niwa, Y.; Hibiya, T. Three-dimensional numerical simulation of m2 internal tides in the east china sea. J. Geophys. Res. Ocean 2004, 109, c04027. [Google Scholar] [CrossRef]
- Zhao, Z.; Klemas, V.; Zheng, Q.; Yan, X.-H. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern south china sea. Geophys. Res. Lett. 2004, 31, l06302. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Alford, M.H. Source and propagation of internal solitary waves in the northeastern south china sea. J. Geophys. Res. Ocean 2006, 111, c11012. [Google Scholar] [CrossRef]
- Jan, S.; Chern, C.-S.; Wang, J.; Chao, S.-Y. Generation of diurnal k1 internal tide in the luzon strait and its influence on surface tide in the south china sea. J. Geophys. Res. Ocean 2007, 112, c06019. [Google Scholar] [CrossRef]
- Alford, M.H.; MacKinnon, J.A.; Nash, J.D.; Simmons, H.; Pickering, A.; Klymak, J.M.; Pinkel, R.; Sun, O.; Rainville, L.; Musgrave, R.; et al. Energy flux and dissipation in luzon strait: Two tales of two ridges. J. Phys. Oceanogr. 2011, 41, 2211–2222. [Google Scholar] [CrossRef]
- Li, Q.; Farmer, D.M. The generation and evolution of nonlinear internal waves in the deep basin of the south china sea. J. Phys. Oceanogr. 2011, 41, 1345–1363. [Google Scholar] [CrossRef]
- Zhang, Z.; Fringer, O.B.; Ramp, S.R. Three-dimensional, nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the south china sea. J. Geophys. Res. Ocean 2011, 116, c05022. [Google Scholar] [CrossRef]
- Guo, C.; Vlasenko, V.; Alpers, W.; Stashchuk, N.; Chen, X. Evidence of short internal waves trailing strong internal solitary waves in the northern south china sea from synthetic aperture radar observations. Remote. Environ. 2012, 124, 542–550. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centuroni, L.R.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Fringer, O.B.; et al. The formation and fate of internal waves in the south china sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef]
- Ramp, S.R.; Yang, Y.J.; Bahr, F.L. Characterizing the nonlinear internal wave climate in the northeastern south china sea. Nonlinear Processes Geophys. 2010, 17, 481–498. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Yin, B.; Hou, Y.; Liu, A.K. Seasonal variability and north–south asymmetry of internal tides in the deep basin west of the luzon strait. J. Mar. Syst. 2014, 134, 101–112. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Kanarska, Y.; McWilliams, J.C. On the generation and evolution of nonlinear internal waves in the south china sea. J. Geophys. Res. Ocean 2010, 115, C02012. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Beardsley, R.C. The generation of long nonlinear internal waves in a weakly stratified shear flow. J. Geophys. Res. 1974, 79, 453–462. [Google Scholar] [CrossRef]
- Maxworthy, T. A note on the internal solitary waves produced by tidal flow over a three-dimensional ridge. J. Geophys. Res. Ocean 1979, 84, 338–346. [Google Scholar] [CrossRef]
- Maxworthy, T. On the formation of nonlinear internal waves from the gravitational collapse of mixed regions in two and three dimensions. J. Fluid Mech. 1980, 96, 47–64. [Google Scholar] [CrossRef]
- Gerkema, T. Internal and interfacial tides: Beam scattering and local generation of solitary waves. J. Mar. Res. 2001, 59, 227–255. [Google Scholar] [CrossRef]
- Jan, S.; Lien, R.-C.; Ting, C.-H. Numerical study of baroclinic tides in luzon strait. J. Oceanogr. 2008, 64, 789–802. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Legg, S.; Klymak, J. Double-ridge internal tide interference and its effect on dissipation in luzon strait. J. Phys. Ocean 2012, 42, 1337–1356. [Google Scholar] [CrossRef]
- Baines, P. On internal tide generation models. Deep. Sea Res. Part Oceanogr. Res. Pap. 1982, 29, 307–338. [Google Scholar] [CrossRef]
- Xing, J.; Davies, A.M. Influence of stratification and topography upon internal wave spectra in the region of sills. Geophys. Res. Lett. 2006, 33, L23606. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A finite-volume, incompressible navier stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Ocean 1997, 102, 5753–5766. [Google Scholar] [CrossRef] [Green Version]
- Large, W.G.; McWilliams, J.C.; Doney, S.C. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef] [Green Version]
- Fang, G. Tide and tidal current charts for the marginal seas adjacent to china. Chin. J. Oceanol. Limnol. 1986, 4, 1–16. [Google Scholar]
- Zu, T.; Gan, J.; Erofeeva, S.Y. Numerical study of the tide and tidal dynamics in the south china sea. Deep. Sea Res. Part Oceanogr. Res. Pap. 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Li, M.; Hou, Y.; Li, Y.; Hu, P. Energetics and temporal variability of internal tides in luzon strait: A nonhydrostatic numerical simulation. Chin. J. Oceanol. Limnol. 2012, 30, 852–867. [Google Scholar] [CrossRef]
- Ray, R.D.; Mitchum, G.T. Surface manifestation of internal tides generated near hawaii. Geophys. Res. Lett. 1996, 23, 2101–2104. [Google Scholar] [CrossRef]
- Cummins, P.F.; Oey, L.-Y. Simulation of barotropic and baroclinic tides off northern british columbia. J. Phys. 1997, 27, 762–781. [Google Scholar] [CrossRef]
- Boon, J.D.; Byrne, R. On basin hypsometry and the morphodynamic response of coastal inlet systems. Mar. Geol. 1981, 40, 27–48. [Google Scholar] [CrossRef]
- Friedrichs, C.T.; Aubrey, D. Non-linear tidal distortion in shallow well-mixed estuaries: A synthesis. Estuar. Coast. Shelf Sci. 1988, 27, 521–545. [Google Scholar] [CrossRef]
- Loder, J.W. Topographic rectification of tidal currents on the sides of Georges Bank. J. Phys. Oceanogr. 1980, 10, 1399–1416. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.S.; Lai, Z.; Beardsley, R.; Xu, Q.; Lin, H.; Viet, N. Current separation and upwelling over the southeast shelf of Vietnam in the South China Sea. J. Geophys. Res. Ocean 2012, 117, C03033. [Google Scholar] [CrossRef] [Green Version]
- Pickering, A.; Alford, M.; Nash, J.; Rainville, L.; Ko, D.S.; Lim, B. Structure and Variability of Internal Tides in Luzon Strait. J. Phys. Oceanogr. 2015, 45, 1574–1594. [Google Scholar] [CrossRef] [Green Version]
- Simpson, J.H.; Crisp, D.J.; Hearn, C. The shelf-sea fronts: Implications of their existence and behaviour [and discussion]. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1981, 302, 531–546. [Google Scholar]
- De Boer, G.J.; Pietrzak, J.D.; Winterwerp, J.C. Using the potential energy anomaly equation to investigate tidal straining and advection of stratification in a region of freshwater influence. Ocean Model. 2008, 22, 1–11. [Google Scholar] [CrossRef]
- Kurapov, A.L.; Egbert, G.D.; Allen, J.S.; Miller, R.N.; Erofeeva, S.Y.; Kosro, P.M. The m2 internal tide off oregon: Inferences from data assimilation. J. Phys. Oceanogr. 2003, 33, 1733–1757. [Google Scholar] [CrossRef]
- Kang, D.; Fringer, O. Energetics of barotropic and baroclinic tides in the monterey bay area. J. Phys. Oceanogr. 2012, 42, 272–290. [Google Scholar] [CrossRef] [Green Version]
- Kelly, S.M.; Nash, J.D. Internal-tide generation and destruction by shoaling internal tides. Geophys. Res. Lett. 2010, 37, l23611. [Google Scholar] [CrossRef] [Green Version]
- Kang, D.; Fringer, O. On the calculation of available potential energy in internal wave fields. J. Phys. Oceanogr. 2010, 40, 2539–2545. [Google Scholar] [CrossRef]
- Jan, S.; Chern, C.-S.; Wang, J.; Chiou, M.-D. Generation and propagation of baroclinic tides modified by the Kuroshio in the Luzon Strait. J. Geophys. Res. Ocean 2012, 117, c02019. [Google Scholar] [CrossRef] [Green Version]
- Ma, B.B.; Lien, R.C.; Ko, D.S. The variability of internal tides in the Northern South China Sea. J. Oceanogr. 2013, 59, 619–630. [Google Scholar] [CrossRef]
- Li, Q.; Wang, B.; Chen, X.; Chen, X.E.; Park, J.H. Variability of nonlinear internal waves in the South China Sea affected by the Kuroshio and mesoscale eddies. J. Geophys. Res. Ocean 2016, 121, 2098–2118. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Chen, X.; Pohlmann, T. The Impact of Fortnightly Stratification Variability on the Generation of Baroclinic Tides in the Luzon Strait. J. Mar. Sci. Eng. 2021, 9, 703. https://doi.org/10.3390/jmse9070703
Zhang Z, Chen X, Pohlmann T. The Impact of Fortnightly Stratification Variability on the Generation of Baroclinic Tides in the Luzon Strait. Journal of Marine Science and Engineering. 2021; 9(7):703. https://doi.org/10.3390/jmse9070703
Chicago/Turabian StyleZhang, Zheen, Xueen Chen, and Thomas Pohlmann. 2021. "The Impact of Fortnightly Stratification Variability on the Generation of Baroclinic Tides in the Luzon Strait" Journal of Marine Science and Engineering 9, no. 7: 703. https://doi.org/10.3390/jmse9070703
APA StyleZhang, Z., Chen, X., & Pohlmann, T. (2021). The Impact of Fortnightly Stratification Variability on the Generation of Baroclinic Tides in the Luzon Strait. Journal of Marine Science and Engineering, 9(7), 703. https://doi.org/10.3390/jmse9070703






