Temporal and Spatial Variability Scales of Salinity at a Large Microtidal Estuary
Abstract
:1. Introduction
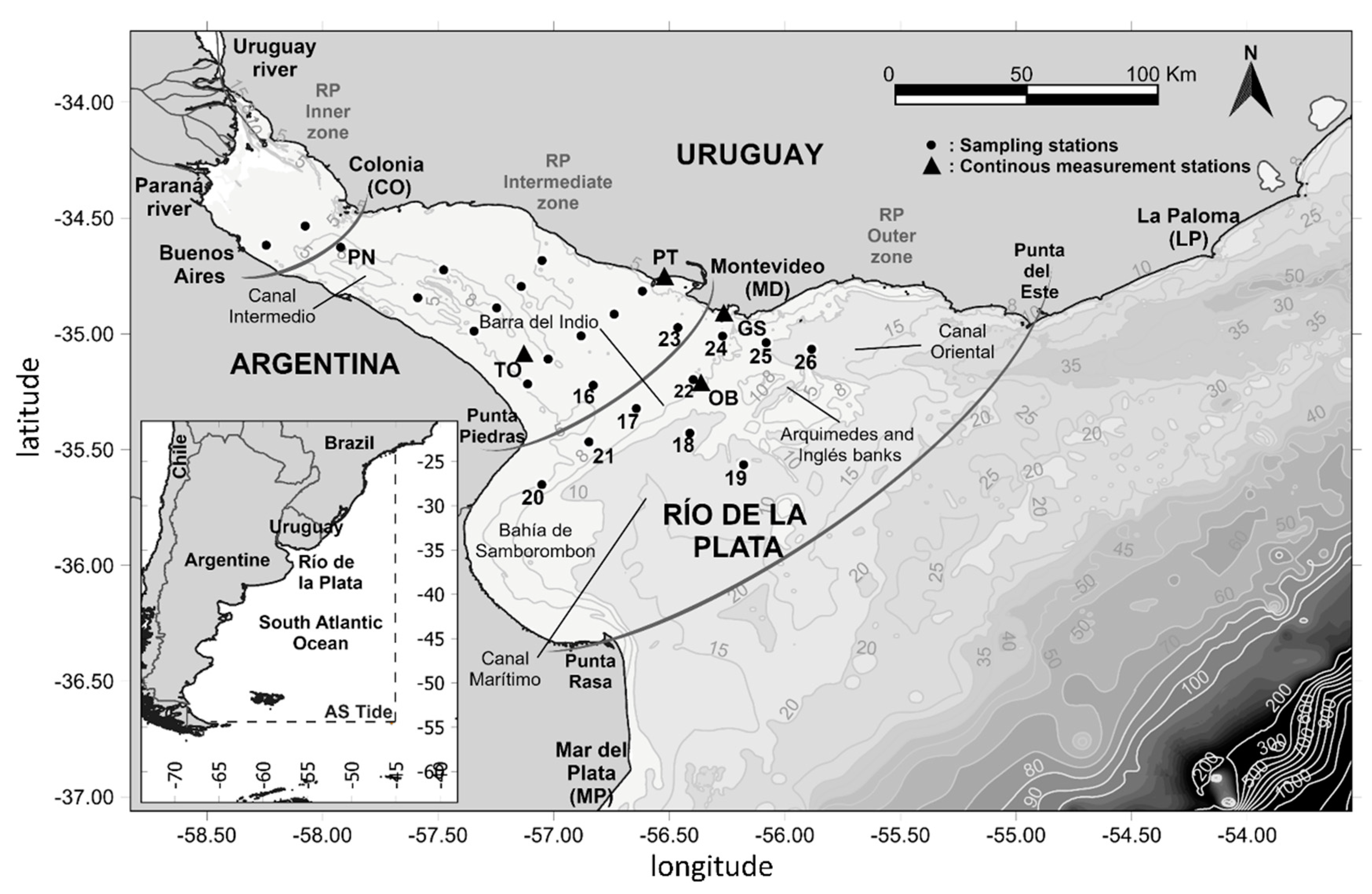
2. The Río de la Plata Estuary
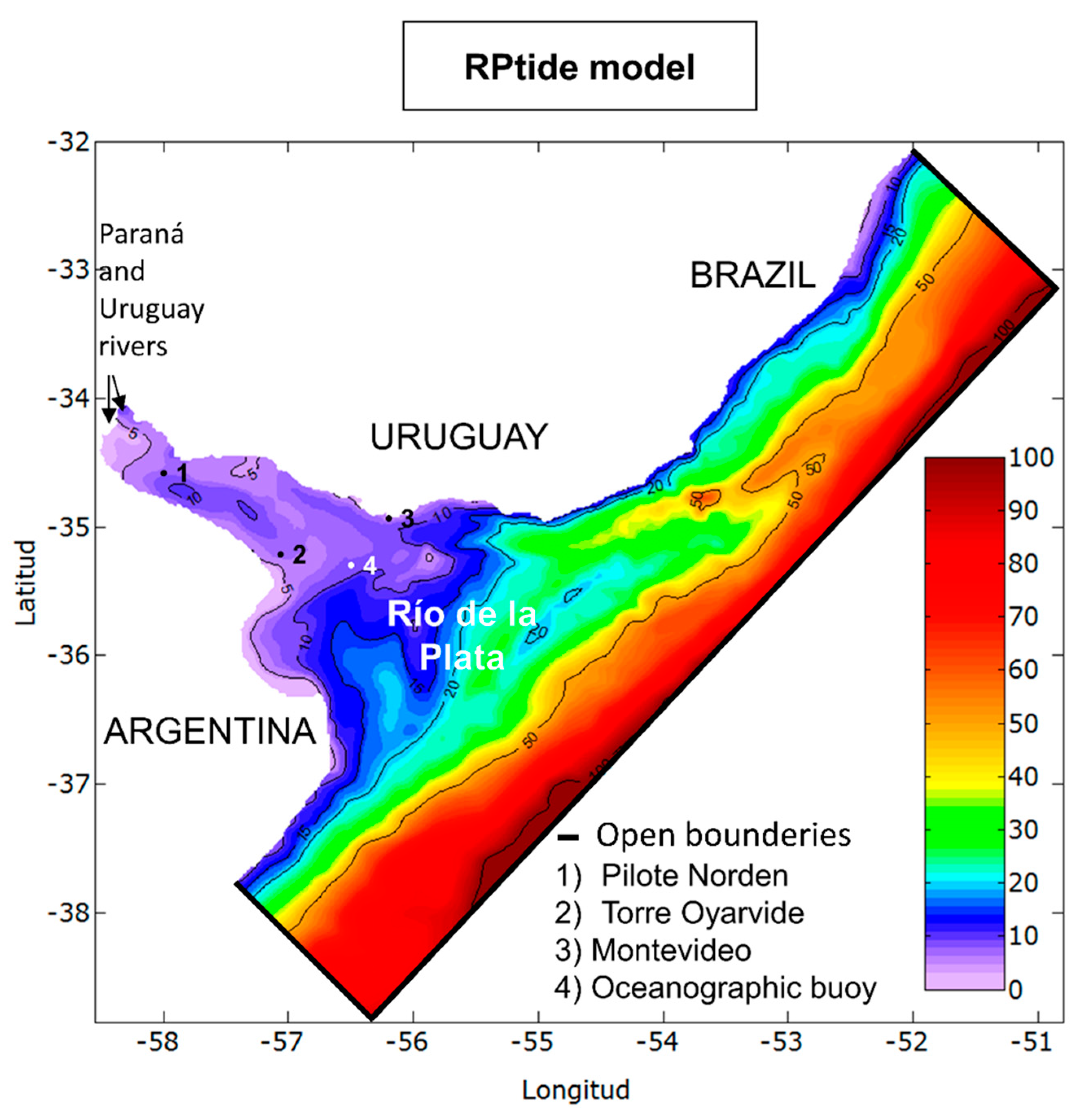
3. Hydrodynamic Numerical Modelling
3.1. Model Description
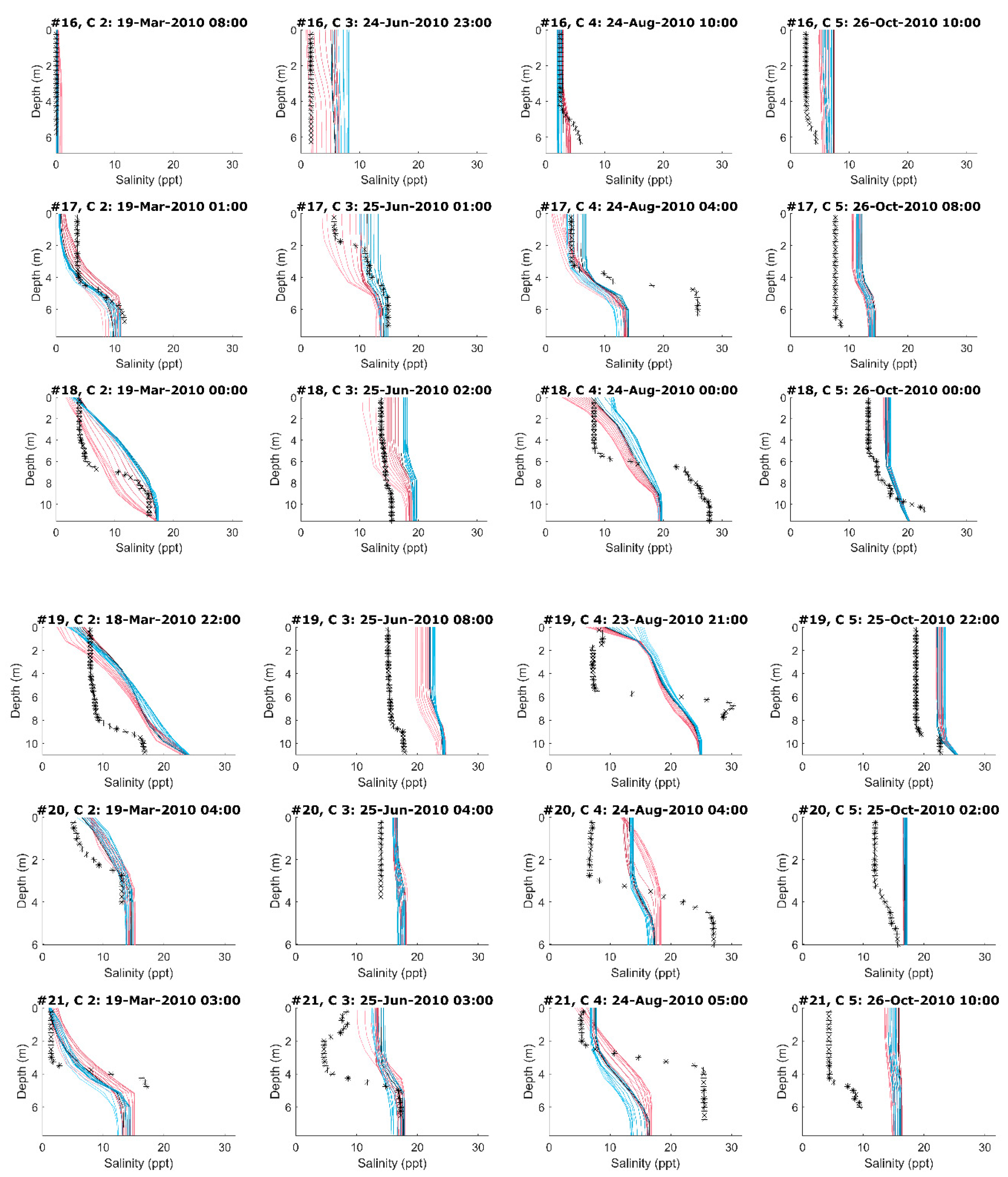
3.2. Model Validation
3.3. Analysis of Model Results
4. Results
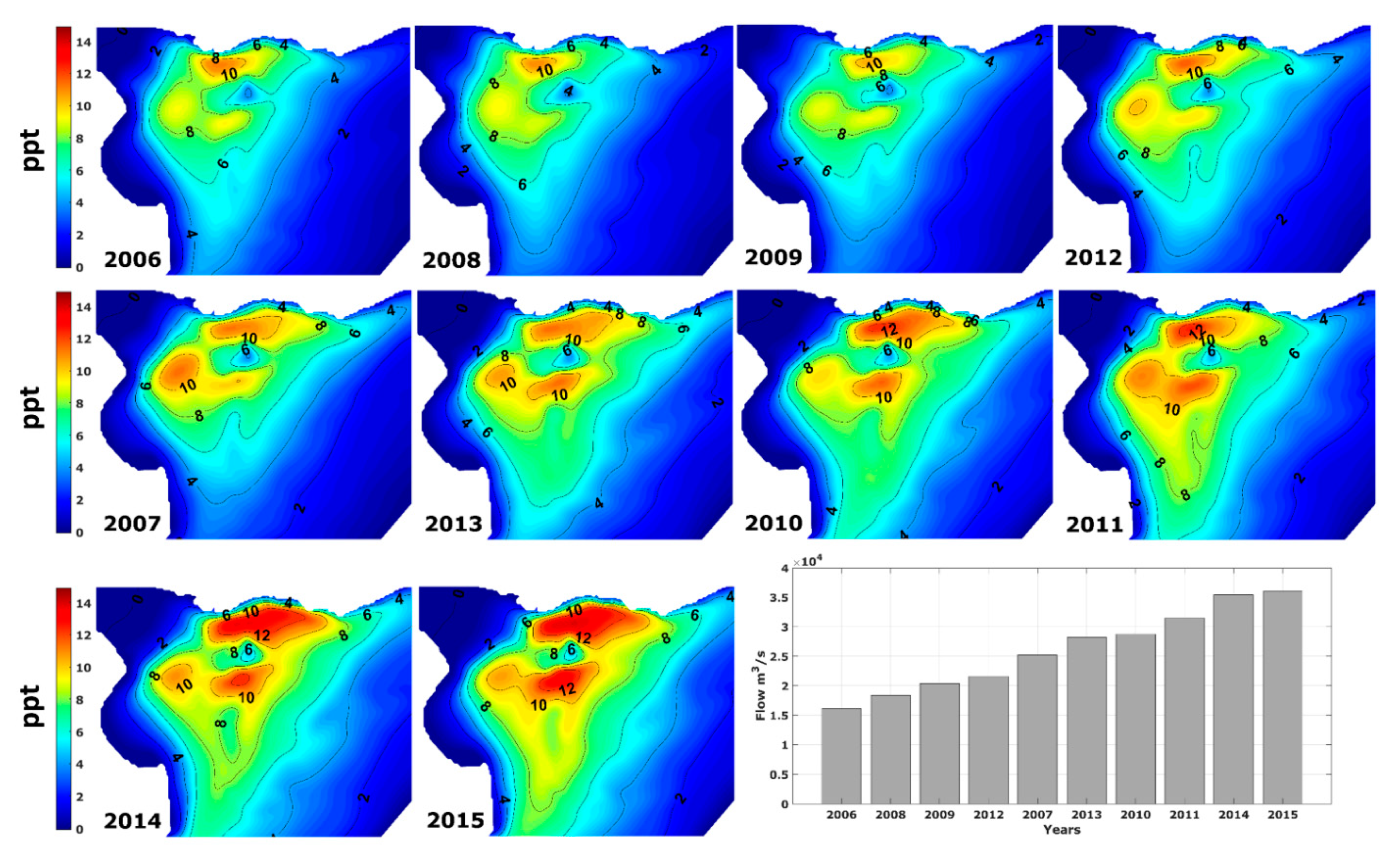
4.1. Fluvial Flow Influence
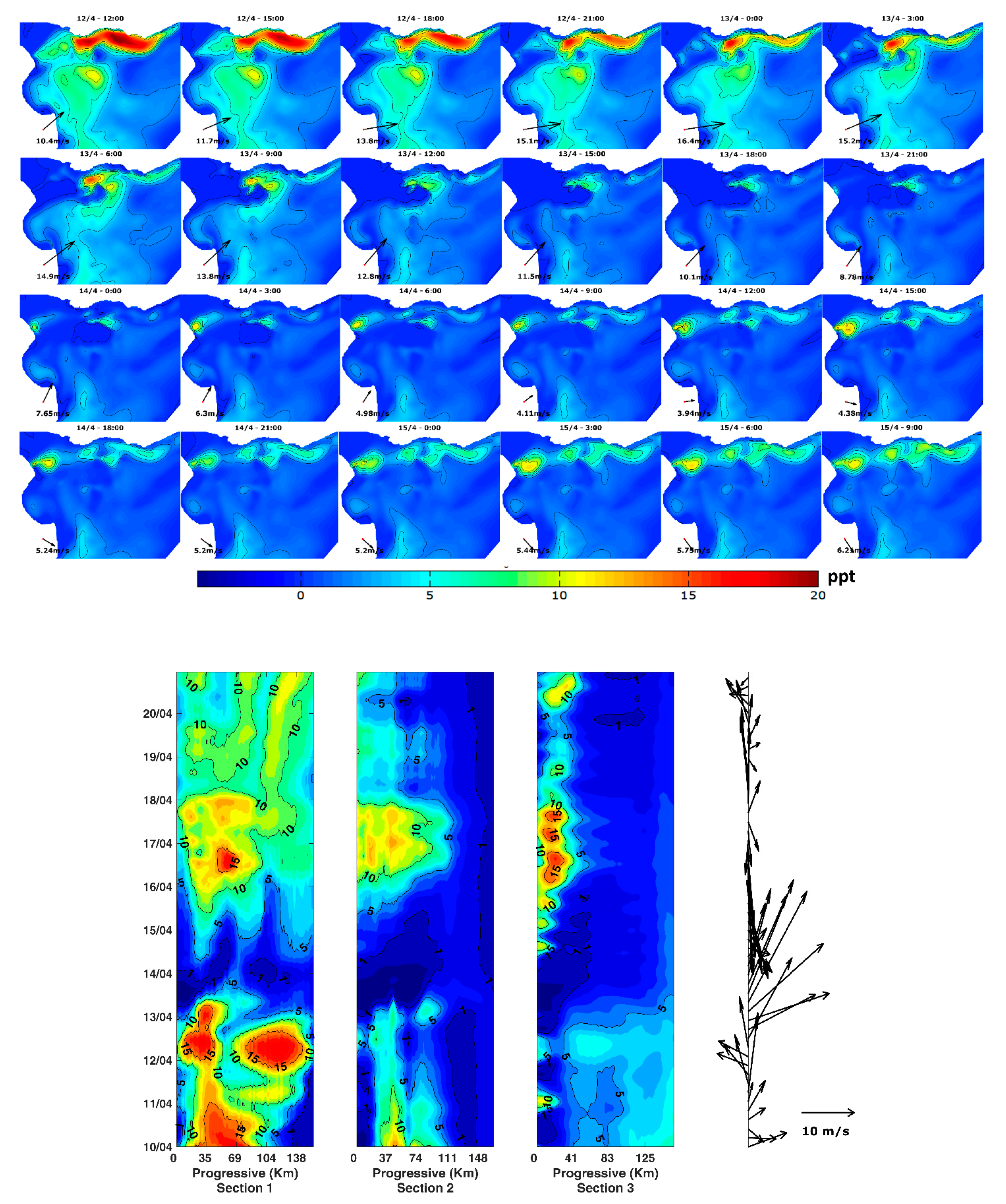
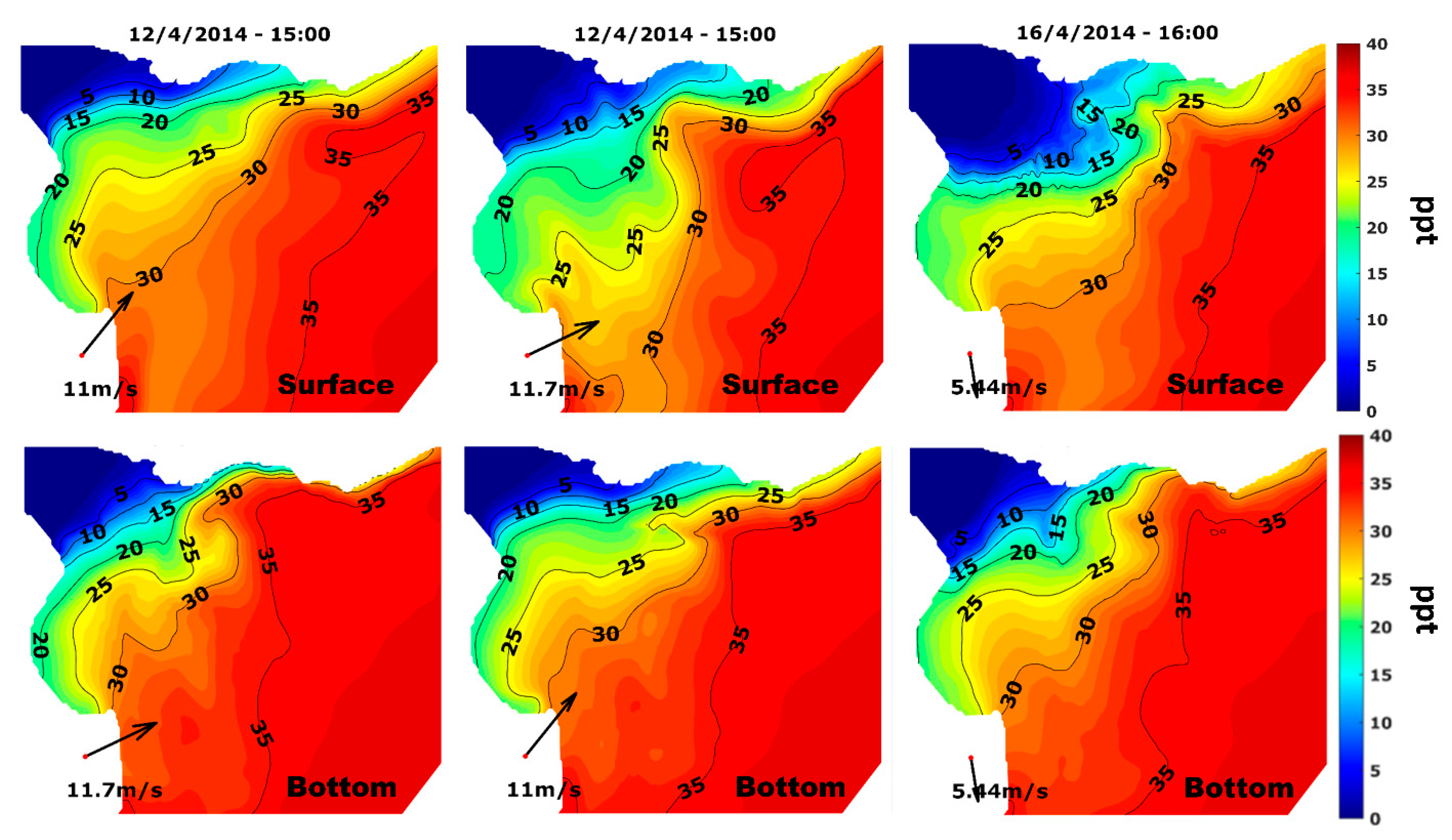
4.2. Influence of Storms
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. RPtide Model Implementation and Calibration
- (1)
- Latitude–longitude coordinate system;
- (2)
- Horizontal grid with constant resolution of 0.02° × 0.02°;
- (3)
- Vertical grid with 10 uniformly distributed sigma layers;
- (4)
- Bathymetry from charts published by the Uruguayan Oceanographic, Hydrographic, and Meteorological Service of the Army (SOHMA) and the Argentinian Naval Hydrographic Service (SHN);
- (5)
- Coastline from the NOAA/NGDC Marine Geology and Geophysics Division database and from local high-resolution measurements;
- (6)
- Bottom stress is computed using a quadratic law formulation with a roughness length;
- (7)
- Free-surface boundary conditions: winds and pressure from global reanalysis of ECMWF (European Centre for Medium-Range Weather Forecast) data, with a spatial resolution of 0.25° and temporal resolution of 6 h;
- (8)
- Oceanic boundary conditions: astronomical and meteorological tides (water level and 2D currents) from the barotropic 2D hydrodynamic model of the South Atlantic Ocean (AStide) in each cell of the southwest and northeast boundaries and every two cells in the southeast boundary;
- (9)
- Continental boundary condition: daily mean values of the fluvial discharges of the Uruguay and Paraná (two branches: Paraná-Guazú and Paraná-Las Palmas) rivers;
- (10)
- Time step of 90 s;
- (11)
- The vertical viscosity is solved by the GOTM model;
- (12)
- The horizontal viscosity is solved by the Smagorinsky model, with a coefficient of 0.1;
- (13)
- The diffusivity (horizontal and vertical) is related with viscosity through the Schmidt number;
- (14)
- The wind stress at the surface is applied and parameterised by a wind drag coefficient, calculated using the formulation of Large and Ponds;
- (15)
- For the salinity, the boundary conditions are freshwater for the continental boundary and a fixed value of 35 ppt for the oceanic boundary;
- (16)
- Initial conditions: zero velocity, constant water level, and uniform salinity;
- (17)
- Spin-up period: a long period (1 year) is required for the initial salinity condition.
| Simulation Name | Rugosity | Nº Schmidt | Oceanic BC | Objective |
|---|---|---|---|---|
| Ref | 0.00065 | 0.2 | Blumber and Kanta Radiation condition Tlag = 1000 s | Reference simulation |
| Sim1 | 0.001 | - | - | Rugosity influence |
| Sim2 | 0.0001 | - | - | Rugosity influence |
| Sim3 | - | 0.1 | - | Nº Sch influence |
| Sim4 | - | 0.5 | - | Nº Sch influence |
| Sim5 | - | 1 | - | Nº Sch influence |
| Sim6 | - | - | Flather condition | Oceanic BC influence |
| Sim7 | - | - | Blumber and Kanta Radiation condition Tlag = 5000 s | Oceanic BC influence |
| Final | 0.001 | 0.2 | Blumber and Kanta Radiation condition Tlag = 1000 s | Selected configuration |
| Simulation Name | RMSE (m) Water Level PN | RMSE (m) Water Level TO | RMSE (ppt) Salinity BO |
|---|---|---|---|
| Ref | 0.34 | 0.24 | 3.39 |
| Sim1 | 0.33 | 0.24 | 3.38 |
| Sim2 | 0.35 | 0.25 | 3.39 |
| Sim3 | 0.34 | 025 | 3.72 |
| Sim4 | 0.33 | 0.24 | 3.23 |
| Sim5 | 0.33 | 0.23 | 3.55 |
| Sim6 | 0.35 | 0.32 | 3.15 |
| Sim7 | 0.36 | 0.24 | 3.03 |
| Final | 0.32 | 0.23 | 3.45 |

| Water Level | 1 November 2009–31 December 2010 | 8 April 2010–25 June 2010 | 26 June 2010–31 July 2010 |
| RMSE (m) PN | 0.24 | 0.20 | 0.23 |
| RMSE (m) TO | 0.23 | 0.23 | |
| RMSE (m) MVD | 0.18 | - | - |
| Velocity | 26 January 2009–18 March 2010 | - | - |
| RMSE (m/s) velocity U BO | 0.17 | - | - |
| RMSE (m/s) velocity V BO | 0.18 | - | - |
| Salinity | 26 November 2009–22 January 2010 | - | 25 June 2010–31 July 2010 |
| RMSE (ppt) BO | 4.57 | - | 3.65 |
References
- Prandle, D. Estuaries: Dynamics, Mixing, Sedimentation and Morphology; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Valle-Levinson, A. (Ed.) Contemporary Issues in Estuarine Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Valle-Levinson, A. Large Estuaries (Effects of Rotation). In Treatise on Estuarine and Coastal Science; Wolanski, E., McLusky, D., Eds.; Academic Press: Cambridge, MA, USA, 2011; pp. 123–140. ISBN 9780080878850. [Google Scholar]
- Pritchard, D.W. Estuarine circulation patterns. Proc. Am. Soc. Civ. Eng. 1955, 81, 1–11. [Google Scholar]
- Cameron, W.M.; Pritchard, D.W. Estuaries. In The Sea; Hill, M.N., Ed.; John Wiley & Sons: New York, NY, USA, 1963; Volume 2, pp. 306–324. [Google Scholar]
- Dyer, K.R. Estuaries. In A Physical Introduction; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Davies, J.H. A morphpgenetic approach to world shorelines. Z. Geomorphol. 1964, 8, 127–142. [Google Scholar] [CrossRef]
- O’Callaghan, J.; Pattiaratchi, C.; Hamilton, D. The response of circulation and salinity in a micro-tidal estuary to sub-tidal oscillations in coastal sea surface elevation. Cont. Shelf Res. 2007, 27, 1947–1965. [Google Scholar] [CrossRef]
- Geyer, W.R. Influence of Wind on Dynamics and Flushing of Shallow Estuaries. Estuar. Coast. Shelf Sci. 1997, 44, 713–722. [Google Scholar] [CrossRef]
- Huang, W.; Li, C.; White, J.R.; Bargu, S.; Milan, B.; Bentley, S. Numerical Experiments on variation of freshwater plume from Mississippi River diversion in Lake Pontchartrain estuary. J. Geophys. Res Ocean. 2020, 125, C2019JC015282. [Google Scholar] [CrossRef]
- Guerrero, R.A.; Acha, E.M.; Framiñan, M.B.; Lasta, C. Physical Oceanography of the Río de la Plata Estuary. Cont. Shelf Res. 1997, 17, 727–742. [Google Scholar] [CrossRef]
- Framiñan, M.B.; Valle-Levinson, A.; Sepúlveda, H.H.; Brown, O.B. Tidal variations of flow convergence, shear, and stratification at the Rio de la Plata estuary turbidity front. J. Geophys. Res. 2008, 113, C08035. [Google Scholar] [CrossRef] [Green Version]
- Sepúlveda, H.; Valle-Levinson, A.; Framiñan, M. Observations of subtidal and tidal flow in the Río de la Plata Estuary. Cont. Shelf Res. 2003, 24, 509–525. [Google Scholar] [CrossRef]
- Simionato, G.C.; Meccia, V.L.; Guerrero, R.; Dragani, W.C.; Nuñez, M. Rio de la Plata estuary response to wind variability in synoptic to intraseasonal scales: 2. Currents’ vertical structure and its implications for the salt wedge structure. J. Geophys. Res. 2007, 112, C07005. [Google Scholar] [CrossRef] [Green Version]
- Simionato, C.; Dragani, W.; Meccia, V.; Núñez, M. A numerical study of the barotropic circulation of the Río de la Plata estuary: Sensitivity to bathymetry, the Earth’s rotation and low frequency wind variability. Estuar. Coast. Shelf Sci. 2004, 61, 261–273. [Google Scholar] [CrossRef]
- Palma, E.; Matano, R.; Piola, A. A numerical study of the Southwestern Atlantic Shelf circulation: Barotropic response to tidal and wind forcing. J. Geophys. Res. 2004, 109, C08014. [Google Scholar] [CrossRef]
- Fossati, M.; Piedra-Cueva, I. Numerical modelling of residual flow and salinity in the Río de la Plata. Appl. Math. Model. 2008, 32, 1066–1086. [Google Scholar] [CrossRef]
- Santoro, P.; Fossati, M.; Piedra-Cueva, I. Study of the meteorological tide in the Río de la Plata. Cont. Shelf Res. 2013, 60, 51–63. [Google Scholar] [CrossRef]
- Meccia, V.L.; Simionato, C.G.; Guerrero, R.A. The Rio de la Plata estuary response to wind variability in synoptic timescale: Salinity fields and salt wedge structure. J. Coast. Res. 2013, 29, 61–77. [Google Scholar] [CrossRef]
- Fossati, M.; Piedra-Cueva, I. A 3D hydrodynamic numerical model of the Río de la Plata and Montevideo’s coastal zone. Appl. Math Modell. 2013, 37, 1310–1332. [Google Scholar] [CrossRef]
- Silva, C.; Marti, C.; Imberger, J. Horizontal transport, mixing and retention in a large, shallow estuary: Río de la Plata. Environ. Fluid Mech. 2014, 14, 1173–1197. [Google Scholar] [CrossRef]
- Alonso, R.; Jackson, M.; Santoro, P.; Fossati, M.; Solari, S. Wave and tidal energy resource assessment in Uruguayan shelf seas. Renew. Energy 2017, 114A, 18–31. [Google Scholar] [CrossRef]
- Fossati, M.; Cayocca, F.; Piedra-Cueva, I. Fine sediment dynamics in the Río de la Plata. Adv. Geosci. 2014, 39, 75–80. [Google Scholar] [CrossRef] [Green Version]
- Fossati, M.; Santoro, P.; Mosquera, R.; Martínez, C.; Ghiardo, F.; Ezzatti, P.; Pedocchi, F.; Piedra-Cueva, I. Dinámica de flujo, del campo salino y de los sedimentos finos en el Río de la Plata. RIBAGUA Rev. Iberoam. Del Agua 2014, 1, 48–63. [Google Scholar]
- Santoro, P.; Fossati, M.; Tassi, T.; Huybrechts, N.; Pham Van Bang, D.; Piedra-Cueva, I. A coupled wave–current–sediment transport model for an estuarine system: Application to the Río de la Plata and Montevideo Bay. Appl. Math. Model. 2017, 52, 107–130. [Google Scholar] [CrossRef]
- Moreira, D.; Simionato, C.G. Modeling the suspended sediment transport in a very wide, shallow, and microtidal estuary, the Río de la Plata, Argentina. J. Adv. Modeling Earth Syst. 2019, 11, 3284–3304. [Google Scholar] [CrossRef]
- Simionato, C.; Moreira, D.; Piedra Cueva, I.; Fossati, M. Proyecto FREPLATA—FFEM Modelado numérico y mediciones insitu y remotas de las transferencias de sedimentos finos a través del Río de la Plata. Parte A: Adquisición de datos. Frente Marítimo 2011, 22, 265–304. [Google Scholar]
- Mateus, M.; Neves, R. (Eds.) Ocean Modelling for Coastal Management—Case Studies with Mohid; IST Press: Lisbon, Potrugal, 2013. [Google Scholar]
- Martínez, C.; Silva, J.P.; Dufrechou, E.; Santoro, P.; Fossati, M.; Ezzati, P.; Piedra-Cueva, I. Towards a 3D Hydrodynamic numerical modeling system for long term simulations of the Río de la Plata dynamic. In Proceedings of the E-Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean. Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bau-er, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Villareal, M.; Karsten, B.; Burchard, H.; Demirov, E. Coupling of the GOTM turbulence module to some three dimensional ocean models. In Marine Turbulence. Theories, Observations, and Models; Cambridge University Press: Cambridge, UK, 2005; pp. 225–237. [Google Scholar]
- Large, W.G.; Pond, S. Open ocean momentum flux measurements in moderate to strong winds. J. Phys. Ocean. 1981, 11, 324–481. [Google Scholar] [CrossRef] [Green Version]
- Santoro, P.; Fernandez, M.; Fossati, M.; Cazes, G.; Terra, R.; Piedra-Cueva, I. Pre-operational forecasting of sea level height for the Río de la Plata. Appl. Math. Modell. 2011, 35, 2462–2478. [Google Scholar] [CrossRef]
- Maciel, F.; Santoro, P.; Pedocchi, F. Spatio-temporal dynamics of the Río de la Plata turbidity front; combining remote sensing with in-situ measurements and numerical modeling. Cont. Shelf Res. 2021, 213, 104301. [Google Scholar] [CrossRef]

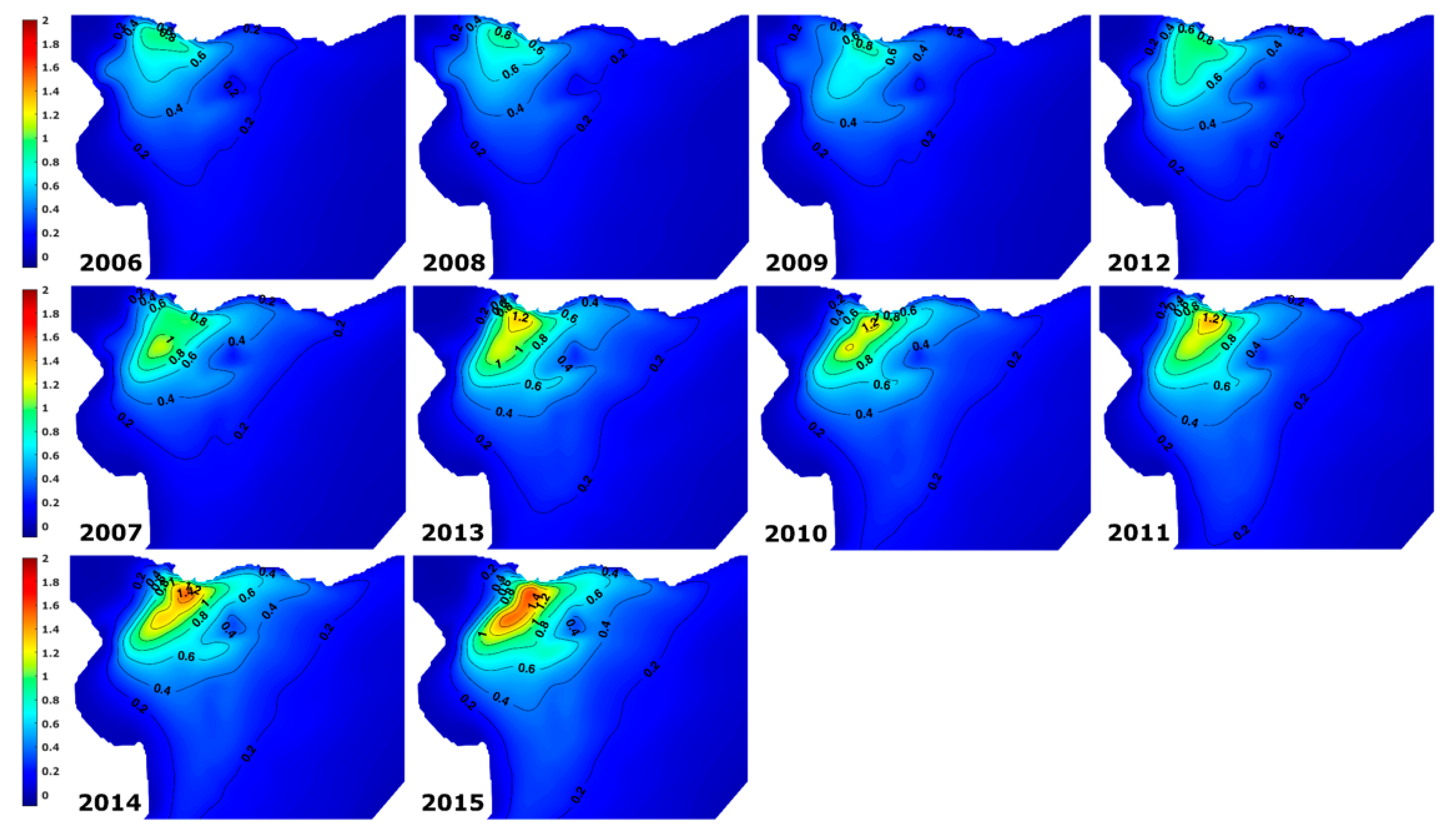
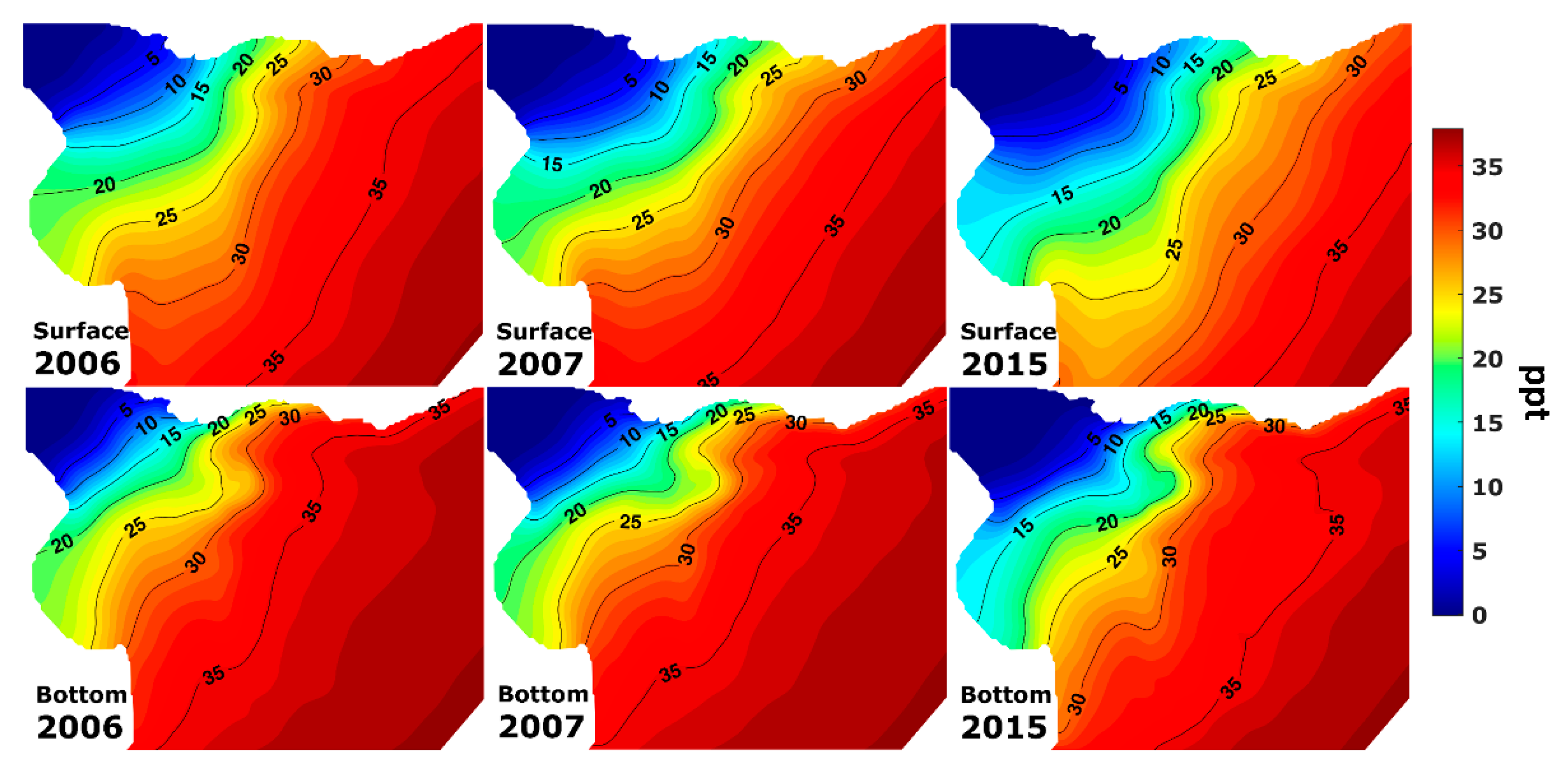
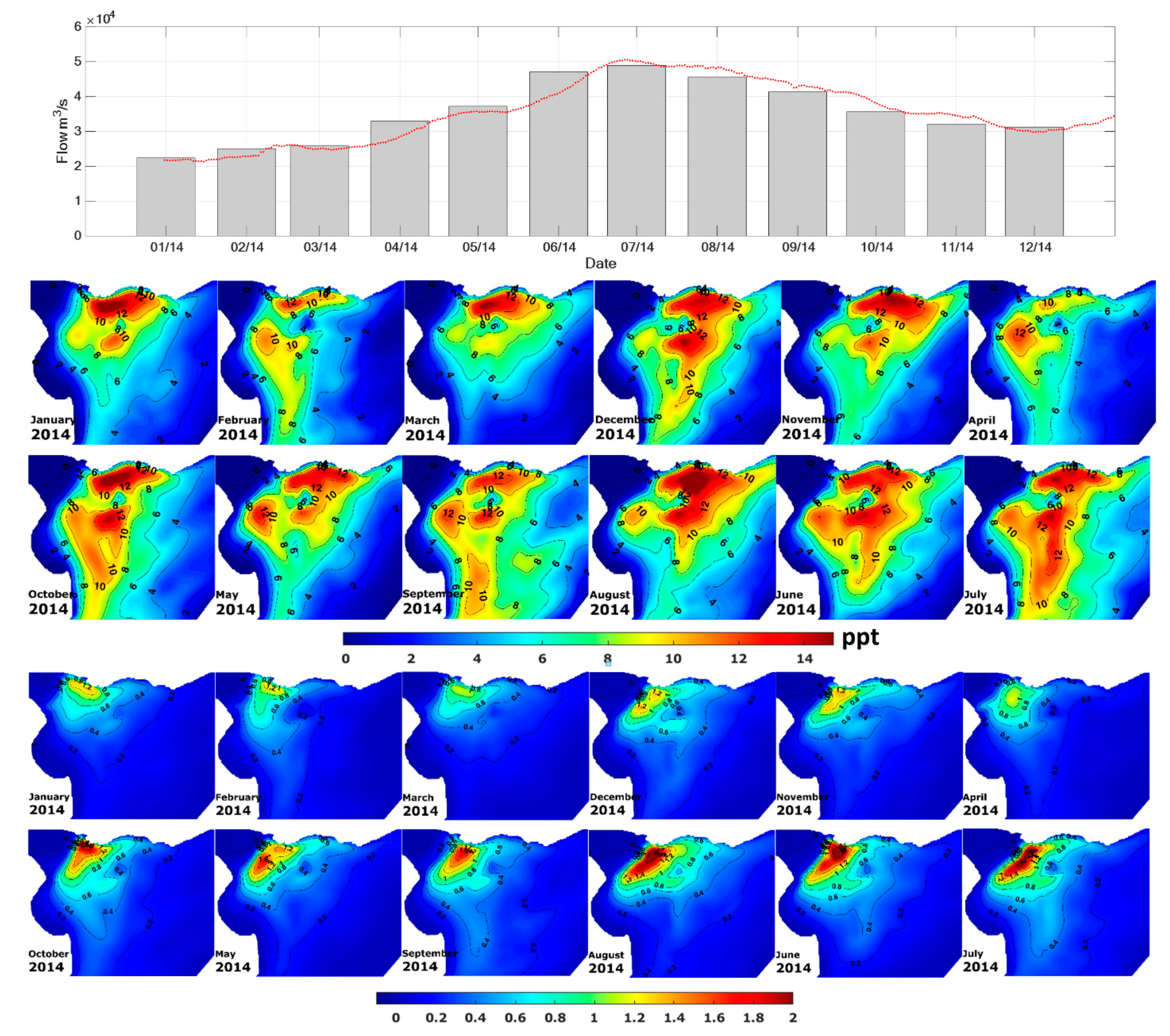
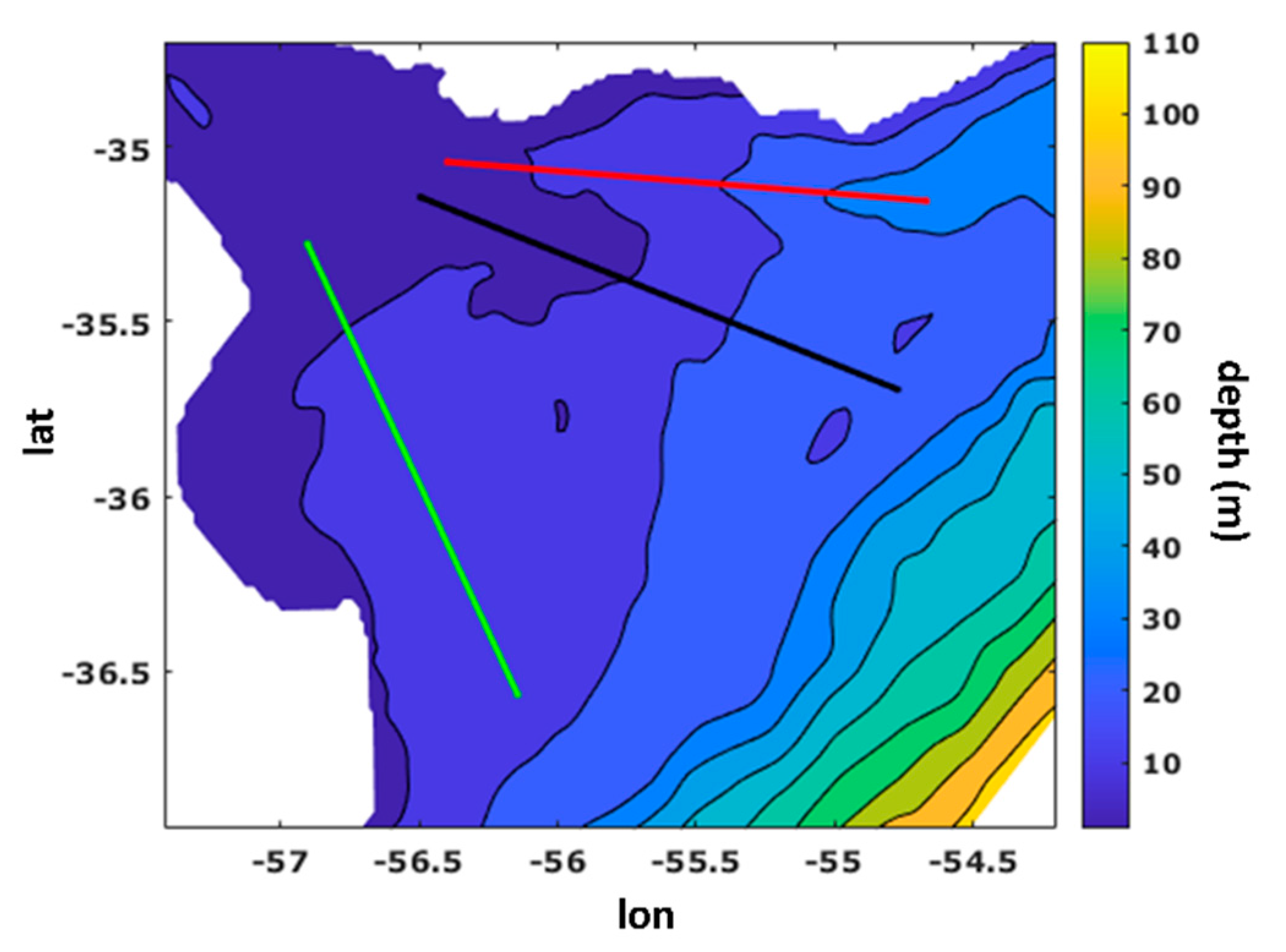
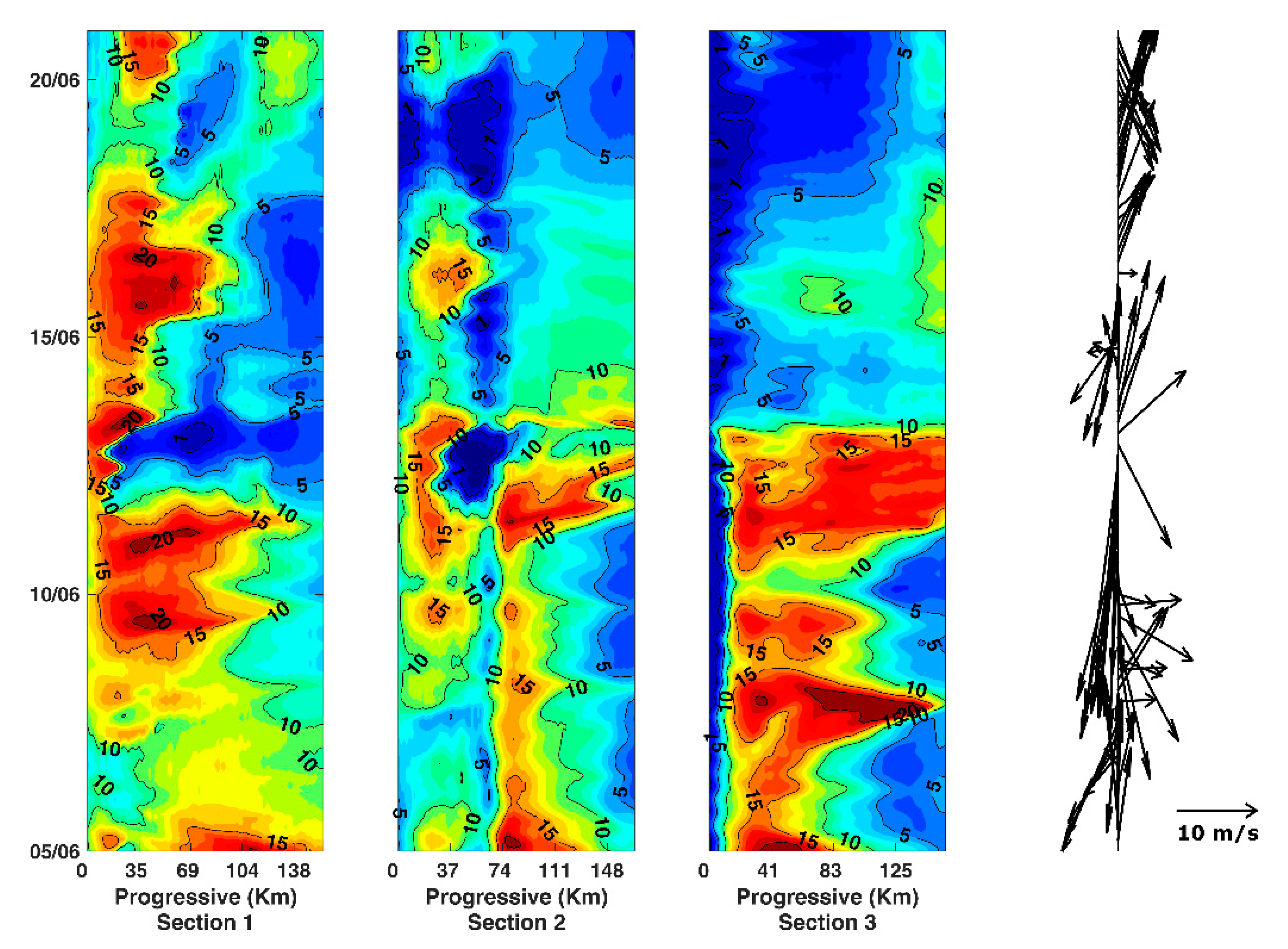
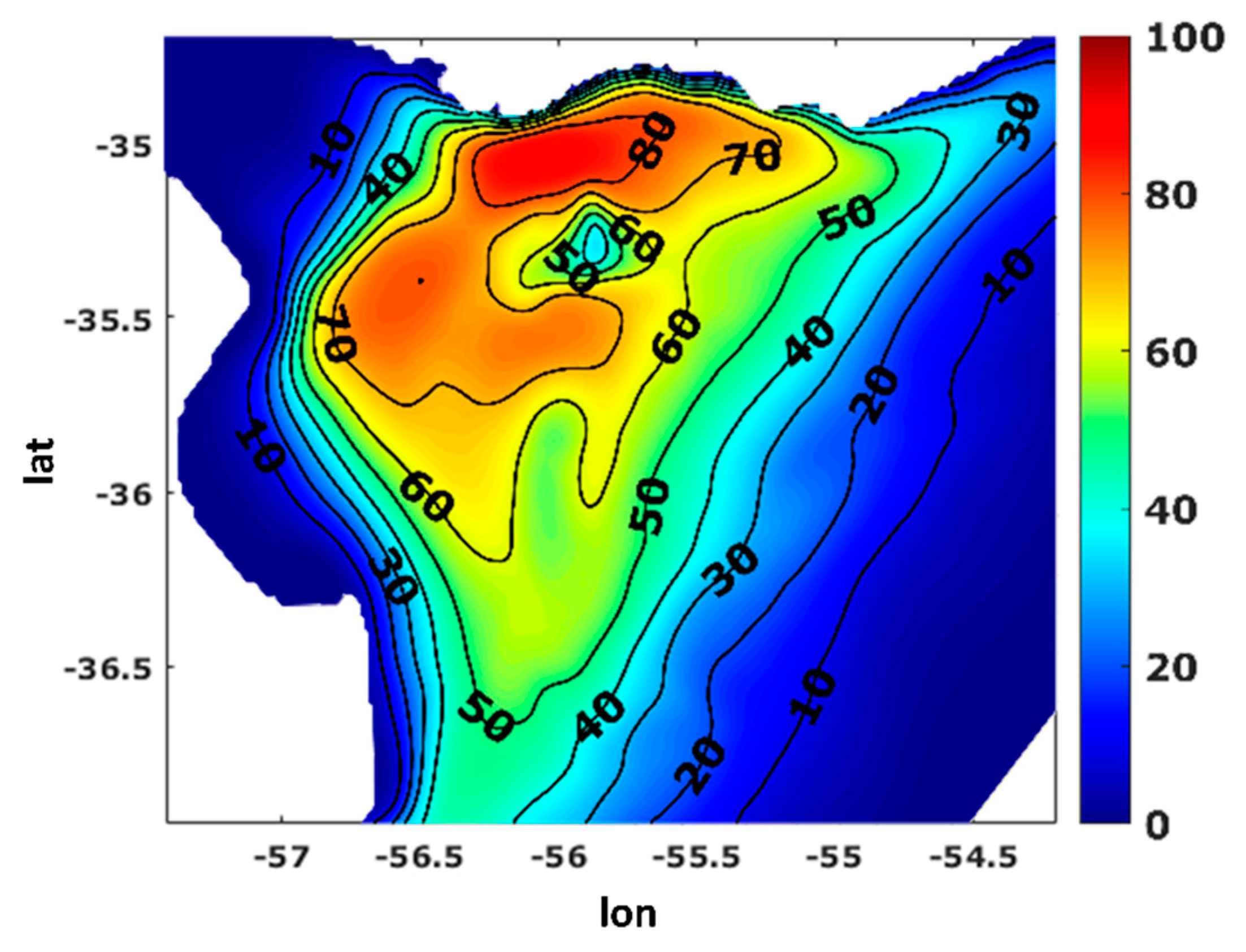
| 2012 | 2014 | ||||||
|---|---|---|---|---|---|---|---|
| Date | Maximum Intensity (m/s) | Approximate Duration (h) | Main Direction | Date | Maximum Intensity (m/s) | Approximate Duration (h) | Main Direction |
| March | 13.7 | 7 | SW | April | 17 | 19 | SW |
| May | 14.2 | 9 | SW | June | 13.5 | 3 | NE |
| June | 13.6 | 8 | SW | July | 15.5 | 11 | NW |
| September | 19.7 | 44 | SE | August | 17.7 | 37 | SW |
| October | 18 | 17 | SW | November | 15 | 17 | EW |
| October | 15 | 4 | SE | - | - | - | - |
| November | 13.7 | 3 | SE–SW | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jackson, M.; Sienra, G.; Santoro, P.; Fossati, M. Temporal and Spatial Variability Scales of Salinity at a Large Microtidal Estuary. J. Mar. Sci. Eng. 2021, 9, 860. https://doi.org/10.3390/jmse9080860
Jackson M, Sienra G, Santoro P, Fossati M. Temporal and Spatial Variability Scales of Salinity at a Large Microtidal Estuary. Journal of Marine Science and Engineering. 2021; 9(8):860. https://doi.org/10.3390/jmse9080860
Chicago/Turabian StyleJackson, Michelle, Gianfranco Sienra, Pablo Santoro, and Mónica Fossati. 2021. "Temporal and Spatial Variability Scales of Salinity at a Large Microtidal Estuary" Journal of Marine Science and Engineering 9, no. 8: 860. https://doi.org/10.3390/jmse9080860
APA StyleJackson, M., Sienra, G., Santoro, P., & Fossati, M. (2021). Temporal and Spatial Variability Scales of Salinity at a Large Microtidal Estuary. Journal of Marine Science and Engineering, 9(8), 860. https://doi.org/10.3390/jmse9080860







