Prediction of Changes in Seafloor Depths Based on Time Series of Bathymetry Observations: Dutch North Sea Case
Abstract
:1. Introduction
2. Methodology
2.1. Preparation of Bathymetry Time Series
- Fixed grid node positions using quadtree DEM, .
- Time series of surveys, where n is the total number of epochs.
- Observed depths values, d for each grid node, p for each epoch.
- Variances of depths, per grid node , per epoch.
2.2. Specification of Stochastic Model
2.2.1. Multibeam Echosounding Variances
2.2.2. Single-Beam Echosounding Variances
2.3. Estimated Parameters
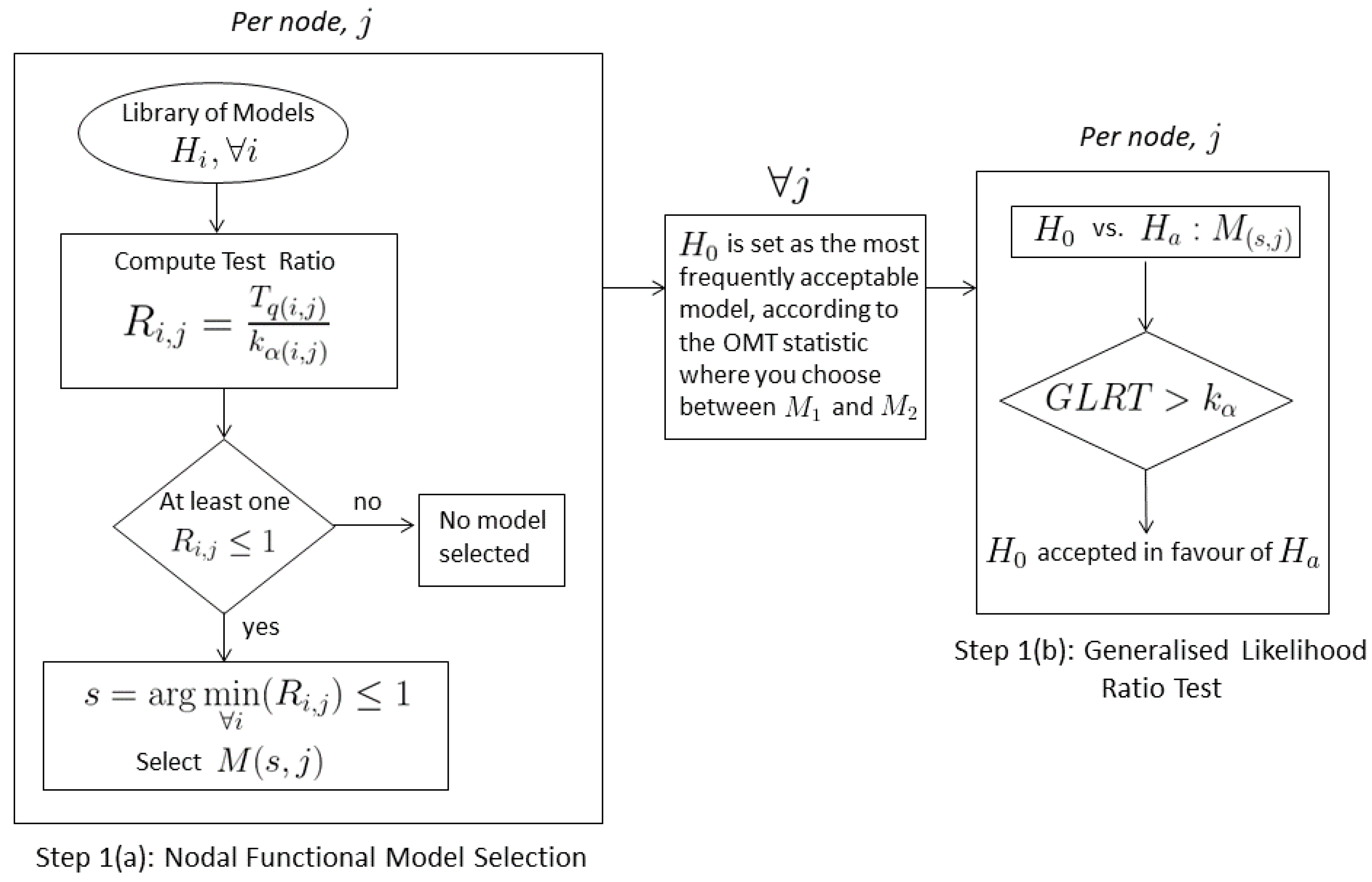
2.4. Functional Model Selection
- Only one model results in . Then, that model is selected for that particular node.
- More than one model can result in . Among the competing models, for each node j, findThen is selected for that node.
- If no model is accepted based on Equation (16), then none of the models is selected for that node.
- The values of two or more of the test ratios can be quite close to each other. Hence the associated models fit almost equally well.
- Due to irregularities in the data it can occur that the piecewise linear model is accepted, although in reality the constant velocity model should be selected. Additionally, the length of the time series and the larger number of unknown parameters in the piecewise linear model can result in over-fitting.
- The spatial correlation between the nodes is not accounted for and hence the selected models in the neighbouring nodes can show inconsistency, especially in areas of high variability.
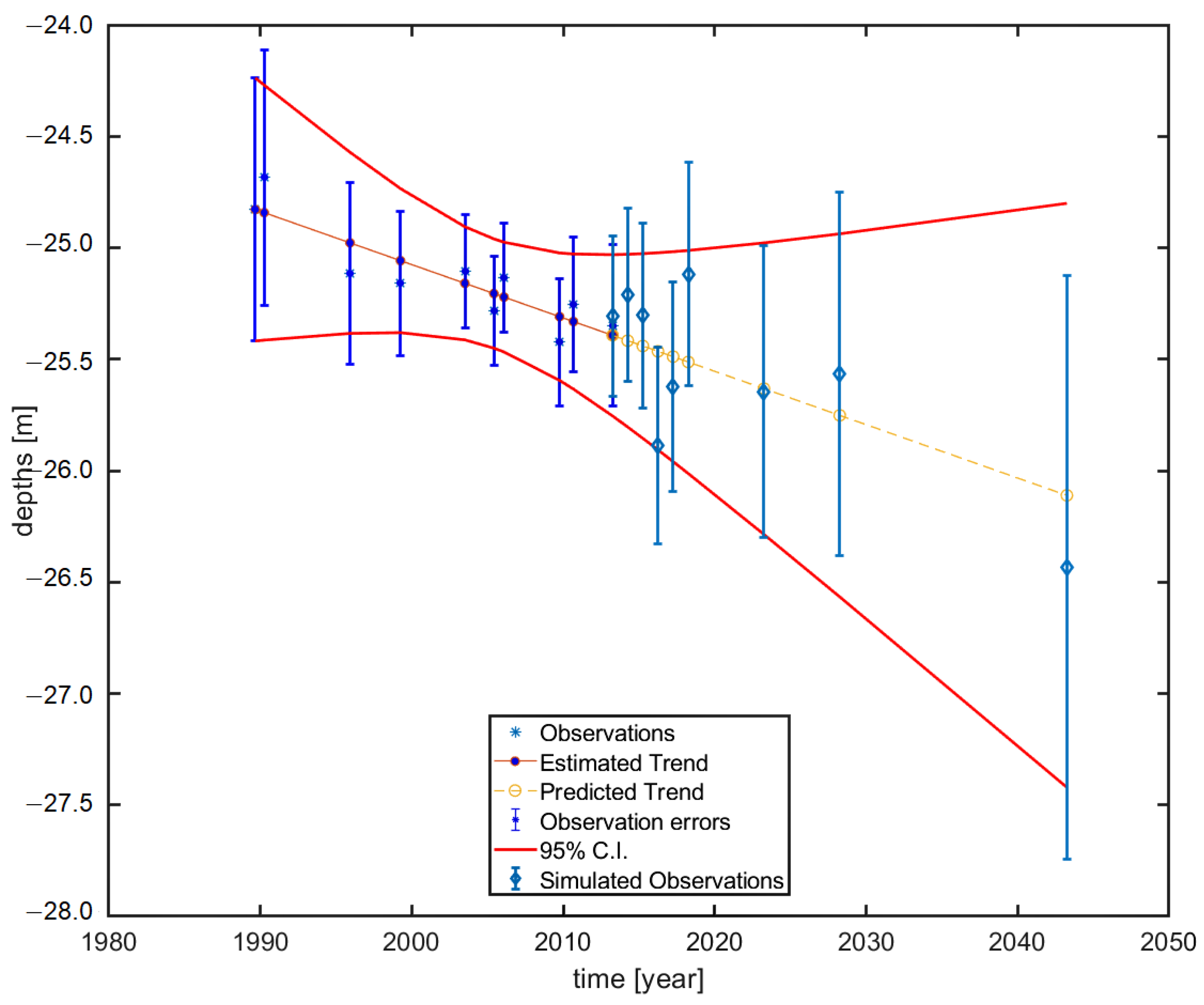
2.5. Prediction and Validation Using Selected Functional Model
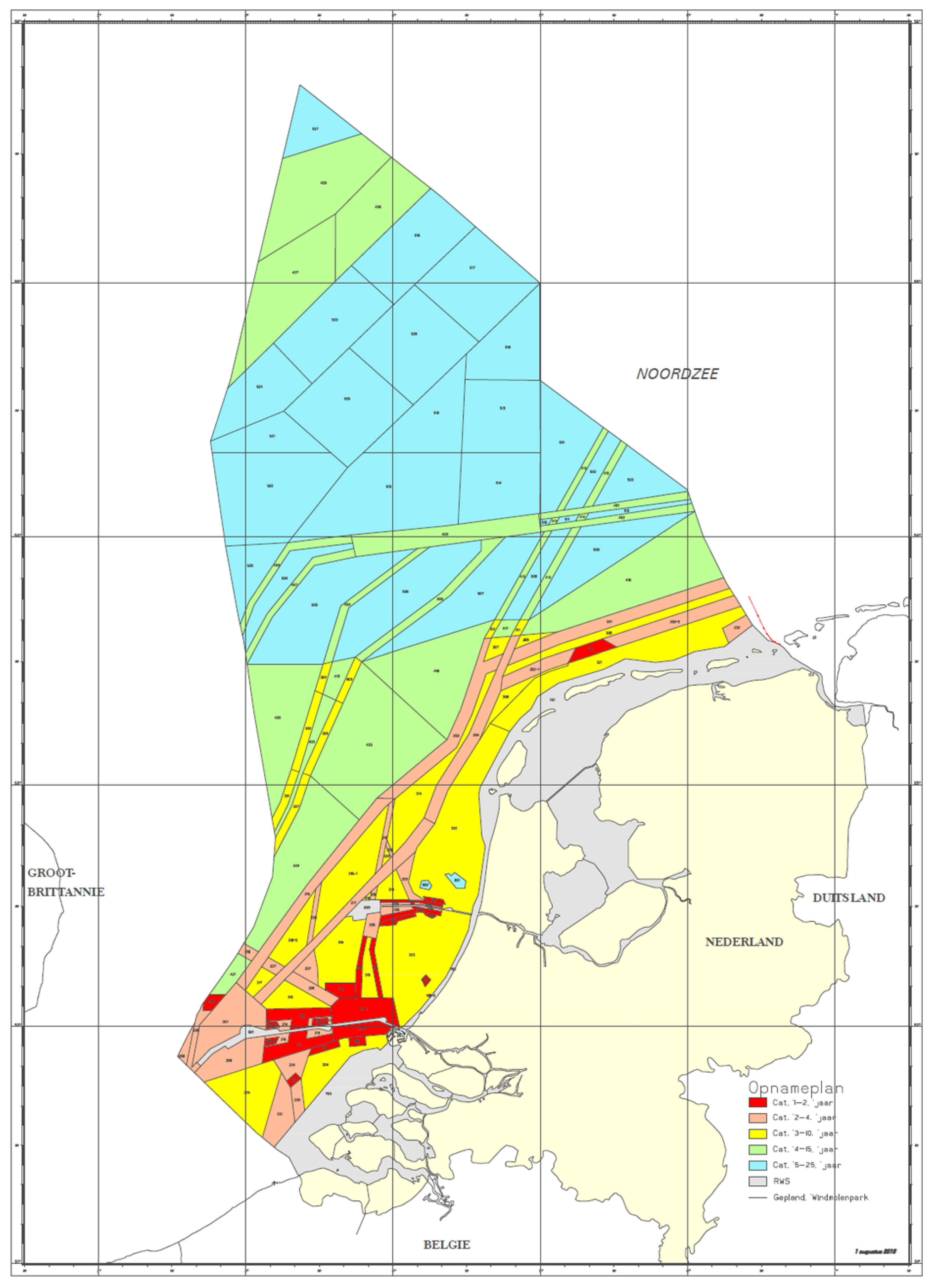
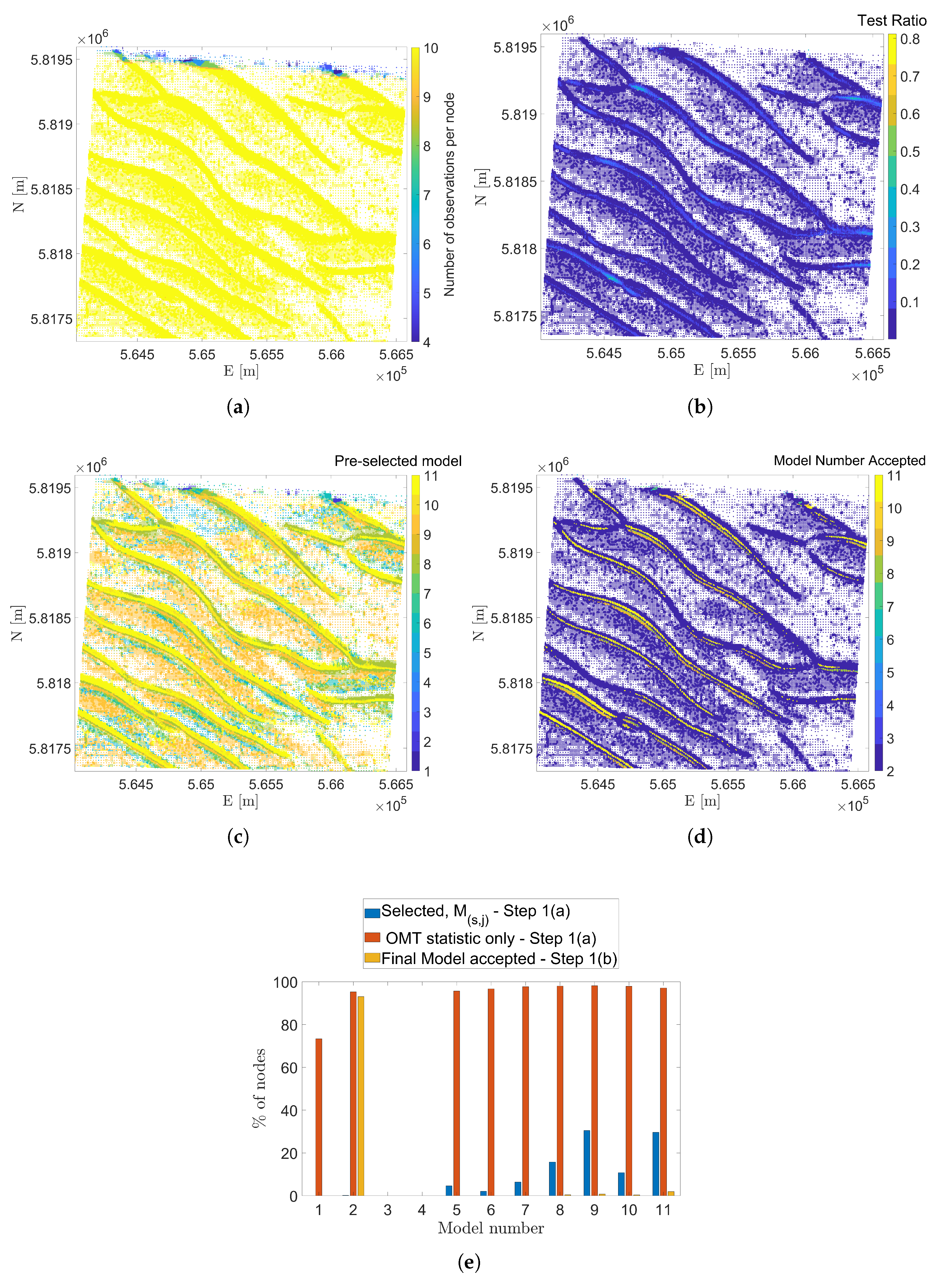
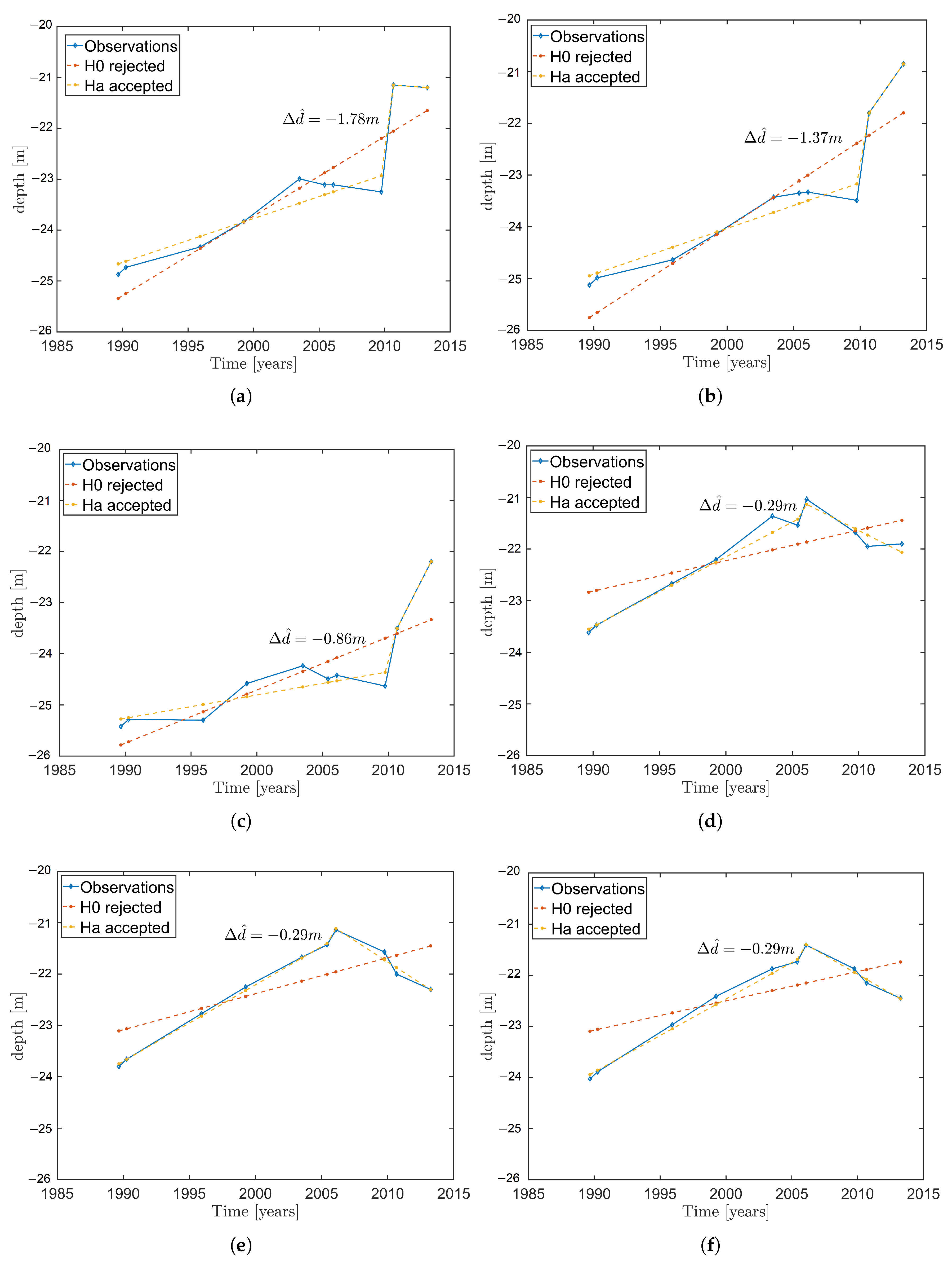
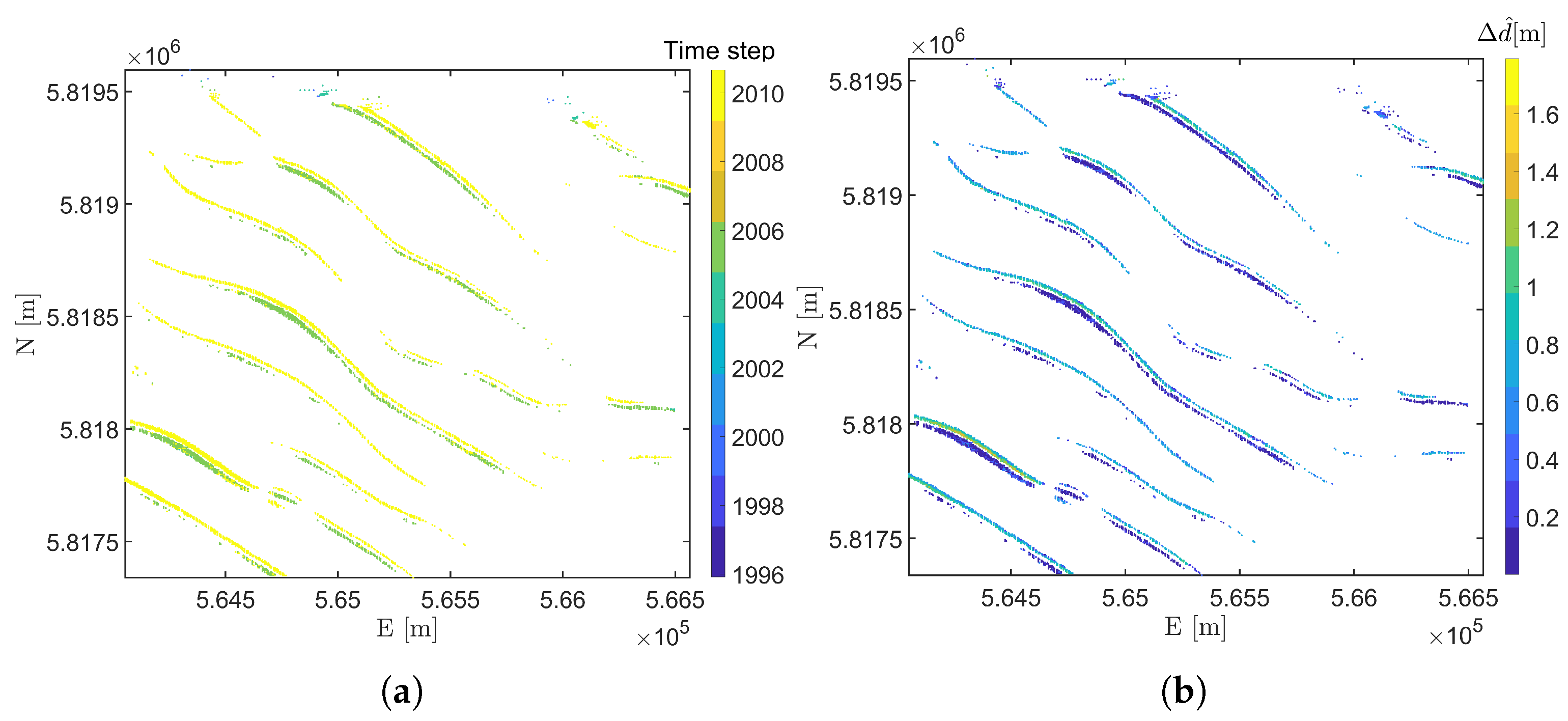
3. Results of Spatial and Temporal Testing
3.1. Area West of IJmuiden
Results for Sub-Area NF
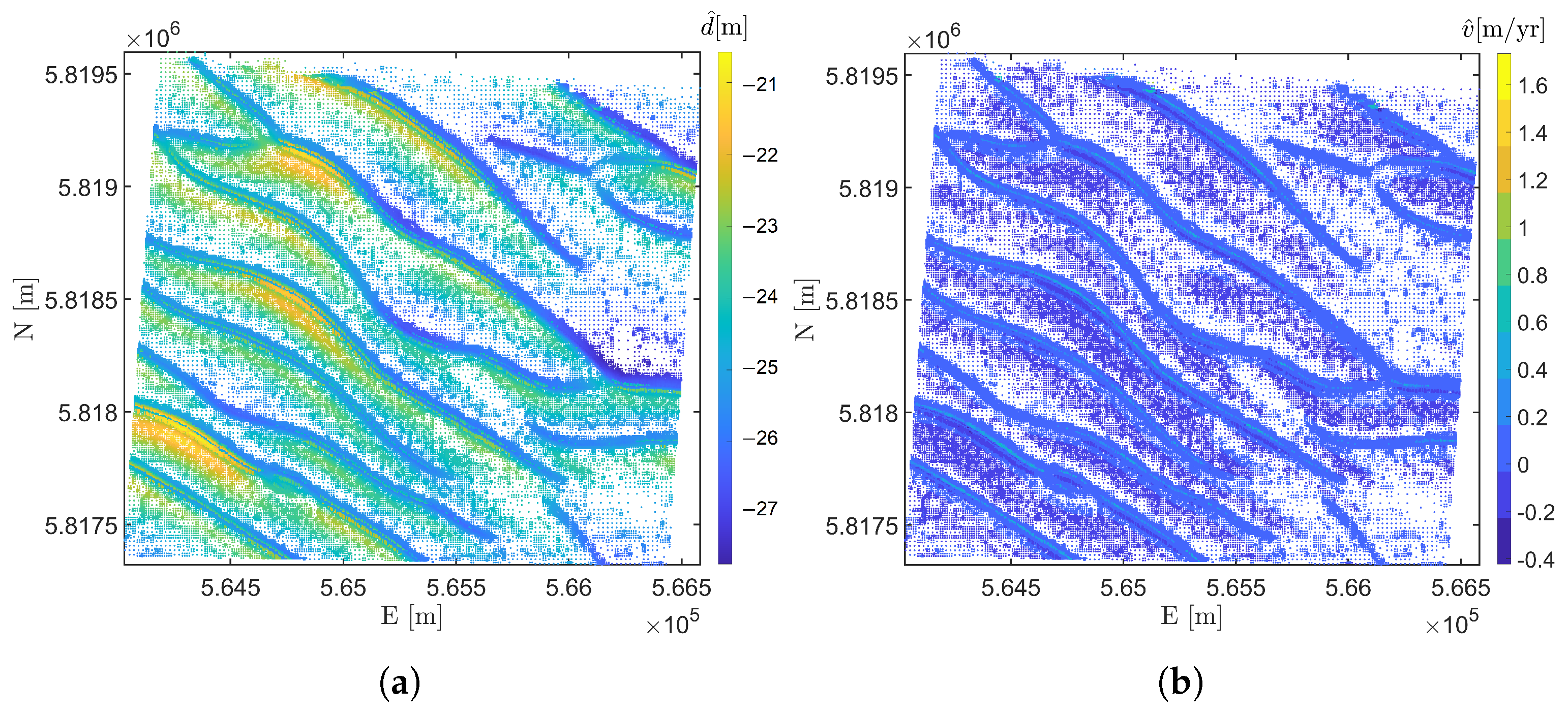
4. Prediction Using the Models Selected: Area NF
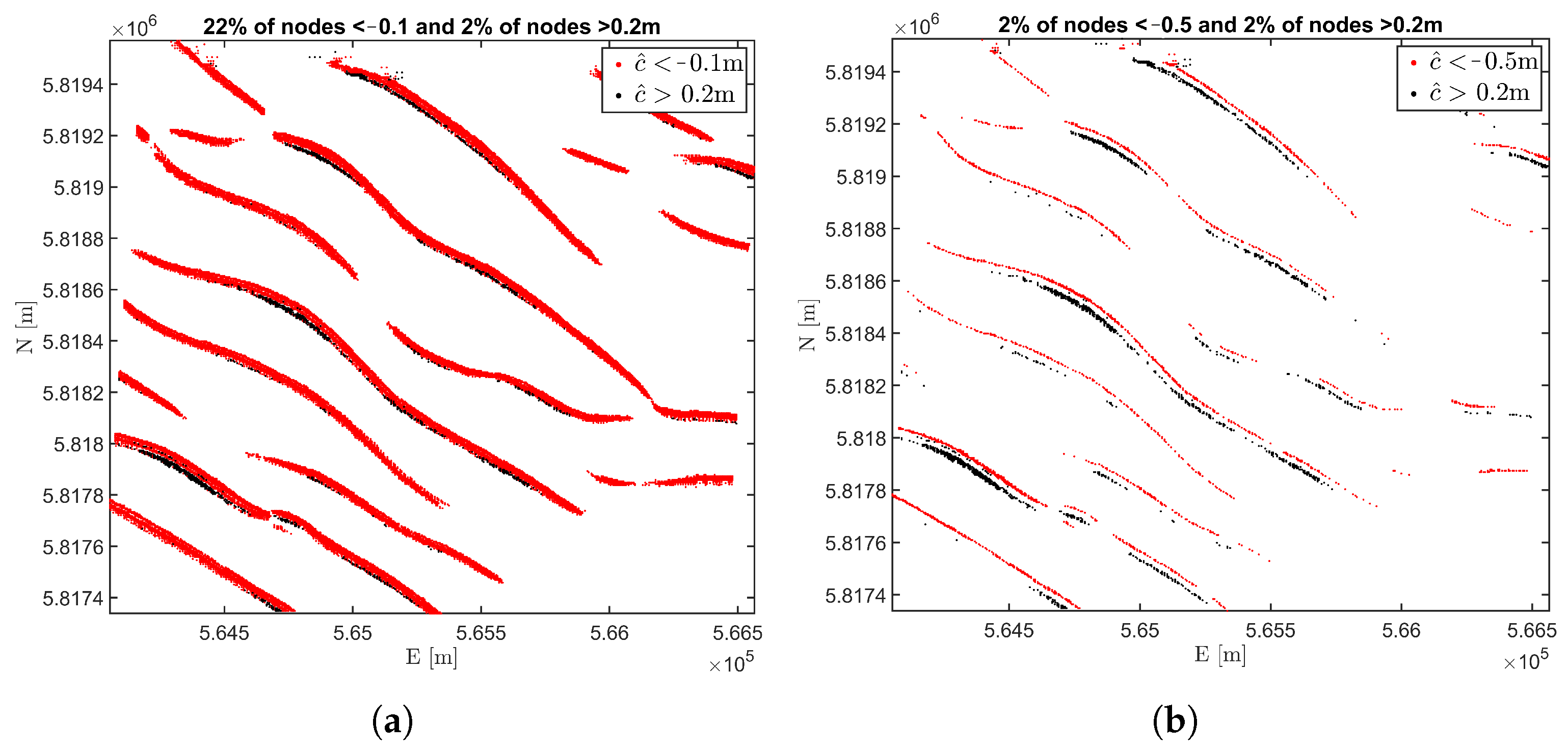
5. Risk-Alert Indicator and Decision Thresholds
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 0D | Zero-dimensional |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| BAS | Bathymetric Archive System |
| BLUE | Best Linear Unbiased Estimation |
| DEM | Digital Elevation Model |
| DGPS | Differential Global Positioning System |
| DIA | Detection, Identification and Adaptation |
| DOF | Degrees of Freedom |
| GLRT | Generalised Likelihood Ratio Test |
| GPS | Global Positioning System |
| IMO | International Maritime Organisation |
| InSAR | Interferometric Synthetic Aperture Radar |
| LAT | Lowest Astronomical Tide |
| LOOCV | Leave-One-Out Cross-Validation |
| MBES | Multibeam Echosounding |
| NCS | Netherlands Continental Shelf |
| NLHS | Netherlands Hydrographic Service |
| OMT | Overall Model Test |
| RWS | Rijkswaterstaat |
| SA | Selective Availability |
| SBES | Single-Beam Echosounding |
| SOLAS | Safety of Life at Sea |
| UTM | Universal Traverse Mercator |
| WGS84 | World Geodetic System 1984 |
| dispersion | |
| expectation | |
| error distribution of simulated observation (Section 2.5) | |
| decision threshold value (Section 5) | |
| probability of incorrectly accepting an alternative hypothesis or | |
| ’level of significance’ | |
| power of test | |
| residuals | |
| adjusted observations | |
| estimated unknown parameters | |
| difference in depth | |
| reference depth of the last survey | |
| ∇ | vector of additional unknown parameters for alternative hypothesis |
| average period between surveys | |
| standard deviation | |
| depth variance | |
| MBES error variance | |
| spatial variance | |
| kriging variance | |
| standard deviation threshold | |
| azimuth East of North | |
| depth observables | |
| random measurement errors | |
| Test statistic with q degrees of freedom | |
| predicted depth | |
| A | design matrix |
| a | acceleration |
| parameters of IHO S44 standards for depth uncertainty | |
| C | specification matrix of alternative hypothesis |
| mean cross-validation error | |
| d | depth parameter |
| seafloor characterisation in time | |
| null hypothesis | |
| alternative hypothesis | |
| i | number of hypotheses; model number |
| j | node index |
| J | total number of nodes |
| k | critical value |
| m | number of observations; number of hypotheses per grid node |
| m | meter |
| M | model |
| N | number of observations per grid cell |
| n | number of unknown parameters; total number of epochs |
| number of piecewise models | |
| p | position; subscript for predicted value (Section 2.5) |
| q | degrees of freedom |
| precision of prediction | |
| precision of the estimator | |
| variance matrix of the observations | |
| R | test ratio |
| r | correlation coefficient |
| S | last survey moment |
| next expected survey | |
| t | time; vector of survey moments |
| v | slope parameter |
| x | unknown parameters (Section 2) |
| Easting and Northing position | |
| simulated observation |
References
- IHO Standards for Hydrographic Surveys. Special Publication No. 44, 6th ed.; Technical Report; International Hydrographic Bureau: Monaco, 2020. [Google Scholar]
- Rijkswaterstaat. Dutch Standards for Hydrographic Surveys. Rijkswaterstaat. 3.0 ed. 2009. Available online: https://puc.overheid.nl/rijkswaterstaat/doc/PUC_158368_31/ (accessed on June 2020).
- McCave, I.N. Sand waves in the North Sea off the coast of Holland. Mar. Geol. 1971, 10, 199–225. [Google Scholar] [CrossRef]
- Nemeth, A.A.; Hulscher, S.J.M.H.; de Vriend, H.J. Modelling sand wave migration in shallow shelf seas. Cont. Shelf Res. 2002, 22, 2795–2806. [Google Scholar] [CrossRef]
- Terwindt, J.H.J. Sand waves in the Southern Bight of the North Sea. Mar. Geol. 1971, 10, 51–67. [Google Scholar] [CrossRef]
- Knaapen, M.A.F. Sandwave Migration Predictor based on shape information. J. Geophys. Res. Earth Surf. 2005, 110, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Dorst, L. Estimating Sea Floor Dynamics in the Southern North Sea to Improve Bathymetric Survey Planning. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2009. [Google Scholar] [CrossRef] [Green Version]
- Van Dijk, T.A.G.P.; Van der Tak, C.; De Boer, W.P.; Kleuskens, M.H.P.; Doornenbal, P.J.; Noorlandt, R.P.; Marges, V.C. The Scientific Validation of the Hydrographic Survey Policy of the Netherlands Hydrographic Office, Royal Netherlands Navy; Technical Report; Deltares: Delft, The Netherlands, 2011. [Google Scholar]
- Besio, G.; Blondeaux, P.; Brocchini, M.; Vittori, G. On the modeling of sand wave migration. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Lindenbergh, R. Parameter estimation and deformation analysis of sand waves and mega ripples. In Proceedings of the 2nd International Workshop on Marine Sand Wave and River Dune Dynamics, Enschede, The Netherlands, 1–2 April 2004. [Google Scholar]
- Pluymaekers, S.; Lindenbergh, R.; Simons, D.; de Ronde, J. A Deformation Analysis of a Dynamic Estuary Using Two-Weekly MBES Surveying. In OCEANS 2007-Europe; Institute of Electrical and Electronics Engineers: Aberdee, UK, 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Huizenga, B. The Interpretation of Seabed Dynamics on the Netherlands Continental Shelf. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2008. [Google Scholar]
- Lindenbergh, R.; Hanssen, R. Eolian deformation detection and modeling using airborne laser altimetry. In Proceedings of the IGARSS 2003, IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1–4. [Google Scholar] [CrossRef]
- Chang, L.; Hanssen, R.F. A Probabilistic Approach for InSAR Time-Series Postprocessing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 421–430. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. Testing Theory; Delft University Press: Delft, The Netherlands, 2000. [Google Scholar]
- Teunissen, P.J.G.; Simons, D.G.; Tiberius, C.C.J.M. Probability and Observation Theory; TU Delft: Delft, The Netherlands, 2009. [Google Scholar]
- Knaapen, M.A.F.; Hulscher, S.J.M.H. Regeneration of sand waves after dredging. Coast. Eng. 2002, 46, 277–289. [Google Scholar] [CrossRef] [Green Version]
- Irish, J.L.; White, T.E. Coastal engineering applications of high-resolution lidar bathymetry. Coast. Eng. 1998, 35, 47–71. [Google Scholar] [CrossRef]
- Brusch, S.; Held, P.; Lehner, S.; Rosenthal, W.; Pleskachevsky, A. Underwater bottom topography in coastal areas from TerraSAR-X data. Int. J. Remote Sens. 2011, 32, 4527–4543. [Google Scholar] [CrossRef]
- Casal, G.; Hedley, J.D.; Monteys, X.; Harris, P.; Cahalane, C.; McCarthy, T. Satellite-derived bathymetry in optically complex waters using a model inversion approach and Sentinel-2 data. Estuar. Coast. Shelf Sci. 2020, 241, 106814. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. SMART-SDB: Sample-specific multiple band ratio technique for satellite-derived bathymetry. Remote Sens. Environ. 2020, 251, 112091. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef] [Green Version]
- Dorst, L. Survey plan improvement by detecting sea floor dynamics in archived echo sounder surveys. Int. Hydrogr. Rev. 2004, 5, 1–15. [Google Scholar]
- Samet, H. An Overview of Quadtrees, Octrees, and Related Hierarchical Data Structures. In Theoretical Foundations of Computer Graphics and CAD; Earnshaw, R.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 51–68. [Google Scholar] [CrossRef] [Green Version]
- Toodesh, R.; Verhagen, S. Adaptive, variable resolution grids for bathymetric applications using a quadtree approach. J. Appl. Geod. 2018, 12, 311–322. [Google Scholar] [CrossRef] [Green Version]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003. [Google Scholar]
- Van Dijk, T.; Kleuskens, M.H.P.; Dorst, L.L.; Van der Tak, C.; Doornenbal, P.J.; Van der Spek, A.J.F.; Hoogendoorn, R.M.; Rodriguez Aguilera, D.; Menninga, P.J.; Noorlandt, R.P. Quantified and applied sea-bed dynamics of the Netherlands Continental Shelf and the Wadden Sea. In Proceedings of the Jubilee Conference Proceedings, NCK-Days 2012: Crossing Borders in Coastal Research, Enschede, The Netherlands, 13–16 March 2012. [Google Scholar]
- Calder, B. On the uncertainty of archive hydrographic data sets. J. Ocean. Eng. IEEE 2006, 31, 249–265. [Google Scholar] [CrossRef]
- Hare, R.; Eakins, B.; Amante, C. Modelling bathymetric uncertainty. Int. Hydrogr. Rev. 2011, 6, 1–30. [Google Scholar]
- Chiles, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; Wiley Series in Probability and Statistics; Applied Probability and Statistics Section; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Digipol, G. Rijkwaterstaat, Rijkstituut voor Kust en Zee, The Hague, The Netherlands; Technical Report; Rijkswaterstaat: Utrecht, The Netherlands, 2007. [Google Scholar]
- Verhagen, S.; Teunissen, P.J.G. Least-Squares Estimation and Kalman Filtering. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 639–660. [Google Scholar] [CrossRef]
- Tukey, J.W. We Need Both Exploratory and Confirmatory. Am. Stat. 1980, 34, 23–25. [Google Scholar] [CrossRef]
- Van Dijk, T.A.G.P.; Lindenbergh, R.C.; Egberts, P.J.P. Separating bathymetric data representing multiscale rhythmic bed forms: A geostatistical and spectral method compared. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Guillen, J. Atlas of Bedforms in the Western Mediterranean; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Velsink, H. The Elements of Deformation Analysis: Blending Geodetic Observations and Deformation Hypotheses. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Velsink, H. On the deformation analysis of point fields. J. Geod. 2015, 89, 1071–1087. [Google Scholar] [CrossRef] [Green Version]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Goovaerts, P.; Webster, R.; Dubois, J.P. Assessing the risk of soil contamination in the Swiss Jura using indicator geostatistics. Environ. Ecol. Stat. 1997, 4, 49–64. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Optimal interpolation and isarithmic mapping of soil properties. VI. Disjunctive kriging and mapping the conditional porbability. J. Soil Sci. 1989, 40, 497–512. [Google Scholar] [CrossRef]
- Armstrong, M.; Matheron, G. Disjunctive kriging revisited: Part I. Math. Geol. 1986, 18, 711–728. [Google Scholar] [CrossRef]
- Journel, A.G. Nonparametric estimation of spatial distributions. J. Int. Assoc. Math. Geol. 1983, 15, 445–468. [Google Scholar] [CrossRef]








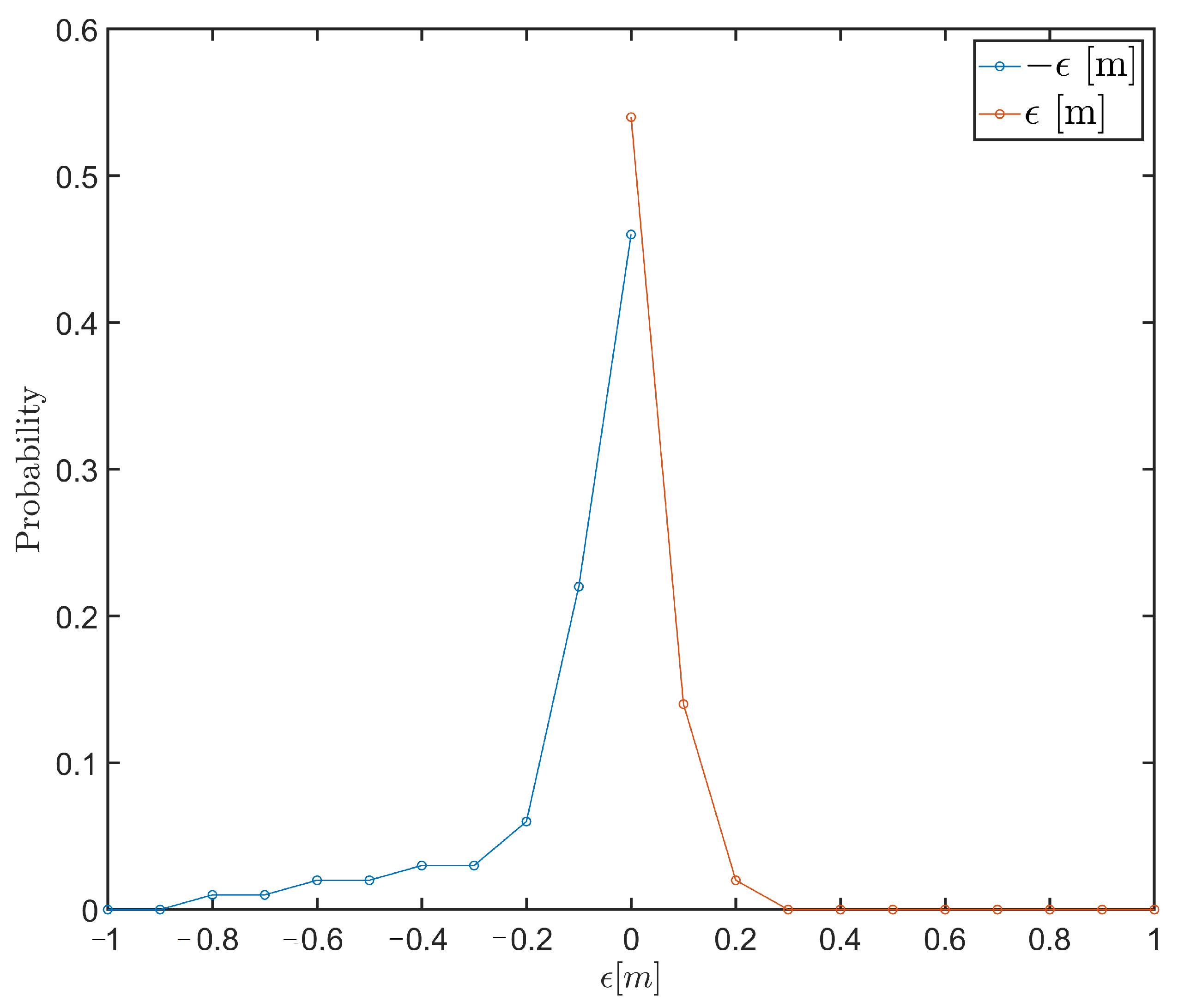
| Hypothesis Number, i | Hypothesis | Unknown Parameters |
|---|---|---|
| 1 | Stable | |
| 2 | Constant Velocity | , |
| 3 | Quadratic | a, , |
| Piecewise Linear | , , , |
| Survey Code | Date [yyyymm] | Line Spacing [m] |
|---|---|---|
| sid8324 | 198908 | 50 |
| HY71lm47-51 | 199003 | 50 |
| HY95069 | 199511 | 125 |
| HY99091 | 199903 | 125 |
| HY02143 | 200306 | 125 |
| HY05166 | 200505 | 5 |
| 021-07 | 200601 | 5 |
| sid12808 | 200909 | 5 |
| 15602 | 201008 | 5 |
| HY13114 | 201303 | 5 |
| sid18294 | 201408 | 5 |
| sid18405 | 201409 | 5 |
| 19244 | 201511 | 5 |
| Water Depth [m] (LAT) | [m] |
|---|---|
| 0 to −20 | −0.1 |
| −21 to −30 | −0.5 |
| <−30 | −1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toodesh, R.; Verhagen, S.; Dagla, A. Prediction of Changes in Seafloor Depths Based on Time Series of Bathymetry Observations: Dutch North Sea Case. J. Mar. Sci. Eng. 2021, 9, 931. https://doi.org/10.3390/jmse9090931
Toodesh R, Verhagen S, Dagla A. Prediction of Changes in Seafloor Depths Based on Time Series of Bathymetry Observations: Dutch North Sea Case. Journal of Marine Science and Engineering. 2021; 9(9):931. https://doi.org/10.3390/jmse9090931
Chicago/Turabian StyleToodesh, Reenu, Sandra Verhagen, and Anastasia Dagla. 2021. "Prediction of Changes in Seafloor Depths Based on Time Series of Bathymetry Observations: Dutch North Sea Case" Journal of Marine Science and Engineering 9, no. 9: 931. https://doi.org/10.3390/jmse9090931
APA StyleToodesh, R., Verhagen, S., & Dagla, A. (2021). Prediction of Changes in Seafloor Depths Based on Time Series of Bathymetry Observations: Dutch North Sea Case. Journal of Marine Science and Engineering, 9(9), 931. https://doi.org/10.3390/jmse9090931






