Reinterpreting the Bruun Rule in the Context of Equilibrium Shoreline Models
Abstract
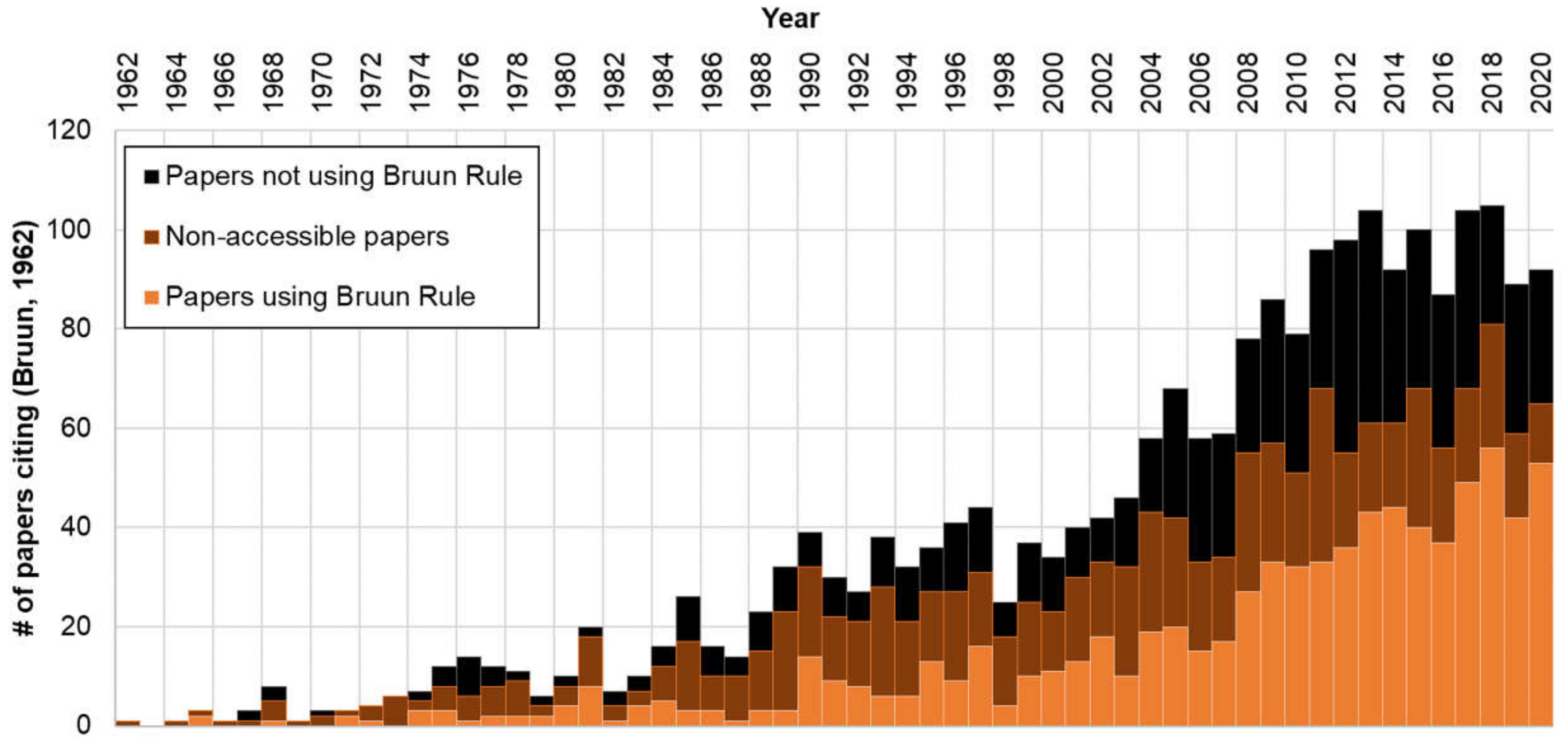
:1. Introduction
2. Sea-Level-Driven Recession and Equilibrium Shoreline Models
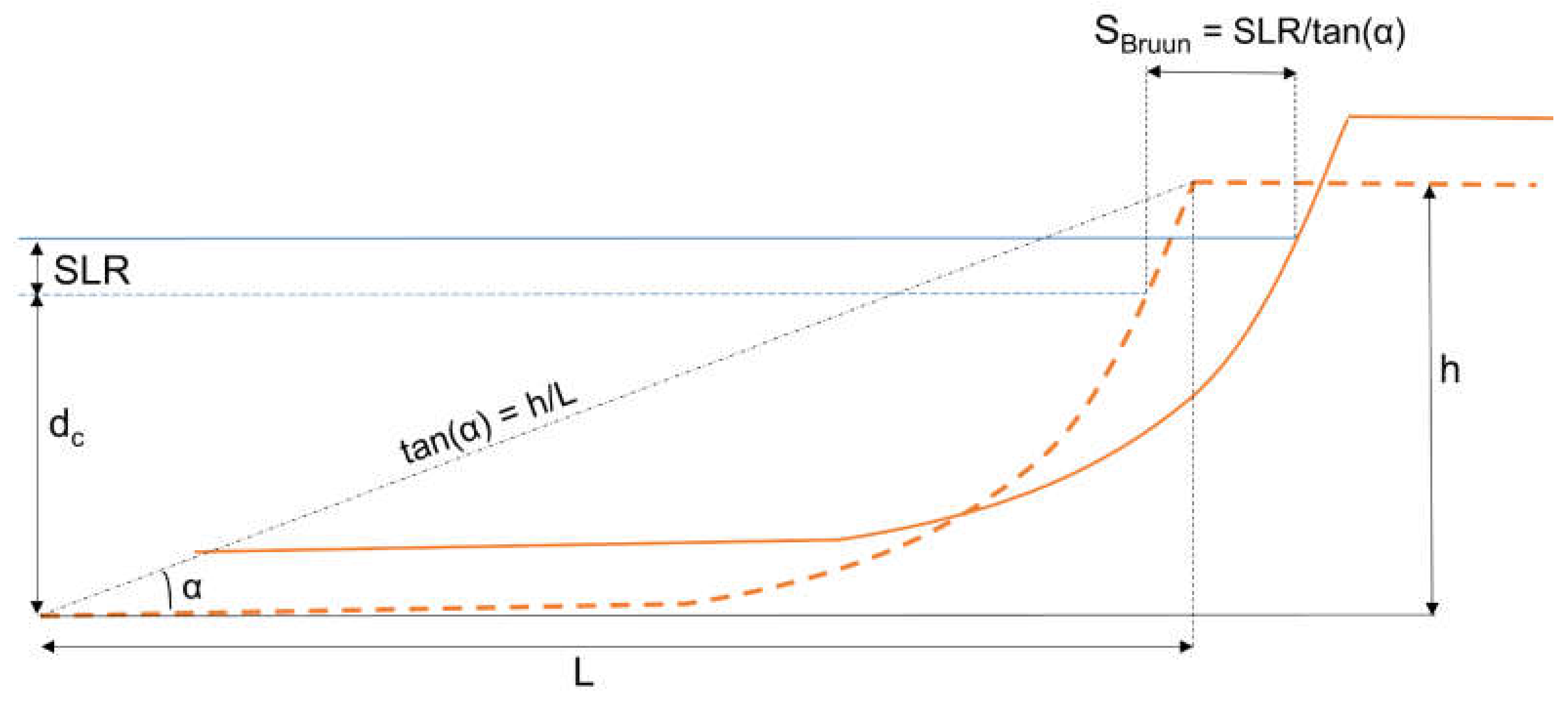
2.1. The Bruun Model
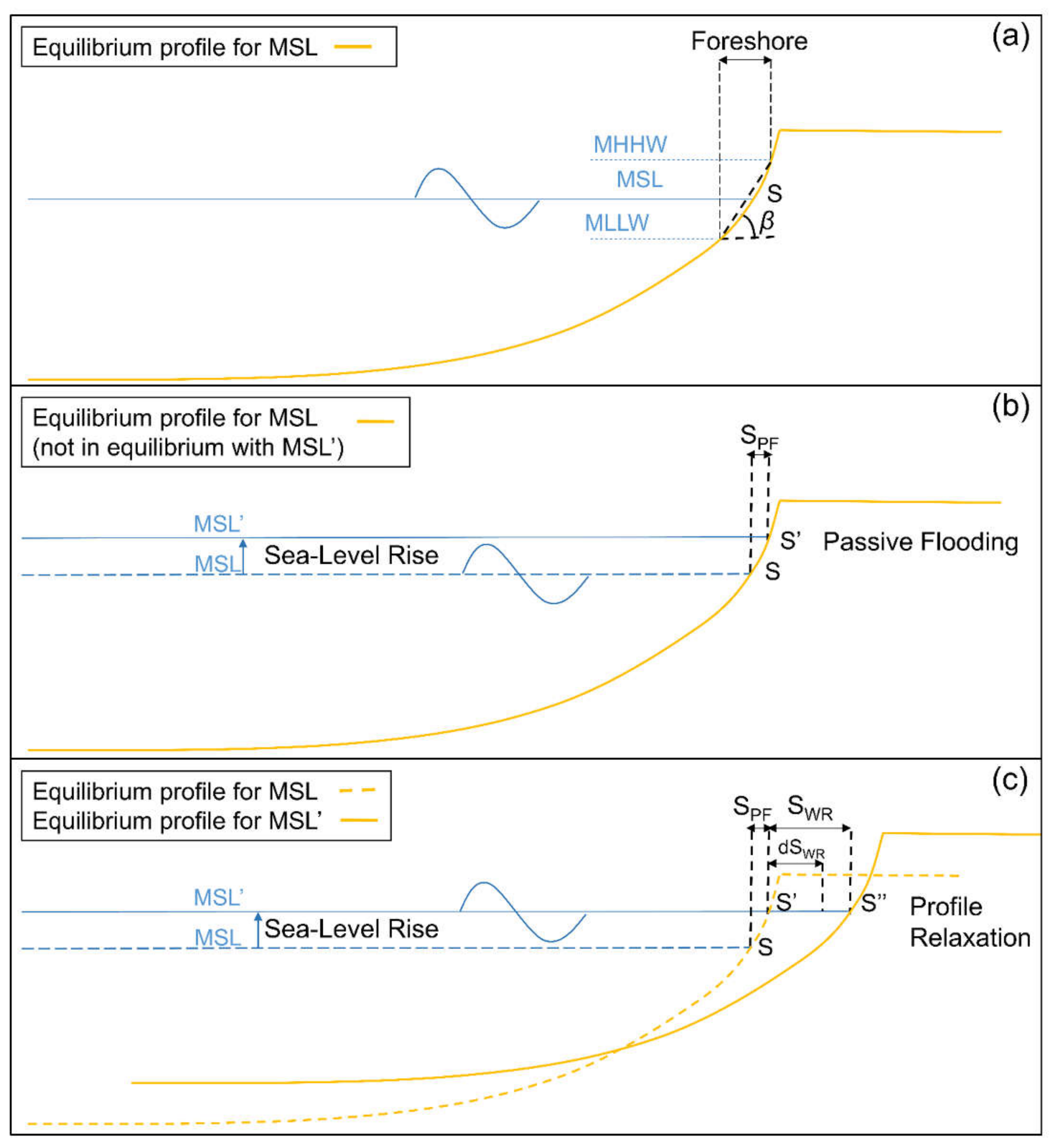
2.2. A physical Interpretation of the Beach Response to Sea-Level Rise
2.3. Disequilibrium and Beach Profile Relaxation in Equilibrium Shoreline Models
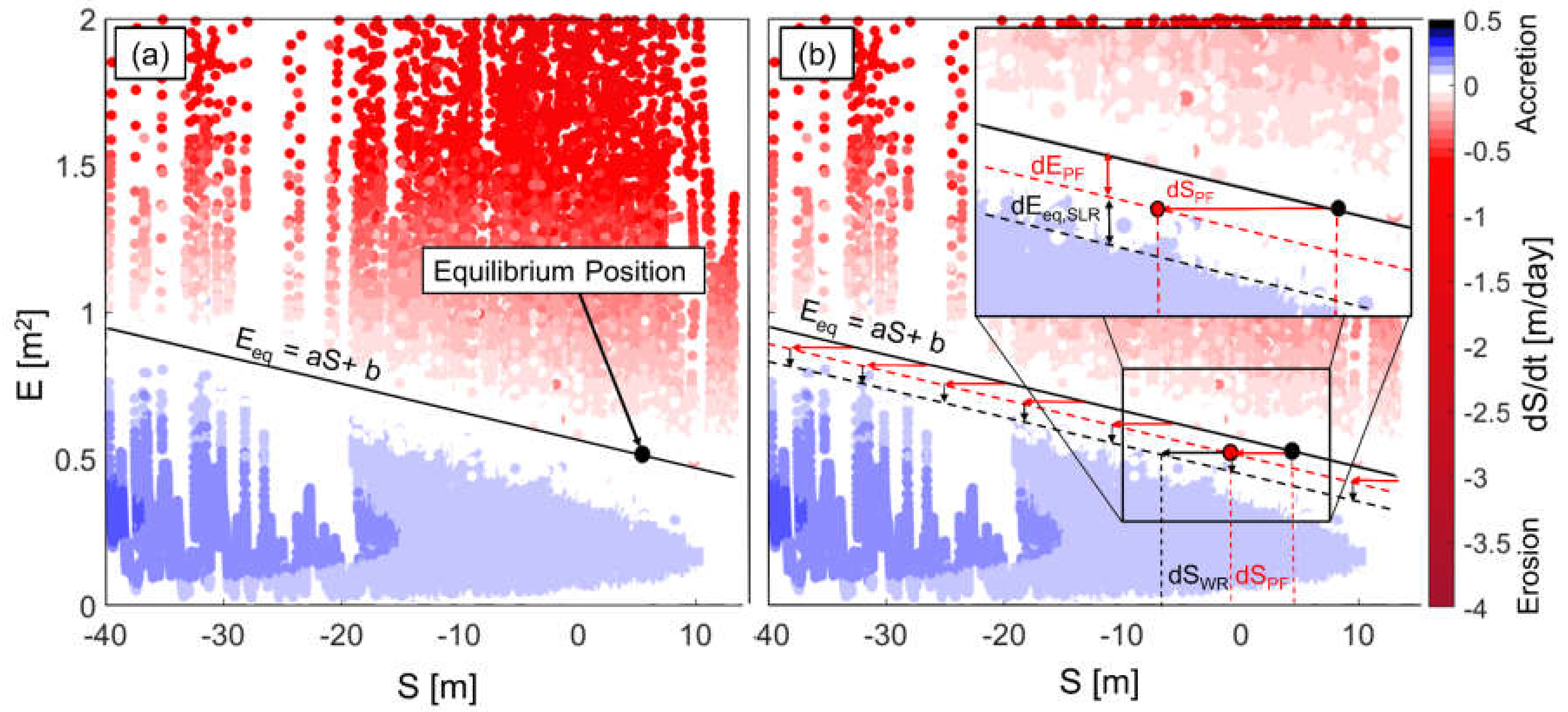
2.4. Sea-Level-Rise-Driven Disequilibrium within ESMs
3. Integrating Sea-Level Rise in Equilibrium Shoreline Models
3.1. Linear Combinations of SLR Effects and ESMs
3.2. SLR Effects and ESMs with Dynamic Interactions
4. Model Application
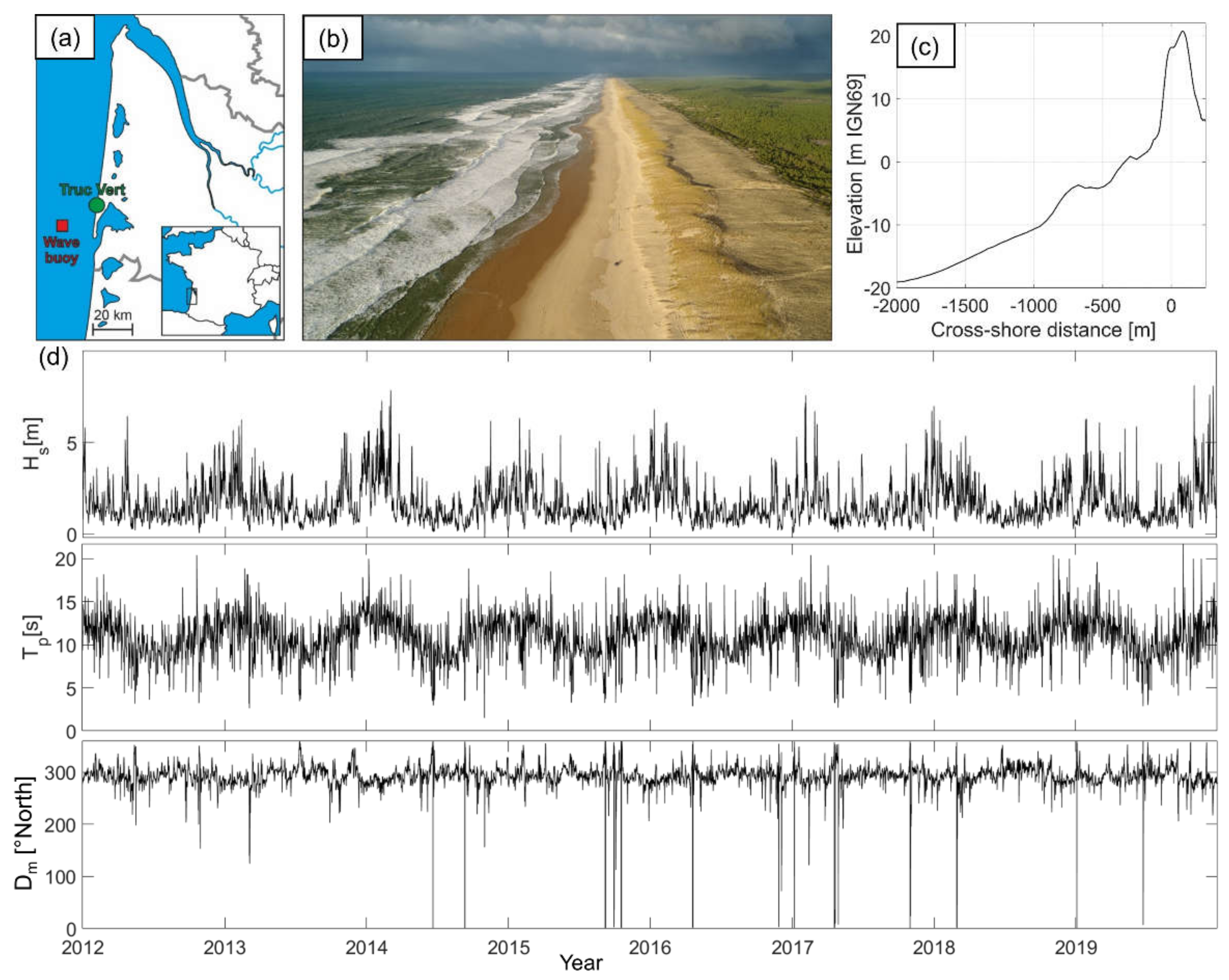
4.1. Test Case
4.2. Integration of SLR Impact Model into ESMs
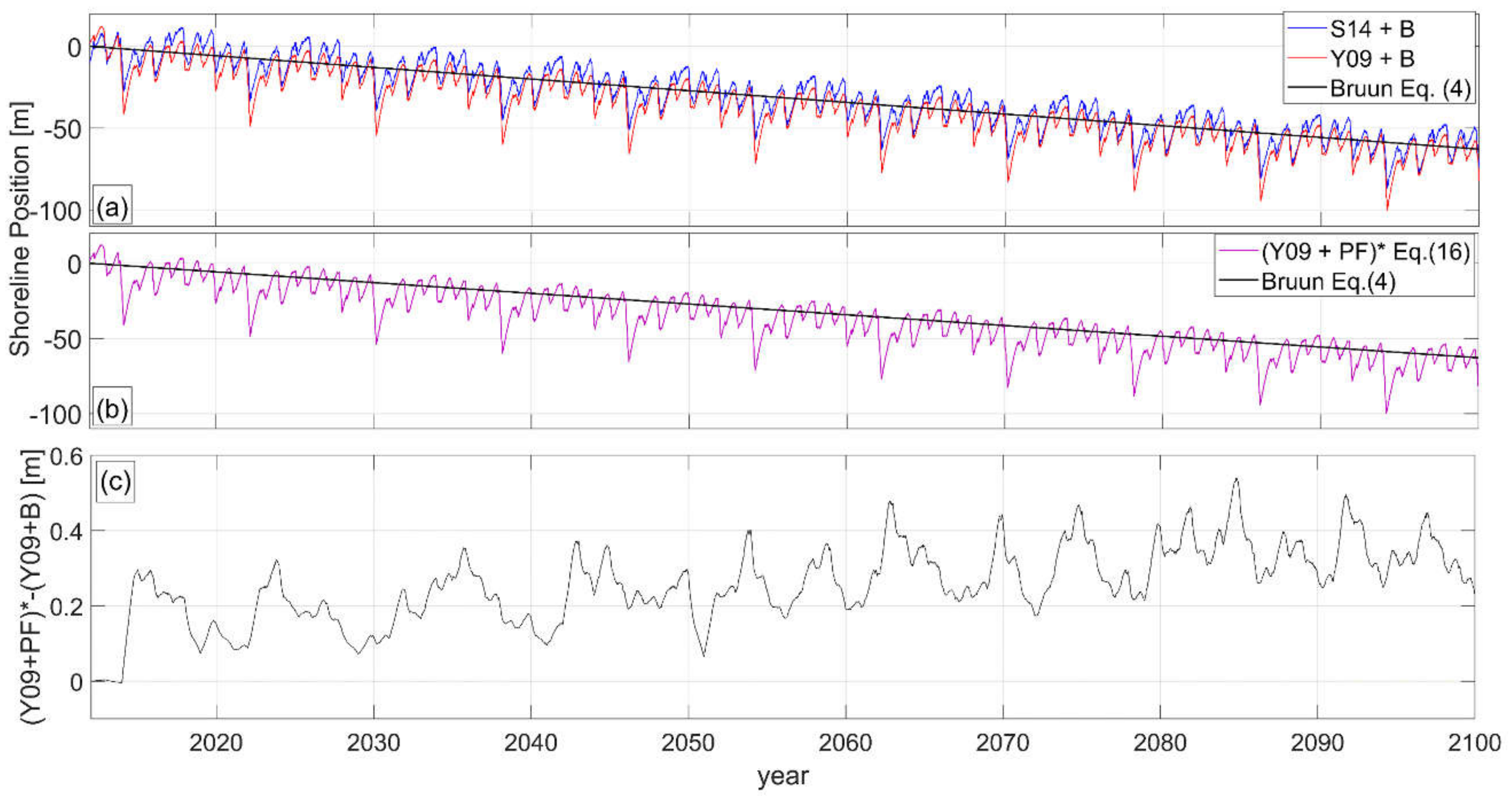
4.3. Results
5. Discussion
5.1. Bruun Rule Interpretation
5.2. Integrating ESMs and SLR-Driven Shoreline Models
5.3. Applications of Integrated Shoreline Models and Uncertainties
5.4. Beyond the Bruun Rule
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
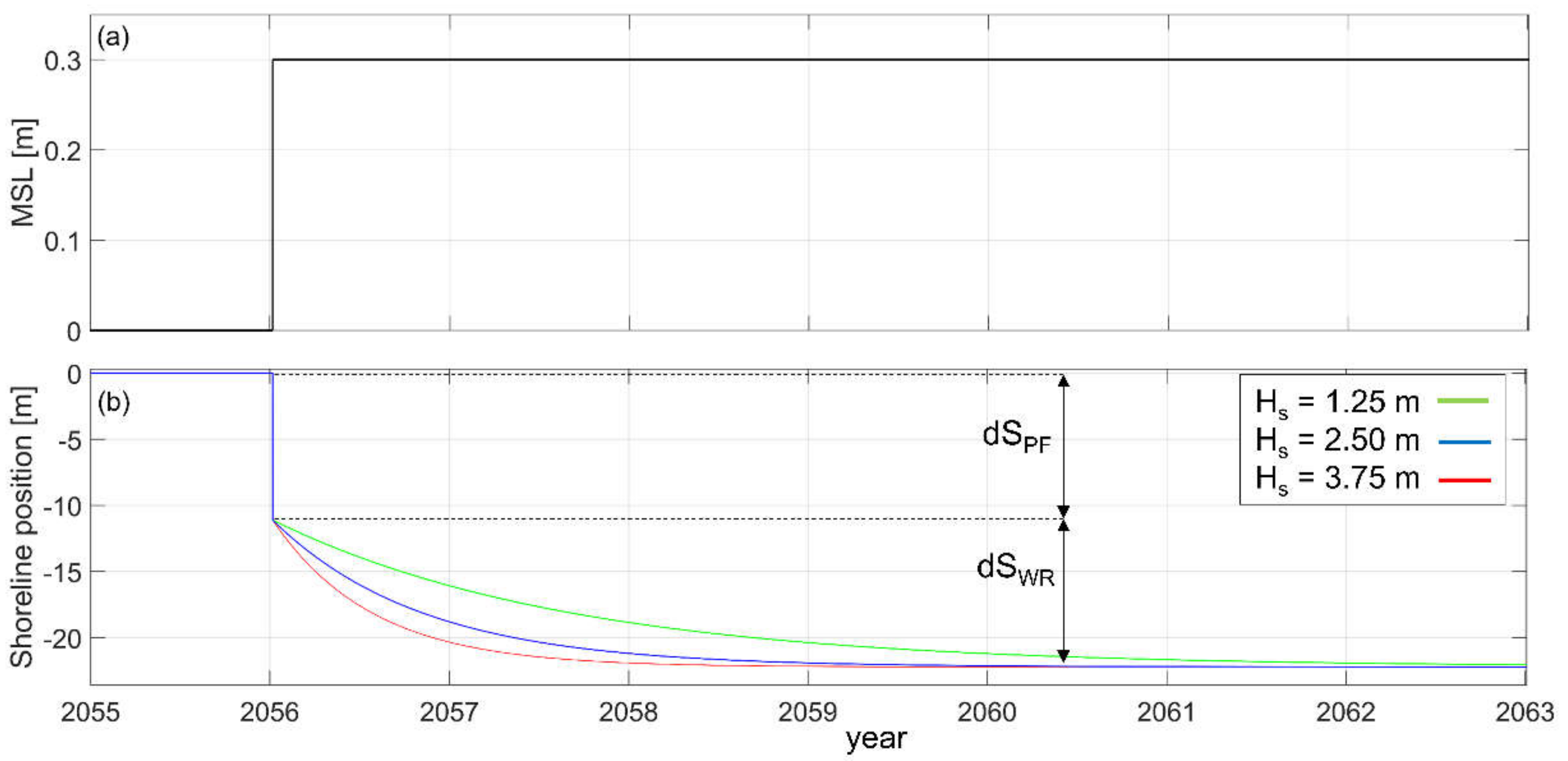
Appendix A. Passive Flooding, Wave Reshaping and the Bruun Rule
Appendix B. Integrating SLR-Driven Disequilibrium into ESMs with Feedback
References
- Ranasinghe, R. Assessing climate change impacts on open sandy coasts: A review. Earth-Sci. Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef] [Green Version]
- Oppenheimer, M.; Glavovic, B.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; Deconto, R.M.; Ghosh, T.; et al. Sea level rise and implications for low-lying islands, coasts and communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., Eds.; 2019. [Google Scholar]
- Toimil, A.; Camus, P.; Losada, I.J.; Le Cozannet, G.; Nicholls, R.J.; Idier, D.; Maspataud, A. Climate change-driven coastal erosion modelling in temperate sandy beaches: Methods and uncertainty treatment. Earth-Sci. Rev. 2020, 202, 103110. [Google Scholar] [CrossRef]
- Vitousek, S.; Barnard, P.L.; Limber, P. Can beaches survive climate change? J. Geophys. Res. Earth Surf. 2017, 122, 1060–1067. [Google Scholar] [CrossRef]
- Bruun, P. Sea-level rise as a cause of shore erosion. J. Waterw. Harb. Div. 1962, 88, 117–130. [Google Scholar] [CrossRef]
- Atkinson, A.L.; Baldock, T.E.; Birrien, F.; Callaghan, D.P.; Nielsen, P.; Beuzen, T.; Turner, I.L.; Blenkinsopp, C.E.; Ranasinghe, R. Laboratory investigation of the Bruun Rule and beach response to sea level rise. Coast. Eng. 2018, 136, 183–202. [Google Scholar] [CrossRef]
- Bayle, P.M.; Beuzen, T.; Blenkinsopp, C.E.; Baldock, T.E.; Turner, I.L. Beach profile changes under sea level rise in laboratory flume experiments at different scale. J. Coast. Res. 2020, 95, 192–196. [Google Scholar] [CrossRef]
- Miller, J.K.; Dean, R.G. A simple new shoreline change model. Coast. Eng. 2004, 51, 531–556. [Google Scholar] [CrossRef]
- Yates, M.L.; Guza, R.T.; O’Reilly, W.C. Equilibrium shoreline response: Observations and modeling. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Davidson, M.A.; Splinter, K.D.; Turner, I.L. A simple equilibrium model for predicting shoreline change. Coast. Eng. 2013, 73, 191–202. [Google Scholar] [CrossRef]
- Splinter, K.D.; Turner, I.L.; Davidson, M.A.; Barnard, P.; Castelle, B.; Oltman-Shay, J. A generalized equilibrium model for predicting daily to interannual shoreline response. J. Geophys. Res. Earth Surf. 2014, 119, 1936–1958. [Google Scholar] [CrossRef] [Green Version]
- Jara, M.S.; González, M.; Medina, R. Shoreline evolution model from a dynamic equilibrium beach profile. Coast. Eng. 2015, 99, 1–14. [Google Scholar] [CrossRef]
- Castelle, B.; Marieu, V.; Bujan, S.; Ferreira, S.; Parisot, J.-P.; Capo, S.; Sénéchal, N.; Chouzenoux, T. Equilibrium shoreline modelling of a high-energy meso-macrotidal multiple-barred beach. Mar. Geol. 2014, 347, 85–94. [Google Scholar] [CrossRef]
- Lemos, C.; Floc’h, F.; Yates, M.; Le Dantec, N.; Marieu, V.; Hamon, K.; Cuq, V.; Suanez, S.; Delacourt, C. Equilibrium modeling of the beach profile on a macrotidal embayed low tide terrace beach. Ocean. Dyn. 2018, 68, 1207–1220. [Google Scholar] [CrossRef]
- Banno, M.; Kuriyama, Y.; Hashimoto, N. Equilibrium-based foreshore beach profile change model for long-term data. In The Proceedings of the Coastal Sediments 2015; World Scientific: Singapore, 2015. [Google Scholar] [CrossRef]
- Dean, R.G.; Houston, J.R. Determining shoreline response to sea level rise. Coast. Eng. 2016, 114, 1–8. [Google Scholar] [CrossRef]
- Vitousek, S.; Barnard, P.L.; Limber, P.; Erikson, L.; Cole, B. A model integrating longshore and cross-shore processes for predicting long-term shoreline response to climate change. J. Geophys. Res. Earth Surf. 2017, 122, 782–806. [Google Scholar] [CrossRef]
- D’Anna, M.; Idier, D.; Castelle, B.; Le Cozannet, G.; Rohmer, J.; Robinet, A. Impact of model free parameters and sea-level rise uncertainties on 20-years shoreline hindcast: The case of Truc Vert beach (SW France). Earth Surf. Process. Landf. 2020, 45, 1895–1907. [Google Scholar] [CrossRef]
- D’Anna, M.; Castelle, B.; Idier, D.; Rohmer, J.; Le Cozannet, G.; Thieblemont, R.; Bricheno, L. Uncertainties in shoreline projections to 2100 at Truc Vert beach (France): Role of sea-level rise and equilibrium model assumptions. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006160. [Google Scholar] [CrossRef]
- Bruun, P. Review of conditions for uses of the Bruun Rule of erosion. Coast. Eng. 1983, 7, 77–89. [Google Scholar] [CrossRef]
- Bruun, P. The Bruun Rule of erosion by sea-level rise: A discussion on large-scale two- and three-dimensional usages. J. Coast. Res. 1988, 4, 627–648. [Google Scholar]
- Dean, R.G. Equilibrium beach profiles: Characteristics and applications. J. Coast. Res. 1991, 7, 53–84. [Google Scholar]
- Hallermeier, R.J. Uses for a calculated limit depth to beach erosion. In Proceedings of the 16th Coastal Engineering Conference; ASCE: New York, NY, USA, 1978; pp. 1493–1512. [Google Scholar]
- Nicholls, R.J. Assessing erosion of sandy beaches due to sea-level rise. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 1998, 15, 71–76. [Google Scholar] [CrossRef]
- Anderson, T.R.; Fletcher, C.H.; Barbee, M.M.; Romine, B.M.; Lemmo, S.; Delevaux, J.M.S. Modeling multiple sea level rise stresses reveals up to twice the land at risk compared to strictly passive flooding methods. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davidson-Arnott, R.G.D. Conceptual model of the effects of sea level rise on sandy coasts. J. Coast. Res. 2005, 216, 1166–1172. [Google Scholar] [CrossRef] [Green Version]
- Cooper, J.A.G.; Pilkey, O.H. Sea-level rise and shoreline retreat: Time to abandon the Bruun Rule. Glob. Planet. Chang. 2004, 43, 157–171. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.; Stive, M.J.F. Estimating coastal recession due to sea level rise: Beyond the Bruun rule. Clim. Chang. 2012, 110, 561–574. [Google Scholar] [CrossRef] [Green Version]
- Rosati, J.D.; Dean, R.G.; Walton, T.L. The modified Bruun Rule extended for landward transport. Mar. Geol. 2013, 340, 71–81. [Google Scholar] [CrossRef] [Green Version]
- Wolinsky, M.A.; Murray, A.B. A unifying framework for shoreline migration: 2. Application to wave-dominated coasts. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Wright, L.; Short, A. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Falqués, A.; Garnier, R.; Ojeda, E.; Ribas, F.; Guillen, J. Q2D-morfo: A medium to long term model for beach morphodynamics. Coast. Estuar. Morphoynamics 2007, 1, 71–78. [Google Scholar]
- Toimil, A.; Losada, I.J.; Camus, P.; Díaz-Simal, P. Managing coastal erosion under climate change at the regional scale. Coast. Eng. 2017, 128, 106–122. [Google Scholar] [CrossRef]
- Robinet, A.; Idier, D.; Castelle, B.; Marieu, V. A reduced-complexity shoreline change model combining longshore and cross-shore processes: The LX-Shore model. Environ. Model. Softw. 2018, 109, 1–16. [Google Scholar] [CrossRef]
- Vitousek, S.; Cagigal, L.; Montaño, J.; Rueda, A.; Mendez, F.; Coco, G.; Barnard, P.L. The application of ensemble wave forcing to quantify uncertainty of shoreline change predictions. J. Geophys. Res. Earth Surf. 2021, 126. [Google Scholar] [CrossRef]
- Robinet, A.; Castelle, B.; Idier, D.; D’Anna, M.; Le Cozannet, G. Simulating the impact of sea-level rise and offshore bathymetry on embayment shoreline changes. J. Coast. Res. 2020, 95, 1263–1267. [Google Scholar] [CrossRef]
- Jaramillo, C.; Jara, M.S.; González, M.; Medina, R. A shoreline evolution model considering the temporal variability of the beach profile sediment volume (sediment gain/loss). Coast. Eng. 2020, 156, 103612. [Google Scholar] [CrossRef]
- Antolínez, J.A.A.; Méndez, F.J.; Anderson, D.; Ruggiero, P.; Kaminsky, G.M. Predicting climate-driven coastlines with a simple and efficient multiscale model. J. Geophys. Res. Earth Surf. 2019, 124, 1596–1624. [Google Scholar] [CrossRef] [Green Version]
- Robinet, A.; Castelle, B.; Idier, D.; Le Cozannet, G.; Déqué, M.; Charles, E. Statistical modeling of interannual shoreline change driven by North Atlantic climate variability spanning 2000–2014 in the Bay of Biscay. Geo-Mar. Lett. 2016, 36, 479–490. [Google Scholar] [CrossRef] [Green Version]
- Larson, M.; Hoan, L.X.; Hanson, H. Direct formula to compute wave height and angle at incipient breaking. J. Waterw. Port Coast. Ocean. Eng. 2010, 136, 119–122. [Google Scholar] [CrossRef]
- Thiéblemont, R.; Le Cozannet, G.; Toimil, A.; Meyssignac, B.; Losada, I.J. Likely and high-end impacts of regional sea-level rise on the shoreline change of European sandy coasts under a high greenhouse gas emissions scenario. Water 2019, 11, 2607. [Google Scholar] [CrossRef] [Green Version]
- Yates, M.L.; Guza, R.T.; O’Reilly, W.C.; Hansen, J.E.; Barnard, P.L. Equilibrium shoreline response of a high wave energy beach. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Ludka, B.C.; Guza, R.T.; O’Reilly, W.C.; Yates, M.L. Field evidence of beach profile evolution toward equilibrium. J. Geophys. Res. Ocean. 2015, 120, 7574–7597. [Google Scholar] [CrossRef] [Green Version]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 20–69. [Google Scholar] [CrossRef]
- Castelle, B.; Bujan, S.; Marieu, V.; Ferreira, S. 16 years of topographic surveys of rip-channelled high-energy meso-macrotidal sandy beach. Sci. Data 2020, 7, 410. [Google Scholar] [CrossRef] [PubMed]
- Banno, M.; Kuriyama, Y. Supermoon drives beach morphological changes in the swash zone. Geophys. Res. Lett. 2020, 47, e2020GL089745. [Google Scholar] [CrossRef]
- SCOR Working group 89. The response of beaches to sea-level changes: A review of predictive models. J. Coast. Res. 1991, 7, 895–921. [Google Scholar]
- Stive, M.; Ranasinghe, R.; Cowell, P.J. Sea level rise and coastal erosion. In Handbook of Coastal and Ocean Engineering; Kim, Y., Ed.; World Scientific: Singapore, 2010; pp. 1023–1037. [Google Scholar]
- Cooper, J.A.G.; Masselink, G.; Coco, G.; Short, A.D.; Castelle, B.; Rogers, K.; Anthony, E.; Green, A.N.; Kelley, J.T.; Pilkey, O.H.; et al. Sandy beaches can survive sea-level rise. Nat. Clim. Chang. 2020, 10, 993–995. [Google Scholar] [CrossRef]
- Morim, J.; Hemer, M.; Wang, X.L.; Cartwright, N.; Trenham, C.; Semedo, A.; Young, I.; Bricheno, L.; Camus, P.; Casas-Prat, M.; et al. Robustness and uncertainties in global multivariate wind-wave climate projections. Nat. Clim. Chang. 2019, 9, 711–718. [Google Scholar] [CrossRef] [Green Version]
- Splinter, K.D.; Turner, I.L.; Reinhardt, M.; Ruessink, G. Rapid adjustment of shoreline behavior to changing seasonality of storms: Observations and modelling at an open-coast beach. Earth Surf. Process. Landf. 2017, 42, 1186–1194. [Google Scholar] [CrossRef]
- Ibaceta, R.; Splinter, K.D.; Harley, M.D.; Turner, I.L. Enhanced coastal shoreline modeling using an ensemble kalman filter to include nonstationarity in future wave climates. Geophys. Res. Lett. 2020, 47, e2020GL090724. [Google Scholar] [CrossRef]
- Splinter, K.D.; Turner, I.L.; Davidson, M.A. How much data is enough? The importance of morphological sampling interval and duration for calibration of empirical shoreline models. Coast. Eng. 2013, 77, 14–27. [Google Scholar] [CrossRef]
- Ruessink, B.G. Predictive uncertainty of a nearshore bed evolution model. Cont. Shelf Res. 2005, 25, 1053–1069. [Google Scholar] [CrossRef]
- Simmons, J.A.; Harley, M.D.; Marshall, L.A.; Turner, I.L.; Splinter, K.D.; Cox, R.J. Calibrating and assessing uncertainty in coastal numerical models. Coast. Eng. 2017, 125, 28–41. [Google Scholar] [CrossRef]
- Kroon, A.; de Schipper, M.A.; van Gelder, P.H.A.J.M.; Aarninkhof, S.G.J. Ranking uncertainty: Wave climate variability versus model uncertainty in probabilistic assessment of coastline change. Coast. Eng. 2020, 158, 103673. [Google Scholar] [CrossRef]
- Cagigal, L.; Rueda, A.; Anderson, D.; Ruggiero, P.; Merrifield, M.A.; Montaño, J.; Coco, G.; Méndez, F.J. A multivariate, stochastic, climate-based wave emulator for shoreline change modelling. Ocean. Model. 2020, 154, 101695. [Google Scholar] [CrossRef]
- Pringle, J.; Stretch, D.D. On a new statistical wave generator based on atmospheric circulation patterns and its applications to coastal shoreline evolution. Comput. Geosci. 2021, 149, 104707. [Google Scholar] [CrossRef]
- Athanasiou, P.; van Dongeren, A.; Giardino, A.; Vousdoukas, M.; Gaytan-Aguilar, S.; Ranasinghe, R. Global distribution of nearshore slopes with implications for coastal retreat. Earth Syst. Sci. Data 2019, 11, 1515–1529. [Google Scholar] [CrossRef] [Green Version]
- Athanasiou, P.; van Dongeren, A.; Giardino, A.; Vousdoukas, M.I.; Ranasinghe, R.; Kwadijk, J. Uncertainties in projections of sandy beach erosion due to sea level rise: An analysis at the European scale. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Le Cozannet, G.; Oliveros, C.; Castelle, B.; Garcin, M.; Idier, D.; Pedreros, R.; Rohmer, J. Uncertainties in sandy shorelines evolution under the Bruun Rule assumption. Front. Mar. Sci. 2016, 3, 49. [Google Scholar] [CrossRef] [Green Version]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Walker, A.; Turner, I.L. Beach slopes from satellite-derived shorelines. Geophys. Res. Lett. 2020, 47, e2020GL088365. [Google Scholar] [CrossRef]
- Davidson, M. Forecasting coastal evolution on time-scales of days to decades. Coast. Eng. 2021, 168, 103928. [Google Scholar] [CrossRef]
- Banno, M.; Nakamura, S.; Kosako, T.; Nakagawa, Y.; Yanagishima, S.; Kuriyama, Y. Long-Term observations of beach variability at Hasaki, Japan. J. Mar. Sci. Eng. 2020, 8, 871. [Google Scholar] [CrossRef]
- Barnard, P.L.; Hoover, D.; Hubbard, D.M.; Snyder, A.; Ludka, B.C.; Allan, J.; Kaminsky, G.M.; Ruggiero, P.; Gallien, T.W.; Gabel, L.; et al. Extreme oceanographic forcing and coastal response due to the 2015–2016 El Niño. Nat. Commun. 2017, 8, 14365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, Y.H.; Barthélemy, E. Combined longshore and cross-shore shoreline model for closed embayed beaches. Coast. Eng. 2020, 158, 103692. [Google Scholar] [CrossRef]


| Simulation | Model | ΔD | SLR-Driven Model | k+ | k− | a | b | Φ |
|---|---|---|---|---|---|---|---|---|
| S14 NoSLR | Equation (4) | ΔD2 | - | 1.01−8 [ms−1(W/m)−0.5] | 4.40−8 [ms−1(W/m)−0.5] | - | - | 1187 [days] |
| S14 + B | Equation (9) | ΔD2 | Bruun | |||||
| Y09 NoSLR | Equation (4) | ΔD1 | - | 0.54 [ms−1/m] | 0.68 [ms−1/m] | −0.01 [m2/m] | 0.55 [m2] | - |
| Y09 + B | Equations (10)–(12) | ΔD1 | Bruun | |||||
| (Y09 + PF)* | Equation (15) | ΔD *1 | PF |
| Shoreline Position | |||
|---|---|---|---|
| Model | 8-Year Mean from at 2100 [m] | [min; Max] Over Last 8-Years [m] | σ Over Last 8-Years [m] |
| (Y09 + PF)* | −58 | [−41; −100] | 8.7 |
| (Y09 + B) | −58.5 | [−41; −100] | 8.7 |
| Bruun | −55 | [−55; −55] | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Anna, M.; Idier, D.; Castelle, B.; Vitousek, S.; Le Cozannet, G. Reinterpreting the Bruun Rule in the Context of Equilibrium Shoreline Models. J. Mar. Sci. Eng. 2021, 9, 974. https://doi.org/10.3390/jmse9090974
D’Anna M, Idier D, Castelle B, Vitousek S, Le Cozannet G. Reinterpreting the Bruun Rule in the Context of Equilibrium Shoreline Models. Journal of Marine Science and Engineering. 2021; 9(9):974. https://doi.org/10.3390/jmse9090974
Chicago/Turabian StyleD’Anna, Maurizio, Deborah Idier, Bruno Castelle, Sean Vitousek, and Goneri Le Cozannet. 2021. "Reinterpreting the Bruun Rule in the Context of Equilibrium Shoreline Models" Journal of Marine Science and Engineering 9, no. 9: 974. https://doi.org/10.3390/jmse9090974
APA StyleD’Anna, M., Idier, D., Castelle, B., Vitousek, S., & Le Cozannet, G. (2021). Reinterpreting the Bruun Rule in the Context of Equilibrium Shoreline Models. Journal of Marine Science and Engineering, 9(9), 974. https://doi.org/10.3390/jmse9090974







