Abstract
In Ying Xian Fogong Si Shijia Ta 應縣佛宮寺釋迦塔 (Sakyamuni Pagoda of Fogong Temple in Ying County), Shanxi, there are statues set on each floor, and 26 exist in total, with six murals painted on the first floor. The pagoda was designed as a vertically rising Buddhist temple, and the interior space of each floor was customized for the statues. Based on previous research and through surveying and mapping of the architecture and statuary (including the murals on the first floor) combined with geometric design analysis, this paper proposes the following: First, there exists a clear geometric proportion among the interior space and statues on each floor of the pagoda. Second, clear proportional relationships also exist among the statues on each floor, and each of the 26 statues has ‘classical’ proportion rules. Third, the height of the giant Buddha statue on the first floor is the module for not only the height of the statues on each floor but also the construction of the whole pagoda such that the height of the statue on the first floor is 1/6 of the total height of the pagoda (excluding the base). And the ratio of the pagoda’s total height to the first floor’s diameter, the ratio of the total height to the top-story height under the column capital, and all the other geometric proportions are closely related to the architectural modeling. And finally, in the construction of the pagoda, statues, and murals, the scale is deduced to be 1 chi 尺 (Chinese foot) = 29.5 cm. These values give clear scale logics not only to the construction but also to the details of the statues. Accordingly, the most frequently used proportions in the architectural space, statues, and murals of the Pagoda of Fogong Temple are , 3:2, 5:3 (or 8:5), and 9:5, which are imbued with cultural messages, like Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument), Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards), the ancient Chinese world view—tian yuan di fang 天圜地方 (the dome-shaped heaven and the flat, square earth) reflected from “ yuan fang tu 圓方圖 (rounded-square map)” and “fang yuan tu 方圓圖 (squared-circle map)”, ancient Chinese ideas that ”san tian liang di er yi shu 參天兩地而倚數 (‘three’ is the number of the heaven and ‘two’ is the number of the earth, and all numbers are based on them)” and “jiu wu zhi zun 九五之尊 (nine and five are the numbers of the honorable central position)”, and most probably related to the “mandala” of Esoteric Buddhism and to the Western “Golden Ratio”, which all need further research in depth.
1. Introduction
The Sakyamuni Pagoda of Fogong Temple in Ying County, Shanxi Province, also recognized as the Timber Pagoda in Ying County, was constructed in the second year of Qingning during the Liao Dynasty (1056). This remarkable structure stands as the sole surviving ancient pagoda with a pure timber framework in China, holding the distinction of being the world’s largest wooden pagoda. Its architectural significance is unparalleled in its historical context.
Notably commendable is the pagoda’s unique architectural feature known as the five “ming ceng 明層 (bright layers)”. These layers, interspersed with “an ceng 暗層 (hidden layers)” give the structure the form of “wai wu nei jiu 外五內九 (outside five inside nine)”.1 Each of these layers, referred to as “ nei cao 內槽” (inner troughs), houses meticulously preserved statues, totaling 26 in number. This arrangement imparts a semblance of a three-dimensional Buddhist temple, enabling devotees to ascend the pagoda’s steps, worshiping Buddha floor by floor. Consequently, the pagoda unfolds as a vertically layered, three-dimensional Buddhist temple.
Liang Sicheng, in his inaugural paper “Wo Men Suo Zhi Dao De Tang Dai Fo Si Yu Gong Dian 我們所知道的唐代佛寺與宮殿 (Buddhist Temples and Palaces in the Tang Dynasty Known to Us)”, published in Zhongguo Yingzao Xueshe Huikan 中國營造學社彙刊 (the Bulletin of the Society for Research in Chinese Architecture) (1932), pointed out that “the Buddhist Hall is the Buddha’s residence…” (). Following Liang’s point, enshrining and worshiping Buddha is the core function of the Pagoda of Fogong Temple. This aligns with the pagoda’s original name, “shijia ta 釋迦塔 (Sakyamuni Pagoda)”, emphasizing its purpose as a vertical Buddhist hall. The intricate interior space is tailored for the statues on each floor, creating a visual and spatial experience that resonates solemnity and harmony.
Building upon prior study on the Pagoda of Fogong Temple, this paper meticulously measures the architecture and statues (including the mural on the first floor),2 conducting a comprehensive surveying and mapping of the structure. The findings reveal clear geometric proportions within the interior space and statue complex on each floor. These proportions are particularly evident in the relationships between the height of stories and statues and between the giant Buddha statue and the murals on the first floor. The geometric relationships also extend to each statue’s and mural’ s proportions. The statue on the first floor is assumed to have a pivotal role, serving as the module for both subsequent statues and the overall architectural design. The construction scale of the pagoda, statues, and murals is speculated as 1 chi = 29.5 cm. From this, the proportional relationships among the height of the pagoda, the base, each story, the pagoda-top finial, and each statue and mural can be inferred. The construction of the pagoda as a whole also has its “classical” ratio control.
The subsequent sections will provide a brief overview of the existing literature, followed by a detailed analysis of the geometric proportions inherent in the pagoda’s interior space and statue complex and the deduction of the scale of construction. This paper will conclude by summarizing various classical geometric proportions adopted in the construction of the architectural space, the statues, and the murals, including , 3:2, 5:3, 8:5, and 9:5, underscoring their cultural significance such as “tian yuan di fang 天圜地方 (a dome-shaped heaven and a flat, square earth)”, “san tian liang di 參天兩地 (three as the heavenly number and two as the earthly number)”, “jiu wu zhi zun 九五之尊 (the numbers nine and five as denoting an honorable position)”, and even concepts like the “Golden Ratio” and “Esoteric Buddhist mandala”.
2. Literature Review
The pioneering investigation of the Pagoda of Fogong Temple and the statues was undertaken by Liang Sicheng 梁思成 and Mo Zongjiang 莫宗江. Their collaborative efforts encompassed a comprehensive examination, yielding a series of pagoda surveys and official sections, visually representing both architectural features and statues (see Figure 1 and Figure 2). Liang Sicheng’s paper, “Shanxi Yingxian Fogong Si Liao Shijia Muta 山西應縣佛宮寺遼釋迦木塔 (Liao Sakya Timber Pagoda of Fogong Temple in Ying County, Shanxi)” (completed in 1936), provides detailed insights. In this work, Liang highlighted the measured values, such as the approximately 12.30 m height of the Buddha on the first floor, the 4 m height of the two-story Buddha and its base, and the approximately 4.85 m height of the four-story Buddha.

Figure 1.
Section of the Pagoda of Fogong Temple. Source: China Academy of Cultural Heritage. (The Chinese character in the fiture says: Sakya Timber Pagoda of Fogong Temple in Ying County, Shanxi, mapped in September 1934 and drawn in June 1935 by the Society for Research in Chinese Architecture. The authors have obtained the copyright of the figure).
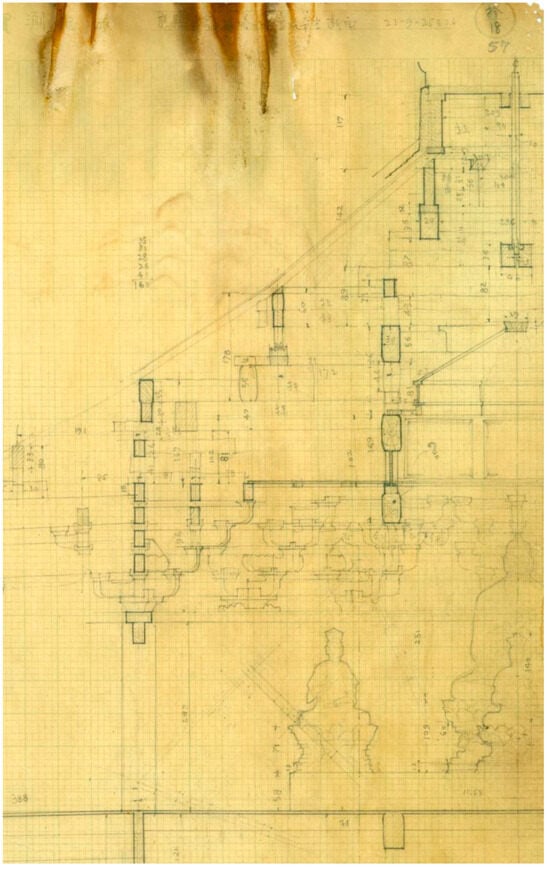
Figure 2.
Surveying draft of the fifth floor and support platform of the Pagoda of Fogong Temple. Source: Memorial Collection of the Society for Research in Chinese Architecture, School of Architecture, Tsinghua University. The authors have obtained the copyright of the figure.
The surveying and mapping drafts (1933) by Liang and Mo, collected in Tsinghua University Archive, have measurements of all statues except the giant Buddha statue on the first floor, which was too big to measure at that time (; ).3 Beyond the Sakyamuni Pagoda of Fogong Temple, Liang Sicheng extended his survey and cartographic endeavors to other Buddhist structures, including the Guanyin Pavilion of Dule Monastery in Ji County, the Three Bodhisattvas Hall of Guangji Monastery in Baodi, the Hall of the Three Sages, Samantabhadra (Puxian) Pavilion, and Mahāvīra Treasure Hall of Shanhua Monastery in Datong, the Bhagavat Sutra Hall of Huayan Lower Monastery in Datong, and the Great East Hall of Foguang Monastery in Mount Wutai. The survey reports authored by Liang often incorporated a dedicated section addressing the aspect of “statues”.
Building upon the preceding research, Chen Mingda 陳明達 conducted a comprehensive examination of the geometric proportions of the Pagoda of Fogong Temple, analyzing the construction from a holistic and detailed perspective, creating a paradigm in the study of the design methodology employed in ancient Chinese timber structures. In his seminal work, Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County) (1966), Chen specified that the first floor of the pagoda reached a height of approximately 11 m. Extending the methodology of Liang and Mo, the section maps in the book depicted the statue complex collectively. Furthermore, Chen also conducted a preliminary exploration of the interior spatial composition of each floor ()4 (Figure 3).
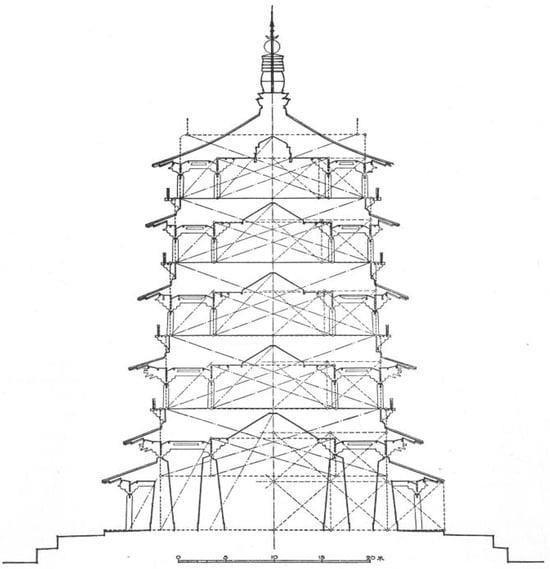
Figure 3.
Composition analysis of Chen Mingda’s sectional drawing of the Pagoda of Fogong Temple. Source: (). The Chinese character 米 means meter, The authors have obtained the copyright of the figure.
In the subsequent “Yingxian Muta Duhou Zhaji 《應縣木塔》讀後札記 (Book Review of Timber Pagoda in Ying County)” (penned shortly after 1980), Mo Zongjiang remarked on the potential influence of Buddhist belief on the interior of the Timber Pagoda (). Mo suggested a parallel with Sutra illustrations and urged a more profound exploration of the “religious functional requirement”, indicating an early awareness of the relationship between interior space, statue layout, and religious function. The archaeologist Su Bai 宿白 later echoed this sentiment, proposing that the Pagoda of Fogong Temple mirrored “the mandala of Mahāvairocana”, inspiring subsequent researchers, which would be expatiated later in the article.
Mo Zongjiang and Chen Mingda’s attention to spatial design and geometric proportions extended to their joint paper “Gongxian Shiku Si Diaoke de Fengge ji Jiqiao 鞏縣石窟雕刻的風格及技巧 (Style and Technique of Carving in Gongxian Cave Temple)” (), focusing on grottoes. The paper underscored deliberate design considerations in cave carving, detailing aspects such as the shape, scale, facade, inner wall, central column, ceiling, and ground. Moreover, it expounded on the geometric proportions of statues in Gongxian Grottoes, exemplified by ratios such as 1:4 and 1:3.5 for the head height to total height in seated Buddha statues, 1:5.5 to 1:6 for the standing Buddha, Disciples, and Bodhisattvas, 1:4.5 to 1:5 for the Vajra, and 1:6 to 1:6.5 for the head height to total height in the side-standing statue featured in the relief sculpture “li fo tu 立佛圖 (Standing Buddha)”.
Chen Mingda’s posthumous manuscript, “Dule Si Guanyin Ge, Shanmen de Damuzuo Zhidu 獨樂寺觀音閣、山門的大木作制度 (The System of Large Wooden Works at the Guanyin Pavilion and the Mountain Gate of Dule Monastery)” (finalized in 1990), marked an early exploration of the geometric relationship between statues and architecture. Notably, he employed an equilateral triangle in the longitudinal sectional analysis for viewing the Avalokitesvara statue of Guanyin Pavilion, contributing to the evolving discourse on the intersection of geometry and giant artistry.
In his 1998 paper titled “Zhongguo Zaoqi Fojiao Jianzhu Buju Yanbian ji Diannei Xiangshe de Buzhi 中國早期佛教建築佈局演變及殿內像設的佈置 (The Evolution of Layout in Early Chinese Buddhist Architecture and Statues)”, Fu Xinian 傅熹年 observed that the establishment of the Buddhist hall, the pagoda, and entire temple serves the purpose of venerating Buddha, providing monks and devotees spaces for meditation and worship. Beyond the architectural layout of Buddhist temples and the external facades of pagodas and halls, the strategic arrangement of statues assumes a crucial role in enhancing the presence of the Buddha statues, constituting a vital aspect of Buddhist architectural art (). This study analyzes the sight elevation angle associated with the “li fo 禮佛 (Buddha worshipping)” concept in various locations, such as Cave 004 of the Grottoes of Mount Maiji, the Great Hall of Nanchan Monastery, the Great East Hall of Foguang Monastery, the Pagoda of Fogong Temple, and the Guanyin Pavilion of Dule Monastery. The findings indicate that the elevation angle of the line of sight between the second to fifth floors of the pagoda typically ranges between 23 and 25°.5 (Figure 4).
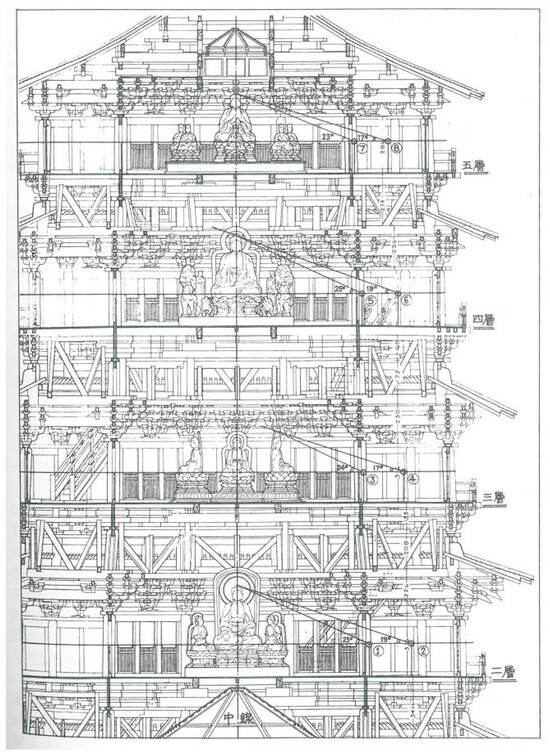
Figure 4.
Analysis of Fu Xinian’s line of sight of the Pagoda of Fogong Temple. Source: (). The Chinese character 二層,三層,四層,五層 means the second third fourth and fifth floor. The authors have obtained the copyright of the figure.
In the paper Yixian Fengguo Si Daxiong Dian Diaocha Baogao 義縣奉國寺大雄殿調查報告 (Investigation Report on the Mahāvīra Hall of Fengguo Monastery in Yi County, Liaoning), Ding Yao 丁垚 and Cheng Li 成麗 conducted a preliminary examination of the scale of seven statues through 3D laser scanning and mapping of the statue complex within the Mahāvīra Hall (). Similarly, in 2012 Shanxi Pingyao Zhenguo Si Wanfo Dian yu Tianwang Dian Jingxi Cehui 山西平遙鎮國寺萬佛殿與天王殿精細測繪報告 (Report on Fine Surveying and Mapping of the 10,000 Buddhas Hall and the Celestial Kings Hall of Zhenguo Monastery in Pingyao, Shanxi), Liu Chang 劉暢 et al. employed 3D laser scanning and color mapping techniques to analyze the standing and seated Attendant Bodhisattva statues situated on the east side of the 10,000 Buddhas Hall and the Celestial Kings Hall of Zhenguo Monastery. The study also briefly discusses the geometric proportions observed among the myriad Buddhas depicted in the mural ().
The author conducts an investigation of the geometric proportions linking architecture, interior space, and statues together. The study also encompasses diverse examples, including the Great East Hall of Foguang Monastery in Mount Wutai, the Guanyin Pavilion, and the Mountain Gate of Dule Monastery in Ji County, the Mahāvīra Hall of Fengguo Monastery in Yi County, the Mahāvīra Treasure Hall, and the Haihui Hall of Shanhua Monastery in Datong, the Bhagavat Sutra Hall of Huayan Lower Monastery in Datong, and the Dasheng Pavilion of Puning Monastery in Chengde. Notably, the examination focuses on ratios related to and /2 derived from the squared-circle map. This paper will introduce and elaborate on the design methodology termed “duo xiang gou wu 度像構屋”, which means designing the interior space of Buddhist architecture—such as halls, pavilions, and pagodas—in accordance with the principal statues (; ; ; ) (Figure 5).
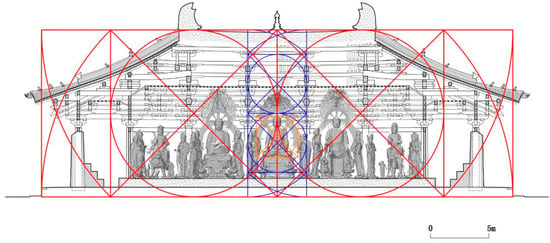
Figure 5.
Design concept analysis diagram of the Great East Hall of Foguang Monastery. Source of the base map: According to the actual map (statue) of the Survey and Research Report of the Great East Hall of Foguang Monastery (2011) by the School of Architecture of Tianjin University. Diagramed by Wang Nan.
In the article Duo Mian Wei Fan Die Fo Hua Ta—Fogong Si Shijia Ta Yi Ti Hua She Ji Mo Shi ji Ying Zao Li Nian Tan Xi 度面為範 疊佛化塔——佛宮寺釋迦塔一體化設計模式及營造理念探析 (Using Buddha Statue’s Facial Length as Modular Measurement and ‘Stacking Buddha Statues’ to Construct the Pagoda: An Exploration of the Integrated Design Model and Building Philosophy for the Sakyamuni Pagoda of Fogong Temple), Chen Siliang 陳斯亮 et al. defined the temple, the pagoda, and the statues of Fogong Temple as a unity and took the facial length of the giant Buddha statue on the ground floor as the modular measurement (1.473 m, equivalent to 5 Liao-dynasty chi) ().
In addition to the aforementioned investigations, insights into Buddhist statues are gleaned from ancient literature. Notably, Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra), translated from Tibetan to Chinese in 1742 during the seventh year of Qianlong in the Qing Dynasty by Gongbu Chabu 工布查布, stands out for its focus on Tibetan Buddhist statue regulations. Furthermore, Wang Shixiang 王世襄’s Compilation of Qingdai Jiangzuo Zeli Huibian: Fozuo, Menshenzuo 清代匠作則例彙編:佛作、門神作 (Handicraft Regulations and Precedents of Qing Dynasty: Buddha and Door God) (2001) provides a compilation addressing the geometric proportions of Buddhist statues in the Qing Dynasty, a subject that will be explored subsequently.
However, in stark contrast to the wealth of Buddhist statues in China, there is a desperate lack of historical documentation, especially monographs on Buddhist statues from the Song, Liao, and Jin Dynasties. Hence, a comprehensive surveying and mapping of extant Buddhist architecture and the statues inside is an indispensable prerequisite for further study. Fu Xinian underscores this need, expressing that due to the limited preservation of original statues and the scarcity of accurate measurements alongside temple structures, it is imperative to conduct detailed surveys of existing Buddhist architecture. Fu contends that only a few of the original statues in the existing Buddhist halls have survived intact and been accurately measured. Still, the layout of statues could be seen as carefully designed, especially in the Tang and Liao Dynasties, when the design techniques were similar. He advocates for expanded surveys and research on Buddhist halls to enhance our comprehension of the architectural achievements in Buddhist culture ().6
Prior scholars have provided initial insights indicating the integration of architecture and interior statues within the design of Buddhist structures, including temples, pavilions, and pagodas, showcasing meticulously arranged proportional relationships between the two. Taking the Pagoda of Fogong Temple as an example, this paper seeks to use survey and mapping techniques to deeply explore the proportional relationships in the construction of Buddhist structures, by analyzing their architectural space, with a particular emphasis on their interior space, statues, and murals located on each floor.
3. Geometric Proportion of the Interior Space and Statue Complex of the Pagoda of Fogong Temple
In the pagoda, there are presently 26 statues distributed across its floors, including 1 on the first floor, 5 on the second floor, 4 on the third floor, 7 on the fourth floor, and 9 on the fifth floor (see Figure 6 and Figure 7). Historical documentation from 1933, when Liang Sicheng and Mo Zongjiang conducted a survey and mapping of the pagoda, indicates that there were 11 statues on the fourth floor at that time, suggesting a total of 30 statues within the entire pagoda ().7 Liang Sicheng posits that while the statues underwent modifications in subsequent periods, they generally adhere to the original form. The most recent restoration occurred in the winter of the 18th year of the Republic of China (). Fu Xinian concurs, asserting that the Buddha statues on each floor are original Liao Dynasty artifacts, albeit subject to later repainting. The discovery of significant relics from the Liao and Northern Song Dynasties on the second and fourth floors during the 1960s and 1970s provides additional evidence, supporting the dating of some statues to the late Liao and early Jin Dynasties ().

Figure 6.
Section of the Pagoda of Fogong Temple. Diagramed by Wang Zhuonan.

Figure 7.
Three-dimensional model of the statues on each floor of the pagoda. Diagramed by Wang Zhuonan.
To repeat, the primary aim of this paper is to discern the distinctive proportional relationships through a comprehensive analysis of the geometric proportions within the interior space and the present state of its statue complex. However, this paper will leave for further discussion the extent to which these proportional relationships accurately reflect the “original state” of the pagoda and statues during the Liao Dynasty, depending on the precise historical epochs and restoration conditions of the 26 sculptures across various dynasties.
The following is the analysis of the geometric proportions of the interior space and the statues on each floor, which is divided into three parts for discussion: first, the proportional relationships between the interior space (especially the inner trough) and the statues; second, the proportional relationships among the statues within the complex; and third, the geometric proportions of each individual statue.
3.1. Analysis of the First-Floor Space and Statues
The first-floor statue within the pagoda depicts a cross-legged seated Buddha, in a sense of solitary and upright grace. Liang Sicheng indicated that the whole body posture and style of the pleated drapery overhang exemplify a high artistic standard (see Figure 8). The base of the Buddha features a Sumeru seat and a three-layered lotus. Notably, the lower two layers are painted with orb patterns, while the top layer has a cross-legged seated Buddha on each petal.

Figure 8.
Giant Buddha on the first floor of the pagoda. Source: Photo by Wang Nan.
Besides the giant Buddha statue, on the first floor, the wall of the pagoda’s central chamber has doors on the south and north sides, and the remaining six walls are fully covered by murals depicting cross-legged seated Buddhas, creating a majestic composition of six Buddhas surrounding the central statue. Liang Sicheng suggested that the six Buddha murals belonged to the same era as the statue in the center. The collective imagery of the six Buddha murals and the central Buddha statue creates a seven-Buddha pattern, reminiscent of the Mahāvīra Hall at Fengguo Monastery in Yi County during the Liao Dynasty, where seven Buddha statues align.
According to surveying and mapping data, from 2021, the dimensions of the six statues and murals on the first floor are as follows (see Table 1).

Table 1.
Dimensions of the giant Buddha on the first floor and the six Buddhas in the murals in the central chamber of the Pagoda of Fogong Temple (unit: m).
The following conclusions can be drawn through the geometric mapping and data analysis of the detailed surveying and mapping of the pagoda’s first-floor space, statues, and murals.
3.1.1. Analysis of the Proportional Relationships between the Space, the Statues, and the Murals
(1) Height of the First Story (14.57 m)8/Total Height of the Giant Buddha (10.32 m) = 1.412 ≈ (99.8% coincidence).
(2) Total Height of the Giant Buddha (10.32 m)/Top Height of the Six Buddhas in the Mural (average 7.28 m) = 1.418 ≈ (99.7% coincidence). Total Height of the Giant Buddha (10.32 m)/Total Height of the Six Buddhas in the Mural (average 6.301 m) = 1.638 ≈ 5:3 (98.3% coincidence).
(3) Height of the First Story (14.57 m)/Top Height of the Six Buddhas in the Mural (average 7.28 m) = 2.001 ≈ 2 (99.9% coincidence).
(4) Total Height of the Giant Buddha (10.32 m)/Inner Diameter of the Central Chamber (10.244 m at the foundation of the wall)9 = 1.007 ≈ 1 (99.3% coincidence).
(5) The Distance from the Top of the Octagonal Caisson Ceiling to the Ground (12.825 m)/Total Height of the Giant Buddha (10.32 m) = 1.243 ≈ 5:4 (99.4% coincidence).
To sum up,
The Height of the First Story/Total Height of the Giant Buddha (equal to the inner diameter of the Central Chamber)/Top Height of the Six Buddhas in the Mural is ≈ 2: :1. Therefore, the space on the first floor (especially the central chamber), the giant Buddha statue, and the six Buddha murals are designed as a whole and have a perfect geometric proportion (Figure 9 and Figure 10).
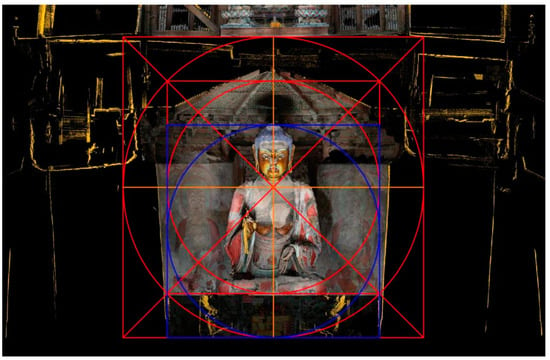
Figure 9.
Proportional analysis of the interior space, the statues, and the murals on the first floor.Diagramed by the author.

Figure 10.
Proportional analysis of the giant Buddha and six Buddhas in the mural on the first floor. Diagramed by the author.
3.1.2. Proportional Analysis of the Statues and the Murals
The following can be seen from Table 2:

Table 2.
Proportional analysis of the giant Buddha on the first floor of the pagoda and the six Buddhas in murals.
(1) The clear height-to-width ratio of the giant Buddha statue is about equal to the total height-to-width ratio (that is, the ratio of the total height to the total width of the base, the same below), both of which are about 3:2, forming a partial and overall harmony of the sculpture of the Giant Buddha shape (Figure 11).
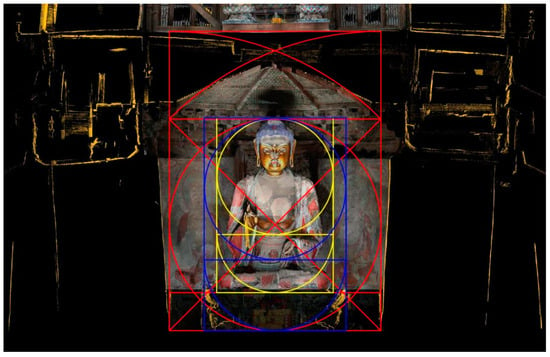
Figure 11.
Geometric proportional analysis of the giant Buddha on the first floor. Diagramed by the author.
(2) Except for the Southeast Wall Buddha, the clear height-to-width ratio of the other five Buddhas is close to 7:5, that is, “fang wu xie qi 方五斜七 (square five, oblique seven)” (close to );10 (Figure 12). The average value of the total height-to-width ratio of the six Buddhas is close to 7:5, but there is a large difference among them; in contrast, the clear-height-to-width ratios are more unified.11
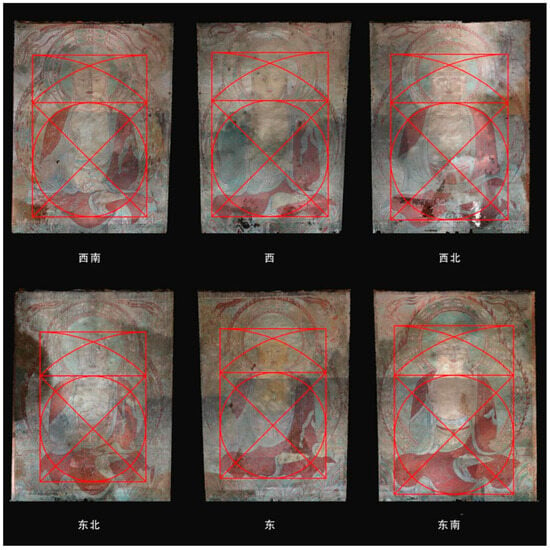
Figure 12.
Geometric proportional analysis of the six Buddhas in the murals on the first floor Diagramed by the author.
(3) The head-to-body ratio of the six Buddhas in the murals is close to 1:3.5, which conforms to the craftsman’s formula of “li qi zuo wu pan san ban 立七坐五盤三半 (seven-heads tall when standing, five-heads tall when sitting, three and a half heads tall when sitting crossed-legged)”. The Six Buddhas’ clear height/height below the head ≈ 3.5:2.5 = 7:5, that is, “fang wu xie qi 方五斜七 (square five, oblique seven).” ()12
(4) The proportion of the head of the giant Buddha statue is significantly higher than that of the six Buddhas in the mural.
3.2. Analysis of the Second-Floor Space and Statues
A square wooden Buddha altar is placed at the center of the second floor. On the altar, the Sakyamuni is sitting cross-legged at the center to the north, with two Attendant Bodhisattvas standing on both sides. The two Bodhisattvas sitting cross-legged on the two sides of the altar are Manjusri and Samantabhadra, respectively (which can be distinguished by the lion and elephant sculptures at the waist of the Sumeru seats) (Figure 13).

Figure 13.
Statue complex on the second floor. Source: Photo by Wang Nan.
According to the 2021 surveying and mapping data, the dimensions of the statues on the second floor are as follows (see Table 3).

Table 3.
Dimensions of the statues on the second floor of the Pagoda of Fogong Temple (unit: m).
The following results can be obtained through the geometric mapping and data analysis of the measured drawings of the space and statues on the second floor.
3.2.1. Analysis of the Proportional Relationship between the Space and the Statue Complex
(1) The Height of the Second Story (8.82 m)/the Top Height of the Buddha (4.42 m) = 1.995 ≈ 2 (99.8% coincidence).
(2) The Height of the Second Story (8.82 m)13/the Width of the Buddha Altar (5.29 m) = 1.667 ≈ 5:3 (100% coincidence).
(3) The Width of the Buddha Altar (5.29 m)/the Width of Each Façade of the Inner Trough (average 5.305 m)14 = 0.997 ≈ 1 (99.7% coincidence).
To sum up,
The second-floor height/the width of the Buddha altar (that is, the width of every side of the inner trough)/the height of the Buddha ≈ 10:6:5. Therefore, the space of the inner trough, the Buddha altar, and the statues on the second floor form an overall design, with obvious and basic proportions (Figure 14).

Figure 14.
Proportional analysis of interior space and statues on the second floor. Diagramed by the author.
3.2.2. Proportional Analysis of Statue Complex
(1) The Total Height of Buddha (4.052 m)/the Total Height of Attendant Bodhisattva (average 2.936 m) = 1.38 ≈ 7:5 (98.6% coincidence, that is, “fang wu xie qi 方五斜七 (square five, oblique seven)”).
(2) The Total Height of the Attendant Bodhisattva (average 2.936 m)/the Total Height of the Manjusri Bodhisattva (average 2.628 m) = 1.117 ≈ 10:9 (99.5% coincidence).
To sum up,
The total height of Buddha/the total height of the Attendant Bodhisattva/the total height of the Manjusri Bodhisattva ≈ 14:10:9. Therefore, the statue complex on the second floor has a clear proportional relationship in elevation design (Figure 15).

Figure 15.
Proportional analysis of the statue complex on the second floor. Diagramed by the author.
3.2.3. Proportional Analysis of the Statues
As can be seen from Table 4,

Table 4.
Proportional analysis of the statues on the second floor of the Pagoda of Fogong Temple.
A: Buddha Statue
(1) The height-to-width ratio (including the clear height-to-width ratio and the total height-to-width ratio) of the Buddha on the second floor is about 3:2, which is the same as the ratio of the Buddha on the first floor.
(2) The head-to-body ratio of the Buddha is about 1:3.5, which is in line with “li qi zuo wu pan san ban 立七坐五盤三半 (seven-heads tall when standing, five-heads tall when sitting, three and a half heads tall when sitting cross-legged)”. The clear height of the Buddha statue/the height below the head ≈ 3.5:2.5 = 7:5, that is, “fang wu xie qi 方五斜七 (square five, oblique seven)”. All the ratios above are the same as the statues on the first floor (Figure 16 and Figure 17).

Figure 16.
Geometric proportional analysis of the Buddha statues on the second floor (1). Diagramed by the author.

Figure 17.
Geometric proportional analysis of the Buddha statues on the second floor (2). Diagramed by the author.
B: Manjusri, Samantabhadra
(1) The clear height-to-width ratio and the total height-to-width ratio of Manjusri and Samantabhadra are about 8:5 or 5:3, both of which are close to the Western “Golden Ratio” (about 1.618).
(2) The ratio of Manjusri’s and Samantabhadra’s total height to their total height is about 10:7, that is, the craftsman’s formula “fang qi xie shi 方七斜十 (square seven, oblique ten)”, which is also the approximate value of .
(3) The head-to-body ratio (excluding the bun) of Manjusri and Samantabhadra is close to 1:4; Manjusri’s head-to-body ratio (including the bun) is about 1:3. By contrast, Samantabhadra’s head-to-body ratio is slightly smaller (Figure 18, Figure 19, Figure 20 and Figure 21).

Figure 18.
Geometric proportional analysis of the Manjusri Bodhisattva on the second floor (1). Diagramed by the author.

Figure 19.
Geometric proportional analysis of the Manjusri Bodhisattva on the second floor (2). Diagramed by the author.

Figure 20.
Geometric proportional analysis of the Samantabhadra Bodhisattva on the second floor (1). Diagramed by the author.

Figure 21.
Geometric proportional analysis of the Samantabhadra Bodhisattva on the second floor (2). Diagramed by the author.
C: Two Attendant Bodhisattvas
(1) The clear height to clear width ratio of two Attendant Bodhisattvas (the clear width is from elbow to elbow) is close to 3.5 (that is, 7:2).
(2) The head-to-body ratio of two Attendant Bodhisattvas (excluding the bun) is about 1:7 (that is, the so-called seven-heads tall), which also conforms to the “li qi zuo wu pan san ban 立七坐五盤三半 (seven-heads tall when standing, five-heads tall when sitting, three and a half heads tall when sitting cross-legged)”. And the golden section of the two Bodhisattvas’ clear height is located near the elbow when the arm is naturally sagging (that is, close to the navel), indicating the proficiency of the craftsman in human body proportions at that time (Figure 22 and Figure 23).
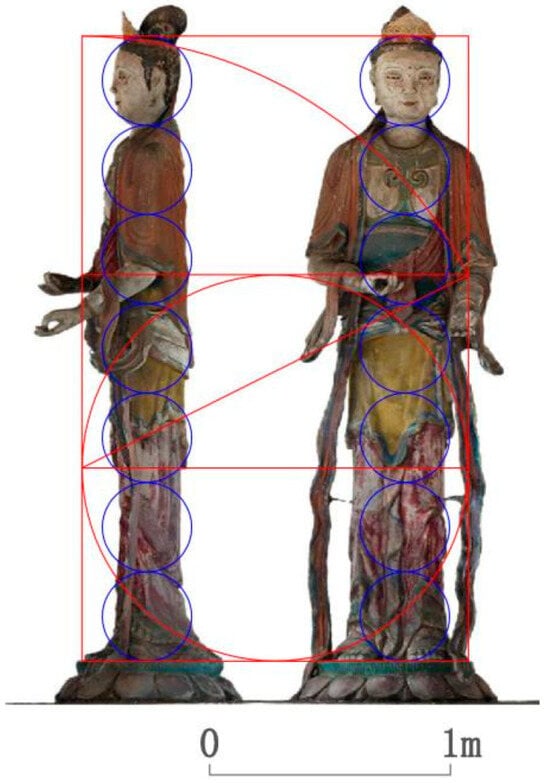
Figure 22.
Geometric proportional analysis of the Attendant Bodhisattva in the northwest on the second floor. Diagramed by the author.
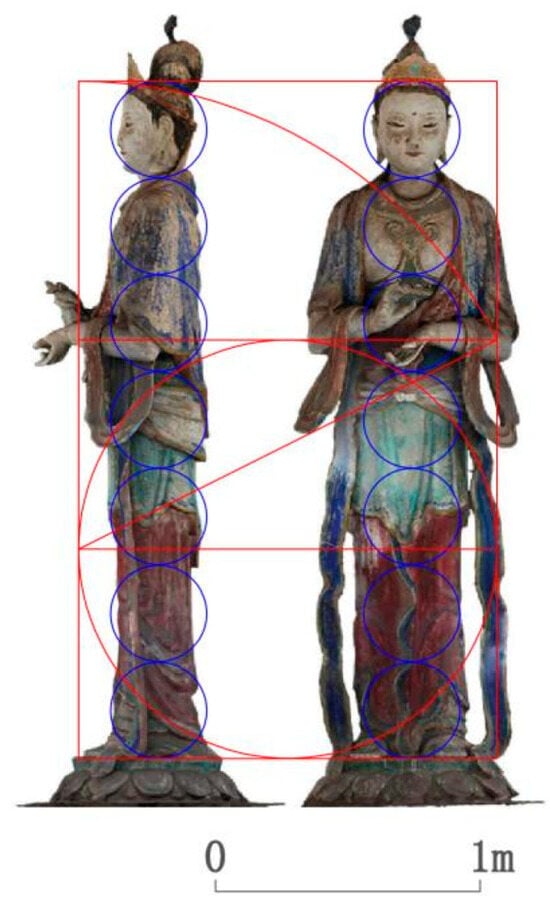
Figure 23.
Geometric proportional analysis of the Attendant Bodhisattva in the northeast on the second floor. Diagramed by the author.
3.3. Analysis of the Third-Floor Space and Statues
The central Buddha altar on the third floor of the pagoda is octagonal, and four seated Buddhas are set on the altar, facing east, south, west, and north, respectively, generally considered to represent the Four Guardian Warriors (namely, the Eastern Akshobhya Buddha, the Southern Ratnasambhava Buddha, the Western Amitabha Buddha, and the Northern Amoghasiddhi Buddha).
Although the size of the four Buddha statues is roughly the same, their mudras are different, and the Sumeru seats under the statues on the north and the south are different from the Sumeru seats under the statues on the east and the west. Under the south and north Buddhas, the seat bottoms are two-layer-corbelled octagons, above which should have been the waist. However, the south Sumeru seat has an eight-horse sculpture (representing the steed of Ratnasambhava) instead of the waist, while the north Sumeru seat has an eight-bird sculpture (representing the steed of Amoghasiddhi: Garuda, the King Golden-winged Birds). Above each sculpture is a four-layer lotus throne supporting the Buddha, and the front petal is covered by the Buddha’s clothes. The east and the west Sumeru seats have two-layer-corbelled octagons at both the top and the bottom. The waist part of the east Sumeru seat is an eight-elephant sculpture (representing the steed of Akshobhya), and that of the west one is an eight-bird sculpture (representing the steed of Amitabha: the peacock). Above each sculpture, a lotus throne stands on the top corbelled octagon, supporting the Buddha (not covered by the Buddha’s clothes) (Figure 24).

Figure 24.
The Four Guardian Warriors on the third floor. Source: Photo by Wang Nan.
According to the 2021 surveying and mapping data, the dimensions of the statues on the third floor are as follows (see Table 5).

Table 5.
Dimensions of the statues on the third floor of the Pagoda of Fogong Temple (unit: m).
3.3.1. Analysis of the Proportional Relationship between the Space and Statue Complex
(1) The Height of the Third Story15 (8.59 m)/the Total Height of Each Buddha (average 2.729 m) = 3.148 ≈ π (99.8% coincidence).
(2) The Total Height of Each Buddha (average 2.729 m)/the side Length of the Altar (average 2.756 m)16 = 0.99 ≈ 1 (99% coincidence).
To sum up,
The height of the third story and the total height of the four Buddhas (equal to the length of the octagonal Buddha altar) are in a unified design. In particular, the height of the third story/the sum of the total height of the four Buddhas ≈ π:4 (that is, the ratio between the perimeters of a circle and its circumscribing square). Drawing a square with the total height of the four Buddhas (which is also equal to the side length of the octagonal Buddha altar) as the side length, the height of the third floor is exactly equal to the circumference of its inscribed circle. This composition is very similar to the “mandala” of Esoteric Buddhism, corresponding to the statues’ layout on the third floor of the Four Guardian Warriors of Esoteric Buddhism (Figure 25).

Figure 25.
Proportional analysis of the interior space and statues on the third floor. Diagramed by the author.
3.3.2. Proportional Analysis of the Statues
As can be seen from Table 6, by taking the average value of the data of the four Buddhas, we can obtain the following:

Table 6.
Proportional analysis of the statues on the third floor of the Pagoda of Fogong Temple.
(1) The height-to-width ratio of each Buddha is close to 3:2, equal to the ratio of the statues on the first and the second floors.
(2) The ratio of the total height to the clear height of each Buddha is about 7:5, that is, the “fang wu xie qi 方五斜七 (square five, oblique seven)”, which is approximately .
(3) The head-to-body ratio of each Buddha is close to 1:3.5, equal to the ratio of the statues on the second floor (Figure 26 and Figure 27).

Figure 26.
Geometric proportional analysis of the Buddha statues on the third floor (1). Diagramed by the author.

Figure 27.
Geometric proportional analysis of the Buddha statues on the third floor (2). Diagramed by the author.
3.4. Analysis of the Fourth-Floor Space and Statues
The layout of the statues on the fourth floor, according to Liang Sicheng, is “the most dramatic one in the pagoda”—the sitting Buddha in the center, with two disciples on either side, Kayah and Ananda. In front of each disciple are, respectively, Manjusri and Samantabhadra Bodhisattvas. Their lion and elephant are standing statues, walking and carrying the Bodhisattvas on lotus thrones, and the Bodhisattvas are all shaped with one foot drooping and one foot sitting cross-legged. In the 1930s, there were also four sculptures of kumara and two sculptures of foreigners on the altar, all in dance poses. In the 1960s, they no longer existed and were replaced by new sculptures of a lion slave and an elephant slave, which survived to the present. From Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), we can see that the head of Manjusri in the 1960s was absent, so the head of Manjusri in the present situation was restored later. The drooping foot of the Samantabhadra was also remolded (Figure 28).

Figure 28.
Statues on the fourth floor. Source: Photo by Wang Nan.
According to the 2021 surveying and mapping data, the dimensions of the statues on the second floor are as follows (see Table 7):

Table 7.
Dimensions of the statues on the fourth floor of the Pagoda of Fogong Temple (unit: m).
3.4.1. Analysis of the Proportional Relationship between the Space and the Statue Complex
(1) The Height of the Fourth Story (7.75 m)17/the Top Height of the Buddha (4.71 m) = 1.645 ≈ 5:3 (98.7% coincidence).
(2) The Top Height of the Buddha (4.71 m)/the Width of the Buddha Altar (5.646 m)18 = 0.834 ≈ 5:6 (99.9% coincidence).
In summary, the height of the fourth story, the Buddha altar, and the Buddha are in a holistic design.19 (Figure 29).

Figure 29.
Proportional analysis of the interior space and the statues on the fourth floor. Diagramed by the author.
3.4.2. Proportional Analysis of the Statue Complex
(1) The Total Height of Buddha (4.274 m)/the Total Height of Samantabhadra (2.842 m) = 1.504 ≈ 3:2 (99.7%). The Total Height of Buddha (4.274 m)/the Total Height of Manjusri (2.812 m) = 1.52 ≈ 3:2 (98.7% coincidence).
(2) The Total Height of Buddha (4.274 m)/the Clear Height of the Two Disciples (average, 2.128 m) = 2.008 ≈ 2 (99.6% coincidence).
(3) The Total Height of Buddha (4.274 m)/the Total Height of the Lion and Elephant (average, 1.075 m) = 3.976 ≈ 4 (99.4% coincidence).
To sum up,
The total height of Buddha/the total height of Bodhisattva/the clear height of the two disciples/the total height of the lion and elephant ≈ 12:8:6:3. Although Manjusri’s head and the lion and elephant are restored or reshaped, there is still a clear proportional relationship between the statues on the fourth floor (Figure 30).

Figure 30.
Proportional analysis of the statue complex on the fourth floor. Diagramed by the author.
3.4.3. Proportional Analysis of the Statues
As can be seen from Table 8,

Table 8.
Proportional analysis of the statues on the fourth floor of the Pagoda of Fogong Temple.
(1) The height-to-width ratio (3:2) and head-to-body ratio (1:3.5) of the Buddha statue on the fourth floor are the same as those of the Buddha statues on the third floor.
(2) Each of the two disciples is about seven heads tall, and each of the two Bodhisattvas is about five heads tall (excluding the bun). If the bun is included, the height of Manjusri and Samantabhadra above the base is about three times the height of the head, which is the same as the layout of Manjusri Bodhisattva sitting cross-legged on the second floor. The two disciples standing on the fourth floor, the two Bodhisattvas, Manjusri and Samantabhadra sitting on one foot, and the giant Buddha sitting cross-legged, exactly constitute the proportion of “li qi zuo wu pan san ban 立七坐五盤三半 (seven-heads tall when standing, five-heads tall when sitting, three and a half heads tall when sitting cross-legged)”, which is consistent with the crafter’s formula. In addition, the lion and elephant remolded in modern times have a moving posture about six heads tall.
(3) The clear height of the Manjusri and Samantabhadra statues is about half of the total height (Figure 31).

Figure 31.
Proportional analysis of the statues on the fourth floor. Diagramed by the author.
3.5. Analysis of the Fifth-Floor Space and Statues
The layout of the statues on the fifth floor is the most solemn and clear. The Buddha altar is nearly square, and at the center is the seated statue of the Dari Tathagata Buddha (also known as the Piluchana Buddha). Liang Sicheng believes that “the head of this Buddha statue seems to be more ancient than statues on the lower floors.” The remaining four sides and four corners set up a total of eight Bodhisattvas’ sitting statues, in an octagonal shape around the central main Buddha. Many scholars believe that this layout reflects the “Foding Zunsheng Mantuoluo 佛頂尊聖曼陀羅” (or “nine-mandala”, “eight Bodhisattvas Mandala”, etc.), that is, according to the “foding zunsheng tuoluoni niansong yigui fa 佛頂尊聖陀羅尼唸誦儀軌法” (translated into Chinese by Bukong不空 in the Tang Dynasty) (),20 the Piluchana Buddha and the eight Bodhisattvas formed a “nine-orientation” statues system (; ; ; ; ). Among them, the Piluchana Buddha is at the center, the Sarvanivāraṇaviṣkambhin and Ākāśagarbha to its south and its north seat, respectively, the Vajrapani and Avalokitesvara (also known as the Guan Zizai Bodhisattva) to the east and the west seat, respectively, the Manjusri and the Ksitigarbha to the southeast and the southwest seat, respectively, and the Samantabhadra and the Maitreya (also known as the Cishi Bodhisattva) to the northeast and the northwest, respectively. The eight Bodhisattvas are headed by the Avalokiteshvara, arranged clockwise around the main statue in turn, ending with Ksitigarbha (Figure 32).

Figure 32.
The statue complex on the fifth floor presented as the pattern of “nine mandala”. Source: Photo by Wang Nan.
From the old photos in Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), it can be seen that in the 1960s, most of the crowns and buns of the heads of the eight Bodhisattvas were incomplete, and all the hands were incomplete; only the crowns and buns of the Sarvanivāraṇaviṣkambhin in the south and the Ksitigarbha in the southwest were more complete. The current ones were mostly remolded later.
According to the 2021 surveying and mapping data, the dimensions of the statues on the fifth floor are as follows (see Table 9):

Table 9.
Dimensions of the statues on the fifth floor of the Pagoda of Fogong Temple (unit: m).
3.5.1. Analysis of the Proportional Relationship between the Space and the Statue Complex
(1) The Height of the Fifth Story (from caisson to the ground, 7.109 m)/the Top Height of the Buddha (3.97 m) = 1.791 ≈ 9:5 (99.5% coincidence).
(2) The Height of the Fifth Story (7.109 m)/the Width of the Lower Buddha Altar (7.111 m)21 = 0.9997 ≈ 1 (100% coincidence).
(3) The Height of the Fifth Story (7.109 m)/the Height of the Ceiling (4.938 m) = 1.44 ≈ (98.2% coincidence).
(4) The Height of the Fifth Story (7.109 m)/the Top Height of Each Bodhisattva (average 2.564 m) = 2.773 ≈ 2 (98% coincidence).
In summary, it can be seen that the foundation, the ceiling, the statue complex, and the Buddha altar are all unified in design, and the proportion is perfect.22 (Figure 33).
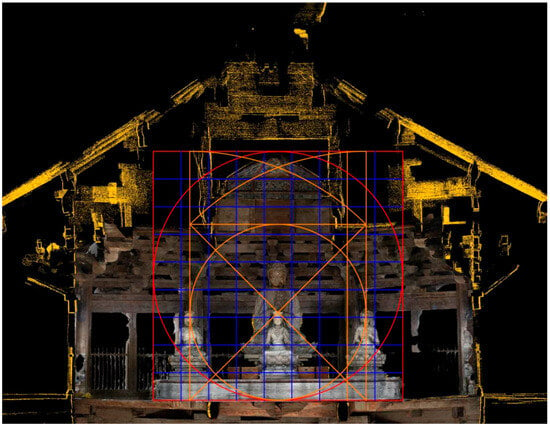
Figure 33.
Proportional analysis of the interior space and the statues on the fifth floor. Diagramed by the author.
3.5.2. Proportional Analysis of the Statue Complex
The Total Height of the Buddha (3.414 m)/the Total Height of the Bodhisattva (average, 2.008 m) = 1.7 ≈ 5:3 (98% coincidence).
3.5.3. Proportional Analysis of the Statues
The following can be seen from Table 10:

Table 10.
Proportional analysis of the statues on the fifth floor of the Pagoda of Fogong Temple.
(1) The height-to-width ratio (3:2) of the Buddha statues on the fifth floor is the same as that on the first to fourth floors; the ratio of the total height to the clear height () is the same as that of the Buddha statues on the third floor (Figure 34 and Figure 35).

Figure 34.
Geometric proportional analysis of the Buddha statues on the fifth floor (1). Diagramed by the author.

Figure 35.
Geometric proportional analysis of the Buddha statues on the fifth floor (2). Diagramed by the author.
(2) The height-to-width ratio of each Bodhisattva (including the clear height-to-width ratio and the total height-to-width ratio, taking the average value) is between 8:5 and 5:3 (close to the Golden Ratio); the head-to-body ratio (including bun) is about 1:3, and the head-to-body ratio without bun is about 1:4. All aspects above are close to the geometric proportion of Manjusri and Samantabhadra on the second floor (Figure 36 and Figure 37).
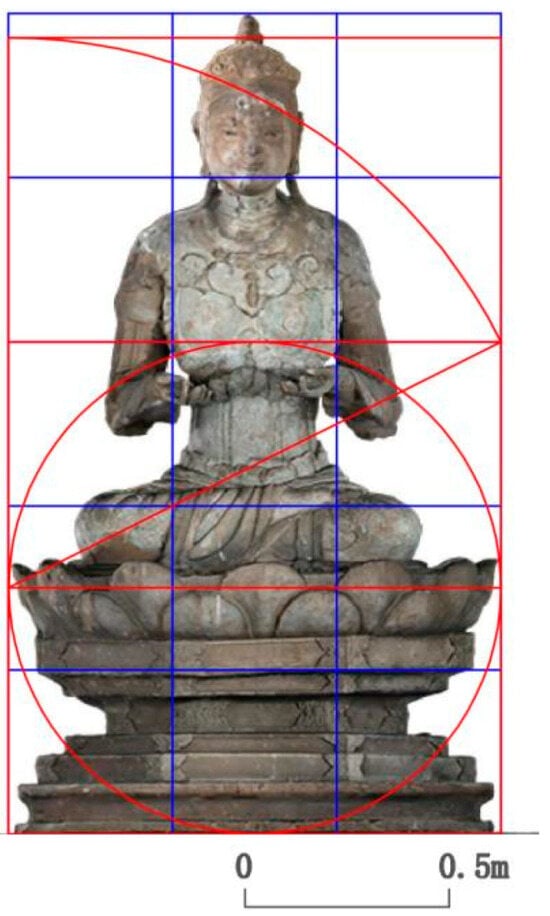
Figure 36.
Geometric proportional analysis of the Bodhisattvas on the fifth floor (1). Diagramed by the author.

Figure 37.
Geometric proportional analysis of the Bodhisattvas on the fifth floor (2). Diagramed by the author.
3.6. Proportional Relationship between the Buddha Statues on Each Floor
In addition to the proportional relationship between the interior space of each floor and the statue complex mentioned above, there are also proportional relationships among the Buddha statues (the main statues) on each floor of the pagoda.
3.6.1. Comparison of the Geometric Proportion of Statues on Each Floor
First of all, there are many similar techniques in the composition ratio of the statues on each floor of the pagoda, as shown in Table 11:

Table 11.
Proportional analysis of the Buddha statues on each floor of the Pagoda of Fogong Temple (A).
The following can be seen from the above table:
(1) The height-to-width ratio (including the clear height-to-width ratio and the total height-to-width ratio) of the Buddha statues on each floor of the pagoda is close to 3:2 (the coincidence degree of most data is higher than 98%, and only the coincidence degree of the clear height-to-width ratio of the Buddha statue on the third floor [taking the average value of the four Buddhas] is 97.8%). The ratio 3:2 is the most common modeling technique for the Buddha statues in the Pagoda of Fogong Temple.
(2) The ratio of the total height to clear height of the four Buddhas on the third floor and the Buddha on the fifth floor is :1 (this ratio also exists on the two seated Bodhisattvas on the second floor, namely Manjusri and Samantabhadra). The ratio of the total height to the clear height of the Buddha statues on the first, second, and fourth floors is also a relatively simple integer ratio.
(3) The head–body ratio of the Buddha statues on the second, third, and fifth floor is close to 1:3.5 (that is, “pan san ban 盤三半 (three and a half heads tall when sitting cross-legged) “, and the six Buddhas in the mural on the first floor also adopt this ratio). The head–body ratio of the Buddhas on the first and the fifth floor is larger, and that of the Buddha on the fifth floor is the largest, with the head occupying one-third of the clear height.
3.6.2. The Total Height Ratio of the Buddha Statues on Each Floor
Secondly, there is a subtler proportion arrangement between the Buddhas on each floor, and it is most likely designed with the giant Buddha on the first floor as the basic module (that is, the modulus). See Table 12:

Table 12.
Proportional analysis of the Buddha statues on each floor of the Pagoda of Fogong Temple (B).
As can be seen from the above table, if the total height of the Buddha on the first floor is 100, the sum of the total height of the Buddhas on the second and the fourth floors is about 80, and the sum of total height of Buddhas on the third and the fifth floors is about 60, the proportion of the above three is 5:4:3, that is, “ gou 3 gu 4 xian 5 勾三股四弦五, the Pythagorean theorem”.
Is this ratio a coincidence? If we carefully consider the Buddhist doctrine and discipline behind the layout of statues on each floor of the pagoda, we will find that this proportional relationship is probably the result of careful arrangement: the themes of the second and the fourth floors of the pagoda belong to Exoteric Buddhism (the second floor is possibly Huayan Sect). The third floor is dedicated to the Four Guardian Warriors, and the fifth floor is dedicated to the so-called “fo ding zun sheng man tuo luo 佛頂尊聖曼陀羅”, all belonging to the Esoteric Buddhism. Each lotus petal on the top of the giant Buddha’s Sumeru seat on the first floor is painted with a small Buddha, which is similar to the Sumeru seat of the Vairocana Buddha in Fengxian Temple of Luoyang Longmen Grottoes and the Tōdai-ji Temple in Nara, Japan ()23 and may also belong to the Huayan Sect. The layout of statues on each floor together constitutes a religious system, which combined Exoteric Buddhism and Esoteric Buddhism, and some scholars have pointed out that this was an important feature of Buddhism in the Liao Dynasty (). Therefore, the statues on the second and the fourth floors (Exoteric Buddhism) are regarded as a group, and their total height is 4/5 of that of the giant Buddha on the first floor; the statues on the third and fifth floors (Esoteric Buddhism) are regarded as a group, and their total height is 3/5 of that of the giant Buddha on the first floor. On the one hand, this layout conforms to the corresponding Buddhist doctrine and discipline of each floor; on the other hand, it presents the proportional relationships between the Buddha statues on each floor clearly.
Further, the sum of the total height of the Buddha statues on the second, the third, the fourth, and the fifth floors (taking the average of the four Buddhas on the third floor) is just 1.4 times the total height of the giant Buddha on the first floor, approximately , and almost equal to the height of the first story of the pagoda (the sum of the total height of the Buddha statues is 14.469 m, and the height of the first story is 14.57 m, in which the coincidence is 99.3%). If we imagine that the Buddha statues on the second to fifth floors are stacked together, the total height is exactly equal to the height of the first story (and is equal to twice the distance between the head of the Buddha on the first floor’s mural); this should also be the result of careful design (Figure 38).
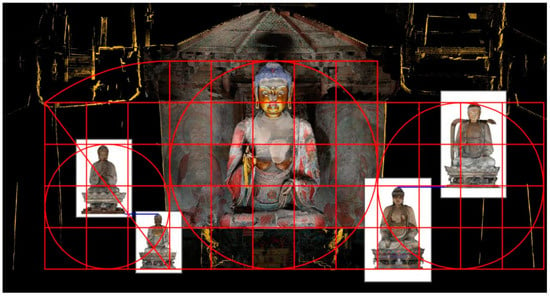
Figure 38.
Analysis of the proportional relationship between Buddha statues on different floors of the pagoda. Diagramed by the author.
3.6.3. Ratio of the Height of the Pagoda to the Total Height of the Giant Buddha on the First Floor
Finally, it is particularly necessary to point out that the total height of the giant Buddha on the first floor is likely not only the module of the total height of the Buddha statues on each floor but also one of the important modules of the pagoda. According to our measured data in 2021, the total height of the pagoda (excluding the base) is 61.99 m. It follows that
The Total Height of the Pagoda (excluding the base, 61.99 m)/the Total Height of the Giant Buddha (10.32 m) = 6.007 ≈ 6 (99.9% coincidence). (; ).24
According to the measured data of Beijing University of Civil Engineering and Architecture in 1991, the total height of the pagoda is 65.88 m, and the height of the base (average) is 3.667 m, so the total height of the pagoda (excluding the base) is 62.213 m. The total height of the giant Buddha on the first floor is about 10.2 m. It follows that
The Total Height of the Pagoda (excluding the base, 62.213 m)/the Total Height of the Giant Buddha (10.2 m) = 6.099 ≈ 6 (98.3% coincidence).
According to the measured data of the China Academy of Cultural Heritage in 2011, the total height of the pagoda is 65.838 m, () and the height of the base (the average value from the terrace to the top on each side) is 3.572 m,25 so the total height of the pagoda (excluding the base) is 62.266 m. The total height of the giant Buddha on the first floor is about 10.375 m. It follows that
The Total Height of the Pagoda (excluding the base, 62.266 m)/the Height of the Giant Buddha (10.375 m) = 6.002 ≈ 6 (the coincidence is close to 100%).
In summary, through the analysis of the measured data from surveying and mapping in 1991, 2011, and 2021, there is a clear proportional relationship between the total height of the pagoda (above the base) and the total height of the giant Buddha on the first floor (6:1).26 (Figure 39). If the total height of the giant Buddha is H, then the total height of the pagoda (above the base) is 6H, and the sum of the total height of four Buddhas on the second to fifth floors is 1.4H, so the sum of the total height of Buddha statues on each floor (the average value of the four Buddhas on the third floor) is 2.4H. The ratio of the sum of the total height of the Buddha statues on each floor to the total height of the pagoda (6H) is 2:5.
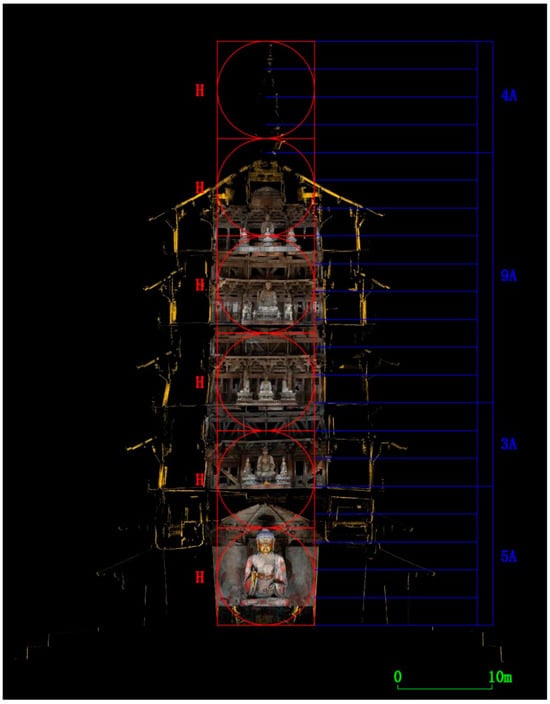
Figure 39.
The total height of the pagoda (without the base) is six times the height of the giant Buddha on the first floor (H). Among them, the height of the first floor, the height of the second floor, the sum of the height of the third, the fourth, and the fifth floors, and the height of the pagoda-top finial are 5A, 3A, 9A, 4A; H = 3.5A; A = 2.952 m. Diagramed by the author.
4. The Construction Scale and Design Methodology Employed in the Architectural Space, the Statue Complex, and the Murals of the Sakyamuni Pagoda of Fogong Temple
4.1. Proportion of the Height of Each Section in the Vertical Direction of the Pagoda
We can further explore that if the total height of the pagoda (excluding the base) is evenly divided into 21 sections, and each is set as A, then A = 61.99/21 = 2.952 m. It follows that
The height of the first story (14.57 m) = 4.936A ≈ 5A (98.7% coincidence);
The height of the second story (8.82 m) = 2.988A ≈ 3A (99.6% coincidence);
The height of the pagoda-top finial (11.571 m) = 3.92A ≈ 4A (98% coincidence);
The sum of the story height of the third, the fourth, and the fifth floors (27.029 m, the height of the fifth story is calculated until the bottom of the finial) = 9.156A ≈ 9A (98.3% coincidence. It can be seen that the average height of the third, the fourth, and the fifth floors is 3A, equal to the height of the second story).
The height of the giant Buddha on the first floor (10.32 m) = 3.496A ≈ 3.5A (99.9% coincidence).
In summary, the layout of the pagoda (above the base) is divided into four parts vertically aligned––the height of the first story/the height of the second story/the sum of the story height of the third, the fourth, and the fifth floors/the height of the pagoda-top finial ≈ 5:3:9:4. Among them, the height of the second story, the pagoda-top finial, and the first story are in the proportion of “gou 3 gu 4 xian 5 勾三股四弦五, the Pythagorean theorem “, which is quite similar to the proportional relationships between the height of the Buddha statues.
4.2. The Deduction of the Construction Scale and the Major Scales Employed in the Pagoda, the Statues, and the Murals
According to the above, A = 2.952 m is the construction module of the Pagoda of Fogong Temple. Significantly, these data are highly probably related to the construction scale.
Fu Xinian deduced that the construction scale used in the Pagoda of Fogong Temple is 1 chi = 29.4 cm (and took this as the performance of the Liao scale followed by Tang). Hence, the major scales on each floor are mainly in full numbers, especially the front width of the third floor (30 chi, equal to the column height on the first floor), which is an important module used in the pagoda’s elevation design (). Zhang Shiqing 張十慶 also holds the view that the “Liao scale is not supposed to be far from Tang scale”, and he deduces that in the Pagoda of Fogong Temple, 1 chi = 29.46 cm, and 1.5 chi is a primary module employed in the design of the plan and section of the pagoda (). Xiao Min 肖旻, () Zhang Yijie 張毅捷, () Chen Siliang, (), and other scholars took numbers between 29.4 cm and 29.5 cm as the pagoda’s construction scale for related studies.
Besides the views mentioned above, Chen Mingda employed the Song scale, 1 chi = 32.9 cm, to adjust the measured data of the wooden materials used in the pagoda (). Xiao Min tried the possibility of 1 chi = 29.4 cm, 30.7 cm, and 31.5 cm (). The team of Liu Chang took 1 chi = 30.6 cm as the construction scale for further study of floor designs (; ; ).
Even though, there are different opinions on the value of the construction scale, the module that A = 2.952 m explored by the team of author could provide a new angle and a solid example for further discussion of the pagoda’s construction scale—module A (2.952 m) is very close to 10 times of the construction scale found by Fu Xinian, Zhang Shiqing, and other scholars (between 29.4 and 29.5 cm), possibly the length of 1 chi in Liao Dynasty.
Hypothetically, given the construction scale used in the Pagoda of Fogong Temple is 1 chi = 29.5 cm, the major scales of the architectural space, the statues, and the murals could all be converted into full numbers (only a few exceptions but also with order), described in Table 13:

Table 13.
Measured values and deduced values (in chi) of the architecture, statues, and the murals of the Pagoda of Fogong Temple.
According to the data above, the following apply:
- (1)
- From the bottom to the top, the height of the base, each story, and the finial are all in full numbers, the total height is 225 chi, and the total height (excluding the base) is 210 chi.
- (2)
- “30 chi” is a major module employed in the design of the pagoda: the front width of each facade on the third floor, the height of the second story, and the average height of the third, the fourth and the fifth stories (including the roof to the fifth story height) are all 30 chi; the total height of the pagoda is 225 chi, 7.5 times 30 chi; and the total height of the pagoda (excluding the base) is 210 chi, 7 times 30 chi. Additionally, Fu Xinian, Zhang Shiqing, and other scholars have noted that the first story column height is 8.85 m, equal to 30 chi.
- (3)
- “15 chi” is another major module: the base is 15 chi high; the total height of the pagoda is 225 chi, 15 times 15 chi; and the total height of the pagoda (excluding the base) is 210 chi, 14 times 15 chi. Additionally, Fu Xinian, Zhang Shiqing, and other scholars have noted that the front width of the central bay on the first floor is 4.42 m, and the colonnade columns are 4.43 m high, both equal to 15 chi.
- (4)
- There is regularity in the diameter of the outer trough and the front width of each facade on each floor. Zhang Shiqing indicated that the front width of each facade on each floor is (from the bottom to the top) 33, 31.5, 30, 28.5, and 27 chi, while taking “30 chi” as a module, and the width is decreased by 1.5 chi floor by floor (from the bottom to the top).
- (5)
- The design of the first story’s architectural space, the giant Buddha, and the pagoda base is in a clear proportional relationship; the central chamber’s inner diameter is 35 chi, the outer chamber’s inner diameter is 70 chi, and the side length of the lower square base (average) is 140 chi, and hence, the ratio between them is 1::2. The side length of the upper octagon base is 50 chi, equal to the height of the first story. The outer trough diameter (excluding the colonnade) is 80 chi, equal to the sum of the first and second stories’ height; including the colonnade, the outer trough diameter is 100 chi, which presents a proportional relationship with the outer chamber’s inner diameter (70 chi), and the side length of the lower square base (140 chi) as 1::2.
- (6)
- As mentioned above, the total height of the giant Buddha is 35 chi (equal to the inner diameter of the central chamber), which is also a major module such that the total height of the pagoda (excluding the base) is 210 chi, 6 times 35 chi. Additionally, the sum of the Buddha’s total heights on the third and the fifth floors is 21 chi, and the sum of the Buddha’s total heights on the second and fourth floors is 28 chi, which present a proportional relationship with the giant Buddha in 3:4:5 (gou 3 gu 4 xian 5 勾三股四弦五, the Pythagorean theorem).
- (7)
- The top height and total height of the Buddhas on the first and the second floors (including the murals on the first floor) are in integral numbers (in chi); the total height of the four Buddhas on the third floor (in average) is 9.3 chi, not in integral number, but could present a ratio to the third-story height (29 chi) as 1: π. The statues on the fourth floor employ “1.2 chi” as the module, presenting a 12:8:6:3 ratio. The central Buddha on the fifth floor is 11.5 chi high in total, and the total height of the Bodhisattvas (in average) is 6.9 chi, presenting a 5:3 ratio. The scale and proportional relationships of the statues on each floor are clear.
- (8)
- Last but not least, the geometric proportions employed in the construction are made obvious by reverting the measured values to the original construction scale: the total height of the pagoda is 225 chi, and the inner diameter of the first-floor outer trough (excluding the colonnade) is 80 chi, which present the ratio 2.8125 ≈ 2 (99.5% coincidence). Moreover, according to the geometric construction, the ratio of the total height of the pagoda and the height from the fifth floor’s column capital to the ground is :1 (see Figure 40). Additionally, the total height of the pagoda (excluding the base) is 210 chi, 6 times the total height of the giant Buddha on the first floor (35 chi), the side length of the lower square base (average) is 140 chi, 4 times the total height of the giant Buddha, and the geometric proportion is 3:2, which also emphasizes the importance of the total height of the giant Buddha, as a module not only in vertical height but also in floor planning.
 Figure 40. Proportional analysis of the facade.Diagramed by the author.
Figure 40. Proportional analysis of the facade.Diagramed by the author.
4.3. Analysis of the Overall Design Methodology of the Sakyamuni Pagoda of Fogong Temple
Based on our analysis, we draw the following conclusions:
Firstly, the design of the whole architectural space starts with the giant Buddha on the first floor such that the height of the Buddha is 35 chi, and the total height of the pagoda (excluding the base) is 210 chi (6 times the height of the giant Buddha); the first story height is 50 chi (the ratio of which to the height of the giant Buddha is 10:7 or :1), and the second-story height is 30 chi, while the average of the third-, the fourth- and the fifth-story heights is also 30 chi, and the height of the pagoda-top finial is 40 chi. Then, the height of the base is determined to be 15 chi, the same as half of the second-story height (also half of the average height of the third to fifth floors). Consequently, the total height of the pagoda is settled to be 225 chi. The major modules are 35 chi, 30 chi, and 15 chi, constantly appearing in the dominant dimensions.
Secondly, the inner diameter of the central chamber on the first floor is determined to be 35 chi (equal to the total height of the giant Buddha). Based on this module, on the same floor, the inner diameter of the outer chamber is determined to be twice the module (70 chi), and the side length of the lower square base is 4 times (140 chi). Then, the side length of the upper octagon base is settled to be 50 chi (equal to the first-story height), and the diameter of the outer trough (excluding the colonnade) is 80 chi, which presents a classical ratio to the total height of the pagoda as 1:2 (its cultural context will be amplified later in the article). Therefore, the front width of each facade is 33 chi. The diameter of the outer trough including the colonnade is 100 chi, presenting a 1: ratio with the side length of the lower square base (140 chi).
Thirdly, the floor plan scale on each floor is determined—the front width of each facade (from the bottom to the top) is 33, 31.5, 30, 28.5, and 27 chi, so the building tapers from base to top. Combined with the design of the story heights, the basic plan and section design are established.
Then, the total height and the layout of the Buddha statues on each floor can be determined, based on the height of the giant Buddha and the proportional relationships between the statues and also because the statues on the second and fourth floors belong to Exoteric Buddhism and the statues on the third and the fifth floors belong to Esoteric Buddhism. The proportional relationship between the top height of the Buddha and the story height on each floor can be further corrected by adjusting altar height (so the altar heights from the second to the fifth floor have no obvious logic). The top height of the Buddhas in the murals on the first floor is 25 chi, 1/ of the giant Buddha, and 1/2 of the first-story height.
Afterward, the proportional relationships between the Buddhas and other attendant statues on each floor can be determined in detail.
Finally, each statue should be shaped according to its own geometric proportion.
Therefore, all the statues and murals are designed as a whole and present harmonious proportions with the architectural space, especially the inner chamber space on each floor. The architectural space, the statues, and the murals are well designed with clear proportions and modulus relations.
5. Conclusions: Classical Proportion and Its Cultural Messages
Through the above analysis of the proportion of the interior space of the pagoda and the composition of the statue complex, some preliminary conclusions can be drawn as follows:
First, there is a very clear proportional relationship between the height of each floor and the top height of the Buddha statue: the first floor is :1, the second floor is 2:1, the fourth floor is 5:3, and the fifth floor is 9:5. In addition, the ratio of the average height of the third floor to the average value of the four Buddhas’ total height is :1. The proportional relationship between the height of each story and the top height (or the total height) of the Buddha statue is one of the most basic geometric proportions between the interior space and statues and is also one of the most important design tools for the coordination between the statues and the interior space of each floor to jointly create the religious atmosphere of “praying to Buddha” and “worshipping Buddha”.28 In addition, the diameter of the inner wall of the central chamber on the first floor of the pagoda is equal to the height of the giant Buddha; the height of the ceiling is approximately 1.25 times that of the giant Buddha, and the top height of the six Buddhas in the mural is half the height of the first floor, etc. These proportional relations reflect a more elaborate design technique. The Buddha altars on each of the second to fifth floors are also integrated with the interior space and statue complex. The above aspects all prove that the interior space of the pagoda, the Buddha altar and the statue complex, and the murals are unified and carefully designed.
Second, the statues on each floor of the pagoda have clear and simple geometric proportions. Although the first floor has only a single giant Buddha, the total height of the giant Buddha is in relation to the top height of the six Buddhas in the murals surrounding the giant Buddha :1. The total height of the main Buddhas, the two attendants, and the Manjusri is related as 14:10:9 (the first two are approximate values of :1). The dimensions of the Buddhas on the third and the fourth floors are the same. The height of the four main Buddhas, Manjusri, Samantabhadra, Anangaye, and the two beasts (taking the clear height of the Anangaye and the total height of the rest) is in a ratio of 12:8:6:3. The total height of the five main Buddhas and the eight Bodhisattvas is 5:3.
Third, the 26 statues of the pagoda each have a clear geometric proportion and, according to different types, have obvious logics. The height-to-width ratio of the Buddhas on each floor (8 in total) is close to 3:2, and the technique is consistent. The height-to-width ratio of the Bodhisattva sitting statues on the second and fifth floor (10 in total) is close to 5:3 or 8:5, which is close to the “Golden Ratio (approximately 1:1.618)”. The two standing Attendant Bodhisattva statues on the second floor and the two disciples on the fourth floor are all seven heads tall. The Manjusri and the two Bodhisattvas sitting on one foot on the fourth floor are all five heads tall (not including buns), and the Buddhas on the second, third, and fifth floors (6 in total) are close to 1:3.5. The above head–body ratios are in line with the craftsman’s formula of “li qi zuo wu pan san ban 立七坐五盤三半 (seven-heads tall when standing, five-heads tall when sitting, three and a half heads tall when sitting cross-legged)”. Of course, there are exceptions, such as the Buddhas on the first and fourth floor, whose head-to-body ratio is between 1:3 and 1:3.25. The ratio of the total height and the clear height of each sitting statue also has a clear proportional relationship, which is most commonly :1 (including the Buddhas on the third and the fifth floor, and Manjusri and Samantabhadra on the second floor) and 3:2 (including the eight Bodhisattvas on the fifth floor). Of course, there are also cases where the ratio of total height to clear height is 6:5 (the Buddha on the first floor), 13:10 (the Buddha on the second floor), and 4:3 (the Buddha on the fourth floor).
Fourth, the height of the Buddhas on each floor may take the height of the giant Buddha on the first floor as the module: the sum of the total height of the Buddhas on the second and fourth floors (Exoteric Buddhism) is 4/5 of the total height of the Buddha on the first floor, the sum of the total height of Buddhas on the third and fifth floors (Esoteric Buddhism) is 3/5 of the total height of the Buddha on the first floor, the sum of the total height of Buddhas on the second to fifth floors is 1.4 times (about times) that of the total height of the Buddha on the first floor. It can be seen that the Buddha on each floor of the pagoda is likely to be a unified design and reflects the harmony of Exoteric Buddhism and Esoteric Buddhism.
Fifth, the total height of the pagoda (excluding the base) is about six times the height of the Buddha on the first floor; it can be seen that the Buddha on the first floor may not only be the module of the Buddhas on each floor but also the module of the architecture. The construction of the entire pagoda can be described as “duo xiang gou ta度像構塔(”designing the interior space of the pagoda, according to the main statues)”.
Sixth, the construction scale is probably 1 chi = 29.5 cm, from which the major scales of the building, the statues, and the murals are in clear and reasonable integral numbers, providing essential clues for the design methodology. The total height of the pagoda is 225 chi, and the total height excluding the base is 210 chi. In the construction, the major modules are 35 chi (the total height of the giant Buddha and the inner diameter of the central chamber on the first floor), 30 chi (the second-story height, the average height of the third, fourth, and fifth floors, the height of the first-story column, and the front width of each facade on the third floor), and 15 chi (the total height of the base, the height of the first-story colonnade column, and the front width of the first-story central bay of the outer trough). The geometric proportion of the total height of the pagoda (225 chi) to the diameter of the first-story outer trough (80 chi) is 2:1.
From the above conclusions, we can sum up several classic ratios that are frequently employed in the design of the interior space and the statues of the pagoda, namely (or 7:5, 10:7), 3:2, 5:3 (or 8:5), and 9:5. Here is a brief discussion of the rich cultural messages behind these classic ratios.
5.1. and the Rules of Square and Circle
In addition to appearing in the interior space of the pagoda and the geometric proportion of the statue, the proportion of also appears in the architectural design of the pagoda, for example, the ratio of the total height of the pagoda to the outer trough diameter (excluding the collonade) is about 2; the ratio of the total height of the pagoda to the distance between the column capital on the fifth floor and the ground below the pagoda is about (). In addition, according to the author’s research, in the Great East Hall of Foguang Monastery in Mount Wutai of the Tang Dynasty and Avalokitesvara Pavilion in the Guanyin Pavilion of Dule Monastery of the Liao Dynasty, the proportion of applies to the architectural design and the geometric proportion of the interior space and statues (complex), showing the design technique of “duo xiang gou wu 度像構屋 (designing the interior space of Buddhist architecture according to the main statues)” just like the Pagoda of Fogong Temple (; ).
One of the earliest scholars to explore the ratio embedded in ancient Chinese architectural design was Wang Guixiang 王貴祥; in his papers Yu Tang Song Jianzhu Zhu Yan Guanxi 與唐宋建築柱簷關係 ( Relationship with Columns and Eaves of Tang and Song Dynasties) (), Tang Song Dan Yan Mugou Jianzhu Pingmian yu Limian Bili Guilv de Tantao 唐宋單簷木構建築平面與立面比例規律的探讨 (A Study on Rules of Proportion in Plans and Facades of Single-Eaved Buildings of Tang-Song Periods) (), and Tang Song Dan Yan Mugou Jianzhu Bili Tanxi 唐宋單簷木構建築比例探析 (A Study on Rules of Proportion of Tang—Song Periods) (), he argued that this compositional ratio can be widely applied to more building types and longer historical periods than the single-eave wooden buildings of the Tang and Song dynasties, as well as to the relationship between building groups and the scale of courtyards, which needs to be explored in depth. In addition, Zhang Shixing further explored the ratio contained in the “caifen system” of the Northern Song Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards) and the “doukou system” of the Qing Dynasty Gongcheng zuofa 工程做法 (Construction Practices) (). Based on relevant works by Wang Guixiang, Feng Shi 馮時, Sun Dazhang 孫大章, Zhang Shiqing, and other scholars (; ; ; ; , ; ; ), the author takes as one of the most common classical proportions in the planning of ancient Chinese capital cities, the layout of architectural groups, and the design of individual buildings, which has been used in various types of cases over five thousand years ().
More importantly, the first “pattern” in Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards) in the Northern Song Dynasty is the Yuan Fang Fang Yuan Tu 圜方方圜圖 (rounded-square and squared-circle map) (Figure 41). It is evident that these drawings are illustrated as the “yuan fang tu 圓方圖 (rounded-square map)” and “fang yuan tu 方圓圖 (squared-circle map)” from Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument) quoted by Li Jie (Figure 42). The “kan xiang 看詳 (Definition)” of Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards), “square and straight” quoted in the Zhou Bi Suan Jing 周髀算經, said,
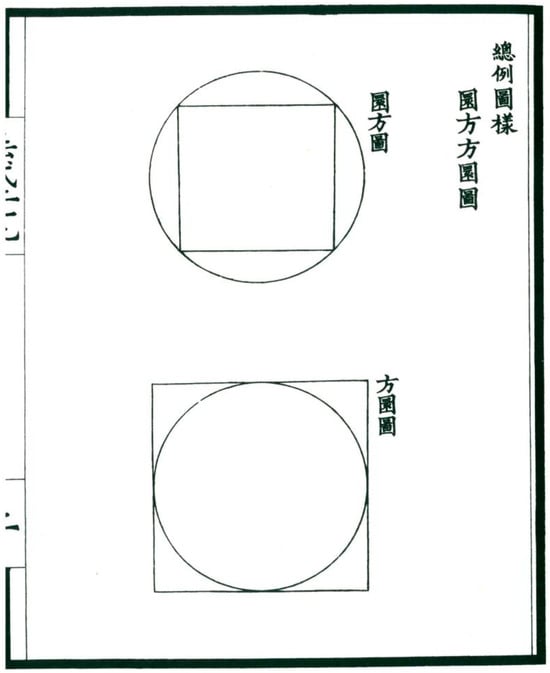
Figure 41.
“Yuan Fang Fang Yuan Tu 圜方方圜圖 (Rounded-Square and Squared-Circle Map)” in Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards). Source: (). 總例圖樣 (diagrams), 圓方圖 (Rounded-Square map), 方圓圖 (Squared-Circle Map).
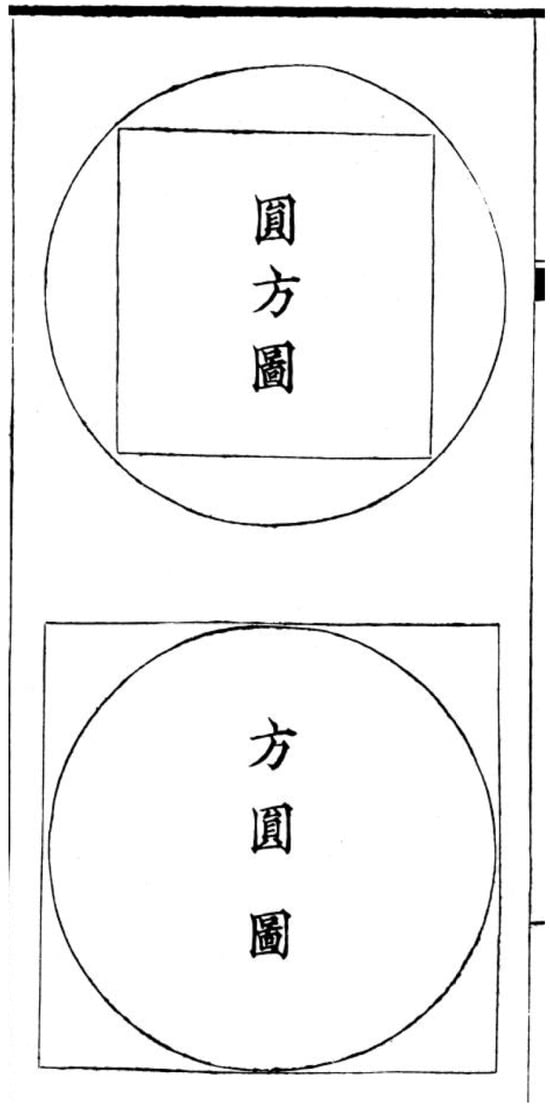
Figure 42.
“Yuan fang tu 圓方圖 (rounded-square map)” and “fang yuan tu 方圓圖 (squared-circle map)” in Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument). Source: ().
“The law of number comes from the square and circle. The circle comes from the square, the square from the rectangle, and the rectangle from ninety-eight and one”.
“To realize that the world can be square and circle, producers must use rules to make goods”.
The ratio of is clear and unmistakable in the ”yuan fang tu 圓方圖 (rounded-square map)” and “fang yuan tu 方圓圖 (squared-circle map)” in Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument) and Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards).29 The drawing technique of the Rule of Square and Circle is a fundamental method in ancient Chinese urban planning, architectural layout, architectural design, and even interior statue layout and statue modeling design in Buddhist architecture. Behind it is the ancient Chinese world view of tian yuan di fang 天圜地方 (a dome-shaped heaven and a flat, square earth) [Zhou Bi Suan Jing said “square belongs to the earth, the circle belongs to heaven, the dome-shaped heaven and the flat, square earth”] and the cultural concept that pursues the harmony of heaven, earth, and humans.
If the “yuan fang tu 圓方圖 (rounded-square map)” more intuitively reflects the proportion of (the ratio of the side length of the square to the diameter of the outer circle is 1:), then the “fang yuan tu 方圓圖 (squared-circle map)” reflects the ratio of the circumference of the square to the diameter of the inscribed circle as 4:π. This is the proportional relationship between the sum of the height of the three floors (the total height of four Buddhas) and the height of the pagoda. Therefore, the ratio of the height of the first floor to the total height of the giant Buddha (:1) and the ratio of the height of the third floor to the total height of the four Buddhas () is exactly corresponding to the “yuan fang tu 圓方圖 (rounded-square map)” and “fang yuan tu 方圓圖 (squared-circle map)” of the Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument).
Further extended, because the ancient people’s approximate algorithm for π is “zhou san jing yi 週三徑一 (circumference three, diameter one)”, that is, π is about equal to 3, the “fang yuan tu 方圓圖 (squared-circle map)” has the ratio of 3:4. Therefore, Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument), after discussing “the law of number comes from the square and circle. The circle comes from the square, the square from the rectangle, and the rectangle from ninety-eight and one”, immediately points out, “In a right triangle where one side is equal to 3 and the other side is equal to 4, the hypotenuse is equal to 5. Half of the square is the rectangle, and it loops around to form 3, 4, and 5. The two rectangles have a total length of 25, which is called the ji ju 積矩 (product-moment). Therefore, the reason why Yu 禹 ruled the world is the source of the numbers.”
Zhao Shuang 趙爽, a mathematician in the Three Kingdoms Period, said, “A circle has a diameter of 1 and a circumference of 3, and a square has a diameter of 1 and a circumference of 4. With the circumference of the circle as the gou (勾), with the circumference of the square as the gu (股), forming a right angle, exactly forming the hypotenuse 5. This is the law of numbers that comes from the square and circle. Therefore, ‘the law of number comes from the square’. Circle and square are the shape of heaven and earth, the number of Yin and Yang” ().
It can be seen that Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument) is based on the relation of 3:4 contained in the “square map”, with 3 (circumference) as the gou (勾) and 4 (square circumference) as the gu (股), and further uses the “product moment method” to deduce the Pythagorean theorem (with “ gou 3 gu 4 xian 5 勾三股四弦五” as an example) to interpret the idea that “the method of number derives from the circle square”. The sum of the height of the Buddha statues on the third and fifth floors of the pagoda mentioned above, the sum of the height of Buddha statues on the second and the fourth floors, and the height of the first floor just meet the ratio of 3:4:5, that is, “ gou 3 gu 4 xian 5 勾三股四弦五”. Based on the above analysis of the relationship between the proportion of the pagoda and the ratio, the relationship of the “gou 3 gu 4 xian 5 勾三股四弦五” among the Buddha statues on various floors (including the proportion of the second floor and the height of the pagoda-top finial and the first floor) seems to be more than a coincidence.
To sum up, the interior space of each floor of the pagoda and the Buddha statue completely and ingeniously interprets the ratio “yuan fang tu 圓方圖 (rounded-square map)”, “fang yuan tu 方圓圖 (squared-circle map)”, and “gou 3 gu 4 xian 5 (勾三股四弦五)” in the “Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument)”; the original book of the Zhou Bi Suan Jing 周髀算經 had the three combined as “ gou gu yuan fang tu 勾股圓方圖 (Pythagorean Rounded-square Map)”, but unfortunately lost, Zhao Shuang made up the “ xian tu 弦图(Hypotenuse Map)” accordingly () (Figure 43).
Figure 43.
“Xian Tu” of Zhou Bi Suan Jing 周髀算經 (The mathematical classic of the Zhou shadow-gauging instrument) by Zhao Shuang. Source: ().The Chinese character in the figure is used to prove the Pythagorean theorem.
It is particularly worth noting that, according to the book Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra), which focuses on the rules of Tibetan Buddhism, the clear height of the cross-legged seated Buddha portrait in Tibetan Buddhism is 70 “zhi 指 (finger)” and the clear width is 50 “zhi” (),30 which is exactly the ratio of “ fang wu xie qi 方五斜七 (square five, oblique seven)”, which is close to the ratio of (Figure 44). The most used proportion of the clear height-to-width ratio of the six Buddhas sitting cross-legged in the mural on the first floor is (only the giant Buddha on the southeast wall is different), which can be regarded as an early example of the geometric technique recorded in the Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra). An earlier example than the pagoda is the Buddha sitting cross-legged in the Great East Hall of Foguang Monastery in Mount Wutai, with a clear height-to-width ratio of , which is also an important representative of this composition in the statue ()31 (Figure 45).
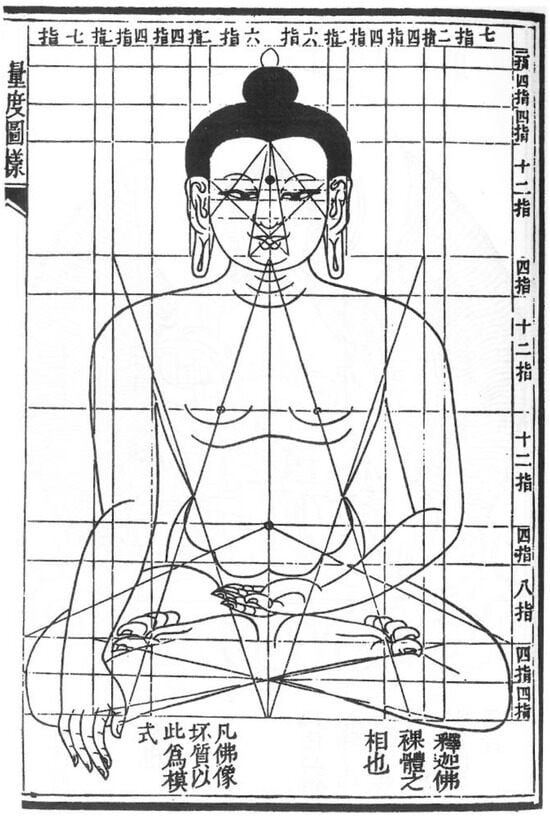
Figure 44.
Illustration of the Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra). Source: (). The Chinese character in the figure use zhi 指 (finger) to measure the Buddha. 二指 means two fingers, 四指 means four fingers, 六指 means six fingers, 七指 means seven fingers, 八指 means eight fingers, 十二指 means twelve fingers, the sentence blow 釋迦佛裸體之相也,凡佛像坏質以此為模式 means this is a standard figure of Buddha, all the Buddha Statue should take this as example.
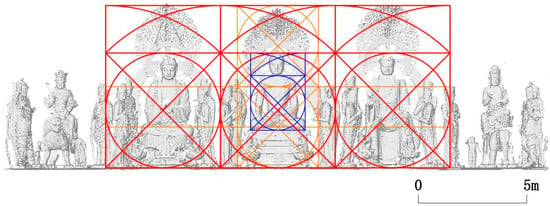
Figure 45.
Geometric proportional analysis of the Buddha statues in the East Main Hall of Foguang Temple on Wutai Mountain. Source: ().
The large number of the ratio of in the Pagoda of Fogong Temple is not only a long-standing tradition in the construction activities in ancient China but also similar to the Buddhist Tantra Mandala schema (which also makes large use of the composition of the Rules of Square and Circle)32 (). It is worthy of further exploration whether the ratio of , which appears in the architectural design of pagodas and the proportion of interior space and statue composition, is the result of the integration of the above two cultural connotations.
5.2. San Tian Liang Di 參天兩地 and 3:2 “(Three as the Heavenly Number and Two as the Earthly Number)”
The ratio 3:2 appears in the height-to-width ratio of the Buddha on each floor of the pagoda, which should be the basic technique of the pagoda’s Buddha modeling.33 Similarly, the height-to-width ratio of the seven giant Buddhas in the Mahāvīra Hall of Fengguo Monastery in Yi County, another Liao Dynasty giant structure (built in 1020, the ninth year of Kaitai in the Liao Dynasty), is also close to 3:2 (specifically, the height-to-width ratio of the central giant Buddha is the closest to 3:2, and the ratio of the two Buddhas at the end is almost 8:5), and the ratio of the total height of the central giant Buddha to the width of the central bay of the Mahāvīra Hall is 3:2 () (Figure 46).
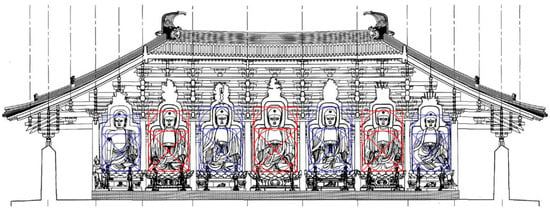
Figure 46.
Geometric proportional analysis of the Buddha statues in the Daxiong Hall of Fengguo Temple at Yixian. Diagramed by Wang Nan.
Similar to the ratio of , 3:2 is also a classic ratio commonly used in urban planning and architectural design in ancient China. It is particularly important that the ratio of “the height of cai” (15 分°) to “the width of cai” (10 分°) of structural carpentry stipulated in Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards) is 3:2.34 According to the book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County) by Chen Mingda, the wood used for pagodas is 25.5 × 17 cm, and the ratio of breadth to thickness is 3:2. In addition, there is no shortage of the 3:2 ratio in the content of “Bai Gong Zhi Qi 百工制器 (Craftsmen Making Utensils) “, mentioned in the Zhouli Kaogongji 周礼·考工记 (The Ritual of Zhou—Records of Artificers).
Wang Qiheng 王其亨 extensively discussed the cultural connotation of the classic ratio of 3:2 in combination with the twelve frequencies of ancient China and especially pointed out its connection with the philosophical concepts of “ san tian liang di er yi shu參天兩地而倚數 (‘three’ is the number of the heaven and ‘two’ is the number of the earth, and all numbers are based on them)” in Zhouyi—Shuo Gua 周易·說卦 (Zhou’s [book of ] Changes—Shuo Gua), which is very enlightening (; ; ). In discussing the -ratio relationship between the diameter of the three-ring stone altar at the Liaoning Niuheliang Hongshan Culture “Circular Mound” site, Feng Shi also pointed out that it is closely related to the thought of “san tian liang di 參天兩地 (three as the heavenly number and two as the earthly number)” in Zhouyi (). Wang Jun further explored and discussed the connotation of “san tian liang di 參天兩地 (three as the heavenly number and two as the earthly number)”, especially its different interpretations ().35 The interpretation of “san tian liang di er yi shu 參天兩地而倚數 (‘three’ is the number of the heaven and ‘two’ is the number of the earth, and all numbers are based on them)” in Zhouyi Ben Yi 周易本義 (Zhou’s [book of ] Changes Ben Yi) by Zhu Xi 朱熹 is as follows:
“The dome-shaped heaven and the flat, square earth. The circle has a diameter of one and a circumference of three, and three is an odd number, so ‘three’ is the number of the heaven; the square has a diameter of one and a circumference of four, which is obtained by adding two numbers of two earth, so ‘two’ is the number of the earth, and all numbers are based on them”.36
This is based on the ancient π of the “zhou san jing yi 週三徑一 (circumference three, diameter one)” to explain “san tian 參天 (three as the heavenly number)”, the mathematical relationship of the square “yi er wei si 一而圍四 (diameter one, circumference four) “ and “er er de si 二二得四 (two and two add up to four)” to explain “liang di 兩地 (two as the earthly number) “. All squares and circles begin with one, the circle is “yi er wei sa一而圍三 (diameter one and circumference three)”, and three is “the heaven (san tian 參天)”; the Square is “yi er wei si 一而圍四 (diameter one, circumference four)”, which is the sum of two numbers of two earth, that is “ two earth(兩地) “. This interpretation links the idea of “san tian liang di 參天兩地 (three as the heavenly number and two as the earthly number)” in the ratio of 3:2 with the idea of “tian yuan di fang 天圜地方 (a dome-shaped heaven and a flat, square earth)“.37
5.3. “Golden Section”, 5:3, and 8:5
The ratio of 5:3 (or 8:5) appears frequently in the ratio of the statues of Buddha sitting cross-legged in the pagoda. Compared with the ratio of 3:2 commonly employed in Buddha statues, it appears slenderer, which is close to the so-called golden section ratio (about 1.618) in the West. The ratio of the Buddha’s total height to the eight Bodhisattvas’ total height on the fifth floor, the ratio of the fourth floor’s height to the Buddha’s top height on the fourth floor, the ratio of second floor’s height to the Buddhist altar’s width (width of each side of the inner trough), the ratio of the front width of the central bay on the first floor to the secondary bay, and the ratio of the first-story height (5 chi) to the second-story height (3 chi) are all 5:3, which shows that the ratio of 5:3 is widely used in the design of the pagoda.
This ratio is also quite common in ancient Chinese architecture, with typical examples that the height-to-width ratio of the Shenwu Gate, the Donghua Gate, and the Xihua Gate of the Forbidden City is 3:5. First of all, the 5:3 ratio is the ratio of “xian 弦” and “gou 勾” in the “ gou 3 gu 4 xian 5 勾三股四弦五” in the Zhou Bi Suan Jing 周髀算經 (The Mathematical classic of the Zhou shadow-gauging instrument), and then, it is likely to be related to the connotation of the so-called “san wu yi bian, cuo zong qi shu 參伍以變,錯綜其數 (explore the changes of three and five, intricately deduce their mathematics)” in Zhouyi·Xi Ci Shang 周易·係辭上 (Zhou’s [book of ] Changes—Xi Ci vol.1), which needs to be further explored. () What is interesting is the close relationship between the ratio of 5:3 (or 8:5) and the Golden Ratio, especially when it is used in sculpture art, how it is related to the technique of using the Golden Ratio in Western sculpture art, and whether it has influenced Chinese Buddhist art with the introduction of Buddhism into China (such as the influence brought by Gandhara art, etc.). These topics are also worth exploring in depth. In the early study of ancient Chinese sculptors using the geometric proportion of 5:3, we can at least find Cave 18 of the Yungang Grottoes in the Northern Wei Dynasty (belonging to the first phase of Yungang) as a typical example: the ratio of the height between the central main Buddha and the Attendant Bodhisattva is 5:3, while the ratio between the central main Buddha, the Attendant Bodhisattva, and the Attendant Bodhisattva is about 10:6:5. This shows that the geometric technique, which gives the statues of different levels in the statue complex a clear proportional relationship, has been used in the Yungang Grottoes (Figure 47).
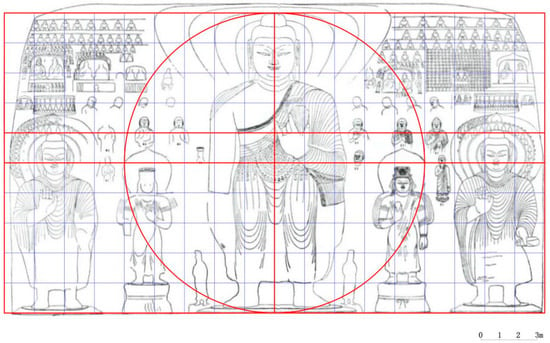
Figure 47.
Geometric proportional analysis of the statue complex in Cave 18 of Yungang Grottoes in Datong. Source: ().
5.4. Jiu Wu Zhi Zun 九五之尊 and 9:5 (Nine and Five Are the Numbers of the Honorable Central Position”
The ratio of 9:5 appears less frequently in the pagoda than the previous ones, but it appears in more important places: first, the ratio of the octagonal caisson ceiling’s height to the Buddha’s top height is 9:5, and the nine statues on the fifth floor (presented as the “nine-mandala”), which contain the connotation of the numbers 9 and 5 from the proportion, adhere to the spatial pattern;38 second, the ratio of the octagonal side length to the “outer trough” and the “inner trough” on the first floor is 9:5 (according to the measured data of the China Academy of Cultural Heritage, the width of the outer trough of the first floor(average 9.561 m)/the width of the inner trough (average 5.319 m) 39 = 1.798 ≈ 9:5 (the coincidence is 99.9%)); third, as mentioned above, the ratio of the total height of the third, the fourth, and the fifth floors of the pagoda to the height of the first floor is 9:5. In addition, the Pagoda of Fogong Temple has five layers on the outside and four hidden layers inside, showing a pattern of “ wai wu nei jiu 外五內九 (outside-five, inside-nine)”, which also contains the numbers 9 and 5.
In the construction of ancient Chinese cities and architecture, the numbers 9 and 5 are frequently used to symbolize the so-called “ jiu wu zhi zun 九五之尊 (nine and five are the numbers of the honorable central position)” ().40 In particular, qian gua jiu wu yao ci 乾卦九五爻辞 (the lines on hexagram 9–5 of the trigrams of the Qian Gua) in Zhouyi 周易 (Zhou’s [book of ] Changes) says “ fei long zai tian, li jian da ren飛龍在天,利見大人 (Dragon appears in the sky. It furthers one to see the great person)”, which further makes the “ jiu wu zhi zun 九五之尊 (nine and five are the numbers of the honorable central position)” a substitute name for the throne. Previous scholars have proved the Pagoda of Fogong Temple as a royal project in the Liao dynasty, (; ), which makes the symbolic meaning of “ jiu wu zhi zun 九五之尊”” here reasonable.
It is worth mentioning that the association between the pagoda and the thought of Zhouyi 周易 is not only implied in 9:5 (symbolizing “ jiu wu zhi zun 九五之尊”) or a series of 3:2 (symbolizing “ san tian liang di 參天兩地 (three as the heavenly number and two as the earthly number)”) but also directly appears in the facade and the interior space of the pagoda: the most prominent ones are the stone Bagua Tu 八卦圖 (Eight Diagrams) on the front of the base of the pagoda (Figure 48) and the painted Bagua Tu 八卦圖 in the center of the octagonal caisson ceiling of the pagoda’s fifth floor (Figure 49). In addition, the pattern in the center of the octagonal caisson ceiling of the pagoda’s first floor is similar to the “Taiji Tu 太極圖 (Taiji Diagram)” of the Song Dynasty Neo-Confucianism master Zhou Dunyi 周敦頤 (derived from the “shui huo kuang huo tu 水火匡廓圖” and “san wu zhi jing tu三五至精圖”). It is also related to the connotation of Zhouyi 周易 and Bagua Tu 八卦圖 () (Figure 50 and Figure 51). Interestingly, the two caisson ceilings individually having Eight Diagrams or “Taiji Diagram” of the pagoda are, respectively, on the fifth floor and the first floor, which is precisely where the 9:5 ratio relationship occurs.41

Figure 48.
The Bagua Tu 八卦圖 (Eight Diagrams) stone carvings embedded in the front of the base of the pagoda (the three characters of “Confucianism, Buddhism, and Taoism” above the Eight Diagram). Source: Memorial Collection of the Society for Research in Chinese Architecture, School of Architecture, Tsinghua University.

Figure 49.
Bagua Tu 八卦圖 drawn in the center of the Douba 鬥八 (octagonal) Caisson Ceiling on the fifth floor. Source: Photo by Wang Nan.

Figure 50.
Zhou Dunyi’s “tai ji tu 太極圖 (Taiji Diagram)” in the center of the Douba Caisson Ceiling on the first floor (can be compared with Figure 51). Source: Photo by Wang Nan.
Figure 51.
“Taiji Tu 太極圖 (Taiji Diagram) and “shui huo kuang huo tu 水火匡廓圖” Source: (). The Chinese characters in the figure show how wu xing 五行 and Yinyang 阴阳 works.
The above are some findings concerning the proportion of the architectural space, the statues, and the murals in the Pagoda of Fogong Temple. This article tries to preliminarily explore the cultural message behind the proportional relationship and points out some directions worth further exploration in the future. With the gradual deepening of the research, it is further revealed that the importance of proportion to the study of ancient Chinese cities, buildings, and even statues and murals should not be underestimated.
In the Qing Dynasty, Gongbu Chabu, the translator of the Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra), wrote Zaoxiang Liangdu Jing Yi 造像量度經引 (Introduction of Buddhist Statue Measurement Sutra), “The Sutra says that if the statue is imprecise, then the right God does not dwell. How can craftsmen change the proportion of Buddha statues at will? Proper proportion is what matters”.
Gongbu Chabu realized the importance of the proportion and scale of Buddhist statues by translating Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra). However, if we want to understand the composition and proportion of those Buddhist statues earlier than the Buddhist Statue Measurement Sutra, we can only find the law by surveying more early examples and analyzing them. This is exactly the main goal of this article.
This article is written on the 120th anniversary of the birth of Mr. Liang Sicheng. I would like to conclude with a comment in Liang’s article Shuo Jianzhu Pinge Jingshen zhi Suozai 說建築品格精神之所在 (Talk about the character and spirit of architecture, 1943)42 to commemorate this date:
“Proportion: This is the most fundamental issue in all creation of art. Everything in a piece of art comes down in the end to the question of proportion, that is, the proportion of the arranged relations between the parts… The issue of beauty is resolved if the proportion is appropriate.”
Author Contributions
Conceptualization, N.W. and Z.W.; methodology, N.W.; software, Z.W. and H.Z.; validation, N.W., Z.W. and H.Z.; formal analysis, N.W.; investigation, N.W., Z.W. and H.Z.; resources, N.W.; writing—original draft preparation, N.W.; writing—review and editing, N.W. and Z.W.; visualization, Z.W. and H.Z.; supervision, N.W.; project administration, N.W. and Z.W.; funding acquisition, N.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
Part of this paper is a translation of “Round Heaven and Square Earth, Unity of Pagoda and Statuary—A Study on the Geometric Proportions of Space and Statues inside the Timber Pagoda in Ying County” originally published in Chinese by “Journal of Architectural History”, 2021, volume 2, pp. 71–94. This translation was prepared by Zhu Shiyi, Zhu Xinrui, Huang Huaqing, and Yang Shu. Permission was granted by Wang Nan, Wang Zhuonan, and Zhenghongyu. The authors have obtained permission from the Journal of Architectural History to translate this article into English, and the journal has transferred the copyright to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | The Pagoda of Fogong Temple in Ying County exhibits an octagonal plane, featuring three rooms on each side across its five floors. The initial floor incorporates a covered corridor encircling the hall, contributing to the pagoda’s overall aesthetic of six eaves. Beyond the first floor, each subsequent level comprises a support platform, housing body, and eaves, characterized by layered indentations. The crowning element is an octagonal pyramidal roof, culminating with an iron pagoda-top finial on the uppermost floor. Positioned atop a dual stone foundation, each floor is delineated by inner and outer columns, totaling 24 outer columns and 8 inner columns. Furthermore, the first floor integrates auxiliary columns into its wall structure. |
| 2 | The research team, comprising scholars from the School of Architecture at Tsinghua University and the School of Architecture at Inner Mongolia University of Technology, conducted an on-site investigation of the Pagoda of Fogong Temple in January 2021. The scope of data collection encompassed the architectural features, statues, and select murals on the first floor. Employing a multifaceted approach, the team utilized three-dimensional laser scanning, UAV oblique photogrammetry, camera close-range photography, and total station measurement methods to procure comprehensive data. For architectural data acquisition, a combination of long- and short-distance 3D laser scanners and a total station facilitated the creation of an accurate point cloud model, with the overall model precision controlled within 10 mm. The acquisition of statue and mural data involved the amalgamation of handheld 3D laser scanning and close-range photogrammetry to produce a color model. To enhance model accuracy, the collected datasets underwent mutual verification. Challenges arose during the data acquisition of the Buddha statues and murals on the first floor due to their considerable height, limited surrounding space, and the presence of protective glass baffles in the lower section. Despite these challenges, the team rigorously maintained data quality. Key contributors within the team included Liu Chang 劉暢, Wang Nan 王南, and Wang Zhuonan 王卓男 in the preliminary planning phase, while Wang Zhuonan, Zheng Hongyu 鄭虹玉, Zhou Jiang 周江, Wang Zhiming 王志明, Cao Min 曹敏, Han Qi 韓琪, Yue Qi 岳祺, Yu Shihao 于世豪, and Zhao Zeyi 趙澤毅 were instrumental in field data collection, post-processing, and mapping. The analysis diagram drawing for this paper was executed by Wang Nan. |
| 3 | Based on Liang Sicheng and Mo Zongjiang’s 1933 survey draft, the Buddha statue’s total height with its base on the fifth floor was 3.6 m, clear height 2.51 m, and Sumeru seat 1.09 m. Comparing this to our 2021 survey data (total height 3.414 m, clear height 2.398 m, Sumeru seat height 1.016 m), the disparity is within 20 cm. Liang Sicheng’s work on Fogong Temple in Ying County, Shanxi, notes the fourth-floor Buddha’s height as 4.85 m, but considering the kāyaprabhā, the 1933 data, which include this, gain significance due to today’s kāyaprabhā damage. Additionally, the 1933 survey reveals Manjusri Bodhishava’s total height on the fourth floor as 2.9 m and the west disciple’s height as 2.33 m, closely aligning with 2021 data (2.812 m and 2.318 m, respectively). Liang Sicheng also mentioned a 4 m total height for the Buddha on the second floor, closely mirrored in the 2021 survey (4.052 m). However, the giant Buddha on the first floor stands out with a height discrepancy (12.3 m in historical records, 10.32 m in 2021), potentially due to historical estimations. Chen Mingda’s 1966 book, alongside 1960s surveys, suggests a 70 cm gap in the first-floor giant Buddha’s height compared to 2021. Constraints in the indoor space hindered accurate measurements, justified by the difficulty even with modern technologies. A 1991 survey by Beijing University of Civil Engineering and Architecture aligns with 2021 data, while the 2011 section drawing from the China Academy of Cultural Heritage closely matches the 2021 measured height of 10.32 m, indicating reliability. |
| 4 | The omission of drawings for the two Bodhisattva statues on the second floor remains unexplained. Furthermore, the “Supplementary Note” accompanying the 1978 publication on Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), as highlighted by Chen Mingda, elucidates that the internal spatial configuration of the pagoda adheres to specific principles. Notably, the height ratio between the inner and outer troughs is governed by the viewing angle. |
| 5 | Fu Xinian emphasizes that in the Grottoes of Mount Maiji Cave 004, the Great Hall of Nanchan Monastery, and the Great East Hall of Foguang Monastery, a deliberate and prevalent design pattern ensures a comfortable viewing angle for the central point of Buddha worship, approximately at 30°. This intentional arrangement, deemed non-coincidental by Fu, reflects a systematic approach characteristic of the era (). Furthermore, Zhang Rong 張榮 and colleagues, in their 2018 paper “Fo Guang Si Dong Da Dian Jian Zhi Yan Ge Yan Jiu 佛光寺東大殿建置沿革研究 (Research on the Construction History of the Great East Hall of Foguang Monastery)”, meticulously validate and extend Fu’s analysis of the Buddha worship line of sight, particularly in the Great East Hall of Foguang Monastery and its statue complex, through detailed surveying and mapping techniques (). |
| 6 | Furthermore, Su Bai advocates for a comprehensive investigation into the proportions of Buddhist statues through precise surveying and mapping methodologies. |
| 7 | In addition, from the old photos of the Society for Research in Chinese Architecture, it can be seen that there is a tiny Buddha statue and a Buddhist pilgrim statue on the second floor of the Buddha altar. The height of these two statues is only slightly higher than the Sumeru seat of Manjusri and Samantabhadra, and they no longer exist today. If you count these two small statues, there were 32 statues in 1933. |
| 8 | In this paper, the “height” value of each floor from the first to the fourth floor takes the distance from the upper floor of the inner trough to the ground of this floor (average value), and the distance from the top of the octagonal caisson ceiling to the ground is taken from the top of the fifth floor. According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the height of the first floor is 14.65 m. According to the data of Beijing University of Civil Engineering and Architecture in 1991, the height of the first floor is 14.678 m, which is relatively close to our surveying data in 2021. |
| 9 | According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the inner diameter of the central chamber is 10.25 m, which is basically the same as the surveying data in 2021. |
| 10 | “Fang wu xie qi 方五斜七 (square five, oblique seven)”, “ Square seven, oblique ten(方七斜十)” and so on are the ancient craftsmen’s formula, similar to ratio. |
| 11 | The pedestal of the giant Buddha in each mural is partially shielded by the glass plate used for protection on the first floor of the pagoda, so the surveying effect is not ideal, and the total aspect ratio is only for reference. |
| 12 | “Li qi zuo wu pan san ban 立七坐五盤三半 (seven-heads tall when standing, five-heads tall when sitting, three and a half heads tall when sitting cross-legged)” is the craftsman’s formula that is still in use today, meaning that the head and body ratio of a standing statue is 1:7, that of a seated statue is 1:5, and that of a statue sitting cross-legged (結跏趺坐) is 1:3.5. Wang Shixiang compiled the Qingdai Jiangzuo Zeli Huibian: Fozuo, Menshenzuo 清代匠作則例彙編:佛作、門神作 (Handicraft Regulations and Precedents of Qing Dynasty: Buddha and Door God), which says, “The statue of Han walks seven-heads tall, sits five-heads tall, squats three and a half heads tall. The statue of foreigner sits five-heads tall, hangs seven-heads tall, stands nine-heads tall”. In addition, there are formulas for calculating the surface area of the statue: “Walk seven, sit five, Nirvana three(行七坐五涅槃三)” and so on. |
| 13 | According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the height of the second floor is 8.84 m. According to the data of Beijing University of Civil Engineering and Architecture in 1991, the height of the second floor (take the average value of the inner trough) is 8.779 m. All of them are similar to the survey data of 2021. |
| 14 | The width of the Buddha altar and the width of the inner trough are taken from the values in the survey draft of Liang Sicheng and Mo Zongjiang in 1933. According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the width of the inner trough is 5.36 m, and the width of the Buddha altar is 5.28 m. According to the data of Beijing University of Civil Engineering and Architecture in 1991, the width of the inner trough is 5.231 m, and the width of the Buddha altar is 5.199 m. The above conclusions remain unchanged after verification. |
| 15 | According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the height of the third floor is 8.85 m. According to the data of Beijing University of Civil Engineering and Architecture in 1991, the height of the third floor (take the average value) is 8.631 m. The 1991 and 2021 survey data are more similar. |
| 16 | According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the Buddha altar side length is 2.75 m; according to the data of Beijing University of Civil Engineering and Architecture in 1991, the Buddha altar side length (take the average value) is 2.68 m. The above conclusions remain unchanged after verification, and the coincidence is above 98%. |
| 17 | According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the height of the fourth floor is 7.83 m; according to the data of Beijing University of Civil Engineering and Architecture in 1991, the height of the fourth floor (take the average value of the inner trough) is 7.765 m. The 1991 and 2021 survey data are more similar. |
| 18 | According to the data of Chen Mingda’s book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), the width of the Buddha altar is 5.8 m. According to the data of Beijing University of Civil Engineering and Architecture in 1991, the width of the Buddha altar is 5.588 m. The 1991 and 2021 survey data are more similar. |
| 19 | In addition, the width of each side of the outer trough on the fourth floor (8.47 m); the width of each side of the inner trough on the fourth floor (5.09 m) = 1.664 ≈ 5:3 (99.8% coincidence), which is equal to the ratio of the height of the fourth floor to the top height of the Buddha. |
| 20 | The original Dhanari Columu building in the north of the pagoda (1194, 4th year of in the Jin Dading) is still visible in the old photos of the Society for Research in Chinese Architecture. According to our field investigation, the column is now broken in a number of pieces, scattered throughout the Fogong Temple, in urgent need of restoration and protection. The relationship between the column and the layout of the pagoda is worth further study. |
| 21 | According to the data of Beijing University of Civil Engineering and Architecture in 1991, the width of the Buddha altar is 6.995 m. The above conclusion remains unchanged after verification. |
| 22 | Chen Mingda once pointed out in his book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County) that “It is impossible to find out how the caisson’s height is determined.” At least we know that the height of the caisson is equal to the width of the Buddha altar and, at the same time, forms a ratio of 9:5 to the height of the Buddha’s top, a ratio of
to the ceiling, a ratio of 2
to the height of the Bodhisattva’s top, and so on. |
| 23 | The little Buddha patterns painted in the lotus petal of the giant Buddha should symbolize the so-called “ World of the Lotus Sanctuary “ in the Avatamsaka Sutra. |
| 24 | In the past, the author calculated the ratio between the total height of the pagoda and the height of the giant Buddha based on the height of the giant Buddha in the book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County) by Chen Mingda. Since the height of the giant Buddha in this book (more than 11 m) is higher than the true value, the conclusion was obviously wrong. This paper corrected it with the latest measured data, hereby explained. |
| 25 | The data is taken from the first floor’s north–south section of the pagoda. |
| 26 | In particular, it should be pointed out that due to the tilt of the pagoda, the total height should be slightly less than the original height before its tilt. Through the examination of the pagoda’s tilting condition, numerous in-depth studies still need to be conducted in order to estimate the pagoda’s original height before tilting. |
| 27 | The total height of the base here is taken from Chen Mingda’s Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), from the ground under the southern platform to the top of the base. The height of the base measured by Beijing Institute of Civil Engineering and Architecture and Chinese Academy of Cultural Heritage is different from the above, which is caused by the different location of the ground. |
| 28 | In the book Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County), Chen Mingda tried to restore the caisson and ceiling on second, third and fourth floor. Regardless of whether the second, third, and fourth floors had caisson or ceiling in the past, from the proportional relationship between the height of the story and the height of the Buddha at present, the pagoda also shows a clearer design intention even if there is no caisson or ceiling. |
| 29 | Li Jie even put forward the integer ratios of 141:100 and 100:71 in Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards), which are more accurate and closer to than the craftsman’s formula of “ fang wu xie qi方五斜七 (square five, oblique seven)”. He wrote in the item “qu jing wei 取徑圍 (Taking the Diameter and Circumference)” in “kan xiang 看詳 (Definition)”: “Today’s work has created objects and systems based on the diameter and circumference. If you want to know the size of a circle, you have to find the diameter from the circumference, or the circumference from the diameter. If we follow the old rules and take ‘zhou san jing yi, fang wu xie qi 週三徑一, 方五斜七 (circumference three, diameter one; square five, oblique seven)’ as the basis, it will be much simpler. This article is hereby amended according to the Jiu Zhang Suan Jing and the approximate diagonal length. A circle with a diameter of 7 has a circumference of 22; A square has a circumference of 100 and a diagonal length of 141; … If you take a square inside the diameter of the circle, you get 71 out of 100”. |
| 30 | According to Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra), “ zhi 指 (finger)” is one of the basic modules of statue making, such as the height of the vertical Buddha is 120 fingers tall, the height of the Buddha sitting cross-legged is 70 fingers tall, and the dimensions of all parts of the body of the statue are based on “finger”. In addition, it is stipulated that twelve fingers are the length of the Zhe 搩, double the length of the Zhe 搩 is the length of the zhou肘 (elbow), and four elbows are the length of the Xun 寻. |
| 31 | In addition, the main Buddha in the Great East Hall of Foguang Monastery in Mount Wutai is times the total height of Attendant Bodhisattvas on both sides. |
| 32 | Wang Guixiang once pointed out, “In Chinese Esoteric Buddhism, especially in Tibetan Buddhism, the mysterious schema “mandala”, is a figure composed of square and circle with cosmic symbolic significance. Its basic concept is “ fang yuan xiang han 方圓相涵 (square and circle contain each other)”, the Tibetan esoteric Chengde Pule Monastery with the round hall and square city of the huge mandala-style architecture, is a typical example. It still needs to be further studied and analyzed whether the relationship between square and circle is also used in the proportion of its architecture. However, in the shape concept, the meaning of creating some cosmic symbol with the form of square and circle is similar to the proportion problem of Tang and Song architectures analyzed by us”. |
| 33 | In addition, the ratio of the total height to the clear height of the eight Bodhisattvas on the fifth floor is also about 3:2. |
| 34 | In addition, Zhang Shiqing’s research pointed out that the ratio of the width of zucai (21 fen) and the width of dancai (15 fen) is 7:5 in Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards), in line with the “fang wu xie qi 方五斜七 (square five, oblique seven)“ ratio (). It can be seen that the scale of “cai” in Ying Zao Fa Shi 營造法式 is the result of the comprehensive application of 7:5 () and 3:2. |
| 35 | Wang Jun 王軍 further pointed out that the three doors of the south wall and the two doors of the north wall of the Yuan Dadu also have the meaning of “ tian nan di bei天南地北 (the sky is in the south, and the earth is in the north) “ and “ san tian liang di 參天兩地 (three as the heavenly number and two as the earthly number) ”. |
| 36 | [Song] Zhu Xi 朱熹: Zhou Yi Ben Yi 周易本義 Volume 4 “Shuogua Zhuan 說卦傳 the Biography of Shuogua”, page 261. |
| 37 | In addition, the height of the first floor (14.57 m)/the height of the second floor (8.82 m) = 1.652 ≈ 5:3 (99.1% coincidence). |
| 38 | In the “nine-mandala” schema on the top floor of the pagoda, there is both the “ si fang wu wei 四方五位 (the four directions and five positions)” relationship between the main Buddha and the four Bodhisattvas of the east, west, south, and north and the “ba fang jiu gong 八方九宮 (the eight directions and nine palaces)” relationship between the main Buddha and the eight Bodhisattvas. The discussion of “si fang wu wei 四方五位” and “ ba fang jiu gong八方九宫” can be found in the first chapter of the reference Zhong Guo Gu Dai de Tian Wen yu Ren Wen 中國古代的天文與人文 Astronomy and Humanity in Ancient China (). |
| 39 | The data are cited from the reference Ying Xian Mu Ta Bao Hu Yan Jiu 應縣木塔保護研究 (Study on the Protection of the Timber Pagoda in Ying County) (). |
| 40 | According to Wang Jun’s research, “ Zhouyi 周易 (the Book of Change) uses 9 and 6 to represent the Yin陰 and Yang陽 attributes of the Yao爻, Yang is 9 and Yin is 6; sixty-four hexagrams are formed by two trigrams, from the bottom to the top of the six lines’ position are called the first, second, third, fourth, fifth, upper, the center line of the upper hexagrams is fifth. If it is Yang line, it is called the 9 and 5; in the six lines, the odd sequence position is Yang, the even sequence position is Yin. The 9 and 5 lines are Yang lines in the Yang position, as well as the center line of the upper hexagrams, that is, the right position in the middle, the ancients regard the middle as the respect, which is the ‘ jiu wu zhi zun 九五之尊 (nine and five are the numbers of the honorable central position) ’”. |
| 41 | It remains to be further studied when these three ba gua tu 八卦圖 (Eight Diagrams) or tai ji tu太極圖 (Taiji Diagrams) appeared in the pagoda. |
| 42 | This article was originally published in the second issue of She Hui Jiao Yu Ji Kan 社會教育季刊 (Sociology of Education), June 1943, and can be found in the article republished in the Jian Zhu Shi Xue Kan 建築史學刊 (Journal of Architectural History). |
References
- Chen, Mingda. 2001. Ying Xian Mu Ta 應縣木塔 (Timber Pagoda in Ying County). Beijing: Cultural Relics Press. [Google Scholar]
- Chen, Mingda. 2002a. Dule Si Guanyin Ge, Shanmen de Damuzuo Zhidu 獨樂寺觀音閣、山門的大木作制度 (The System of Large Wooden Works at the Guanyin Pavilion and the Mountain Gate of Dule Mon-astery) (Vol. I). In Jian Zhu Shi Lun Wen Ji 建築史論文集 (Treatises on History of Architecture). Edited by Zhang Fuhe. Beijing: Tsinghua University Press, vol. 15, pp. 71–88. [Google Scholar]
- Chen, Mingda. 2002b. Dule Si Guanyin Ge, Shanmen de Damuzuo Zhidu 獨樂寺觀音閣、山門的大木作制度 (The System of Large Wooden Works at the Guanyin Pavilion and the Mountain Gate of Dule Mon-astery) (Vol. II). In Jian Zhu Shi Lun Wen Ji 建築史論文集 (Treatises on History of Architecture). Edited by Zhang Fuhe. Beijing: Tsinghua University Press, vol. 16, pp. 10–30. [Google Scholar]
- Chen, Siliang, Mengzhe Yu, Xinyue Xu, Kaiyu Sun, and Chen Peng. 2023. Duo Mian Wei Fan Die Fo Hua Ta—Fogong Si Shijia Ta Yi Ti Hua She Ji Mo Shi ji Ying Zao Li Nian Tan Xi 度面為範 疊佛化塔—佛宮寺釋迦塔一體化設計模式及營造理念探析 (Using Buddha Statue’s Facial Length as Modular Measurement and ‘Stacking Buddha Statues’ to Construct the Pagoda: An Exploration of the Integrated Design Model and Building Philosophy for the Sakyamuni Pagoda of Fogong Temple). Jian Zhu Yi Chan 建築遺產 (Heritage Architecture) 2023: 65–76. [Google Scholar]
- Cheng, Xuyong. 2017. Study on Eight Bodhisattvas of Liao Dynasty. Liao and Jin History and Archaeology 1: 81–109. [Google Scholar]
- Cheng, Zhenyi, and Renjun Wen. 2012. Zhou Bi Suan Jing Yi Zhu 周髀算經譯註 (The Translation and Annotation of the Mathematical Classic of the Zhou Shadow-Gauging Instrument). Shanghai: Shanghai Guji Press. [Google Scholar]
- Ding, Yao, and Li Cheng. 2008. Yixian Fengguo Si Daxiong Dian Diaocha Baogao 義縣奉國寺大雄殿調查報告 (Investigation Report on the Mahāvīra Hall of Fengguo Monastery in Yi County, Liaoning). In Yi Xian Feng Guo Si 義縣奉國寺 (Fengguo Monastery in Yi County). Edited by Architectural Culture Investigation Group. Tianjin: Tianjin University Press. [Google Scholar]
- Feng, Shi. 1993. Hongshan Wenhua San Huan Shi Tan de Tian Wen Xue Yanjiu—Jian Lun Zhong Guo Zui Zao de Yuan Qiu yu Fang Qiu 紅山文化三環石壇的天文學研究—兼論中國最早的圜丘與方丘 (Astronomical Research on the Three Ring Stone Altars of Hongshan Culture—On the earliest Circular Mound and Fang Mound in China). Bei Fang Wen Wu 北方文物 (Northern Cultural Relics) 1: 9–17. [Google Scholar]
- Feng, Shi. 2006. Zhong Guo Gu Dai de Ren Wen yu Tian Wen 中國古代的天文與人文 (Astronomy and Humanity in Ancient China). Beijing: China Social Sciences Press. [Google Scholar]
- Feng, Shi. 2010. Zhong Guo Tian Wen Kao Gu Xue 中國天文考古學 (Chinese Astroarchaeology), 2nd ed. Beijing: China Social Sciences Press. [Google Scholar]
- Feng, Shi. 2018. Wen Ming Yi Zhi: Shang Gu de Tian Wen, Si Xiang yu Zhi Du 文明以止:上古的天文、思想與制度 (Continuity of the Illustrious Culture: Astronomy, Thoughts, and Institutions in Ancient China). Beijing: China Social Sciences Press. [Google Scholar]
- Fu, Xinian. 1998. Zhongguo Zaoqi Fojiao Jianzhu Buju Yanbian ji Diannei Xiangshe de Buzhi 中國早期佛教建築佈局演變及殿內像設的佈置 (The Evolution of Layout in Early Chinese Buddhist Architecture and Statues). In Fu Xinian Jian Zhu Shi Lun Wen Ji 傅熹年建築史論文集 (Fu Xinian’s Treatises on History of Architecture). Edited by Fu Xinian. Beijing: Cultural Relics Press. [Google Scholar]
- Gongbu, Chabu, trans. 2016. Foshuo Zaoxiang Liangdu Jing 佛說造像量度經 (Buddhist Statue Measurement Sutra). Beijing: Cultural Relics Press. [Google Scholar]
- Guo, Youmeng. 2007. Dun Huang Shi Ku “Lushena Fo bing Bada Pusa Mantuoluo” Chu Tan 敦煌石窟“盧舍那佛並八大菩薩曼陀羅”初探 (Preliminary study on “Lushena Buddha and Eight Bodhisattvas Mandala” in Dunhuang Grottoes). Dunhuang Xue Ji Kan 敦煌學輯刊 (Journal of Dunhuang Studies) 1: 45–63. [Google Scholar]
- Hou, Weidong, Linan Wang, and Xinqun Yong. 2016. Ying Xian Mu Ta Bao Hu Yan Jiu 應縣木塔保護研究 (Study on the Protection of the Timber Pagoda in Ying County). Beijing: Cultural Relics Press. [Google Scholar]
- 國家文物局文物保護科學技術研究所 (Institute of Antiquities Preservation Sciences and Techniques of National Cultural Heritage Administration), 山西省古代建築保護研究所 (Shanxi Ancient Architecture Provincial Institute), 山西省雁北地區文物工作站 (Shanxi Yanbei Cultural Relics Workstation), and 山西省應縣木塔文物保管所 (Shanxi Pagoda of Fogong Temple Relics Storage). 1982. Shan Xi Ying Xian Fo Gong Si Mu Ta nei Fa Xian Liao Dai Wen Wu 山西應縣佛宮寺木塔內發現遼代珍貴文物 (Precious Cultural Relics of the Liao Dynasty were found in the Pagoda of Fogong Temple). Wen Wu 文物 (Cultural Relics) 6: 97–101. [Google Scholar]
- Li, Jie. 2006. Ying Zao Fa Shi 營造法式 (Treatise on Architectural Methods or State Building Standards) (Photocopy by Tao Xiang). Beijing: China Architecture Publishing. [Google Scholar]
- Li, Zehui, Dawei Li, and Chang Liu. 2022. 營造尺和材分制:應縣木塔五層木構表裏數據採集與試解 (Construction Ruler and/or Modular caifen System: Data Acquisition and Interpretation of the Structural Design of Sakyamini Pagoda, Ying County, Shanxi Province). 建築史學刊 (Journal of Architecturual History) 3: 36–53. [Google Scholar]
- Li, Zehui, Shoutang Zhao, Qinyuan Li, Dawei Li, Yang Xu, Tong Chen, and Chang Liu. 2021. 應縣木塔平面尺丈假說:從1933年的舊照說起 (A Design Hypothesis for the Floor-Plan Dimensions of Sakyamuni Pagoda, Ying County, Shanxi Province: Starting with an Old Photo Taken in 1933). 建築史學刊 (Journal of Architecturual History) 2: 56–70+177. [Google Scholar]
- Liang, Sicheng. 1932. Wo Men Suo Zhi Dao De Tang Dai Fo Si Yu Gong Dian 我們所知道的唐代佛寺與宮殿 (Buddhist Temples and Palaces in the Tang Dynasty Known to Us). Zhongguo Yingzao Xueshe Huikan 中國營造學社彙刊 (The Bulletin of the Society for Research in Chinese Architecture) 3: 1. [Google Scholar]
- Liang, Sicheng. 2007. Shanxi Yingxian Fogong Si Liao Shijia Muta 山西應縣佛宮寺遼釋迦木塔 (Liao Sakya Timber Pagoda of Fogong Temple in Ying County, Shanxi). In Liang Sicheng Quan Ji 梁思成全集 (The Complete Works of Liang Sicheng). Edited by Liang Sicheng. Beijing: China Architecture Publishing. [Google Scholar]
- Liu, Chang, Dawei Li, Zehui Li, and Shoutang Zhao. 2022. 算法在儒匠之間:應縣木塔平面丈尺假說續輪 (Algorithm Toned by the Learned and the Craftspeople: Re-interpreting the Hypothesis about the Dimensional Design of the Plan of Sakyamuni Pagoda, Ying County, Shanxi Province). 建築史學刊 (Journal of Architecturual History) 3: 126–35. [Google Scholar]
- Liu, Chang, Huinong Liao, and Shusheng Li. 2012. Shanxi Pingyao Zhenguo Si Wanfo Dian yu Tianwang Dian Jingxi Cehui 山西平遙鎮國寺萬佛殿與天王殿精細測繪報告 (Report on Fine Surveying and Mapping of the 10,000 Buddhas Hall and the Celestial Kings Hall of Zhengguo Monastery in Pingyao, Shanxi). Beijing: Tsinghua University Press. [Google Scholar]
- Luo, Zhao. 2010. Ying Xian Mu Ta Su Xiang de Zong Jiao Chong Bai Ti Xi 應縣木塔塑像的宗教崇拜體系 (Religious Worship System of Statues in Pagoda of Fogong Temple). In Yi Shu Shi Yan Jiu 藝術史研究 (The Study of Art History). Guangzhou: Sun Yat-sen University Press, vol. 12, pp. 189–216. [Google Scholar]
- Mo, Zongjiang. 2002. Yingxian Muta Duhou Zhaji 《應縣木塔》讀後札記 (Book Review of Timber Pagoda in Ying County). In Jian Zhu Shi Lun Wen Ji 建築史論文集 (Treatises on Architectural History). Edited by Zhang Fuhe. Beijing: Tsinghua University Press, vol. 15. [Google Scholar]
- Mo, Zongjiang, and Mingda Chen. 1989. Gongxian Shiku Si Diaoke de Fengge ji Jiqiao 鞏縣石窟雕刻的風格及技巧 (Style and Tech-nique of Carving in Gongxian Cave Temple). In Zhong Guo Shiku: Gongxian Shiku Si 中國石窟:鞏縣石窟寺 (Grottoes in China: Gongxian Cave Temple). Edited by Henan Provincial Institute of Cultural Heritage and Archaeology. Beijing: Cultural Relics Press. [Google Scholar]
- Nara National Museum, Todai-Ji Temple, and Asahi Shimbun Company. 2002. The Consecration of the Great Buddha 125 Years: Todaiji Temple. Osaka: Asahi Shimbun. [Google Scholar]
- Seiichi, Mizuno, Nagahiro Toshio, and Institute of Archaeology, Chinese Academy of Social Sciences. 2016. 雲岡石窟 (Yungang Grottoes). Beijing: China Science Publishing, vol. 12. [Google Scholar]
- Shi, Zhen, and Yu Zhang. 2013. Song “Ying Zao Fa Shi” Cai Fen Zhi Du de Shu Li Han Yi ji Lv Du Xie He de Shen Mei Yi Xiang Tan Xi 宋《營造法式》材分制度的數理含義及律度協和的審美意象探析 (Aesthetic lmage Analysis of the Cai Fen System in the Song Dynasty Yingzaofashi on its Meaning of Numbers and the Harmony between Music Temperament and Metrology). 建築師 (The Architect) 3: 58–75. [Google Scholar]
- Song Ke Suan Jing Liu Zhong 宋刻算經六種 (Suan Jing Liu Zhong in Song Dynasty). 1981. Beijing: Cultural Relics Press.
- Su, Bai. 1985. Dule Si Guanyin Ge yu Ji Zhou Yutian Han Jia 獨樂寺觀音閣與薊州玉田韓家 (Avalokitesvara Pavilion of Dule Temple and Han Clan in Yutian, Jizhou). Wen Wu 文物 (Cultural Relics) 7: 32–48. [Google Scholar]
- Sun, Dazhang. 2008. Chengde Puning Si—Qing Dai Fo Jiao Jian Zhu zhi Jie Zuo 承德普寧寺—清代佛教建築之傑作 (Puning Temple in Chengde—A Masterpiece of Buddhist Architecture in the Qing Dynasty). Beijing: China Architecture Publishing. [Google Scholar]
- Wang, Guixiang. 1984. Yu Tang Song Jianzhu Zhu Yan Guanxi 与唐宋建築柱簷關係 ( Relationship with Columns and Eaves of Tang and Song Dynasties). In 建築歷史與理論 (Architectural History and Theory) (Series 3 and 4). Edited by Academic Committee of Architectural History of Architectural Society of China. Nanjing: Jiangsu People’s Publishing House, pp. 137–44. [Google Scholar]
- Wang, Guixiang. 1989. Tang Song Dan Yan Mugou Jianzhu Pingmian yu Limian Bili Guilv de Tantao 唐宋單簷木構建築平面與立面比例規律的探討 (A Study on Rules of Proportion in Plans and Facades of Single-Eaved Buildings of Tang-Song Periods). 北京建築工程學院學報 (Journal of Beijing University of Civil Engineering and Architecture) 12: 49–70. [Google Scholar]
- Wang, Guixiang. 1998. Tang Song Dan Yan Mugou Jianzhu Bili Tanxi 唐宋單簷木構建築比例探析 (A Study on Rules of Proportion of Tang—Song Periods). In Ying Zao 營造 (No. 1: Selected Papers of the First International Symposium on Chinese Architectural History). Beijing: Wenjin Publishing House, pp. 226–47. [Google Scholar]
- Wang, Jun. 2022a. Yao Feng Shun Yu: Yuan Dadu Gui Hua Si Xiang yu Gu Dai Zhong Guo 堯風舜雨:元大都規劃思想與古代中國 (Yao Feng Shun Yu: The Planning Thought of Yuan Dadu and Ancient China). Beijing: SDX Joint Publishing Company. [Google Scholar]
- Wang, Jun. 2022b. “Zhouyi” yu Zijin Cheng Ping Mian Gui Hua 《周易》與紫禁城平面規劃 (“Zhou’s [Book of ] Changes” and the Plan of the Forbidden City). In The International Forum on the History of Ming and Qing Dynasties in China in Commemoration of the 600th Anniversary of the Forbidden City Proceedings. Edited by the Palace Museum. Beijing: Palace Museum Press. [Google Scholar]
- Wang, Nan. 2017. Guiju Fangyuan Fo zhi Ju Suo: Wutai Shan Foguang Si Dong Da Dian Gou Tu Bi Li Tan Xi 規矩方圓 佛之居所—五台山佛光寺東大殿構圖比例探析 (Circles, Squares, and the Place Where Buddha Lives: An Explorative Study on Compositional Proportion of the Main Hall of Foguangsi). 建築學報 (Architectural Journal) 6: 29–36. [Google Scholar]
- Wang, Nan. 2018a. Guiju Fangyuan Duo Xiang Gou Wu: Dule Si Guanyin Ge, Shan Men ji Su Xiang zhi Gou Tu Bi Li Tan Xi 規矩方圓 度像構屋—薊縣獨樂寺觀音閣、山門及塑像之構圖比例探析 (Rules of Square and Circle, Sculpture Sizes in Architectural Composition: An Analysis on the Composition Ratio of Guanyin Hall, Entrance Gateway and Statues in Dule Temple). In 建築史 (History of Architecture). Edited by Jia Jun. Beijing: China Architecture Publishing, vol. 41, pp. 103–25. [Google Scholar]
- Wang, Nan. 2018b. Guiju Fangyuan Futu Wan Qian: Zhong Guo Gu Di Fo Ta Gou Tu Bi Li Tan Xi (shang) 規矩方圓 浮屠萬千—中國古代佛塔構圖比例探析(上)(Rules of Square and Circle, Thousands of Different Pagodas: The Composition Ratio of Traditional Chinese Buddhist Pagodas (Part 1)). In 建築史學刊 (Journal of Chinese Architecture History). Edited by Wang Guixiang. Beijing: China Architecture Publishing, vol. 16, pp. 216–56. [Google Scholar]
- Wang, Nan. 2018c. Guiju Fangyuan Tiandi zhi He: Zhong Guo Gu Dai Du Cheng, Jian Zhu Qun yu Dan Ti Jian Zhu zhi Gou Tu Bi Li Yan Jiu 規矩方圓 天地之合—中國古代都城、建築群與單體建築之構圖比例研究 (The Principle of the Use of Square and Circle in Traditional Chinese Architecture Review of the Academic Symposium on Square and Circle, Heaven and Earth). Beijing: China City Press and China Architecture Publishing. [Google Scholar]
- Wang, Qiheng. 1990. “Ying Zao Fa Shi” Cai Fen Zhi Du de Shu Li Han Yi ji Shen Mei Guan Zhao Tan Xi 《營造法式》材分制度的數理含義及審美關照探析 (The Mathematical Meaning and Aesthetic Observation of the Material Division System in Ying Zao Fa Shi). 建築學報 (Architectural Journal) 3: 50–54. [Google Scholar]
- Wang, Qiheng. 2014. Song “Ying Zao Fa Shi” Cai Fen Zhi Du de Shu Li Han Yi ji Lv Du Xie He de Shen Mei Yi Xiang Tan Xi 宋《營造法式》材分制度的數理含義及律度協和的審美意象探析 (Aesthetic lmage Analysis of the Cai fen System in the Song Dynasty Ying Zao Fa Shi on its Meaning of Numbers and the Harmony between Music Temperament and Metrology). In Dang Dai Zhong Guo Jian Zhu Shi Jia Shi Shu: Wang Qiheng Zhong Guo Jian Zhu Shi Lun Xuan Ji 當代中國建築史家十書:王其亨中國建築史論選集 (Ten Books of Chinese Contemporary Architectural Historians: Wang Qiheng’s Treatises on Chinese Architectural History). Edited by Wang Qiheng. Shenyang: Liaoning Fine Arts Publishing House. [Google Scholar]
- Wang, Shixiang. 2001. Compilation of Qingdai Jiangzuo Zeli Huibian: Fozuo, Menshenzuo 清代匠作則例彙編:佛作、門神作 (Handicraft Regulations and Precedents of Qing Dynasty: Buddha and Door God). Beijing: Beijing Guji Press. [Google Scholar]
- Xi, Lin. 2014. Tubo Chanding Yin Piluzhena yu Bada Pusa Zu He Tu Xiang Yan Jiu 吐蕃禪定印毗盧遮那與八大菩薩組合圖像研究 (A Study of the lconographic Combination of Dhyana-Mudra Vairocana and Eight Bodhisattvas in the Tubo Period). Kao Gu yu Wen Wu 考古與文物 (Archaeology and Cultural Relics) 6: 41–48. [Google Scholar]
- Xiao, Min. 2006. Tang Song Gu Jian Zhu Chi Du Gui Lv Yan Jiu 唐宋古建築尺度規律研究 (The Study of Scale Regulation in Ancient Architecture of Tang and Song Dynasties). Nanjing: Southeast University Press. [Google Scholar]
- Yang, Tiancai, and Shanwen Zhang. 2011. Zhouyi 周易 (Zhou’s [Book of ] Changes). Beijing: Zhonghua Book Company. [Google Scholar]
- You, Li. 2013. Ying Xian Mu Ta Suo Cang “Ru Fa Jie Pin” ji qi Xiang Guan Wen Ti Kao Lun 應縣木塔所藏 《入法界品》及其相關問題考論 (Research on Ru Fa Jie Pin in Wooden Buddhist Pagoda in Ying County). Shan Xi Dang An 山西檔案 (Shanxi Archives) 6: 27–32. [Google Scholar]
- Zhang, Shiqing. 2004. Zhong Ri Gu Dai Jian Zhu Da Mu Ji Shu de Yuan Liu yu Bian Qian 中日古代建築大木技術的源流與變遷 (The Origin and Change of Timber Construction Technology in Ancient Architecture in China and Japan). Tianjin: Tianjin University Press. [Google Scholar]
- Zhang, Shiqing. 2013. “Ying Zao Fa Shi” Cai Bi Li de Xing Shi yu Te Dian: Chuan Tong Shu Li Bei Jing Xia de Gu Dai Jian Zhu Ji Shu Fen Xi 《營造法式》材比例的形式與特點—傳統數理背景下的古代建築技術分析 (The Form and Characteristics of Timber Proportion in Ying Zao Fa Shi: The Technical Analysis of Ancient Architecture under the Background of Traditional Mathematics). 建築史 (History of Architecture) 31: 9–14. [Google Scholar]
- Zhang, Yijie, Haoran Ye, and Xiao Han. 2018b. Dui Ying Xian Mu Ta 1962nian Shi Ce Shu Ju de Zai Fen Xi 對應縣木塔1962年實測數據的再分析 (Reanalysis of the Measured Data of Sakyamuni Pagoda, Ying County, Shanxi Province in 1962). Xi Bu Ren Ju Huan Jing Xue Kan 西部人居環境學刊 (Journal of Human Settlements in West China) 33: 80–85. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).