A Model for the Spread of Infectious Diseases with Application to COVID-19
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
- (1)
- An approximating function based on the proposed for the actual data that enables to predict near future outcomes and also enables to backtrack to estimate the initial values that might have been in those cases where the early or initial data on the pandemic outbreak is not available or was not reported or recorded.
- (2)
- A time-constant of the first order system that determines the time for which the number of deceased people will reach a particular percentage of the peak value. Recall that the response of a first-order system would reach a plateau value asymptotically. For example, the population will reach 99.33% of the plateau (or saturation) value for a period of time equal to five time constants or ; 99.75% of for , etc.
- (3)
- The asymptote’s (maximum) value that corresponds to the maximum number of people that would be deceased in the long run or for a long period of time.
- (4)
- The inflection point of the estimated curve at which the sigmoid changes concavity in Figure 1a. This point corresponds also to the time for which the maximum rate of deaths per day (i.e., ) occur.
2.2. Death Rates
3. Results
3.1. Simulation Results
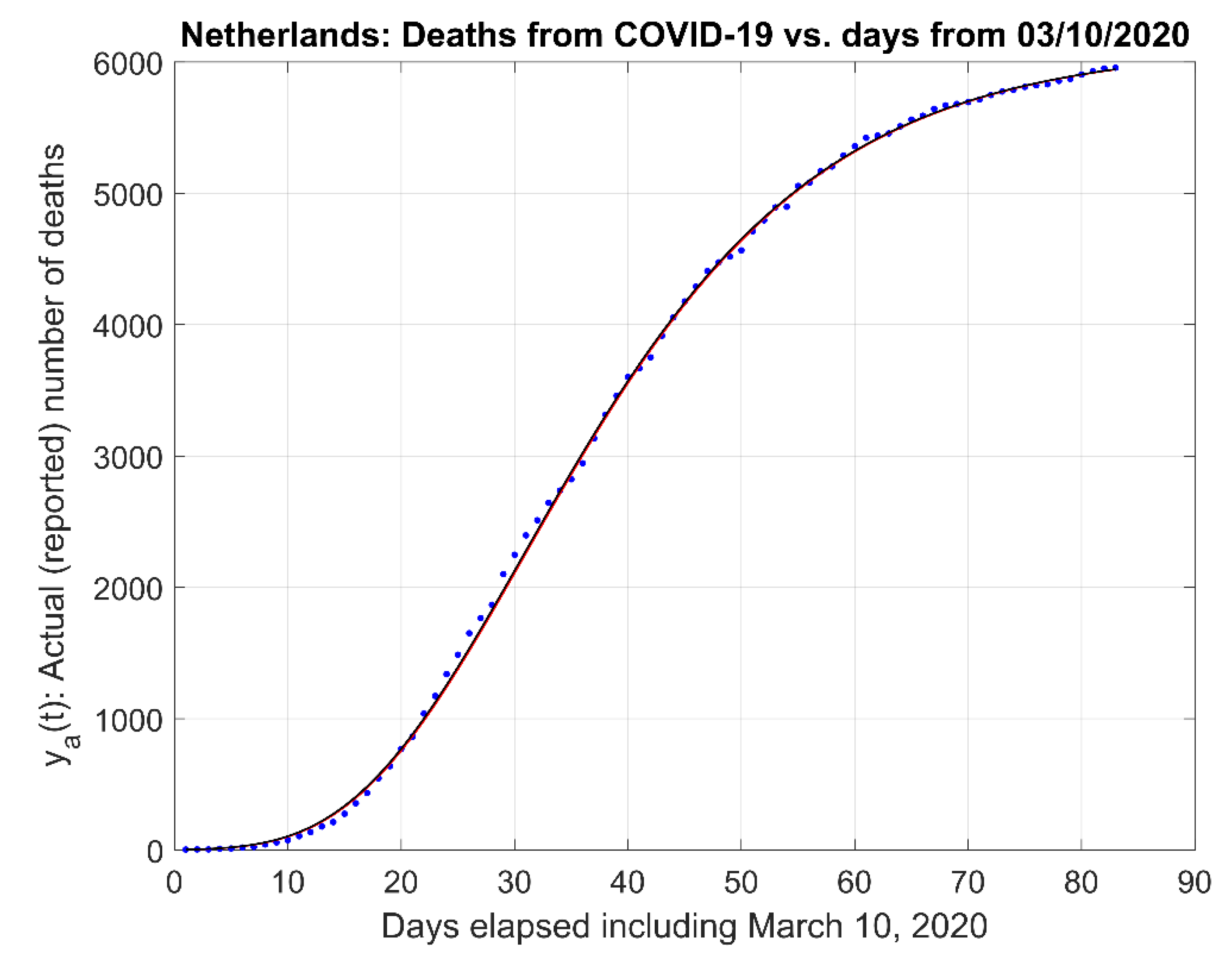
- (1)
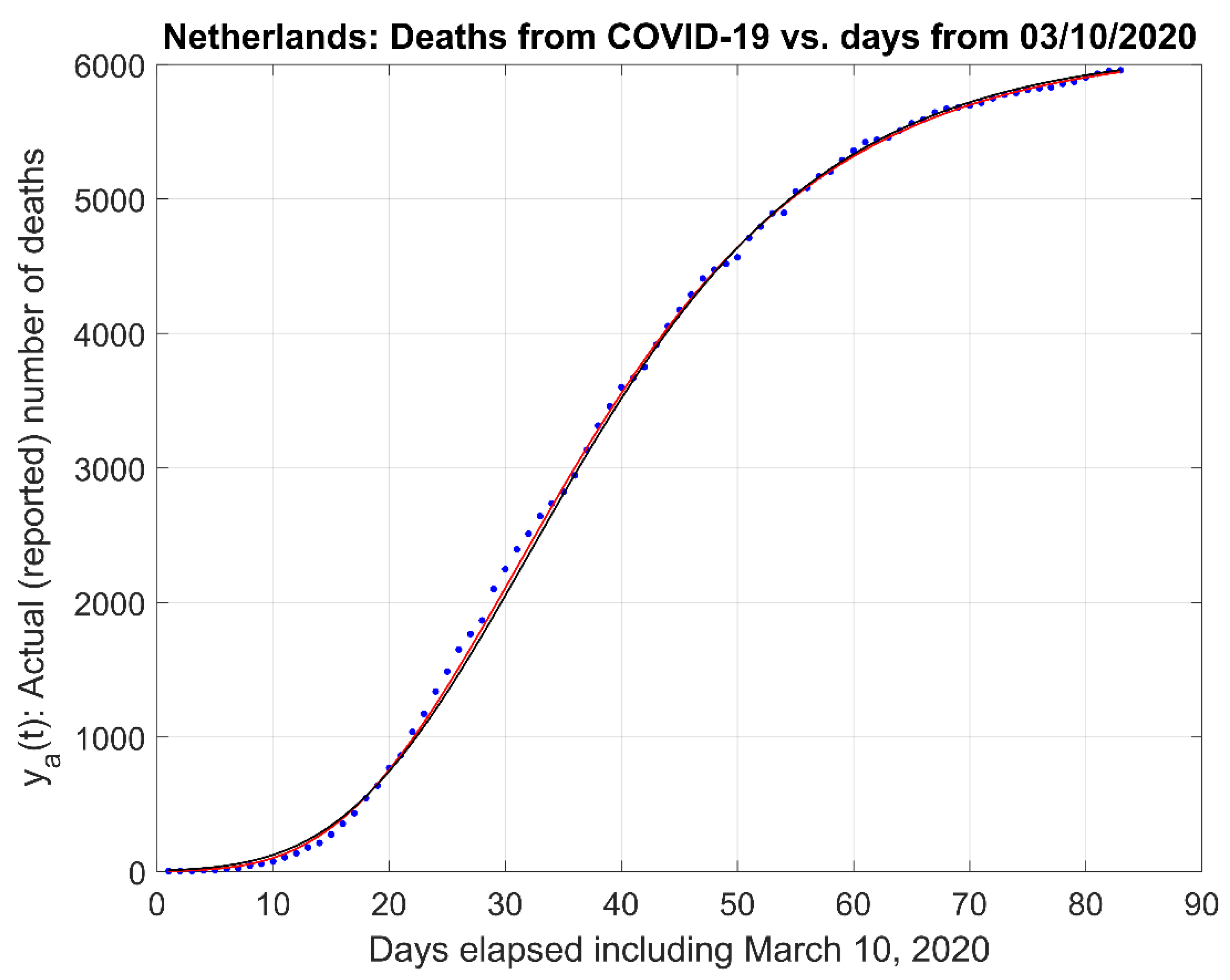
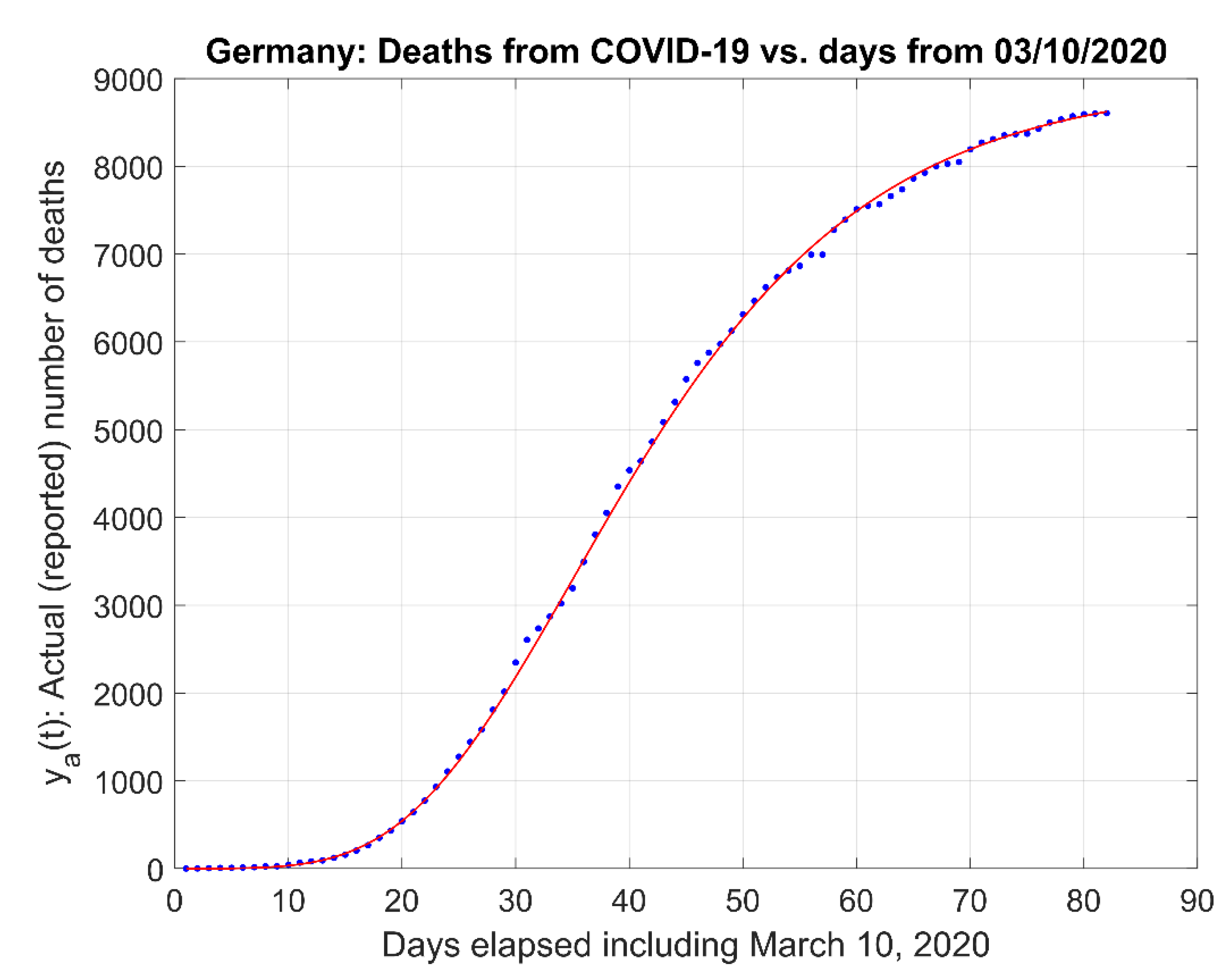
- Actual data and the actual data model estimates curve .
- (2)
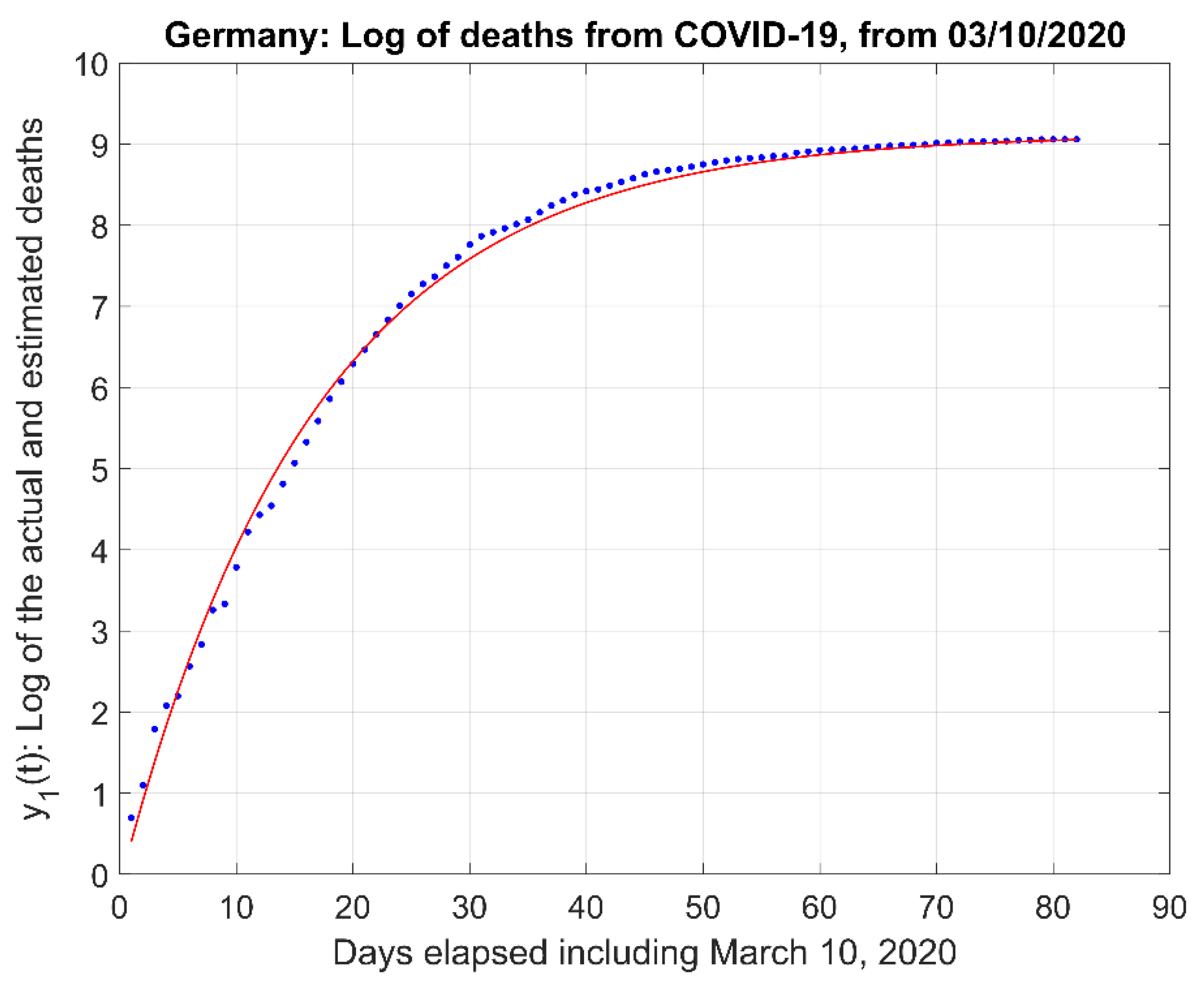
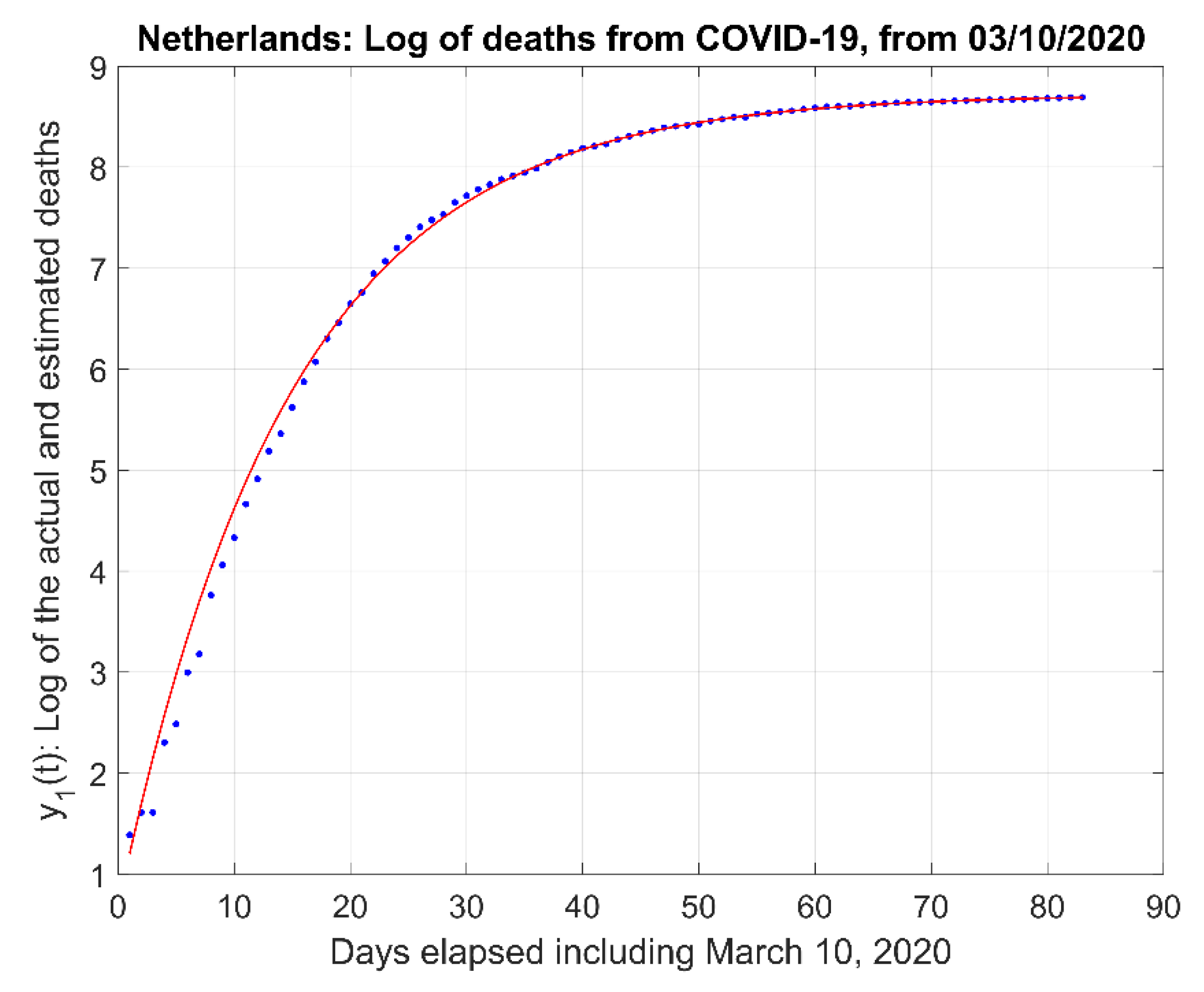
- The natural logarithm of the actual data and the model estimate curve .
- (3)
- The linearization of the actual data logarithm and the linear fit .
- (4)
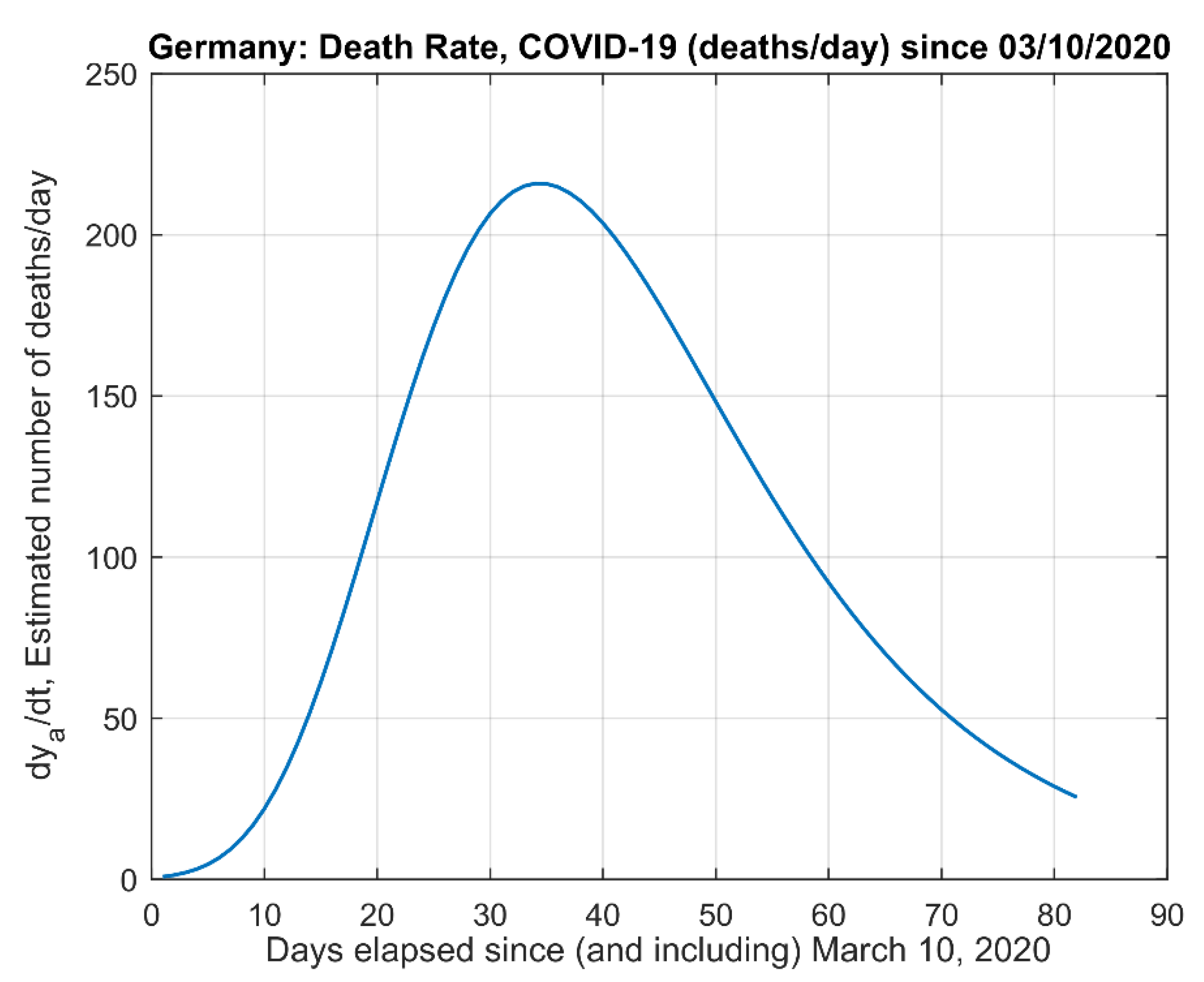
- The derivative of the actual data model .
- (5)
- Additional graphs of interest, like fit residuals n some of the cases analyzed.
3.2. Comparison to Other Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Details on the Least-Square Model Parameter Estimates
Appendix B



References
- Anderson, R.M.; Anderson, B.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Nowak, M.A.; May, R. Virus Dynamics: Mathematical Principles of Immunology and Virology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Adiga, A.; Dubhashi, D.; Lewis, B.; Marathe, M.; Venkatramanan, S.; Vullikanti, A. Mathematical Models for COVID-19 Pandemic: A Comparative Analysis. J. Indian Inst. Sci. 2020, 100, 793–807. [Google Scholar] [CrossRef] [PubMed]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; di Filippo, A.; di Matteo, A.; Colaneri, M. Modelling the COVID-19 Epidemic and Implementation of Population-Wide Interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, J.F.; Jorge, D.C.P.; Veiga, R.V.; Rodrigues, M.S.; Torquato, M.F.; da Silva, N.B.; Fiaccone, R.L.; Cardim, L.L.; Pereira, F.A.C.; de Castro, C.P.; et al. Mathematical Modeling of COVID-19 in 14.8 Million Individuals in Bahia, Brazil. Nat. Commun. 2021, 12, 333. [Google Scholar] [CrossRef] [PubMed]
- Baek, Y.J.; Lee, T.; Cho, Y.; Hyun, J.H.; Kim, M.H.; Sohn, Y.; Kim, J.H.; Ahn, J.Y.; Jeong, S.J.; Ku, N.S.; et al. A Mathematical Model of COVID-19 Transmission in a Tertiary Hospital and Assessment of the Effects of Different Intervention Strategies. PLoS ONE 2020, 15, e0241169. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, V.; Deyal, N.; Bisht, N.S. Mathematical Modeling Based Study and Prediction of COVID-19 Epidemic Dissemination Under the Impact of Lockdown in India. Front. Phys. 2020, 8, 586899. [Google Scholar] [CrossRef]
- Kyrychko, Y.N.; Blyuss, K.B.; Brovchenko, I. Mathematical Modelling of the Dynamics and Containment of COVID-19 in Ukraine. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Iboi, E.; Sharomi, O.O.; Ngonghala, C.; Gumel, A.B. Mathematical Modeling and Analysis of COVID-19 Pandemic in Nigeria. Math. Biosci. Eng. 2020, 17, 7192–7220. [Google Scholar] [CrossRef] [PubMed]
- Cherniha, R.; Davydovych, V. A Mathematical Model for the COVID-19 Outbreak and Its Applications. Symmetry 2020, 12, 990. [Google Scholar] [CrossRef]
- COVID-19 Coronavirus Pandemic|Worldometer. Available online: https://www.worldometers.info/coronavirus/ (accessed on 27 October 2020).
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; van’t Riet, K. Modeling of the Bacterial Growth Curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Addison Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Brauer, F.; van den Driessche, P.; Wu, J. Mathematical Epidemiology (Lecture Notes in Mathematics); Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Sperschneider, V. Bioinformatics: Problem Solving Paradigms; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Iglesias, P.A.; Ingalls, B.P. Control. Theory and Systems Biology; The MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Nowak, M.A. Evolutionary Dynamics: Exploring the Equations of Life; The Belknap Press of Harvard University Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Bohner, M.; Streipert, S.; Torres, D.F.M. Exact Solution to a Dynamic SIR Model. Nonlinear Anal. Hybrid. Syst. 2018, 32, 228–238. [Google Scholar] [CrossRef] [Green Version]
- Murray, C.J. Forecasting the Impact of the First Wave of the COVID-19 Pandemic on Hospital Demand and Deaths for the USA and European Economic Area Countries. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Phillips, C.; Parr, J.; Riskin, E. Signals, Systems, & Transforms; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- da Silva, A.P.R.; Longhi, D.A.; Dalcanton, F.; de Aragão, G.M.F. Modelling the Growth of Lactic Acid Bacteria at Different Temperatures. Braz. Arch. Biol. Technol. 2018, 61, 18160159. [Google Scholar] [CrossRef]
- COVID-19 Forecasts: Deaths | CDC. Available online: https://www.cdc.gov/coronavirus/2019-ncov/covid-data/forecasting-us.html (accessed on 27 October 2020).
- COVID-19-Forecasts/GitHub. Available online: https://github.com/cdcepi/COVID-19-Forecasts/blob/6768f5dbc09dd03833584f9f2dc156c157b2247f/COVID-19_Forecast_Model_Descriptions.md (accessed on 30 October 2020).
- COVID 19 Forecast Hub. Available online: https://covid19forecasthub.org/ (accessed on 27 October 2020).
- Kalantari, R.; Zhou, M. Graph Gamma Process Generalized Linear Dynamical Systems. arXiv 2020, arXiv:2007.12852. [Google Scholar]
- Holmdahl, I.; Buckee, C. Wrong but Useful—What Covid-19 Epidemiologic Models Can and Cannot Tell Us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]



| Date | CN | SK | IT | IR | US | SP | FR | DE | UK | NE |
|---|---|---|---|---|---|---|---|---|---|---|
| 01/21 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 01/22 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 01/23 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| … | ||||||||||
| 05/29 | 4634 | 269 | 33,229 | 7677 | 104,542 | 27,121 | 28,714 | 8594 | 38,593 | 5931 |
| 05/30 | 4634 | 269 | 33,340 | 7734 | 105,557 | 27,125 | 28,771 | 8600 | 38,819 | 5951 |
| 05/31 | 4634 | 270 | 33,415 | 7797 | 106,195 | 27,127 | 28,802 | 8605 | 38,934 | 5956 |
| Date | CN | SK | IT | IR | US | SP | FR | DE | UK | NE |
| Parameter Country | RSS | ||||
|---|---|---|---|---|---|
| CN | 8.4480 | 4664 | 14.15 | 0.39 | 0.4399 |
| SK | 5.6173 | 275 | 19.42 | 0.06 | 0.5745 |
| IT | 10.4574 | 34,801 | 18.00 | 1.26 | 1.4644 |
| IR | 9.0025 | 8124 | 20.53 | 1.39 | 1.0933 |
| US | 11.6622 | 116,099 | 17.13 | 1.10 | 0.3230 |
| SP | 10.2858 | 29,315 | 14.04 | 1.38 | 1.1376 |
| FR | 10.3182 | 30,279 | 17.89 | 1.93 | 2.2950 |
| DE | 9.1235 | 9168 | 16.70 | 1.57 | 1.2356 |
| UK | 10.6360 | 41,606 | 17.16 | 2.28 | 1.2653 |
| NE | 8.720 | 6124 | 14.85 | 1.37 | 1.2483 |
| Model/Parameters | Residuals Mean Value | Residuals RSS |
|---|---|---|
| First-Order α = 0.0674; td = 1.37 | 0.0414 | 1.2483 |
| Gompertz b = 2.0755; c = −0.0674 | 0.0541 | 1.3919 |
| Richards ν = 0.01; τ = 31; k = 0.07 | 0.0057 | 0.8451 |
| Logistic b = 3.65; c = 0.099 | 86.6 | 1.53 × 102 |
| Stannard k = 0.74; l = 1.0; p = 10.50 | 0.1102 | 1.4161 |
| Schnute a = 0.0655; b = 0.055; y1 = 7.274; τ1 = 3.79; τ2 = 138 | 0.0179 | 1.8290 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unglaub, R.A.G.; Spendier, K. A Model for the Spread of Infectious Diseases with Application to COVID-19. Challenges 2021, 12, 3. https://doi.org/10.3390/challe12010003
Unglaub RAG, Spendier K. A Model for the Spread of Infectious Diseases with Application to COVID-19. Challenges. 2021; 12(1):3. https://doi.org/10.3390/challe12010003
Chicago/Turabian StyleUnglaub, Ricardo A. G., and Kathrin Spendier. 2021. "A Model for the Spread of Infectious Diseases with Application to COVID-19" Challenges 12, no. 1: 3. https://doi.org/10.3390/challe12010003
APA StyleUnglaub, R. A. G., & Spendier, K. (2021). A Model for the Spread of Infectious Diseases with Application to COVID-19. Challenges, 12(1), 3. https://doi.org/10.3390/challe12010003





