Abstract
This paper investigates the problem of the task-space synchronization control for networked Euler-Lagrange systems. In the considered systems, there are time-varying delays existing in the networking links and every subsystem contains uncertainties in both kinematics and dynamics. By adding new time-varying coupling gains, the negative effects caused by time-varying delays are eliminated. Moreover, to address the difficulties of parametric calibration, an adaptively synchronous protocol and adaptive laws are designed to online estimate kinematics and dynamic uncertainties. Through a Lyapunov candidate and a Lyapunov-Krasovskii functional, the asymptotic convergences of tracking errors and synchronous errors are rigorously proved. The simulation results demonstrate the proposed protocol guaranteeing the cooperative tracking control of the uncalibrated networked Euler-Lagrange systems in the existence of time-varying delays.
1. Introduction
Recent years have witnessed rapid progress of networked coupling systems, e.g., Internet [1], Internet of Things (IoT) [2], Network Physiology [3], and satellite remote sensing. The innovative thinking of networking structure combined with conventional technologies is profoundly influencing various fields and results in technical evolutions. For instance, some outstanding studies are proposed to solve some technical issues in physiology [4,5]. Also, in industry, networked control systems (NCSs) attract increasing interests. As a representative class of NCSs, multi-agent system (MAS) is a hot subject of research. Generally speaking, it consists of different subsystems (nodes) including integrator-type nodes, autonomous vehicle, manipulators, and mobile robots, et al. Many mechanical systems could be formulated by Euler-Lagrange equations. Naturally, to find a unified control approach for all Euler-Lagrange rigid body systems is practical as well as interesting.
The synchronization is a concept in the field of MAS, which is originally inspiring from cooperative behaviors in biological universe, such as, animal flocking, the ants cooperation, etc. Inspired from these biological behaviors [6,7,8], studies of synchronization are promising and have been widely used in industrial applciations. For instance, teleoperating control [9,10,11], formation control of multiple vehicles, cooperative control of multiple mainpulators [8,12,13,14,15,16,17,18,19,20], et al. In the study of Euler-Lagrange systems, many results concentrate on mechanical dynamics, systematic kinematics, and uncertainties. Accordingly, various approaches of control have been proposed to address different technical issues in past decades [12,13,21,22,23,24,25,26]. Due to the widespread Euler-Lagrange systems, the combination of cooperative control techniques and Euler-Lagrange systems naturally becomes attractive. By cooperatively and synchronously accomplishing a task, MASs are capable to finish many industrial tasks, such as collaborating transportation, formation control, goal seeking, et al. Numerous results of the cooperative control were published in the past years. As a matter of fact, there is no distinct boundary line between synchronization and consensus. That is to say that consensus can be regarded as a basic problem of synchronization. As a distinctive feature, the synchronization usually requires the consensus of velocity. Many publications [16,17,18,19,20] are devoted to the study of consensus. Also, studies of consensus of networked Euler-Lagrange systems are reported. For instance, refs. [8,27] consider the leaderless lead-following consensus under directed topology. Regarding the study of synchronization for networking Euler-Lagrange systems, ref [28] proposes a synchronization tracking control scheme for multi-robotic manipulators. Using a passivity-based approach, which is a conveniently theoretic tool to study synchronization, enormous literature [29,30,31] has been devoted to this field, where ref. [29] considers balanced graphs and its post-study [30] further studies strongly connected graphs. Additionally, in ref. [31], a cascade scheme is presented to achieve synchronization of multiple Euler-Lagrange systems.
In NCSs, the communication issue is regarded as a key factor. That is to say that communication topologies, communicating delays, communicating noise, etc., are expected to be addressed. As a matter of fact, the communication flows are inevitably delayed and to investigate communicating delays is practical and meaningful. Some investigations propose various approaches. In the work of Liu and Chopra [32], the constant delays on networks are considered for networked robotic systems. Taking more uncertainties into consideration, Wang [33] introduces a passivity-based protocol to cope with constant communicating delays in networked robotic systems. Liang [34] proposes an uncalibrated control protocol for multiple Euler-Lagrange systems with constant networking delays. The problems of delays also are extensively investigated in neural networks [35,36,37,38]. Wang et al. [37], investigates the delayed Cohen-Grossberg neural networks by pinning control and achieves the generalized pinning synchronization. Considering output constraints and actuator nonlinearities, ref. [38] proposed an adaptive neural output-feedback control for delayed fractional-order systems. Note that all above-mentioned methods either regard communicating delay as the constant or consider the system parameters as known.
Specifically, from Equation (19) in [33] and Equation (11) in [34], it is not hard to observe that the negative effects of the communicating delays will arise when the delays become time-varying. One may argue why not tune control gains with a big enough one to guarantee the stability even under the upper bound of delays. It is common knowledge that the objective of control design is a good dynamical performance and a low control cost. To obtain less conservative results, the adaptive approach of synchronization for the delayed MAS is expected to be investigated.
Apart from the issues of the delayed networks, the control problem of uncalibrated Euler-Lagrange systems is significant and challenging. With the advances of sensor fusion, visual servoing control is widely used in robotics. The controllers which servo Euler-Lagrange systems through state errors on image-plane have been widely discussed [13,22,39]. For servoing control, the transformation matrices from task-space to actuator control input vector space usually are the key and they are usually derived from manipulator kinematics. Hence, accurate calibration is crucial for the success of control tasks. Unfortunately, calibration of kinematic parameters is not easy. Many publications mentioned the tediousness and difficulties of calibration. This explains why the control of uncalibrated Euler-Lagrange systems is of significance and of challenges. To handle such a problem, non-calibration naturally becomes an alternative. The non-calibration, also known as the uncalibrated control, plays an important role in the nowadays research of rigid body mechanical systems. Due to its extensive results, we omit the literature review about single Euler-Lagrange system here and we will concentrate on the results of networked Euler-Lagrange systems. Without using the task-space velocities, ref. [23] proposes a synchronous protocol for network robotic systems under strongly connected topology. Ref. [40] considers that multiple manipulators contain uncertain kinematic parameters and solves the problem by using the projection method and the adaptive updating law. In ref. [32], the dynamics of networked robotic systems is regarded as uncertain and an adaptive control scheme is proposed to address the uncertainties. Ref. [41] proposes a bearing-based formation control method for networked robotic systems and considers the kinematic and dynamic uncertainties on the network with the bearing Laplacian matrix. Ref. [42] investigates the separation of the kinematic and dynamic loops in the case of no task-space velocity measurement and the quantification of the manipulability of the system. From the literature review, it is not hard to observe that the synchronous control protocols which are capable to deal with the mechanical uncertainties possess both academic and engineering significance. In a word, the technical issues in nowadays Euler-Lagrange systems usually lie in kinematic transformation with uncertainties and dynamic uncertainties. Therefore, it is necessary to solve these issues in the NCS of Euler-Lagrange systems.
Basing on the above two challenges, the networking Euler-Lagrange systems to be considered have the following characteristics: There are time-varying delays existing in communicating link and the Euler-Lagrange systems are uncalibrated. In the existing literature, the article [30] presents cooperative controllers for networking Euler-Lagrange systems. The scheme considers the time-varying delays among agents (see Equation (22) in ref. [30]). Nevertheless, for the control of the Euler-Lagrange agent, accurate parameters of kinematics are needed. Moreover, the restriction of requiring a balanced and strong connection on network topology limits the application of the control scheme. To the best of our knowledge, however, the above control problems have not been investigated yet. We conclude the main difficulties in the control design of the networked Euler-Lagrange system: Non-calibration, time-varying delays of links, and the issues of velocity on task-space. The main contributions of this paper are summarized in the following three aspects. (a) It is first considered that there exist time-varying delays in communication links in the strongly connected Euler-Lagrange networking systems; (b) The problem of uncalibrated heterogeneous Euler-Lagrange systems for NCSs is addressed; (c) The task-space velocities are avoided in the protocol design to minimize the effects of noise.
2. Preliminaries
For a better understanding of this paper, some lemmas and algebraic graph theory are given in this section.
Lemma 1.
Let be a uniformly continuous function on . Suppose that exists and is finite. Then,
Graph can be conveniently used to represent the information flow [43] between agents. Let to represent an undirected graph or directed graph (digraph) of order n with the set of nodes , the set of edges , and a weighted adjacency matrix with non-negative adjacency elements . The edge indicates the information flow is from j to i. For a undirected graph, , if , then . But for digraph, it does not hold. The set of neighbors of agent i is defined as . The graph weighted adjacency matrix is such that if , and otherwise. Furthermore, conventionally, assume there is no self-loop contained i.e., , and hence for all , . The in-degree of vertex vi is denoted by , Similarly, the out-degree of a vertex is denoted by . If the in-degree equals the out degree, the graph is said to be balanced.
The Laplacian matrix is defined as
Note that the topology of a strongly connected network satisfies the following lemma, which facilitates the analysis of this paper.
Lemma 2.
If a topology is strongly connected, for its Laplacian matrix , there exist a positive vector such that
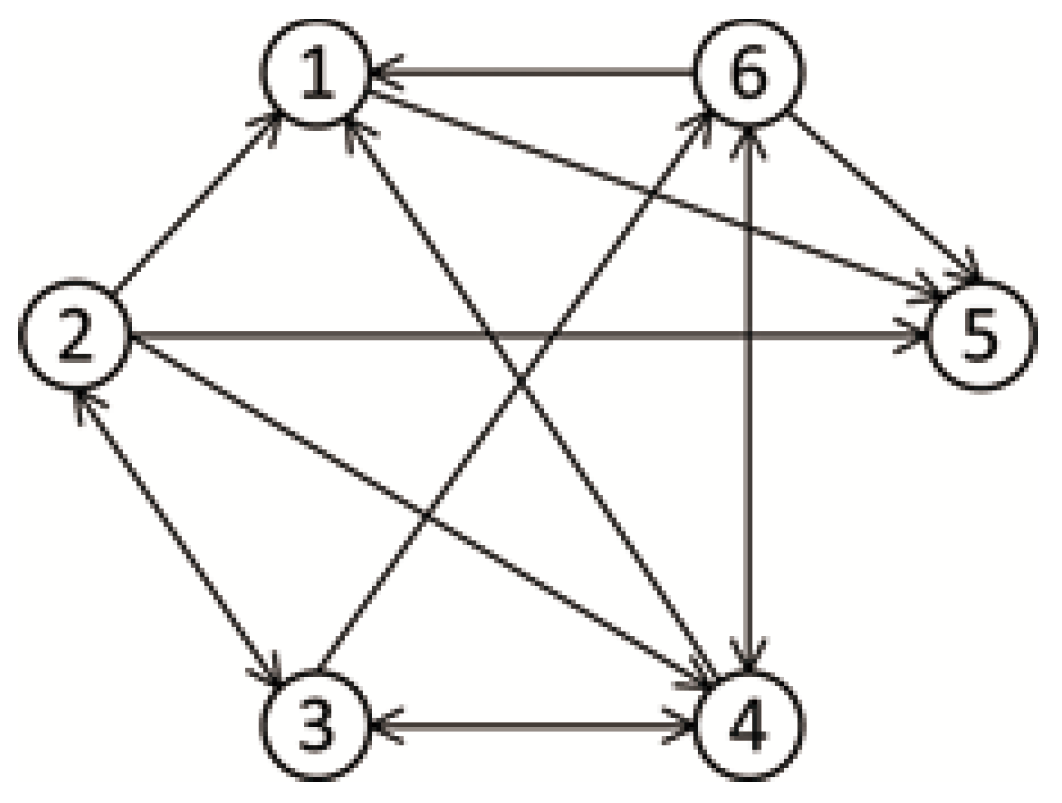
A typical strongly connected network topology is presented in Figure 1.
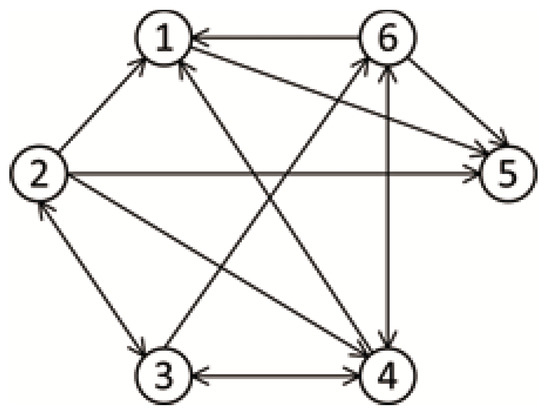
Figure 1.
The topology of a strongly connected network.
3. Modelling and Problem Formulation
3.1. Euler-Lagrange Dynamics
Consider the ith Euler-Lagrange dynamics on a network, whose behavior is described by the following well-known equation [44]
where is a vector of generalized coordinates and the measuring output; n denotes the dimension of generalized coordinate; denotes inertia matrix which is positive-define and symmetric; is the gravitational force; is Coriolis and centrifugal matrix; is the vector of torques produced by the actuators associated with the ith system. is a skew-symmetric matrix.
For any properly dimensional vector , the following holds
Furthermore, when the accelerations in the mechanical system are bounded, the states of the system (3) are also bounded. Owing to the Euler-Lagrange dynamic structure, (3) exhibits certain fundamental properties as follows [44].
Property 1.
The dynamics of an Euler-Lagrange rigid body system can be linearizing parameterized as follows
where ; is called dynamic regression matrix; the vector includes all unknown dynamic parameters which are constant; is the dimension of vector .
3.2. Kinematics
Let be the position vector on task-space of the ith agent, where m denotes the dimension of task-space. For instance, for image-plane, the dimension and for Cartesian space, . The kinematics of ith agent can be overall formulated by
where the function maps the positions from the generalized coordinates frame of Euler-lagrange systems to the task space frame. Differentiating (6) yields the task-space velocity,
where the matrix , called the Jacobian matrix, characterizes the mapping between the joint velocities and task-space velocities of the ith manipulator, also known as Jacobian matrix. The Jacobian matrix describes the kinematics of a Euler-Lagrange system. Note that (6) exhibits certain fundamental propertie the following linear parameterization property [13].
Property 2.
The kinematics (7) can be linearly parameterized as the following form
where is called the kinematic regression matrix and is the unknown vector which is constant.
Hereafter, to facilitate understanding, is simplified by and by .
3.3. Control Objective
The network considered in this paper is digraph with strongly connected topology and time-varying delays on its links. The upper bound of the changing rate of delays is assumed to be not larger than 1. The dynamics of agents is of Euler-Lagrange with uncertainties. The kinematic parameters also contain uncertainties.
Our control goal is to design a proper cooperative protocol for asymptotically and synchronously tracking a task-space trajectory . Namely, and velocity tracking errors as . The synchronization means the cooperative position synchronization error and velocity synchronization error as .
In addition, from the perspective of control performance, using task-space velocities obtained from numerical differentiation of positions may deteriorate the stability performance and the protocol is expected to be free of using task-space velocities.
4. Cooperative Task-Space Synchronous Protocol Design
Based on the above analysis, Jacobian matrix is unknown due to the absence of knowing accurate kinematic parameters. As an alternative, the estimated Jacobian matrix makes the protocol design possible. is derived according to Property 2 from the following equation,
where denotes the estimate of . Define to denote the estimated error of kinematic unknown. The adaptive law is the key of the estimation and will be designed later. With estimated , we now present the observer to estimate task-space velocity,
where to be determined later; denotes observed errors; and are positive constants. Note that the observer is to estimate the task-space velocity for avoiding directly using task-space velocity.
Differentiating yields
Define the delay of coupling signals from agent j to agent i by and it satisfies
where denotes the upper bound of the delay rate.
Remark 1.
In the case of that the knowledge of delay rates is available, using accurate delay rates makes the protocol less conservative. In the case of that delay rates is unknown, taking the upper bound as 1 can also achieve systematic stability.
Furthermore, we define references of joint-space velocities and task-space velocities for i-agent, respectively, by
where ; ; is the pseudo-inverse of ; ; is short for .
Then differentiating (13) yields
Following the typical application in ref. [45], we define a sliding vector of generalized coordinates
In view of many different vectors of error values in formulation, we denote by hereafter. Accordingly, Combining (9)–(15), the following holds
Likewise, the estimates of dynamic parameters are accordingly derived from Property 1,
The updating law for will be introduced later. Define called estimating errors. To unify, we number it with .
Now we propose the synchronous protocol for the ith Euler-Lagrange sub-system as follow
where and are control gain matrices with proper dimensions. Additionally, the gain of task-space velocity observer can therefore be determined by .
Remark 2.
It can be seen from (20) that the protocol has a form of PD+ (Proportional Differential plus dynamics compensation). Due to the extensive use of PD+ controller in rigid body systems, the proposed protocol for the networked Euler-Lagrange systems control could be easily applied to the traditional control scheme. That is to say that the synchronous protocol for multi-manipulator can be transplanted to the separated manipulator control system by revising reference task-space velocity.
Remark 3.
Note that it can be observed that the task-space velocities are not used in (20). Alternatively, task space reference velocities , including the observed velocities , are used. The protocol presented in (20) is free of the task-space positions despite the fact that they actually are available. The significance is better steady-state performance when the positions are noisy as well.
Remark 4.
Compared with the existing results, the first advantage is the processing of time-varying delays. In reality, most of the delays existing in the network usually are time-varying rather than constant. In existing results, delays are regarded as constants and the constant tends to be the upper bound of the time-varying delays in order to guarantee the overall stability. Obviously, it is conservative due to the choice of the upper bound. In this work, the control protocol is designed to adapt the varying delays such that the control approach could be less conservative. The second advantage is non-calibration. Many existing results dealing with the delays for MAS whose parameters are calibrated or bounded, (e.g., [35,36,37,38]). In a real application, for many nodes in MASs, in particular, for Euler-Lagrange systems, calibration is difficult and error-prone.
After substituting controller (20) into the dynamic Equation (3), the close-loop system is given by
where , are simplified , respectively; is short for .
Now, we are at the position to present the updating laws above mentioned, for and .
5. Stability Analysis
In this section, the rigorously mathematic proof of asymptotic and synchronous stability of the overall coupled Euler-Lagrange systems is given. The following theorem presents the main results.
Theorem 1.
Consider N-agent Euler-Lagrange systems on the network with a strongly connected topology graph. Under the synschronous protocol formulated (18) and the updating laws (22) and (23), the asymptotic stability and synchronization of the systems can be guaranteed. Namely, for the i-th agent, as . For the networked Euler-Lagrange system, , as , , with the time-varying delays which satisfies .
Proof.
For the ith Euler-Lagrange system, we propose the Lyapunov-like positive definite function as follow
Differentiating the (24) yields
Note that the unknown parameters are constant, namely, and , it is easy to obtain , By invoking (4), (16), (17), and (21), it can be rewritten
According to the definition of and , the following holds
For the overall networked system, the following Lyapunov-Krasovskii functional (LKF) is constructed,
Differentiating (28) along with the system, one has
Here, with assumption and Lemma 2, the following holds
Then (29) can be further derived as
Recalling (12), one has , leading to . The nagetive semi-definition of means that V will not increase its values. Namely, it is upper-bounded. The boundedness of exist. Hence , . From (22) and (23), . Note that , thus . Invoking (13), one obtains and . With , holds. It leads to . Under the condition of the boundedness of into (10), one derives . With bounded , holds. From (14), it is observed that . From (21), then holds. By differentiating w.r.t. time, it yields . So far, it is derived that is uniformly continuous. From Lemma 1, as can be easily derived. Consequently, for as .
The convergence of variable indicates , , for as . Similarly, one can easily derive . Due to the strongly connected graph, one has for as . □
6. Simulation Results
In this section, we conduct simulations to verify the main results of this paper. In simulations, planar manipulators are taken as examples of Euler-Lagrange systems. The mechanical parameters, including the mass of links, D-H parameters, are assumed as unknown, for the purpose of verifying the effectiveness of non-calibration. Regarding the network, the communication topology is strongly connected as mentioned above. Meanwhile, there exist delays on the network and the delays are time-varying whose rates of change are bounded by 1.
The control objective is defined on image-space. Namely, the task-space is on image, , where represents the coordinates on X-axis of image-plane and represents coordinates on Y-axis of image-plane. The associated graph Laplacian matrix is set as
The man-made communicating time-varying delays are randomly generated by computer. Accordingly, the strengths and can be derived. Note that the model parameters of agents can be different from each other. This is to say that the proposed protocol also can be employed on the networks with heterogeneous agents.
For estimating parameters of dynamics and kinematics, Property 1 and Property 2 should be used with the adaptive laws (22) and (23). Constructing the regression matrices will be the first step and the detailed procedures are provided in many existing publications, so we omit it. In this simulation, the regression matrix consists of time-varying functions with independent variables: (i.e., joint space position vector and its velocity vector); the regression matrix consists of time-varying functions with independent variables: (i.e., joint space position vector, its velocity vector, the defined references of joint velocity and the differential reference). After constructing the regression matrices, one has the differential equations formulated in (22) and (23). By setting the initial values of unknown vectors and , the unknowns can converge to certain values by iteration, leading to asymptotic convergence of Euler-Lagrange systems. To show the global convergence, the initial values of the unknowns are chosen randomly as well.
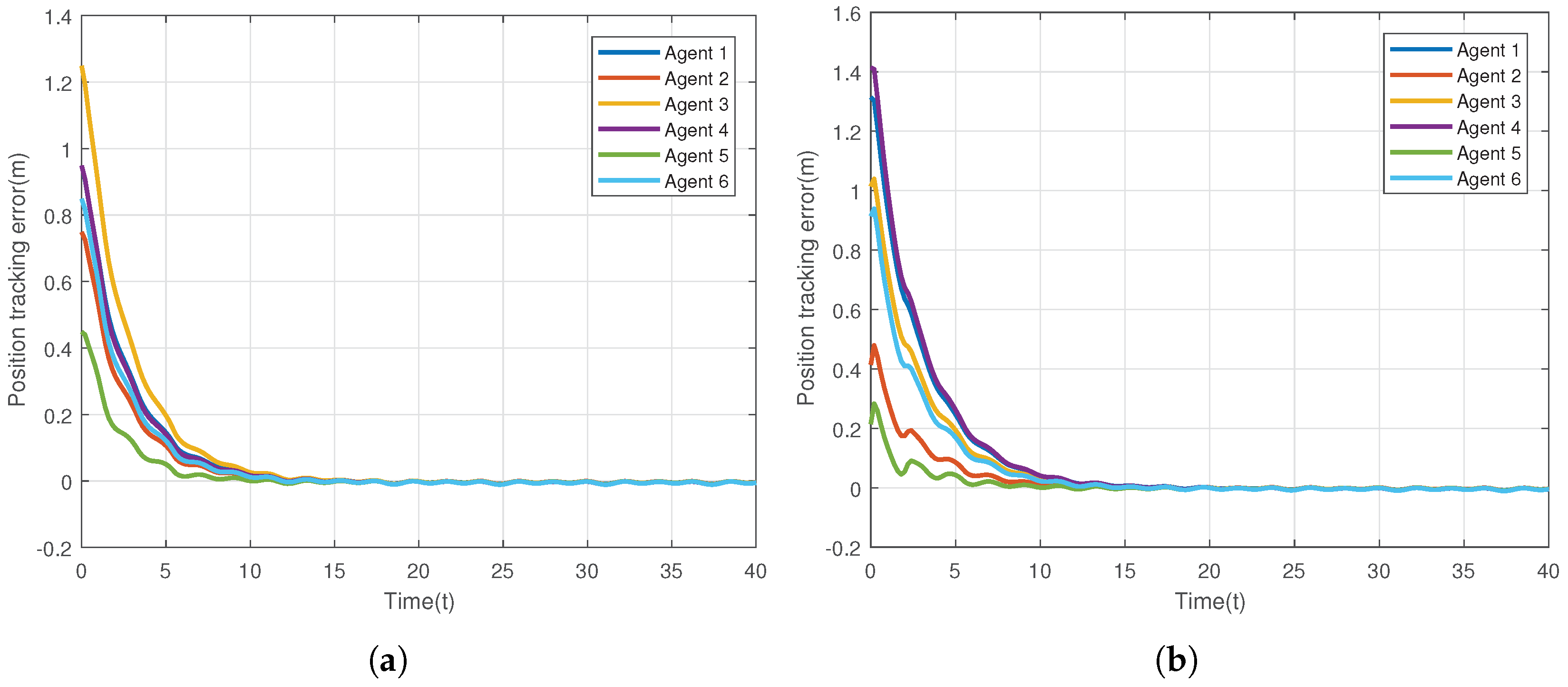
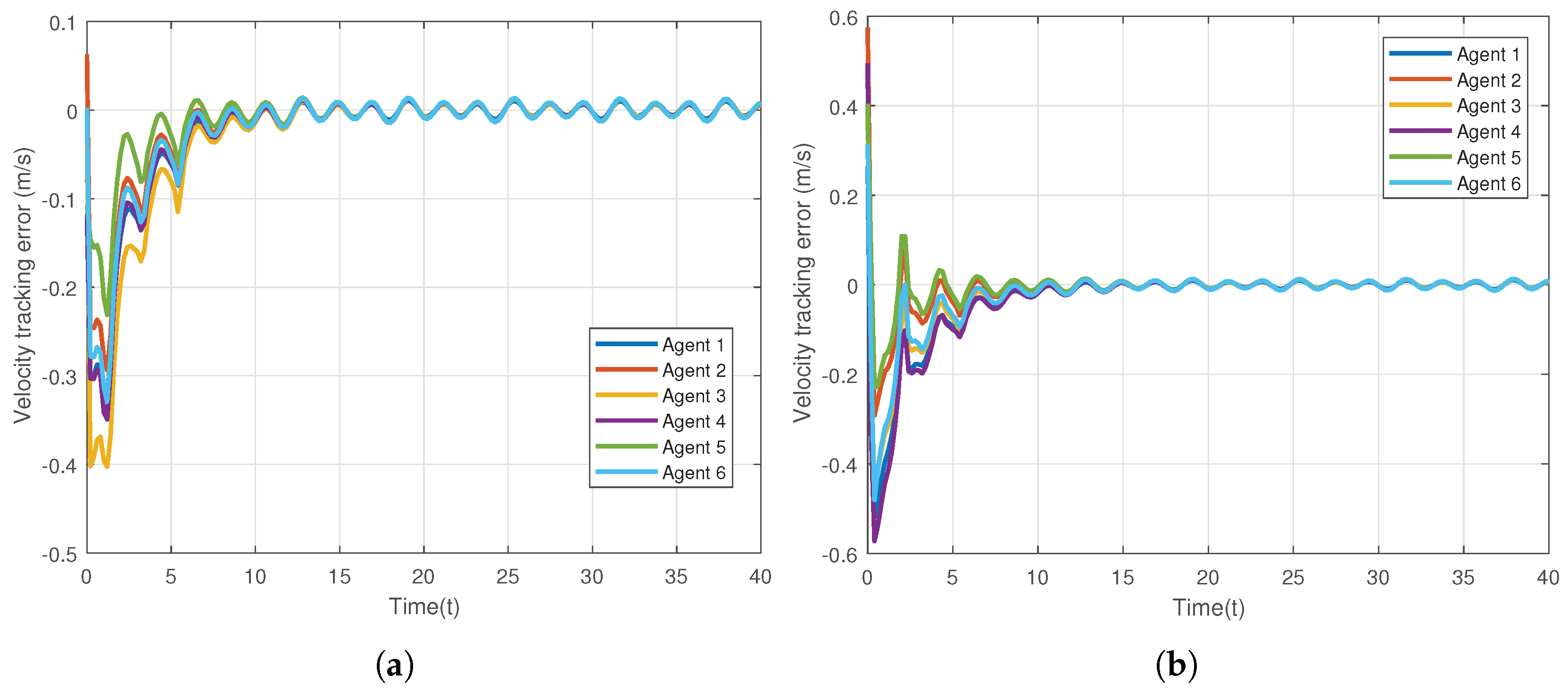
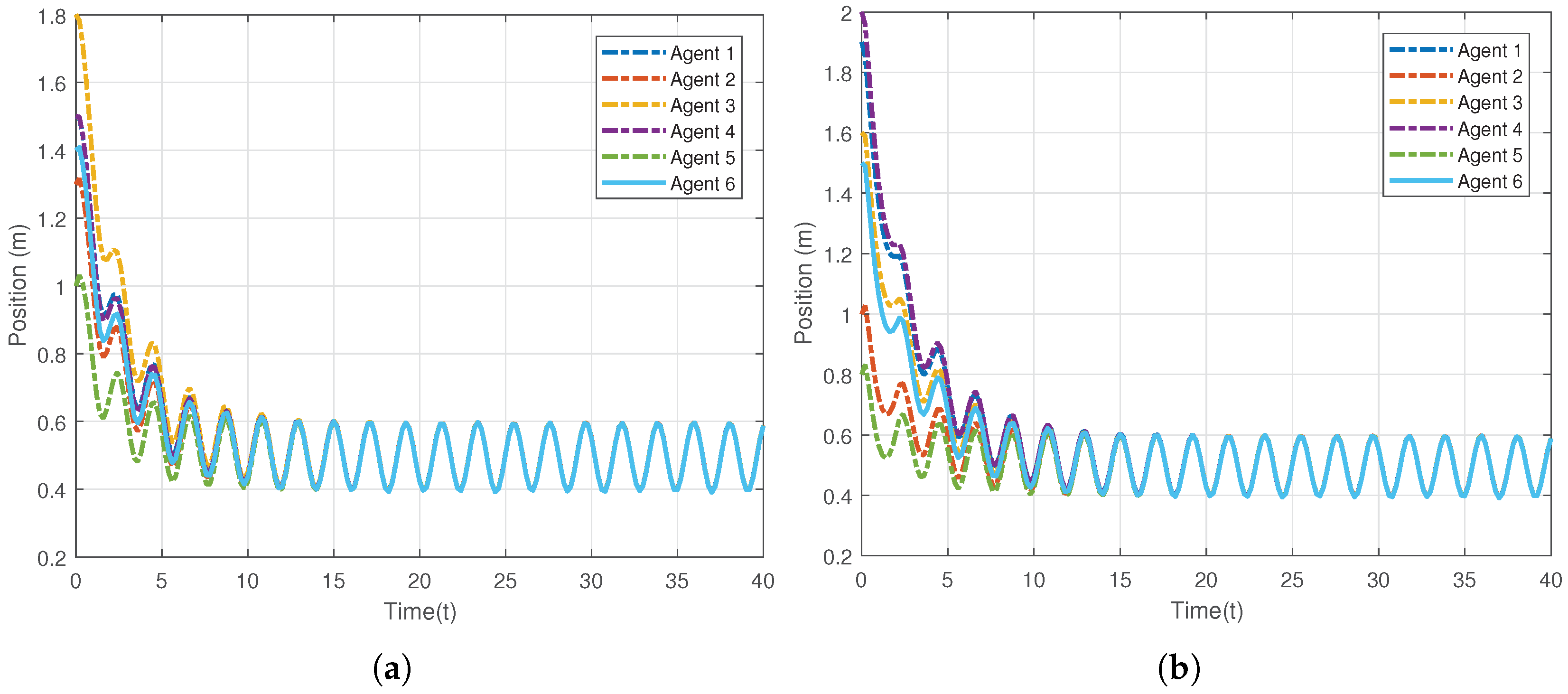
The control gains are chosen as , and the constants in the protocol are set as . The given desired trajectory is on image-plane, which is the circle, . The results of the first simulation are present in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. Figure 2 is presented to show the convergence of positions of 6 agents on the network. Figure 3 exhibits the velocity tracking errors of the 6 followers. Intuitively, the actual positions and velocities on X-axis and Y-axis of the 6 agents are given in Figure 4 and Figure 5, respectively. From Figure 2, Figure 3, Figure 4 and Figure 5, it can be observed that the proposed controller (20) can guarantee the whole system’s tracking errors asymptotically convergent and synchronous. For better illustrating the positions and velocities of agents on image-plane, their motions are plotted on X-axis and Y-axis separately.
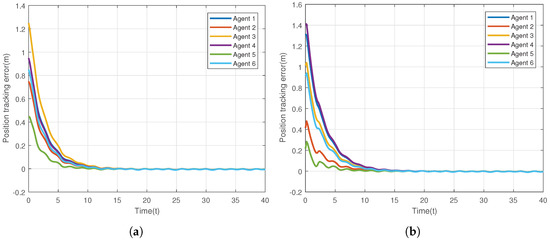
Figure 2.
Position tracking errors of 6 agents in the networked Euler-Lagrange system. (a) Position tracking errors for X-axis; (b) Position tracking errors for Y-axis.
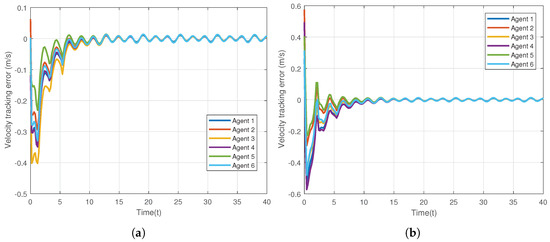
Figure 3.
Tracking errors of velocities of 6 agents in the networked Euler-Lagrange system. (a) Tracking errors for X-axis; (b) Tracking errors for Y-axis.
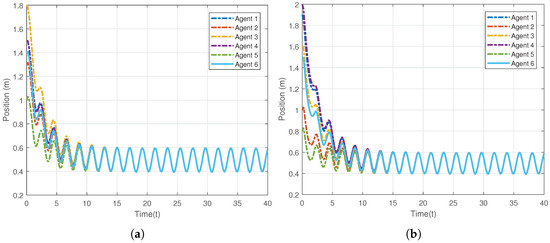
Figure 4.
Positions of the agents in the networked Euler-Lagrange system. (a) Actual positions on X-axis; (b) Actual positions on Y-axis.
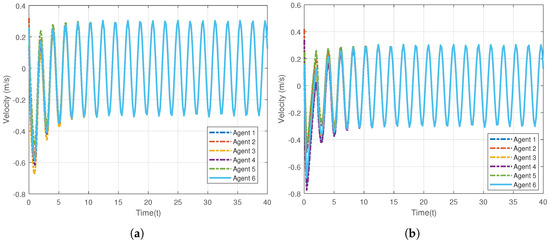
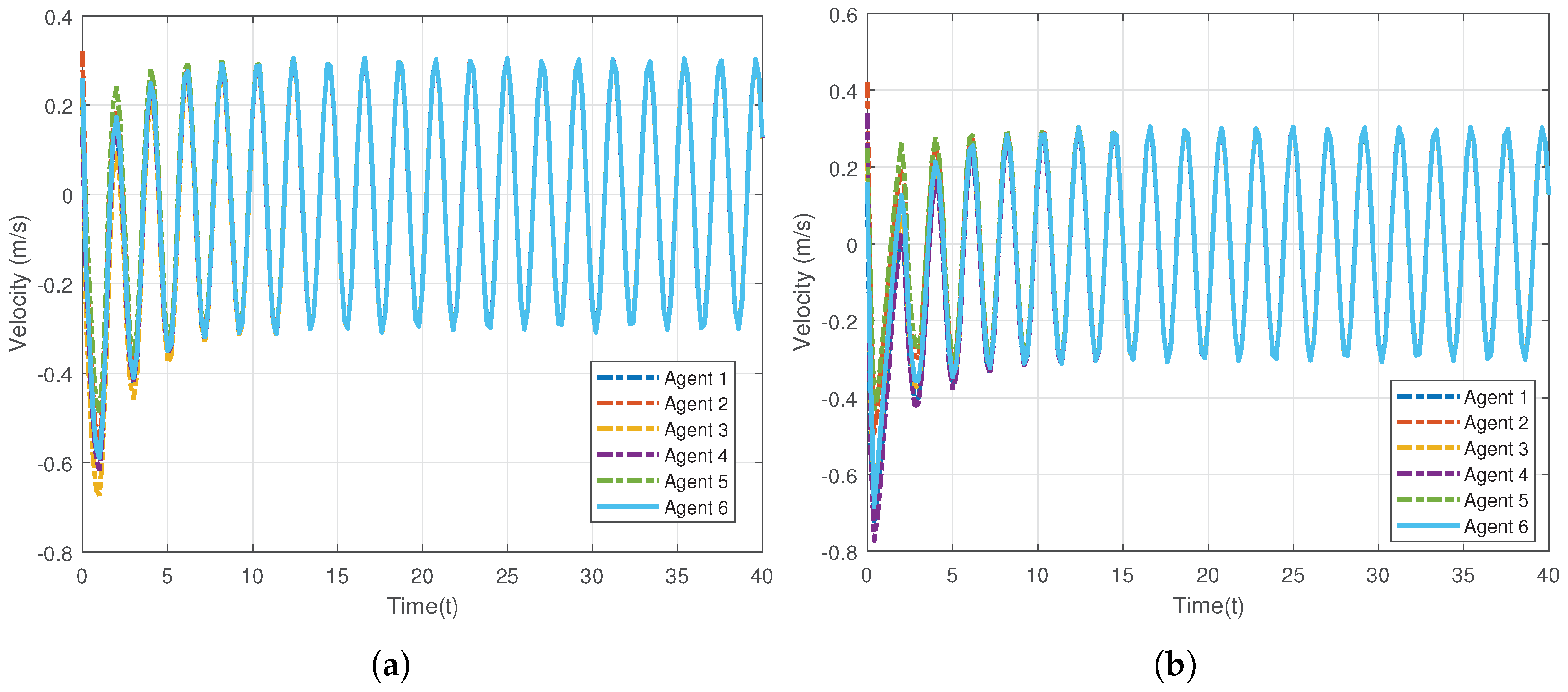
Figure 5.
Velocities of 6 agents of the coupled Euler-Lagrange system. (a) Actual velocities on X-axis; (b) Actual velocities on Y-axis.
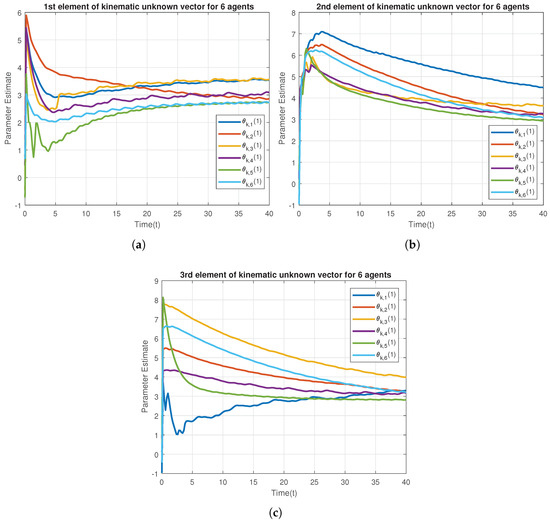
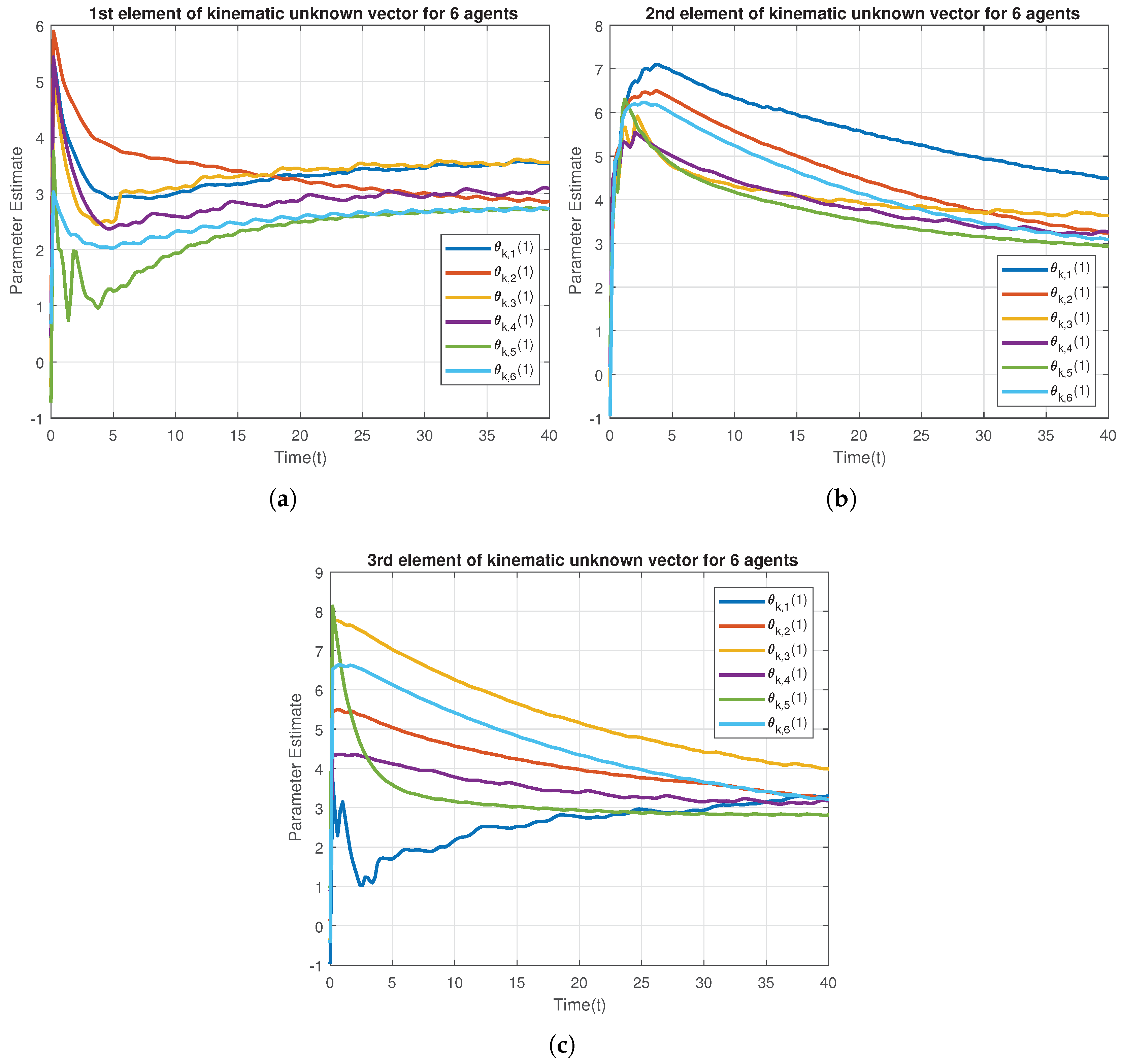
Figure 6.
Kinematic parameter estimates of the Euler-Lagrange agents. (a) 1st element; (b) 2nd element; (c) 3rd element.
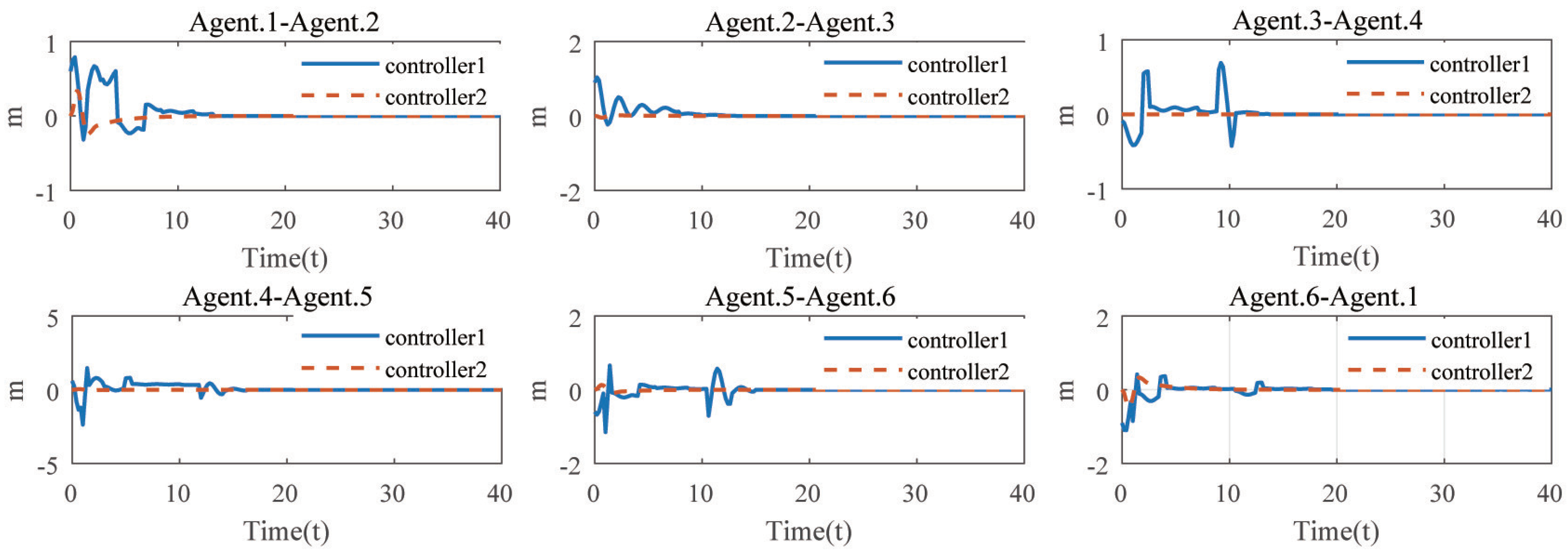
To further verify the superiority of the result, a comparison has been made in the second simulation between the proposed control protocol and the protocol proposed in [34]. The results of the second simulation are plotted in Figure 7. The X-axis synchronization error curves (the dotted line) of every two agents are under the proposed protocol (20), i.e., controller 2 in Figure 7. It can be observed that the synchronization between the agents is guaranteed. By contrast, the synchronization error curves represent the synchronous errors of the controller proposed in [34].
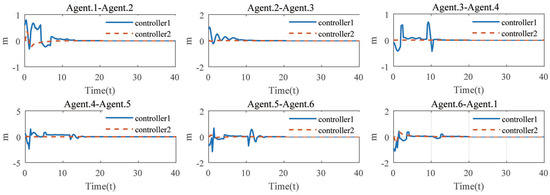
Figure 7.
Synchronization errors on X-axis.
From Figure 7, although the synchronization can finally be achieved, it can be observed that it exhibits some abnormal oscillations for controller 1, due to the effects of the time-varying delays. By contrast, the synchronous errors of controller 2, however, are relatively smooth.
Figure 6 provides the profile of the estimates of the kinematic parameters. Note that these estimates are not well convergent, resulting from the lack of persistent excitation.
7. Conclusions
A novel adaptively synchronous protocol is presented for the networking Euler-Lagrange systems with mechanical uncertainties. Furthermore, the time-varying delays are considered on the network.
To address this problem, a velocity observer on task-space and a reference velocity are first proposed. Moreover, the updating laws of estimates of kinematic parameters and estimates of dynamic parameters are proposed to cope with mechanical uncertainties accordingly. Compared with the results of existing literature, the proposed unified protocol addresses the synchronous problem of the MAS of Euler-Lagrange systems with uncalibrated parameters and even with networking time-varying delays. In this paper, the advantages of the proposed protocol can be summarized as the following aspects.
First, the capability of dealing with time-varying delays. In existing literature [33,34], only constant delays are considered, which makes the design of networking protocol conservative. The proposed protocol achieves less conservativeness on the coupling gains of the synchronous protocol.
Second, non-calibration. The work of calibration is tedious and error-prone. The non-calibration scheme is promising and convenient in industry. By the proposed protocol, MAS of uncalibrated Euler-Lagrange systems can be synchronous and cooperative to perform control objective in task-space.
Third, it is free of task-space velocities. Through the observer in the protocol, the task-space velocity can therefore be avoided, which makes the overall system robust to noise.
The analysis of Lyapunov stability is also provided in this paper to prove the mathematic correctness. To verify the effectiveness of this protocol, the simulation results of the proposed cooperative control scheme are presented.
Author Contributions
Conceptualization, H.W. and T.L.; methodology, H.W. and Z.Z; software, T.L. and Z.Z.; validation, H.W., Z.Z. and T.L.; resources, Z.Z.; data curation, T.L.; writing—original draft preparation, H.W.; writing—review and editing, Z.Z. and T.L.; supervision, Z.Z.; project administration, Z.Z.; funding acquisition, H.W.
Funding
This research and the APC were funded by Science and Technology Program of Tianjin (major project), China, under Grant 15ZXZNGX00290.
Acknowledgments
The authors would like to thank the editor and the anonymous reviewers for their valuable suggestions to improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rahman, A.A.; Ashraf, M.; Van Oorschot, P.C. CPV: Delay-Based Location Verification for the Internet. IEEE Trans. Dependable Secure Comput. 2017, 14, 130–144. [Google Scholar]
- Liu, Y.; Liu, A.; Hu, Y.; Li, Z.; Choi, Y.; Sekiya, H.; Li, J. FFSC: An Energy Efficiency Communications Approach for Delay Minimizing in Internet of Things. IEEE Access 2017, 4, 3775–3793. [Google Scholar] [CrossRef]
- Bashan, A.; Bartsch, R.P.; Kantelhardt, J.W.; Havlin, S.; Ivanov, P. Network physiology reveals relations between network topology and physiological function. Nat. Commun. 2012, 3, 702. [Google Scholar] [CrossRef] [PubMed]
- Bartsch, R.P.; Liu, K.K.; Bashan, A.; Pch, I. Network Physiology: How Organ Systems Dynamically Interact. PLoS ONE 2015, 10, e0142143. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.L.; Bartsch Ronny, P.; Lin, A.; Mantegna Rosario, N.; Plamen, C.I. Plasticity of brain wave network interactions and evolution across physiologic states. Front. Neural Circuits 2015, 9, 62. [Google Scholar] [CrossRef]
- Chase Ivan, D. Cooperative and Noncooperative Behavior in Animals. Am. Nat. 1980, 115, 827–857. [Google Scholar] [CrossRef]
- Rilling, J.K.; Demarco, A.C.; Hackett, P.D.; Thompson, R.; Ditzen, B.; Patel, R.; Pagnoni, G. Effects of intranasal oxytocin and vasopressin on cooperative behavior and associated brain activity in men. Psychoneuroendocrinology 2012, 37, 447–461. [Google Scholar] [CrossRef]
- Wang, H. Consensus of Networked Mechanical Systems with Time Delays: A Unified Framework. IEEE Trans. Autom. Control 2013. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; Saddik Abdulmotaleb, E. Observer-based force reflecting robust coordination control for networked bilateral shared telerobotic system. Int. J. Control 2018. [Google Scholar] [CrossRef]
- Chopra, N.; Spong Mark, W. Adaptive Synchronization of Bilateral Teleoperators with Time Delay. Automatica 2008, 44, 2142–2148. [Google Scholar] [CrossRef]
- Nitendra, N.; Enver, T.; Darren, D. Teleoperation with kinematically redundant robot manipulators with sub-task objectives. Robotica 2009, 27, 1027–1038. [Google Scholar]
- Lorenzo, S.; Cristian, S.; Alessio, L.; Cesare, F. Decentralized Control of Cooperative Robotic Systems for Arbitrary Setpoint Tracking while Avoiding Collisions. IFAC-Pap. Online 2015, 48, 57–62. [Google Scholar]
- Cheah, C.C.; Liu, C.; Slotine, J.J.E. Adaptive Tracking Control for Robots with Unknown Kinematic and Dynamic Properties; Sage Publications Inc.: Thousand Oaks, CA, USA, 2006. [Google Scholar]
- Nikhil, C.; Chen, L.Y. Controlled Synchronization of Mechanical Systems. In Proceedings of the ASME 2008 Dynamic Systems and Control Conference, Ann Arbor, MI, USA, 20–22 October 2008; pp. 1221–1228. [Google Scholar]
- Alexander, F.J.; Murray Richard, M. Information flow and cooperative control of vehicle formations. IFAC Proc. 2002, 35, 115–120. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Lin, Z.; Broucke, M.; Francis, B. Local control strategies for groups of mobile autonomous agents. IEEE Trans. Autom. Control 2004, 49, 622–629. [Google Scholar] [CrossRef]
- Olfatisaber, R.; Murray Richard, M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ziyang, M.; Zhongkui, L.; Athanasios, V.; Shiming, C. Delay-Induced Synchronization of Identical Linear Multiagent Systems. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 43, 476–489. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, T.; Yang, G.H.; Liang, H. Distributed Cooperative Optimal Control for Multiagent Systems on Directed Graphs: An Inverse Optimal Approach. IEEE Trans. Cybern. 2015, 45, 1315–1326. [Google Scholar] [CrossRef]
- Wang, T.; Qiu, J.; Shen, Y.; Gao, H.; Fan, J.; Chai, T. Performance-Based Adaptive Fuzzy Tracking Control for Networked Industrial Processes. IEEE Trans. Cybern. 2016, 46, 1760–1770. [Google Scholar] [CrossRef]
- Li, T.; Zhao, H. Global finite-time adaptive control for uncalibrated robot manipulator based on visual servoing. ISA Trans. 2017. [Google Scholar] [CrossRef]
- Wang, H. Adaptive visual tracking for robotic systems without image-space velocity measurement. Automatica 2015, 55, 294–301. [Google Scholar] [CrossRef]
- Wang, H. Adaptive Control of Robot Manipulators With Uncertain Kinematics and Dynamics. IEEE Trans. Autom. Control 2017, 62, 948–954. [Google Scholar] [CrossRef]
- Wang, T.; Qiu, J.; Gao, H. Adaptive Neural Control of Stochastic Nonlinear Time-Delay Systems with Multiple Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2016, 99, 1–9. [Google Scholar] [CrossRef]
- Zhang, F.; Dawson, D.M.; De Queiroz, M.S.; Dixon, W.E. Global adaptive output feedback tracking control of robot manipulators. IEEE Trans. Autom. Control 2002, 45, 1203–1208. [Google Scholar] [CrossRef]
- Ren, W. Distributed leaderless consensus algorithms for networked Euler–Lagrange systems. Int. J. Control 2009, 82, 2137–2149. [Google Scholar] [CrossRef]
- Jo, C.S.; Jacques, S.J. Cooperative Robot Control and Concurrent Synchronization of Lagrangian Systems. IEEE Trans. Robot. 2007, 25, 686–700. [Google Scholar]
- Chopra, N.; Spong, M.W. Output Synchronization of Nonlinear Systems with Time Delay in Communication. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4986–4992. [Google Scholar]
- Liu, Y.C.; Chopra, N. Controlled Synchronization of Heterogeneous Robotic Manipulators in the Task Space. IEEE Trans. Robot. 2012, 28, 268–275. [Google Scholar] [CrossRef]
- Emmanuel, N.; Romeo, O.; Luis, B.; David, H. Synchronization of Networks of Nonidentical Euler-Lagrange Systems with Uncertain Parameters and Communication Delays. IEEE Trans. Autom. Control 2011, 56, 935–941. [Google Scholar]
- Liu, Y.C.; Chopra, N. Synchronization of networked robotic systems on strongly connected graphs. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 3194–3199. [Google Scholar]
- Wang, H. Passivity based synchronization for networked robotic systems with uncertain kinematics and dynamics. Automatica 2013, 49, 755–761. [Google Scholar] [CrossRef]
- Liang, X.; Wang, H.; Liu, Y.H.; Chen, W.; Hu, G.; Zhao, J. Adaptive Task-Space Cooperative Tracking Control of Networked Robotic Manipulators Without Task-Space Velocity Measurements. IEEE Trans. Cybern. 2015, 46, 2386–2398. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Min, X.; Ahmed, A.; Tasawar, H. Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 2017, 292, 210–227. [Google Scholar] [CrossRef]
- Fei, Z.; Guan, C.; Gao, H. Exponential Synchronization of Networked Chaotic Delayed Neural Network by a Hybrid Event Trigger Scheme. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2558–2567. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Huang, L.; Tang, L.; Zhuang, J. Generalized pinning synchronization of delayed Cohen-Grossberg neural networks with discontinuous activations. Neural Netw. 2018, 104, 80–92. [Google Scholar] [CrossRef] [PubMed]
- Zouari, F.; Ibeas, A.; Boulkroune, A.; Cao, J.; Mehdi, M.A. Adaptive neural output-feedback control for nonstrict-feedback time-delay fractional-order systems with output constraints and actuator nonlinearities. Neural Netw. 2018, 105, 256–276. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Wang, H.; Chen, W.; Zhou, D. Adaptive visual servoing using common image features with unknown geometric parameters. Automatica 2013, 49, 2453–2460. [Google Scholar] [CrossRef]
- Cheng, L.; Hou, Z.G.; Tan, M.; Liu, D. Multi-Agent Based Adaptive Consensus Control for Multiple Manipulators with Kinematic Uncertainties. In Proceedings of the 2008 IEEE International Symposium on Intelligent Control, San Antonio, TX, USA, 3–5 September 2008; pp. 189–194. [Google Scholar]
- Li, X.; Luo, X.; Wang, J.; Zhu, Y.; Guan, X. Bearing-Based Formation Control of Networked Robotic Systems with Parametric Uncertainties. Neurocomputing 2018. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Y. Task-Space Consensus of Networked Robotic Systems: Separation and Manipulability. arXiv, 2018; arXiv:1702.06265. [Google Scholar]
- Chris, G.; Gordon, R. Algebraic Graph Theory; World Book Inc.: Chicago, IL, USA, 2004. [Google Scholar]
- Slotine, J.-J.E.; Jean-Jacques, E.; Li, W. Applied Nonlinear Control; China Machine Press: Beijing, China, 2004. [Google Scholar]
- Wang, H.; Liu, Y.H. Adaptive Visual Servoing of Robot Manipulators Using Uncalibrated Eye-in-hand Visual Feedback. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 386–391. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).