Abstract
The adaptability of an in-progress business process is an essential requirement for any business process management system in dynamic business process environments. Over the last two decades, the artifact-centric approach for business process management has been evidenced to have higher level of flexibility. However, the adaptation of a model of an artifact-centric business process instance is still inevitable and pervasive due to the complex and ever-changing business environments. Almost all works of artifact-centric business process neglect this issue. To fill this gap, we propose a special business rule called adaptation rule to address the dynamic adaptation problem and describe the adaptation by a global adaptation model. Moreover, we provide a validation mechanism over our proposed adaptation rule of the global adaptation model to guarantee the behavior correctness of the adaptation. Through this validation approach, computing the lifecycle of the global adaptation model can be avoided.
1. Introduction
A critical challenge for the competitive enterprise is its ability to quickly react to business process changes and adequately address them. The adaptability of in-progress business process is an essential requirement for any business process management system in dynamic business process environments [1]. Adaptation of a business process (also referred to as process adaptation) refers to the action of customizing a process instance to make it applicable to a particular situation [2].
In the past two decades, a new business process modeling paradigm has emerged, i.e., artifact-centric business process modeling [3,4]. It has been proved that this approach provides a higher level of flexibility of workflow enactment and evolution [5]. However, few works have developed artifact-centric business process paradigms for the adaptation of business processes. Wang et al. [6] proposed a taxonomy of changes of artifact-centric business processes based on a three-level workflow implementation and an analysis of the impact of changes. Yongchareon et al. [5] addressed the requirements of private artifact-centric business processes change and provided a verification mechanism to preserve the correctness of public business processes in interorganizational business process circumstances based on a view framework. Li and Yu [7] proposed three primitive changes (add, delete and modify) of activities of artifact-centric workflow model in the execution level and proposed guidelines to guarantee the execution of business process instances that are adapted. However, the change of artifact information model is not discussed and theoretical validation of the adaptation is not presented. Eshuis et al. [8] formally reasoned about properties of a process model that are preserved after the model is changed and defined several change operations that preserve certain properties based on Case Management Model and Notation (CMMN), which is an artifact-centric business process model based on the Guard–Stage–Milestone (GSM) model [9,10]. Although flexibility is naturally considered by artifact-centric business process modeling approach, dynamic adaptation of a model of a business process instance is still inevitable because of the turbulent business process environments [11,12,13]. However, almost all works in artifact-centric business process community neglect this issue. It is difficult to address this issue, mainly for the following two reasons. First, both data and process should be considered during the adaptation of business process instances. Second, due to the flexible and the declarative properties of artifact-centric business processes, it is hard to guarantee the correctness of the adaptation, i.e., a business process instance that is adapted can still reach an acceptable business goal without deadlock.
Many efforts in activity-centric business process community have addressed this issue. Vasilecas et al. [14] proposed a rule- and context-based approach to dynamically define a business process model. The adaptations of business process instances are implemented by changing contexts, rules and activities. Hu et al. [15] proposed a rule-, context- and goal-based approach for the adaptation of business process instances. Ayora et al. [16] proposed nine change patterns to enable the modeling and evolution of process families at a high level of abstraction. They extended these change patterns to 10 change patterns in [17] and verified that these change patterns can guarantee the structure and the correct behavior of the variants by case study. Policies are used to decide whether a business process instance should be adapted. Nunes et al. [18] proposed the adaptation of business process instances based on context. Patiniotakis et al. [19] used a multi-criteria decision-making approach for the adaptation of event-driven business process instances. Oberhauser [20] proposed adaptation processes to adapt business process instances. Artifact-centric business processes focus on what can be done (goals and progresses) instead of what should be done (tasks or corresponding services) that activity-centric business processes focus on [21]. Nevertheless, due to this difference between activity-centric and artifact-centric modeling approaches, the adaptation methods in activity-centric modeling paradigm are not applicable for artifact-centric business processes.
To solve the issue, we present a taxonomy of changes of artifact-centric business processes and analysis characteristics of these changes. Considering these characteristics, we propose a special business rule called adaptation rule to implement the dynamic adaptation of a model of an artifact-centric business process instance and describe the adaptation by a global adaptation model. Although a global adaptation model can be converted into an artifact-centric business process model, we provide an incremental validation method to verify behavior properties of the business process instances that are adapted by an adaptation rule. As such, the traditional lifecycle composition process of model validation can be avoided. Note that our proposed solution partially solves the problem of adaptation of an artifact-centric business process. How to adapt a business process model to create a new business process model is not discussed in this paper.
2. Artifact-Centric Business Process Model
There are abundant artifact-centric business process models defined formally or informally, but they reach a consensus that business processes are dominated by business artifacts [22]. In this study, we adopt the ACP model with some modifications as it reflects the original idea of artifact-centric approach faithfully [22,23,24].
Definition 1
(modified from [23]). An artifact-centric business process model is a triple M = (Z, V, R), where Z is an artifact schema. An artifact schema is a set of artifact classes Z = {C1, C2, …, Cn}, Ci (1≤i≤n) is an artifact class that defined by a tetrad (A, s0, S, Sf), where A is a set of name-value paired attributes; s0 is the default start state; S is a set of states; and Sf ⊂ S is the set of final states. V is a set of services. R is a set of business rules over Z. A business rule is a triple (λ, β, v), where λ is the precondition; β is the postcondition; and v ∊ V is a service that operates one or more artifacts c1, c2, …, cn of artifact classes C1, C2, …, Cn, respectively.
Artifacts are business-relevant entities that are created and evolved through business processes. An artifact class (hereafter artifact) defines an information model and its lifecycle [3]. A business rule associates service(s) with artifact(s) in a Condition–Action style. Each business rule describes which service is invoked and which state of an artifact is changed under what precondition and postcondition [23]. λ and β are defined by quantifier free first order logic formula. In the formula, there are two types of proposition over schema Z: (1) state proposition (the instate predicate); and (2) attribute proposition (the defined predicate and scalar comparison).
- Example 1.
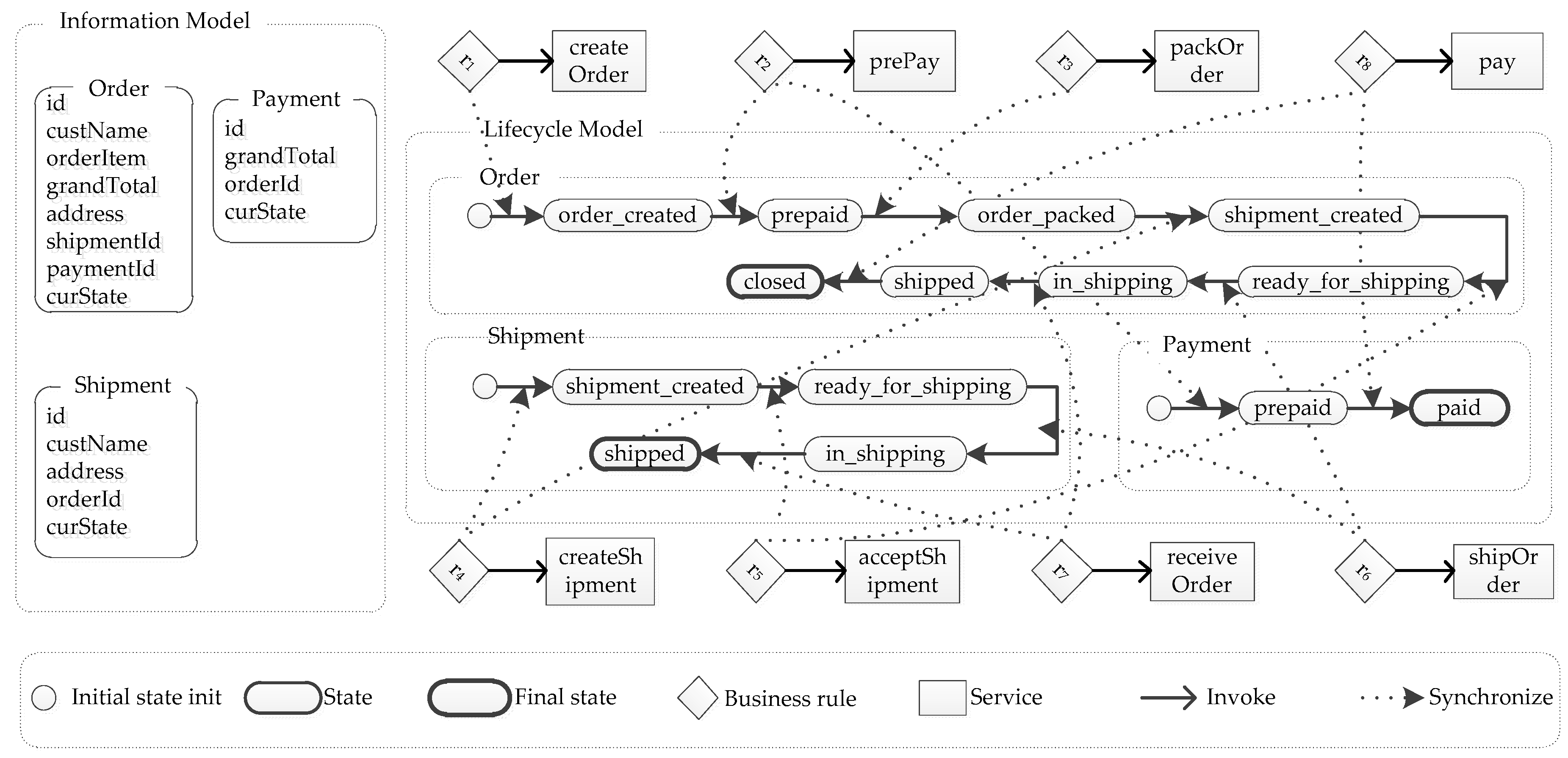
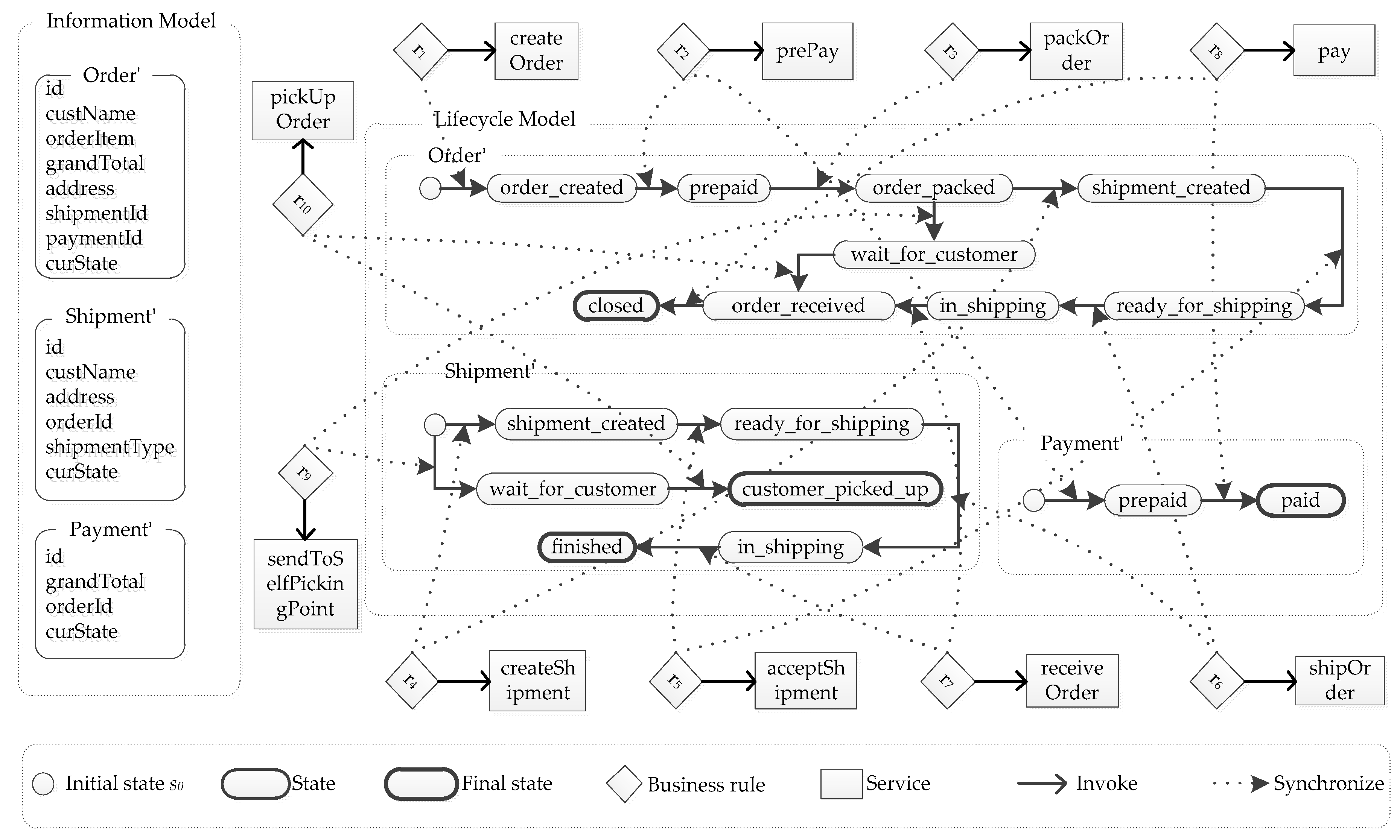
We use a purchase business process [23] to illustrate the concept of the artifact-centric business processes. Its artifact-centric representation is described in Figure 1.
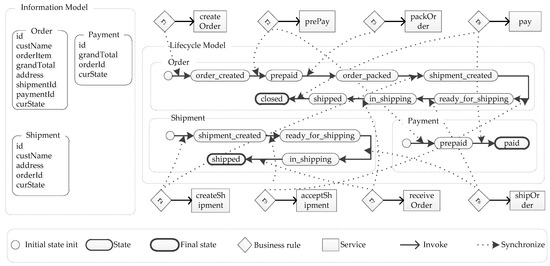
Figure 1.
Artifact-centric representation of a purchase business process.
A purchase business process consists of an information model (Figure 1, top left) and a lifecycle model (Figure 1, top right). There are three artifacts, namely Order, Payment and Shipment, in the process. A customer can instantiate the process by selecting some products and creating an order artifact instance, and follows the process to prepay the order. At this moment, a payment artifact instance is created and move to the prepaid state. A seller can accept the order and get ready to ship the order after the order has been packed, and follow the process to ship the order. Now, a shipment artifact instance is created. After the seller ships the order, the customer can receive the order and follow the process to finish the payment. Eight business rules and eight services work together to update the information model of the process and move three artifacts from one state to another along their lifecycles.
There is an example of business rules in the purchase process (Table 1). In Table 1, state proposition instate(O, order_created) holds if state of O is order_created, i.e., O.curState = order_created; and attribute proposition defined(O.custName) holds if custName of O has been defined.

Table 1.
An example of business rules in the purchase process (Figure 1).
3. Adaptation of a Model of an Artifact-Centric Business Process Instance
In this section, we present a taxonomy of changes of an artifact-centric business process and discuss characteristics of these changes. Considering characteristics of these changes, we propose a global adaptation model for the adaptation of a model of an artifact-centric business process instance.
3.1. Taxonomy of Changes of an Artifact-Centric Business Process
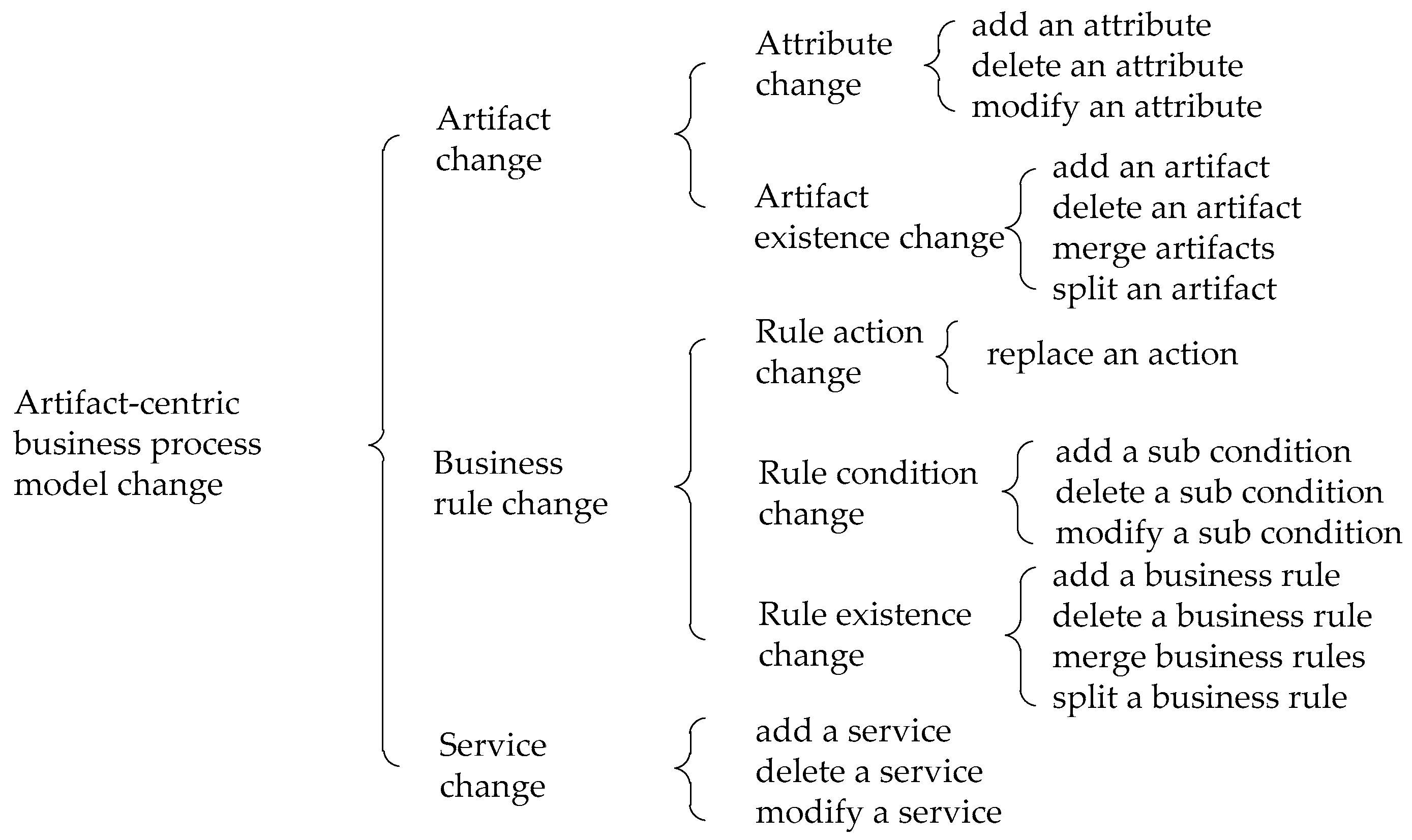
According to key components of an artifact-centric business process, we present the taxonomy of changes of an artifact-centric business process in Figure 2. These changes are inspired from the work of Wang et al [6]. However, we focus on model level changes.
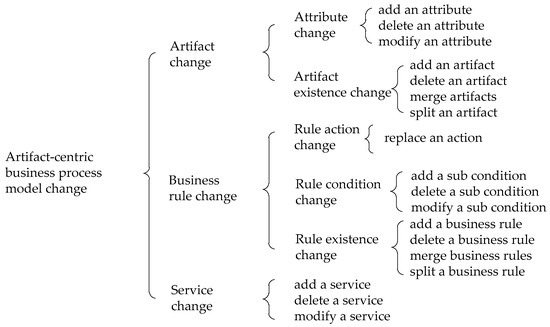
Figure 2.
The taxonomy of changes of an artifact-centric business process.
Artifact change contains two types of sub changes: attribute change and artifact existence change. Attribute change may add an attribute to an artifact, delete an attribute from an artifact and modify an attribute of an artifact. Artifact existence change includes add an artifact, delete an artifact, merge artifacts and split an artifact.
Business rule change includes rule action change, rule condition change and rule existence change. Rule action change refers to replacement of an action. Rule condition change refers to modification of conditions. A sub condition could be added to λ or β of a business rule. A sub condition may be deleted from λ or β of a business rule. A sub condition of λ or β of a business rule may be modified. Business rule existence change includes add a business rule, delete a business rule, merge business rules and split a business rule.
Service change includes: add a service, delete a service and modify a service.
Suppose we want to adapt a business process instance from model M to model M’. According to the taxonomy, we can see that artifacts of M and M’ may have following differences.
From view of information models of artifacts:
(1) An artifact of M may map to one artifact of M’ if attribute changes are used alone. Nevertheless, the cardinality of attributes may be different if changes of add an attribute or delete an attribute are used.
(2) An artifact of M may map to multiple artifacts of M’ if changes of split an artifact are used alone.
(3) Multiple artifacts of M may map to one artifact of M’ if changes of merge artifacts are used alone.
(4) Multiple artifacts of M may map to multiple artifacts of M’ if combination of changes is used.
(5) Artifacts of M may map partially to artifacts of M’ if change of add an artifact or delete an artifact is used.
(6) Attributes of artifacts of M map partially to attributes of artifacts of M’ while considering Characteristics (1)–(5).
Similarly, from view of lifecycles of artifacts, relationships of artifacts between M and M’ may be one-to-one, one-to-many, many-to-one, many-to-many and partial mapping. Usually, mappings between states do not exist if changes of merge artifacts and split an artifact are used because both the cardinality of states and the names of states may be changed due to these changes. As a result, states of artifacts of M map partially to states of artifacts of M’.
From former analysis, we can see that relationships of artifacts between two models are complex from perspectives of both information models of artifacts and lifecycles of artifacts. Because data and states of artifacts of business process instances that should be adapted cannot be decided according to relationships of artifacts between M and M’, it is hard to decide when and how to adapt a model of a business process instance automatically. This circumstance is common for most changes in Figure 2, for example, add an attribute, add an artifact, merge artifacts, and split an artifact.
Note that these changes are interleaving [6]; coordination of changes of artifacts, business rules and services should be done to generate a new version of business process that is modeled as M’. How to generate M’ by these changes is omitted, as it is not the interests of this paper. Next, we present our method for the adaptation of a model of an artifact-centric business process instance semi-automatically.
3.2. The Proposed Global Adaptation Model
There are two operations while implementing the adaptation of a model of an artifact-centric business process instance when considering perspectives of data and process of an artifact-centric business process. Suppose the instance is adapted from model M to model M’. One operation is to convert the information models of artifacts of the instance from M to M’. The other operation is to set the converted artifact instances with proper data (attributes with proper values and artifact instances with proper states).
Considering complex relationships of artifacts of M and M’ while adapting a business process instance from M to M’, we propose special user-defined business rules called adaptation rule for deciding when and how to implement the adaptation. After an adaptation rule is defined and deployed to the business process system, a business process instance will be adapted dynamically by the adaptation rule if the precondition and the postcondition of the adaptation rule are satisfied. We use a global adaptation model to describe the adaptation.
Definition 2.
A global adaptation model is a tetrad Γ = (M, M’, va, ra), where M and M’ are two artifact-centric business process models; va is a service that implement the two operations while adapting a business process instance of M to M’; and ra is a special business rule called adaptation rule that is a tuple (λM, λM’, βM, βM’, va), where λM is the sub condition of ra on M in the precondition of ra; λM’ is the sub condition of ra on M’ in the precondition of ra; βM is the sub condition of ra on M in the postcondition of ra; and βM’ is the sub condition of ra on M’ in the postcondition of ra. λM ∧ λM’ formulates the precondition of ra; and βM ∧ βM’ formulates the postcondition of ra.
In Definition 2, va is a service that implements a partial function f: M.Z.C1 × … × M.Z.Cm … ↦ M’.Z.C1 × … × M’.Z.Cn, m = |M.Z| and n = |M’.Z|. λM’ takes formula instate(M’.Z.C1, s0) ∧ … ∧ instate(M’.Z.Cn, s0) (n = |M’.Z|) as default. Note that there is a special final state sgf in Ci.Sf, where Ci ∊ M.Z. State proposition in βM takes formula instate(M.Z.C1, sgf) ∧ … ∧ instate(M.Z.Cm, sgf) (m = |M.Z|) as default. If state of an artifact instance was logged as sgf, it means that the corresponding process instance of this artifact instance has been adapted.
Given a global adaptation model Γ, it can be mapped to an artifact-centric business process model MΓ, where MΓ.Z = Γ.M.Z ∪ Γ.M’.Z, MΓ.V = Γ.M.V ∪ Γ.M’.V ∪ {Γ.va} and MΓ.R = Γ.M.R ∪ Γ.M’.R ∪ {Γ.ra}. Compare MΓ with M and M’, we can see that only Γ.ra needs to be defined as we suppose Γ.va has been provided. From definition of an adaptation rule, we can see that an adaptation rule dominates artifacts of two business process models, instead of artifacts of the same business process model as compared with general business rules. Another difference is that an adaptation rule synchronizes all artifacts of both business process models as contrast to part of artifacts within one business process model. In this paper, we suppose Γ.M.Z ∩ Γ.M’.Z = ∅.
- Example 2.
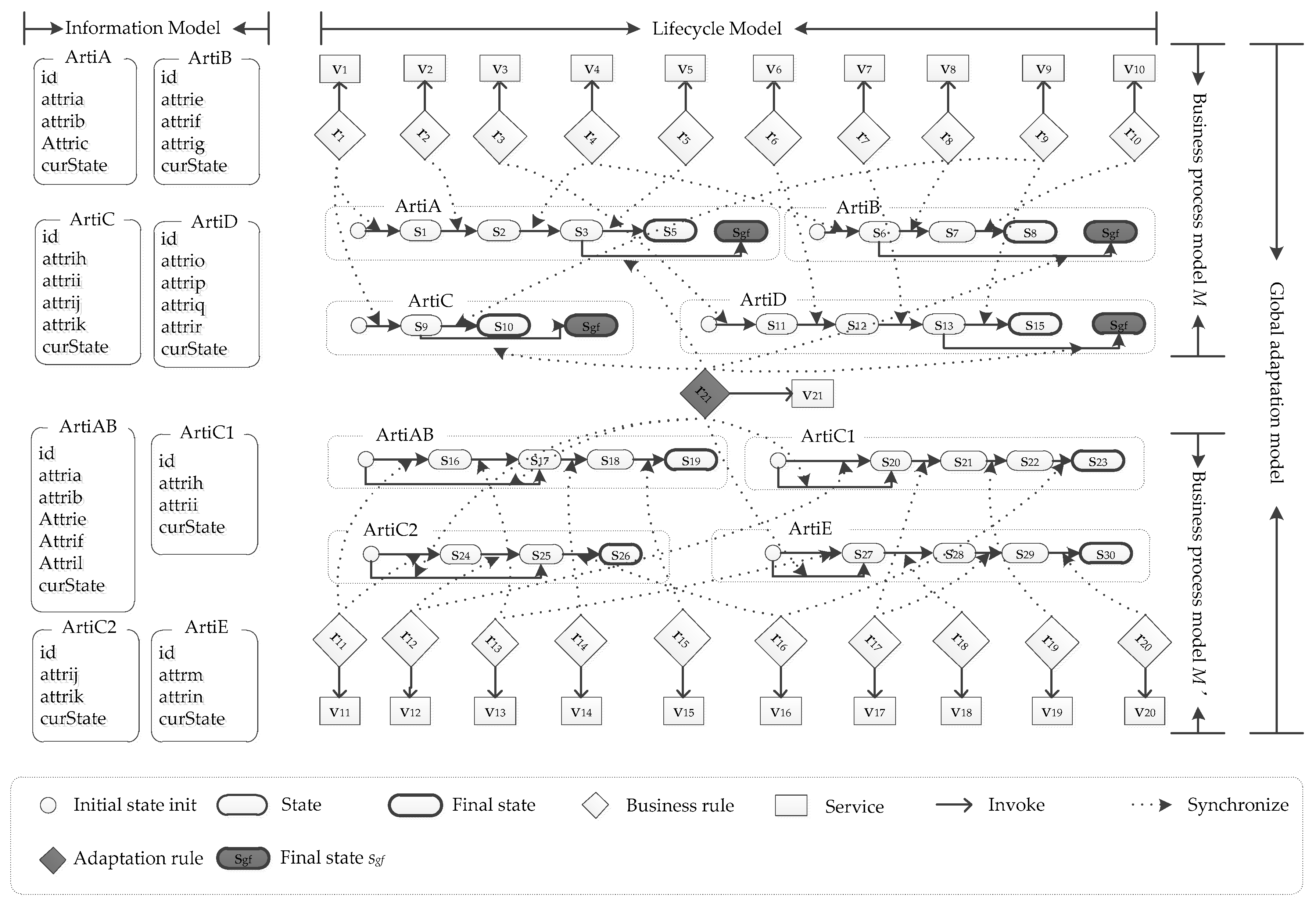
It is hard to find a real-world business process to illustrate all circumstances. In this example, we use two domain independent process models to illustrate the concept of our global adaptation model (Figure 3).
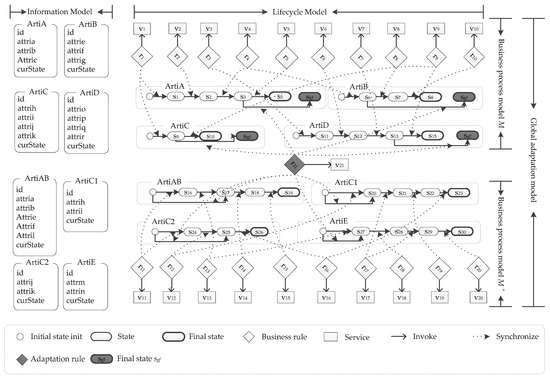
Figure 3.
Artifact-centric representation of a global adaptation model.
Compare two business process models M and M’ in Figure 3. two artifacts ArtiA and ArtiB are merged as artifact ArtiAB. Further attribute changes are used on ArtiAB, where the changes are delete attributes Attric and Attrig and add attribute Attril. Artifact ArtiC splits as two artifacts ArtiC1 and ArtiC2. Artifact ArtiD is deleted and a new artifact ArtiE is added in model M’.
In Figure 3, we can see that, if adaptation rule r21 is evaluated, a business process instance of M will be adapted to model M’ and continues to run according to definition of M’. Note that some complementary sub services may be incorporated in v21 to remedy losses and supplement gains of the business process instance due to the adaptation. For instance, a seller returns postage fee if type of shipment of an order is changed from express to self-pick-up in a purchasing process. On the contrary, a customer pays postage fee if type of shipment of an order is changed from self-pick-up to express.
From Example 2, we can see that an adaptation rule combines two business process models as one brand new business process model MΓ. Next, we validate a global adaptation model through its corresponding artifact-centric business process model.
The adaptation rule of Example 2 is defined in Table 2.

Table 2.
The adaptation rule of Example 2.
4. Verification of a Global Adaptation Model
Verification of a global adaptation model Γ is crucial to guarantee the correctness of execution of a business process [24]. In this section, we use the soundness of a global adaptation model Γ to guarantee that business process instances of Γ.M that are adapted by Γ.ra can reach business goals without deadlock. Considering flexible and declarative properties of artifact-centric business process, we use the correctness of an adaptation rule to guarantee that a business process instance that is adapted by the adaptation rule can reach an acceptable business goal.
4.1. Soundness of an Artifact-Centric Business Process Model
Before presenting the soundness of a global adaptation model, we introduce the soundness of an artifact-centric business process model as a foundation in this subsection.
It is known that verifying artifact behaviors is undecidable when the ability of creating new artifacts is considered [24]. However, the verification is decidable when artifact behaviors, i.e., the lifecycle of an artifact, are represented by finite states [5]. Differently, we generate the lifecycle of an artifact-centric business process directly as opposed to pair-wise composition of the lifecycles of two artifacts.
Definition 3
(modified from [5]). Given an artifact-centric business process model M, the lifecycle of an artifact C (C ∊ M.Z), denoted as LC is a triple (s0, Vs, Et), where s0 is the default start state of C; Vs = C.S ∪ {s0}; and Et ⊂ Vs × M.R × Vs is the set of transitions.
Given a transition (sx, r, sy) ∊ Et, it means that state of an artifact will be updated from sx to sy if business rule r is evaluated.
Definition 4.
Given an artifact-centric business process model M, the lifecycle of M, marked as LM, is a triple (s0, Vs, Et), where s0 = (.s0, …, .s0), n = |M.Z| and Ci ≠ Cj (i ≠ j). Vs ⊂ .Vs × , …, ×.Vs. Given a state s ∊ Vs, s is a final state of LM if s[i] is a final state of for i in [1,n]. Et ⊂ Vs ×R ×Vs is a set of transitions, where R is a set of business rules that transformed from M.R.
Given a lifecycle LM and a state s ∊ LM.Vs, we call s as a business goal of LM if there is a business process instance of M that is completed, where Ci ∊ M.Z and instate(Ci,s[i]) (1 ≤ I ≤ |s|) holds for the process instance. If not specified clearly, the sequence of states in s are determined by lexicography order of artifact names, which take marks of artifacts as default. Note that a business goal of LM is equivalent to a final state of LM if M is a general artifact-centric business process model; and not equivalent if M is an artifact-centric business process model that derives from a global adaptation model. In the second circumstance, a final state of LM must be a business goal of LM, but a business goal of LM may not be a final state. For instance, state (s0, s0, s0, s0, s19 s23 s26, s30) is a business goal, not a final state of (Γ is the global adaptation model of Figure 3). We call lifecycle as the lifecycle of Γ.
Let cv(r, sx, sy) be a transformation function. cv(r, sx, sy) returns a new business rule denoted as r[sx,sy], where sub condition of state proposition in the precondition of r is substituted by instate(CM, sx) and sub condition of state proposition in the postcondition of r is substituted by instate(CM, sy). CM is a virtual artifact that composites all the artifacts of model M, where their states appear in sx. Given an artifact-centric business process model M, LM can be generated iteratively from LM.s0.
- Example 3.
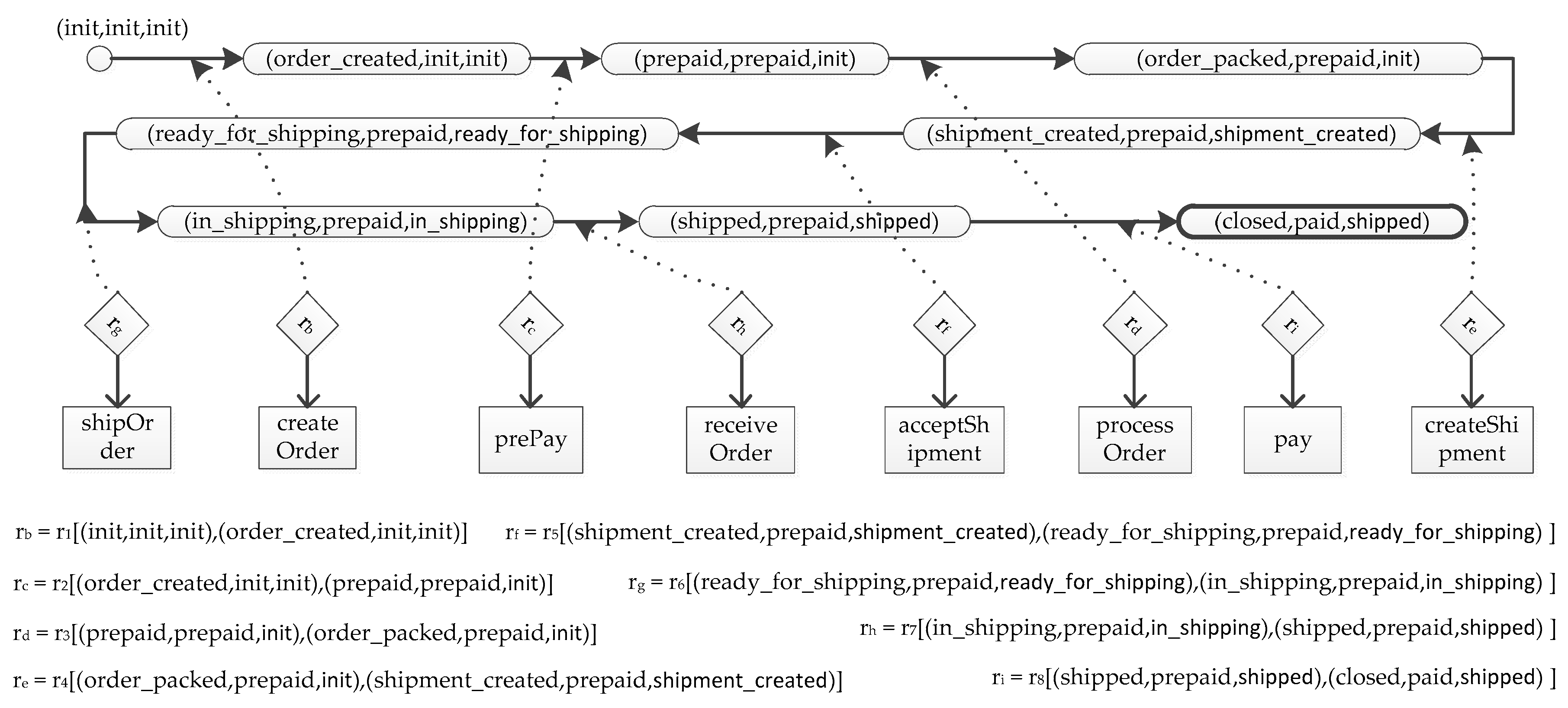
In this example, we use aforementioned purchase business process that is modeled as MP to illustrate the process of generating the lifecycle of MP, which is marked as . The initial state of the lifecycle is (init, init, init) for there are three artifacts in the model. At present, only precondition of r1 holds. Because r1 induces Order from init to order_created, state of a process instance will change from (init, init, init) to (order_created, init, init) if r1 is evaluated. To make r1 suitable for the lifecycle, the sub condition of state propositions of the precondition and the postcondition of r1 are substituted by instate(, (init, init, init)) and instate(, (order_created, init, init)), respectively. As such, it generates a new business rule, i.e., cv(r1, (init, init, init), (order_created, init, init)). Consequently, transition ((init, init, init), r1[(init, init, init), (order_created, init, init)], (order_created, init, init)) belongs to and state (order_created, init, init) belongs to . Similarly, the lifecycle of MP is derived iteratively until and are fixed. Finally, is generated as Figure 4.
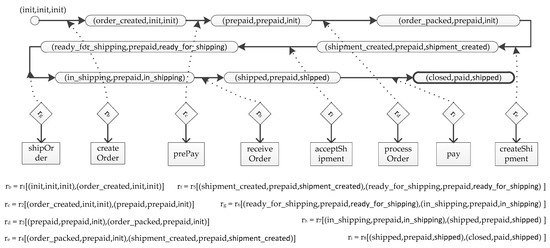
Figure 4.
The lifecycle of the purchase business process model MP (Figure 1).
Next, we introduce the soundness of a lifecycle with some modifications [5]. Given a lifecycle L, L is sound if and only if following two conditions are satisfied: (1) business rule r ∊ rule(L) such that r induces one and only one transition, i.e.,
and (2) for every none final state s in L.Vs, s can be reached from L.s0 and s can reach a final state, i.e.,
∀r ∊ rule(L), (sx, r, sy) ∊ L.Et ∧ (sm, r, sn) ∉ L.Et;
∀ s ∊ L.Vs ∧ ¬fi(s), ∃sf, sf ∊ L.Vs ∧ fi(sf) ∧ L.s0 ⇒* s ∧ s ⇒* sf.
rule(L) returns a set of business rules that appear in L. Function fi(s) returns true if s is a final state of L. A transition (sx, r, sy) can be equivalently marked as sx ⇒r sy. The superscript of ⇒r is omitted if it is not the concern. We write sx ⇒* sy if state sy can be reached from state sx by some sequence of business rules in rule(L). Condition (2) implies connectivity and goal-reachable of the lifecycle of an artifact or a business process model.
Definition 5.
Given an artifact-centric business process model M, M is sound if and only if LM is sound.
If an artifact-centric business process model M is sound, all business process instances that are regulated by M can reach some final states of LM without deadlock [5].
4.2. Verification
In this sub section, we define the soundness of a global adaptation model Γ and verify it. We prove that the global adaptation model is sound if the adaptation rule in the model is sound. Here, we suppose Γ.M and Γ.M’ are sound. Furthermore, we use an adaptation goal to define the acceptable business goals for business process instances that are adapted by an adaptation rule. Then, we use the correctness of the adaptation rule to guarantee that the business process instances can reach some acceptable business goals.
Definition 6.
Given a global adaptation model Γ, we say that Γ.ra is sound if and only if: (1) sx is a reachable state from LM.s0 in the lifecycle of Γ.M; and (2) sy is a reachable state from LM’.s0 in the lifecycle of Γ.M’. Given a global adaptation model Γ, let the artifact-centric business process model derived from Γ as MΓ, Γ is sound if MΓ is sound.
sx is a state of M according to sub condition Γ.ra.λM, and sy is a state of M’ according to sub condition Γ.ra.βM’. For example, sx = (s3, s6, s9, s13) and sy = (s17, s20, s25, s27) in Example 2 (Figure 3).
Theorem 1.
Given a global adaptation model Γ, Γ is sound if Γ.M, Γ.M’ and Γ.ra are sound.
Proof.
By definition of the soundness of a global adaptation model, proof of Theorem 1 is equivalent to prove that MΓ is sound if Γ.M, Γ.M’ and Γ.ra are sound. By Definition 5 and definition of the soundness of a lifecycle, MΓ is sound if and only if Formulas (1) and (2) hold for the lifecycle of MΓ, i.e.,
Therefore, Theorem 1 holds if we can confirm the following hypothesis: Formulas (3) and (4) hold if Γ.M, Γ.M’ and Γ.ra are sound. This hypothesis can be divided as two parts: (I) Formula (3) holds if Γ.M, Γ.M’ and Γ.ra are sound; and (II) Formula (4) holds if Γ.M, Γ.M’ and Γ.ra are sound. Next, we prove these two parts separately. Suppose the lifecycle of Γ.M is LM; the lifecycle of Γ.M’ is LM’; and Γ.ra = (λM, λM’, βM, βM’, va). Note that the sequence of states of artifacts in a state of may not be in lexicography order of artifact names, because we put states of artifacts of LM before states of artifacts of LM’ in a state of for convenience of description.
Proof of Hypothesis Part (I). To prove Hypothesis Part (I), we divide transitions of as three types. Rules appear in , i.e., rule() can be divided as three sub sets, rules derive from Γ.M.R, marked as RM; rules derive from Γ.M’.R, marked as RM’ and {Γ.ra}. According to construction process of the lifecycle of an artifact-centric business process model, there are three types of transitions in that correspond to these three sub sets of rules. These transitions have the form of (sm_a∘sm’_init, r, sm_b∘sm’_init), (sm_init_gf∘sm’_a, r’, sm_init_gf∘sm’_b) and (sm_a∘sm’_init, Γ.ra, sm_gf∘sm’_b), respectively. sm_a and sm_b are two states of LM and sm’_init is the initial state LM’.s0. Notation ∘ represents concatenation operation. sm_init_gf is either the initial state or a state sm_gf of LM, where sm_gf[i] = sgf (1≤i≤|M.Z|). sm’_a and sm’_b are two states of LM’. According to Definition 4 and the construction process of the lifecycle (omitted in this paper), we have following two facts:
Since Γ.M and Γ.M’ are sound, the following two formulas
hold while considering Formulas (1), (5) and (6). Since Γ.ra is sound and transition (sm_x∘sm’_init, Γ.ra, sm_gf∘sm’_y) is unique in , we have that
sm_x is an state of LM according to Γ.ra.λM, denoted as prestate(Γ.ra); sm’_y is a state of LM’ according to Γ.ra.βM’, denoted as poststate(Γ.ra). Here, we confirm Hypothesis Part (I) when transitions confine to the same type by Formulas (7)–(9). Next, we release this restriction. Since Γ.M.Z ∩ Γ.M’.Z = ∅, we have rx ≠ ry, rx ∊ Γ.M.R and ry ∊ Γ.M’.R. Therefore, we can have r ≠ r’, where r and r’ belong to different rule sets RM, RM’ and {Γ.ra}. Here, it is sufficient to show that Hypothesis Part (I) holds while considering Formulas (7)–(9). Proof of Hypothesis Part (I) is complete.
Proof of Hypothesis Part (II). To prove Hypothesis Part (II), we divide lifecycle as two parts: lifecycle fragments that process instances are not adapted; and lifecycle fragments that process instances are adapted. Because M and M’ are sound, by Formulas (2), (5) and (6), we can have that
and
sm_init = LM.s0. sm’_sf and sm_sf are final states in LM’ and LM, respectively. Formulas (10) and (11) depict the lifecycle fragments that process instances are not adapted. Note that sm_sf∘sm’_init and sm_init∘sm’_sf are seen as final states in for the fact that sm_sf∘sm’_init and sm_init∘sm’_sf are business goals of business process instances that are not adapted. Therefore, both fi(sm_sf∘sm’_init) and fi(sm_init∘sm’_sf) return true in Formulas (10) and (11). Next, we discuss the lifecycle fragment that business process instances are adapted. Because M’ and Γ.ra are sound, by Formulas (2) and (6), we can have that:
Because M is sound, by Formulas (2) and (5), we can have that .s0 ⇒* sm_x∘sm’_init. As (sm_x∘sm’_init, Γ.ra, sm_gf∘sm’_y) and sm_gf∘sm’_y ⇒* sm_gf∘sm’_c, we can have that .s0 ⇒* sm_gf∘sm’_c. Since .s0 ⇒* sm_gf∘sm’_c and Formula (12) hold, it is sufficient to show that following formula
holds. By Formulas (10), (11) and (13), it is sufficient to show that Hypothesis Part (II) holds. The proof of Theorem 1 is complete. □
It is known that the evolution of a business process instance is nondeterministic due to the flexibility and declarative properties of artifact-centric business processes [25]. A business process instance will reach a completely different final state even with the same business data. Furthermore, there exists unexpected business goals of M’. Therefore, we must guarantee that a business process instance that is adapted by an adaptation rule can reach an acceptable business goal, i.e., business goal that are acceptable for a customer. We provide the correctness of an adaptation rule to guarantee this constraint.
Before presenting the correctness of an adaptation rule, we provide a definition of an adaptation goal, which is used to define the acceptable business goals. An adaptation goal is defined by domain experts.
Definition 7.
Given a global adaptation model Γ, an adaptation goal of business process instances that are adapted by Γ.ra is a set of final states Sbg = {s1, …, sn}, where si (1 ≤ I ≤ n) is a final state of the lifecycle of Γ.M’.
Definition 8.
Given a global adaptation model Γ and an adaptation goal Sbg of business process instances that are adapted by Γ.ra, Γ.ra is correct if reach(Γ) ⊆ Sbg.
In Definition 8, reach(Γ) returns a set of reachable final states from state srp in the lifecycle of Γ.M’, where srp = poststate(Γ.ra). For example, reach(Γ) = {(s19, s23, s26, s30)}, srp = poststate(r21) = (s17, s20, s25, s27) in Example 2 (Figure 3).
We provide an algorithm iscorrect() to check the correctness of an adaptation rule. In the algorithm, we suppose Γ.M, Γ.M’ and Γ.ra are sound. The algorithm is described as Algorithm 1.
| Algorithm 1. Correctness checking algorithm |
| Input: a global adaptation model Γ and an adaptation goal Sbg. |
| Output: true or false. |
| 0. Begin |
| 1. srp← poststate(Γ.ra) |
| 2. q.add(srp), Sf← null, S← S∪ {srp} |
| 3. While q is not null |
| 4. sx ← q.remove() |
| 5. M’ ←Γ.M’ |
| 6. For each (sa, r, sb) in LM’.Et |
| 7. If sa = sx and sb not in S |
| 8. q.add(sb), S ← S ∪ {sb} |
| 9. If fi(sb) |
| 10. Sf ← Sf ∪ {sb} |
| 11. End |
| 12. End |
| 13. End |
| 14. End |
| 15. If Sf ⊆ Sf |
| 16. Return true |
| 17. Return False |
| 18. End |
In the algorithm, q is a queue. Lines 3–14 compute the set of reachable final states Sf from state srp in LM’ transitively, i.e.,
∀ sm’_sf ∊ Sf, srp ⇒* sm’_sf ∧ fi(sm’_sf).
Since Γ.M, Γ.M’ and Γ.ra are sound, by Theorem 1, we have Γ is sound. From semantics of function reach(), we can see that Sf = reach(Γ). By Definition 8 and Lines 15–17, Algorithm 1 is correct. Let N = max(|S|) and K = |LM’.Et|, the time complexity of Algorithm 1 is O(NK).
In Theorem 2, there is a function adaptgoal(). adaptgoal(Γ.ra) returns the adaptation goal of business process instances that are adapted by Γ.ra.
Theorem 2.
Given a global adaptation model Γ, if Γ is sound and Γ.ra is correct, a business process instance that is adapted by Γ.ra can reach one business goal s of LM’, where s ∊ adaptgoal(Γ.ra).
Proof.
Since Γ is sound, we have a set of reachable final states by reach(Γ). By Formulas (6) and (13), we have that state sm_gf∘s (s ∊ reach(Γ)) can be reached from sm_gf∘poststate(Γ.ra) in . Reversely, by Formulas (13) and (6), we have that a process instance of Γ.M that is adapted to Γ.M’ by Γ.ra can reach a final state s’ of LM’, where s’ must be in reach(Γ). Since Γ.ra is correct, it is obvious that reach(Γ) ⊆ adaptgoal(Γ.ra) by Definition 8. Therefore, s’ ∊ adaptgoal(Γ.ra). The proof of Theorem 2 is complete. □
- Example 4.
In this example, we use aforementioned purchase business process to illustrate our proposed global adaptation model. Suppose the purchase business process is improved by providing options for a customer to pick up an order by him/herself or deliver the order by an express. The old model of the purchase business process is marked as MP (Figure 1) and the new model of the purchase business process is marked as MP’ (Figure 5).
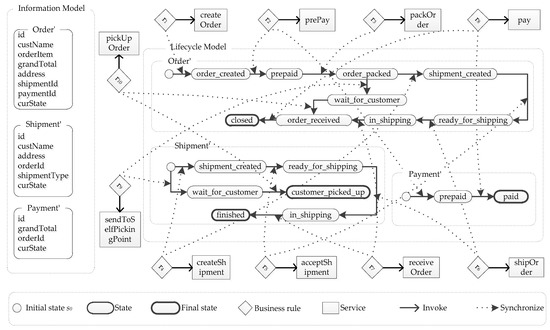
Figure 5.
The purchase business process model MP’.
Compare with MP, a new attribute shipmentType is added in artifact Shipment’; two business rules r9 and r10 are added in Mp’; and two states are added to artifacts Order’ and Shipment’. After the new model is deployed, a business process instance can be adapted from MP to MP’ by our proposed adaptation rule. Here, we only discuss one circumstance. That is, a customer selects to change the type of shipment to self-pick-up and the order is at state shipment_created. Note that, after the new model has been deployed, there is a user interface for a customer to change the type of shipment, i.e., self-pick-up or express, if an order has not reached state ready_for_shipping. To implement the adaptation in this circumstance, we define an adaptation rule in Table 3.

Table 3.
The adaptation rule ra that is used for the adaptation.
In Table 3, the type of a shipment is self-pick-up if shipmentType equals to 1. According to the definition of the adaptation rule, we can have that prestate(ra) = (shipment_created, prepaid, shipment_created) and poststate(ra) = (wait_for_customer, prepaid, wait_for_customer). According to (Figure 4), state (shipment_created, prepaid, shipment_created) is reachable in . Similarly, state (wait_for_customer, prepaid, wait_for_customer) is reachable in . As such, ra is sound by Definition 6. Therefore, all purchase process instances that are adapted by the adaption rule can reach some business goals of .
In the proposed circumstance, a customer selects to pick up the order by him/herself, such that the order should be closed after the order is picked up and paid by the customer, i.e., the adaptation goal for a business process instance that is adapted by ra is adaptgoal(ra) = {(closed, paid, customer_picked_up)}. The state of a purchase process instance is poststate(ra) after ra is evaluated. According to Lines 3–14 of Algorithm 1 and , we can have that the set of reachable states from state (wait_for_customer, prepaid, wait_for_customer) in is reach(Γ) = {(closed, paid, customer_picked_up)}, where Γ = (MP, MP’, ra.va, ra). Because reach(Γ) ⊆ adaptgoal(ra), ra is correct by Definition 8. By Theorem 2, a purchase process instance of MP that is adapted by ra can finally reach an acceptable business goal that belongs to adaptgoal(ra). In this example, there is only one business goal (closed, paid, customer_picked_up), which is expected by customers.
5. Tool Prototype
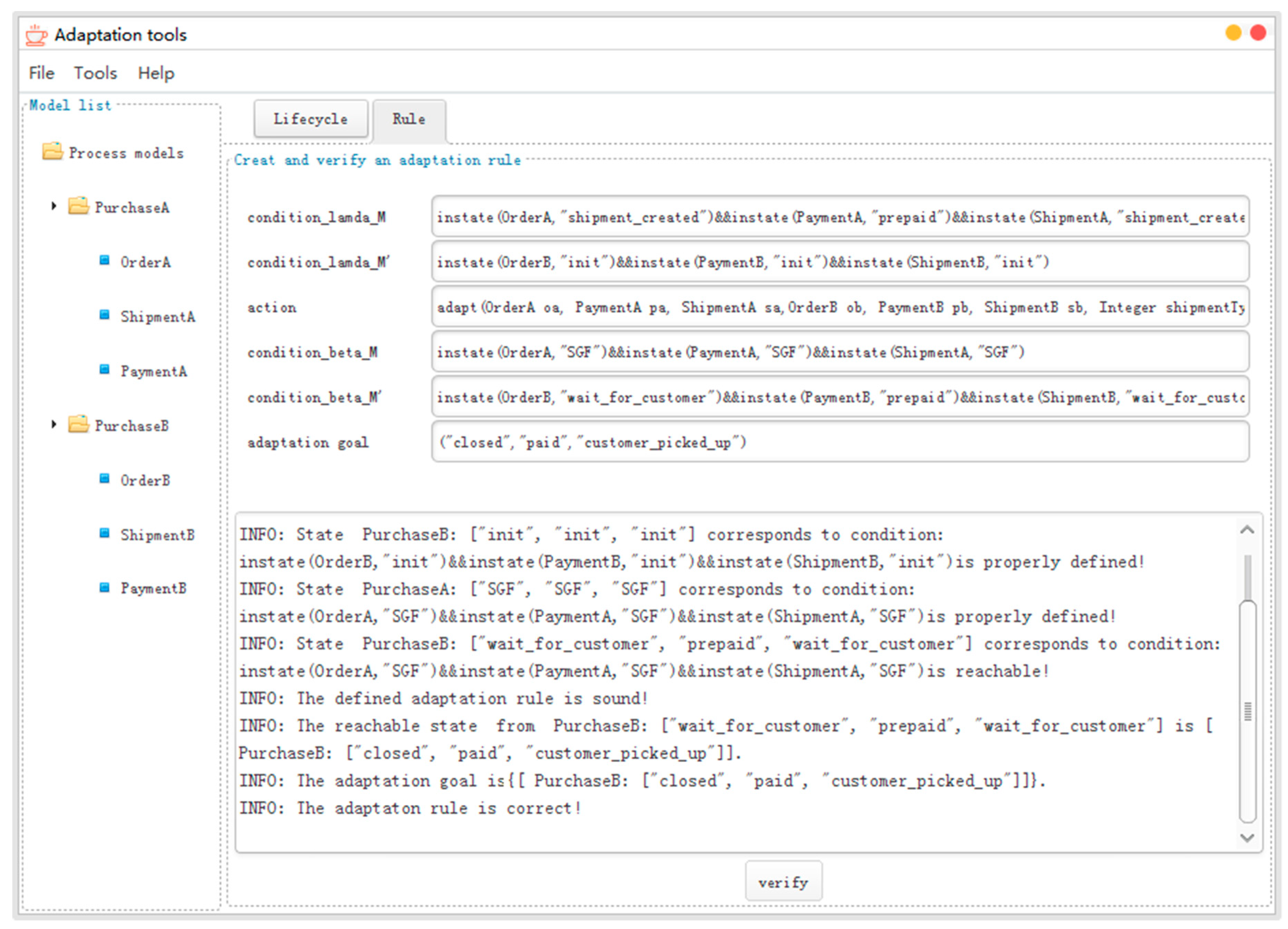
From Example 4, we can see that it is relatively easy for a process designer to define an adaptation rule and an adaptation goal when implementing the adaptation of a model of an artifact-centric business process instance. However, it is a hard work for process designer to judge whether an adaptation rule is sound and correct. To solve this, we developed a tool prototype for helping a process designer to define a sound and correct adaptation rule.
In the tool, we implemented a function to compute the lifecycle of a process model according to lifecycles of artifacts of the process model. We also implemented a function to judge whether the state that corresponds to a condition of an adaptation rule is reachable. Based on these two functions, we implemented Algorithm 1 as one of the main features of the tool. The tool was developed based on Java 1.8, Java Universal Network/Graph Framework (JUNG) 2.1.1 and BeautyEye 3.7 [26,27]. Figure 6 demonstrates the screenshot of verification result of Example 4. Note that names of artifacts of MP end with “A” and names of artifacts of MP’ end with “B”.
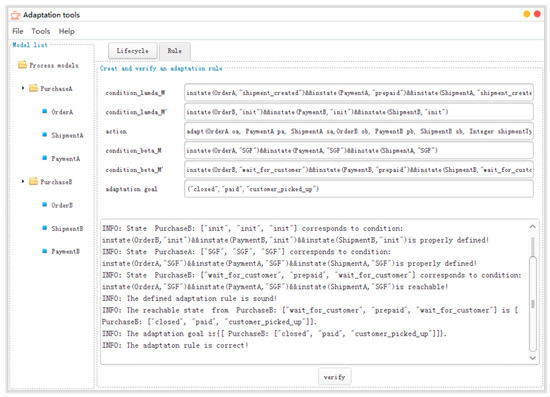
Figure 6.
The screenshot of the verification results of Example 4 through the tool.
A process designer can import two or more artifact-centric business process models through File menu of the tool, where these models are stored as APMT (Artifact-Centric Process Model based on Label Transition System) document [5]. An APMT document, which is based on XML format, captures the behavior of an artifact-centric business process based on the definitions of lifecycles of artifacts and their synchronization. A process designer can click on the name of an artifact on the left of the main panel to check the lifecycle of the artifact, where the lifecycle is presented in the tabbed panel that is named as “Lifecycle”.
A process designer can define an adaptation rule through Tools menu or click on the title of the tabbed panel that is named as “Rule”. The defined adaptation rule and these imported business process models are used as input of the tool. Verification results for the defined adaptation rule are presented at the bottom of the tabbed panel that is named as “Rule”.
6. Discussions
In this paper, we propose an adaptation rule for adapting a model of an artifact-centric business process instance dynamically and use a global adaptation model to describe the adaptation. We prove that a global adaptation model is sound if the adaptation rule and the two artifact-centric business process models in the global adaptation model are sound. Business process instances that are adapted by the adaptation rule can reach some acceptable business goals if the adaptation rule is correct and the global adaptation model is sound. During the adaptation, both changes of data (artifact information model) and process (lifecycles of artifacts) are considered.
Although we discuss the adaptation of a model of an artifact-centric business process instance theoretically, our theoretical results can be used directly to support the adaptation of business process instances in the execution level if business processes are running on the framework proposed in [25]. Because they claim that the framework supports execution of artifact-centric business process model (ACP model) directly without model transformation. Furthermore, our proposed global adaptation model can be seen as an artifact-centric business process model. Comparison of the framework with other works can be found in [25].
In this paper, our proposed adaptation rule is used to adapt a model of a business process instance. From another perspective, our adaptation rule can also be used to combine lifecycle fragments of different business process models to construct complex business processes, because a global adaptation model can be seen as an equivalent artifact-centric business process model according to its definition. From this perspective, artifact-centric business process model is improved with the ability of modeling sub business processes, which, to our best knowledge, has not been addressed in the artifact-centric business process community.
However, in a global adaptation model, there is only one adaptation rule. In real-world, multiple adaptation rules should be defined to adapt business process instances of different circumstances. Moreover, transitive adaptation, i.e., a process instance is adapted more than one time, is not discussed. Nevertheless, the same results can also be derived when multiple adaptation rules are defined in one global adaptation model. Because a global adaptation model with one adaptation rule can be seen as an ordinary artifact-centric business process model, such that the soundness of the global adaptation model can be proved recursively. Furthermore, the adaptation goal of business process instances that are adapted by an adaptation rule is restricted locally to the adaptation rule, such that the correctness of an adaptation rule is independent of other adaptation rules.
There are also some limitations of our proposed method. First, an adaptation rule and the adaptation goal of business process instances that are adapted by the adaptation rule are defined by human. Second, our proposed method is closed related to ACP model [25]. There are some other similar artifact-centric business process modeling approaches, such as GSM and CMMN [3,9,10], where a milestone (state in ACP model) is reached if a guard (a condition for opening a stage) of a stage (action in ACP model) is satisfied and the stage is executed and condition of the sentry that corresponds to the milestone is satisfied. Comparing ACP model with GSM and CMMN models, they all depict artifact behaviors by lifecycles of artifacts. Differently, a lifecycle of an artifact in ACP model is driven by Condition–Action business rules, and a lifecycle of an artifact in GSM and CMMN models is driven by variants of Event–Condition–Action rules. We try to adapt our proposed method to apply to GSM and CMMN models.
7. Conclusions
In this paper, we propose an adaptation rule for adapting a model of an artifact-centric business process instance and describe the adaptation by a global adaptation model. We prove that the business process instance can reach an acceptable business goal without deadlock if the adaptation rule is sound and correct. We developed a tool prototype for helping a process designer to define a sound and correct adaptation rule. Possible applications and limitations of our proposed method are discussed in the Discussion Section. Our future work will try to adapt our proposed approach to other models, like GSM and CMMN.
Author Contributions
Conceptualization, J.Z.; Methodology, J.Z.; Software, J.Z.; Writing-Original Draft Preparation, J.Z.; Writing-Review & Editing, J.Z. and G.L.; Supervision, G.L.
Funding
This research received no external funding.
Acknowledgments
The authors gratefully acknowledge the editors and the anonymous reviewers for their detailed and constructive criticisms, which have helped us to improve the quality and presentation of our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rinderle, S.; Reichert, M.; Dadam, P. Correctness criteria for dynamic changes in workflow systems—A survey. Data Knowl. Eng. 2004, 50, 9–34. [Google Scholar] [CrossRef]
- Nunes, V.T.; Santoro, F.M.; Werner, C.M.; Ralha, C.G. Real-time process adaptation: A context-aware replanning approach. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 99–118. [Google Scholar] [CrossRef]
- Cohn, D.; Hull, R. Business artifacts: A data-centric approach to modeling business operations and processes. IEEE Data Eng. Bull. 2009, 32, 3–9. [Google Scholar]
- Kunchala, J.; Yu, J.; Yongchareon, S. A survey on approaches to modeling artifact-centric business processes. In Proceedings of the International Conference on Web Information Systems Engineering Workshops (WISE), Thessaloniki, Greece, 12–14 October 2014; Volume 9051, pp. 117–132. [Google Scholar]
- Yongchareon, S.; Liu, C.F.; Yu, J.; Zhao, X.H. A view framework for modeling and change validation of artifact-centric inter-organizational business processes. Inf. Syst. 2015, 47, 51–81. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y. Change analysis for artifact-centric business processes. In Proceedings of the International Conference on Business Information Systems (BIS), Larnaca, Cyprus, 22–23 May 2014; Volume 176, pp. 98–109. [Google Scholar]
- Li, S.; Yu, S.J. Research on change adaptation technology of data-centric business process models. Intell. Comput. Appl. 2016, 6, 36–43. [Google Scholar]
- Eshuis, R.; Hull, R.; Yi, M.F. Property preservation in adaptive case management. In Proceedings of the International Conference on Service-Oriented Computing (ICSOC), Goa, India, 16–19 November 2015; Volume 9435, pp. 285–302. [Google Scholar]
- Damaggio, E.; Hull, R.; Vaculín, R. On the equivalence of incremental and fixpoint semantics for business artifacts with Guard-Stage-Milestone lifecycles. In Proceedings of the International Conference on Business Process Management (BPM), Clermont-Ferrand, France, 30 August–2 September 2011; Volume 6896, pp. 396–412. [Google Scholar]
- About the Case Management Model and Notation Specification Version 1.1. Available online: https://www.omg.org/spec/cmmn/1.1/ (accessed on 15 October 2018).
- Cognini, R.; Corradini, F.; Gnesi, S.; Polini, A.; Re, B. Business process flexibility—A systematic literature review with a software systems perspective. Inf. Syst. Front. 2016, 20, 343–371. [Google Scholar] [CrossRef]
- Song, W.; Jacobsen, H.A. Static and dynamic process change. IEEE Trans. Serv. Comput. 2018, 11, 215–231. [Google Scholar] [CrossRef]
- Rosa, M.L.; Aalast, W.M.; Dumas, M.; Milani, F.P. Business process variability modeling: A survey. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Vasilecas, O.; Kalibatiene, D.; Lavbič, D. Rule- and context-based dynamic business process modelling and simulation. J. Syst. Softw. 2016, 122, 1–15. [Google Scholar] [CrossRef]
- Hu, G.C.; Wu, B.D.; Chen, J.L. Dynamic adaptation of business process based on context changes: A rule-oriented approach. In Proceedings of the International Conference on Service-Oriented Computing Workshops (ICSOC), Berlin, Germany, 2–5 December 2013; Volume 8377, pp. 492–504. [Google Scholar]
- Ayora, C.; Torres, V.; Weber, B.; Reichert, M.; Pelechano, V. Enhancing modeling and change support for process families through change patterns. In Proceedings of the International Workshop on Business Process Modeling, Development and Support (BPMDS), Valencia, Spain, 17–18 June 2013; Volume 147, pp. 246–260. [Google Scholar]
- Ayora, C.; Torres, V.; Vara, J.L.; Pelechanoa, V. Variability management in process families through change patterns. Inf. Softw. Technol. 2016, 74, 86–104. [Google Scholar] [CrossRef]
- Patiniotakis, I.; Apostolou, D.; Verginadis, Y.; Papageorgiou, N.; Mentzas, G. Assessing flexibility in event-driven process adaptation. Inf. Syst. 2017, 1–19. [Google Scholar] [CrossRef]
- Oberhauser, R. Adapting processes via adaptation processes: A flexible and cloud-capable adaptation approach for dynamic business process management. In Proceedings of the International Symposium on Business Modeling and Software Design (BMSD), Milan, Italy, 6–8 July 2015; pp. 9–18. [Google Scholar]
- Bhattacharya, K.; Gerede, C.; Hull, R.; Liu, R.; Su, J.W. Towards formal analysis of artifact-centric business process models. In Proceedings of the International Conference on Business Process Management (BPM), Brisbane, Australia, 24–28 September 2007; Volume 4714, pp. 24–28. [Google Scholar]
- Lei, J.K.; Bai, R.F.; Guo, L.P.; Zhang, L. Towards a scalable framework for artifact-centric business process management systems. Proceedings of International Conference on Web Information Systems Engineering (WISE), Shanghai, China, 8–10 November 2016; Volume 10042, pp. 309–323. [Google Scholar]
- Yongchareon, S.; Liu, C.F. A process view framework for artifact-centric business processes. In Proceedings of the International Conference on “On the Move to Meaningful Internet Systems” (OTM), Crete, Greece, 25–29 October 2010; Volume 6426, pp. 26–43. [Google Scholar]
- Nigam, A. Business artifacts: An approach to operational specification. IBM Syst. J. 2003, 42, 428–445. [Google Scholar] [CrossRef]
- Gerede, C.E.; Bhattacharya, K.; Su, J.W. Static analysis of business artifact-centric operational models. In Proceedings of the IEEE International Conference on Service-oriented Computing & Applications (SOCA), Newport Beach, CA, USA, 19–20 June 2007; pp. 133–140. [Google Scholar]
- Ngamakeur, K.; Yongchareon, S.; Liu, C.F. A framework for realizing artifact-centric business processes in service-oriented architecture. In Proceedings of the International Conference on Database Systems for Advanced Applications (DASFAA), Busan, South Korea, 15–19 April 2012; Volume 7238, pp. 63–78. [Google Scholar]
- Java Universal Network/Graph Framework Version 2.1.1. Available online: https://github.com/jrtom/jung/releases/tag/jung-2.1.1 (accessed on 11 July 2018).
- BeautyEye Version 3.7. Available online: https://github.com/JackJiang2011/beautyeye (accessed on 11 July 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).