Evolution, Robustness and Generality of a Team of Simple Agents with Asymmetric Morphology in Predator-Prey Pursuit Problem †
Abstract
:1. Introduction
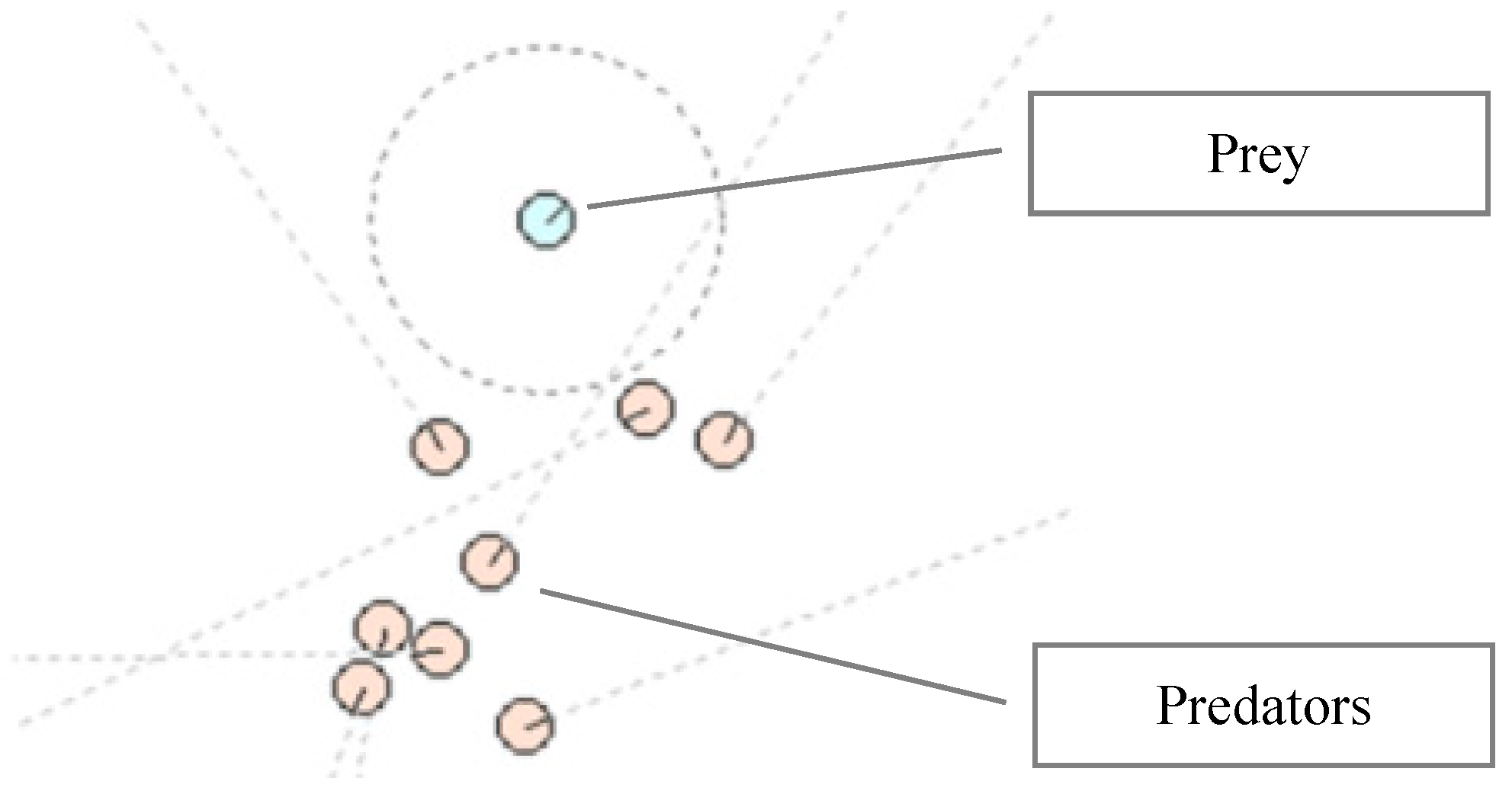
2. The Entities
2.1. The Predators
2.2. The Prey
2.3. The World
3. Evolving the Behavior of Predator Agents
3.1. Evolutionary Setup
| Algorithm 1. Main steps of genetic algorithms (GA). |
| Step 1: Creating the initial population of random chromosomes; |
| Step 2: Evaluating the population; |
| Step 3: WHILE not (Termination Criteria) DO Steps 4–7: |
| Step 4: Selecting the mating pool of the next generation; |
| Step 5: Crossing over random pairs of chromosomes of the mating pool; |
| Step 6: Mutating the newly created offspring; |
| Step 7: Evaluating the population. |
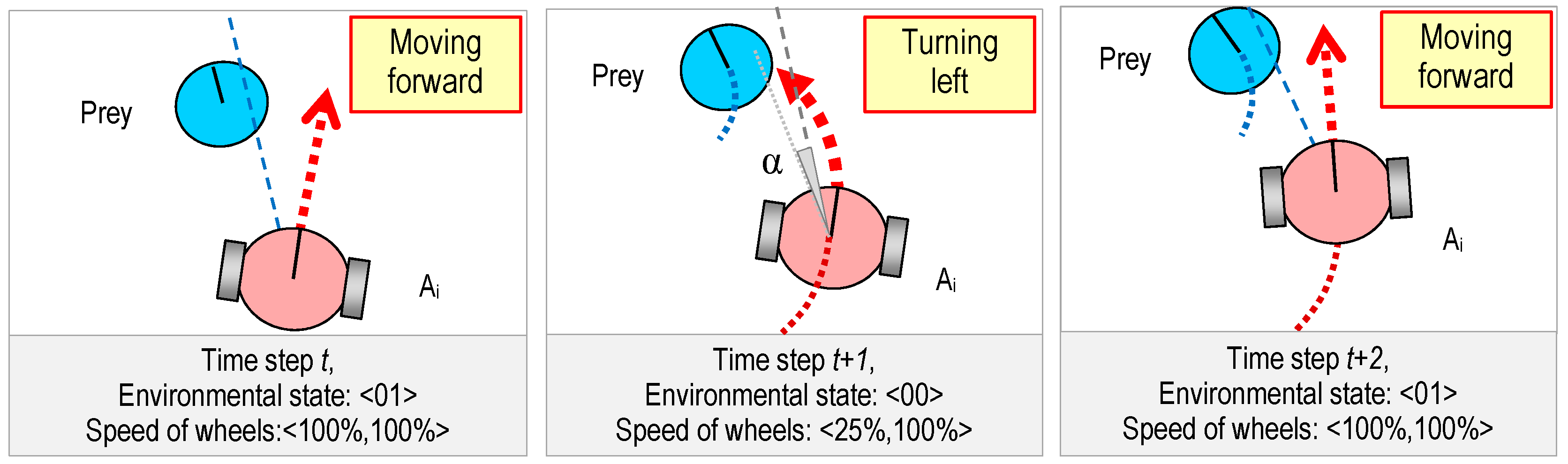
3.2. Genetic Representation
3.3. Genetic Operations
3.4. Fitness Evaluation
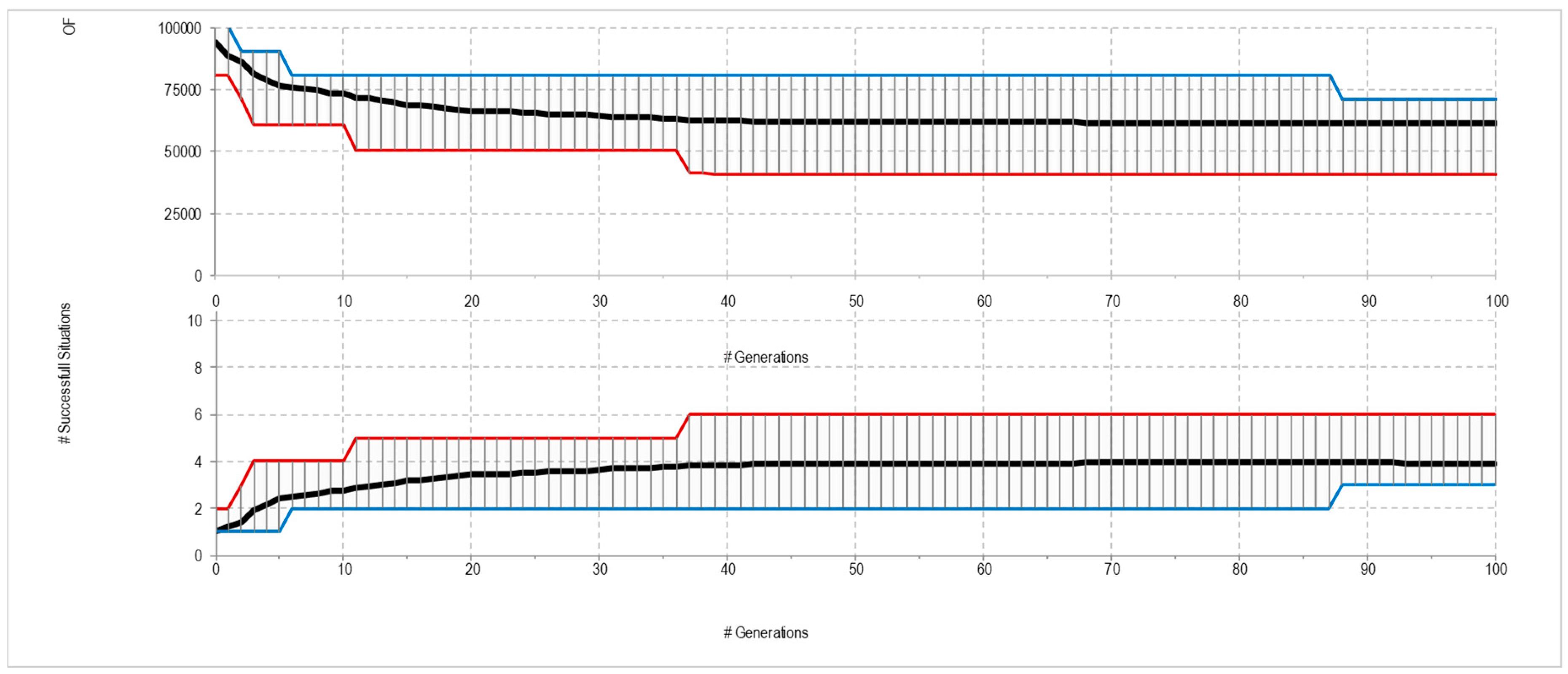
4. Experimental Results
4.1. Canonical Predators
4.2. Enhancing the Morphology of Predators
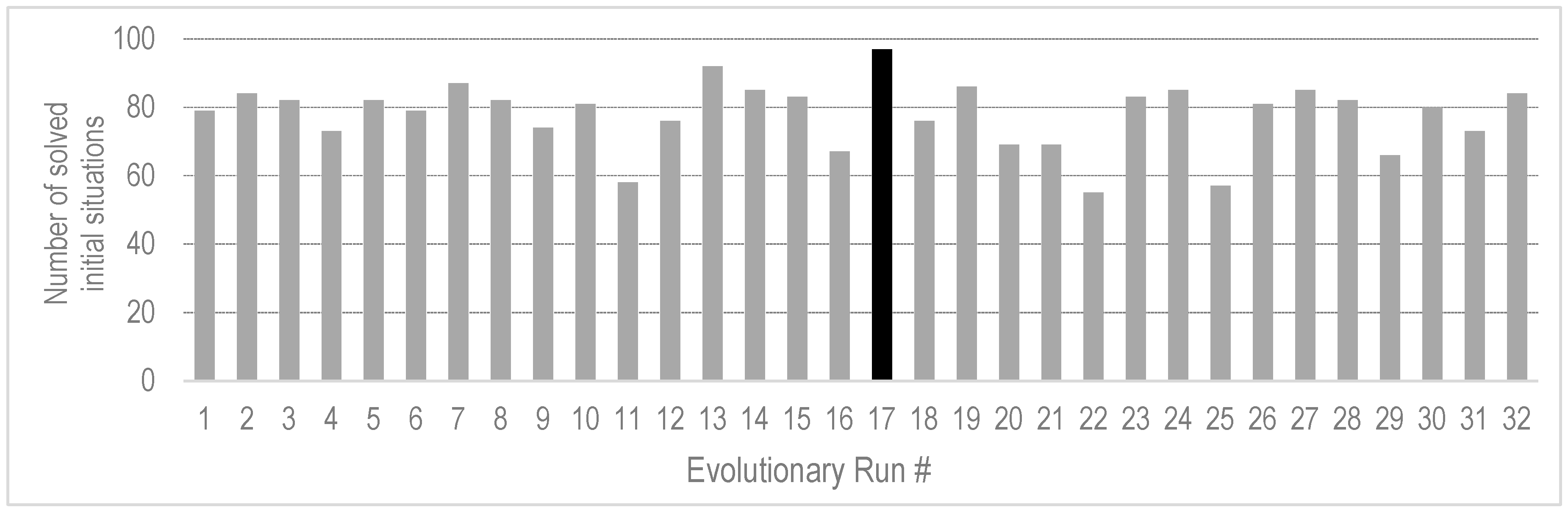
4.3. Generality of the Evolved Behavior
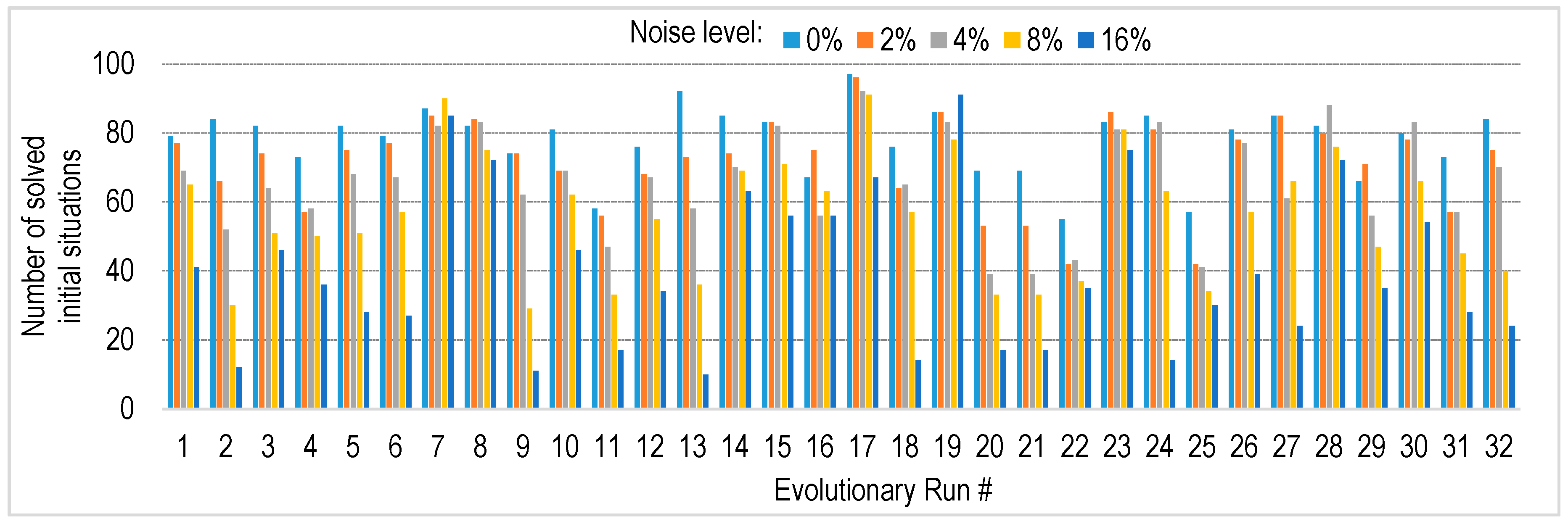
4.4. Robustness to Sensory Noise
5. Discussion
5.1. Advantages of the Proposed Asymmetric Morphology
5.2. Emergent Behavioral Strategies
5.3. Alternative Approaches
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhattacharya, S.; Murrieta-Cid, R.; Hutchinson, S. Optimal paths for landmark-based navigation by differential-drive vehicles with field-of-view constraints. IEEE Trans. Robot. 2007, 23, 47–59. [Google Scholar] [CrossRef]
- Yu, J.; LaValle, S.M.; Liberzon, D. Rendezvous without coordinates. IEEE Trans. Autom. Control. 2012, 57, 421–434. [Google Scholar]
- Tanev, I.; Georgiev, M.; Shimohara, K.; Ray, T. Evolving a Team of Asymmetric Predator Agents That Do Not Compute in Predator-Prey Pursuit Problem. In Proceedings of the 18th International Conference on Artificial Intelligence: Methodology, Systems, Applications, Varna, Bulgaria, 12–14 September 2018. [Google Scholar]
- Georgiev, M.; Tanev, I.; Shimohara, K. Coevolving behavior and morphology of simple agents that model small-scale robots. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018. [Google Scholar]
- Gauci, M. Swarm Robotic Systems with Minimal Information Processing. Ph.D. Thesis, University of Sheffield, Sheffield, UK, September 2014. [Google Scholar]
- Gauci, M.; Chen, J.; Li, W.; Dodd, T.J.; Groß, R. Self-organized aggregation without computation. Int. J. Robot. Res. 2014, 33, 1145–1161. [Google Scholar] [CrossRef]
- Gauci, M.; Chen, J.; Li, W.; Dodd, T.J.; Groß, R. Clustering objects with robots that do not compute. In Proceedings of the 2014 International Conference on Autonomous Agents and Multi-agent Systems, Paris, France, 5–9 May 2014. [Google Scholar]
- Özdemir, A.; Gauci, M.; Groß, R. Shepherding with Robots That Do Not Compute. In Proceedings of the 14th European Conference on Artificial Life, Lyon, France, 4–8 September 2017; pp. 332–339. [Google Scholar]
- Brown, D.S.; Turner, R.; Hennigh, O.; Loscalzo, S. Discovery and exploration of novel swarm behaviors given limited robot capabilities. In Proceedings of the 13th International Symposium on Distributed Autonomous Robotic Systems, London, UK, 7–9 November 2016; pp. 447–460. [Google Scholar]
- Benda, M.; Jagannathan, V.; Dodhiawala, R. An Optimal Cooperation of Knowledge Sources; Technical Report BCS-G2010-28; Boeing AI Center, Boeing Computer Services: Bellevue, WA, USA, 1986. [Google Scholar]
- Haynes, T.; Sen, S. Evolving behavioral strategies in predators and prey. In Proceedings of the 1995 International Joint Conference on AI, Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Luke, S.; Spector, L. Evolving Teamwork and Coordination with Genetic Programming. In Proceedings of the First Annual Conference on Genetic Programming, Stanford, CA, USA, 28–31 July 1996; pp. 150–156. [Google Scholar]
- Tanev, I.; Brzozowski, M.; Shimohara, K. Evolution, generality and robustness of emerged surrounding behavior in continuous predators-prey pursuit problem. Genet. Progr. Evolvable Mach. 2005, 6, 301–318. [Google Scholar] [CrossRef]
- Rubenstein, M.; Cabrera, A.; Werfel, J.; Habibi, G.; McLurkin, J.; Nagpal, R. Collective transport of complex objects by simple robots: Theory and experiments. In Proceedings of the 2013 International Conference on Autonomous Agents and Multiagent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 47–54. [Google Scholar]
- Lien, J.M.; Rodriguez, S.; Malric, J.P.; Amato, N.M. Shepherding Behaviors with Multiple Shepherds. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Requicha, A.A. Nanorobots, NEMS, and Nanoassembly. Proc. IEEE 2013, 91, 1922–1933. [Google Scholar] [CrossRef]
- Niu, R.; Botin, D.; Weber, J.; Reinmüller, A.; Palberg, T. Assembly and Speed in Ion-Exchange-Based Modular Phoretic Microswimmers. Langmuir 2017, 33, 3450–3457. [Google Scholar] [CrossRef] [PubMed]
- Ibele, M.; Mallouk, T.E.; Sen, A. Schooling Behavior of Light-Powered Autonomous Micromotors in Water. Angewandte Chemie Int. Ed. 2009, 48, 3308–3312. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Pedrero, F.; Massana-Cid, H.; Tierno, P. Assembly and Transport of Microscopic Cargos via Reconfigurable Photoactivated Magnetic Microdockers. Small 2017, 13, 1603449. [Google Scholar] [CrossRef] [PubMed]
- Holland, J. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Goldberg, E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Nolfi, S.; Floreano, D. Evolutionary Robotics: The Biology, Intelligence, and Technology of Selforganizing Machines; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Angeline, P.J.E.; Kinnear, K.E., Jr. Genetic Programming and Emergent Intelligence. In Advances in Genetic Programming; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Georgiev, M.; Tanev, I.; Shimohara, K. Performance Analysis and Comparison on Heterogeneous and Homogeneous Multi-Agent Societies in Correlation to Their Average Capabilities. In Proceedings of the 2018 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, Japan, 11–14 September 2018. [Google Scholar]
- Georgiev, M.; Tanev, I.; Shimohara, K. Exploration of the effect of uncertainty in homogeneous and heterogeneous multi-agent societies with regard to their average characteristics. In Proceedings of the Genetic and Evolutionary Computation Conference Companion GECCO (Companion), Kyoto, Japan, 15–19 July 2018. [Google Scholar]




| Feature | Value of the Feature | |
|---|---|---|
| Predators | Prey | |
| Number of agents | 8 | 1 |
| Diameter (and wheel axle track), units | 8 | 8 |
| Max linear velocity of wheels, units/s | 10 | 10 |
| Max speed of agents, units/s | 10 | 10 |
| Type of sensor | Single line-of-sight | Omni-directional |
| Range of visibility of the sensor, units | 200 | 50 |
| Orientation of sensor | Parallel to longitudinal axis | NA |
| Parameter | Value |
|---|---|
| Genotype | Eight integer values of the velocities of wheels (V00L, V00R, V01L, V01R, V10L, V10R, V11L, and V11R) |
| Population size | 400 chromosomes |
| Breeding strategy | Homogeneous: the chromosome is cloned to all predator agents before the trial |
| Selection | Binary tournament |
| Selection ratio | 10% |
| Elitism | Best 1% (4 chromosomes) |
| Crossover | Both single- and two-point |
| Mutation | Single-point |
| Mutation ratio | 5% |
| Fitness cases | 10 initial situations |
| Duration of the fitness trial | 120 s per initial situation |
| Fitness value | Sum of fitness values of each situation: (a) Successful situation: time needed to capture the prey (b) Unsuccessful situation: 10,000 + the shortest distance between the prey and any predator during the trial |
| Termination criterion | (# Generations = 200) or (Stagnation of fitness for 32 consecutive generations) or (Fitness < 600) |
| Sensor Offset | Terminal Value of Objective Function | Successful Runs | # Generations Needed to Reach 90% Probability of Success | ||||
|---|---|---|---|---|---|---|---|
| Best | Worst | Mean | Standard Deviation | Number | % (of 32 Runs) | ||
| 0° | 40,928 | 70,729 | 61,064 | 8516 | 0 | 0 | NA |
| 10° | 504 | 10,987 | 1310 | 2531 | 30 | 93.75 | 60 |
| 20° | 468 | 818 | 588 | 57.2 | 32 | 100 | 9 |
| 30° | 495 | 713 | 574 | 38.5 | 32 | 100 | 12 |
| 40° | 475 | 40,903 | 1840 | 7128 | 31 | 96.875 | 15 |
| V00L | V00R | V01L | V01R | V10L | V10R | V11L | V11R |
| 25% | 100% | 100% | 100% | −25% | −20% | 100% | 100% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, M.; Tanev, I.; Shimohara, K.; Ray, T. Evolution, Robustness and Generality of a Team of Simple Agents with Asymmetric Morphology in Predator-Prey Pursuit Problem. Information 2019, 10, 72. https://doi.org/10.3390/info10020072
Georgiev M, Tanev I, Shimohara K, Ray T. Evolution, Robustness and Generality of a Team of Simple Agents with Asymmetric Morphology in Predator-Prey Pursuit Problem. Information. 2019; 10(2):72. https://doi.org/10.3390/info10020072
Chicago/Turabian StyleGeorgiev, Milen, Ivan Tanev, Katsunori Shimohara, and Thomas Ray. 2019. "Evolution, Robustness and Generality of a Team of Simple Agents with Asymmetric Morphology in Predator-Prey Pursuit Problem" Information 10, no. 2: 72. https://doi.org/10.3390/info10020072
APA StyleGeorgiev, M., Tanev, I., Shimohara, K., & Ray, T. (2019). Evolution, Robustness and Generality of a Team of Simple Agents with Asymmetric Morphology in Predator-Prey Pursuit Problem. Information, 10(2), 72. https://doi.org/10.3390/info10020072





