2. Related Work
In DDBS design, it is consensually agreed-upon that the more precise the data partitioning and allocation techniques, the better the performance and the lower the response time are likely to be obtained [
8]. In [
8], a comprehensive taxonomy was given. This taxonomy was fine-grained and comprehensively analyzed in both static and dynamic environments. The main issues addressed in this taxonomy includes data fragmentation, data allocation, and replication. These issues have been examined to classify and analyze a huge number of previously-made DDBSs works. The observation of earlier works’ drawbacks was the drive aim of this taxonomy to produce more productive methods to improve DDBS performance. It was found that TC minimization (including communication costs) has been the key objective, for which most of old and recent works have been striving to achieve by maximizing data locality and minimizing remote data access. Nevertheless, it was noted in taxonomy that most of these works failed to provide a clear definition for TC as a performance metric, which is considered as a huge shortcoming.
An improved system to fragment data at the initial stage of DDBS design and allocate fragmented data at runtime over the cloud environment was presented in [
4]. A Cloud Based Distributed Database System (CB-DDBS) architecture over a cloud environment was developed. CB-DDBS adopted a replication scenario so that DDBSMs are allowed to work in parallel to meet the client’s orders. Even though the proposed algorithm of CB-DDBS was hugely driven by the Performance Optimality Enhancement Algorithm (POEA) [
9], authors had never indicated this inspiration. Moreover, selecting a cluster leader was not practical enough to work in a real-world environment as most DDBSs have the same specification for all of its members (nodes), specifically in the Peer-2-Peer network. On the other hand, the data replication problem (DRP) was deeply addressed by [
6] and formulated as an integer linear problem, with an assumption of having overlapping horizontally-divided data. In fact, the replication problem was looked at as an optimization problem to gain the intended aim of having fragments’ copies and sites kept at a minimum. On the other extreme, [
10] drew a method based on the particle swarm optimization (PSO) algorithm to shorten TC. The core of this study was to solve a data allocation problem (DAP) by utilizing the PSO algorithm. Fragments allocation over sites had been done with the PSO algorithm, and its performance was evaluated on 20 different tested problems.
On the same line, in [
2], an enhanced version of [
3] was developed. The work sought to incorporate a site clustering algorithm, for network sites, and a mathematical replication model for cost-effective data allocation [
3]. A significant enhancement was observed in terms of overall DDBSs performance through decreasing TC among network sites. The constraints of clusters and sites were also taken into account to strengthen the proposed efficiency. In-depth experiments were carried out to solely prove the effectiveness of this technique, with respect to minimizing TC and promoting DDBS performance. As a matter of fact, an evidential reduction in TC and clear enhancement in DDBSs performance had been demonstrated. Additionally, this work was profoundly evaluated against [
3], with respect to the objective function of [
2]. Results positively proved that [
2] far outperformed [
3], in terms of decreasing TC and significantly increasing the overall DDBS productivity.
On the other hand, [
11] used a Genetic Algorithm (GA) with Mahalanobis distance along with the K-means clustering algorithm as an influential combination to propose a two-phase clustering algorithm for distributed datasets. In first phase, GA is utilized in parallel on fragments, which were assigned to different sites. Mahalanobis distance was used as fitness value in GA. To draw a better representation of initial data, covariance between data points were considered in Mahalanobis distance. In second phase, to find final results, K-means with K-means++ initialization was applied on intermediate output. To conduct experiments and measure performance, multiple real-life and synthetic datasets were used to implement the technique in the framework of Hadoop.
On the same page, in [
5], an enhanced vertical fragmentation approach was presented using the K-means Rough (KR) clustering technique. Several experiments were conducted and results using KR showed that: (1) the smaller the number of clusters K, the larger the total time and the satisfactory error average cost and memory cost K-means algorithm were obtained; (2) the larger the number of clusters of k, the more optimized were these three criteria in comparison with the normal k-Means algorithm. Lastly, in [
12,
13], the authors proposed an approach of a greedy nature to fragment and allocate fragments in DDBS. While they used an aggregated similarity to cluster similar queries and find fragments, they were planning to use a greedy algorithm to assign resulted fragments into relative sites. However, they neither demonstrated the approach mechanism nor conducted experiments to verify the approach effectiveness.
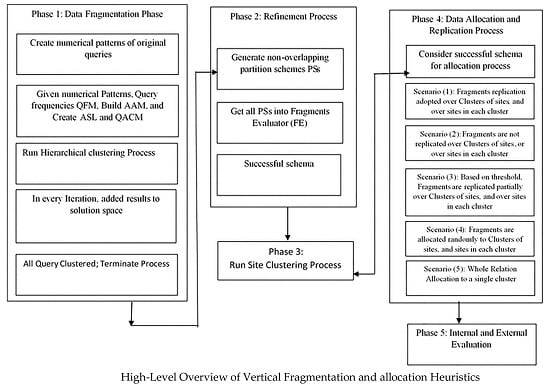
In the proposed work of this paper, a comprehensive approach is released for the purpose of finding the best fitting technique for DDBS design. The intended technique is meant to further minimize TC while giving an obvious definition for TC. It is worth mentioning that the criteria involved in taxonomy [
7] are also considered in this paper. TC is being lessened by increasing data locality and decreasing remote data access, while communication overhead is significantly reduced by adopting replication scenarios.
4. Practical Experiment
This experiment was conducted using a machine with a Intel core i3 duo processor, with a speed of 2.80 GHz, 4 GB RAM, and a Windows 7, 32-bit operating system. C-sharp language was used to analyze and interpret data given as initial input represented in the queries, query frequency matrix (QFM) and communication costs matrix. To highlight the contribution of this work in terms of TC reduction, we made an external evaluation with [
7]. We created an environment that ensured a fair comparison between our work of this paper and [
7]. In other words, the same simulation environment in which [
7] was been implemented, was also adopted in this paper. To illustrate the mechanism of our approach, one experiment was performed. The virtual network was assumed to be fully-connected network of sites, as shown in
Figure 2.
It worth mentioning here that, in the first experiment, the proposed employee (Emp) dataset was created in accordance with the description provided in
Table 3. For the first experiment, the dataset had six attributes and 300 rows. For the sake of simplifying computation and completeness, the schema and attributes were re-drawn in this work. The Emp-no, Emp-name, Job-id, Salary, Location and Dept-id, were referred to as A1, A2, A5, A6, A5, and A6, respectively.
For this experiment, it was assumed that the queries under consideration were eight queries running against the dataset, say 50% to 85% of all queries.
Q1: Select A1, A2, A5, A6 from Emp where A1 in (1234, 261, 1239) and A3 = “Mang222”;
Q2: Select A3, A5 from Em where A5 in (‘site 1’, ‘site 3’, ‘site 6’);
Q3: Select A2, A4, A5 from Em;
Q4: Select A1, A3, A6 from Em where A6 = ‘dept2’;
Q5: Select A1, A2, A5 from Emp where A2 = “Jane” and A5 in (‘site 2’,‘site 5’);
Q6: Select A3, A4, A6 from Emp where A4 > 4500;
Q7: Select A2, A6 from Emp where A1 > 1234;
Q8: Select A1, A3, A5, A6 from Emp;
5. Results and Discussion
We evaluated the performance of this work by conducting several experiments, among which just eleven are presented in this section for demonstration purposes. Relation cardinality, number of sites, number of queries, and rate of query types were all varied in each experiment. In doing so, both our proposed work and that of [
7] were set to be examined under different circumstances. As mentioned earlier, this work had the aim of increasing data locality to the greatest possible extent so that TC was going to be maximally reduced. In other words, data fragments were placed in the cluster/site where it was highly and frequently required. As consequences, transmission costs (TC), including communication costs, and response time were substantially mitigated. To validate and verify these claims, internal and external evaluations were made. For the sake of ensuring a fair comparison, we tried to create the same environment in which [
7] had been tested. Thus, for first part of this evaluation, the same five problems addressed in [
7] were also considered in this work, namely queries 8, 16, 24, 30, and 40, respectively. While the first problem was separately done in both works, it was exclusively restricted for retrieval queries (read-type). The second and third problems considered a mixture of retrieval and update queries, but with retrieval queries having a larger portion. Finally, the last two problems also were a mixture, but with update queries taking a larger share. The evaluation process was made in terms of many design-related performance factors. Among these factors was (1) the TC reduction rate, which is of paramount importance to be investigated; and (2) DDBS performance, which is calculated as (1—averaged TC), where averaged TC is the averaged costs incurred as the query set of the certain experiment is being processed. That is, performance had a inversely proportional relationship with TC in this work. For each problem, meeting the minimization of (TC) along with the objective function was considered.
For the first problem,
Figure 4,
Figure 5,
Figure 6 and
Figure 7 show the experiments that were carried out and which reflect the clear contribution of work of this paper. While
Figure 4 and
Figure 5 display TC rate for both works as per site clustering of [
8];
Figure 6 and
Figure 7 show results of TC rate when applying the new proposed site clustering of this paper, on both [
7] and our work of this paper. According to the results obtained, our work proved to be highly efficient with respect to TC minimization. Every query, among those under consideration, was tested on employee dataset in accordance to five data allocation scenarios: (1) hybrid replication-based Scenario (HAS); (2) full replication Scenario (FAS); (3) no replication over clusters of sites Scenario (NAS); (4) random allocation Scenario; and (5) random allocation for the whole dataset. These experiments were done using C#, to determine which fragmentation and allocation scenario gave better results for DDBS performance. It is worth indicating that we refer to reference [
7] as [
7] and [Adel et al, 2017] interchangeably, and we refer to the proposed work of this paper as “present” (in figures) to facilitate comparison and make it clearly understood.
It was clearly evident form
Figure 4 and
Figure 5 that scenario (1) outperformed its peers, particularly when communication cost between clusters was considered,
Figure 7. While scenario (2), for the first problem, came in second place with a slight difference followed by scenario (3). Scenario (5), on the other hand, was recorded to be the worst for DDBS performance. Needless to say, it was possibly true that scenario (1) was the best for the first three problems, since all data were available in all clusters and were of read type queries that had the larger space of queries under consideration. These facts were not surprising since it agreed with results observed in [
7]. However, in the proposed work of this paper, as per results on all drawn figures, TC reduction was clearly observed to be greatly lessened when compared to [
7]. In the sense that it can be confidently deduced that the enhancement of the present work proved to be highly valuable and effective.
In [
7], communication costs between clusters were taken as the average of all points of intended clusters. This justifies why [
7] recorded great results in this work. In other words, comparing [
7] in
Figure 4 with [
7] in
Figure 5, it was evidential that the LDV-based clustering process for network sites showed to be highly effective in terms of TC reduction. On the other hand, in most cases, our work of this paper showed to perform better than [
7] in all scenarios of communication, as shown in
Figure 6 and
Figure 7.
From the results shown in
Figure 4,
Figure 5,
Figure 6 and
Figure 7, it can be concluded that data replication had a huge impact on communication cost minimization, mainly when retrieval queries established the largest portion of the considered queries. To emphasize this claim, four more experiments (P1, P2, P3, and P4) were performed with 16, 24, 30, and 40 queries, respectively. The obtained results presented in
Figure 8 and
Figure 9 confirmed that scenarios (1) and (2) were the best scenarios, whereby retrieval queries represented the largest portion of considered queries, as they were in P1, P2, and P3. However, scenario (3), followed by scenario (4), were considered to be, by far, the best options when updated queries constituted the largest percentage of the queries under consideration, as they were in P4 and P5.
Our proposed site clustering technique played a key role in balancing clusters and thus in increasing data compactness, locality, and availability in each cluster. These factors, in fact, contributed highly in reducing TC and heightening DDBS performance, as revealed in
Figure 10 and
Figure 11. All problems described previously were evaluated in the same pattern in which problem (1) was examined. It was clear from the results illustrated in
Figure 10 and
Figure 11 that our proposed method performed better than [
7], for all problems tackled and all considered scenarios regarding TC minimization.
Approach Complexity of Computation
Similarly, like [
7] and [
17], the complexity of time was bounded by O (NF*QN*M), at the best case, and O (N2), at the worst case. Where NF, QN, M and N stand for Number of Fragments, Number of Query clusters, number of sites and number of queries respectively.