End to End Delay and Energy Consumption in a Two Tier Cluster Hierarchical Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Work
3. WSN Scenario
Cells, Sensors and Cell Head Selection
4. Communication
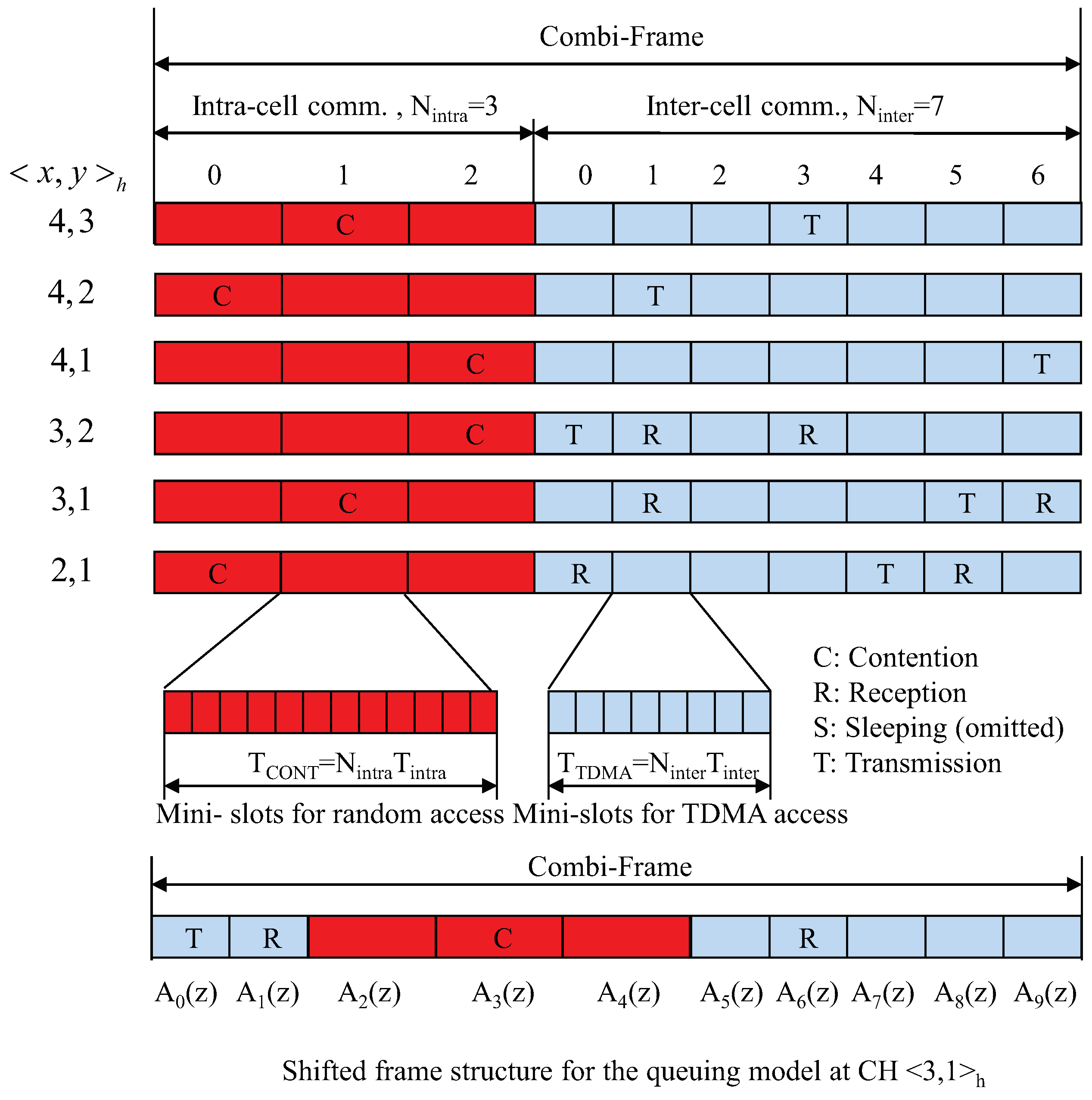
4.1. Frame Structure
4.2. Slot Assignment for Intra-Cell and Inter-Cell Communications
4.3. The Communication Range
4.4. Inter-Cell Routing and Load Balancing
4.5. Synchronization of the WSN
5. The Intra-Cluster Communication
5.1. Traffic Model
5.2. The Contention Process
6. The Inter-Cluster Communication
6.1. The Traffic Load and the Stability Conditions
6.2. The Embedded Markov Chain
6.3. On the Input Process in the Inter-Cluster Communication
6.4. On the Output Process in the Inter-Cluster Communication
7. End-To-End Delay Analysis
7.1. Sojourn Times in a CH
7.2. Local and Exogenous Traffic
7.3. Delay of a Tagged Data Packet
7.4. Algorithmic Procedure
7.5. Model Validation
8. The Energy Consumption Model
9. Numerical Results
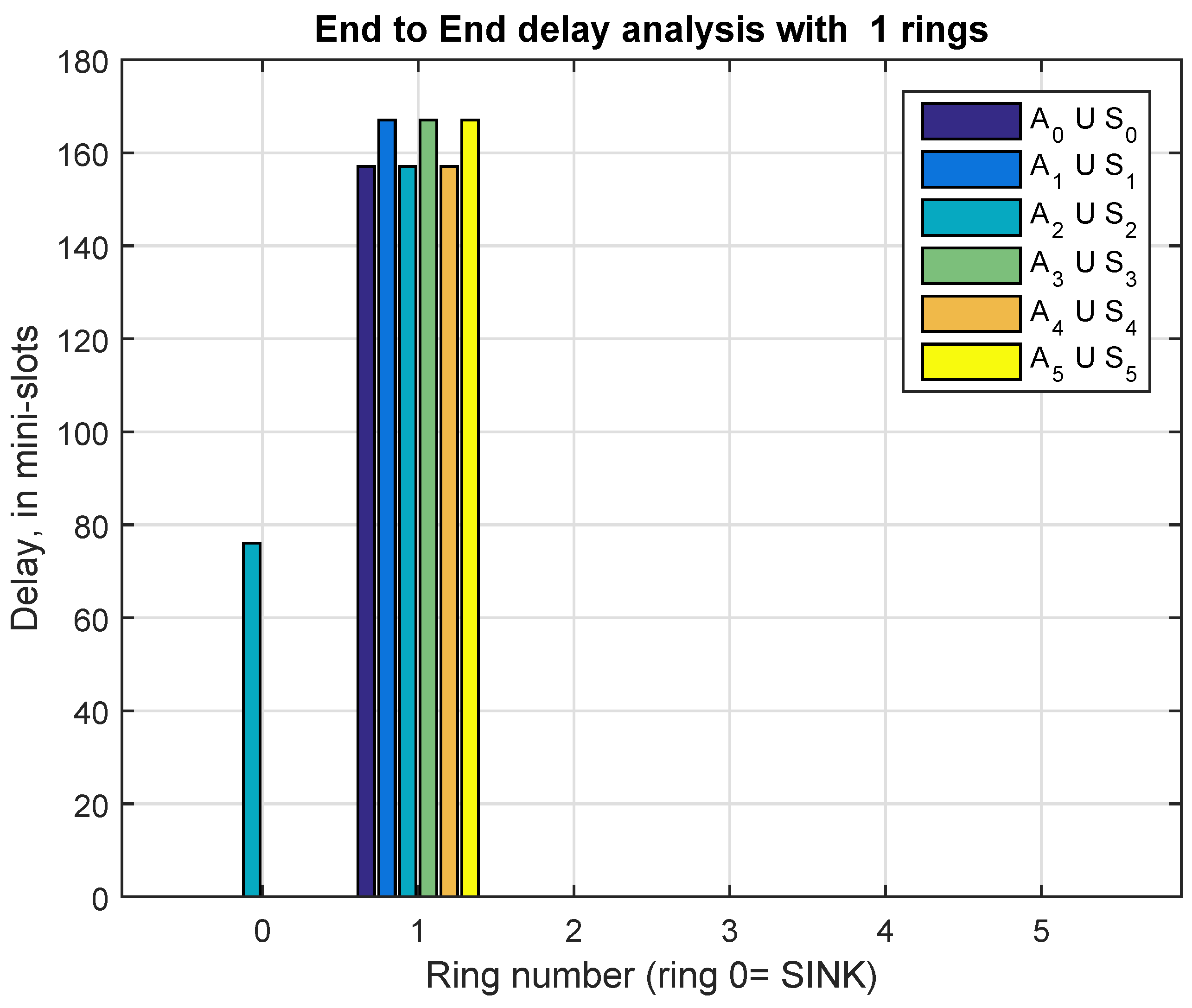
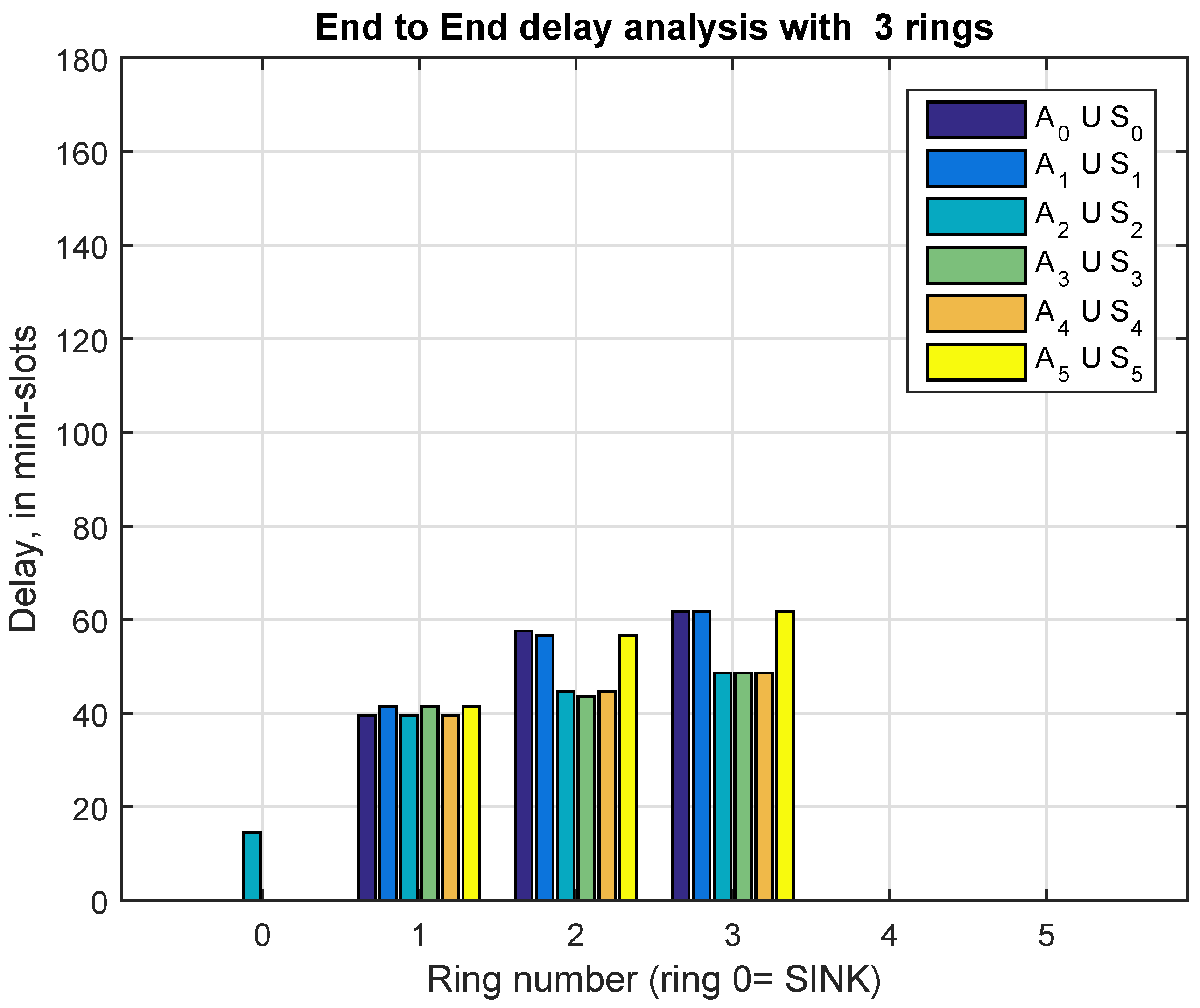
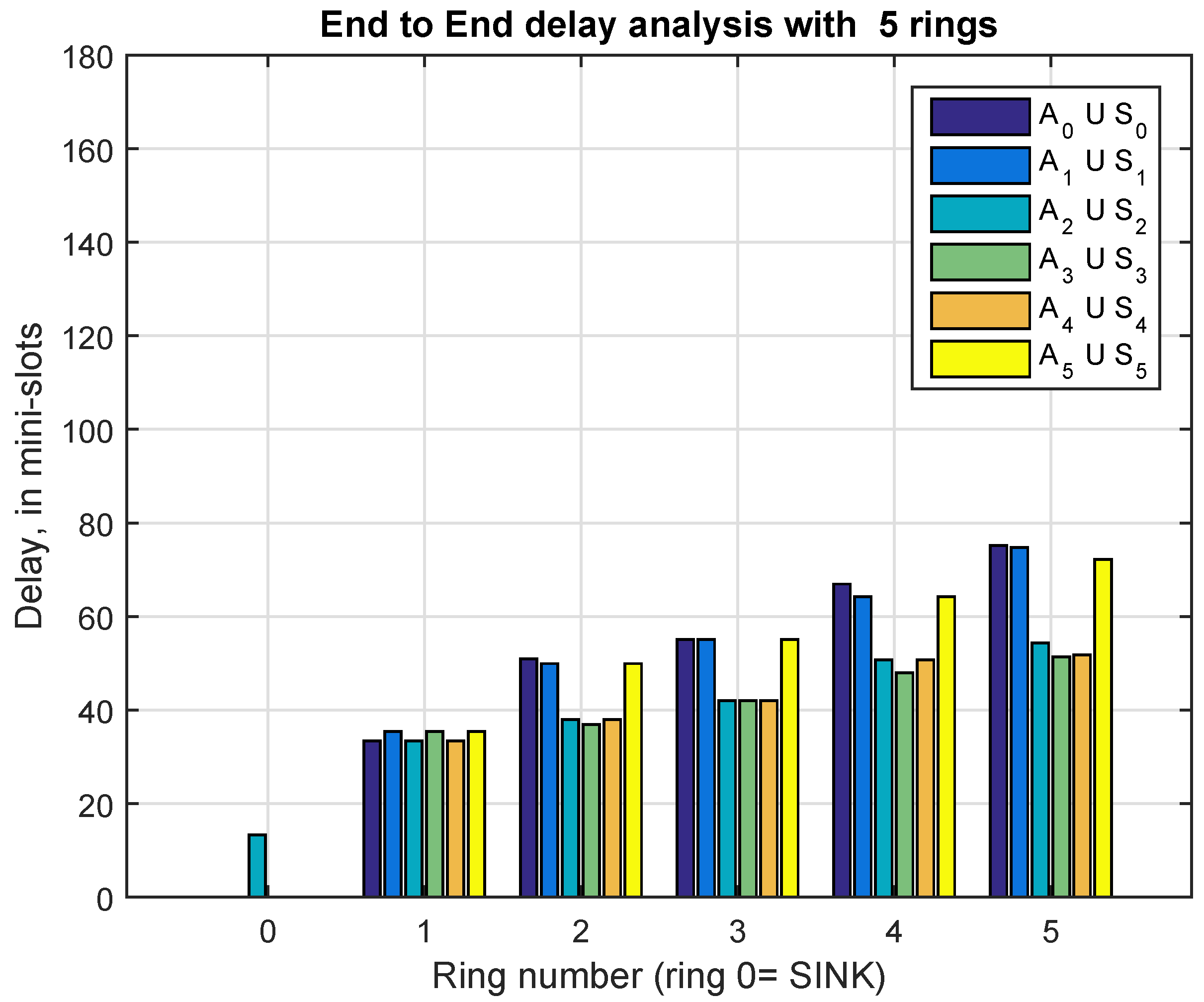
9.1. Delay Analysis
9.2. Energy Consumption
10. Conclusions and Further Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Hexagonal coordinates for a cluster | |
| Polar coordinates for a cluster | |
| Maximum number of rings in the WSN area | |
| Minimum range of intra-cell communication | |
| Minimum range of inter-cell communication | |
| Total number of sensors or motes in the WSN area | |
| Total number of members per cluster | |
| Number of slots per sub-frame | |
| Number of mini-slots per slot | |
| Number of slots per sub-frame | |
| Number of mini-slots per slot | |
| Number of slots per Combi-Frame | |
| Number of mini-slots per Combi-Frame | |
| Time duration of the mini-slot | |
| Time duration of the mini-slot | |
| Time duration of the sub-frame | |
| Time duration of the sub-frame | |
| Time duration of the Combi-Frame | |
| Poisson arrival rate of data packets per sensor | |
| Probability a sensor becomes active during one mini-slot | |
| PGF of the input process at a CH | |
| PGF of the output process after a slot | |
| PGF of the arrival data packets at CH during slot i | |
| PGF of the departure process at a CH after a slot | |
| Normalized traffic load at any CH of ring k |
References
- Shi, L.; Fapojuwo, A.O. TDMA Scheduling with Optimized Energy Efficiency and Minimum Delay in Clustered Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2010, 9, 927–940. [Google Scholar] [CrossRef]
- Rom, R.; Sidi, M. Multiple Access Protocols—Performance and Analysis; Springer: New York, NY, USA, 1990. [Google Scholar]
- Hammond, J.L.; O’Reilly, P.J.P. Performance Analysis of Local Computer Networks; Addison-Wesley Publishing Company: Boston, MA, USA, 1986. [Google Scholar]
- Sari, A. Two-Tier Hierarchical Cluster Based Topology in Wireless Sensor Networks for Contention Based Protocol Suite. Int. J. Commun. Netw. Syst. Sci. 2015, 8, 29–42. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, H. Balancing Energy Consumption to Maximize Net-work Lifetime in Data-Gathering Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1526–1539. [Google Scholar] [CrossRef]
- Bjornemo, E.; Johansson, M.; Ahlen, A. Two Hops is One too Many in an Energy-Limited Wireless Sensor Network. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP ’07), Honolulu, HI, USA, 15–20 April 2007; Volume 3, pp. III-181–III-184. [Google Scholar]
- Kheireddine, M.; Abdellatif, R. Analysis of Hops Length in Wireless Sensor Networks. Wirel. Sens. Netw. 2014, 6, 109–117. [Google Scholar] [CrossRef]
- Wieselthier, J.E.; Ephremides, A.; Michaels, L.A. An Exact Analysis and Performance Evaluation of Framed ALOHA with Capture. IEEE Trans. Commun. 1989, 37, 125–137. [Google Scholar] [CrossRef]
- Song, W.; Huang, R.; Shirazi, B.; LaHusen, R. TreeMAC: Localized TDMA MAC protocol for real-time high-data-rate sensor networks. In Proceedings of the PERCOM 2009, IEEE International Conference on Pervasive Computing and Communications, Galveston, TX, USA, 9–13 March 2009; pp. 1–10. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, D.; Zhu, G. End-to-end delay and packet drop rate performance for a wireless sensor network with a cluster-tree topology. Wirel. Commun. Mob. Comput. 2014, 14, 729–744. [Google Scholar] [CrossRef]
- Alabdulmohsin, I.; Hyadi, A.; Afify, L.; Shihada, B. End-to-end delay analysis in wireless sensor networks with service vacation. In Proceedings of the WCNC 2014, IEEE Wireless Communications and Networking Conference, Istanbul, Turkey, 6–9 April 2014; pp. 2798–2804. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Yoo, S. Time slot assignment for convergecast in wireless sensor networks. J. Parallel Distrib. Comput. 2015, 83, 70–82. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.; Xie, J.; Zhang, Z. Energy Efficiency TDMA/CSMA Hybrid Protocol with Power Control for WSN. Wirel. Commun. Mob. Comput. 2018, 2018, 1–7. [Google Scholar] [CrossRef]
- Olariu, S.; Stojmenovic, I. Design guidelines for maximizing lifetime and avoiding energy holes in sensor networks with uniform distribution and uniform reporting. In Proceedings of the IEEE INFOCOM 2006, 25th IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006; pp. 1–10. [Google Scholar] [CrossRef]
- Sgora, A.; Vergados, D.J.; Vergados, D.D. A Survey of TDMA Scheduling Schemes in Wireless Multihop Networks. ACM Comput. Surv. 2015, 47, 53:1–53:38. [Google Scholar] [CrossRef]
- Martin, E.; Liu, L.; Covington, M.; Pesti, P.; Weber, M. Location-Based Services Handbook—Applications, Technologies, and Security; Chapter Positioning Technologies in Location-Based Services; Ahson, S.A., Ilyas, M., Eds.; CRC Press: Boca Raton, FL, USA, 2010; pp. 1–45. [Google Scholar] [CrossRef]
- Pal, A. Localization Algorithms in Wireless Sensor Networks: Current Approaches and Future Challenges. Netw. Protoc. Algorithms 2010, 2, 45–74. [Google Scholar] [CrossRef]
- Pestana Leao de Brito, L.M.; Rodriguez Peralta, L.M. An Analysis of Localization Problems and Solutions in Wireless Sensor Networks. Revista de Estudos Politécnicos 2008, 6, 1–27. [Google Scholar]
- Gerla, M.; Kwon, T.J.; Pei, G. On demand routing in large ad hoc wireless networks with passive clustering. In Proceedings of the 2000 IEEE Wireless Communications and Networking Conference, Chicago, IL, USA, 23–28 September 2003; pp. 100–105. [Google Scholar]
- Aziz, N.A.A.; Aziz, K.A.; Ismail, W.Z.W. Coverage Strategies for Wireless Sensor Networks. World Acad. Sci. Eng. Technol. Int. J. Electron. Commun. Eng. 2009, 3, 171–176. [Google Scholar]
- Alonso, E.; Meier-Hellstern, K.S.; Pollini, G. Influence of cell geometry on handover and registration rates in cellular and universal personal telecommunication networks. In Proceedings of the 8th International Teletraffic Congress (ITC), Specialists Seminar on Universal Personal Telecommunications, Genova, Italy, 12–14 October 1992; pp. 261–270. [Google Scholar]
- Kusdaryono, A.; Oh Lee, K. A Clustering Protocol with Mode Selection for Wireless Sensor Network. J. Inf. Process. Syst. 2011, 7, 29–42. [Google Scholar] [CrossRef]
- MacDonald, V.H. Advanced Mobile Phone Service: The Cellular Concept. Bell Syst. Tech. J. 1979, 58, 15–41. [Google Scholar]
- Casares-Giner, V.; Wuchner, P.; Pacheco-Paramo, D.; de Meer, H. Combined Contention and TDMA-Based Communication in Wireless Sensor Networks. In Proceedings of the NGI’12 Conference, Karlskrona, Sweden, 25–27 June 2012. [Google Scholar] [CrossRef]
- Elson, J.; Girod, L.; Estrin, D. Fine-Grained Network Time Synchronization using Reference Broadcasts. In Proceedings of the Fifth Symposium on Operating Systems Design and Implementation (OSDI), Boston, MA, USA, 9–11 December 2002. [Google Scholar]
- Ganeriwal, S.; Kumar, R.; Srivastava, M.B. Timing-Sync Protocol for Sensor Networks. In Proceedings of the ACM SenSys’03, Los Angeles, CA, USA, 5–7 November 2003. [Google Scholar]
- Maróti, M.; Kusy, B.; Simon, G.; Lédeczi, A. The Flooding Time Synchronization Protocol. In Proceedings of the ACM SenSys’04, Proceedings Second International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 3–5 November 2004; pp. 39–49. [Google Scholar]
- Ranganathan, P.; Nygard, K. Time Synchronization in Wireless Sensor Networks: A Survey. Int. J. UbiCOmp 2010, 1, 92–102. [Google Scholar] [CrossRef]
- Shanti, C.; Sahoo, A. DGRAM: A Delay Guaranteed Routing and MAC Protocol for Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2010, 9, 1407–1423. [Google Scholar] [CrossRef]
- European Telecommunications Standards Institute; ETSI Secretariat. Digital Cellular Telecommunications System (Phase 2+); Physical Layer on the Radio Path; General Description (GSM 05.01 Version 5.4.0); GSM Technical Specification; ETSI: Sophia Antipolis, France, 1998. [Google Scholar]
- Redl, S.M.; Weber, M.K.; Oliphant, M.W. An Introduction to GSM; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Wu, Y.-C.; Chaudhari, Q.; Erchin Serpedin, E. Clock Synchronization of Wireless Sensor Networks. IEEE Signal Process. Mag. 2011, 1, 124–138. [Google Scholar] [CrossRef]
- Casares-Giner, V.; Sempere-Paya, V.; Todoli-Ferrandis, D. Framed ALOHA Protocol with FIFO-Blocking and LIFO-Push out Discipline. Netw. Protoc. Algorithms 2014, 6, 82–102. [Google Scholar] [CrossRef]
- Tello, L.; Pla, V.; Leyva-Mayorga, I.; Martinez-Bauset, L.; Casares-Giner, V.; Guijarro, L. Efficient Random Access Channel Evaluation and Load Estimation in LTE-A With Massive MTC. IEEE Trans. Veh. Technol. 2019, 68, 1998–2002. [Google Scholar] [CrossRef]
- Adan, I.; van Leeuwaarden, J.; Winands, E. On the application of Rouché’s theorem in queueing theory. Oper. Res. Lett. 2006, 34, 355–360. [Google Scholar] [CrossRef]
- Casares-Giner, V.; Martínez-Bauset, J.; Portillo, C. Performance Evaluation of Framed Slotted ALOHA with Reservation Packets and Succesive Interference Cancelation for M2M Networks. Comput. Networks. 2019, 155, 15–30. [Google Scholar] [CrossRef]
- Bhardwaj, M.; Garnett, T.; Chandrakasan, A.P. Upper bounds on the lifetime of sensor networks. In Proceedings of the ICC 2001, IEEE International Conference on Communications. Conference Record, Helsinki, Finland, 11–14 June 2001; Volume 3, pp. 785–790. [Google Scholar] [CrossRef]
- Wu, D.; He, J.; Wang, H.; Wang, C.; Wang, R. A Hierarchical Packet Forwarding Mechanism for Energy Harvesting Wireless Sensor Networks. IEEE Commun. Mag. 2015, 8, 92–98. [Google Scholar] [CrossRef]








| Sector | Condition | Axes | Condition |
|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | ||||||||||
| 1 | 1 | 3 | |||||||||
| 2 | 4 | 7 | 12 | ||||||||
| 3 | 9 | 13 | 19 | 27 | |||||||
| 4 | 16 | 21 | 28 | 37 | 48 | ||||||
| 5 | 25 | 31 | 39 | 49 | 61 | 75 | |||||
| 6 | 36 | 43 | 52 | 63 | 76 | 91 | 108 | ||||
| 7 | 49 | 57 | 67 | 79 | 93 | 109 | 127 | 147 | |||
| 8 | 64 | 73 | 84 | 97 | 112 | 129 | 148 | 169 | 192 | ||
| 9 | 81 | 91 | 103 | 117 | 133 | 151 | 171 | 193 | 217 | 243 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ |
| 1 | 1 | 3 | |
| 2 | 0 | 4 | |
| 2 | 1 | 7 | |
| 2 | 2 | 12 | |
| 3 | 0 | 9 | |
| 3 | 1 | 13 | |
| 3 | 2 | 19 | |
| 3 | 3 | 27 | |
| 4 | 0 | 16 | |
| 4 | 1 | 21 | |
| 4 | 2 | 28 | |
| 4 | 3 | 37 | |
| 4 | 4 | 48 | |
| 5 | 0 | 25 | |
| 5 | 1 | 31 | |
| 5 | 2 | 39 | |
| 5 | 3 | 49 | |
| 5 | 4 | 61 | |
| 5 | 5 | 75 | |
| 6 | 0 | 36 | |
| 6 | 1 | 43 | |
| 6 | 2 | 52 | |
| 6 | 3 | 63 | |
| 6 | 4 | 76 | |
| 6 | 5 | 91 | |
| 6 | 6 | 108 | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| -- | -- | 9 | |
| -- | -- | 6 | |
| -- | -- | 5 | |
| -- | -- | 9 | |
| -- | -- | 8 | |
| -- | -- | 3 | |
| -- | -- | 2 | |
| -- | -- | 6 | |
| -- | -- | 5 | |
| -- | -- | 10 | |
| -- | -- | 7 | |
| -- | -- | 6 | |
| -- | -- | 4 | |
| -- | -- | 3 |
| Ring k | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 (1) | 1 (6) | 2 (12) | 3 (18) | 4 (24) | 5 (30) | 6 (36) | 7 (42) | ... | |
| 0 | 1 (sink) | ||||||||
| 1 | 1 + 6 | 1 | |||||||
| 2 | 1 + 18 | 3 | 1 | ||||||
| 3 | 1 + 36 | 6 | 1 | ||||||
| 4 | 1 + 60 | 10 | 1 | ||||||
| 5 | 1 + 90 | 15 | 1 | ||||||
| 6 | 1 + 126 | 21 | 1 | ||||||
| 7 | 1 + 168 | 28 | 1 | ||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ |
| RING | CH | ||
|---|---|---|---|
| 4 | -- | -- | |
| -- | -- | ||
| -- | -- | ||
| -- | -- | ||
| -- | -- | ||
| 3 | -- | -- | |
| -- | -- | ||
| -- | -- | ||
| -- | -- | ||
| 2 | -- | -- | |
| -- | -- | ||
| -- | -- | ||
| 1 | -- | -- | |
| -- | -- |
| 0 | 363 | 364 | (63, 0) | 63 | - | - | - | - | - |
| 1 | 51 | 364 | (10, 3) | 51 | 0.8254 | - | - | - | - |
| 2 | 18 | 361 | (3, 1) | 16 | 0.8552 | 0.2850 | - | - | - |
| 3 | 9 | 370 | (2, 1) | 13 | 0.6967 | 0.2903 | 0.1161 | - | - |
| 4 | 5 | 366 | (2, 1) | 13 | 0.6456 | 0.2905 | 0.1506 | 0.0645 | - |
| 5 | 3 | 364 | (2, 1) | 13 | 0.5813 | 0.2712 | 0.1550 | 0.0871 | 0.0387 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casares-Giner, V.; Inés Navas, T.; Smith Flórez, D.; Vargas Hernández, T.R. End to End Delay and Energy Consumption in a Two Tier Cluster Hierarchical Wireless Sensor Networks. Information 2019, 10, 135. https://doi.org/10.3390/info10040135
Casares-Giner V, Inés Navas T, Smith Flórez D, Vargas Hernández TR. End to End Delay and Energy Consumption in a Two Tier Cluster Hierarchical Wireless Sensor Networks. Information. 2019; 10(4):135. https://doi.org/10.3390/info10040135
Chicago/Turabian StyleCasares-Giner, Vicente, Tatiana Inés Navas, Dolly Smith Flórez, and Tito Raúl Vargas Hernández. 2019. "End to End Delay and Energy Consumption in a Two Tier Cluster Hierarchical Wireless Sensor Networks" Information 10, no. 4: 135. https://doi.org/10.3390/info10040135
APA StyleCasares-Giner, V., Inés Navas, T., Smith Flórez, D., & Vargas Hernández, T. R. (2019). End to End Delay and Energy Consumption in a Two Tier Cluster Hierarchical Wireless Sensor Networks. Information, 10(4), 135. https://doi.org/10.3390/info10040135





