A Method of Ultra-Large-Scale Matrix Inversion Using Block Recursion

Abstract

Ultra-large-scale matrix inversion has been applied as the fundamental operation of numerous domains, owing to the growth of big data and matrix applications. Using cryptography as an example, the solution of ultra-large-scale linear equations over finite fields is important in many cryptanalysis schemes. However, inverting matrices of extremely high order, such as in millions, is challenging; nonetheless, the need has become increasingly urgent. Hence, we propose a parallel distributed block recursive computing method that can process matrices at a significantly increased scale, based on Strassen’s method; furthermore, we describe the related well-designed algorithm herein. Additionally, the experimental results based on comparison show the efficiency and the superiority of our method. Using our method, up to 140,000 dimensions can be processed in a supercomputing center.

1. Introduction

With the growth of computer applications, matrix inversion has become a basic operation that is widely used in various industries. For example, online video service providers (such as YouTube) use various types of the matrices to store user and item information [1]; in satellite navigation and positioning, matrix inversion is used to solve positioning equations [2]; triangular matrix inversion is used in the fast algorithm of radar pulse compression (based on reiterative minimum mean-square error); and, matrices are also used in multivariate public key encryption [3], etc. Next, the application of matrix in cryptography is described in detail. In some of existing cryptographic algorithms, a matrix is used to directly encrypt a message. When the process is duplicated, it is found that the encrypted message can be obtained by solving the inversion of the encryption matrix. Additionally, some algorithms can be transfromed into multiple linear equations, represented as $Ax=b$, where A is an $n\times n$ matrix; x and b are $n\times 1$ vectors. Subsequently, the equation can be solved by computing the inverse of the matrix A, denoted by $A^{-1}$, in order to obtain $x=A^{-1}\times b$. For general matrices, some common inversion algorithms exist such as Gaussian elimination, Gauss-Jordan elimination [4], Cholesky decomposition [5], QR decomposition [6], LU decomposition [6], and so on. Meanwhile, other algorithms focus on special types of matrices, such as the positive definite matrix [7], tridiagonal matrix [8], adjacent pentadiagonal matric [9], and triangular matrix [10]. However, these algorithms for general matrices are computationally intensive and they require a cubic number of operations. Hence, many studies have been performed to reduce the complexity. In 1969, Strassen [11] presented a method that reduces the complexity from $O\left(n^3\right)$ to $O\left(n^{2.808}\right)$, where n denotes the order of the matrix. In 1978, Pan et al. [12] proved that the complexity can be less than $O\left(n^{2.796}\right)$. Coppersmith and Winograd [13] were the first to reduce the index of n less than $2.5$: the obtained time complexity was $O\left(n^{2.496}\right)$. Despite various optimizations, the index of n had never been less than 2. However, with increasing matrix dimensions and the exponential growth of data volume, it is impossible to solve the problem that is mentioned above by using only these methods proposed previously and their optimizations. With the rapid development of parallel computing, the problem of designing an efficient algorithm for large scale distributed matrix inversion has garnered the significant attention of researchers.

Message Passing Interface (MPI) is a programming model that can effectively support parallel matrix inversion. Apart from MPI, plenty of new distributed computing technologies have emerged as platforms for large data processing tasks in recent years; the most popular ones are MapReduce and Spark, which exhibit outstanding scalability and fault-tolerance capabilitys. Xiang et al. [14] proposed a scalable matrix inversion method that was implemented on MapReduce and discussed some optimizations. Liu et al. 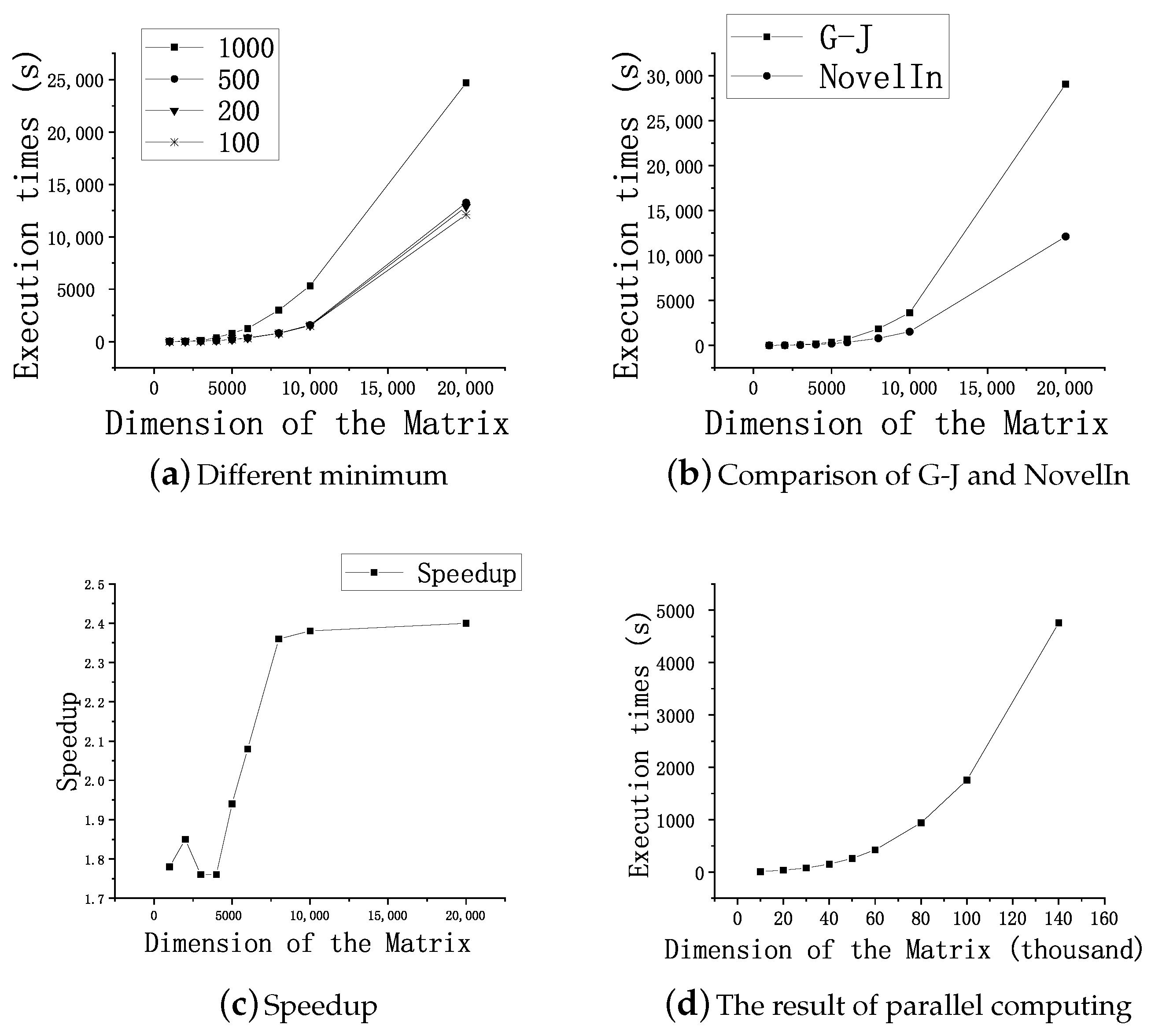[15] described an inversion algorithm using LU decomposition on Spark. In this paper, we propose a novel distributed matrix inversion algorithm for a large-scale matrix that is based on Strassen’s original serial inversion scheme and implement it on the MPI. Essentially, it is a block-recursive method to decompose the original matrix into a series of small ones that can be processed on a single server. We present a detailed derivation and the detailed steps of the algorithm and then show the experimental results on the MPI. However, it is noteworthy that the primary aim of this paper is not to compare the performance of the MPI, Spark, and MapReduce. In summary:

• We propose and implement a large-scale matrix block-recursive inversion algorithm based on the Strassen’s method while using distributed and parallel technologies.
• We describe the theorem used in our algorithm; furthermore, we prove the theorem and describe the algorithm steps.
• Through numerous experiments, we prove that the proposed method is superior to LU decomposition and Gauss-Jordan elimination under the same conditions.

Note that the all operations for solving matrix inversion is based on finite fields and only for a square matrix.

The remainder of this paper is structured, as follows. Section 2 provides a literature review. Our method is presented in Section 3 and the experimental evaluation results in Section 4. In Section 5, we conclude the paper and discuss future works.

2. Related Work

Owing to the numerous existed methods for matrix inversion, we focus on only two representational methods: Gauss-Jordan Elimination and LU decomposition. In the rest of this section, we introduce the key ideas of the two methods briefly and analyze their deficiency in solving the inversion of high-order matrix as compared with our presented methods. Some of the other methods are applied to special matrices, e.g., SVD decomposition is used for the pseudo inversion of non-square matrix, and Cholesky decomposition is used in symmetric positive definite linear equations. Additionally, we omit some other methods that are substantially similar to the two most representative methods mentioned above. Furthermore, we selected the two methods, because they are the most frequently used in matrix inversion parallel computing of the existing papers.

At the beginning of the section, we give the basic definition of an inverse matrix:

Definition 1.

Given an n-th order square matrix A, if an n-th order square matrix B exists satisfying $AB=BA=I_n$, where $I_n$ is the n-th indentity matrix, the matrix A is invertible, and its inverse matrix is B, written as $A^{-1}$.

2.1. Gauss-Jordan Elimination

Gauss-Jordan is an efficient, classic, and well-known method for solving low order matrix inversion. It has two common forms that are based on either row transformation or column transformation. The row-based version is more widely used in daily life. As the two methods have the same principle, we will only briefly introduce the row-based one here.

In the row transformation method, the given $n\times n$ matrix A is connected with I, which is an identity matrix having the same order as A, to obtain an augmented matrix W, denoted as $w=\left[A\right|I]$, whose dimension becomes $n\times 2n$. Then, we apply row transformation operations on the matrix W to convert W from $\left[A\right|I]$ to $\left[I\right|B]$, and the matrix B is equal to $A^{-1}$. The proof is shown below. As the operations performed on the matrix W contain only the row transformations, the entire process can be viewed as multiplying W by an invertible matrix P to satisfy $PW=P\left[A\right|I]=[PA\left|P\right]=\left[I\right|B]$. We can obtain $P=B$ and $PA=I$ and infer that $BA=I$. Therefore, the matrix B is equal to $A^{-1}$. The process can be divided into the following four steps:

Step 1: transform the left part of the matrix W into an upper triangular matrix by applying row transformations from the top to the bottom. The specific steps are as follows:

(1)

Multiply the first row by a constant, such that $a_{11}$ becomes 1 (initially, if this element is zero, add any other row whose first element is not zero to this row).

(2)

Subtract the first row multiplied by a constant from the second row such that $a_{21}$ become zero. Perform the same operation for the remaining rows, written as $r_i-r_1\times j$.

(3)

Repeat steps (1)–(2) for each column sequentially to transform the left half into an upper triangular matrix.

Step 2: transform the left part of the matrix W into a diagonal triangular matrix by performing row transformations from the bottom to the top. This is similar to step 1.

Step 3: multiply each line by a coefficient to transform the left part of the augmented matrix into an identity matrix.

Step 4: the right part of the augmented matrix W is the inverse of matrix A.

Apparently, the time complexity of the program is $O\left(n^3\right)$ without any parallelization. For the Gauss–Jordan, the operations on rows are sequential, and the parallelization of this method is not highly effective.

2.2. LU Decomposition

LU decomposition can be viewed as another form of Gauss elimination in essence. Multiple types of decomposition have been proposed, e.g., PLE decomposition, PLS decomposition, CUP decomposition, LQUP decomposition, and LUP decomposition. Among them, PLE decomposition breaks the initial matrix A into the product of permutation matrix P, unit lower triangular matrix L (i.e., the lower triangular matrix whose diagonal elements are all 1) and row elementary transformation matrix E. Meanwhile, CUP decomposition resolves A into the product of column elementary transformation matrix C, unit lower triangular matrix U, and permutation matrix P.

These forms have been shown to be equivalent: it is sufficient to use a permutation matrix to obtain different decomposition forms that are based on LU decomposition. Their mutual conversion required no domain operation; only the permutation operation is involved, which can be scaled to matrix multiplication. Hence, we only discuss the most direct LU decomposition. LU decomposition essentially transforms the original matrix A into an upper triangular matrix through elementary row transformation, and the transformation matrix is a unit lower triangular matrix. Inverting the two matrices respectively and multiplying their inverses to get the inverse of A is known as the Doolittle algorithm. In addition, the Crout algorithm only replaces the two decomposed matrices with a lower triangular matrix and unit upper triangular matrix, which is similar to the Doolittle algorithm in essence. We only present the Doolittle as an example. Note that it has been proven in linear algebra that LU decomposition is existent and unique provided that the square matrix is non-singular.

The critical step in LU decomposition is to obtain the ‘L’ and ‘U’. Subsequently, we use Gauss-Jordan (or other methods) to get the inversion of ‘L’ and ‘U’. The main purpose of decomposition is to reduce the computational cost of elimination and ease the storage within computer programs. The decomposed forms are shown below:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]\hfill \\ \hfill =& \left[\begin{array}{cc}{l}_{11}& \\ l_{21}& l_{22}\\ ⋮& ⋮& \ddots \\ l_{n1}& l_{n2}& \cdots & l_{nn}\end{array}\right]\left[\begin{array}{cccc}{u}_{11}& u_{12}& \cdots & u_{1n}\\ & u_{22}& \cdots & u_{2n}\\ & & \ddots & ⋮\\ & & & u_{nn}\end{array}\right]\hfill \end{array}$$

(1)

As shown in Equation (1), we can deduce the following formulas according to the rules of matrix multiplication and the equality of matrices on both sides of the equations:

$$\left\{\begin{array}{ccc}\hfill & u_{1j}=a_{1j}\hfill & \hfill j=1,2,3,\dots ,n\\ & l_{i1}=a_{i1}/u_{11}\hfill & \hfill i=2,3,\dots ,n\\ & u_{ij}=a_{ij}-\sum _{k=1}^{i-1}{l}_{ik}{u}_{kj}\hfill & \hfill j=i,i+1,\dots ,n;i=2,3,\dots ,n\\ & l_{ij}=(a_{ij}-\sum _{k=1}^{j-1}{l}_{ik}{u}_{kj})/u_{jj}\hfill & \hfill i=j+1,j+2,\dots ,n;j=2,3,\dots ,n\end{array}\right.$$

Matrix L and U can be calculated by the formula above. Subsequently, we calculate the inverse of L and U, respectively, and multiply them to get the inverse of original matrix. The formula to calculation every element of L and U has been provided, and it is obvious that the time complexity is $O\left(n^3\right)$. The worst complexity of multiplying matrices is still $O\left(n^3\right)$. In conclusion, the complexity of LU decomposition is $O\left(n^3\right)$ without parallelization. However, in the actual implementation of LU decomposition, the row-permuted matrix $PA$ is decomposed instead of the original matrix A, when considering that the LU decomposition of the original matrix may fail to materialize in some cases. The permutation matrix P can render the factorization more stable. Therefore, the inverse matrix $A^{-1}$ can be obtained by calculating $U^{-1}{L}^{-1}P$. Obviously, the complexity has not changed.

It is impractical to calculate the inversion by the formula above directly when the dimension of the matrix is extremely large. Liu et al. [13] presented a method that is based on LU decomposition in detail and we will only mention their formula for inversion. Their method first used the following equation:

$$\left(\begin{array}{cc}{P}_1& O\\ o& P_2\end{array}\right)\left(\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right)=\left(\begin{array}{cc}{L}_1& O\\ L_2& L_3\end{array}\right)\left(\begin{array}{cc}{U}_1& U_2\\ O& U_3\end{array}\right)$$

Here, $\left(\begin{array}{cc}{P}_1& O\\ o& P_2\end{array}\right)$ is the permutation matrix P mentioned previously that renders the factorization to be more stable. Subsequently, performing multiplication for the equation above, the result are as follows:

$$\left(\begin{array}{cc}{P}_1{M}_1& P_1{M}_2\\ P_2{M}_3& P_2{M}_4\end{array}\right)=\left(\begin{array}{cc}{L}_1{U}_1& L_1{U}_2\\ L_2{U}_1& L_2{U}_2+L_3{U}_3\end{array}\right)$$

The details of the intermediate substitution are not unrolled here, and the final equations are the following:

$$\begin{array}{cc}\hfill L^{-1}& =\left(\begin{array}{cc}{L}_1^{-1}& O\\ -L_3^{-1}{L}_2{L}_1^{-1}& L_3^{-1}\end{array}\right)\hfill \\ \hfill U^{-1}& =\left(\begin{array}{cc}{U}_1^{-1}& -U_1^{-1}{U}_2{U}_3^{-1}\\ O& U_3^{-1}\end{array}\right)\hfill \\ \hfill P& =\left(\begin{array}{cc}{P}_1& O\\ O& P_2\end{array}\right)\hfill \end{array}$$

By comparing the most optimized LU decomposition (Algorithms 5–7 in [13]) with the proposed method, it is clear that in the primary parts the number of basic operation, such as multiplication and inversion, of the two methods has a difference and the cost of LU is larger than the latter.

3. Theoretical Demonstration and Algorithm Design

In this section, we present the detailed theoretical derivation that is required for our proposed method and describe the algorithm. The process can be divided into two parts: matrix completion and block recursive inversion. After partitioning the original matrix, we obtained four submatrices of the same order. Next, we analyze the process, formulate the theorem, and provide the revelant proofs of each part.

3.1. Matrix Completion

For a more general conclusion, we assume that the order of the given square matrix is $2^r\times s$, where r is a natural number and s is the order of the block matrix that can be decomposed on a single server. The original matrix does not always satisfy this criterion, and we must fill the matrix in this case. The completion lemma is as follows:

Lemma 1.

Fill the original matrix H with null matrix O and identity matrix I, whose order is subject to specific circumstances. The form after filling is as follows: $\left[\begin{array}{cc}H& O\\ O& I\end{array}\right]$. Apparently, the revision of filling matrix can be obtained easily:

$${\left(\begin{array}{cc}H& O\\ O& I\end{array}\right)}^{-1}=\left(\begin{array}{cc}{H}^{-1}& O\\ O& I^{-1}\end{array}\right)$$

Subsequently, we obtain the inversion of the original matrix directly.

3.2. Block Inversion Theorem

In this section, we present and prove the theorem for obtaining the inversion of the original matrix by invertible submatrices. We first introduce the following lemmas before proving the inverse theorems.

Lemma 2.

If the square matrices A and D are invertible, then the block matrix $H=\left(\begin{array}{cc}A& O\\ C& D\end{array}\right)$ is invertible and its inverse matrix is

$$H^{-1}={\left(\begin{array}{cc}A& O\\ C& D\end{array}\right)}^{-1}=\left(\begin{array}{cc}{A}^{-1}& O\\ -D^{-1}C{A}^{-1}& D^{-1}\end{array}\right)$$

Proof. 

Firstly, submatrix A is invertible, based on the preconditions; therefore, we have the following equation:

$$\left(\begin{array}{cc}{I}_m& O\\ C{A}^{-1}& I_n\end{array}\right)\left(\begin{array}{cc}A& O\\ C& D\end{array}\right)=\left(\begin{array}{cc}A& O\\ O& D\end{array}\right)$$

Apparently, the matrix $\left(\begin{array}{cc}A& O\\ O& D\end{array}\right)$ has the inversion, which is $\left(\begin{array}{cc}{A}^{-1}& O\\ O& D^{-1}\end{array}\right)$. Multiply both sides of this equation by it, and the following is obtaied:

$$\left(\begin{array}{cc}{A}^{-1}& O\\ O& D^{-1}\end{array}\right)\left(\begin{array}{cc}{I}_m& O\\ C{A}^{-1}& I_n\end{array}\right)\left(\begin{array}{cc}A& O\\ C& D\end{array}\right)=I$$

Based on the equation, H is invertible and its inversion is

$$\begin{array}{cc}\hfill H^{-1}& =\left(\begin{array}{cc}{A}^{-1}& O\\ O& D^{-1}\end{array}\right)\left(\begin{array}{cc}{I}_m& O\\ C{A}^{-1}& I_n\end{array}\right)\hfill \\ & =\left(\begin{array}{cc}{A}^{-1}& O\\ -D^{-1}C{A}^{-1}& D^{-1}\end{array}\right)\hfill \end{array}$$

□

The following theorem can be proved similarly:

Lemma 3.

If the square matrices A and D are invertible, then the block matrix $H=\left(\begin{array}{cc}A& B\\ O& D\end{array}\right)$ is invertible and its inverse matrix is

$$H^{-1}={\left(\begin{array}{cc}A& B\\ O& D\end{array}\right)}^{-1}=\left(\begin{array}{cc}{A}^{-1}& -A^{-1}B{D}^{-1}\\ O& D^{-1}\end{array}\right)$$

Lemma 4.

If the square matrices B and C are invertible, then the block matrix $H=\left(\begin{array}{cc}A& B\\ C& O\end{array}\right)$ is invertible and its inverse matrix is

$$H^{-1}={\left(\begin{array}{cc}A& B\\ C& O\end{array}\right)}^{-1}=\left(\begin{array}{cc}O& C^{-1}\\ B^{-1}& -B^{-1}A{C}^{-1}\end{array}\right)$$

Lemma 5.

If the square matrices B and C are invertible, then the block matrix $H=\left(\begin{array}{cc}O& B\\ C& D\end{array}\right)$ is invertible and its inverse matrix is

$$H^{-1}={\left(\begin{array}{cc}O& B\\ C& D\end{array}\right)}^{-1}=\left(\begin{array}{cc}-C^{-1}D{B}^{-1}& C^{-1}\\ B^{-1}& O\end{array}\right)$$

By the lemmas above, we prove the following theorem:

Theorem 1.

If the block matrix $H=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ and sub-matrix A are invertible, then matrix ${(D-C{A}^{-1}B)}^{-1}$ exists and the inversion of H is:

$$\begin{array}{c}\hfill H^{-1}=\left(\begin{array}{cc}{A}^{-1}+A^{-1}B{(D-C{A}^{-1}B)}^{-1}C{A}^{-1}& -A^{-1}B{(D-C{A}^{-1}B)}^{-1}\\ -{(D-C{A}^{-1}B)}^{-1}C{A}^{-1}& {(D-C{A}^{-1}B)}^{-1}\end{array}\right)\end{array}$$

Proof. 

We record the inversion of H as $H^{-1}={\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)}^{-1}=\left(\begin{array}{cc}X& Y\\ Z& W\end{array}\right)$. According to the definition of the invertible matrix, $H{H}^{-1}=H^{-1}H=I$. Performing the matrix multiplication results in the following:

$$\begin{array}{cc}\hfill H{H}^{-1}& =\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\left(\begin{array}{cc}X& Y\\ Z& W\end{array}\right)\hfill \\ & =\left(\begin{array}{cc}AX+BZ& AY+BW\\ CX+DZ& CY+DW\end{array}\right)=\left(\begin{array}{cc}{I}_m& O\\ O& I_n\end{array}\right)\hfill \end{array}$$

This results in the following equations:

$$\left\{\begin{array}{ccc}\hfill & AX+BZ=I_m\hfill & \hfill \left(\mathrm{a}\right)\\ \hfill & AY+BW=O\hfill & \hfill \left(\mathrm{b}\right)\\ \hfill & CX+DZ=O\hfill & \hfill \left(\mathrm{c}\right)\\ \hfill & CY+DW=I_n\hfill & \hfill \left(\mathrm{d}\right)\end{array}\right.$$

(2)

Based on Equation (2b), we have

$$Y=-A^{-1}BW$$

(3)

By substituting Equation (3) into Equation (2d), we obtain

$$W={(D-C{A}^{-1}B)}^{-1}$$

(4)

Subsequently, we can obtain Y by substituting Equation (4) into Equation (3):

$$Y=-A^{-1}B{(D-C{A}^{-1}B)}^{-1}$$

(5)

According to Equation (2a), we have

$$X=A^{-1}(I_m-AZ)$$

(6)

By substituting Equation (6) into Equation (2c), we obtain

$$Z=-{(D-C{A}^{-1}B)}^{-1}C{A}^{-1}$$

(7)

Finally, we obtain the Z by substituting Equation (7) into Equation (6):

$$X=A^{-1}+A^{-1}B{(D-C{A}^{-1}B)}^{-1}C{A}^{-1}$$

(8)

To summarize, we obtain the inversion of H, as follows:

$$\begin{array}{c}\hfill H^{-1}=\left(\begin{array}{cc}{A}^{-1}+A^{-1}B{(D-C{A}^{-1}B)}^{-1}C{A}^{-1}& -A^{-1}B{(D-C{A}^{-1}B)}^{-1}\\ -{(D-C{A}^{-1}B)}^{-1}C{A}^{-1}& {(D-C{A}^{-1}B)}^{-1}\end{array}\right)\end{array}$$

□

Similarly, we can prove the following theorems:

Theorem 2.

If the block matrix $H=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ and sub-matrix B are invertible, then matrix ${(C-D{B}^{-1}A)}^{-1}$ exists and the inversion of H is

$$\begin{array}{c}\hfill H^{-1}=\left(\begin{array}{cc}-{(C-D{B}^{-1}A)}^{-1}D{B}^{-1}& {(C-D{B}^{-1}A)}^{-1}\\ B^{-1}+B^{-1}A{(C-D{B}^{-1}A)}^{-1}D{B}^{-1}& -B^{-1}A{(C-D{B}^{-1}A)}^{-1}\end{array}\right)\end{array}$$

Theorem 3.

If the block matrix $H=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ and sub-matrix C are invertible, then matrix ${(B-A{C}^{-1}D)}^{-1}$ exists and the inversion of H is

$$\begin{array}{c}\hfill H^{-1}=\left(\begin{array}{cc}-C^{-1}D{(B-A{C}^{-1}D)}^{-1}& C^{-1}+C^{-1}D{(B-A{C}^{-1}D)}^{-1}A{C}^{-1}\\ {(B-A{C}^{-1}D)}^{-1}& -{(B-A{C}^{-1}D)}^{-1}A{C}^{-1}\end{array}\right)\end{array}$$

Theorem 4.

If the block matrix $H=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ and sub-matrix D are invertible, then matrix ${(A-B{D}^{-1}C)}^{-1}$ exists and the inversion of H is

$$\begin{array}{c}\hfill H^{-1}=\left(\begin{array}{cc}{(A-B{D}^{-1}C)}^{-1}& -{(A-B{D}^{-1}C)}^{-1}B{D}^{-1}\\ -D^{-1}C{(A-B{D}^{-1}C)}^{-1}& D^{-1}+D^{-1}C{(A-B{D}^{-1}C)}^{-1}B{D}^{-1}\end{array}\right)\end{array}$$

3.3. Recursive Algorithm

Algorithm 1 shows the corresponding deterministic algorithm, and the partition of original matrix is presented in the Figure 1. As shown, we stored the partition process as a tree. For a more concise and clear figure, the first and last nodes illustrate the partition results at every layer, and the partition of the other blocks is similar. Although we have only divided it by a certain number of times, the actual number is much higher. Information regarding each node is represented in a three-tuple, written as $(n,i,j)$, where n is the dimension of the matrix contained in the node; i and j are the row and column of the first element of the matrix, respectively. Finally, we attempt to find a path, which is called the inversion chain, where the matrix contained in each node is invertible.

Algorithm 1 The recursion algorithm.

Input: $H\to$ The original matrix; $s\to$ the dimension solved by a single server output: $H^{-1}\to$ the inversion of H step 1: For the given matrix H, determine whether it needs to be filled according to $Lemma1$ and write the augmented matrix as $H^{*}$; step 2: Divide the n-dimensional H or $H^{*}$ obtained in the step 1 into $\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]$; step 3: Repeat the division of step 2 for each sub-block matrix until the dimension of them is less than s; step 4: Find the inversion chain, e.g., $(s,q,k),\cdots ,(m,i,j),\cdots ,$ $(n,0,0)$ step 5: Calculate the inversion of the parent nodes from the leaf $(s,q,k)$ along the path sequentially, finally get the matrix M, i.e., inversion of root $(n,0,0)$; step 6: if the matrix is not filled then             goto step 7;          else             take the first n rows and the first n columns of M to form the             new matrix, which is $H^{-1}$;          end if; step 7: Return $H^{-1}$.

It is noteworthy that the method that we adopted to obtain the inversion of the leaf node was Gauss-Jordan elimination. Theoretically, $2\times n\times (n-1)$ threads exist to reduce the time complexity from $O\left(n^3\right)$ to $O\left(n\right)$ when the program is executed in a supercomputing center. However, the real complexity is slightly more than $O\left(n\right)$ because of some bottlenecks such as memory access. Meanwhile, we use the shared memory of the GPU to reduce excessive access times due to the large matrix order.

To more clearly describe the process, we take a 16-dimensional matrix as an example.

The following matrix instance is a 16-dimensional square matrix H based on $GF\left(2\right)$, denoted as $(16,0,0)$. When the entire process is replicated next, step 1 is skipped, which means no padding is required, in order to obtain a more distinct presentation. The value of s is set to 2. For a more concise process, we use a known inversion chain as an example: divide one of the submatrices each time, although the same operation is required for all submatrices.

First we divide the matrix H into four submatrices, as shown below:

$$\begin{array}{cc}\hfill & A_8=\left(\begin{array}{cccccccc}1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\\ 1& 0& 0& 1& 1& 0& 1& 1\end{array}\right),B_8=\left(\begin{array}{cccccccc}1& 0& 1& 0& 1& 1& 0& 0\\ 1& 0& 1& 0& 1& 1& 1& 1\\ 1& 0& 1& 0& 0& 0& 0& 1\\ 1& 0& 1& 0& 0& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 0& 0& 1& 0& 1& 1& 0& 1\\ 0& 1& 1& 0& 1& 1& 0& 1\\ 0& 0& 1& 1& 1& 1& 0& 1\end{array}\right),\hfill \\ \hfill & C_8=\left(\begin{array}{cccccccc}1& 0& 0& 1& 1& 0& 1& 0\\ 1& 0& 0& 1& 1& 0& 0& 1\\ 1& 0& 0& 1& 1& 1& 1& 1\\ 1& 0& 0& 1& 0& 1& 1& 1\\ 1& 0& 0& 0& 1& 0& 1& 1\\ 1& 0& 1& 1& 1& 0& 1& 1\\ 1& 1& 0& 1& 1& 0& 1& 1\\ 0& 0& 0& 1& 1& 0& 1& 1\end{array}\right),D_8=\left(\begin{array}{cccccccc}1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\\ 1& 0& 1& 0& 1& 1& 0& 1\end{array}\right)\hfill \end{array}$$

The submatrices above are written as $(8,0,0),(8,0,8),(8,8,0)$ and $(8,8,8)$, individually. After continuing to divide matrix $B_8$, four submatries can be obtained, i.e., $(4,0,8)$, $(4,0,12),(4,4,8),(4,4,12)$. In the subsequent partition, a subscript denotes the dimension of the matrix to distinguish the same mark, i.e., $A,B,C,D$.

$$\begin{array}{c}\hfill A_4=\left(\begin{array}{cccc}1& 0& 1& 0\\ 1& 0& 1& 0\\ 1& 0& 1& 0\\ 1& 0& 1& 0\end{array}\right),B_4=\left(\begin{array}{cccc}1& 1& 0& 0\\ 1& 1& 1& 1\\ 1& 0& 0& 1\\ 0& 1& 0& 1\end{array}\right)\\ \hfill C_4=\left(\begin{array}{cccc}1& 0& 1& 0\\ 0& 0& 1& 0\\ 0& 1& 1& 0\\ 0& 0& 1& 1\end{array}\right),D_4=\left(\begin{array}{cccc}1& 1& 0& 1\\ 1& 1& 0& 1\\ 1& 1& 0& 1\\ 1& 1& 0& 1\end{array}\right)\end{array}$$

Through the last division, the four matrices that we obtained are recorded as $(2,4,8),(2,4,10),(2,6,8),(2,6,10)$.

$$\begin{array}{c}\hfill A_2=\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right),B_2=\left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right),C_2=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right),D_2=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)\end{array}$$

The matrix satisfies the condition to be computed on a single server. Furthermore, matrix $D_2=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)$, also written as $(2,6,10)$, is invertible. It can be inferred that, after all the divisions are completed, the number of 2-dimensional matrix, whose probability of irreversibility is $\frac{5}{8}$, is a total of 64. Therefore, it is almost impossible that all of them are irreversible simultaneously. To simplify our description, the two-dimensial matrix $D_2$ obtained at the final step is invertible. After calculating the inversion of intermediate nodes sequentially, we finally get a chain, where the matrix on each node is invertible, denoted as $D_2:(2,6,10)⟶C_4:(4,4,8)⟶B_8:(8,0,8)⟶H:(16,0,0)$, which are highlighted in the follow matrix. Along the chain, the inversion of H can be deduced according to the theorems of the previous section. The final inversion is omitted here.

4. Experimental Evaluation

We performed experiments on personal computers in order to evaluate the performance of the proposed algorithm (later written as NovelIn) and compared it with the Gauss-Jordan Elimination (later written as G-J). In this section, except the comparison with the G-J, the performance about applying the algorithm to different matrix sizes is also presented. Finally, we present the results of executing the NovelIn on GPU clusters.

4.1. Experimental Environment

Firstly, we implement G-J and NovelIn on the personal computer, which has a 2.3 GHz Intel CPU with four physical cores and NVIDIA GTX960M. On the personal computer, we measure the runtime for solving the general matrix, whose order is not large than 20,000, to compare the performance of G-J and NovelIn. Owing to the limitations of the personal computer, the operations with high order matrices mentioned before were performed on a parallel computing platform, namely GPU clusters that were composed of servers that are deployed in a data center with well designed architecture. Each server has 128 GB RAM and two 2.4 GHz Inter Xeon CPUs with 20 physical cores.

In order to investigate the performance of the algorithms, we generated different matrices of different orders, as shown in

Table 1. Order of matrices.

Matrix	Order (PC)	Order (GPUs)
M1	1000	10,000
M2	2000	20,000
M3	3000	30,000
M4	4000	40,000
M5	5000	50,000
M6	6000	60,000
M7	7000	70,000
M8	8000	80,000
M9	10,000	100,000
M10	20,000	140,000

.

4.2. Comparison of Performance

In consideration of the actual situation, we evaluate the performance of the two methods, i.e., G-J and NovelIn, on $GF\left(2^8\right),GF\left(2^{16}\right)$ and $GF\left(2^{32}\right)$. For $GF\left(2^8\right),GF\left(2^{16}\right)$, which contain fewer elements, its matrix elements are inversed by looking up the tables, which consist of a positive table, storing the polynomial value of the element, and a negative table, storing the opposite. It is obvious that the memory that tables required is 512 B and 64 KB for $GF\left(2^8\right)$ and $GF\left(2^{16}\right)$ individually. For $GF\left(2^{32}\right)$, the memory required is enormous; therefore, we take the algorithm of exponentiating by squaring in order to obtain the inversion of each element, and its time complexity is $O\left(n^2\right)$. The specifical experimental data on the different finite fields are shown in the following tables.

Table 2. The results on $GF\left(2^8\right)$.

		Method	G-J (4 Threads)	G-J (8 Threads)	NovelIn (1000)	NovelIn (500)	NovelIn (200)	NovelIn (100)	Speedup
	Times (s)
Dimension
1000			9	3.2	10	4.6	2.2	1.8	1.78
2000			52	24	30	17	14	13	1.85
3000			192	74	98	48	46	42	1.76
4000			745	174	375	101	101	99	1.76
5000			990	374	810	200	196	193	1.94
6000			1842	692	1253	358	337	332	2.08
8000			9621	1839	3000	810	782	780	2.36
10,000			22,100	3625	5320	1580	1530	1526	2.38
20,000			29,090.4	24,700	13,521	12,862	12,121	2.40

presents the data used on $GF\left(2^8\right)$.

Most of our experiments are based on $GF\left(2^8\right)$, when considering that $GF\left(2^8\right)$ has the least number of elements, as shown in Table 2. For the G-J, we set the recursive threshold, namely the order solved by personal computer, to 100. We present the comparison in Figure 2 to show the effects of number of threads on runtime; we discovered that it is not as simple as cutting it in half when the number of threads increases from four to eight. In the case of four threads, we did not provide the running time of the 20,000 dimensional matrix because it is extremely large. Hence, we then set the number of threads to eight. The number followed by the word “NovelIn” is the corresponding recursive threshold when using NovelIn.

For the NovelIn, we set four recursive thresholds and measured their runtimes to obtain the best one. The result is presented in Figure 3a. It is not difficult to find that, with the decrease of recursive threshold, the runtime gap of the process, which deals with the same order matrix, becomes gradually unclear. Therefore, in the experiments based on the $GF\left(2^{16}\right)$ and $GF\left(2^{32}\right)$, the recursive threshold is set to 100 directly. Figure 3b shows that the runtime of NovelIn is superior than that of the other, and the gap becomes wider with a higher dimension of the matrix when the experimental environment remains the same. To reflect the advantage more directly, the speedup—the time required by G-J divided by the time required by NovelIn—is shown in Figure 3c. Comparing the performance of the two methods, it is evident that the performance of NovelIn is more superior. Next, we execute the algorithm in a supercomputing center.

Table 3. The results on the supercomputing center.

		Finite Field	$\mathit{GF}\left(2^8\right)$	$\mathit{GF}\left(2^{16}\right)$	$\mathit{GF}\left(2^{32}\right)$
	Times (s)
Dimension
10,000			9	20	20
20,000			35	94	94
30,000			77	273	273
40,000			152	545	545
50,000			260	1066	1066
60,000			424	1870	1870
80,000			940	4058	4058
100,000			1754	7898	7898
140,000			4757

shows the relative data based on all the finite fields. Given the capability of the supercomputing center, we set the recursive threshold to 2000. The results from the supercomputing center are presented in Figure 3d, and its effect is remarkable. For the 140,000 dimensional matrix, NovelIn only requires 4700 s in order to obtain its inversion.

We mentioned that the recursive threshold is set to 100 directly in the experiments based on $GF\left(2^{16}\right)$ and $GF\left(2^{32}\right)$; additionally, the relevant experimental results are listed in

Table 4. The results on $GF\left(2^{16}\right)$ and $GF\left(2^{32}\right)$.

		Finite Field	G-J ($\mathit{GF}\left(2^{16}\right)$)	NovelIn ($\mathit{GF}\left(2^{16}\right)$)	Speedup ($\mathit{GF}\left(2^{16}\right)$)	G-J ($\mathit{GF}\left(2^{32}\right)$)	NovelIn ($\mathit{GF}\left(2^{32}\right)$)	Speedup ($\mathit{GF}\left(2^{32}\right)$)
	Times (s)
Dimension
1000			3.9	1.8	2.17	3.9	85	0.05
2000			32	13	2.46	32	328	0.10
3000			116	40	2.90	116	40	2.90
4000			310	94	3.30	310	1809	0.17
5000			583	181	3.22	583	3592	0.16
6000			1048	310	3.38	1048	310	3.38
8000			2601	731	3.56	2601	12,908	0.20
10,000			4910	1426	3.44	4910	25452	0.19
12,000			8827	2452	3.60	8827	2452	3.60
20,000			46,082	11,326	4.07	46,082	11,326	4.07

. The results are presented in Figure 4 and Figure 5, respectively. According to Figure 4a, it is obvious that NovelIn performed better than the other. By contrast, Figure 5a shows an interesting result, in that the performance of NovelIn is inferior to that of the G-J when the matrix order is not large enough on the $GF\left(2^{32}\right)$. Additionally, we depict the change in the speedup with the growth of the matrix order in the Figure 4b. As expected, the speedup shows an upward trend in general, which resembles the change on $GF\left(2^8\right)$. Otherwise, Figure 4c and Figure 5b show the time of applying NovelIn to a real high order matrix on the supercomputing center, where the specific data are shown in Table 3. The performance and scalability of NovleIn are apparent.

5. Conclusions

In this paper, we have focused on the problem of large-scale matrix inversion, which has become increasingly fundamental, owing to the constant growth of the data in various fields. We presented an efficient inversion algorithm for large-scale matrices and its implementation. The key idea is to breakdown the large-scale matrices into a set of sub-blocks and then calculate the inversion by the proposed method. Our experimental evaluation demonstrated that the excellent performance of our method. Specifically, it performed better when executing the program on the supercomputing center. This algorithm, which is aimed at large-scale matrix inversion, may render some existing encryption algorithms no longer secure, such as an algebraic attack. Because the essence of an algebraic attack is matrix inversion, the method that is proposed in this paper can make the algorithms that rely solely on ultra-large-scale matrix to resist algebraic attacks no longer secure.

The analysis of evaluation results on clusters with varied dimensions demonstrated the good scalability of our algorithm. For the future work, we will attempt to utilize multi-GPU collaborative computing, such that matrices can be distributed to different GPUs, in order to further extend the practicability of this algorithm for larger matrices.