A Real-World-Oriented Multi-Task Allocation Approach Based on Multi-Agent Reinforcement Learning in Mobile Crowd Sensing
Abstract
:1. Introduction
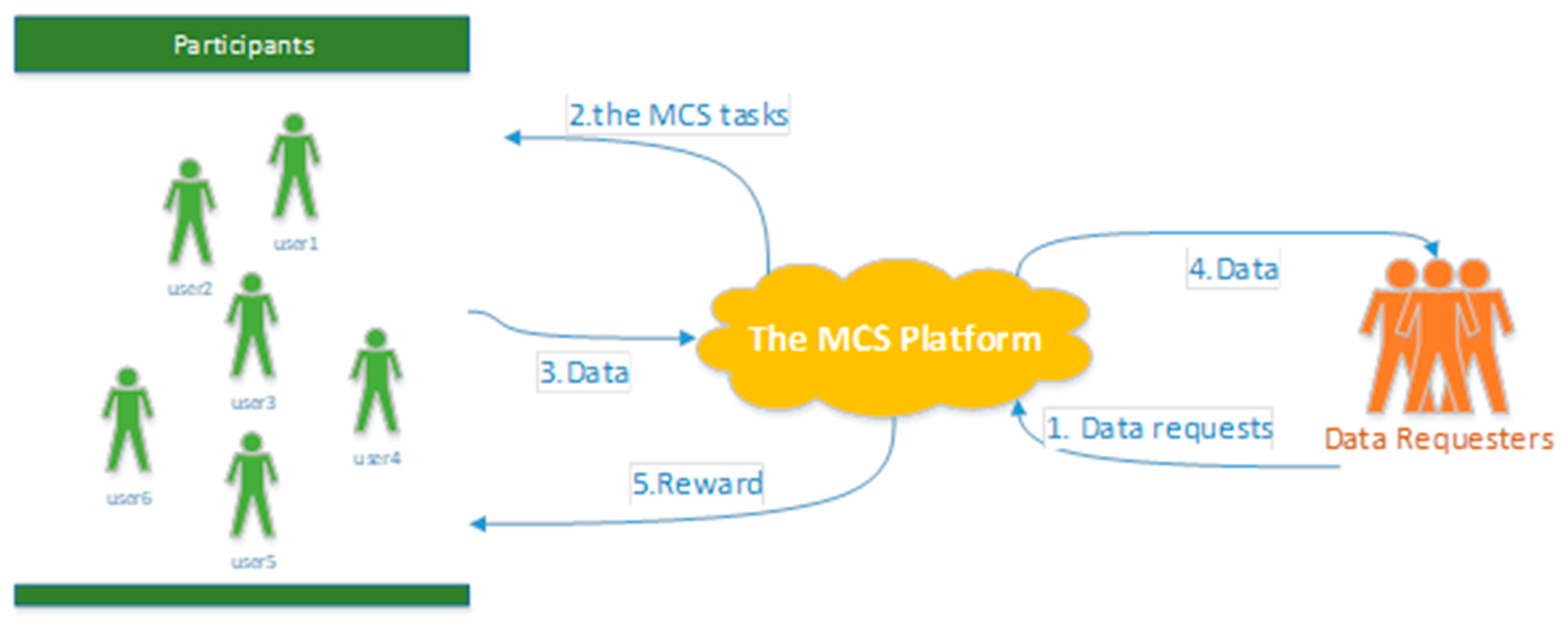
1.1. Molile Crowd Sensing
- 1)
- The data requester sends a request to the platform. The data request will be designed by the MCS platform as a corresponding mobile crowd sensing task;
- 2)
- Based on the real-time information of users and tasks, the platform adopts a certain method to achieve task allocation;
- 3)
- Participants move to the target area to perform MCS tasks and upload data to the platform;
- 4)
- The platform receives and processes the data which are uploaded by participants. In addition, the platform pays participants a certain amount of rewards.
1.2. Task Allocation in the MCS
- 1)
- Multi-task real-time concurrency. In a typical MCS architecture, there is a centralized platform to publish MCS tasks and collect sensing data. Data requests come from different objects, such as government, individual user, scientific research department. Therefore, in a certain period of time, an MCS platform will encounter multi-task real-time concurrency. (Considering the above situation, we design an optimal path for each participant to accomplish multiple tasks, which minimizes the total sensing time while optimizing the quality of MCS tasks);
- 2)
- The heterogeneity of participants. Above all, the participants vary in mobility by taking different vehicles. In addition, the participants vary in ability to complete MCS tasks due to the device power, device capacity, storage space, etc. In other words, the number of tasks that each participant can actually perform is different, and the sensing time cost is determined by the distance and the speed, which greatly increases the difficulty of multi-task allocation;
- 3)
- The heterogeneity of tasks. The data requesters are different, and include governments, enterprises, and individual users. Therefore, the tasks vary in priority and importance weight. For example, the real-time perception of accidents requested by the government is more important than the user’s perceived task. On the other hand, MSC tasks vary in the number of required participants and the target location;
- 4)
- Poor participant resources. Since the target area of the MCS task is uncertain, there may not be enough participant resources in the area of low population density. In the above case, all tasks are not guaranteed to be performed. In addition, under constraints of cost, the performed tasks cannot be completely accomplished. How to optimize the efficiency and quality of the tasks in the case of poor participant resource is a very challenging problem;
- 5)
- Accident and emergency. There are uncertain factors in the execution of the MCS tasks. In particular, two typical accidents are studied: (1) participant cannot reach the designated task area according to the planned path due to traffic jam; (2) participant quits halfway due to equipment failure, network paralysis, dishonest behavior, etc. The above accidents have an adverse effect on the completion of tasks and reduce the overall efficiency of the MCS platform.
1.3. Reinforcement Learning
1.4. Contributions in This Work
2. Problem Model
2.1. Problem Formalization
2.2. Problem Analysis
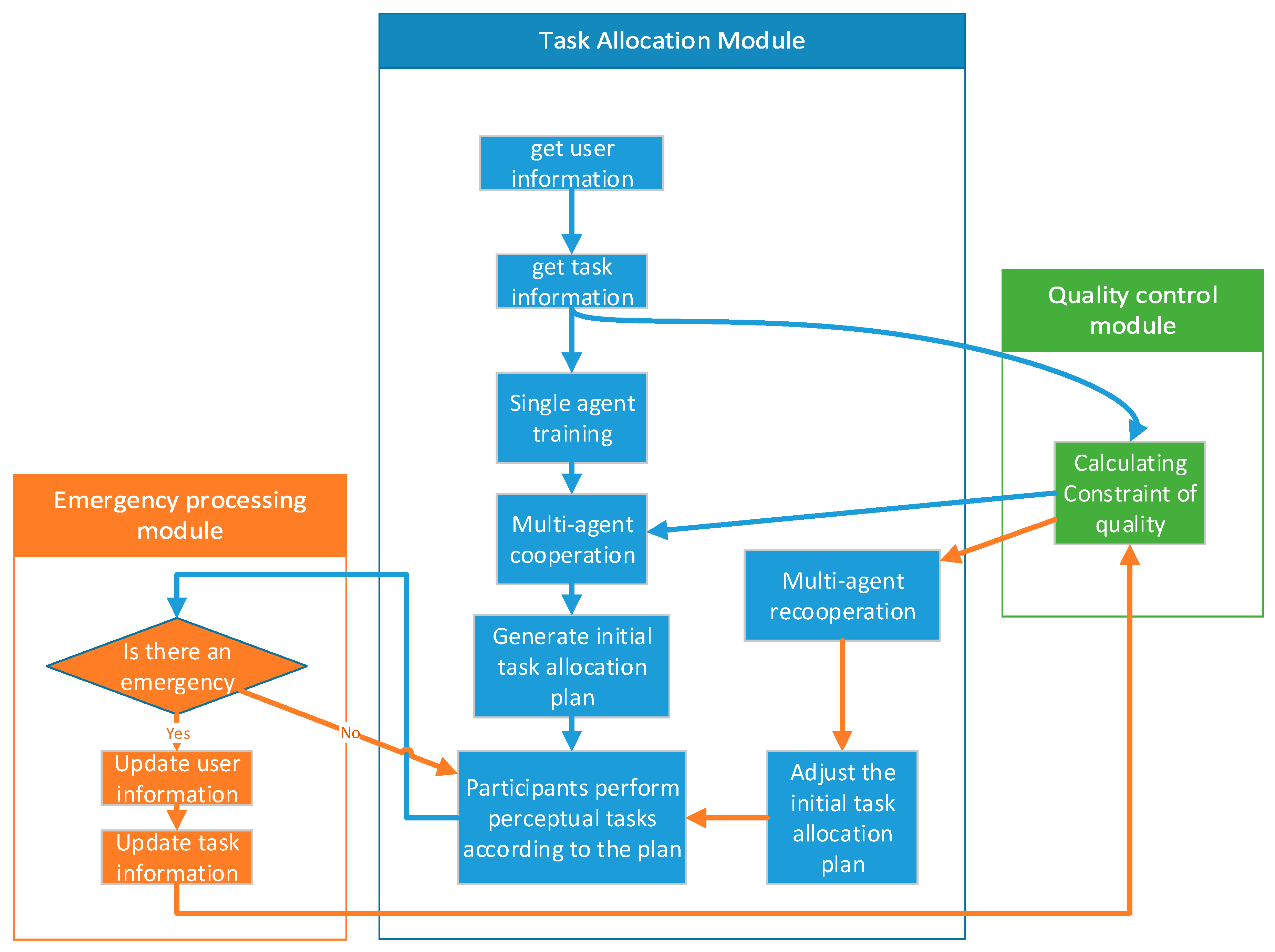
3. Proposed Approaches
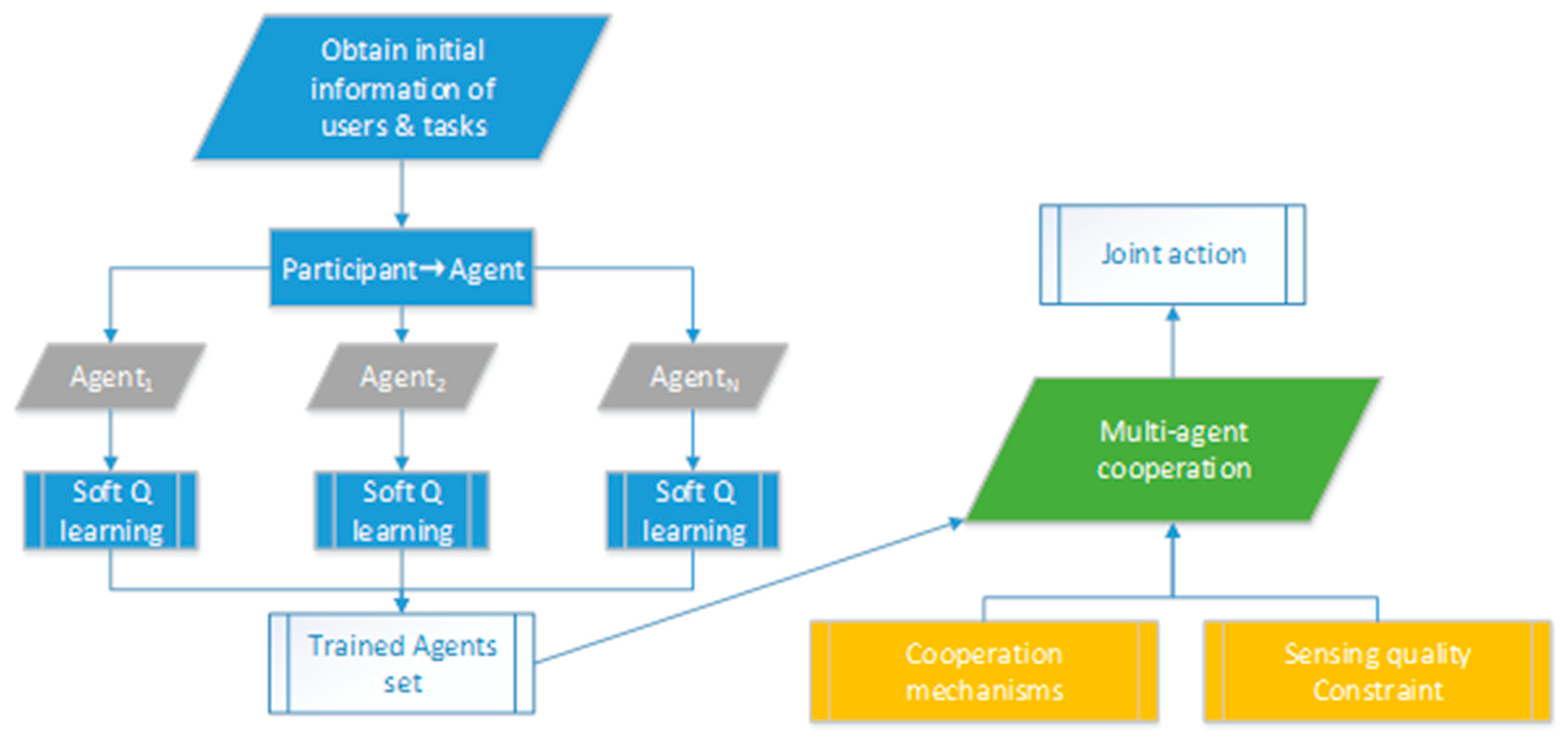
3.1. An RL Model for a Single Agent.
| Algorithm 1: Modified Soft Q-learning |
| Input: the user set U, the task set T |
| Output: the Q Table set Q Tables |
| Initialize the Q Tables is |
| for episode e = 1 to E do |
| Initialize the Q Table let the Q value is 0 |
| while the number of performed tasks is not equal to the number of executable tasks do |
| Update |
| end for |
| Q Tables join Q Table |
| parallel execute the above code for each user in U |
3.2. Obtain the Sensing Quality Constraint
| Algorithm 2: Dynamic programming for multipack problem |
| Input: the user set U, the task set T |
| Output:ConstraintSQ |
| Initialize MaxNE, W, N, TW according to the U&T |
| Initialize F |
| fori = 1 to m do |
| for v = TW to 0 do step −1 |
| end for |
| end for |
| Obtain ConstraintSQ according to F |
3.3. Multi-Agent Cooperation for Optimal Joint Action
3.3.1. Cooperation Mechanism Based on Social Convention
| Algorithm 3: Cooperation mechanism based on social convention |
| Input: the user set U, the task set T, ConstraintSQ, Q Tables |
| Output: Λ |
| Sort U in ascending order according to speed |
| while participants can continue to execute tasks do |
| for u in U do |
| if u can no longer continue the task then |
| Add the into the Λ |
| end if |
| u select the task t with the largest Q value in when meet ConstraintSQ |
| Update |
| Update ConstraintSQ |
| Add task t into the |
| end for |
| return Λ |
3.3.2. Cooperation Mechanism Based on Joint Action-Value Function
| Algorithm 4: Cooperation mechanism based on joint action-value function |
| Input: the user set U, the task set T, ConstraintSQ, Q Tables |
| Output: Λ |
| while participants can continue to execute tasks do |
| Obtain the depends on the recursion on ConstraintSQ |
| for in do |
| If u can no longer continue the task then |
| Add the into the Λ |
| end if |
| for in do |
| Select the actions of a certain users according to Q value |
| Add actions (tasks) into the |
| end for |
| Update |
| Update ConstraintSQ |
| end for |
| return Λ |
3.4. Emergency Response Mechanism
4. Experiment and Analysis
4.1. Experiment Data Preparation
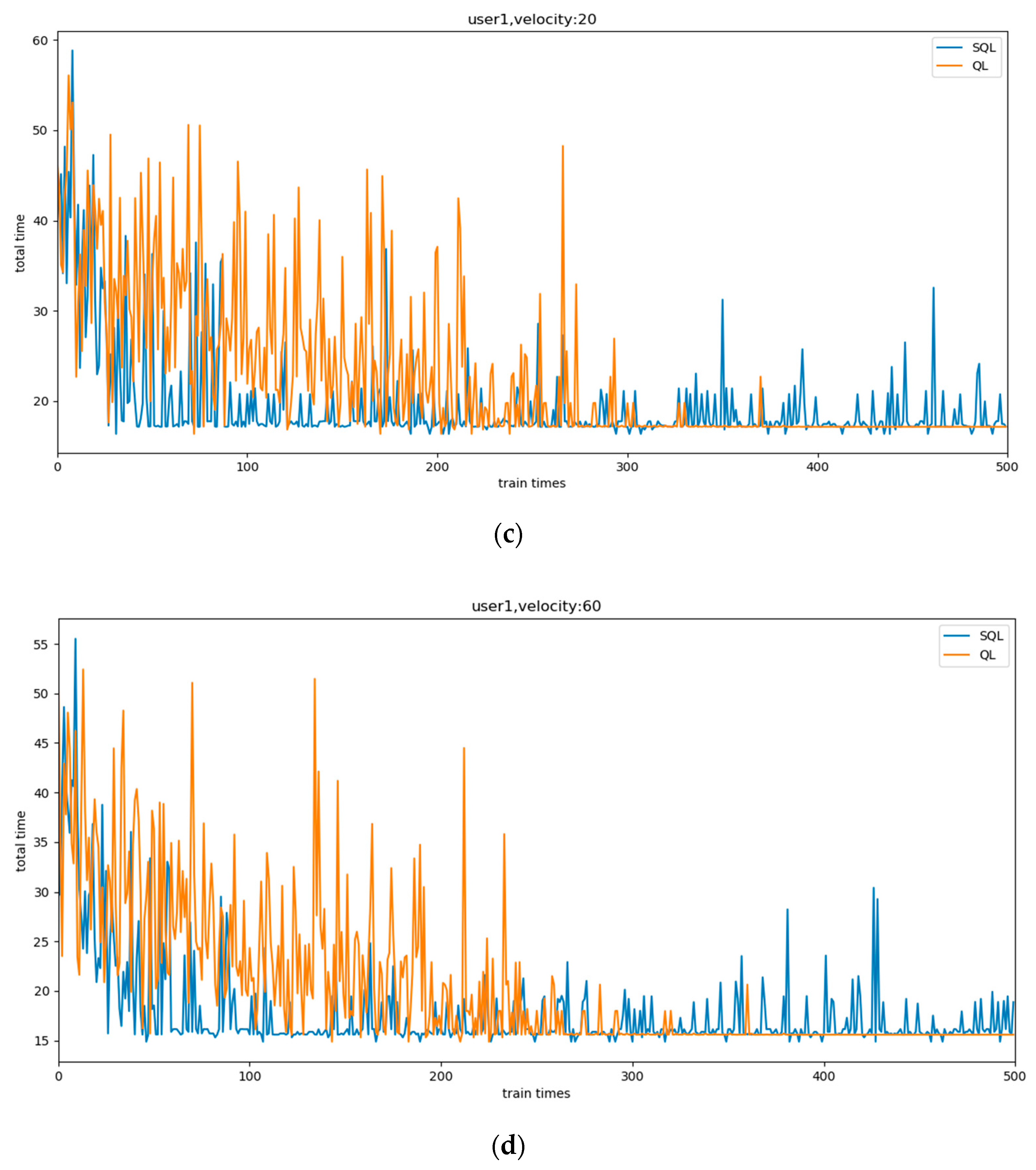
4.2. Evaluation of RL Model for Single Agentx
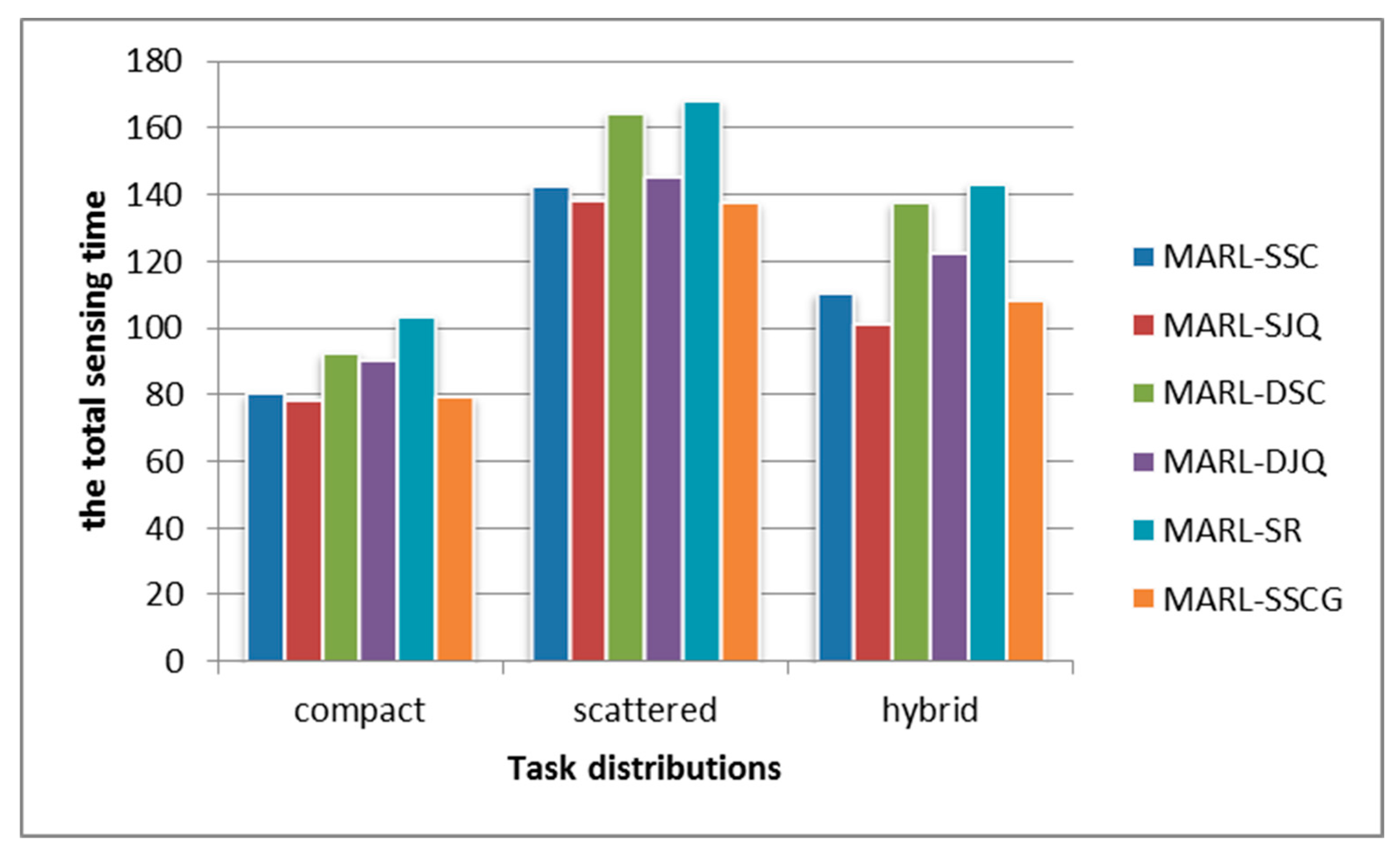
4.3. Evaluation of Multi-Agent Reinforcement Learning Framework
4.4. Evaluation of the MARL Framework in Case of Emergencies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Y. Crowd sensing computation. Commun. CCF 2012, 8, 38–41. [Google Scholar]
- Ganti, R.K.; Ye, F.; Lei, H. Mobile crowd sensing: Current state and future challenges. IEEE Commun. Mag. 2011, 49, 32–39. [Google Scholar] [CrossRef]
- Rana, R.K.; Chou, C.T.; Kanhere, S.S.; Bulusu, N.; Hu, W. Ear-phone: An end-to-end participatory urban noise mapping system. In Proceedings of the ACM/IEEE International Conference on Information Processing in Sensor Networks, Stockholm, Sweden, 12–15 April 2010; pp. 105–116. [Google Scholar]
- Liu, S.; Liu, Y.; Ni, L.; Li, M.; Fan, J. Detecting crowdedness spot in city transportation. IEEE Trans. Veh. Technol. 2013, 62, 1527–1539. [Google Scholar] [CrossRef]
- Altshuler, Y.; Fire, M.; Aharony, N.; Volkovich, Z.; Elovici, Y.; Pentland, A.S. Trade-offs in social and behavioral modeling in mobile networks. Int. Conf. Soc. Comput. 2013, 78, 412–423. [Google Scholar]
- Pryss, R.; Reichert, M.; Herrmann, J.; Langguth, B.; Schlee, W. Mobile crowd sensing in clinical and psychological trials--a case study. In Proceedings of the IEEE International Symposium on Computer-Based Medical Systems, Sao Carlos, Brazil, 22–25 June 2015; pp. 23–24. [Google Scholar]
- Ra, M.R.; Liu, B.; La Porta, T.F.; Govindan, R. Medusa: A programming framework for crowd-sensing applications. In Proceedings of the 10th International Conference on Mobile Systems, Lake District, UK, 25–29 June 2012; pp. 337–350. [Google Scholar]
- Qi, L.; Dou, W.; Wang, W.; Li, G.; Yu, H.; Wan, S. Dynamic mobile crowdsourcing selection for electricity load forecasting. IEEE Access 2018, 6, 46926–46937. [Google Scholar] [CrossRef]
- Gao, Z.; Xuan, H.Z.; Zhang, H.; Wan, S.; Choo, K.K.R. Adaptive fusion and category-level dictionary learning model for multi-view human action recognition. IEEE. Intern. Things. J. 2019, 6, 1–14. [Google Scholar]
- Wang, J.; Wang, Y.; Zhang, D.; Wang, F.; Xiong, H.; Chen, C.; Lv, Q.; Qiu, Z. Multi-task allocation in mobile crowd sensing with individual task quality assurance. IEEE Trans. Mob. Comput. 2018, 17, 2101–2113. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B.; Wang, Y.; Wu, W.; Yu, Z.; Zhang, D. TaskMe: Multi-task allocation in mobile crowd sensing. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 403–414. [Google Scholar]
- Xiong, J.; Chen, X.; Tian, Y.; Ma, R.; Chen, L.; Yao, Z. MAIM: A novel incentive mechanism based on multi-attribute user selection in mobile crowd sensing. IEEE Access 2018, 6, 65384–65396. [Google Scholar] [CrossRef]
- Reddy, S.; Estrin, D.; Srivastava, M. Recruitment framework for participatory sensing data collection. In Proceedings of the Eighth International Conference on Pervasive Computing, Helsinki, Finland, 17–20 May 2010; pp. 138–155. [Google Scholar]
- Zhang, D.; Xiong, H.; Wang, L.; Chen, G. CrowdRecruiter: Selecting participants for piggyback crowd sensing under probabilistic coverage constraint. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 703–714. [Google Scholar]
- Cardone, G.; Foschini, L.; Bellavista, P.; Corradi, A.; Borcea, C.; Talasila, M.; Curtmola, R. Fostering participaction in smart cities: A geo-social crowdsensing platform. IEEE Commun. Mag. 2013, 51, 112–119. [Google Scholar] [CrossRef]



| Time | State | Actions | Selected Action | New State |
|---|---|---|---|---|
| 1 | (0,0,0,0,0,0) | (1,2,3,4,5) | 1 | (1,1,0,0,0,0) |
| 2 | (1,1,0,0,0,0) | (2,3,4,5) | 3 | (3,1,0,1,0,0) |
| 3 | (3,1,0,1,0,0) | (2,4,5) | 5 | (5,1,0,1,0,1) |
| 4 | (5,1,0,1,0,1) | (2,4) | 2 | (2,1,1,1,0,1) |
| 5 | (2,1,1,1,0,1) | (4) | 4 | (4,1,1,1,1,1) |
| Number of Tasks | Soft Q-Learnig | Q-Learning | Deep Q Network | Sarsa |
|---|---|---|---|---|
| 5 | 0.061 | 0.483 | 0.131 | 0.171 |
| 10 | 0.132 | 0.561 | 0.233 | 0.522 |
| 20 | 0.188 | 0.902 | 0.335 | 0.734 |
| Name | Single RL Model | Cooperation Mechanism | The Sensing Quality Constraint |
|---|---|---|---|
| MARL-SSC | SQL | Social Convention | Multipack |
| MARL-SJQ | SQL | Multipack | |
| MARL-DSC | DQN | Social Convention | Multipack |
| MARL-DJQ | DQN | Multipack | |
| MARL-SR | SQL | Random queue | Multipack |
| MARL-SSCG | SQL | Social Convention | Greedy* |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Zhang, Z.; Wu, X. A Real-World-Oriented Multi-Task Allocation Approach Based on Multi-Agent Reinforcement Learning in Mobile Crowd Sensing. Information 2020, 11, 101. https://doi.org/10.3390/info11020101
Han J, Zhang Z, Wu X. A Real-World-Oriented Multi-Task Allocation Approach Based on Multi-Agent Reinforcement Learning in Mobile Crowd Sensing. Information. 2020; 11(2):101. https://doi.org/10.3390/info11020101
Chicago/Turabian StyleHan, Junying, Zhenyu Zhang, and Xiaohong Wu. 2020. "A Real-World-Oriented Multi-Task Allocation Approach Based on Multi-Agent Reinforcement Learning in Mobile Crowd Sensing" Information 11, no. 2: 101. https://doi.org/10.3390/info11020101
APA StyleHan, J., Zhang, Z., & Wu, X. (2020). A Real-World-Oriented Multi-Task Allocation Approach Based on Multi-Agent Reinforcement Learning in Mobile Crowd Sensing. Information, 11(2), 101. https://doi.org/10.3390/info11020101




