Grade Setting of a Timber Logistics Center Based on a Complex Network: A Case Study of 47 Timber Trading Markets in China
Abstract
:1. Introduction
2. Methods
2.1. Basic Types of Networks
2.2. Basic Characteristics of Networks
2.3. Analysis Method for the Timber Logistics Transportation Network Based on a Complex Network
Problem Description
- (1)
- The freight volume and transportation capacity of nodes are the main factors that affect the accessibility of the logistics transportation network.
- (2)
- The distance, route and time between nodes are based on the existing transportation network.
- (3)
- Intercity freight transportation mainly adopts the multimodal transportation of air and railway transportation, while highway transportation is used in the same city.
- (4)
- The freight capacity of each node (market) settled enterprise is equivalent, so the number of enterprises in the market is used as the indicator for measuring its freight capacity.
- (5)
- The direction of transportation is not considered in the course of transportation.
2.4. Transportation Network Models
2.4.1. Data Acquisition
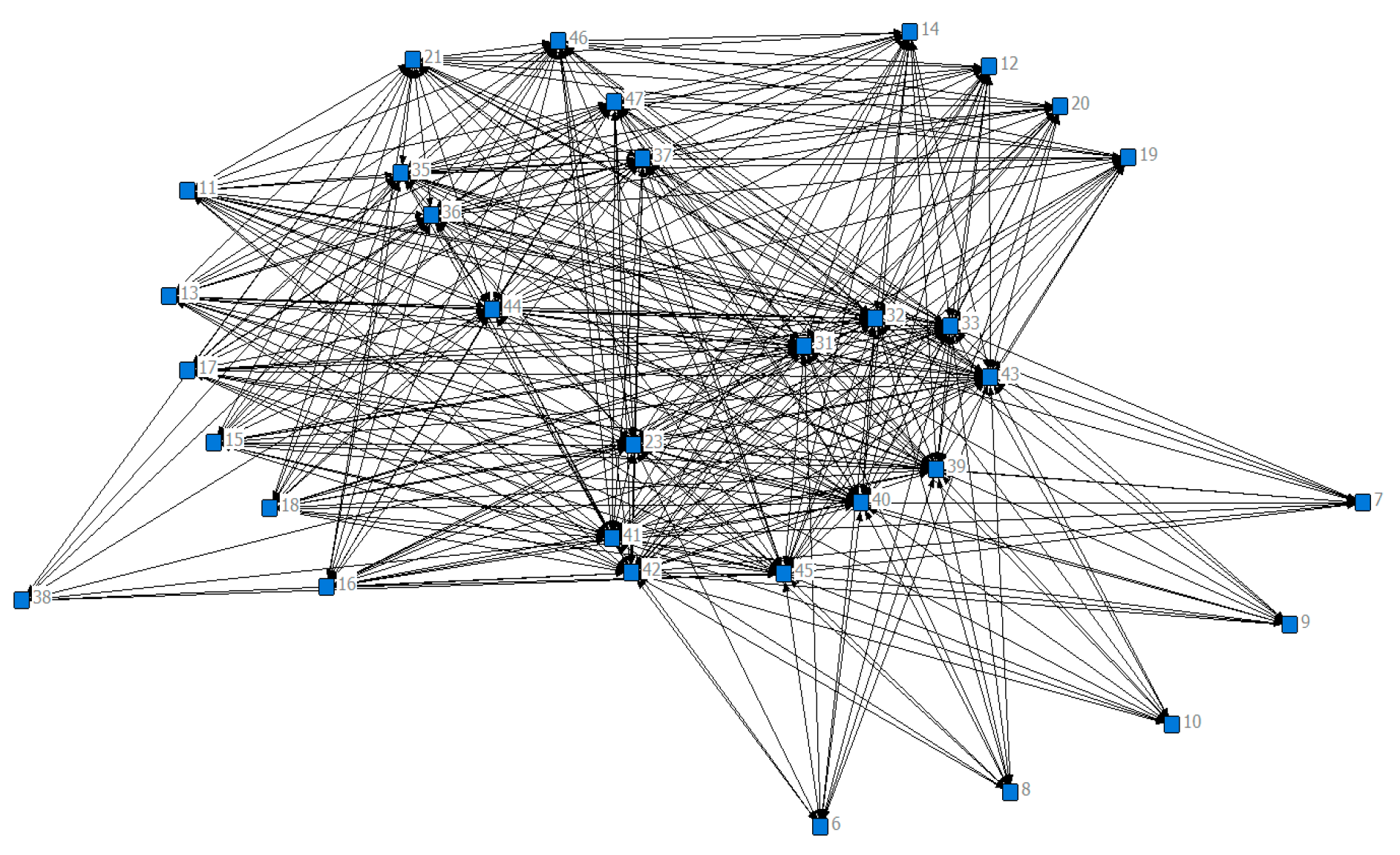
2.4.2. Complex Transportation Network Model
2.4.3. Freight Volume Analysis and Indicator Processing
- (1)
- The four transportation indicators and freight volume indicators measured by Ucinet are processed by the Z-score to make them dimensionless.
- (2)
- The four indicators under the three modes of transportation are summed to obtain the corresponding transportation capacity value. Then, the comprehensive transportation capacity of each node is calculated by weighting the transportation capacities of railway and air and adding the transportation capacity of highway. Combined with the freight volume indicator, the logistics capacity coefficient of each node is obtained.
- (3)
- The city is selected as the unit to formulate the rules of network construction. The first 10% of cities are scored as the highest level, the second 20% of cities are scored as the second level, the next 30% of cities are scored as the third level and the last 40% of cities are scored as the fourth level. The node with the highest score is selected as the logistics center in each city.
3. Empirical Study of the Complex Structural Characteristics of the Timber Transportation Network
3.1. Problem Description
3.2. Analysis of the Complex Transportation Network Model
3.2.1. Analysis of the Air Transportation Network
3.2.2. Analysis of the Railway Transportation Network
3.2.3. Highway Transportation Network Analysis
3.3. Analysis of the Logistics Capacity Coefficient Combined with the Freight Volume
3.4. Grade Setting of the Timber Logistics Center
4. Comparative Analysis with Other Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, H.; Gao, Z.; Wu, J. A bi-level programming model and solution algorithm for the location of logistics distribution centers. Appl. Math. Model. 2008, 32, 610–616. [Google Scholar] [CrossRef]
- Marković, G.; Gašić, M.; Kolarević, M.; Savković, M.; Marinković, Z. Application of the MODIPROM method to the final solution of logistics centre location. Transport 2013, 28, 341–351. [Google Scholar] [CrossRef]
- Önden, İ.; Acar, A.Z.; Eldemir, F. Evaluation of the logistics center locations using a multi-criteria spatial approach. Transport 2016, 33, 322–334. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, Y.; Li, Y.; Liu, S.; Yang, J. A Study of Rural Logistics Center Location Based on Intuitionistic Fuzzy TOPSIS. Available online: https://www.hindawi.com/journals/mpe/2017/2323057/ (accessed on 16 February 2020).
- Guimaraes, V.D.; Ribeiro, G.M.; do Forte, V.L.; Lucena, A. A location-allocation model for Logistics Integration Centers. Int. J. Transp. Econ. 2017, 44, 273–292. [Google Scholar]
- Zhao, S.X. A study on the Location Determinants and Performance of Pharmaceutical industry’s Logistics Center. J. Korea Res. Assoc. Int. Commer. 2018, 18, 145–166. [Google Scholar]
- Mousavi, S.M.; Antuchevičienė, J.; Zavadskas, E.K.; Vahdani, B.; Hashemi, H. A new decision model for cross-docking center location in logistics networks under interval-valued intuitionistic fuzzy uncertainty. Transport 2019, 34, 30–40. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Hill, D. Optimal capacity distribution on complex networks. Epl (Europhys. Lett.) 2010, 89, 58004. [Google Scholar] [CrossRef]
- Cardillo, A.; Gómez-Gardeñes, J.; Zanin, M.; Romance, M.; Papo, D.; Del Pozo, F.; Boccaletti, S. Emergence of network features from multiplexity. Sci. Rep. 2013, 3, 1344–1349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Couto, G.S.; Silva, A.P.; Ruiz, L.B.; Benevenuto, F. Structural Properties of the Brazilian Air Transportation Network. An. Da Acad. Bras. De Ciências 2015, 87, 1653–1674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Mburu, L.; Wang, S. Analysis of community properties and node properties to understand the structure of the bus transport network. Phys. A Stat. Mech. Its Appl. 2016, 450, 523–530. [Google Scholar] [CrossRef]
- Ducruet, C. Multilayer dynamics of complex spatial networks: The case of global maritime flows (1977–2008). J. Transp. Geogr. 2017, 60, 47–58. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Chen, J.; Yan, X.C. Space‒Time Evolution Analysis of the Nanjing Metro Network Based on a Complex Network. Sustainability 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Hao, J.; Ji, X.; Liu, L. Research on the Complex Characteristics of Freight Transportation from a Multiscale Perspective Using Freight Vehicle Trip Data. Sustainability 2019, 11, 1897. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.Y.; Zhang, K.M.; Hua, G.W. The Study on Site Selection of Coal Distribution Center based on Logistics Green Grade. In Proceedings of the 1st International Conference on Logistics, Informatics and Service Science (LISS 2011), Beijing, China, 8–11 June 2011; Insticc-inst Syst Technologies Information Control & Communication: Setubal, Portugal, 2011; pp. 28–34. [Google Scholar]
- Yang, F.; Zhao, Z.B.; Jiang, T.Y.; Dong, Y.C. Evaluation Research on Military Logistics Distribution Center Based on SVM. In Proceedings of the 5th International Symposium on Knowledge Acquisition and Modeling (KAM), London, England, 27–28 June 2015; Atlantis Press: Paris, France, 2015; pp. 210–212. [Google Scholar]
- Wu, Z.B.; Xu, J.P.; Xu, Z.S. A multiple attribute group decision making framework for the evaluation of lean practices at logistics distribution centers. Ann. Oper. Res. 2016, 247, 735–757. [Google Scholar] [CrossRef]
- Chen, J.H. Establishment on Evaluation Index System for Urban Logistics Center Location Scheme. In Proceedings of the 5th International Education, Economics, Social Science, Arts, Sports and Management Engineering Conference (IEESASM), Qingdao, China, 28–29 December 2017; Atlantis Press: Paris, France, 2017; pp. 555–559. [Google Scholar]
- Liu, B.H.; Li, J.; Zheng, S.D. Competitiveness Evaluation of Pharmaceutical Logistics Centres Based on Combined Weight and Cumulative Prospect Theory. In Proceedings of the 4th International Conference on Environmental Science and Material Application (ESMA), Xian, China, 15–16 December 2018; IOP Publishing LTD: Bristol, England, 2019. [Google Scholar]
- Li, X.; Wang, Y. Evaluation of the Operation System of the Sales Logistics Distribution Center in Steel Enterprises Based on AHP. In Proceedings of the 1st International Symposium on Management and Social Sciences (ISMSS), Wuhan, China, 13–14 April 2019; Atlantis Press: Paris, France, 2019; pp. 44–48. [Google Scholar]
- Lin, Y.H.; Chen, Q.Y.; Qiu, R.Z. Visual supervision of wood transport behavior based on K-means clustering. J. Qinghai Norm. Univ. (Nat. Sci. Ed.) 2016, 32, 54–59. [Google Scholar]
- Long, T.; Pan, H.X.; Ma, P.; Shi, X.L. Dynamic Analysis of International Wood Forest Products Trade Based on Complex Network. Explor. Econ. Issues 2016, 182, 170–175. [Google Scholar]
- Lin, Y.Y.; Qiu, R.Z. Analysis and design of wood logistics network optimization system. For. Eng. 2017, 87–91. [Google Scholar]
- Sarrazin, F.; LeBel, L.; Lehoux, N. Analyzing the impact of implementing a logistics center for a complex forest network. Can. J. For. Res. 2019, 49, 179–189. [Google Scholar] [CrossRef]
- Long, T.; Pan, H.; Dong, C.; Qin, T.; Ma, P. Exploring the competitive evolution of global wood product trade based on complex network analysis. Phys. A Stat. Mech. Its Appl. 2019, 525, 1224–1232. [Google Scholar] [CrossRef]



| Node Number | Timber Market Name |
|---|---|
| 1 | Dongguan Houjie·Xingye Timber Market |
| 2 | Dongguan Jiaye Timber Market |
| 3 | Dongguan Houjie·Oriental Xingye City |
| 4 | Guangdong Dongguan Jilong Timber Market |
| 5 | Dongguan Chashan Fengye Timber Market |
| 6 | Foshan Shunde ShuiTeng Timber Market |
| 7 | Foshan Big Turn Splint Market |
| 8 | Foshan Shunde Asia Pacific Timber Market |
| 9 | Foshan Shunde Longshan Decorative Materials Market |
| 10 | Guangdong Foshan Nanhai Bomei Market |
| 11 | Guangzhou Xintang Yueshun Decoration Materials City |
| 12 | Guangzhou Tianma Decoration Materials Market |
| 13 | Guangzhou Panyu Wuzhou Decoration World |
| 14 | Guangdong Guangzhou Yuzhu International Timber Market |
| 15 | Guangzhou Yangcheng Decorative Materials Market |
| 16 | Guangzhou Xilong Building Materials Market |
| 17 | Guangzhou B&Q Building Materials Supermarket |
| 18 | Guangzhou Tianjian Decoration Materials Market |
| 19 | Guangzhou Anhua Decorative Materials Market |
| 20 | Guangzhou Yiheng Timber Market |
| 21 | Hangzhou Timber Trading Market |
| 22 | Shaoxing Tashan Timber Market |
| 23 | Wenzhou Timber Exchange Market |
| 24 | Jiaxing Jiashan International Timber Market |
| 25 | Jiaxing Jiashan·Oriental Xingye City |
| 26 | Huzhou Nanxun Building Materials Market |
| 27 | Huzhou Timber Market |
| 28 | Zhangjiagang Timber Exchange Market |
| 29 | Taicang City Port District Huachen Logistics Center |
| 30 | Zhenjiang Yangzhong Venus Timber Market |
| 31 | Tianjin Xinzhong Building Materials Trade Market |
| 32 | Tianjin Bohai Bay Timber Market |
| 33 | Tianjin Beichen District Hanjiashu Timber Market |
| 34 | Shandong Dezhou Timber Market |
| 35 | Qingdao Jiaozhou Timber Market |
| 36 | Qingdao Licang District Wantou First Timber Market |
| 37 | Hunan Changsha Zhongnan Timber Market |
| 38 | Yueyang City Sun Bridge Building Materials Market |
| 39 | Shijiazhuang Zhengding Hengshan Plate Market |
| 40 | Shijiazhuang City Timber Trading Market |
| 41 | Shanghai Jiading District Donghua Global Building Materials Market |
| 42 | Shanghai Baoshan Furen Timber Market |
| 43 | Beijing Dongba Imported Timber Market |
| 44 | Heilongjiang Suifenhe Imported Timber market |
| 45 | Inner Mongolia Manzhouli City Timber Market |
| 46 | Anhui Jieshou Lvzhai Timber Market |
| 47 | Jiangxi Jinxian Wengang Wild Chicken Cage Timber Market |
| Node Number | City Name | Air Transportation Conditions | Node Number | City Name | Air Transportation Conditions |
|---|---|---|---|---|---|
| 6 | Foshan | Foshan Shadi Airport | 30 | Zhenjiang | No Airport |
| 7 | Foshan | Foshan Shadi Airport | 31 | Tianjin | Tianjin Binhai Airport |
| 10 | Foshan | Foshan Shadi Airport | 34 | Dezhou | No Airport |
| 11 | Guangzhou | Guangzhou Baiyun Airport | 35 | Qingdao | Qingdao Liuting Airport |
| 13 | Guangzhou | Guangzhou Baiyun Airport | 37 | Changsha | Changsha Huanghua Airport |
| 14 | Guangzhou | Guangzhou Baiyun Airport | 38 | Yueyang | Yueyang Sanhe Airport |
| 16 | Guangzhou | Guangzhou Baiyun Airport | 40 | Shijiazhuang | Shijiazhuang Zhengding Airport |
| 17 | Guangzhou | Guangzhou Baiyun Airport | 41 | Shanghai | Shanghai Hongqiao Airport |
| 19 | Guangzhou | Guangzhou Baiyun Airport | 43 | Beijing | Beijing Capital Airport |
| 21 | Hangzhou | Hangzhou Xiaoshan Airport | 45 | Hulun Buir | Western suburbs of Manchuria |
| 22 | Shaoxing | No Airport | 46 | Fuyang | Fuyang Xiguan Airport |
| 23 | Wenzhou | Wenzhou Longwan Airport | 47 | Nanchang | Nanchang Changbei Airport |
| Node Number | nDegree | nBetweenness | ||
|---|---|---|---|---|
| 1 | 0.000 | 0.000 | 0 | 0 |
| 2 | 0.000 | 0.000 | 0 | 0 |
| 3 | 0.000 | 0.000 | 0 | 0 |
| 4 | 0.000 | 0.000 | 0 | 0 |
| 5 | 0.000 | 0.000 | 0 | 0 |
| 6 | 10.000 | 0.217 | 0.456 | 0.044 |
| 7 | 10.000 | 0.217 | 0.456 | 0.044 |
| 8 | 10.000 | 0.217 | 0.456 | 0.044 |
| 9 | 10.000 | 0.217 | 0.456 | 0.044 |
| 10 | 10.000 | 0.217 | 0.456 | 0.044 |
| Distance | Node Number | ||||||
|---|---|---|---|---|---|---|---|
| 6 | 20 | 21 | 23 | 33 | 35 | ||
| Node Number | 6 | 0 | 0 | 0 | 947 | 1909 | 0 |
| 20 | 0 | 0 | 1099 | 1015 | 1910 | 1867 | |
| 21 | 0 | 1099 | 0 | 0 | 1133 | 792 | |
| 23 | 947 | 1015 | 0 | 0 | 1545 | 1102 | |
| 33 | 1909 | 1910 | 1133 | 1545 | 0 | 477 | |
| 35 | 0 | 1867 | 792 | 1102 | 477 | 0 | |
| Node Number | nDegree | |||
|---|---|---|---|---|
| 6 | 61.174 | 0.051 | 6.1174 | 0.10904 |
| 16 | 123.546 | 0.103 | 7.267412 | 0.072937 |
| 22 | 0 | 0 | 0 | 0 |
| 23 | 315.359 | 0.263 | 10.51197 | 0.038922 |
| 31 | 248.807 | 0.208 | 8.885964 | 0.053532 |
| 35 | 257.028 | 0.215 | 10.28112 | 0.05123 |
| 37 | 273.933 | 0.229 | 11.41388 | 0.047883 |
| 38 | 80.944 | 0.068 | 10.118 | 0.141036 |
| 39 | 246.417 | 0.206 | 9.126556 | 0.054719 |
| 40 | 246.417 | 0.206 | 9.126556 | 0.054719 |
| 41 | 284.556 | 0.238 | 9.4852 | 0.039101 |
| 42 | 284.556 | 0.238 | 9.4852 | 0.039101 |
| 43 | 182.136 | 0.152 | 7.005231 | 0.045508 |
| 45 | 124.420 | 0.104 | 4.443571 | 0.040796 |
| 46 | 248.838 | 0.208 | 11.31082 | 0.050837 |
| 47 | 270.548 | 0.226 | 11.76296 | 0.049055 |
| Node Number | Betweenness (B) | Comprehensive Weights (T) | |||
|---|---|---|---|---|---|
| 23 | 1.4007 | 2.0910 | 1.1711 | −0.2254 | 4.4373 |
| 41 | 1.4007 | 2.1903 | 0.9198 | −0.2207 | 4.2901 |
| 42 | 1.4007 | 2.1903 | 0.9198 | −0.2207 | 4.2901 |
| 31 | 1.2208 | 1.6516 | 0.7732 | 0.1596 | 3.8052 |
| 32 | 1.2208 | 1.6516 | 0.7732 | 0.1596 | 3.8052 |
| 33 | 1.2208 | 1.6516 | 0.7732 | 0.1596 | 3.8052 |
| 39 | 1.1309 | 1.4903 | 0.8321 | 0.1908 | 3.6441 |
| 40 | 1.1309 | 1.4903 | 0.8321 | 0.1908 | 3.6441 |
| 43 | 1.0409 | 1.6134 | 0.3130 | −0.0519 | 2.9155 |
| 45 | 1.2208 | 2.0326 | −0.3137 | −0.1760 | 2.7637 |
| Node Number | Railway Station | Node Number | Railway Station | Node Number | Railway Station | Node Number | Railway Station |
|---|---|---|---|---|---|---|---|
| 1 | Dongguan | 13 | Guangzhou South | 25 | JiaXing | 37 | Changsha West |
| 2 | Dongguan | 14 | Guangzhou East | 26 | Huzhou | 38 | Yueyang East |
| 3 | Dongguan | 15 | Guangzhou West | 27 | Huzhou | 39 | Shijiazhuang North |
| 4 | Dongguan East | 16 | Guangzhou North | 28 | Suzhou North | 40 | Shijiazhuang North |
| 5 | Dongguan | 17 | Guangzhou East | 29 | Suzhou North | 41 | Shanghai West |
| 6 | Foshan | 18 | Guangzhou East | 30 | Zhenjiang | 42 | Shanghai West |
| 7 | Foshan | 19 | Guangzhou | 31 | Tianjin North | 43 | Beijing East |
| 8 | Foshan | 20 | Guangzhou west | 32 | Tianjin | 44 | Mudanjiang |
| 9 | Foshan | 21 | Hangzhou | 33 | Tianjin West | 45 | Manzhouli |
| 10 | Foshan | 22 | Shaoxing | 34 | Dezhou | 46 | Fu-Yang |
| 11 | Guangzhou East | 23 | Wenzhou South | 35 | Qingdao North | 47 | Nam Cheong |
| 12 | GuangZhou East | 24 | JiaXing | 36 | Qingdao North |
| Node Number | Betweenness (B) | Comprehensive Weights (T) | |||
|---|---|---|---|---|---|
| 33 | 1.7773 | 3.2841 | −0.8686 | 0.2919 | 4.4847 |
| 32 | 1.7773 | 3.2841 | −1.0086 | −0.9868 | 3.0661 |
| 31 | 1.7773 | 3.2841 | −0.9997 | −1.0138 | 3.0479 |
| 43 | 1.3467 | 1.7569 | −0.8147 | 0.3273 | 2.6162 |
| 21 | 1.2391 | 0.9607 | −0.4172 | −0.0307 | 1.7518 |
| 42 | 1.0238 | 0.4129 | −0.5016 | 0.5034 | 1.4385 |
| 41 | 1.0238 | 0.4129 | −0.4942 | 0.4558 | 1.3983 |
| 47 | 1.5620 | 1.1924 | −0.9599 | −1.3303 | 0.4643 |
| 15 | 0.0550 | −0.2140 | 0.6177 | 0.0040 | 0.4627 |
| 16 | 0.0550 | −0.2140 | 0.6177 | 0.0040 | 0.4627 |
| Node Number | K | U | Y | Comprehensive Weights (T) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 208.946 | 52.2365 | 0.6715 | 0.2512 | 4.0946 | 0.4939 | 4.8396 |
| 2 | 4 | 204.788 | 51.197 | 0.6936 | 0.2512 | 3.9994 | 0.5433 | 4.7939 |
| 3 | 4 | 66.9 | 16.725 | 0.3726 | 0.2512 | 0.8443 | −0.1737 | 0.9218 |
| 4 | 4 | 23.579 | 5.8948 | 0.2531 | 0.2512 | −0.1469 | −0.4406 | −0.3363 |
| 5 | 4 | 16.733 | 4.1833 | 0.2521 | 0.2512 | −0.3036 | −0.4428 | −0.4951 |
| 6 | 4 | 78.505 | 19.6263 | 0.5407 | 0.2512 | 1.1099 | 0.2018 | 1.5628 |
| 7 | 4 | 32.642 | 8.1605 | 0.4657 | 0.2512 | 0.0605 | 0.0343 | 0.3460 |
| 8 | 4 | 83.414 | 20.8535 | 0.5055 | 0.2512 | 1.2222 | 0.1231 | 1.5966 |
| 9 | 4 | 41.061 | 10.2653 | 0.3746 | 0.2512 | 0.2531 | −0.1692 | 0.3352 |
| 10 | 4 | 32.796 | 8.199 | 0.4624 | 0.2512 | 0.0640 | 0.0269 | 0.3422 |
| Node Number | Number of Enterprises | P | Node Number | Number of Enterprises | P | Node Number | Number of Enterprises | P |
|---|---|---|---|---|---|---|---|---|
| 1 | 346 | 1.95 | 17 | 7 | −0.54 | 33 | 32 | −0.36 |
| 2 | 26 | −0.40 | 18 | 12 | −0.50 | 34 | 136 | 0.41 |
| 3 | 771 | 5.07 | 19 | 5 | −0.55 | 35 | 37 | −0.32 |
| 4 | 292 | 1.55 | 20 | 9 | −0.52 | 36 | 44 | −0.27 |
| 5 | 6 | −0.55 | 21 | 59 | −0.16 | 37 | 102 | 0.16 |
| 6 | 66 | −0.11 | 22 | 10 | −0.52 | 38 | 8 | −0.53 |
| 7 | 69 | −0.08 | 23 | 20 | −0.44 | 39 | 44 | −0.27 |
| 8 | 54 | −0.19 | 24 | 29 | −0.38 | 40 | 37 | −0.32 |
| 9 | 10 | −0.52 | 25 | 14 | −0.49 | 41 | 90 | 0.07 |
| 10 | 8 | −0.53 | 26 | 33 | −0.35 | 42 | 384 | 2.23 |
| 11 | 4 | −0.56 | 27 | 24 | −0.41 | 43 | 116 | 0.26 |
| 12 | 10 | −0.52 | 28 | 224 | 1.05 | 44 | 140 | 0.44 |
| 13 | 11 | −0.51 | 29 | 33 | −0.35 | 45 | 83 | 0.02 |
| 14 | 228 | 1.08 | 30 | 30 | −0.37 | 46 | 31 | −0.36 |
| 15 | 10 | −0.52 | 31 | 35 | −0.33 | 47 | 8 | −0.53 |
| 16 | 7 | −0.54 | 32 | 30 | −0.37 |
| Node Number | Comprehensive Weight of Air Transportation | Comprehensive Weight of Railway Transportation | Comprehensive Weight of Highway Transportation | Transportation Capability Coefficient | Comprehensive Weight of Freight Volume | Logistics Capacity Coefficient |
|---|---|---|---|---|---|---|
| 1 | −4.6581 | 0.4279 | 4.8396 | 5.2583 | 1.9480 | 7.2062 |
| 3 | −4.6581 | 0.4279 | 0.9218 | 1.3405 | 5.0663 | 6.4068 |
| 2 | −4.6581 | 0.4279 | 4.7939 | 5.2125 | −0.4000 | 4.8125 |
| 42 | 4.2901 | 1.4385 | 0.4041 | 1.8479 | 2.2268 | 4.0747 |
| 33 | 3.8052 | 4.4847 | −0.1875 | 4.2960 | −0.3559 | 3.9401 |
| 14 | 0.7542 | 0.4596 | 1.1079 | 1.5681 | 1.0822 | 2.6503 |
| 31 | 3.8052 | 3.0479 | −0.2881 | 2.7612 | −0.3339 | 2.4273 |
| 18 | 0.7542 | 0.4596 | 2.3145 | 2.7747 | −0.5027 | 2.2720 |
| 12 | 0.7542 | 0.4596 | 2.3201 | 2.7802 | −0.5174 | 2.2629 |
| 32 | 3.8052 | 3.0661 | −0.6708 | 2.3966 | −0.3706 | 2.0260 |
| Node Number | City Name | City Number | Node Number | City Name | City Number |
|---|---|---|---|---|---|
| 1 | Dongguan | 1 | 11 | Guangzhou | 13 |
| 2 | Dongguan | 1 | 12 | Guangzhou | 13 |
| 3 | Dongguan | 1 | 13 | Guangzhou | 13 |
| 4 | Dongguan | 1 | 14 | Guangzhou | 13 |
| 5 | Dongguan | 1 | 15 | Guangzhou | 13 |
| 6 | Foshan | 2 | 16 | Guangzhou | 13 |
| 7 | Foshan | 2 | 17 | Guangzhou | 13 |
| 8 | Foshan | 2 | 18 | Guangzhou | 13 |
| 9 | Foshan | 2 | 19 | Guangzhou | 13 |
| 10 | Foshan | 2 | 20 | Guangzhou | 13 |
| 21 | Hangzhou | 3 | 31 | Tianjin | 14 |
| 22 | Shaoxing | 4 | 32 | Tianjin | 14 |
| 23 | Wenzhou | 5 | 33 | Tianjin | 14 |
| 24 | Jiaxing | 6 | 34 | Dezhou | 15 |
| 25 | Jiaxing | 6 | 35 | Qingdao | 16 |
| 26 | Huzhou | 7 | 36 | Qingdao | 16 |
| 27 | Huzhou | 7 | 37 | Changsha | 17 |
| 28 | Suzhou | 8 | 38 | Yueyang | 18 |
| 29 | Suzhou | 8 | 39 | Shijiazhuang | 19 |
| 30 | Zhenjiang | 9 | 40 | Shijiazhuang | 19 |
| 41 | Shanghai | 10 | 45 | Manzhouli | 20 |
| 42 | Shanghai | 10 | 46 | Fuyang | 21 |
| 43 | Beijing | 11 | 47 | Nanchang | 22 |
| 44 | Mudanjiang | 12 |
| City Number | Grade of Logistics Center | City Name | Logistics Capacity Coefficient |
|---|---|---|---|
| 1 | Level 1 | Dongguan | 3.625992 |
| 10 | Shanghai | 2.976004 | |
| 14 | Level 2 | Tianjin | 2.797807 |
| 13 | Guangzhou | 1.315718 | |
| 2 | Foshan | 0.779902 | |
| 8 | Suzhou | 0.381721 | |
| 11 | Beijing | 0.255385 | |
| 19 | Level 3 | Shijiazhuang | 0.100643 |
| 7 | Huzhou | −0.18127 | |
| 6 | Jiaxing | −0.30508 | |
| 3 | Hangzhou | −1.02727 | |
| 22 | Nanchang | −2.68646 | |
| 16 | Qingdao | −2.71568 | |
| 20 | Manzhouli | −3.37272 | |
| 4 | Level 4 | Shaoxing | −3.3756 |
| 17 | Changsha | −3.83059 | |
| 9 | Zhenjiang | −4.19341 | |
| 12 | Mudanjiang | −4.58568 | |
| 15 | Dezhou | −4.8129 | |
| 21 | Fuyang | −5.22204 | |
| 5 | Wenzhou | −5.5914 | |
| 18 | Yueyang | −5.65007 |
| Method | Brief Description | Advantages | Disadvantages | Applicability |
|---|---|---|---|---|
| With subjective weight assignment | All of these methods are based on the combination of different mathematical models and subjective evaluation indicator system, so as to achieve the location of logistics center. | These methods consider specific objectives, such as the lowest cost or the closest distance, and the assignment of subjective evaluation indicators. | It is difficult to construct the evaluation indicator system comprehensively. The quantization method is not easy to obtain. | This kind of method is suitable for long-term planning and in a small region. |
| No subjective weight assignment | These methods make use of different mathematical models and algorithms to study location quantitatively. | These methods mainly consider economic benefit and time benefit. | Customer needs and costs will vary with time and location. | This kind of method is suitable for industries with small market changes, otherwise dynamic planning should be used as an assistant. |
| Subjective weighting of complex networks | This kind of method is based on complex network method and subjective evaluation indicator. | According to the complex network characteristics of each node, it is more objective. | The subjective evaluation indicator is difficult to obtain and the accuracy needs to be improved. | It is suitable for the node selection of long-term planning with small area, which constitute the nodes of complex network. |
| Objective weighting of complex networks (method used in this paper) | The method of this paper is to use the complex network method, combined with the comprehensive weight of freight volume, which can determine the important nodes and grade settings. | According to the characteristics of nodes and the weighting of main objective data, the conclusion is not interfered by subjective factors. | The weighting method can be improved. | This method is suitable for the initial planning of the project, the data of the research object is difficult to obtain, the research object is special, and there are alternative positions in a large area. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, L.; Huang, X.; Wu, Y.; Yan, X.; Zheng, Y. Grade Setting of a Timber Logistics Center Based on a Complex Network: A Case Study of 47 Timber Trading Markets in China. Information 2020, 11, 107. https://doi.org/10.3390/info11020107
Xue L, Huang X, Wu Y, Yan X, Zheng Y. Grade Setting of a Timber Logistics Center Based on a Complex Network: A Case Study of 47 Timber Trading Markets in China. Information. 2020; 11(2):107. https://doi.org/10.3390/info11020107
Chicago/Turabian StyleXue, Liang, Xin Huang, Yuchun Wu, Xingchen Yan, and Yan Zheng. 2020. "Grade Setting of a Timber Logistics Center Based on a Complex Network: A Case Study of 47 Timber Trading Markets in China" Information 11, no. 2: 107. https://doi.org/10.3390/info11020107
APA StyleXue, L., Huang, X., Wu, Y., Yan, X., & Zheng, Y. (2020). Grade Setting of a Timber Logistics Center Based on a Complex Network: A Case Study of 47 Timber Trading Markets in China. Information, 11(2), 107. https://doi.org/10.3390/info11020107





