Deep Reinforcement Learning Based Left-Turn Connected and Automated Vehicle Control at Signalized Intersection in Vehicle-to-Infrastructure Environment
Abstract
:1. Introduction
- Aiming at the micro-control problem of a left-turning CAV at a signalized intersection, a control method based on an improved deep deterministic policy gradient (DDPG) is presented in this paper. The left-turn connected and automated vehicle (CAV) approaching, inside, and leaving an intersection is integrated in the control method. In addition, unlike the current research methods of RL for vehicle control at signalized intersections, this paper controls the action of left-turn CAV as a continuous action, rather than dividing the action space into discrete action, which is more suitable for the actual situation.
- In view of the instability of the DDPG algorithm, this paper divides the total experience replay buffer into positive reward experience replay buffer and negative reward experience replay buffer. Then, sampled from the positive negative reward experience replay buffer according to the ratio of 1:1, both excellent and not-excellent experiences can be sampled each time. At the same time, in order to avoid the overestimation of the critic network in the DDPG algorithm and accelerate the training of the actor network, the DDPG algorithm used in this paper is designed with a multi-critic structure.
- Aiming at the problems studied in this paper, a DRL model is established. When constructing the DRL model, considering the particularity of the problem, the state of the model is processed. In addition, this paper uses micro-simulation software VISSIM to build a virtual environment and takes it as an agent-learning environment. The left-turn vehicle in the simulation environment is used as the learning agent, so that the agent can learn independently in the virtual environment. Finally, in order to verify the effectiveness of agent training in different environments, this paper analyzed the train and test results under different market penetration under 0.2, 0.5, and 0.7 saturation degrees of a signalized intersection.
2. Literature Review
3. Problem Description
3.1. Description of the Left-Turning CAV Control Problem in V2I Environment
- (1)
- Within the control range, vehicles are not allowed to turn around, overtake, change lanes, etc.
- (2)
- Each vehicle has determined the exit road before entering the control area of the intersection.
- (3)
- Communication devices are installed in the CAV and RSU to ensure real-time communication between the vehicle, RSU, and the control center.
- (4)
- There is no communication delay or packet loss between the CAV, RSU, and control centers.
- (5)
- The CAV drives in full accordance with the driving behavior of the central control system.
3.2. Deep Reinforcement Learning Problem Description
3.2.1. State Description
3.2.2. Action Description
3.2.3. Reward Function Description
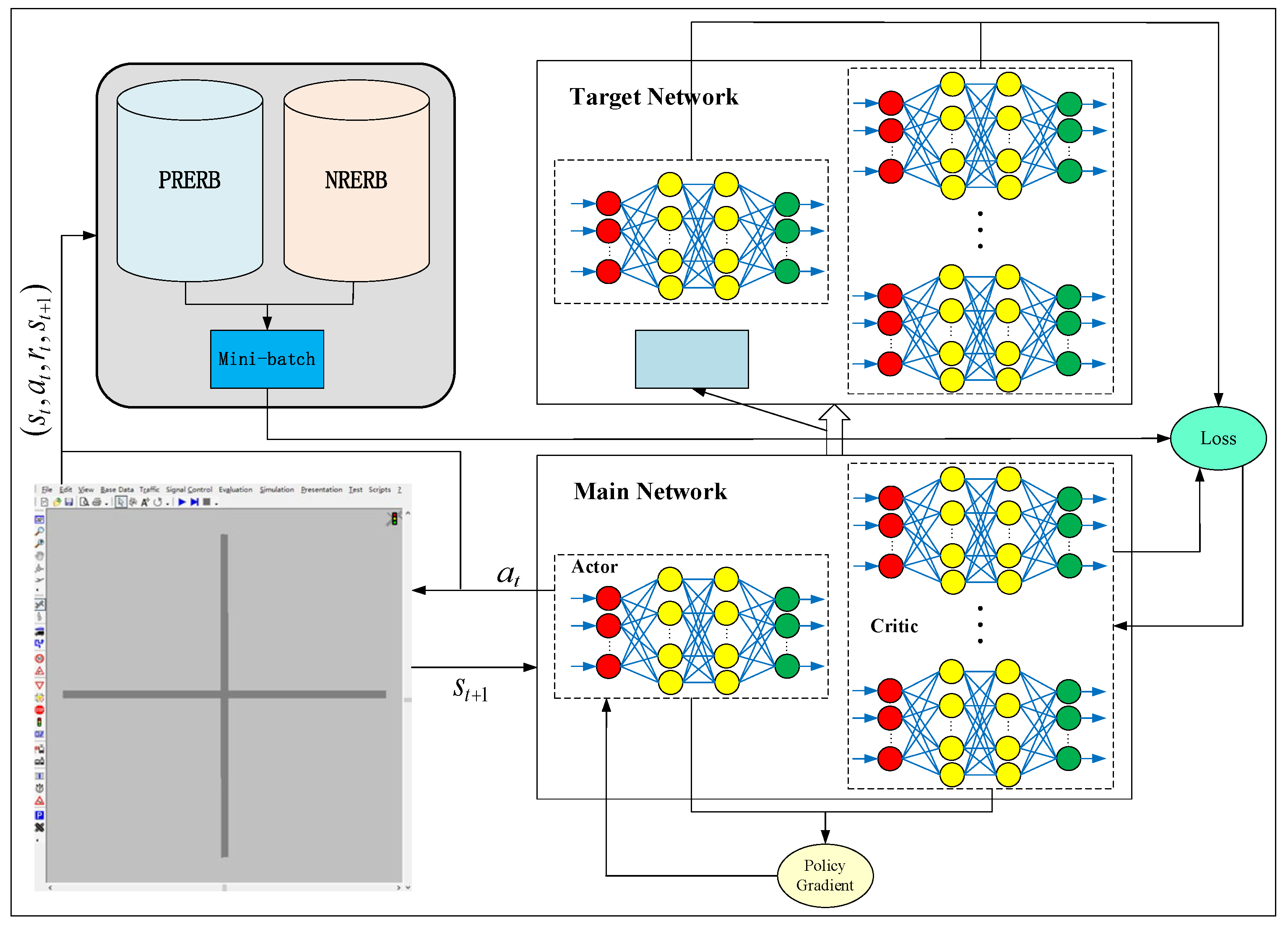
4. Multi-Critic DDPG Method Based on Positive and Negative Reward Experience Replay Buffer
4.1. Reinforcement Learning
4.2. Multi-Critic DDPG Method Based on Positive and Negative Reward Experience Replay Buffer (PNRERB-MC-DDPG)
| Algorithm 1 PNRERB-MC-DDPG method |
| Step 1: Initialize the critic network and actor network of the main network, give parameters and . |
| Step 2: Initialize the critic network and actor network of the target network, give parameters and . |
| Step 3: Initialize PRERB , NPERB , mini-batch , discount factor , the learning rate of critic network , the learning rate of the actor network , pretraining size , noise , noise reduction rate , training time , and random probability value . |
| Step 4: Infinite loop |
| Step 5: If there is no CAV in the current network |
| Step 6: If the maximum cycle time is reached, stop. |
| Step 7: If the detects the entry of the vehicle, add the vehicle number, and use the random probability to determine whether the vehicle is a CAV. |
| Step 8: If the detects a vehicle leaving, remove the vehicle number. |
| Step 9: Judge whether there are CAVs at present. If there is (there is a CAV ID stored in the RSU), enter line 10; otherwise, step by step simulation and jump back to Step 6. |
| Step 10: If there are CAVs in the current network |
| Step 11: Gets the current states of each CAV |
| Step 12: Infinite loop |
| Step 13: If the maximum cycle time is reached, stop. |
| Step 14: Select actions based on the current policy and exploration noise |
| Step 15: Execute action ; then, get the immediate reward value and the next state . |
| Step 16: For the current network of all CAVs |
| Step 17: if |
| Step 18: Put experience into |
| Step 19: else |
| Step 20: Put experience into |
| Step 21: If the number of experiences in is greater than |
| Step 22: |
| Step 23: Sample data were randomly selected from and |
| Step 24: Set . |
| Step 25: Calculate the loss of the critic network for the main network by Equation (7). |
| Step 26: Calculate the gradient of the actor network by Equation (11). |
| Step 27: Update the main network by Equations (12) and (13). |
| Step 28: Update the main network by Equations (14) and (15). |
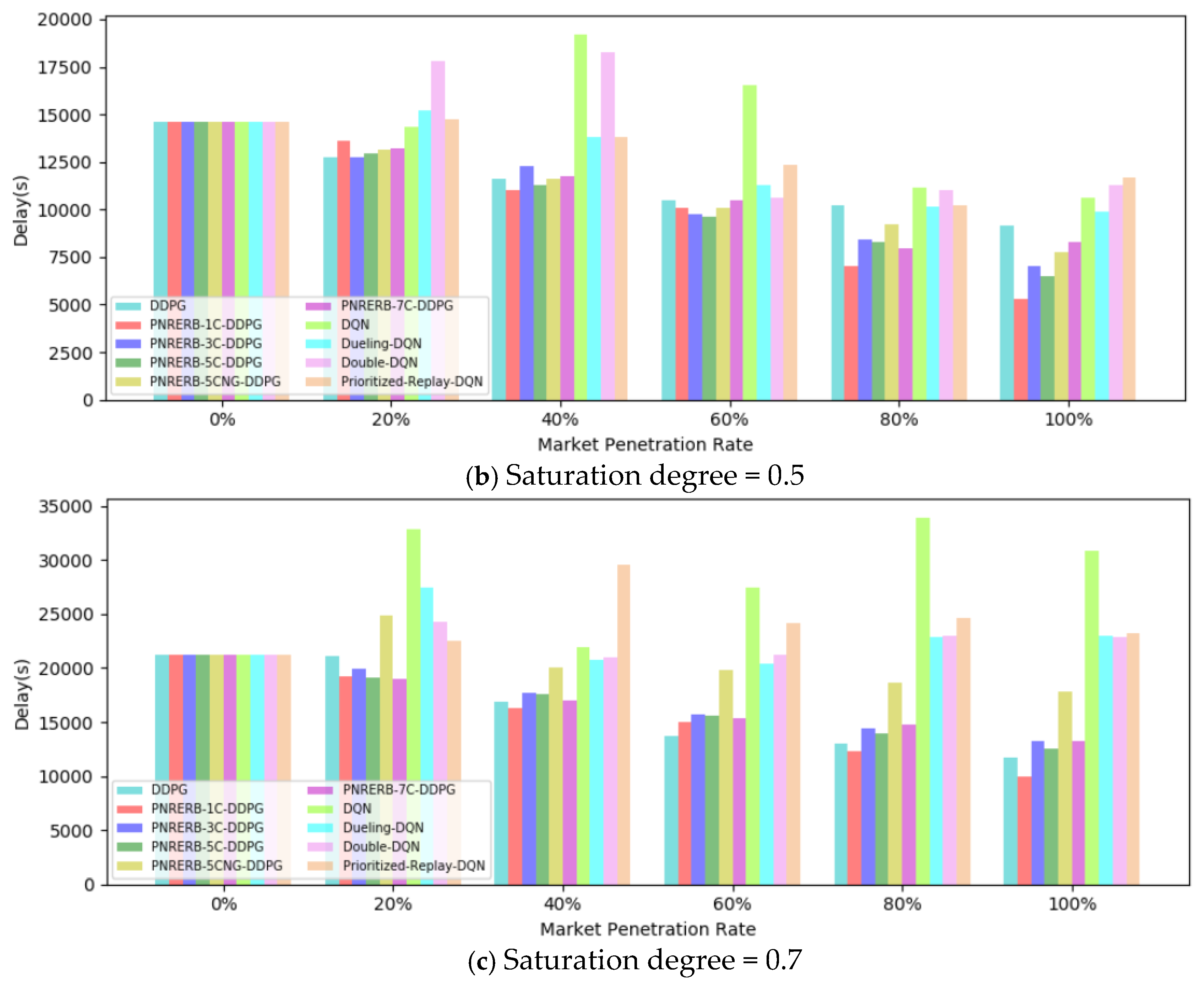
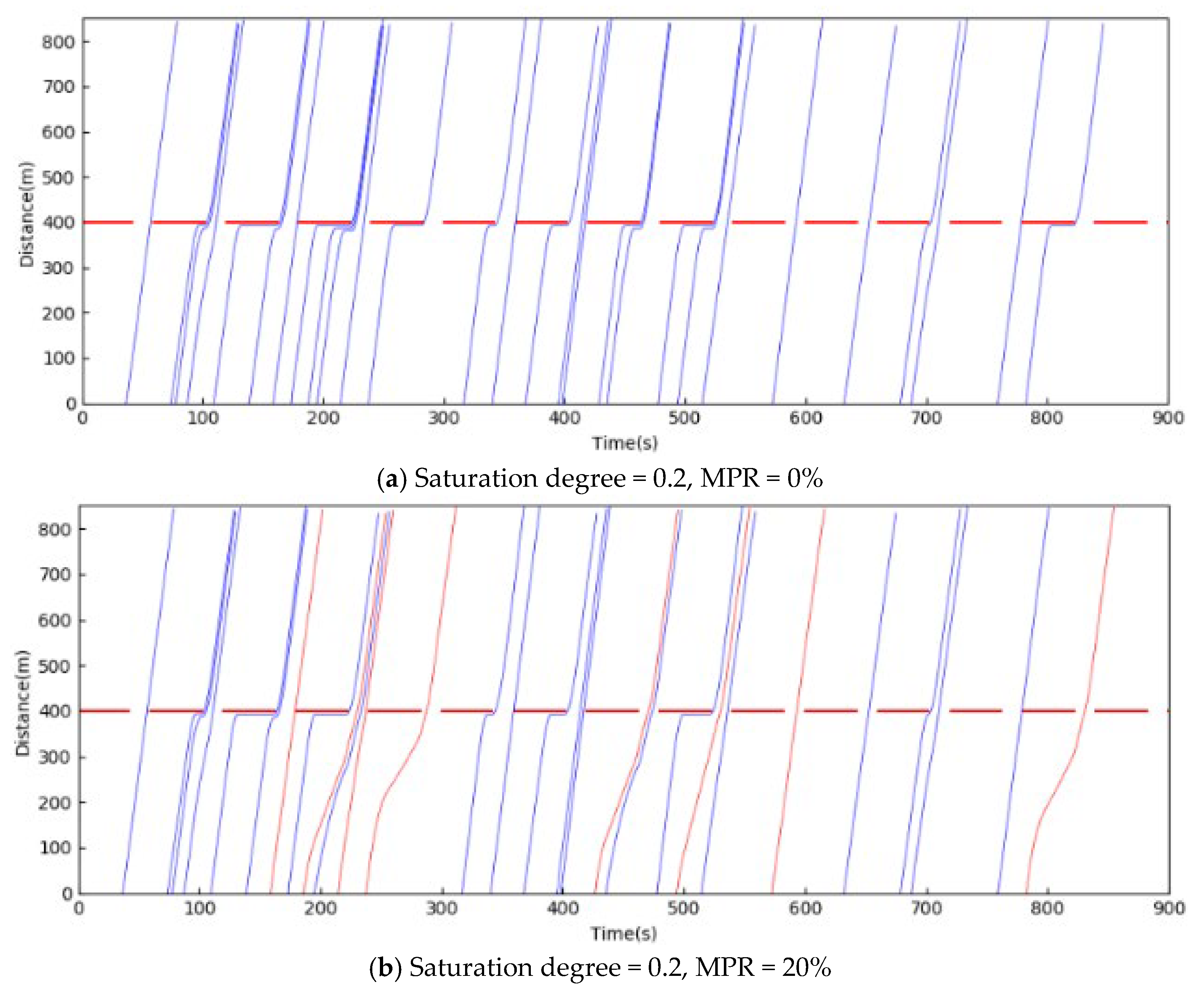
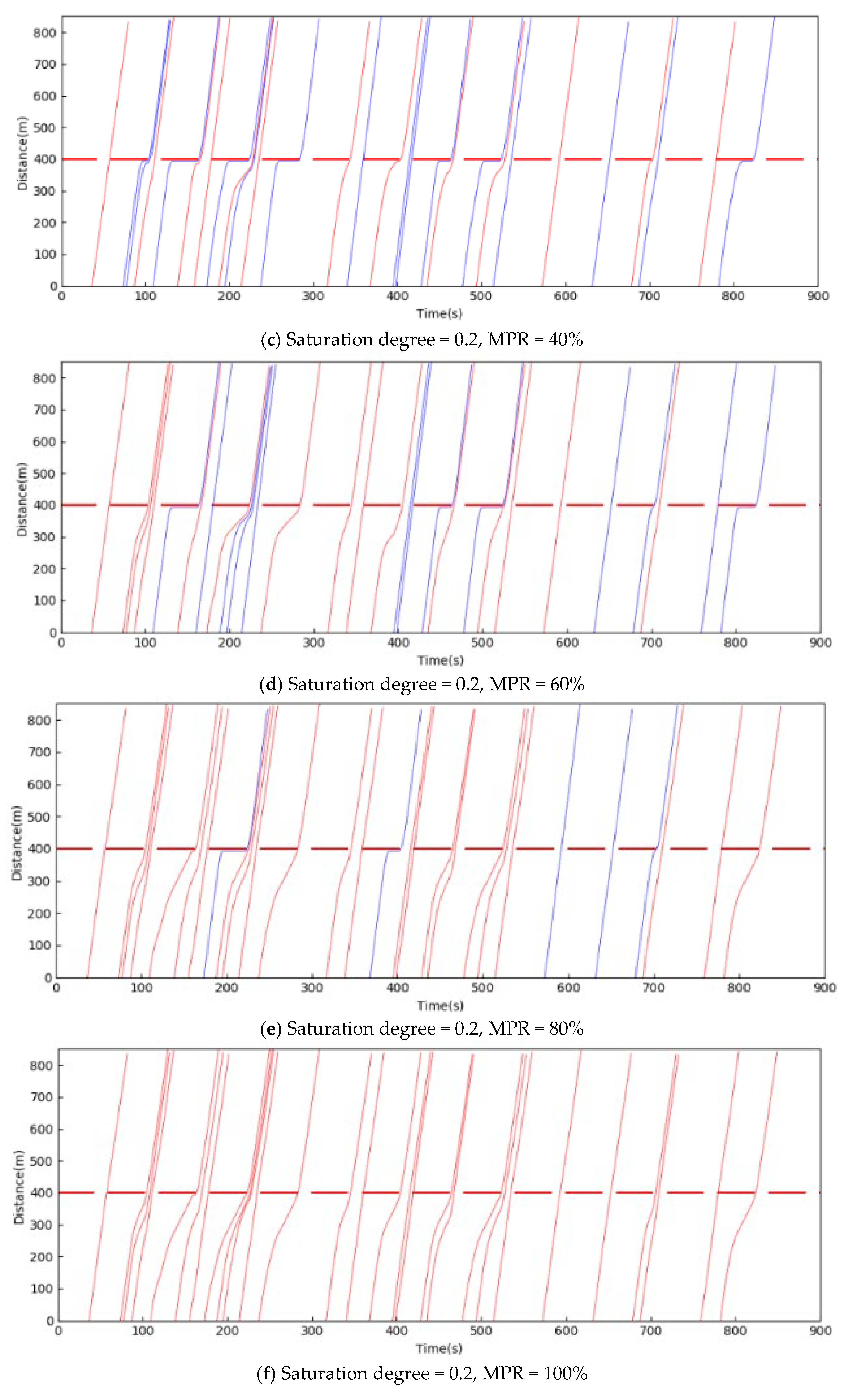
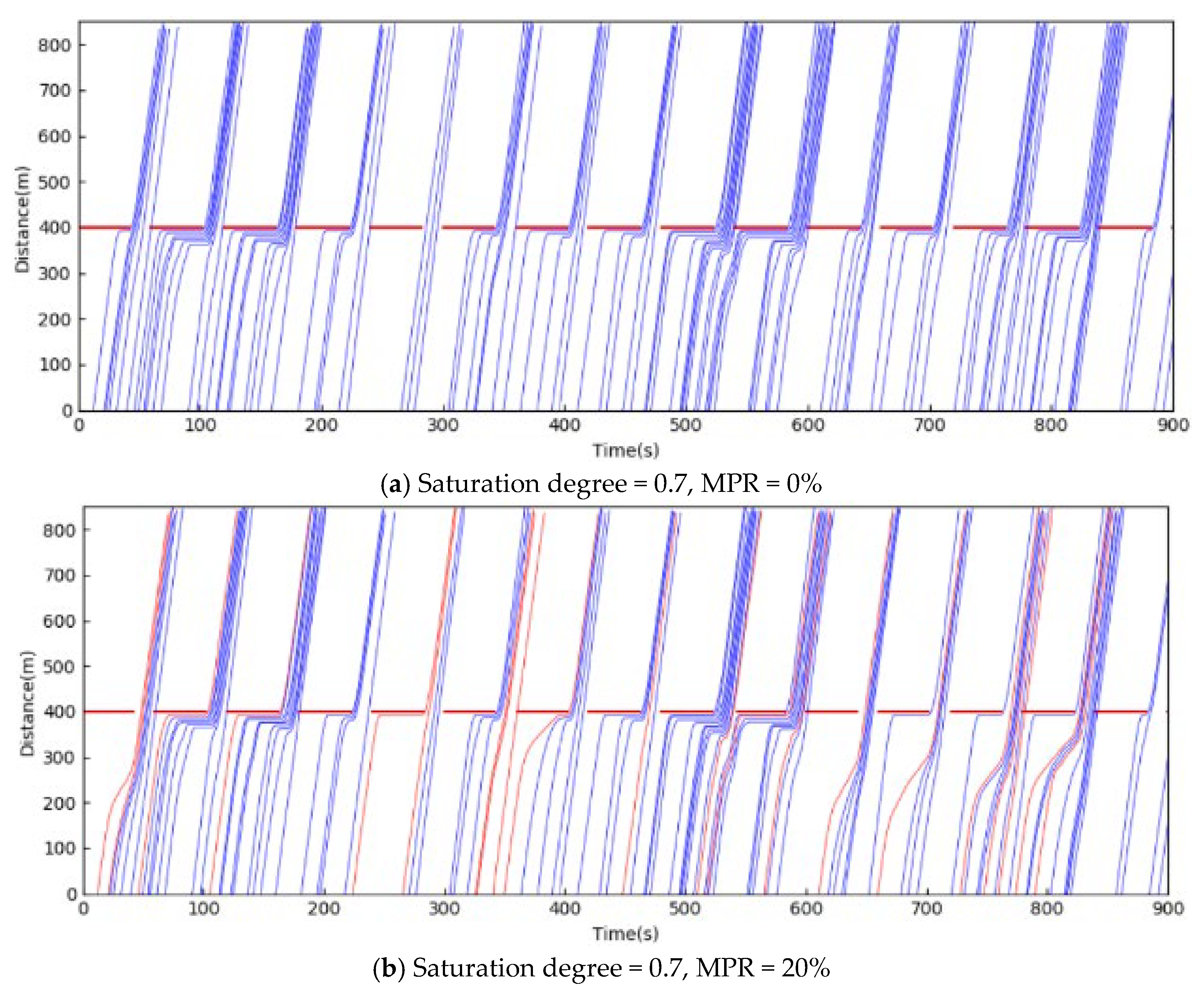
5. Simulation
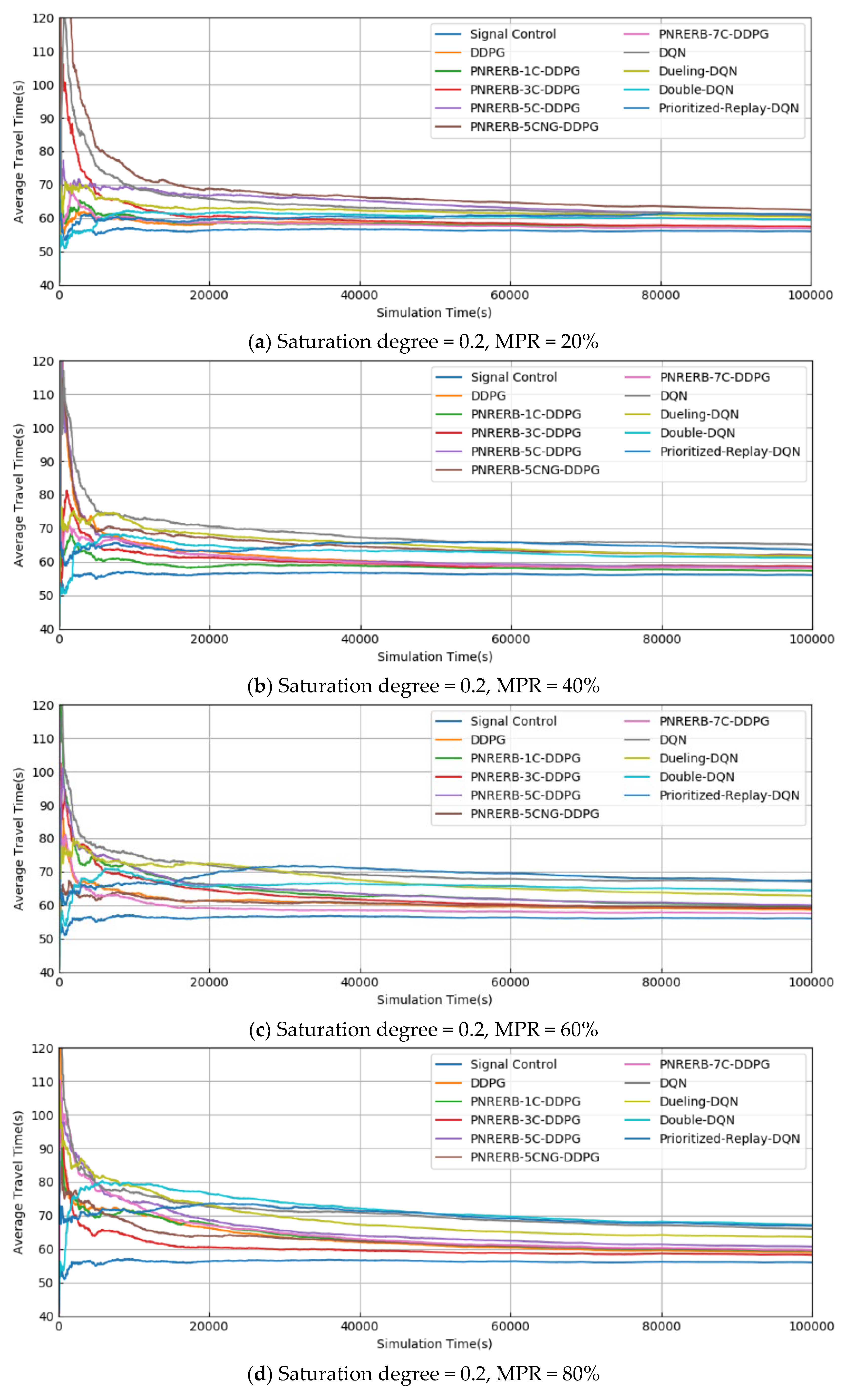
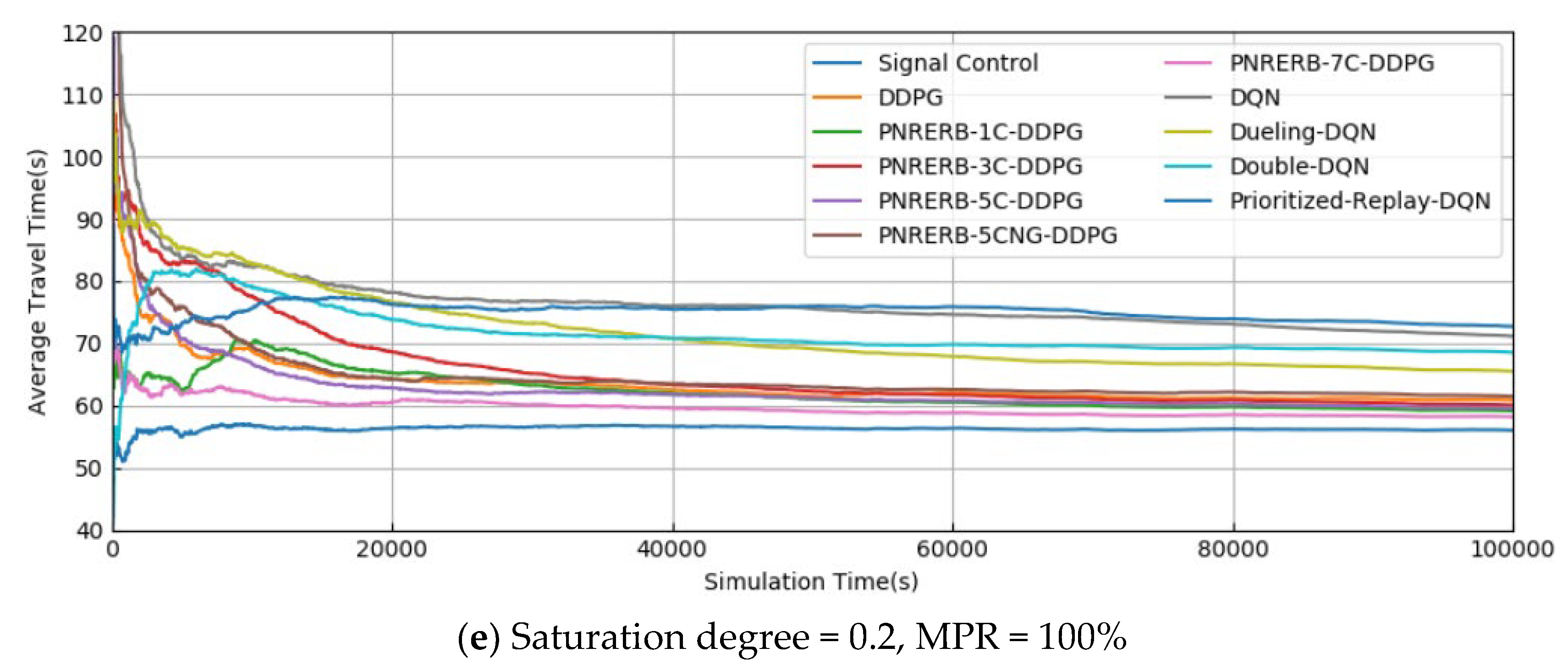
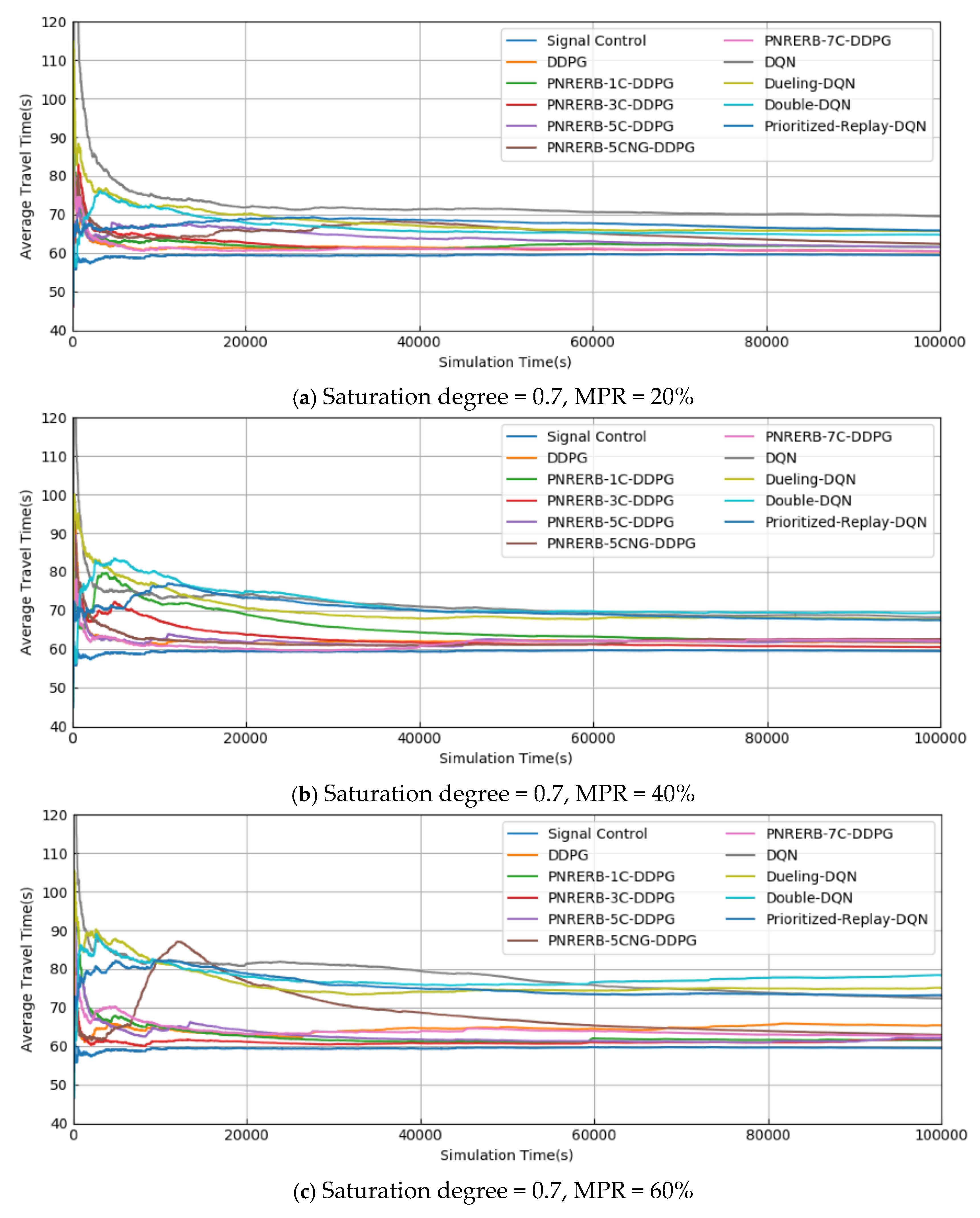
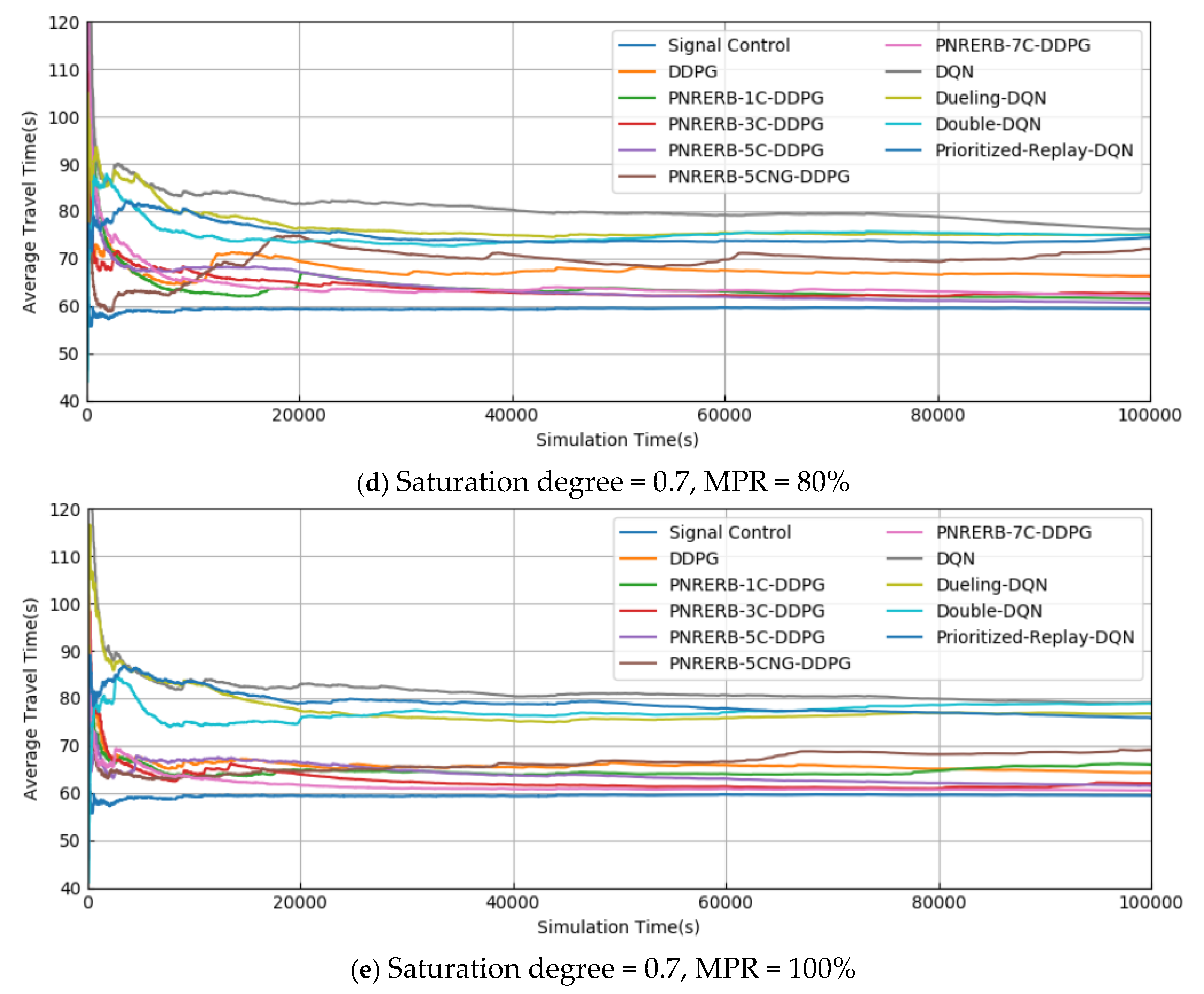
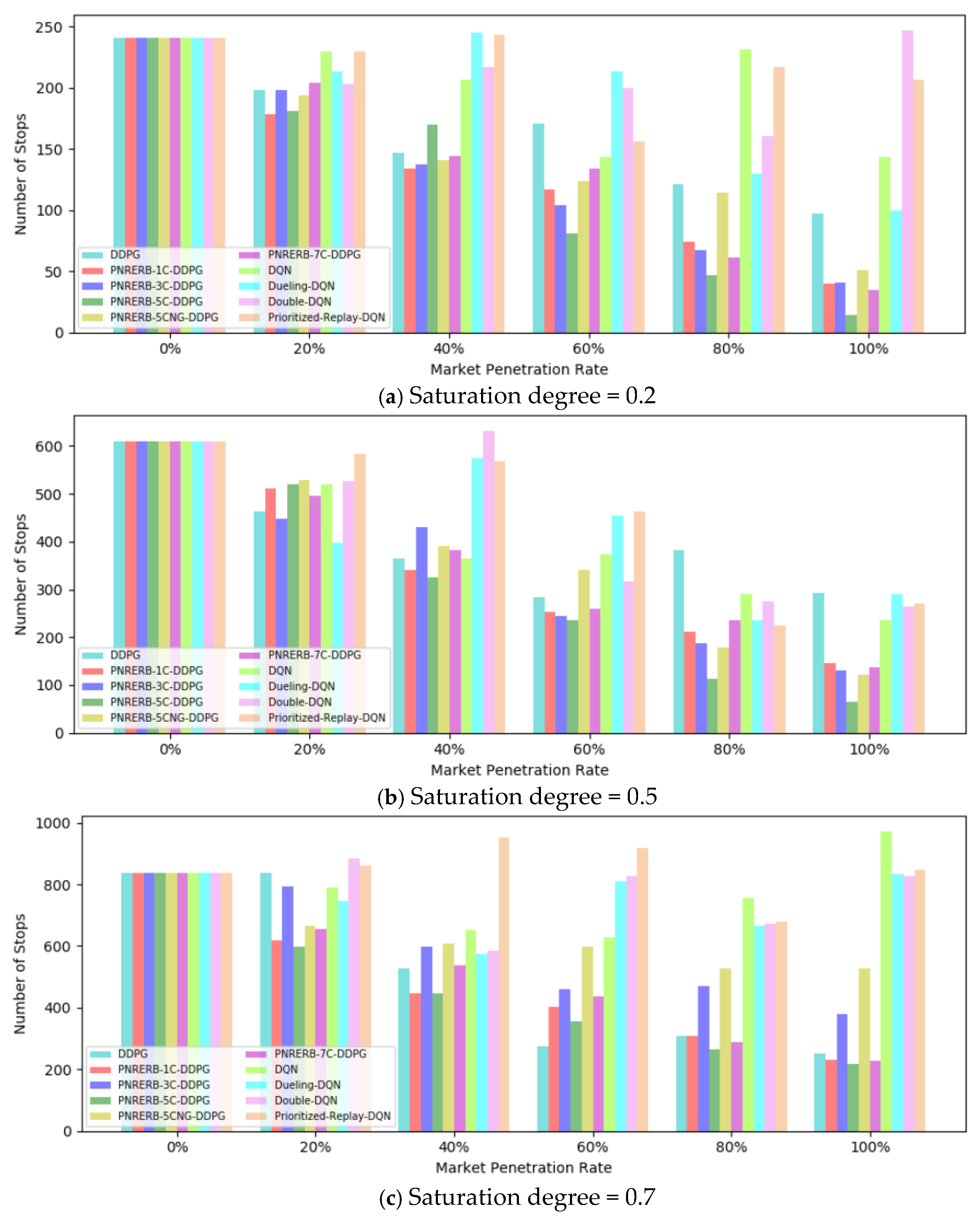
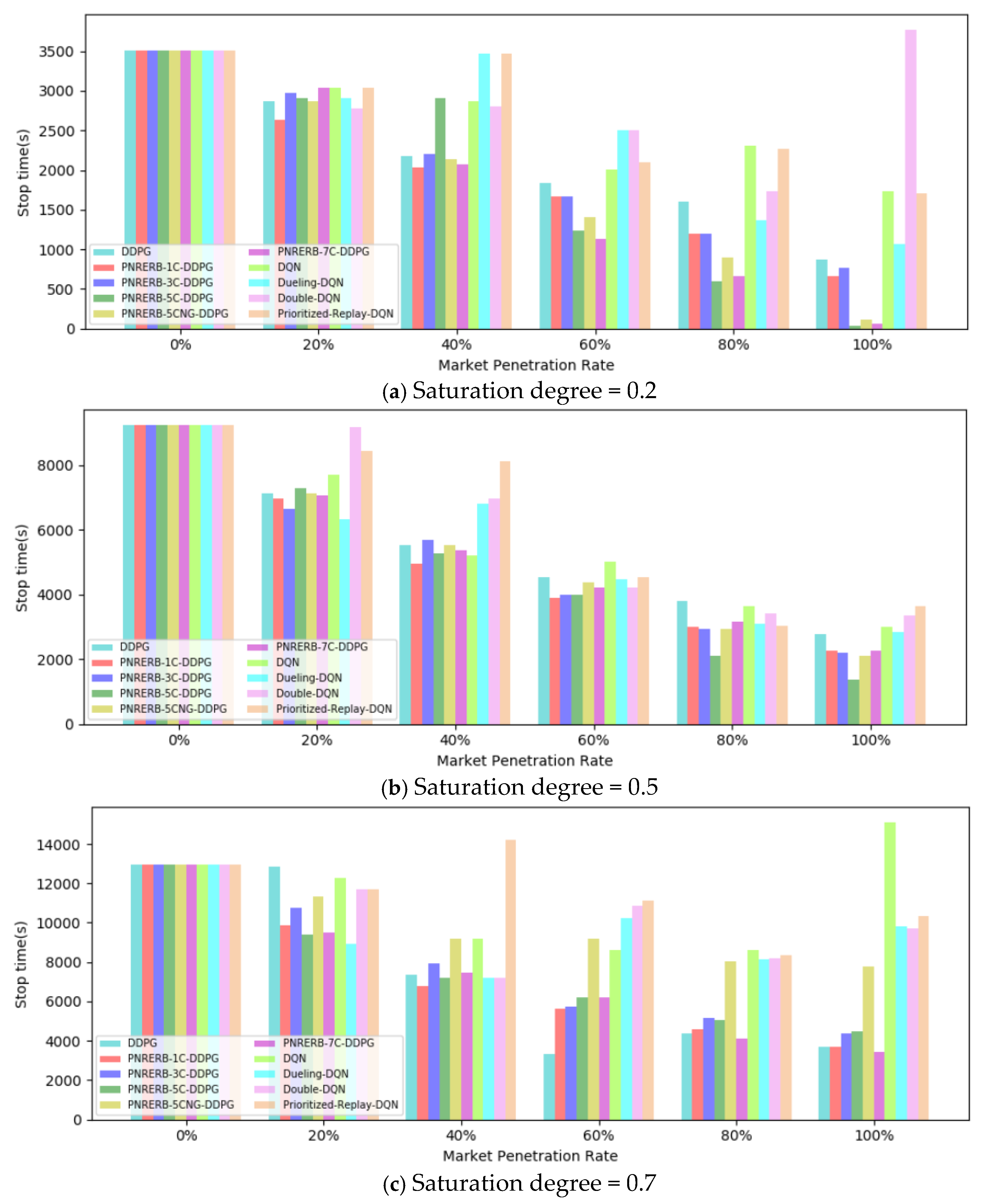
5.1. Training Results
5.2. Test Results
6. Conclusions and Prospect
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Methods | Actor Network Structure and Parameters | Critic Network Structure and Parameters |
|---|---|---|
| DDPG method | 100(relu) + 100(relu) + Dropout(0.8) + 50(sigmoid) | 128(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) |
| PNRERB-1C-DDPG method | 100(relu) + 100(relu) + Dropout(0.8) + 50(sigmoid) | 128(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) |
| PNRERB-3C-DDPG method | 100(relu) + 100(relu) + Dropout(0.8) + 50(sigmoid) | 100(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 128(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 128(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) |
| PNRERB-5C-DDPG method | 100(relu) + 100(relu) + Dropout(0.8) + 50(sigmoid) | 100(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 128(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 128(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 100(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 118(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) |
| PNRERB-5CNG-DDPG method | 100(relu) + 100(relu) + Dropout(0.8) + 50(sigmoid) | 100(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 128(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 128(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 100(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 118(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) |
| PNRERB-7C-DDPG method | 100(relu) + 100(relu) + Dropout(0.8) + 50(sigmoid) | 100(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 128(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 128(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 100(relu) + 128(relu) + Dropout(0.8) + 64(leaky_relu) 118(relu) + 100(relu) + Dropout(0.9) + 50(leaky_relu) 130(relu) + 100(relu) + Dropout(0.8) + 64(leaky_relu) 120(relu) + 118(relu) + Dropout(0.9) + 50(leaky_relu) |
| Methods | Critic Network Structure and Parameters |
|---|---|
| DQN method | 128(relu)+100(relu)+ Dropout(0.9)+50(leaky_relu) |
| Dueling-DQN method | 128(relu)+100(relu)+ dropout(0.9)+50(leaky_relu) |
| Double-DQN method | 128(relu)+100(relu)+ dropout(0.9)+50(leaky_relu) |
| Prioritized-Replay-DQN method | 128(relu)+100(relu)+ dropout(0.9)+50(leaky_relu) |
References
- Zhang, M.; Wang, Y.; Zheng, B.; Zhang, K. Application of artificial intelligence in autonomous vehicles. Auto Ind. Res. 2019, 3, 2–7. [Google Scholar]
- Zhou, B. 2019 autonomous vehicle maturity index report. China Information World, 9 September 2019. [Google Scholar]
- Xie, X.; Wang, Z. SIV-DSS: Smart In-Vehicle Decision Support System for driving at signalized intersections with V2I communication. Transp. Res. C 2018, 90, 181–197. [Google Scholar] [CrossRef]
- Vahidi, A.; Sciarretta, A. Energy saving potentials of connected and automated vehicles. Transp. Res. C 2018, 95, 822–843. [Google Scholar] [CrossRef]
- Hou, X.; Wang, L.; Zhang, Q. Thoughts on the development path of auto insurance in the era of 5G driverless cars. Technol. Econ. Guide 2019, 25, 4–6. [Google Scholar]
- Zhang, Z.; Li, M.; Lin, X.; Wang, Y.; He, F. Multistep speed prediction on traffic networks: A deep learning approach considering spatio-temporal dependencies. Transp. Res. C 2019, 105, 297–322. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Hou, Z.; Feng, Y.; Yin, C. Data-driven approximate Q-learning stabilization with optimality error bound analysis. Automatica 2019, 103, 435–442. [Google Scholar] [CrossRef]
- Zhang, W.; Gai, J.; Zhang, Z.; Tang, L.; Liao, Q.; Ding, Y. Double-DQN based path smoothing and tracking control method for robotic vehicle navigation. Comput. Electron. Agric. 2019, 166, 104985. [Google Scholar] [CrossRef]
- Aslani, M.; Seipel, S.; Mesgari, M.S.; Wiering, M. Traffic signal optimization through discrete and continuous reinforcement learning with robustness analysis in downtown Tehran. Adv. Eng. Infor. 2018, 38, 639–655. [Google Scholar] [CrossRef]
- Genders, W.; Razavi, S. Evaluating reinforcement learning state representations for adaptive traffic signal control. Procedia Comput. Sci. 2018, 130, 26–33. [Google Scholar] [CrossRef]
- Belletti, F.; Haziza, D.; Gomes, G.; Bayen, A.M. Expert Level control of Ramp Metering based on Multi-task Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1198–1207. [Google Scholar] [CrossRef]
- Wang, P.; Chan, C. Formulation of Deep Reinforcement Learning Architecture Toward Autonomous Driving for On-Ramp Merge. In Proceedings of the IEEE 20th International Conference on ITS, Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep Reinforcement Learning framework for Autonomous Driving. Electron. Imag. 2017, 19, 70–76. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y. Research of Traffic Signal Control in Urban Area based on Cooperative Vehicle Infrastructure System. Master’s Thesis, North China University of Technology, Beijing, China, 2017. [Google Scholar]
- Li, Z.; Elefteriadou, L.; Ranka, S. Signal control optimization for automated vehicles at isolated signalized intersections. Transp. Res. C 2014, 49, 1–18. [Google Scholar] [CrossRef]
- Sun, X. Estimation of Emission at Signalized Intersection with Vehicle to Infrastructure Communication. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Guo, Y. Research and Implementation of Eco-Driving Guidance System for Intersection. Master’s Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Wang, X. Traffic Signal Coordination Control and Optimization for Urban Arterials Considering the Emission of Platoon. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- Li, D. Distinguishing Method of Arterial Fleet Considering Minor Traffic Flow. Master’s Thesis, Jilin University, Changchun, China, 2017. [Google Scholar]
- Zhou, B. Urban Traffic Signal Control Based on Connected Vehicle Simulation Platform. Master’s Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Yu, C.; Feng, Y.; Liu, H.X.; Ma, W.; Yang, X. Integrated optimization of traffic signals and vehicle trajectories at isolated urban intersections. Transp. Res. B 2018, 112, 89–112. [Google Scholar] [CrossRef] [Green Version]
- Liao, R. Eco-Driving of Vehicle Platoons in Cooperative Vehicle-Infrastructure System at Signalized Intersections. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Zhao, W.M.; Ngoduy, D.; Shepherd, S.; Liu, R.; Papageorgiou, M. A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalised intersection. Transp. Res. C 2018, 95, 802–821. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Wu, X. Eco-driving advisory strategies for a platoon of mixed gasoline and electric vehicles in a connected vehicle system. Transp. Res. D 2018, 63, 907–922. [Google Scholar] [CrossRef]
- Gong, S.; Du, L. Cooperative platoon control for a mixed traffic flow including human drive vehicles and connected and autonomous vehicles. Transp. Res. B 2018, 116, 25–61. [Google Scholar] [CrossRef]
- Kalantari, R.; Motro, M.; Ghosh, J.; Bhat, C. A distributed, collective intelligence framework for collision-free navigation through busy intersections. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1378–1383. [Google Scholar]
- Shi, J.; Qiao, F.; Li, Q.; Yu, L.; Hu, Y. Application and Evaluation of the Reinforcement Learning Approach to Eco-Driving at Intersections under Infrastructure-to-Vehicle Communications. Transp. Res. Rec. 2018, 2672, 89–98. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Nishio, K. Reinforcement Learning of Driver Receiving Traffic Signal Information for Passing through Signalized Intersection at Arterial Road. Transp. Res. Procedia 2019, 37, 449–456. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. Comput. Sci. 2015, 8, A187. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on Machine Learning (ICML), Beijing, China, 21–26 June 2014. [Google Scholar]
- Witten, I.H. An adaptive optimal controller for discrete-time Markov environments. Inf. Control 1977, 34, 286–295. [Google Scholar] [CrossRef] [Green Version]
- Zuo, S.; Wang, Z.; Zhu, X.; Ou, Y. Continuous reinforcement learning from human demonstrations with integrated experience replay for autonomous driving. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, 5–8 December 2017; pp. 2450–2455. [Google Scholar]
- Zhu, M.; Wang, X.; Wang, Y. Human-like autonomous car-following model with deep reinforcement learning. Transp. Res. C 2018, 97, 348–368. [Google Scholar] [CrossRef] [Green Version]
- Xu, J. Intersection blind spot collision avoidance technology based on Vehicle Infrastructure Cooperative Systems. Master’s Thesis, Tianjin University of Technology and Education, Tianjin, China, 2016. [Google Scholar]
- Jiang, H. Research on eco-driving control at signalized intersections under connected and automated vehicles environment. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Sutton, R.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Wang, X.; He, H.; Xu, X. Reinforcement learning algorithm for partially observable Markov decision processes. Control Decis. 2004, 19, 1263–1266. [Google Scholar]
- Lin, L.J. Reinforcement Learning for Robots Using Neural Networks; School of Computer Science, Carnegie-Mellon Univ.: Pittsburgh, PA, USA, 1993. [Google Scholar]
- Wu, J.; Wang, R.; Li, R.; Zhang, H.; Hu, X. Multi-critic DDPG Method and Double Experience Replay. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 165–171. [Google Scholar]







| CAV | HV | ||
|---|---|---|---|
| Desired speed limit | 70 km/h | Desired speed | 70 km/h |
| Minimum speed limit | 0 km/h | Minimum speed | 0 km/h |
| Maximum acceleration | 3.5 m/s2 | ||
| Minimum deceleration | −4 m/s2 | ||
| Saturation Degree = 0.2 | |||||||||||
| Benchmark | DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M0 | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 0% | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 | 56.0 |
| 20% | / | 57.3 | 57.3 | 57.4 | 60.5 | 62.4 | 56.9 | 61.0 | 60.2 | 59.4 | 61.0 |
| 40% | / | 58.0 | 57.3 | 58.5 | 58.2 | 61.9 | 58.0 | 65.0 | 61.5 | 61.1 | 63.4 |
| 60% | / | 58.6 | 59.7 | 59.0 | 60.0 | 59.3 | 57.5 | 67.0 | 62.8 | 64.3 | 67.5 |
| 80% | / | 59.0 | 59.4 | 58.3 | 60.7 | 59.6 | 59.7 | 66.0 | 63.6 | 67.1 | 66.9 |
| 100% | / | 60.9 | 59.1 | 60.0 | 59.5 | 61.4 | 58.2 | 71.1 | 65.5 | 68.5 | 72.7 |
| Saturation Degree = 0.5 | |||||||||||
| Benchmark | DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M0 | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 0% | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 | 57.6 |
| 20% | / | 58.7 | 59.9 | 58.8 | 58.7 | 61.2 | 58.7 | 63.3 | 63.2 | 62.7 | 62.8 |
| 40% | / | 61.1 | 58.5 | 58.8 | 57.9 | 61.9 | 58.9 | 64.4 | 63.5 | 67.8 | 65.2 |
| 60% | / | 60.2 | 59.4 | 59.2 | 59.1 | 64.2 | 60.7 | 70.6 | 66.7 | 70.0 | 74.5 |
| 80% | / | 60.9 | 60.6 | 60.3 | 59.9 | 68.4 | 59.6 | 75.3 | 68.3 | 72.0 | 64.6 |
| 100% | / | 66.6 | 62.2 | 62.8 | 58.8 | 69.8 | 61.5 | 75.3 | 73.1 | 74.2 | 67.6 |
| Saturation Degree = 0.7 | |||||||||||
| Benchmark | DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M0 | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 0% | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 | 59.4 |
| 20% | / | 60.3 | 61.5 | 60.4 | 61.5 | 62.4 | 60.4 | 69.5 | 65.7 | 64.7 | 65.8 |
| 40% | / | 62.1 | 62.3 | 60.9 | 62.3 | 62.5 | 62.6 | 73.1 | 70.5 | 72.4 | 69.4 |
| 60% | / | 65.3 | 61.6 | 61.8 | 62.0 | 62.8 | 62.6 | 72.4 | 75.0 | 78.3 | 73.2 |
| 80% | / | 66.3 | 61.5 | 62.6 | 60.6 | 72.0 | 62.0 | 76.1 | 75.1 | 75.0 | 74.4 |
| 100% | / | 64.7 | 66.5 | 62.5 | 62.0 | 69.1 | 61.0 | 78.0 | 76.7 | 76.8 | 75.8 |
| Saturation Degree = 0.2 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 17 | 26 | 17 | 24 | 19 | 15 | 4 | 11 | 15 | 4 |
| 40% | 39 | 44 | 43 | 29 | 41 | 40 | 14 | −1 | 10 | −1 |
| 60% | 29 | 51 | 56 | 66 | 48 | 44 | 40 | 11 | 17 | 35 |
| 80% | 49 | 69 | 72 | 80 | 52 | 74 | 4 | 46 | 33 | 10 |
| 100% | 59 | 83 | 82 | 94 | 78 | 85 | 40 | 58 | −2 | 14 |
| Saturation Degree = 0.5 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 23 | 16 | 26 | 14 | 13 | 18 | 14 | 34 | 13 | 4 |
| 40% | 40 | 44 | 29 | 46 | 35 | 37 | 40 | 5 | −3 | 6 |
| 60% | 53 | 58 | 59 | 61 | 44 | 57 | 38 | 25 | 48 | 24 |
| 80% | 37 | 65 | 69 | 81 | 70 | 61 | 52 | 61 | 54 | 63 |
| 100% | 52 | 76 | 78 | 89 | 79 | 77 | 61 | 52 | 56 | 55 |
| Saturation Degree = 0.7 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 0 | 26 | 5 | 28 | 20 | 21 | 5 | 11 | −5 | −2 |
| 40% | 36 | 46 | 28 | 46 | 27 | 35 | 22 | 31 | 30 | −13 |
| 60% | 67 | 52 | 45 | 57 | 28 | 47 | 24 | 3 | 1 | −9 |
| 80% | 63 | 63 | 43 | 68 | 36 | 65 | 9 | 20 | 19 | 18 |
| 100% | 69 | 72 | 54 | 73 | 36 | 72 | −16 | 0 | 1 | −1 |
| Saturation Degree = 0.2 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 18 | 24 | 15 | 17 | 18 | 13 | 13 | 17 | 20 | 13 |
| 40% | 38 | 41 | 37 | 17 | 39 | 40 | 18 | 1 | 20 | 1 |
| 60% | 47 | 52 | 52 | 64 | 59 | 67 | 42 | 28 | 28 | 40 |
| 80% | 54 | 65 | 65 | 82 | 74 | 80 | 34 | 60 | 50 | 35 |
| 100% | 75 | 80 | 78 | 99 | 96 | 98 | 50 | 69 | −7 | 51 |
| Saturation Degree = 0.5 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 22 | 24 | 28 | 21 | 22 | 23 | 16 | 31 | 1 | 8 |
| 40% | 40 | 46 | 38 | 42 | 40 | 42 | 43 | 26 | 24 | 12 |
| 60% | 50 | 57 | 57 | 57 | 52 | 54 | 45 | 51 | 54 | 50 |
| 80% | 58 | 67 | 68 | 77 | 68 | 65 | 60 | 66 | 62 | 67 |
| 100% | 70 | 75 | 76 | 85 | 77 | 75 | 67 | 69 | 63 | 60 |
| Saturation Degree = 0.7 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 1 | 23 | 16 | 27 | 12 | 26 | 5 | 30 | 9 | 9 |
| 40% | 43 | 47 | 38 | 44 | 29 | 42 | 29 | 44 | 44 | −9 |
| 60% | 74 | 56 | 55 | 52 | 29 | 52 | 33 | 20 | 16 | 14 |
| 80% | 66 | 64 | 60 | 61 | 38 | 68 | 33 | 37 | 36 | 35 |
| 100% | 71 | 71 | 66 | 65 | 39 | 73 | −16 | 24 | 24 | 20 |
| Saturation Degree = 0.2 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 12 | 16 | 11 | 12 | 8 | 12 | 6 | 7 | 11 | −3 |
| 40% | 26 | 31 | 28 | 18 | 13 | 33 | 12 | −2 | 8 | −1 |
| 60% | 41 | 41 | 41 | 51 | 31 | 41 | 25 | 20 | 16 | 18 |
| 80% | 43 | 61 | 57 | 73 | 50 | 63 | 18 | 33 | 36 | 18 |
| 100% | 64 | 72 | 69 | 93 | 64 | 67 | 26 | 51 | −2 | 33 |
| Saturation Degree = 0.5 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 12 | 6 | 12 | 11 | 10 | 9 | 1 | −4 | −21 | −1 |
| 40% | 20 | 24 | 16 | 22 | 20 | 19 | −31 | 5 | −25 | 5 |
| 60% | 28 | 31 | 33 | 33 | 31 | 28 | −13 | 22 | 27 | 15 |
| 80% | 30 | 51 | 42 | 43 | 36 | 45 | 23 | 30 | 24 | 30 |
| 100% | 37 | 63 | 51 | 55 | 46 | 43 | 27 | 32 | 22 | 19 |
| Saturation Degree = 0.7 (%) | ||||||||||
| DDPG-Based Methods | DQN-Based Methods | |||||||||
| MPR | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
| 20% | 1 | 9 | 5 | 9 | −17 | 10 | −54 | −29 | −14 | −5 |
| 40% | 20 | 23 | 16 | 17 | 5 | 20 | −3 | 2 | 1 | −39 |
| 60% | 35 | 29 | 25 | 26 | 6 | 27 | −29 | 3 | −0 | −13 |
| 80% | 38 | 42 | 31 | 34 | 11 | 30 | −60 | −8 | −8 | −16 |
| 100% | 44 | 52 | 37 | 41 | 16 | 37 | −45 | −8 | −7 | −9 |
| Methods | MPR | Saturation Degree = 0.2 | Saturation Degree = 0.5 | Saturation Degree = 0.7 | ||||
|---|---|---|---|---|---|---|---|---|
| TFC (L) | TEE (kg) | TFC (L) | TEE (kg) | TFC (L) | TEE (kg) | |||
| Benchmark | M0 | 0% | 13.66 | 31.57 | 34.38 | 79.54 | 49.18 | 113.80 |
| DDPG-based methods | M1 | 20% | 13.77 | 31.83 | 34.87 | 80.69 | 49.22 | 113.89 |
| M2 | 13.67 | 31.60 | 34.40 | 79.59 | 49.39 | 114.29 | ||
| M3 | 13.71 | 31.70 | 34.29 | 79.32 | 49.14 | 113.71 | ||
| M4 | 13.82 | 31.94 | 34.36 | 79.49 | 49.39 | 114.31 | ||
| M5 | 14.02 | 32.43 | 34.37 | 79.51 | 52.56 | 121.65 | ||
| M6 | 13.65 | 31.54 | 34.50 | 79.82 | 49.00 | 113.39 | ||
| DQN-based methods | M7 | 14.17 | 32.79 | 35.97 | 83.31 | 59.82 | 138.72 | |
| M8 | 14.18 | 32.82 | 37.07 | 85.92 | 56.62 | 131.21 | ||
| M9 | 13.99 | 32.37 | 38.12 | 88.28 | 53.64 | 124.24 | ||
| M10 | 14.91 | 34.52 | 35.89 | 83.12 | 52.45 | 121.54 | ||
| DDPG-based methods | M1 | 40% | 13.66 | 31.57 | 34.48 | 79.79 | 49.38 | 114.30 |
| M2 | 13.63 | 31.51 | 34.38 | 79.53 | 48.96 | 113.28 | ||
| M3 | 14.44 | 33.39 | 34.40 | 79.59 | 48.89 | 113.15 | ||
| M4 | 13.63 | 31.54 | 34.40 | 79.59 | 49.94 | 115.59 | ||
| M5 | 14.46 | 33.43 | 34.43 | 79.67 | 50.27 | 116.35 | ||
| M6 | 13.63 | 31.52 | 34.56 | 79.97 | 49.17 | 113.80 | ||
| DQN-based methods | M7 | 14.56 | 33.74 | 43.36 | 100.68 | 54.38 | 126.15 | |
| M8 | 14.50 | 33.62 | 36.69 | 84.99 | 53.57 | 124.12 | ||
| M9 | 14.77 | 34.18 | 39.93 | 92.46 | 53.62 | 124.27 | ||
| M10 | 14.52 | 33.62 | 35.73 | 82.75 | 61.12 | 141.98 | ||
| DDPG-based methods | M1 | 60% | 13.76 | 31.81 | 34.27 | 79.29 | 50.53 | 116.97 |
| M2 | 13.62 | 31.48 | 34.38 | 79.53 | 49.36 | 114.24 | ||
| M3 | 13.63 | 31.52 | 35.23 | 81.53 | 48.75 | 112.82 | ||
| M4 | 13.68 | 31.63 | 34.86 | 80.68 | 50.00 | 115.72 | ||
| M5 | 14.06 | 32.50 | 35.00 | 80.98 | 50.44 | 116.73 | ||
| M6 | 13.68 | 31.64 | 35.16 | 81.36 | 49.31 | 114.11 | ||
| DQN-based methods | M7 | 15.31 | 35.48 | 41.05 | 95.27 | 59.98 | 139.14 | |
| M8 | 14.15 | 32.76 | 36.31 | 84.16 | 52.12 | 128.73 | ||
| M9 | 14.79 | 34.26 | 36.61 | 84.86 | 53.34 | 128.99 | ||
| M10 | 15.81 | 36.72 | 37.23 | 85.02 | 58.53 | 135.74 | ||
| DDPG-based methods | M1 | 80% | 13.65 | 31.55 | 34.23 | 79.20 | 49.41 | 114.37 |
| M2 | 13.91 | 32.16 | 34.43 | 79.66 | 48.91 | 113.17 | ||
| M3 | 13.76 | 31.81 | 34.27 | 79.27 | 48.87 | 113.07 | ||
| M4 | 13.71 | 31.70 | 35.38 | 81.85 | 50.70 | 114.73 | ||
| M5 | 14.02 | 32.41 | 37.87 | 87.83 | 50.32 | 116.43 | ||
| M6 | 13.98 | 32.32 | 35.75 | 82.78 | 49.09 | 113.59 | ||
| DQN-based methods | M7 | 15.11 | 34.86 | 37.52 | 87.10 | 64.33 | 149.35 | |
| M8 | 16.00 | 37.07 | 37.45 | 86.84 | 52.34 | 123.54 | ||
| M9 | 14.60 | 33.81 | 37.34 | 87.02 | 52.69 | 124.63 | ||
| M10 | 14.98 | 34.73 | 37.41 | 86.72 | 55.64 | 132.56 | ||
| DDPG-based methods | M1 | 100% | 13.69 | 31.656 | 34. 45 | 79.70 | 49.64 | 114.91 |
| M2 | 13.71 | 31.697 | 34. 26 | 79.26 | 49.09 | 113.58 | ||
| M3 | 13.71 | 31.707 | 34.16 | 79.02 | 49.08 | 113.57 | ||
| M4 | 14.17 | 32.783 | 35.58 | 82.30 | 51.29 | 118.69 | ||
| M5 | 14.21 | 32.855 | 38.38 | 89.04 | 50.03 | 115.76 | ||
| M6 | 13.76 | 31.816 | 35.25 | 81.53 | 49.12 | 113.64 | ||
| DQN-based methods | M7 | 17.83 | 41.360 | 38.08 | 88.43 | 69.53 | 161.24 | |
| M8 | 14.43 | 33.426 | 41.78 | 96.78 | 58.12 | 132.94 | ||
| M9 | 14.48 | 33.511 | 39.72 | 89.75 | 58.02 | 132.85 | ||
| M10 | 17.67 | 40.984 | 40.01 | 90.15 | 58.32 | 135.21 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Xue, Z.; Fan, D. Deep Reinforcement Learning Based Left-Turn Connected and Automated Vehicle Control at Signalized Intersection in Vehicle-to-Infrastructure Environment. Information 2020, 11, 77. https://doi.org/10.3390/info11020077
Chen J, Xue Z, Fan D. Deep Reinforcement Learning Based Left-Turn Connected and Automated Vehicle Control at Signalized Intersection in Vehicle-to-Infrastructure Environment. Information. 2020; 11(2):77. https://doi.org/10.3390/info11020077
Chicago/Turabian StyleChen, Juan, Zhengxuan Xue, and Daiqian Fan. 2020. "Deep Reinforcement Learning Based Left-Turn Connected and Automated Vehicle Control at Signalized Intersection in Vehicle-to-Infrastructure Environment" Information 11, no. 2: 77. https://doi.org/10.3390/info11020077
APA StyleChen, J., Xue, Z., & Fan, D. (2020). Deep Reinforcement Learning Based Left-Turn Connected and Automated Vehicle Control at Signalized Intersection in Vehicle-to-Infrastructure Environment. Information, 11(2), 77. https://doi.org/10.3390/info11020077





