2. Methods
This article presents a relation of the function in a congruence form , with and being the real and imaginary parts of , respectively, and, and being independent functions of Zeta, which are dependent only on and . This congruence has its source in the Riemann’s functional equation and the Gamma function whose variations and dependencies are investigated. The study is based on the specificities of the Zeta function, the Ksi function and the Gamma function, by analyzing them with respect to the aforementioned relations. The components and , formed of ripples, cancel each other out periodically and alternately, and thus cause on the critical line, in the neighborhood of these undulations, the emergence of an additional zero but, this time, common to both curves. The article thus provides a numerical illustration of the Riemann Hypothesis (RH).
The methodology flow chart is summarized in
Figure 1:
3. Materials and Preparatory Calculations
It is assumed that the reader is already familiar with the fundamentals of mathematics. There are many books that the reader can consult: a classic or standard book, which can be recommended to the reader interested in the specific subjects, is proposed in each following paragraph.
It is crucial to understand the behavior of the Zeta, Ksi and Gamma functions in the critical strip, in particular the values for which the real and imaginary parts cross zero, and the angles between the two parts, because they play an essential role in the RH. In this article, we use basic theorems to dissipate the illustration’s complexity. We therefore use the following theorems, results and formulas: Bézout’s theorem, Stirling’s formula, Taylor’s formula, and operations on complex numbers.
In order to facilitate the reading of the following sections, preparatory calculations by computer are grouped in this section. The reader can skip the development of the calculations at first reading, although they bring together the formation of the tools necessary for reasoning and understanding latter sections. In addition, this section represents a more substantial part of the computer work of this article. The study of the Ksi function’s numerical behavior requires power series expansions as a function of
, assuming that
is small compared to
. These computational developments require rigor and significant efforts; the calculations were checked by computer. We use the Python language [
22] and the SciPy ecosystem [
23] for all the computations and we visualize them using the matplotlib library [
24]; we use mpmath [
25] as an arbitrary-precision substitute for Python’s float/complex types and for functions (Gamma, Zeta), with arbitrary precision.
3.7. The Ksi Function of the Functional Equation
The Ksi function (
Figure 4) has remarkable properties that should be elucidated if we want to understand the RH. The Ksi function manages the symmetry in
and
of the Zeta function:
. The functional relationship, presented in various forms, is as follows:
However, to analyze the synchronization of the zeroing of the real and imaginary parts, the relation can be written symmetrically:
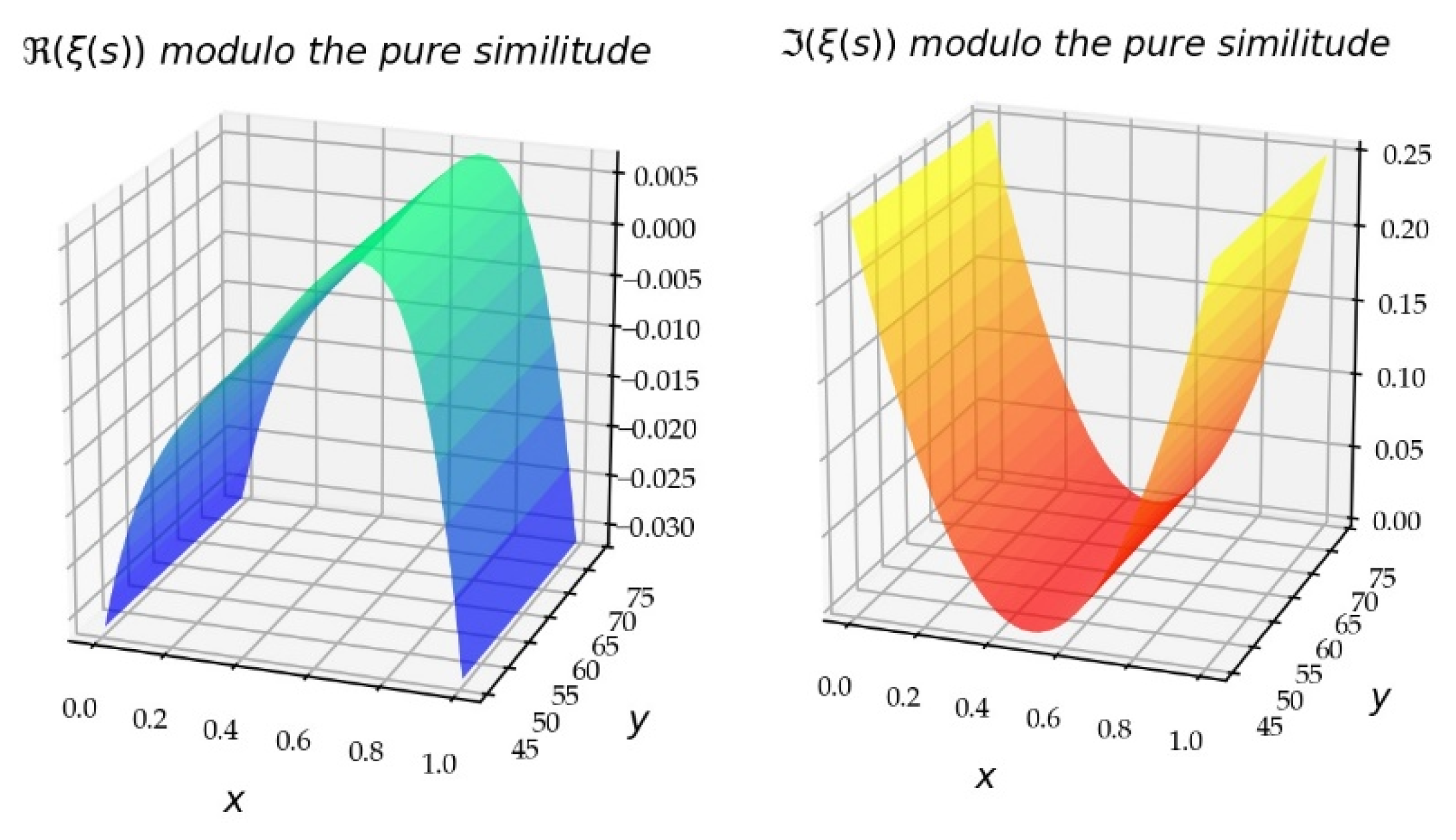
It is essential to focus on the various components of this function to observe the formation and gestation of this symmetry. The complex formation of symmetry is in fact located at the core of the Gamma function, which intermingles the variables and so vigorously that it is naive to hope to split all the components of this function into both independent parts, one function of , and the other of .
The set-up used in this article is: . The function , which is within a factor, a Gamma function ratio, intermingles the variables and , but the local angle between both surfaces (real and imaginary) shows a lesser degree of dependence compared to .
On the critical line, the ratio becomes the ratio of two conjugated Gamma functions, and the modulus of the function is . The function then behaves like undulations which vary between and . It is not, however, a perfect classic trigonometric function. The functional relation distorts the relationship between the Gamma functions, and therefore, the result between and , outside the critical line. In the Ksi formula, the ratio of Gamma functions severely destroys, along the axis, the obliquity of the undulations of the Gamma function, but this does not disappear completely. This is a primary result of this analysis of the Ksi function. In addition, the inverse of this function is: . In the decomposition of Ksi into elements, we must be able to find the inverse elements and better understand how symmetry works.
4. Results
This section first presents the computer results and the formula on the critical line and continues with a graphical presentation and a numerical calculation. Then, the section apprehends the calculations in the critical strip in order to prove that the points of the critical line are located on the limit of a property of the functional relation. Finally, the section presents a geometric interpretation of the functional equation, which clarifies the RH.
To understand the arrangements of both surfaces which contribute to the RH, the mechanisms of the joint undulations of the real and imaginary surfaces of the Zeta function and the Ksi function must be demystified. The local behavior of the Zeta and Ksi functions is mainly constructed in relation to the Gamma function. The Ksi function, which brings two symmetric values of the Zeta function into constant , is essentially a ratio of two Gamma functions. It is therefore essential to analyze and visualize the behavior of the Gamma function and the Ksi function in the critical strip, and to focus attention on the specific case of the critical line. The essential constraint is the functional equation which imposes a strong requirement to constant , between and .
4.3. Synthesis
The summary of formulas in critical strip
is as follows:
The summary of the formulas on the critical line
is as follows:
The decomposition architecture of angles in the critical strip and on the critical line, with the associated series angles, is summarized in
Table 3.
Our method extracts and disconnects from the Ksi function
, a homothety of ratio
and pure rotations of angle
, since the subgroup of the group of similarities, composed of homotheties and rotations, leaves non-trivial zeros invariant:
. The analysis is concentrated on the remainder
, in particular the existence of a potential symmetry in
and
, in the series of the remainder
. The Ksi function congruence, via this homothety and these rotations, is justified by a fundamental property of the Zeta function, which is the existence of an equivalence relation on the
axis. We split the critical line
:
into contiguous intervals
. In the interval
, we find the nth non-trivial zero with high probability. This segmentation organizes an equivalence relationship taking into account the fractional part
of the anamorphosed variable
, which we associate with two rotations
of angle
. These rotations drop the Ksi function undulations. This rotation angle
corresponds, on the critical line, to the alternative undulations (real part and imaginary part) of the function
. The ratio
also structures the Zeta function, with the particular values of
from
Table 4:
This angle arises in the distribution function of the presence of non-trivial zeros and in the ratio of the Gamma functions, at the origin of the Ksi function. The ratio is derived, among other things, from the Bernoulli number in the Gamma function series expansion. The rotation of angle dissolves the first term bias in the Riemann series.
The demonstration outline is therefore as follows. We are looking for a class of functions
, which cancels out the Zeta function, in order to identify the kernel of the morphism
. If such a function exists, it must satisfy the identity
for the pair of points
and
with coordinates
and
. Unfortunately the way in which the
and
coordinates are entangled at the heart of the Zeta function and of the Ksi function make it impossible to disentangle them, in order to exhibit a function
in the whole critical strip, both for the pair
and for the pair (
). Both non-separable coordinates in the ratio
unfortunately make this operation fruitless. This inability to decompose into unbreakable components of the relationship is evident in the expansion into series
. It is also explained by examining the Zeta derivative whose term
reveals that each term in the series muddles up coordinates with regard to the term
. This impossibility is also interpreted by the holomorphic function structure which is a conformal transformation (by locally preserving angles) whose angles in the critical strip are intimately linked to the unbreakable pair
. On the other hand, when
, the ratio becomes
and the angle
simply depends on
, so that
. So, there is indeed a relation on the critical line
:
The angle series , a function of , of sum function , is written as:
; warning:
In the class of functions , the two series, or , may be chosen, since in an underlying way, the relation governs the stability of both elements. The RH seems to be strengthened, since this identity is null only for .
The formula, decomposed into Ksi series, splits the influence of and coordinates: On the one hand, the amplitude of is , and on the other hand, the phase (the argument) of is more difficult to analyze because the pair is indissoluble. The deforming mechanism between and is generated by a similarity whose rotation angle is generated by the two pure rotations of angle and two digressive rotations of angle . The angle of rotations depends only on the fractional part of the anamorphosis of , and the angle depends inextricably on the pair . By the deformation of these lenses, the functions and become out of sync, because of the angle , more precisely because of , and this crisscross does not allow the conception of a Bézout identity between both parts, real and imaginary, of the Zeta function. However, the entanglement and the complexity of the angle disappear for . The angle no longer depends on at all.
In the critical strip, the functional equation makes it possible to write the Zeta function, within a homothety and a rotation, in a congruent manner:
The ratio of the two equivalent Zeta functions is a digressive series, which is unfortunately not a composition of perfect rotations . The remainder is a digressive series , the first order of which shows that the sum function of the angle inevitably entangles and. This residue prevents the conception of a relation in the critical strip (except ), but gives its holomorphic property to the Zeta function (conformal transformation: the angles are locally preserved, the small circle image is a circle). The characteristics (Riemann functional equation and Hadamard product formula) make it possible to distinctly separate the properties on both complementary sets, and . On the other hand, on the critical line, this remainder becomes , which is absorbed in a multiplicative digressive series, since , and this property makes it possible to write a relation .
6. Conclusions
It is conceptually difficult to mathematically conceive of a set of points on a complex surface, isolated from each other in a domain of the plane, especially if these regular points have no characteristics other than being located on the 0-level contours of the intersection of two wavy surfaces, real and imaginary, locally smooth and without singularity. One solution is to wrap this set of isolated points into a connected superset and to think about the algebraic properties of this superset. In the case of the Riemann function, the critical line is the superset that covers non-trivial zeros. The existence of a class of functions in the critical strip of which the kernel is the critical line makes it possible to complete the proof, without attempting to determine these zeros more precisely. Following this step, by using the analytical properties of the points of this function, non-trivial zeros can be identified and calculated.
In conclusion, the article presents a RH analysis with numerical computation methods. The study contribution follows from the examination of the two-angle conjunction of the Zeta function and of the Ksi function. On the one hand, the Zeta function has a remarkable property on the critical line: The real/imaginary ratio of the Zeta function is interpreted as the angle tangent that generates an equivalence class along the axis. On the other hand, the Ksi function is congruent, to within a homothety and a rotation, to a remainder series, whose sum function angle is not symmetrical with respect to the line . On the contrary, the residual congruent series intrinsically contains this symmetry on the line . This trigonometric property of the remainder series undoubtedly exists only on the critical line. It is therefore essentially an angular functional constraint of the holomorphic Zeta function and of the associated Ksi function, which is at the origin of the property of the RH. This constraint enigma is contained in the Gamma functions’ ratio .
The calculations made it possible to highlight, by a ring morphism , the formula , valid only on the critical line, which brings out an irreducible numerical series. This formula is an identity representing a synchronous balance between both parts , real and imaginary, of the Zeta function. This equipoise () is stable along the critical line , and topples outside of it, in the critical strip.
On the critical line, the elements and of the Zeta function cancel each other out alternately and periodically, in the middle of the interval , and at the start of the interval .
Stability allows both parts to systematically cancel themselves out at the same time, at an additional point, a non-trivial zero, in the neighborhood of each periodic and alternative zeroing of both parts . This cyclical phenomenon thus attests to the existence of equivalence classes of the zeroing of both surfaces according to the angle . It also substantiates the occurrence number of these representatives of equivalence classes, that is to say the potential number of zeros on this line .
In the critical strip, the Zeta function happens as two surfaces intersect irregularly. A
anamorphosis makes it possible to restore quasi-periodic waves. These waves are reflected isometrically on both sides
and
of the critical line, which act as a rectilinear mirror (
Figure 16). On the contrary, these waves are distorted by the prism of a convex lens that emphasizes the folds for
, and a concave lens that diminishes them for
. The Riemann functional equation provides the distortion link between the two lenses. The congruent transformation in the subgroup of similarities of the Ksi function makes it possible to remove the structural waves and reveal its background, which is a power series
whose angle is not symmetrical in
and
.
From Sainte-Pélagie prison, in 1831, Évariste Galois [
33], pioneer of the set theory outlook, mocking those who got lost in the maze of quadratures, advised researchers to “not jump with both feet into the calculations”. May this article prove that we have learned the lesson against this usual shortcoming, and that we have, at each step of the process, geometrically interpreted the transformations and clarified the path taken by the method.