A Self-Operating Time Crystal Model of the Human Brain: Can We Replace Entire Brain Hardware with a 3D Fractal Architecture of Clocks Alone?

Abstract

Time crystal was conceived in the 1970s as an autonomous engine made of only clocks to explain the life-like features of a virus. Later, time crystal was extended to living cells like neurons. The brain controls most biological clocks that regenerate the living cells continuously. Most cognitive tasks and learning in the brain run by periodic clock-like oscillations. Can we integrate all cognitive tasks in terms of running clocks of the hardware? Since the existing concept of time crystal has only one clock with a singularity point, we generalize the basic idea of time crystal so that we could bond many clocks in a 3D architecture. Harvesting inside phase singularity is the key. Since clocks reset continuously in the brain–body system, during reset, other clocks take over. So, we insert clock architecture inside singularity resembling brain components bottom-up and top-down. Instead of one clock, the time crystal turns to a composite, so it is poly-time crystal. We used century-old research on brain rhythms to compile the first hardware-free pure clock reconstruction of the human brain. Similar to the global effort on connectome, a spatial reconstruction of the brain, we advocate a global effort for more intricate mapping of all brain clocks, to fill missing links with respect to the brain’s temporal map. Once made, reverse engineering the brain would remain a mere engineering challenge.

1. Introduction

The universal quest to understand how a life form runs by itself gave birth to the concept of a time crystal in the 1970s [1,2]. A time crystal is a distinct periodic oscillation produced by a system when an external agent disrupts its natural periodic oscillation. A spatial crystal has three orthogonal axes, X, Y, and Z. A singularity in space is where mass is located, which builds a unit lattice. A time crystal has three orthogonal axes of phase, a singularity in phase is the domain where a new clock appears, and time symmetry breaks. Since a biological clock runs by itself, along the periodic path, it can do some work along its path, like an automated machine. Now, if the clock is disturbed, yet it returns to the original path, after a certain time, that’s not conventional programming, because one could disrupt the system in infinite possible ways. Still, the system figures out how to return to the original path [3]. That is life, a true autonomous engine. For nearly half a century, time crystal research to find an autonomous engine that would replace a life form has explored varieties of rhythmic cellular systems like heartbeats, lungs, ovulation, neuron spikes, etc. To re-assemble the disintegrated parts of a time crystal, reviving the initial phase difference between clocks is essential. Such a phase reset is abundant in biology [4,5]. Thus, biological systems have a memory to remember the phase gaps of various clocks. When the biological clocks are disturbed, chemically, physically, or by other means, they return following a unique path along the return route [6,7]; it creates new clocks. The intermediate clock, if returns periodically every time when the system is perturbed, the phase plots look like a crystal, so it was called time crystal in the 1970s [8]. To make a crystal, one has to fit multiple phase cycles inside a longer phase cycle, such nesting of phase is meticulously designed in biology [9]. The advancement of time crystal research was so profound that the researchers started mapping a catalog of intermediate or inherent clocks in the system. A pair of clocks, one that represents the system’s original periodic event and the perturbation clock, could change the relative diameter of the two, and that alone could give rise to infinite possible outcomes [10]. The attempts were made to catalog all significant outcomes in a singular plot. Since the system output looked like a meander flower, the plot used to be called meander flower garden [11]. The angle between the successive petals is exactly 2π⁄integer; the entire landscape is an array of integers [12]. A time crystal is an artwork of singularity points connected by phase, not a single point in it is real (real part of a complex number). There is no time, space, or mass; it is a network of phase [13]. The phase shift is the only event in the information processing, caused either by changing the input frequency [14] or by the intensity of the light pulse [15]. Time crystal represents any information as topology, and every topology or geometric shape is a single point or corner point in its higher topology.

One of the significant problems of time crystal research has been that it considered only one perturbation to the original clock, which could reset phase and move the system towards a singularity point, where the state that defines the clock becomes undefined [16,17]. The undefined biological clock means no decision could be made regarding the state of that periodically oscillating system. One could note that if there is only one perturbation, then only one singularity point would be active. However, if there are multiple perturbations one after the other, each perturbation would cause a distinct singularity point. It would mean that a single original clock would have multiple singularity points. Such a provision was never proposed or explored. It is necessary to generalize the number of participating clocks, if we want to integrate all clocks in a system using an integrated clock architecture. Since a pair of clocks, the original and the perturbing one, builds a meander flower garden [11,12], we need to introduce a concept whereby the petals of meander flowers could be isolated and built into one new meander flower. The idea would be like constructing a garden of garden of meander flowers, and the human brain model we propose here would be a generalization of earlier proposed meander flower garden [11,12].

There could be two primary events when we try to bind multiple clocks operating simultaneously in a system. First, a host clock’s system point would reach a sequence of singularity points one after another [18]. Second, in the singularity domain, another clock might get active. Exploring singularity domain as a region where the conditions for multiple clocks coexist [17,19,20,21] enables one to design an architecture of clocks representing all dynamic clocks that govern an entire system, as complex as a life form.

Different kinds of resonance properties are explored to build clocks [10]. One could use a cavity and trap ions, electrons, or any other forms or carriers. At specific frequencies, the carriers trapped inside the cavity would vibrate at the maximum amplitude, and then beyond that frequency, we would find that amplitude of vibration decreases. This particular frequency is resonance frequency, and at resonance, we could well imagine that the carriers in the cavity would vibrate like a clocking material with minimum damping, this clock could be our element to build a time crystal [10]. Instead of a cavity, a dielectric slab could also vibrate with the maximum amplitude when it absorbs the signals of the right frequency that matches the energy of its gap between two vibrational energy states. It is a particular form of dielectric resonance [22,23,24,25,26]. Therefore, two kinds of resonances, the dielectric resonance and the cavity resonance, could be used to design clocks that run by noise. When noise or a mixture of electromagnetic signals of various frequencies are pumped together to a system [27], the signals with right frequencies are trapped into the cavity, and it builds up resonant oscillations of carriers or the vibrations of the resonating slab itself. Other signals are not absorbed. The entire human brain is a biomaterial-based integrated system of cavity resonator and the dielectric resonators. Singh et al. [28] have modeled the entire brain architecture by taking every component one by one, separately, and then simulating the resonant oscillations of each component from the smallest to the largest.

2. The Inventions of a Universal Time Crystal (UTC), Time Polycrystal and Space-Time-Topology-Symmetry (STts) Metric: Background Works on Brain Model

2.1. Resonance and Time Crystal

2.1.1. Noise Driven Clocks: Harvesting the Geometry of Cavity and Dielectric Resonators

A clock-like oscillation cannot be perpetual; we need to supply a particular kind of noise or a pure signal to a cavity or a dielectric slab continuously from outside so that the clocks run forever. White noise is a good energy source since it contains signals of the entire operating frequency range; a single source would supply continuous trigger to all clocks at a time. Thenceforth, we want an engineering system that harvests only noise (vertical parallel processor, JP-5,187,804 patent 2006), and due to the geometric arrangement of the cavity and the dielectric resonators, the architecture converts noise into a meaningful signal. The next part is to generate singularity [10], when we add one or more singularities to the clock, we need to find a guest clock that would interfere with the periodic oscillatory path of the host clock. At a particular phase region, both the clocks would destructively interfere and neutralize each other, but not totally, only for a particular set of measuring clocks. In other words, the undefined function would be limited to a certain time domain, and the lower-upper time limits of this undefined time domain would be the key region for setting up the assembly of clocks. This needs to be understood properly. If phased out by a destructive interference completely, then, no existence of the clocks would be left [2], so we would not be able to define what would happen next.

2.1.2. A Paradigm Shift in the Half-A-Century Old Concept of a Time Crystal

Therefore, an absolute singularity is not acceptable to build an architecture of clocks, or universal time crystal UTC proposed by Reddy et al. [10]. In Reddy et al.’s version [10] of a time crystal, the interference happens in a particular time domain; in all other time domains, the clocks survive. It means both the clocks interact in a particular time domain destructively, and beyond that phase region of the host clock, the host returns to its original path. Hosting a new clock in the singularity is the feature where UTC (universal time crystal) differs from both Winfree’s version [2] of time crystal and the Wilczek’s version of time crystal [29]. Both Winfree and Wilczek versions of time crystals were limited to only one clock. They never had to be concerned with the nature and features of the singularity domain. However, here we have to do that. Hence, UTC is of utmost essential to building a time crystal model of a human brain.

2.1.3. Representing Resonance-Based UTC, Time Polycrystals Using Circles

Once we define that two clocks would interact, the model device would be a cavity or dielectric resonator made of a smaller cavity or dielectric resonators, i.e., the host oscillator is made of guest oscillators. The particular condition that the host oscillators resonance property is a dependent function of the guest oscillator is important. The activation condition has an embedded sub-condition that we cannot define a host without the guest and vice versa [10]. If the condition is not followed in the hardware, we cannot build singularity in the host clock at a common phase domain with the guest clock. The common phase domain is a range of phase values of the host clock, where the system point of host clock passes through 360° phases of the guest clock. One could realize nested clocks by drawing a small circle on the perimeter of a large circle. However, while meeting this particular condition, we also set another consequence for the hardware, for host A, the constituent B would be in the imaginary world. For B, the host A would be in the imaginary world so that the system could be represented as A + iB. The shape of the cavities determines the amplitude variation pattern of the resonance frequencies, the number of constituent cavities determines the number of frequencies, size of the cavities determines the time domain where the resonance frequencies would reside. One could create an astronomically large assembly of the cavity and dielectric resonators, one inside another.

2.1.4. Twelve Classes of Rhythms Proposed or Reported in the Brain That Could Produce Vortices or Clocks to Build Time Crystal

Twelve ways biological systems could build circular ring like distribution of fields, called vortex, when energy is trapped in the cavity or in a dielectric resonator. These rings resemble clocks, since along the perimeter of the ring, the high intensity field rotates. (1) Magnetic vortices could be produced by spiral molecular structures, e.g., DNA, microtubule, hippocampus spiral nerve fiber. THz thermal noise could activate such particle like fields, when carriers transmit through a spiral path. (2) Spin wave vortex made by beating of quantum wavefunctions triggered by electromagnetic resonance. At electromagnetic resonance, often the quantum properties survive and could lead to interference of signals, and lead to beating. (3) A flux of density of electronic states trapped in a cavity is leaked in a control way produces spiral flow of density of states. It leads to vortices or atom like virtual distribution of fields. Geometric arrangement of protein complexes or molecular structures could produce such vortices. (4) Van der Waal’s mechanical oscillation could undergo fluctuations in the perturbation of induced dipole-dipole interaction in a medium where crystal like ordered arrangement of dipoles build a continuum of dipoles. (5) Electromagnetic resonance generate evanescent wave due to the geometry and inhomogeneous distribution of dielectric constants. Electric field and magnetic field split. The inversion of the symmetry of arranged dielectric resonators could reshape evanescent emission into a periodic burst. (6) Electric potential bursts across a cylindrical path would naturally generate circular rings of electric fields. Nerve spikes are electric field vortices. (7) Quasi-particles generated by mechanical defects in the ordered arrangement could build soliton vortices if the cavity that hosts the ordered arrangement of dielectric resonators hold a vortex shape. (8) Quasi-particles generated in the homogeneous distribution of charge domain as a defect of non-linear charge distribution could form polariton or polaron like particle based vortices in a hexagonal close packed 2D sheets. Cortical columns in the hexagonal 2D arrangement in the brain and in the hippocampus has this ability. (9) Diffusion of ions through spirally leaky pathways could generate twister like ionic vortices. Alfa helices of proteins, axons and neural network, nerve bundles are potential domains for synthesizing such vortices. (10) Chemical sensing of molecules could flow molecules through fluids following a periodically repeating loop. The closed path would follow time limit, generating clocks, in effect vortices of chemical sensors. Enzyme and hormones build such vortices. (11) Electromagnetic resonance often triggers a mechanical resonance of the dielectric resonator, which is called a electromechanical resonator. The biological systems are rich in mechanical resonators that build electromechanical vortices. (12) Spring like elastic materials generate pure sound like mechanical waves in the fluid. These pure mechanical waves are found in the protein’s alfa helices, in the domain of tertiary structures.

2.2. Background Human Brain Model Studies as a Precursor to the Proposed Time Crystal Brain Model

2.2.1. Triplet of Triplet Resonance Chain Model of the Human Brain

When a systems vibrational response is plotted in terms of the frequency spectrum, one could observe a wide resonance frequency peak with a low, quality factor. If the measurement apparatus is more sensitive, one could observe discrete sharp resonance frequency peaks inside that wide resonance peak. Sahu et al.’s study of microtubule’s resonance frequency band showed that microtubule has three resonance bands, in the kHz, MHz, and GHz frequency domains [26]. However, if one zooms each resonance band, measuring signals at a very low-frequency gap, one could find three more resonance frequency bands in each of them. This phenomenon is not limited to a single microtubule. It is observed in tubulin proteins that construct microtubule and single neurons too. Therefore, a scale-free triplet of triplet resonance is observed from 2nm wide protein to 25nm wide and micrometer long microfilament, finally, nearly a millimeter-long neuron [26]. The resonant oscillations of microtubule like filaments deliver the ability to fine tune nerve spike timing to a neuron membrane [30,31]. The experimental finding of a mathematical symmetric relationship spanning over a space of 10³ orders and a temporal range of 10⁶ orders prompted the development of the resonance chain model [20]. In the resonance chain model, 12 brain components were taken into account to cover a space of 10¹² orders and a temporal domain of 10²⁴ orders. Note that triplet of triplet assembly of resonance peaks is the most dominating groups of vibrations. There are a doublet of pentates, triplet of pentates, and several elementary grouping of resonance bands present in the spectrum. However, their intensity is very low.

2.2.2. Rebuilding Real Brain Components in the Simulator and Solving Maxwell’s Equations to Find Resonance Frequencies and Clock-Like Oscillation of Fields

When Singh et al. [28] attempted to model the entire human brain in terms of the cavity and dielectric resonators, they took the 3D model of Rajat Jain imaged by UCSD. They painstakingly recreated all components one by one, a similar size, a similar shape, and a similar dielectric property. While simulating the resonance properties of objects, one has to solve Maxwell’s equations and find the frequencies at which transmission and reflection of electromagnetic signals are maximum, i.e., resonance frequencies. Singh et al. [28] found that 12 layers of oscillators need to be assembled one inside another to model the entire brain from the largest (entire skin nerve network connected to midbrain) to the smallest (helical secondary structures of proteins). Rutuja Chhajed (co-authored of Reddy et al. [10]) first mapped the cavities of every single component in the brain. She noted the biological necessity of 12 layers, which were recreated by Singh et al. [28] in the CST computer simulator. We observed that while building the brain, nature has used a few geometric shapes repeatedly, and the teardrop to ellipsoid transition could be represented using a single mathematical equation. We have also found that the prime number of cavities or resonating centers or oscillators were assembled to build a higher organ.

2.2.3. Identification of Primes in the Ratio of Resonance Frequencies: Experiment and Theory

The preference of primes suggests that the number of cavities within a cavity determines the number of vibrating nodes, the prime number of nodes could interact in all possible ways in a cavity and generate all possible integers. Reddy et al. [10] argued that 12–15 primes could generate 99.99% of all possible integers in the universe. Singh et al. [32] have recently shown proposed a space-time-topology-symmetry (stTS) metric that provides 11D composition of tensors representing the geometric information structure of a self-operating mathematical universe. The reason for self-operation is that the pattern of primes called a phase prime metric, PPM that links all events represented as geometric shapes embedded in the time crystals [10], builds stereographic projection to infinity. The feedback from infinity returns the topological fraction of the projection to infinity. Thus, mostly the feedback is not defined in the set of stereographic projection to infinity [33]. Therefore, solutions of the self-operating universe are undefined in its own input set, and the projection-feedback network is non-computable. Finally, Singh et al. [28] showed that brain components are designed to isolate electric and magnetic parts and produce evanescent wave. Two orthogonal fields electric E and magnetic M components in the electromagnetic wave, interact with matter differently due to material’s dielectric constant distribution and geometry. In some regions, the E vector is absorbed more; in some regions, the M vector is absorbed more. The output of white noise interaction with the brain components is the creation of an evanescent wave [34,35], which generates vortex or free atom-like-structure of fields [36]. One prime example of the vortex field is the nerve spike made of an electric field; around the axon, it propagates like a hollow ring. Thus, a nerve impulse is one example of an electric vortex.

2.3. A Space-Time-Topology-Prime Metric for Analyzing the Human Thought and Conscious Experiences

2.3.1. Quaternion, Octonion and Dodecanion Tensors: Stereographic Projection to Infinity and Feedback from Infinity (PF Network)

Singh et al.’s [33] study also suggested that the human brain if modeled over a self-operating mathematical universe then it should have three primary regions where the distinct stereographic projections of information structure to infinity and feedback of that information structure from infinity to the operating system would carry out three distinct, independent to each other operations, along three orthogonal axes. We have placed three distinct projection-feedback, PF networks orthogonal to each other along a line, as shown in Figure 1a. The first PF network is located at the sensors, the system of sensors is designed to capture 11D data and with 4D quaternion tensors $h_{1,3}$ [37]. Second PF network is the midbrain cross-over, where 11D data is represented with octonion tensors $h_{4,2}$ [38]. Third PF network is the cortex domain made of 47 Brodman’s regions [39,40] where 11D data is represented with dodecanion tensors $h_{3,4}$ [32,33,41]. At three different dimensions, three PF networks operate continuously. The environment sends input, which is read as spatial streams of pulses as a function of time (space-time, 4D). Internally fed 15 topologies are searched outside, so the data is then placed on a proper Euclidian surface (space-time-topology, 8D). Finally, the symmetry of primes embedded in the topology is determined, and we get a proper metric of primes, called phase prime metric, PPM ([10], JP-2017-150173; World patent WO 2019/026984) (space, s-time, t-topology, T-symmetry, S; 11D). The state of the brain is defined as an output of the stTS metric, namely $\mathscr{H}$, and we define it below.

2.3.2. Construction and Decomposition of Space-Time-Topology-Prime or Space-Time-Topology-Symmetry (sTtS) Metric

Normally, a metric measures the spatial distance, for self-assembly of time polycrystals, which is the information processing unit in the brain, polycrystal’s growth within and above hardware is represented by three PF networks that could be measured using the space $d{s}^2\left(h_3\right)$, time $d{t}^2\left(h_{1,2}\right)$, topology $d{T}^2\left(h_5\right)$ and symmetry $d{S}^2\left(h_7\right)$. Here, the combinations of dual, triple, and quad features are as follows.

When a time crystal is formed at the sensors, we get quaternions, that could have information like, space-time $st\left(h_3,h_{1,2}\right)$, with 3 + 1 or 2 = 5 or 6 dimensions; in the midbrain, for octonions, we could have information of Space-topology $sT\left(h_3,h_5\right)$, with 3 + 5 = 8 dimensions; time-symmetry $tS\left(h_{1,2},h_7\right),$ with 1 or 2 + 7 = 8 or 9 dimensions. Finally, at the highest level in the cortex region, a dodecanion would represent the information content. therein information type would be topology-symmetry $TS\left(h_5,h_7\right)$, with 5 + 7 = 12 dimensions; $stST\left(h_3,h_{1,2},h_5,h_7\right)$, with 3 + 1/2 + 5 + 7 = 16 or 17 dimensions. Space-symmetry $sS\left(h_3,h_7\right)$, with 3 + 7 = 10 dimensions; Space-topology $tT\left(h_{1,2},h_5\right)$, with 1 or 2 + 5 = 6 or 7 dimensions; space-symmetry-time $sSt\left(h_3,h_7,h_{1,2}\right)$ with 3 + 7 + 1 or 2 = 11 or 12 dimensions; space-time-topology $stT\left(h_3,h_{1,2},h_5\right)$ with 2 + 1 or 2 + 5 = 8 or 9 dimensions; space-symmetry-topology $sST\left(h_3,h_7,h_5\right)$ with 3 + 7 + 5 = 15 dimensions; symmetry-time-topology $tST\left(h_{1,2},h_7,h_5\right)$ with 1 or 2 + 7 + 5 = 13 or 14 dimensions; symmetry-space-time $sSt\left(h_3,h_7,h_{1,2}\right)$ 3 + 7 + 1 or 2 = 11 or 12 dimensions. Therefore, two kinds of dimensions are taken into account, when a new kind of dynamic feature is added to a new axis, we go up to 20D (icosanion). Still, when we consider the dimension of dynamics for time crystals one inside another, then the maximum dimension is 12D (dodecanion) [32]. In three PF layers of Figure 1a, all noted tensors listed above generate continuously generate various distinct dynamics represented as time polycrystals, and those virtual particle-like elements would interact with the phase prime metric, PPM ${\mathsf{\Delta }}_{PPMi} \left(i=1 to \infty \right)$. The mathematical operation is defined as Ж (see Appendix A for details). In this mathematical operation time crystals are matched [41].

Hence, $stST$ would be confined in one imaginary world, i.e., it would represent the projected and the feedback time crystal “to and from” the PPM. The metric representing the time crystal in $stST=S2T2$ universe of 12 nested worlds is given by [32].

$$\begin{array}{l}\mathscr{H}={\mathsf{\Delta }}_{PPM1}st\left(h_3,h_{1,2}\right)+{\mathsf{\Delta }}_{PPM2}sT\left(h_3,h_5\right)+{\mathsf{\Delta }}_{PPM3}tS\left(h_{1,2},h_7\right)+{\mathsf{\Delta }}_{PPM4}TS\left(h_5,h_7\right)\\ +{\mathsf{\Delta }}_{PPM5}sS\left(h_3,h_7\right)+{\mathsf{\Delta }}_{PPM6}tT\left(h_{1,2},h_5\right)+{\mathsf{\Delta }}_{PPM7}sST\left(h_3,h_7,h_5\right)\hfill \\ +{\mathsf{\Delta }}_{PPM8}stT\left(h_3,h_{1,2},h_5\right)+{\mathsf{\Delta }}_{PPM9}tST\left(h_{1,2},h_7,h_5\right)\hfill \\ +{\mathsf{\Delta }}_{PPM10}sSt\left(h_3,h_7,h_{1,2}\right)+{\mathsf{\Delta }}_{Project-Feedback}stST\left(h_3,h_{1,2},h_5,h_7\right)\hfill \end{array}$$

2.4. Tensor Analysis of the Human Brain and the Thought Process

2.4.1. How to Bind Different Clocks Using the Singularity Domains

Our brain modeling task becomes a bit clearer now. We would map the motion of electrical vortices transmitting alone all over the brain as nerve spikes [43], the clocks or rhythms of electric vortices. And develop how clocks are interconnected to each other. The nerve spike transmission pathways are reported in detail in the brain rhythm literature [44,45]. We connect the components that activate in a sequence to run a biological rhythm and represent it using a set of interconnected circles. Once we determine the conditional phase relationships between different such rhythms or clocks, we could bind different clocks in 3D orientations. We now discuss how to bind different clocks using singularity.

One typical electric pulse (say, nerve impulse, i.e., electric circular vortex) could be represented by a circular path covering 360°. Figure 1b shows that between two limiting phases (say 30° to 40°) of periodic oscillations of the host clock, the exact point of phase change is the singularity point (at 35° phase of the host) where the state of the clock gets undefined [10]. When one measures a pulse stream, from beginning to the end of the pulse is 360°. The sphere in Figure 1b shows that a particular area on this surface is the singularity domain (here it would be 30° to 40°). By geometric musical language, GML [18,46], around a circular path on the phase sphere, the singularity points or domains represent the corners of the embedded geometric shape. The circular path on the sphere is represented by a 2 × 2 tensor, a pair of primes depicts the row of tensor, and a shift in the prime symmetry resides along the vertical axis. The diagonal values are −1 for tensors of any dimension since we divide one into many parts to define the complex vector. There is a mirror symmetry of elements (i.e., a C2 symmetry) across the diagonal [32,33]. The 2 × 2 tensor could hold at most four singularity points, since it has four elements, due to C2 symmetry, the tensor represents a loop of singularity points. Higher-dimensional complex numbers could hold more complex structures.

2.4.2. Tensors of Different Dimensions in Different Parts of the Brain: Data Format

At the sensors, when the elementary time crystals are produced, they are not linked, 1D, 2D, 3D, and 4D tensors [37] are sent to the midbrain. In the midbrain, by a feedforward network between the midbrain and the sensors, 5D, 6D, 7D, and 8D tensors [38] are produced which links the time crystals using PPM or the pattern of primes that assists by providing the symmetry and modulating the sensor by shifting the primes (Figure 1c, middle). The third PF network that runs in the higher brain region converts 1D-8D elements by creating 9D, 10D, 11D, and 12D data, the manifolds suggested by Singh et al. [32,33] are generated to bind the tensors (Figure 1c, right). In Figure 1b, we have noted the shifting of primes along the vertical axis. We need to learn what is prime shifting. In the geometric musical language, GML [18], information is written as time polycrystals. One of the primary elements of a time polycrystal is the singularity domain, as shown in Figure 1b.

2.4.3. How Tensor Elements are Filled during Interaction of Vortices or Particle-like Field Structure

Now, for any tensor product, horizontal elements and the vertical elements are identical; however, not in GML [46]. One of the key aspects of GML is that tensor products are generated every moment for carrying out information processing. The number of singularity points on the primary phase cycle of a host is the number of guest clocks [47]. It is the number of different time flows experienced by a system point as it moves 360°. Each clock can have its system point and can grow its phase cycle structure or time crystal inside by making a new guest-host system. It can connect with neighboring time crystals or phase cycles as guests of a larger phase cycle. It is the self-assembly of time crystals side by side [48,49]. When two vortices interact, constructive or destructive interferences happen. The structural symmetry of the vortices is represented by a set of frequencies, and the ratio of frequencies is represented in terms of nearest primes. During the destructive interference of vortex atoms (nerve spike) around the undefined phase region where the signal disappears, the symmetry that is normally changed is written in terms of associative primes change. Therefore, when a vector of any dimension encounters a singularity point [50], one could notice changes in the tensor elements, and the corresponding change in primes is called the prime shift. The origin of prime shift is the in-situ updates of time crystals perpetually in the brain. The effect of information exchange, learning, and plasticity, decision making, i.e., for any brain event, a change in the symmetry or creation or editing of singularity points is an inevitable process [10].

2.4.4. A Nerve Spike and Time Crystal in a Neuron

The event that happens at the smallest scale during the information processing stage is the creation or editing of time crystals [2]. Time crystals were identified for neuron decades back [51]; however, not so intricately as we do here for modeling the human brain. When a set of nerve spikes carry information in the brain [30,31,42], it edits the time gap between the nerve spikes. What does it mean? A neuron spike, if it does not change its rate of firing with time, would have only one clock with no singularity. Still, if it adds an undefined region during firing or singularity point where the spikes are no more, it means there is a host clock that runs for a much longer time, and that 360° phase path would develop a singularity. Therefore, editing the time gap between the spikes could generate n number of host clocks [10]. One could write a singular clock pathway in a 3D architecture of clocks using a 1D stream of nerve spikes. On the other hand, from a 3D architecture of clocks, one could generate an astronomically large number of the 1D network of clocks, which then could be represented by a widely time-varying stream of nerve spikes.

3. Garden of Gardens (GOG): Meander Flower Garden

3.1. Definition of a Meander Flower Garden

The complexity of events that a pair of clocks could encode in a time crystal is enormous. In Figure 2a, a map is created on the interaction of a pair of clocks. A clock could be represented using a circle. Now, when a pair of clocks interact, two circles could make external contact, internal contact, or one top of another. The motion path for the combined system point looks like a meander flower. The plot that summarizes all possible contacts between interacting clocks is called a meander flower garden [12,52,53]. A time crystal is not the host clock that runs perpetually in the system, and it is not the perturbation clock. However, when the host clock is perturbed, then, a new clock is generated that slowly changes its diameter to return to the unperturbed clock state [6,7,54]. The newly born temporary clock that is fundamental to the hardware of the primary clock is the time crystal [10]. Any clock that we see in the system is not the time crystal, but the clock that is generated by the systemic clocks is the time crystal. Figure 2a plot has two axes. The horizontal axis denotes the recovery time, the time during which the time crystal survives in the system. The ratio of recovery time to excitation time is plotted. The vertical axis depicts the frequency. We can look at a meander flower garden as rows of identical frequencies to explain how a change in recovery time modifies the time crystal or meander flower.

3.2. Hopf Bifurcation and Isochrones to Classify Time Crystals Built in a Meander Flower Garden

We could also look into the garden plot as the columns of identical recovery time to excitation ratio [11,12,41]. One could notice that along the column, the flowers are nearly identical, and along the horizontal row, the complexity of flowers is nearly the same. Therefore, Hopf bifurcation or the lines of synchronization selects time crystals that have similar complexities, i.e., the number of petals of meander flower is similar. Note that Hopf bifurcation is a point where the system loses equilibrium and oscillates between two complex planes, i.e., a new clock appears within a limiting ϵ, so it is called a limit cycle. It is mathematically presented as $\frac{dz}{dt}=z\left(\left(\lambda +i\right)+b{\left|z\right|}^2\right)$, here $b=\alpha +i\beta$, α is Lyapunov constant. When information is written, the perturbation frequency of the garden is fixed, depending on which carrier was used in which cavity, the recovery, and the excitation ratio varies, which changes the time crystals produced following the garden. Note that a clock and a singular perturbation clock and a host clock (PH) system builds a garden. Therefore, an astronomically large number of gardens would be produced in the brain. A surprising feature is the “linear looping” between the flowers with inward petals and those with outward petals [42]. The lines with similar dynamics of flowers are isochrons [55].

3.3. Constructing Garden of Garden (GOG) from the Flower Petals of a Meander Flower Garden

One could estimate that for creating one geometric shape, say a triangle, three singularity points are required as per GML [46]. Now, it would lead to a complex composition of frequencies of time crystals in the meander flower garden. Most importantly, when composite structures form by the self-assembly of time crystals within and above [41], then, either we need to build a 3D garden of meander flowers or collect petals from multiple gardens of meander flowers and build a new garden as shown in the Figure 2b [11,12]. The garden of garden (GOG) has several applications for a brain operation. First, when petals of different flowers are taken and attached to create a new flower, then, this is exactly the operation we need to create PF derived decision in the brain. As discussed above, to create stereographic projection and feedback from infinity, we need to shift the infinity. Then infinite geometric series that is projected to infinity finds that some unique geometric shapes appear dominating in the series [33]. Two geometric series could be represented by two meander flower gardens, and then collecting petals from the flowers of two gardens would be equivalent to the operation of PF. As described above and previously by Singh et al. [33], two infinite geometric series are deducted, and the uncommon time crystal parts (or flower parts; flower = time crystal) are selected from the deducted output series of clock geometries. The selection is such that if they are combined, the output time crystal will get richer in symmetry. Thus, Figure 2b represents the stereographic projection and feedback from infinity, namely PF operation [32].

3.4. Selection of 12 Brain Components as Meander Flower Garden for Developing a Human Brain Model

Garden of gardens (GOG) is synthesized in 12 major organs of the brain, each to be represented by 12 systems of time crystals. When we mapped the network of clocks for all the organs, we found that the 12 system of clocks repeatedly appears in some systems. Here, 12 is an important number when manifolds form in 12 dimensions, and a system could generate three distinct compositions of manifolds at a time. Twelve different dimensions in those manifolds could operate independently by combining 2 × 2 × 3, 2 × 3 × 2, and 3 × 2 × 2 imaginary worlds. Triplet of manifolds has been described by Singh et al. [32] as a fundamental minimum criterion for a self-operating mathematical universe. Twelve organs that demonstrate triplet manifolds are (1) skin nerve net, (2) cranial nerve, (3) Blood vessel, (4) Cortical branches, (5) cortex layers, (6) cerebellum, (7) thoracic nerves, (8) hypothalamus, (9) thalamic bodies, (10) hippocampus, (11) neuron, (12) microtubule. Here, in our proposed brain model of time crystals, we primarily emphasize on these organs, and it does not mean that other components cannot synthesis complex time crystals. It simply suggests that at least 12 manifold triplet systems are there in the human brain, as listed in Figure 2c. One of the primary differences between our model and existing brain models is that all existing models consider only the neuron as the key circuit element for neural network’s decision making (component number 11).

Here we do understand that blood vessel may not be very important to make decisions in the brain. However, we strictly follow the principle, whoever generates triplet of manifolds or pentate of manifolds, should be a part of our brain model. Triplet forms a topology (triangle), so does pentate (pentagon). In a general statement, whenever manifolds generated by resonance frequencies of a brain component form a group that could further integrate into a higher-order topology allowed by GML [45], we consider that brain component as an integral decision-making organ of the human brain.

4. Fourth Circuit Element: Hinductor

4.1. Looking beyond Memristor: Inventing a New Kind of Fourth Circuit Element Inspired by Microtubule, DNA and Several Basic Information Processing Devices in Biology

Thus far, we have discussed that the basic unit of information in the brain is a time crystal, which has a finite number of singularity points in each clock to build the geometric shapes prescribed by GML [18]. The basic decision-making device is described in Figure 3a. The smallest information processing unit would be an alfa-helix or DNA. We call three concentric spiral layers as a new class of fourth circuit element, H (Hinductor, not memristor) [10,41,56]. Three layers of self-assembly of H within and above lead to H1, the first-generation output of H. Then three layers of self-assembly within and above leads to H2, the second generation of H. Finally, self-assembly of H2 would lead to H3. Starting from alfa helix, one could reach tubulin protein, which self-assembles again into microtubule H1, the first generation Hinductor. Microtubule forms a bundle to build the skeleton of a neuron. Several such filamentary bundles in the axonal and dendritic branches orient themselves creating a 3D network. Several such networks build a column or sphere (teardrop to ellipsoid structures self-assemble to build them), we get three-layered self-assembly of H1 devices, it is second generation Hinductor, H2 device. These columns or spheres self-assemble three times in a hexagonal close packing in three layers, and we get a 2D sheet, this third-generation Hinductor or H3 device, as shown in the Figure 3a [41]. In our brain model, we cover the entire neural network of the whole body, and Figure 3b lists how H3 devices build the key components of multiple brain organs. All 12 components selected above are made of different versions of H.

4.2. Synthesis of Time Crystals and Multi-Dimensional Tensors Using Fourth Circuit Element, Hinductor

H is a particularly designed device to generate electrical, magnetic, and mechanical vortices, to build three classes of time crystals necessary for operating the brain. Electrical vortices regulate the energy transmission; the mechanical vortices regulate the physical motion, and the magnetic vortices transport the key information since they are not destroyed by water and ions, which happens with electrical vortices often. H1 is the first generation Hinductor device that builds quaternion; three layers of basic Hinductor device develop three imaginary worlds, as shown in Figure 3c (left). H2 is the second generation Hinductor device, with the three additional imaginary layers it processes octonions. H3 is the third generation Hinductor device, with three more layers one above another, it could process dodecanion and manifold triplet. In Figure 3c right, we have demonstrated how manifold triplets look like in terms of three versions of the same dodecanion tensors. Inputs in the brain are structured as a quaternion made of sensor derived quaternions; midbrain derived octonions and the higher brain cortex region developed dodecanion, depicted as $Q$ (to the extreme right of Figure 3c). We have defined above the metric $\mathscr{H}$, which acquires tensors of various dimensions and builds a space-time-topology-prime metric that decomposes the input tensors and expands it using phase prime metric, PPM [32]. Finally, the brain output is structured as quaternion $Q$, shown in Figure 3c. Therefore, the human brain, following our proposed model, follows a global linguistic structure of four questions, namely who, when, where, and why, distributed over one real and three imaginary worlds. However, the elements of the quaternion linguistic tensor are filled up by $\mathscr{H}$, which explores 2D to 20D tensors during its operation.

5. Key Principles for the Development of the Human Brain: Assumptions and Mathematical Criterion for Consciousness

For developing a functional model of the human brain, we need to link the brain components with the generation of 2D to 20D tensors. The generation of vibrations should happen naturally in the brain components so that $\mathscr{H}$ metric activates manifold triplets, input, and output quaternions integrate the tensors produced by $\mathscr{H}$. Therefore, we follow the principles of designing a brain, as described above. First, we would count the number of dielectric and cavity resonators in a cluster for every functionally distinct region or wherever the global arrangement of resonators is similar, i.e., follow a particular symmetry. Second, we investigate the dominating number of cavities assembled within and above for every new functional domain. Thus, we map every functional organ in terms of statistically dominating primes in its structure, two classes of arrangements, side-by-side SS, and within-and-above WA assembly.

5.1. From Tensors to Primes in the Global Design of the Brain

5.1.1. Integration of 12 Brain Components and Their Parts: The Role of Primes

The number of cavities that build the brain components is not random. Moreover, since the number of components is too large, we select a special mathematical criterion to select components. These special supporting components or brain regions have 12 number of SS and WA assembly of cavities. The most important part is linking cavities. How 12 constituents are connected to the 12 regions of primary decision-making systems is an interesting mathematical arrangement. In all the 12 layers, GML proposed 15 geometric shapes are enough to rewrite the information in the universe in terms of geometric shapes [10]. Fifteen basic geometric shapes are matched with the external data, GML has five 1D structures (straight I/II, corner V/U, angle T/L, cross X/x, spiral/vortex S). GML has five 2D structures (triangle, square, pentagon, hexagon, circle). GML has five 3D structures (tetrahedron, cube squares, octahedron, dodecahedron, icosahedron) [32].

5.1.2. Tensors in the Brain: Hierarchy of Tensor Dimensions for Integrating the Time Crystals

In Figure 4a, we have explained the emergence of primes from sensors to the eventual 47 cortex regions. If an event happens to follow this mathematical universe, one has to assign time, space, topology, and primes. Then the information transmits from sensors to the Brodman’s 47 cortex regions. Note that when we say a cavity is following prime 2, it means a 2 × 2 tensor could hold all periodic oscillations in 4 distinct values. For simplicity, we mention only the prime number. A sensor in the human body receives spikes from the neurons that fill the periodic spike information as elements of four tensors. These four tensors follow the primes 2, 3, 5, and 7 as fundamental classes of tensors, which captures the physical significance of periodic oscillations in the input signal. Here 2 × 2 tensor is assigned as time, 3 × 3 tensor is assigned as space, 5 × 5 tensor is assigned as topology, 7 × 7 tensor is assigned as primes. It means by using a 2 × 2 tensor or two basic values, one real and the other imaginary; we define time. Then, using a 3 × 3 tensor, we define space, basically three spatial coordinates. Then, using 5 × 5 tensor, we choose five topologies from 15, and using 7 × 7 tensor, we choose 7 of the first 15 primes of the number system. Information processing in the brain takes place in three layers, as shown in Figure 4b.

In the first step, we show that six primes 2,3,5,7,11,13, dominate sensors packing of periodic oscillation data. The dynamics of SS elements incorporated in the sensor data is 12 dimensional, i.e., represented by a 12 × 12 tensor. However, the dynamics of WA assembly (layer inside a layer) is up to 4D only. In the second phase, midbrain dynamics reach 8D. Sensors stereographically project the input information to the midbrain, and midbrain sends feedback to enhance information from 4D to 8D. Finally, in the third step, its 12D. Just below the dimension evolution chart of Figure 4b, we demonstrate the temporal evolution chart for the brain, 4D information accessing speed of the sensors is rapid. In contrast, integrated global synchronization for the 4D to 8D conversion happens within milliseconds, and 8D to 12D conversion takes hundreds of milliseconds to seconds.

5.1.3. Midbrain as the Interface between Sensors and the Higher-Level Cortex

Sensory geometry to the nerve spike to be transmitted to the brain follows the implementation of the primes 2, 3, 5, 7, 11, and 13. And this is done uniquely, a pair of sensors is used for every single data capture, C2 symmetry. Three major frequency domains are isolated and processed separately for the particular kind of sensing in the next step. Five functional classifications are made for each of the three frequency classes, and seven (hexagonal close packing) node 2D regions make sure input data is 11D. Then C11 and C13 symmetries are synthesized by the sensory nerve bundles. The 2D surface area could generate from 8 kinds of sensory systems in the brain model of Figure 4a is converged by a semi-circular disc containing 31 spinal nerves, 12 cranial nerves, and midbrain 1, which has 37 effective cavities.

In contrast, midbrain 2 has 47 types of cavities. All the midbrain cavities and components are listed in Figure 4c. Midbrain 1 is a pentagon (limbic system, hypothalamus, amygdala, basal ganglion, thalamus, and mammillary body), while Midbrain 2 is a quadrilateral (Hippocampus, cerebellum, brain stem and reticular formation) [44]. We enter inside each corner of these geometric shapes and find more complex geometric shapes hidden inside.

The effort of globally linking components in various groups, as we did above, two sets of midbrain groups, reveals a telling story that brain activation topology is fundamentally different than the nerve fiber connection-based brain map. Two very interesting examples are shown for the cranial nerve and spinal nerve control topology. Based on the origin in the brain, we have created the topology of cranial nerves, and based on the origin in the spinal cord, we have created the organizational topology of 31 spinal nerves. To the extreme right of Figure 4c, we observe the topology of these controls.

5.2. Assumptions and Key Principles of Our Human Brain Model

Here, we summarize the key assumptions and principles of operation of our proposed human brain model:

• Operational language: Periodic clocks prepared by brain cavities at 10⁹ order spatial scale to build an architecture of clocks spread over 10¹⁸ orders of time scale, regulate brain operation using a geometric language (geometric musical language, GML). Dielectric and cavity resonators self-assemble within and above to build the spatial architecture. Undefined phase regions of a clock allow other clocks to activate and run. Thus, clocks self-assemble within and above to cover 10¹⁸ orders of time scale. GML is the machine language, and it regulates brain operation.
• Unit of information & fundamental information processing device: Clock architecture breaking time symmetry is a unit of information of the brain. A spiral of three concentric cylinders, two water, and one material layer, build the fundamental information processing device H of the brain. H self-assembles to build another H, it’s the first generation H or H1. H1 builds H2, and hexagonal close packing of H2 in the form of a 2D sheet is the fundamental decision-making unit of the brain.
• Decision making: All input information is converted into the architecture of clocks, which changes its 11D dynamics following the StTs metric. The metric incorporates a pattern of primes (Phase prime metric, PPM; JP-2017-150173; World patent WO 2019/026984) to let the clock architecture transform its shape as a function of time. The transformation of clock architecture is the solution to the problem. It is the brain’s simulation of the future. Projection of clock architecture to infinity by creating an infinite series of structures using StTs metric and transforming the clock architecture by receiving feedback from infinity is the thought process of the brain.
• Memory, learning, and principle of circuit evolution: Clocks made of 12 types of carriers building 12 types of vortices (ring of fields act as particles). These vortices act as clocks or memories that transmits through dielectric and cavity resonator-based structures. As the brain learns, the cavity and dielectric resonators change arrangement following a resonance frequency identity that remains constant during brain evolution. The ratio of electrical resonance frequencies is $e$ (2.73…), the ratio of magnetic resonance frequencies is $\varphi$ (golden ratio, 1.61….), the ratio of mechanical resonance frequencies is $\pi$, the relation of linking the resonances is $e^2+{\varphi }^2={\pi }^2$.
• Origin of consciousness: Each of the 12 major brain organs assembled one inside another, has twelve, time crystal-based information architecture. Since one could rearrange 12 clock architectures in 2 × 2 × 3, 2 × 3 × 2, and 3 × 2 × 2 format, the hardware could operate using three information architectures simultaneously. In this model of the human brain, the ability of the hardware to create, evolve, and operate three distinct, complete information structures simultaneously would be considered as one of the primary requirements of self-awareness.

6. Organs and Statistically Dominating Primes

6.1. Primes in Our Sensory System

We observe the 3D structure, often the bundle of nerve fiber, the number of apparently isolated fiber assemblies in the brain, and the neural network of the entire human body. We count the number of structurally isolated regions as cavities and zoom each cavity to find structurally isolated regions inside. Entering inside, we count the number of cavities again. If N cavities assemble side by side (we call it SS assembly) to build an organ, we go inside one of the cavities and find M cavities inside. So, we write the system as N(M). The journey continues with N(M)((Q))…

6.1.1. Eyes

Optical nerve bundles from a pair of eyes crossover following a mirror symmetry (C₂). The other end of this fiber is connected to the V1-4 cortex region via five sectional pathways (dominating primes are 2, 5, and nature of the assembly is side-by-side SS) [57]. Since each eye has seven cavities (cornea, aqueous chamber, lens, ciliary body, retina, phobia centralis) and retina has five layers inside (lipid bilayer, cone bipolar, rhodopsin, upper and lower coating). Cone bipolar follows hexagonal close packing, just like the cortical column assembly in the cortex region or the tubulin proteins on the microtubule surface. Unit cells of cone bipolar have seven cone cells. Seven columns of rhodopsins have a sensory molecule made of 11 carbon chain [58]. If we make a journey within and above in the eye, we have 2(7)((5))(((7)))((((11)))), therefore in five layers of within and above assemblies, we get the sensory architecture of an eye, if we include cross over and V4 regions for left and right brain, then the within and above (WA) assembly needs to be edited. We would get finally 2(7)((5))(((7)))((((11))))(((((5))))).

6.1.2. Ears

In one of the ears, three semicircular ducts, and three spirals of the cochlea are connected by a common cavity, above fenestra ovalis, we get a total of 7 cavities (SS primes 2 and 7). In the cochlea is made of three cavities, vestibular canal, tympanic canal, and cochlear duct (3 cavities, SS). Cochlear duct is made of the organ of Corti, tectorial membrane, tectorial membrane, and auditory nerve (3 cavities, SS). The organ of Corti is made of 3 types of cells, inner hair cells, outer hair cells, and supporting cells (3 types of cavities, SS). Complete ear architecture now could be written as within and above assembly WA 2(7) ((3)) (((3))) ((((3)))) [59]. Auditory nerves move to the spinal cord. In the spinal cord, the sound signal passes through five cavities (left ventral cochlear nucleus, medial superior olive, right ventral cochlear nucleus, lateral superior olive). Two outputs are generated in this lower brain stem. Finally, three cavities work together, inferior colliculus of the midbrain, complex group of pathways, namely lateral lemniscus, and finally thalamus (we get 7, 3 as SS assembly in the final level). We edit above noted WA assembly WA 2(7) ((3)) (((3))) ((((3)))) ((((7,3)))) [44].

6.1.3. Nose

A pair of nasal cavities (2 cavities, SS), the front part of the nose to the cranial bone, there are three cavities (front cavity has aloe cartilage; second from the front has Dorsum nasi, the third cavity has ethmoid sinuses, three cavities, SS). The cross-sectional view of the nose shows seven layers of neurons (7 layers, first, olfactory bulb; second, receptor cell; third, Basal cell; fourth, cilia in mucus; fifth, mucus-secreting gland & extended pathway; sixth, glomerulus; seventh, ethmoid bone; each layer holds a distinct symmetry of neuron arrangement; SS). Nose receptors are plenty, but they are divided into seven gene classes, and it covers 23 sub-classes of receptors (7, 23, two primes belong to SS category). The entire hardware for smell is built following 2(3) ((7)) (((23))) primes for the within and above assembly. Finally, three types of cavities are active, olfactory tract, amygdala, and olfactory cortex, which completes the smell processing in the brain [60], so we edit the WA prime path as 2(3) ((7))(((23)))((((3)))).

6.1.4. Touch

There are seven types of touch sensors located all over the skin (7 types of cavities make SS assembly) [61]. Thermo-receptors, which senses heat (Ruffini’s corpuscles) and cold (Krause’s corpuscles); Meissner’s corpuscle senses touch; nociceptor, senses pain; Pacinian corpuscle senses pressure, Merkle’s disc for touch and finally the seventh, root hair plexus that senses touch [62]. Touch senses come from all over the body and reach the spinal cord, where five spinal tracts pathways [63] (1. Dorsal root ganglion, 2. Dorsal horn, 3. Dorsal column nuclei, 4. Medulla, 5. Raphe nucleus (descending signal); 5 types of cavities SS) arranged in C2 symmetry or divided in a pair of cavities, where each side has three cavities, i.e., C3 symmetry. Beyond the spinal cord, the ventral posterior nucleus and somatosensory cortex make the final decision (2 types of cavities). If we think of within and above assembly, then 2,5) (7) ((5)) (((2))) is the WA assembly, where the first 2,5 represents C2 symmetry of the entire body, and five represents, pair of hands, legs, and the main body.

6.1.5. Tongue

The tongue has two symmetric parts, five, sensory regions (sweet, salty, sour, hot, and umami); there are three layers (epithelium, filiform papilla, and fungiform paila). One bud is made of five cavities, pore, hair, gustatory receptor cell, supporting cell and nerve fiber. In the last three steps, the signal is processed, the nucleus of the solitary tract, thalamus, taste area of the somatosensory cortex. The sensory molecules have seven secondary structures of proteins arranged in such a way that the molecules to test are trapped within sending a signal of single-molecule detection. Therefore, the within and above assembly for tongue is 2(5) ((3)) (((5))) ((((3)))) (((((7))))).

7. Twelve Major Brain Components, 12 Key Dynamic Centers, and Primes in Their Structure Design

7.1. Why Did We Choose 12 Brain Components and Left Others?

We created a complete clock-based architecture of the entire human brain functions, how different elementary components of the brain transmit nerve spikes [30,31,43], and generate cognitive functions. We found that 12 brain components are there whose clock architectures are self-similar; they all have at least 12 key functional parts activating at the same time (Figure 5a). Since we did not follow any pre-meditated model of the human brain at the beginning of our study, we selected all 12 components. We started the investigation, how and why 12, why this number is so important in the brain. When we see the number of cavities, we find that brain prefers to select a prime number of cavities, when we look for generating the clock architecture or time crystal architecture, then, the brain prefers to assemble clocks in multiples of 12 (2 × 2 × 3; Figure 5b), 18(2 × 3 × 3), 20(2 × 2 × 5) and 30(2 × 3 × 5). Specially assembling clocks within and above by taking two hosts, then inside each clock, it puts two more, and then inside every two clocks, they put three more clocks. Thus, we get the WA assembly of cavities in various ways for 12.

7.2. Scale Free Universal Integration of Space, Time, Topology and Prime

The topological organization of brain components is charted in Figure 5c. Of course, we do not rule out the possibility that one could design brain-like hardware based on 18, 20, and/or 30 basic components (18 = 2 × 3 × 3; 20 = 2 × 2 × 5 and 2 × 3 × 5). Currently, we present the human brain that explores 12 components varying 1.5 nm (single protein) to 1.6meters (neural net of the whole body), i.e., 10⁹ orders of spatial scale. The time range operated in the brain 10⁻¹⁵ (alkyl and amine periodic oscillations in $\alpha$-helices, a secondary protein structure) seconds to 10⁹ (heart cell replacement cycle) seconds or 10²⁴ orders. One could take a small bandwidth of time and model the human brain. We would discuss in a separate article exhaustive theoretical simulation of all brain components by Singh et al. How 10⁹ orders of spatial scale change could process 10²⁴ orders change in the temporal scale, using these 12 components, is a mystery. All the components follow a time-bandwidth strongly overlapping a wide time width in the resonance spectra of all brain components. There are no continuously linked resonance frequencies, but Ghosh et al. [20] proposed a resonance chain to simplify the non-linear time domain linking of all triplet of triplet resonance bands representing the entire human brain. The current time crystal model of the human brain could be considered as an extension of vibrations of the resonance chain proposed by Ghosh et al. [20]. The clocks in a neural system self-assemble to modulate the time [64]. For this purpose, a need for three clocks is observed in some bio-systems [65]. Saxena et al. has shown experimentally that such scale free triplet of triplet resonance chain does exit in tubulin, microtubule and neuron [26].

7.3. Different Brain Components and How Do They Process Different Primes

7.3.1. Microtubule and Tubulin Protein, DNA, RNA (Molecular Spirals)

Spiral pathways exhibit clock arithmetic. All animals on the planet have 13 protofilaments in their cellular microtubule. Sahu et al.’s quantum tunneling images suggest that a microtubule has 13 dielectric resonators and 12 cavities in between. A signal could flow though the microtubule surface following spiral ring-like paths at a gap of 2, 3, 5, 7, and 11 and 13 as if the modulo is 13. The gap is the number of tubulin proteins along the perimeter of a microtubule. We can convert a series of circular transmission 7, 14, 21, 28, and 35 loops into 7, 1, 8, 2, 9… These numbers we get when we complete the circle and continue counting (14 = 1, and so on). Let’s take another example, two spirals begin transmission from the perimeter at a gap of 10 tubulins we get a series, 11, 22, 33, 44, 55… and translates to 11, 9, 7, 5, 3… due to clock arithmetic. We devised a generalized route to find alfa-helix assembly functioning as an independent circuit. A group of helices, when isolated by beta sheets, act as a single group [66]. The electric, magnetic, electromagnetic, thermal, mechanical any kind of energy absorbed by these helical structures would get trapped in the cavity created by the beta-sheet, and we would observe cavity and dielectric resonance. The numbers of loops in the helices are counted to find how integers group to play PPM. We have investigated 26,000 proteins to find that the proteins primarily adapt to the various number of cavities from 1 to 23 [66]. DNA and RNA play with the coding using a pattern of prime [67,68]. We did not do much because already available researches on these topics are plenty. Junk DNA or repeated coding of DNA has a close relationship with the pattern of primes. The synonymous quartets of codons = 4n + 1 primes doublets (mostly) = primes with quaternary remainder 3.

7.3.2. Neuron

Often in textbooks, we find 23 types of branching in the neurons, 23 types of glial cells, and 13 types of oligodendrocytes. The Bloomfield study seems the most complete [69], where 22 different ganglion cells types, reminiscent of the cat and human retina’s ganglion cells, are described [69,70,71,72].

7.3.3. Cortical Column and Cortex

Cortical columns arrange in a hexagonal close packing, the number of columns increases from the center of a 2D sheet as 1, 7, 19, 37, and so on (dominating primes of the cortex 2D sheet, 1, 7, 19 and 37…SS). Since each cortical column has seven distinct layers, five of them process key information, two layers engage in acquiring input from the lower brain. Three specific layers take the output (primes for input and output 2, 3 SS) to other 47 Brodmann’s functional regions [73,74]. If we write how primes constitute WA symmetry it would be 47(1,7,19,37) ((7)) (((2,3))), therefore in four layers the primes govern the cavity network, left to right represents top to bottom or a journey within. A series of primes, 1,7,19,37…, around 200,000 hexagonal close packings of cortical columns make our decisions in 47 Brodmann’s functional regions.

7.3.4. Cerebellum

Eleven semicircular regions or primary folds in the cerebellum creates 11 primary cavities (10 physical folds and one deep cerebellar nuclei). The five inner materials inside the cavities create five types of cavities (five types of cavities, pia mater, molecular layer, Purkinje cell layer, Internal granule layer, white matter). The cerebellum is made of crossbar architecture, horizontally two major layers, anterior lobe, and posterior lobe. Simultaneously, the cerebellum is composed of vertically three layers, vermis, paravermis, and edge hemispheres. There is a total of five types of cavities. If we include posterolateral fissure and flocculonodular lobe, a total of seven types of cavities [44].

7.3.5. Hippocampus

There are 17 distinct functional regions in the hippocampus, which could be structurally identified as distinct geometries of nerve fiber arrangement. The central part of the hippocampus is a cylindrical spiral nerve fiber-based structure where 37 helical rings filter the brain’s input-output signal. From these 37 helical pathways, nerve fibers move out all over the brain like a corona. Seventeen types of cavities compose the hippocampus (Alveus, stratum oriens, stratum pyramidale, stratum lucidum, stratum radiatum, stratum lacunosum, stratum moleculare, hippocampal sulcus, temporal horn, stratum granulosum, Polymorphic layer, Fimbria, Margo denticulutatus, Fimbriodentate sulcus, Hippocampal sulcus, Subiculum, CA2-CA3) [75].

7.3.6. Hypothalamus

Thirteen types of cavities make hypothalamus. 1. The paraventricular nucleus for water balance and stress. 2. Medial preoptic for blood pressure, 3. 4. Anterior commissure and Anterior hypothalamic area for body temperature. 5. The supraoptic nucleus for water balance. 6. suprachiasmatic nuclei for the biological clock. 7. 8. 9. Dorsomedial nucleus, ventromedial nucleus, and mammillary body for feeding, 10. Posterior hypothalamic area for shivering, 11. Dorsal hypothalamic area, 12. Lateral hypothalamic area, 13. pituitary gland controlling hormonal and enzyme rhythms [76].

7.3.7. Thalamus

Seven connection pathways between 12 thalamic relay nuclei in the midbrain and their seven corresponding cortical areas in the cortex are linked through the thalamic reticular nucleus [77]. Two types of pathways, corticothalamic connections, and thalamocortical connections. 12 thalamocortical nucleus A: anterior thalamic nucleus, M: medial thalamic nucleus, VA: ventral anterior nucleus, VL: ventral lateral nucleus, VP: ventral posterior nucleus, LP: lateral posterior nucleus, Pu: pulvinar, C: centromedial nucleus, P: parafascicular nucleus, LGN: lateral geniculate nucleus, MGN: medial geniculate nucleus, TRN: thalamic reticular nucleus. The nuclei are connected by interthalamic nuclei. It could be the 13th cavity.

7.3.8. Thoracic Nerve System

Among 31 pairs of spinal nerves, we have isolated 12 thoracic nerves connected to breathing and heartbeat rhythms that build a triangular topology. There are two classes of thoracic parts of the spinal nerve system, anterior and posterior [44]. Within anterior (Intercostal-Intercostobrachial—T2: Thoraco-abdominal nerves—T7–T11: Subcostal—T12); within the posterior class, there are posterior branches of thoracic nerves. T fiber extensions direct signals from the brain to various parts of the upper body, including the muscles, deep inside the tissues, skin, and the blood vessels, and take the feedback. T1 and T2 (top two thoracic nerves) top of the chest as well as into the arm and hand. T3, T4, and T5 spread over the chest wall and aid in breathing. T6, T7, and T8 spreads into the chest and/or down into the abdomen. T9, T10, T11, and T12 spreads into the abdomen and/or lower in the back.

7.3.9. Cranial Nerve System (4 Sensors)

There are 31 spinal nerves; with 12 cranial nerves, we have a 43-peripheral nervous system (PNS) to sense the world around us. 31 and 43 are primes, and 12 is the key seed number used by the human brain in its hardware. Out of 12, only the olfactory nerve (CN I) and optic nerve (CN II) originate from the cerebrum. While Cranial nerves III–XII arise from the brain stem (midbrain, pons, or medulla) or branches out from a junction between the two parts. Midbrain—the trochlear nerve (IV) originates from the posterior side of midbrain. Midbrain-pontine junction—oculomotor (III). Pons—trigeminal (V). Pontine-medulla junction—abducens, facial, vestibulocochlear (VI–VIII). Medulla oblongata—posterior to the olive: glossopharyngeal, vagus, accessory (IX-XI). Anterior to the olive: hypoglossal (XII). At seven different layers of midbrain and cerebellum, they originate [78].

7.3.10. Blood Vessel Network in the Brain (Mechanical Rhythm Generator, Flow of Magnetic Element)

Seven primary branches of the external carotid artery enter the brain. The occipital artery that moves towards the backside of the head, and then there are transverse facial artery, posterior, and anterior auricular artery, frontal artery, parietal artery. The occipital artery extends to five more regions of the brain, generating five more symmetries (supraorbital, anterior and posterior communicating arteries, basilar artery, vertebral artery). A total of 13 symmetries of the blood vessel network encompasses the entire brain [44]. We leave the blood vessel network of the whole body because it resembles the geometric arrangement of the skin-nerve network. Since our brain model is geometric, we look for a unique composition of geometries at all scales.

7.3.11. Cortical Branches or Connectome Geometry

Water molecule diffuses in the brain all along with the nerve fiber, using which one could map the wiring diagram of possible circuits (the basis of the connectome project, follow the water flow). We have three major parts of the cortex, and one could notice five distinct domains [79] in the connectome branches [80]. If we count both sides of the brain (left and right), the connectome nerve fiber network is made of 12 distinct domains divided into five regions. The top corticospinal tract that has four regions from the front to the back of the human head and the rest four domains described below have two regions. One part is on the left side of the brain and the other on the right side of the brain [79]. First, the corticospinal tract, U shape around corpus callosum, which is divided into 37 regions (including left-right) through the top brain central from front to back. Second, splenium of the corpus callosum, V shape around U coming from the spinal region to the top. It has six sub-regions (including left-right). Third, extreme capsule fiber system, a pair of fish-like structure from front to the back of the brain, each fish is a composition of five distinctly folded sub-fibers domain (ten including left and right). Fourth, arcuate fasciculus, semicircular shape S fibers at the extreme left and right sides of the brain, seven sub-regions are there on each side (fourteen sub-regions including left and right brain). Fifth, uncinate fasciculus, a local curve connecting the fish and the extreme left-right semi-circular shape, each side has five sub-regions (ten, including left and right brain).

7.3.12. Skin & Sensory Nerve Network (One Sensor)

There are 31 spinal nerves; within that, 12 thoracic nerves are already separated functionally, and we discussed it above. Now, we are left with 19 pairs [81], which is also a prime. In humans, there are 31 pairs of mixed (sensory + motor) nerve fibers: 8 cervical, 12 thoracic, five lumbar, five sacral, and one coccygeal. Here 5-fold symmetry of the body is reflected in the entire neural network. Note that when we want to investigate the motor + sensory nerve bundle of the spinal cord, we include thoracic too. One element could participate in defining multiple symmetric structures.

7.4. A Summary, How the Brain Has Used 15 Prime Symmetries in Building Its Hardware

Normally, while explaining the mirror symmetry in a hardware Prime 2 is brought into the picture, we understand that brain triggers the formation of crossing parallel lines into a rhombus, balances unwanted growth delivering a C2 symmetry. Its lowest integer holds another rhombus, and this fractal feature continues. Similarly, triplets of resonance bands or nesting of clocks expand fractally, the first loop of a teardrop-like a triplet in the phase prime metric contains another similar triplet, we call it triplet of the triplet [10]; a result of C3 and prime 3. Prime 5 builds S-shaped open-end curves, spiral, and vortices, the key to several such structures we find in the brain, including DNA, microtubule, and even protein’s secondary structures. Prime 7 embeds the circles in the curves, and this is the first step towards the optimization of 1D or 2D assembly of organic sensors. Imagine, cortical column, rhodopsin, 2D sheets of cortical columns, seven sets the limiting assembly unit. Together prime 5 and prime 7 creates a fractal of a flowerpot repeated over the entire integer space, and we find that in the phase prime metric plot. Prime 11 builds a fractal of reverse petals in the phase prime matrix. Prime 13 builds a fractal of hearts; for the first time, duality and coexistence of multiple solutions in a singular vibrating unit are realized.

From prime 17, we start making a journey beyond Prime 17 builds a fractal of spiral, that primarily looks like a vortex. Prime 19 builds a fractal of a spiral; Prime 23 builds a fractal of multi-directional vortex generator. Prime 29 builds a fractal of a toroid Prime 31 builds a fractal of crossed petals Prime 37 builds a fractal of parallel lines. Prime 41 builds a meander flower, Prime 43 reflects a garden of meander flower. Prime 47 signifies a complete meander flower garden.

To make sense, the brain may predict the future [82] for PPM-hardware, in the metric that maps the past-present-future of an event. As soon as the space for “present” is filled up, the infinite series of future events is redefined.

8. Time Crystal Map of the Whole Brain

We start our journey to build a complete, time crystal model of the whole brain with the very basic components. We follow the standard textbooks [2,41,44] with respect to how different brain components activate in a temporal and spatial sequence. The majority of biological clocks follow the temporal and spatial activation of key elements in a sequence. However, such activations are of two types. Within and above (WA) as we see in the suprachiasmatic nuclei, for regulating the circadian rhythm. Side by side, as it happens, memory and skill learning pathways in the midbrain. These ionic and molecular communication pathways are very well established. Each sequence is converted into a cycle so that if the clock runs, i.e., system point moves along the closed path; the biological process is executed. Two circular clocks connect at a particular phase point to conditionally connect two biological processes. Following this simple principle, we have made an effort to cover all reported clock like oscillations into an integrated architecture. It may be possible that we might have missed some of the clocks. However, later, the missing ones could be added. Our effort to build a time crystal map of the whole brain cannot be completed in a single attempt. The time crystal brain model is our second attempt to build a generalized integrated functional model of the brain. Ghosh et al. [20] proposed a resonance chain experimentally verified by Saxena et al. [26]. However, that effort was too global. It did not look into the process of neurogenesis or linking the function of a bio-system using its structure in detail. Therefore, for many reasons, the current effort is much more complete, enriched, and detailed in its intricacy.

8.1. Time Crystal Architecture of 12 Key Brain Components: Each Forms a Meander Flower Garden

8.1.1. Skin & Sensory Nerve Network (Largest Organ of the Human Body)

From Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, we have provided the database of a time crystal architecture or temporal representation of the whole brain. Figure 6 starts with the skin-nerve network. Normally, we would expect that 31 spinal nerve pairs would process this time crystal, and based on the integration of information data available already with the literature [44], we have compiled this chart. The first interesting feature of this time crystal chart is the composition of heat, touch, pain-sensing in the skin, at the same time, the chart also takes into account the events that should happen in the midbrain components. The second interesting feature of this time crystal architecture is proprioception, positioning of different organs, hand, leg, finger, etc. changes the 3D orientation of the neural nerve network. Proprioception plays a key role in the emergence of consciousness in a life form, as it determines the sense of the existence of a body in an environment. The third key feature is the spinal cord, where continuously the motor and sensory nerve signals interplay and carries out a key decision making about the critical features of the sensory input. Brain signals continuously cross-check what kind of signal is it, and technical detail of the sensory input is judged in the spiral cored. Though we discovered GML [18,46] while studying the resonant oscillations of the microtubule [66], often cross-checking of interactive signal transformation between sensory input and the motor response, reveals that GML could have major application almost at every level of information processing in the brain.

8.1.2. Cortical Branches and the Connectome: Connecting Organs

Figure 7 describes the cortical branches in the most simplistic form. It is not difficult to complicate the time crystal architecture using an enormous amount of research data available [2,41,44,45]. We have discussed above the role of primes in the cortical branches; however, here, we have emphasized three key points. Often, we think ventricles in the brain do nothing. In the previous studies on the cavities of the Rajat Jain’s brain, Singh et al. [28] found that, on the contrary, the energy transmission is regulated directionally by the cavities. Therefore, while building the time crystal architecture, we have kept one of the three parts of the architecture for ventricles. The second key feature that is often neglected in the studies of cortical branches is the junction between the cortical branches and the cortex region. Internal brain cavity made by folded cortex layers has nine components, in a triplet of triplet [20] assembly (it means, primarily one finds three major cavities, and inside each cavity, there are three cavities). Therefore, the time crystal model needs to take into account how hexagonal lattices of cortical columns [73], cortical columns and the cortex branches of nerve fibers obtained from the connectome database [83,84] three factors play an important role in the coupled transfer of energy between the three components. Third and finally, the key prime branches of how the symmetries of different functionally known brain regions and cortical branches are coupled. Not just the Brodmann’s regions, detailed fMRI and PET scans have revealed how functional brain regions and cortex branches are linked together. In summary, Figure 7, time crystal concentrates on the links between cortex branches and the cognitive functional regions of cortical layers.

8.1.3. Functional Loops and Cavity Regions Are Put Together into One, Time Crystal

Figure 8 shows the time crystal for the cortex domain or cortical layers. The cortex region could be divided or classified in various ways. However, we have concentrated on the 20 primary consciousness tasks [44] that we would outline in the Figure 16, Figure 17 and Figure 18. One could consider Figure 8 as the key hardware-software link, time crystal for the brain operation. The first interesting feature about this time crystal is linking different functional regions. The possibilities are infinite; however, when we limit ourselves to only 20 conscious responses as outlined in the Figure 16, Figure 17 and Figure 18, then we could search for links between different functional regions as reported in the literature and build an integration map. Therefore, Figure 8 is an effort to bind hardware response to functional property; similar to neurogenesis. We may call it brain genesis, where each independent function of the brain could be related to the other functions. When we note time crystal inside this chart, it refers to multiple local components, which are not listed in detail.

• D1 Consciousness: Central Executive, CE; Olfactory lobe, OL; Mamillary body, MB; Parietal lobe, PL; Corpus Calosum, CC; Temporal lobe, TL; Fusi form gyrus, FFG; Corpus calosum, CC; Primary sensory pad, PSP; Superior temporal, ST; Sensory pads, SP; Caudate nucleus, CN; Putamen, P; Amygdala, A; Hippocampus, H; Reticular formation, RF; Thalamus, T; Limbic system, LS; Superior caliculus, SC; Orbito-frontal cortex, OFC; Frontal lobe, FL; Parietal cortex, PC.
• D2. Memory: Protein secondary structure, PSS; $\alpha$- helix, $\alpha$; $\beta$- sheet, $\beta$; Microtubule, M; Actin, A; Neurofilament, N; Neuron, NN; Glia-Astrocyte, GA; Oligo-dendrocyte, OD; Pyramidal & polar, PP; Tear-drop transform, TDT; Super structures of neuron, SSN
• D3, Language and conversation: Arcuate fasciculus, AF; Temporal lobe, TL; Frontal lobe, FL; Dorsal Pre frontal cortex, DPFC; Motor cortex, MC; Broca’s area, BA; Gesdiwind territory, GT; Cerebellum, C; Wernicke’s area, WA; Visual cortex, VC
• D4. Thinking and intelligence: Extrastriate cortex, EC; Fusiform gyrus, FG; Wernicke’s area, WA; angular gyrus, AG; supramarginal gyrus, SG; superior parietal lobule, SPL; Anterior Cingulate, AC; Working memory, WM; Procedural memory, PM; Episodic memory, EM; Semantic memory, SM; Implicit memory, IM
• D5 Sense of universal time, symmetry
• 10 Metrices of prime, 10MP; Statistical prime contribution, SPC; Striatum amygdala, SA; Temporal lobe, TL; Thalamus, T; Parietal lobe, PL; Hippocampus long memory, HLM; Topological projected time, TPt; Frontal lobe, FL; Corpus calosum, CC; Reticular formation, RF; Hippocampus min time filtered pattern, HMTFP
• D6. Fear, threat, anger, hate
• Medical dorsal nucleus, MDN; Limbic system, LS; Thalamus, Th; Posterior portion, PP; Accessory basal, AB; Middle gyrus, Mg; Basal nucleus, BN; Cingulate cortex, CC; Cortex, C; Medical, M; Amygdala, A; Hypothalamus, H; Input lateral terminal, ILT; Olfactory lobe, OL; Fornix, F; Mammillary body, MB; Basal ganglia, BG; Frontal cortex, FC; Superior- Frontal cortex, SFC; Pre-frontal cortex, PFC; Ventral tangential array, VTA; Dopamine level, DL; Styria terminalis, ST; Nucleus acumens, NA; Orbitofrontal cortex, OC; Insula, In.
• D7. Reward
• Basal ganglia, BG; Nucleus accumbens, NA; Ventral tegmental area, VTA; Mid brain, MB; Pre-frontal cortex, PFC; Dopamine cycle, DC; Striatum, S; Pallidum, P; Thalamus, T; Cortex, C; Ventral pallidum, VP; parabrachial nucleus, PN; orbitofrontal cortex OFC; and insular cortex, IC

• D8 Mimicry, skill, adaptation
• Parietal lobe, PL; Thalamus, Th; Cerebellum, C; Hippocampus, H; Amygdala, A; Temporal lobe, TL; Caudate nucleus, CN; Mammillary body, MB; Putamen, P; Frontal lobe, FL; Primary visual cortex, PVC; Temporal lobe, TL; Dorsolateral Pre-frontal, DPF; Orbito frontal cortex, OFC; Motor cortex, MC; Reticular formation, RF; Supplementary Motor cortex, SMC; Thalamus sensor cross-over, TSC; Tempo-parietal junction, TPJ; Hippocampal memory encoding, HME
• D9. Creativity & Humor
• ACC Anterior Cingulate, AC; Temporal sulcus, TS; Caudate nucleus, CN; Central executive, CE; Left Amygdala, LA; Pre-frontal cortex, PFC; Motor cortex, MC; Posterior Temporal region, PTR; Motor cortex, MC; Ventral brain stem, VBS; Cerebellum, C; Pyramidal tract, PT
• D10. Personality
• Supplementary motor cortex, SMC; Creativity time crystal, CTC; Personality time crystal, PTC; Insula, I; Cingulate, C; Striatum, S; ACC Anterior Cingulate, AC; Temporal sulcus, TS; Thalamus, Th; Amygdala, A; Reticular formation, RF; Temporo-parietal junction, TPJ; Temporal lobe, TL; Desolation prefrontal, DP; Orbitofrontal cortex, OFC; Thyroid, Thy
• D11 Love and pain
• Lateral nucleus, LN; Medial ventral posterior nucleus, MVPN; Cingulate cortex, CC; Spindle cells, SC; Olfactory lobe, OL; limbic system, LS; Superior temporal cortex, STC; orbito-frontal cortex, OFC; Amygdala, A; Primary visual cortex, PVC; Fusiform gyrus, FFG; ventral tegmental area, VTA; nucleus accumbens, NA; Prefrontal cortex, PFC
• D12 Learning dreaming defragmentation
• Nucleus Accumbens, NA; Thalamus, Th; Caudate nucleus, CN; Reticular formation, RF; Central executive. CE; Prefrontal cortex, PrC; Putamen, P; Parietal cortex, PaC; Hippocampus, H; Broca’s area, BA; Visual scratch pad, VSP; Mamillary body, MB; Amygdala, A; Parietal lobe, PL; ventrolateral preoptic nucleus, VLPO; Parafacial zone, PF; Nucleus accumbens core, NAC; Lateral hypothalamic MCH neurons, LHMN
• O1 Fusion of elementary sensor into single time crystal
• Optic cranial nerve, II; trochlear nerve (IV); abducens nerve (VI); oculomotor nerve (III); Optic Chiasm, OC; Thalamus, Th; Optic Chiasm, OC; Optical nerve, ON; Retinal ganglion cell axon, RGCA; Lateral geniculate nucleus, LGN; Optical radiation, OR
• Cortex domain, CD; Ventral posterior nucleus, VPN; Dorsal column nuclei, DCN; Ventral horn, VH; Dorsal root ganglion, DRG; Touch, Pressure, Vibration, heat/cold, pain, proprioception (muscle), S1-S6
• Receptor cell nerve fiber, RCNF; Medial orbitofrontal, MOF; Tract, T; Amygdala, A; Lateral orbitofrontal, LOF; Hippocampus, H; Midbrain, M; Olfactory nerve, I
• Facial nerve (cranial nerve VII), the lingual branch of the glossopharyngeal nerve (cranial nerve IX), and the superior laryngeal branch of the vagus nerve (Cranial nerve X); Nucleus of medullary tract, NMT; Taste area of somatosensory, TAS; Taste area of insula, TAI; Medulla, M; Gustatory Cortex, GC; Thalamus, Th; Epiglottis, E
• Superior olivary nucleus, SON; Primary auditory cortex, PAC; Superior olive complex, SOC; Mid brain, MB; Lateral lemniscus, LL; Medulla, M; Inferior Colliculus, IC; Ventral Cochlear nucleus, VCN; Semicircular canals, SCC; Auditory nerve, AN; Medial geniculate body, MGB; Inferior colliculus, IC; Cochlear nucleus, CN; Auditory nerve, AN
• O2: Proprioception: Proprioception cells, PC; Pressure, P; Spinal cord, SC; Conscious, Co; Un-conscious, UC; Temperature, T; Cerebellum, C; Thalamus, Th; Vibration, V; Pons, Po; Pain, Pn; Touch, T; Dorsal root axon, DRA; Ventral Posterior nuclei, VPN; Dorsal root ganglion, DRG; Dorsal Column nuclei, DCN.

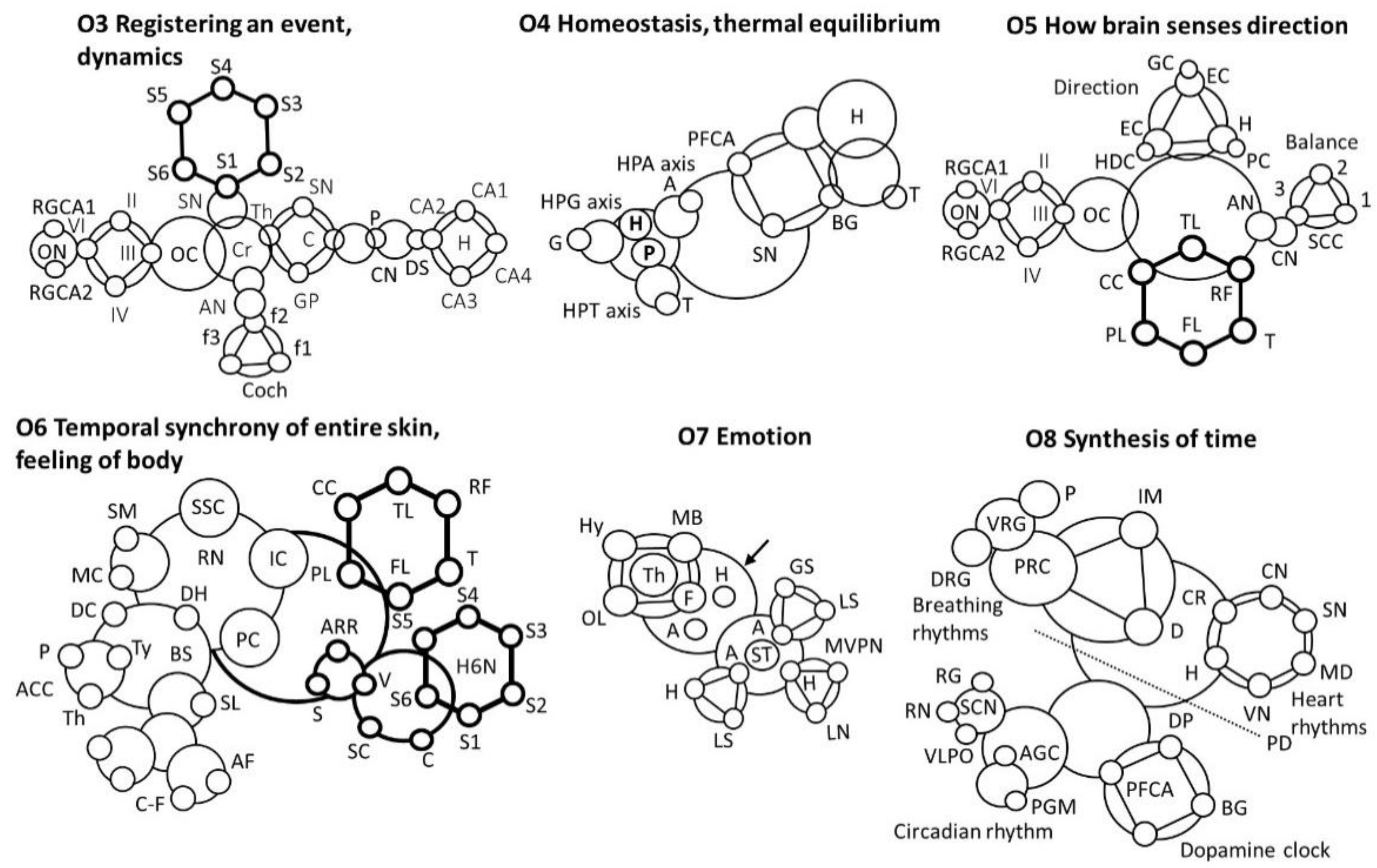
• O3 Motion or movement, audio+visual + time
• Registering an event
• Putamen, P; Caudate nucleus, CN; dorsal stratium, DS; Substantia Nigra, SN; Globus pallidus, GP; Claustrum, C; thalamus; Optical nerve, ON; Cochlea, Coch; Auditory nerve, AN; Retinal ganglion cell axon, RGCA; Spinal nerve, SN; Cerebellum, Cr.
• O4 Homeostasis, thermal equilibrium
• Pituitary, P; Gonad, G; Adrenal, A; Thyroid, T; Retina, R; Basal Ganglia, BG; Hypothalamus, H; Pituitary gland, PG; Melatomic level, ML; Superchiasmatic nucleus, SCN
• O5 How brain senses direction
• Semicircular canals, SCC; Cochlear nucleus, CN; Auditory nerve, AN; Optic cranial nerve, II; trochlear nerve (IV); abducens nerve (VI); oculomotor nerve (III), Optic Chiasm, OC; Retinal ganglion cell axon, RGCA; Temporal lobe, TL; Thalamus, T; Parietal lobe, PL; Frontal lobe, FL; Corpus calosum, CC; Reticular formation, RF; Place cells, PC; Hippocampus, H; Grid cells, GC; Entorhinal cortex, EC; Head direction cell, EDC
• O6 Temporal synchrony of entire skin cover, feeling of body
• Somato sensory Cortex, SSC; Supple mentary motor, SM; Raphe Nucleus, RN; Motor cortex, MC; Spinal loop, SL; Insular Cortex, IC; Descending connection, DC; Analgesic chemical cycles, ACC; Parietal Cortex, PC; Pituitary, P; C- fibre, C-F; Thyroid, Ty; Brain stain, BS; Nerve fibre, NF; Dorsal horn, DH; A-delta fiber, AF; Thalamus, Th; Activate automated response, AAR; Spinal cord, SC; Hippocampus, (6 nucleus), H6N; Shiver, S; Voluntary, V; Cerebral, C; Temporal lobe, TL; Thalamus, T; Parietal lobe, PL; Frontal lobe, FL; Corpus calosum, CC; Reticular formation, RF
• O7 Emotion
• Medial ventral posterior nucleus, MVPN; Amygdala, A; limbic system, LS; GABA secretion, GS; Hippocampus, H; Hypothalamus, H; Mamillary body, MB; Olfactory lobe, OL; Lateral nucleus, LN; Fornix, F; Thalamus, Th; Stria terminalis, ST
• O8 Time
• Medulla, MD; Pons, P; Internal muscle, IM; Internal muscle, IM; Vagus nerve, VN; Diaphragm, D; Ventral Respiratory Group, VRG; Pontine Respiratory Center, PRC; Dorsal Respiratory Group, DRG; Sinoatrial node, SN; Cardiac nerve, CN; Cardio Regulator, CR; Hypothalamus, H; Basal Ganglia, BG; Dopamin Path, DP; Pre-frontal cortex, anterior, PFCA; Substantia Nigra, SN; Pyramidal decussation, PD; Raphe nuclei, RN; Superchiasmatic nuclei, SCN; Adrenal gland cortisol, AGC; Pineal gland melatonin, PGM; Ventro-lateral preoptic nucleus, VLPO; Retina ganglion, RG; Tuberomammillary nucleus, TMN.

8.1.4. Time Crystal of a Neuron

Figure 9 is another important milestone because of two reasons. In the conventional brain models, the smallest decision-making unit in the neuron [85,86]. However, for us, the smallest component is alfa-helices or DNA spiral. Therefore, in Figure 9, time crystal to replace the neuron membrane response holds a promise to change the century-old concept of information processing via neuron. One of the key features in the time crystal representation is the inclusion of ordered architectures of beta-spectrin and actin network that resides just below the membrane. Ordered, unidirectional arrangement of filaments in the axon initial segment [87]. The massive network of filaments that were considered silent was also taken into account [31]. The lattice arrangement of proteins could change the potential distribution all along the microtubule surface. Finally, the protein structure and the role of water channels inside a single protein, across the filaments, and with the flow of water across the nerve bundles, we find that there are enormous contributions of water arrangement and flow in governing the neuron properties. Therefore, Figure 9 is a journey beyond existing neuroscience.

8.1.5. Time Crystal of a Single Microtubule

Figure 10 describes a complete representation of microtubule, the most important and the most complex system among all other filaments found in the neuron [66,88,89]. Sahu et al. [89] have carried out important studies on the single microtubule, especially finding the contributions of structural symmetries. Some of the key dynamic features included in the time crystal of microtubule are spiral transmission with variable periods. Secondary structures of tubulin protein generate local clusters that act as pockets of energy trap, i.e., these local orientations or $\alpha$-helical structures are considered as a circuit of helical elements. Water channels of neuron fibers are the very exciting topic of research, equally important is the water channels of microtubule inside its core, and similarly important is the external water layer around it. We have developed a new kind of fourth circuit element, Hinductor, H, in our lab inspired by the lattice arrangement and its dynamic symmetry [10,56]. Therefore, circuit, protein lattice arrangement, and water channel constitute three key architectural features that provide three major sections of the time crystal.

8.1.6. Time Crystal of the Cerebellum, Thalamic Body, Hippocampus, and the Hypothalamus

Figure 11 combines the time crystal of the cerebellum, thalamic body, hippocampus, and the hypothalamus into one integrated architecture. These four fundamental elements could silent one and operate with the other three to build a hierarchical control on the brain’s decision making. Similarly, Figure 12 combines the cranial nerve, the brain’s blood vessel, the thoracic nerve, and the skin nerve net, four key brain components that combine and build a hierarchical time crystal network. Figure 13 builds the third and final quartet assembly of time crystals, microtubule, neuron, cortical branches, and the cortex domain. If one notices the combinations we have used for 4 × 3 assemblies in Figure 11, Figure 12 and Figure 13, they will find that we have concentrated most environmentally sensitive, emotion sensitive, and logic sensitive parts separately.

8.1.7. The Time Crystal of the Complete Brain

Figure 14 and Figure 15 combine the 4 × 3 assemblies, and this is the time crystal map of the complete brain. Therefore, we start our journey from elementary helices of proteins, DNA, following up with the spirals of the hippocampus and end up with the giant organ skin of the entire human body. We do not want to leave any component that might affect the evolution of universal time crystal of the whole brain.

8.2. The Coexistence of Biological Clocks of Various Kinds with the Materials Key Resonances: Could Both Be Linked?

One major striking point in our effort to combine the clocks is that the clocks for the regeneration of cells and different periodic tasks for essential life-tasks are linked to the clocks formed by the natural resonance of dielectric materials. This effort to link all form of clocks have clear advantages, and many points could be listed, however, we would like to note justifications for bridging the two.

In the literature, biological clocks [2] begin with the bursting neurons or membranes [43]. The time-domain of brain operation is limited from milliseconds to seconds. Enzymes follow chemical sensing pathways to detect signals and activate the next. However, molecular-scale dynamics, resonant features were never included to find the clocks inside a neuron so that a neuron’s firing could be explained further, using faster clocks. Another query that often remains unanswered is how unique designs of brain components (think about fornix or cingulate gyrus) are created, what their purpose is. Singh et al. [28] have carried out extensive origins of these geometries, and these original contributions to the understanding of human brain geometry would remain as a seminal contribution. The impact of such studies would be manifold. We would not only link the geometries of key components like a neuron, but we would expand our studies beyond, for example, how typical folding of the hippocampus helps in acquiring key information processing decisions in the brain. Why C7 symmetry of cortical columns help, how would have the information processing changed if it would have followed a C8 symmetry. Therefore, so-called inactive components that had no role in decision making of the brain may turn important. Therefore, the quest to find a periodic clock like oscillations in every component, without pre-judging what the key is, would help in understanding the origin of components too.

9. Garden of Gardens of Meander Flowers: 20 Conscious Experiences and Their Time Crystal as Reported in the Literature

We have explained the garden of gardens or meander flower garden [2,90] in Figure 2. We have explained the same mechanism using the time crystals presented above for all organs, and then we collected some parts to build 20 conscious experiences [44]. There are five columns in Figure 19, primary time crystals are summarized in the first column of Figure 19 We have taken a simplified version as a meander flower garden. Then we combine the components time crystal to build fusion time crystals representing the entire system. One of the primary advantages of a fusion time crystal is that the stereographic projection to infinity and the feedback from infinity delivers the unique functional derivatives [33]. These derivatives are “petals collected from gardens of meander flowers,” and a new flower is built. The garden of gardens is 20 in number as summarized in the 4th and 5th columns of Figure 16.

• Hypothalamus: MT-Mammilothalamic tract, LS-Limbic system, HR-Heart rate, PN-Posterior nucleus, DMN-Dorso medial nucleus, AN-Arcuate nucleus, VN-Ventromedial nucleus, BP-Blood pressure, AP-Anterior Proptic, MP-Medial proptic, SN-Supraoptic nucleus, PVN-Paraventricular nucleus, LN-Lateral nucleus, HT-Hypothalamic nucleus, SC-Suprachiasmatic, O-Oxytocin,
• Cerebellum: SV-Superior vermis, P-Pyramid, AL-Anterior lobule, N-Nodule, U-Uvula, AGL- Anterior Graduate Lobule, A-Posterior quadrate lobule, SQL-Superior quadrate lobule, FL-Flocculonodular Lobe, B-Folia, D-Horizontal Fissure, E-Middle lobule, F-Dorsolateral fissure, G-Postlunate Fissure, H-Inferior semilunar lobule, I-Tonsil
• Hippocampus: DG-Dentate Gyrus, GCL-Granulate Cell Layer, H-Hilus, PL-Pyramidal Layer, PML-Polymorphic layer, Cavity of spatial and temporal pole is made of UT and VT, UT-U Trap, VT-V Trap, LEC(5)-Lateral Enthorhinal Cortex, (Pre/Parasubiculum, Pirifrom Cortex, Olfactory area, Amygdala). MEC(6)-Medial Enthorhinal cortex, (Perihinal cortex, frontal cortex, insular cortex, postrhinal cortex, cingulate gyrus, Parietal, Occipital cortex)
• Thoracic nerve: MNR-Motor nerve rootlet, SRN-Sensory root Ganglion, SNR-Sensory nerve root, NF-Nerve Fiber, A-Arachnoid matter, DM-Dura matter, PM-Pia matter, SCS-Suprachnoid space, CC-Central canal, WM-White matter, GM-Gray matter, AT-Anterior Tissue.
• Thalamic body: LVPN-Lateral ventral posterior nucleus, LDN-Lateral dorsal nucleus, LAN-Lateral anterior nucleus, IN-Intralaminor nucleus, LL-Lateral lamina, NM-Nuclei of midbrain, CMN-Centro median nucleus, AN-Anterior nucleus, MVPN-Medial ventral posterior nucleus. RN-Reticular nucleus, LPN-Lateral posterior nucleus, MDN-Medial dorsal nucleus, LVN-Lateral ventral nucleus.
• Cranial nerve: TN: Trochlear nerve, ON-Oculomotor nerve, AN-Abducens nerve, ON-Optic nerve, HN-Hypoglossal nerve, GN-Glossopharyngeal nerve, VC-Vestibulo-cochlear, VN-Vagus nerve, FN-Facial nerve, ON-Olfactory nerve, TN-Trigeminal nerve, SAN-Spinal accessory nerve.
• Blood Vessel’s branches: Circular shape (ACA-Anterior commutatory artery, ICA-Internal carotid artery, MCA-Middle cerebral artery, ASA-Anterior spinal artery), $\lambda$-shape(PA-Pontine Arteries, BA-Basilar artery, PA-Posterior Artery, SCA-Superior cerebral artery), T-shape (ICA-Interior cerebral artery, ASA-Anterior spinal artery, PCA-Posterior cerebral artery, AICA-Anterior Interior cerebral artery)
• Microtubule: Tubulin protein structure
• Secondary protein [$\alpha$-helices (LPD-Length pitch and diameter; CHRNO-alkyl, amine), $\beta ,\gamma ,\delta$]. Cavity[Conic, vortex, dumb-bell or tear drop, spiral]. Water layer [Random arrangement, cluster, ordered] Sim on the lattice surface, S(lattice type A, B and AB) and Protofilaments (numbers, 6–9, 10–14, 15–19).
• Topological morphogenesis of microtubule surface
• Helical transport path (periodicity helical gap 2,3, (returns on 13); gap 4 (returns on 16)); Central water channel (Longitudinal, transverse and normal); Surface tubulin lattice (six distinct classes of lattices observed in the tunnelling images)
• Interface between sub-helices & surfaces
• Secondary protein water channel (triplet of triplet domains, 8 tubulin cavities have 9 interfaces with H₂O); external surface water layer (1-2molecular layer of water in three modes, normal, disperse, interfered source); Inner core water channel (longitudinal, transverse and normal modes of water).
• Skin nerve network: Homeostatic primary clock network
• HoS- Homeostatic; Fb- Feedback; C* [4]- Brain stem, dorsal horn, spinal loop, descending connections; Fls[4]- Feedback local time crystal (Thyroid, Pituitary, thalamus); B*[3]- Motor cortex, parietal cortex, raphe nucleus, Hs- Homeostatic; Co- Cold; He- Heat; Mo- Moderate; Ac [5]- Activated; (Touch, vibration, pain, pressure, temp); V[3]- Voluntary, (Spinal loop, cortex, nerve fiber); Sh- Shiver (Sharp, week, moderate)
• Brain controlled higher level network connected to skin
• PrM- Proprioception manospeech; Ce- Cerebellum; Sp- Spinal; Th- Thalamus; D[3]- Dorsal, (Pons, Thalamus, Ventral posterior nucleus); D1- Dorsal root axon; D2-Dorsal root ganglion; D3- Dorsal columns; PrC- Propriception cells; K[3]- Kinesthesia (Trigeminal nerve, GSA fiber, Mesencephalic nucleus); Ex[4]- External haptic perception (Lateral, Pressure, following contour, exposure); N*[3]- Consciousness, non-consciousness
• Proprioception
• Sensory pathway via spinal cord
• Se – Sensory; Sp -Spinal system; Wh- White matter; Gr-Gray matter; Sc[3]- Spinal cord, (C- fiber, A delta, fiber) Mc- Meissner’s corpuscle; Ep- Epidermis layer; De-Dermis layer; Hy-Hypodermis layer; Nb-Nerve bundle; Sa-sacral; Lu-Lumber; Ca- Cervical
• Cortical branches: Ventricular and geometric cavities
• Aq-Aqueduct, Body, At-Atrium, LV-Lateral Ventricle, VS-Ventricular system, IV-V = IV Ventricle, III-V = III Ventricle, PH-Posterior Horn, IH-Interior Horn, AH-Anterior Horn,
• Top folded hexagonal lattice domains (47 Brodman’s regions)
• CS-Cortical system; SVL-Seven vertical layers of cortical column, N(4), Hexagonal lattice, Mc, Vc, Sc. Folded cavity, Sl-Sulus, Gy-Gyrus, Cc(4).
• Nerve bundle for different functional region.
• E(6), F(6), G(6), L(6), I(6), J(6), H(6), K(6), Three types of branches B, X-S=X-shape, Semi-circular-SC, and U-S-U shape.
• A = Occipital lobe, B = Frontal lobe, C = Temporal lobe, D = Perietal lobe, E (6) = Neurological function, F(6) = Lateral brodmann area, G(6) = Medial brodmann area, H(6) = Gyrus nuclei, I(6) = Formation sulus, J(6) = Function sulus, K(6) = Depth sulus, L(6) = Gingival sulus, Cc(4) = cortical columns (left, right, left right), N(4) = Neuron (Multipolar neuron, Motor neuron, Sensory neuron, Anaxonic neuron, 23 types of neural branches are studied), Vc = Visual cortex, Mc = Motor cortex, Sc = somatosensory cortex
• Cortex domain: MGB(2) = Median germiculate body (Thalamus, Cerebellum); Gp(2) = Glossopheringal (left part and right part); Mr = Medullary tract; Th = Thalamus; Me = Medulla; Ti = Taste area of insula; Tr = Tongue area of cortex; So = Somatosansory; E1(6) = Eye 1; E2(6) = Eye 2; A(6) = 6 nucleus; (v1,v2, v3, v4, v5, v6); Th = Thalamus; Op = Optic radiation; Ic = Inferior colliculus; e1,e2 = ear 1,ear 2.
• Em = Emotional pathways (details in functional time crystals); Tc = Time crystal clusters of hippocampal output, Thy = Thyroid, Pe = Personality time crystal, Tha = Thalamus, In = Insula, Ci = Cingulate gyrus learning pathway, St = striatum, ACC=, B(3) = Temporoparietal junction, reticular formation, supplementary; C(3) = Amygdala, Desolation, temporal lobe; Am, Mb = Amygdala, midbrain; Ols(2) = Olfactory system (lobe, tract); N1(6) = Nose1 (6 sensor, +one controller 6 + 1 = 7); N2(6) = Nose2(6 sensors +one controller, 6 + 1 = 7); Olc(2) = Olfactory cortex (Medial and lateral orbit frontal); PTC = Personality time crystal.
• Sc = 31 Spinal cord cavity’s time crystal; Th = thalamus, Cb = cerebellum, Pc = Proprioception cell based network, Se(4) = Sensor (Pressure, pain, touch, vibration); Vpn = Ventral post. Nuclei, DC = Dorsal column
• Ax = Axonal branches connecting cortical columns, Ga = Ganglion, Po = Pons brain stem, Ce = Cerebral
• Vo = Voluntary, Three sensations of homeostasis trigger large scale information processing, Sh = Shiver; He = Heat; Co = Cold
• Hp (6) = Hippocampus; (6 nucleus, +one controller 6 + 1 = 7); Rn = raphe nucleus, Nf = Nerve fiber singular time crystal, Sp = Spinal loop time crystal built by cross sectional components; Ic = Insula cortex; Ss = Somato sensory; Ma = Motor area, Mo = Motor cortex; Pc = Perietal cortex; Dh(3) = Dorsal horn, (Descending connection, Analgesic chemical cycle)
• All components of the column 4 and column 5 are described in the Figures following this presentation.

Figure 17 shows dodecanion tensor-based D1-D12 super meander flowers, then octonion O1-O8, little flowers, and finally, Q1-Q4, the quaternary flowers. Figure 17, Figure 18 and Figure 19 represents the signaling pathways for the corresponding brain functions. These pathways are well established. However, we have linked the pathways that affect one another. Instead of unique time crystals presented as conscious experiences, we could use tensors with clocking elements. For geometric musical language, GML [45], the elementary 2 × 2 tensor represents a cycloid like systems, i.e., a pair of circles connected and having a relative rotation, which means, their symmetries change differently. The quaternion, octonion, dodecanion, Hexa-decanions (multiple of 4) are most suited to explaining rotation in a 3D system, i.e., effective tools to present a clock architecture operating on a 3D Euclidean system. Conscious cognitive experiences have the geometric boundary or a cage in which geometric information made of 15 geometric shapes are placed.

Here, we have built a time crystal of 12 hardware covering the entire operational time domain. The biological rhythms run by brain associated components are converted into time crystals, and since cognitive response generating rhythms of the brain are also converted into time crystals. Two distinct kinds of time crystals are compared side by side to discover that time crystal generated as cognitive experience. The hardware version of the rhythm-based time crystals follows a simple pattern of primes, namely, phase prime metric, PPM ([10], JP-2017-150173; World patent WO 2019/026984). We conclude that the human brain components are designed as clocks, and the prime number of clocks are arranged to deliver a cognitive response. For readers, we have listed 47 Brodmann’s regions [39,40] which generate the garden of gardens flowers eventually, as described in Figure 17, Figure 18 and Figure 19 [11,12].

Brodmann’s 47 Functional Regions [39,40,91,92]

• Somatosensory, sensitive vibration, proprioception and fine touch, temperature, vibration, and pain. Deep proprioception. Intermediate postcentral.
• Somatosensory, sensitive vibration, proprioception and fine touch, temperature, vibration, and pain. Deep proprioception. Rostral postcentral.
• Somatosensory, sensitive vibration, proprioception and fine touch, temperature, vibration, and pain. Deep proprioception. Caudal postcentral.
• The motor fibers originate from the precentral gyrus. Searches for periodic events and joins multiple clocking events into a single clocking event. Proprioception.
• Somatosensory coordinating region; Perception of personal space. Processing chaotic pattern, Self-reflection during decision making, temporal context recognition.
• The initiation of movement arises here. Selective attention to rhythmic responses. Generating melodic phrases. Language processing and speech perception. Topographic memory.
• Attention, geometry-based deductive reasoning. Mental rotation, temporal context detection. The recollection of the experience, pains.
• Activates for coherent movement of the visual field, working memory. Still, since this region is responsible for planning and perceptual priming, it is affected by several diseases, executive dysfunction, Schizophrenia, and Alzheimer’s. Proprioception.
• Executive control of behavior. Detect error, identify the difference between conflict and reward. Social judgment, executive memory, abstract thinking, and intentionality.
• The executive function of event and time-based prospective memory. Multiple attentions at a time, expressing intention and response to the thermal stimuli. Forget intentionally.
• It is involved in emotional decision making and processing rewards, planning, encoding new information into long-term memory, and reasoning. Listening without talking.
• Orbitofrontal area, taste, Social Cognition, stabilize mood to a fixed state, and Mental Time. This region is indirectly connected to the global Palladius as well as the substantia nigra, due to efferent to the striatum.
• Insular cortex, behavioral inhibition, calculation, response to fear, feeling pain. Compassion and empathy, perception, motor control, self-awareness, cognitive functioning, and interpersonal experience. It is involved in psychopathology.
• Insular cortex, behavioral inhibition, calculation, response to fear, feeling pain. Compassion and empathy, perception, motor control, self-awareness, cognitive functioning, and interpersonal experience. It is involved in psychopathology.
• Anterior temporal lobe, behavioral inhibition, calculation, response to fear, feeling pain.
• Insular cortex, behavioral inhibition, calculation, response to fear, feeling pain; Compassion and empathy, perception, motor control, self-awareness, cognitive functioning, and interpersonal experience. It is involved in psychopathology.
• V1, primary, calcarine, or striate cortex) is the end organ of the afferent visual system, pattern, and orientation of objects.
• V2, Visual, confronting color and shape, correlating form and name, motion (shape + time).
• V3, Visual mental imagery, connecting words or sentences, and build an associative structure.
• Comprehending metaphor, abstract events, objects; visual to the perceptual whole, thus, processing the task of visual memory processing.
• Complex composition of sounds processing, correlating texts to words, build sentences for language processing.
• Part of the superior temporal gyrus included in the language processing region known as Wernicke’s area. Prosody comprehension. Detecting key tone features of multiple languages.
• Ventral posterior cingulate cortex, comprehension of the concept, emotional language; dynamics of geometric shapes (topokinetics).
• Ventral anterior cingulate cortex, expression; behavioral & motor inhibition, mental timekeeping, feeling pain.
• Subgenual area (part of the Ventromedial prefrontal cortex).
• Ectosplenial portion of the retrosplenial region of the cerebral cortex; dynamics of geometric shapes (topokinetics), comprehension of feelings in the words.
• Piriform cortex, experiencing and realization of emotion.
• Ventral entorhinal cortex, experiencing and realization of emotion.
• Retrosplenial cingulate cortex, comprehension by retrieving memory; dynamics of geometric shapes (topokinetics).
• Part of cingulate cortex, comprehension by retrieving memory; dynamics of geometric shapes (topokinetics).
• Dorsal Posterior cingulate cortex, comprehension by retrieving memory; dynamics of geometric shapes (topokinetics).
• Dorsal anterior cingulate cortex, smell related differentiation, comprehension by retrieving memory; behavioral & motor inhibition, various emotional stimuli, mental timekeeping, feeling pain.
• Part of anterior cingulate cortex, comprehension by retrieving memory; behavioral & motor inhibition, various emotional stimuli, feeling pain, mental timekeeping.
• Dorsal entorhinal cortex (on the Parahippocampal gyrus), comprehension by retrieving memory; experiencing and realization of emotion; Novelty discrimination.
• Perirhinal cortex (in the rhinal sulcus), comprehension by retrieving memory; experiencing and realization of emotion; Novelty discrimination.
• Ectorhinal area, now part of the perirhinal cortex (in the rhinal sulcus); working memory; experiencing and realization of emotion; Novelty discrimination.
• Recognizing true and false memories, episodic encoding. Judging minute changes of known events, objects, face recognition. Semantic relationship extraction.
• The junction that links hearing, vision, memory, emotional awareness, and reactions. Diverse language functions. (11, 38, 47 emotions). Comprehending humor, inferential reasoning to fear, threat, emotional attachment. Comprehending narrative, the composition of voice tone, music.
• Mathematics, abstract reasoning. Executive control of systematic behavior, the sequence of words, and the sequence of tasks organized.
• Region of creativity. Comparing past, present events, memory, images, music, etc. Detecting conflict between intention and sensory drive; often compare tactile and proprioceptive response. Performing music.
• The critical technical parameters of a complex sound are analyzed. Rapid bursts of sounds are decomposed, and all essential parameters are retrieved.
• Retrieving and simulating missing auditory patterns. Segregating isolated parts of the sound, repetition priming effect.
• Digit or abstract numbers, integers, primes stimulate this region. Understanding codes.
• Executive function on identifying grammar rules, retrieving unintelligible speech, expressing emotion, compose music, triggering expressive movement.
• Broca’s area, aesthetic appreciation, editing, or modulating the emotional response. Inhibiting or hiding response, build a filtered sequence of facts, events, data for the rapid expression.
• Executive control on behavior, calculating in mind, estimating self-reflection, detecting conflict and changing strategy and exhibiting empathy.
• Meticulous sensing of stimuli, inhibiting emotional response. Sensitive temporal coherence among various signals, like language, music, etc.

10. The Operational Mechanism of the Brain: Frequently Asked Questions

10.1. How Brain Structures Evolve, How Learning or Thinking Changes the Brain Circuits? What Is Wrong with the Current Neuroscience Model and How Our Model Helps in Bridging Those Missing Links?

In our brain model, we have a couple of key ingredients. (1) There is a complete temporal pattern as a time crystal architecture of the whole brain. It is the memory (there is no separate space or resource for memory); it is the architecture of generic decision making; the time crystal architecture represents the defining features of various patterns of primes (PPMs). The symmetry of time crystal arrangement selects the dominating integers and primes required to construct a typical PPM ([10], JP-2017-150173; World patent WO 2019/026984). Every brain component is an assembly of time crystal or a time polycrystal; just by looking at a time crystal architecture, one could draw its equivalent PPM. Three trees (Why three? 2 × 2 × 3, 2 × 3 × 2, 3 × 2 × 2) whose branches are made of PPMs edit their structures simultaneously as the brain processes information. (2) Brain processes information means the trees grow new branches or PPMs when PPM converts input time polycrystals into an integrated architecture of clocks and sends it to the external world. Three trees continuously produce wide varieties of time crystals by linking time crystals as thoughts. (3) Time polycrystals operate in all time domains at a time, hence memory is written everywhere, together with information is processed everywhere, at a time. Most importantly, several copies or replicas of information leaves its signature everywhere. Hence, all kinds of carriers and all kinds of mediums operate to utilize the time domain as widely as possible.

Current neuroscience models consider the brain as a circuit of switches made of neurons, so it requires an algorithm to run it. Algorithms need human intuition, so the models are machines. In our model, tensors with dimensions 2D to 20D follows a metric STts [33], carry out stereographic projection to infinity, and incorporates the feedback [32], to generate decisions for the human brain. The self-operational universe [32,33] model enables our brain model, avoiding the need for any external interference and run on its own. No brain model integrates constituents as elementary prime numbers. The brain operates as if the non-repeating pattern of primes, generating unique composition of integers. Linking the choice of arranging the events to the ordered factor of integers with the prime number of brain components enables our model brain to operate by itself. Moving from membrane only transmission and junction limited decision to decentralized decision making of temporal expressions of organs is a major difference with current neuroscience. For our model, the neuron membrane is one of twelve major components involved in decision making.

10.2. Do All Humans Have Same Time Crystal Architecture? Same PPM Architecture for the Brain? How Do Two Humans Differ?

As far as generic hardware is concerned, all humans have identical host clock architectures, but when we start making a journey through the structure of the guest clocks, we find that details of guest clocks vary. Interhuman differences are in the detailing of the local clocks, which a living system acquires during the journey.

10.3. How Does a Change in the Arrangement of Clocks Affect Brain Hardware? The Foundation of Neurogenesis in Our Brain Model

At the very local levels, throughout the clock architecture representing the brain, we would find clocks are being added, subtracted. During brain operation, the PPMs born, unwanted PPMs disappears, how does that affect the neural circuits? A clock represents a particular symmetry, where, in the symmetry-time-domain co-ordinate, a newborn or deleted lock is located, depending on that a particular clock system is identified [20,21]. Note that if it is found in the synthesis of a new time crystal or a thought that major changes need to be done, it is like the coexistence of two 3D clock architectures in a local domain of the 3D time crystal map of the human brain. It is interesting to note that if a set of neurons or proteins that would change does not vibrate in a new pattern, future time crystal pattern won’t get created in the first place. So, time crystal coexists in two forms, and the material pathway vibrates in two modes, periodically (classical or quantum). The dual-mode oscillations try to reach synchrony, and that happens if the future form of a time crystal is built brilliantly.

Now we come to the most interesting part of our brain model. In all existing brain models [93,94], one has to rewire neural junctions or build a new circuit to edit brain learning. Here, junction editing is not an absolute necessity; the geometric arrangement of neural branches or a minor shift in the nerve fiber orientation could add, subtract, or edit a clock. Furthermore, a minor change in the ordering of arrangements would be enough to edit a clock, add a new one, or even delete a clock. Change in symmetry is everything we need to do at all scales for all purposes of brain functioning. If one wants to edit the nerve spike rate, then it would be sufficient to change the length, width, and pitch of helical assemblies around the axon. Plasticity is not limited to junction editing anymore. There are plenty of geometry editing options that could deliver a similar or much more profound effect.

If one wants to edit protein, then change the symmetry of arranging the secondary structure of proteins. For editing much shorter clocks like that is represented by a nerve fiber, one could just simply reorient or bend it by a short angle. The 3D transmittance and reflectance of the concerned fields through the 3D architecture of the fibers would require a minor change, a little tilt. Singh et al. [28] have carried out extensive studies using CST to find how a little change, even in the curvature of a structure, changes the evanescent wave [34,35] and time crystal map significantly. There is one to one correspondence between the angular momentum map created by a structure when a signal of a particular frequency falls on a structure. Thus, reverse construction of the neural network to the deformation of subtle folds in the cortex to reshaping of the hypothalamus to axon length, there is a one to one map between the information content (time crystal) and the physical structure. It is neurogenesis in our model. One could easily build the neural network or equivalent hardware from the time crystal map of the system.

10.4. Digital Reconstruction of the Time Crystal Reconstruction of the Human Brain Is Possible? Could Our Brain Model Be Integrated with Modern Neuroscience?

We have made a mathematically significant statement above. The time crystal map of the whole brain provides two important information: first, the integrated architecture of PPMs and second, the symmetry of the cavities [41], and dielectric resonator arrangements [28]. We have to note here that unlike a conventional digital computer, here, information with physical significance is not logically compiled. The architecture of many PPMs independently and in a combined manner, sends stereographic projections to infinity and acquires feedback from infinity [33]. Therefore, the time crystals continuously generated as output are non-computable and cannot be written as an algorithm [10]. All PPMs are of infinite lengths, even if numbers of cavities are finite, and projection-feedback estimates how the effect of the shift in infinity point (described above in detail) changes the topology [33]. Shifting infinity cannot be defined.

Moreover, all outputs are fundamentally different than the input topology sets. Therefore, the brain’s decisions from the time crystal reconstructions appear as if it is the output of finite ordered circuit elements, but, in our model, the digital reconstruction is not possible. One has to replicate the topology of clocks at least so that after vibrations of various kinds, the similar time crystal architecture of the brain is regenerated. In that hardware, one could study the elementary effects of addition and subtraction of time crystals of the brain.

In modern neuroscience, membrane skin transmits the signal, the key to the brain’s cognitive response, gap junctions hold the memory. Cognition, perception, intelligence, and creativity, all key brain features, are attributed to the membrane and junction. How neural network build branches are important only to map the junctions, branches resemble wiring in an integrated chip. For us, branches are the hologram-like projector of vortices [41], every single component, from secondary structures of proteins to the entire body’s neural network, act as hologram-like projectors of 12 different kinds of vortices. These vortices are the generators of clocks.

In modern neuroscience, all components inside the membrane are silent, do not play any role in cognition. The fine-tuning of time gaps between nerve spikes is carried out by membrane alone. We have experimentally established that the membrane does transmit axon potential even if all filaments inside the axon are dissolved into cell fluids. However, neurons lose the ability to fine-tune the time gap between spikes [30,31]. Moreover, the ionic diffusion generated electric nerve impulse frequencies exhibit triplet of triplet frequency bands. So does the quasi-charge transmitted microtubule under electromagnetic resonance. More surprisingly, a similar triplet of triplet resonance is found under electromechanical oscillations of secondary structures of tubulin protein. The scale-free triplet of triplet resonance band across a large scale [26] suggests that existing neuroscience is a single pixel in a giant picture that nature paints as a function of time in brain science.

10.5. In Conventional Time Crystal Known for 50 Years, the Unit Cell Is Made of Only One Kind of Atoms or Clocks, Now Many Atoms Participate. How Polycrystals Are Born, Why Are They Necessary?

For 50 years, time crystal meant only constructing one unit cell of time crystal made of one kind of atom or one kind of clock [2,29]. Now, we also build one unit cell made of several (for brain 537 types of atoms or clocks) atoms. Its a unit cell for a polycrystal [41]. However, we used the word polycrystal only to reflect the view that the unit cell does not repeat in biological time crystals. But when a unit cell is made of different kinds of atoms, even in nature, we find polycrystals. Here, PPM that delivers symmetry repeats the unit cell but often with a difference [10]. A subtle change in symmetry changes the arrangement of unit cells, and since PPM extends to infinity, possibilities of rearrangement are astronomical. Thus, robust polycrystals are naturally synthesized by PPM assemblies of the human brain.

10.6. Two Different Concepts of Dimensions Are Applied Together in the Brain Model, Was Introducing 12 Dimensions Necessary?

Often in the literature, we find that Octonions [38,95] are used in quantum mechanics to explain seven distinct dynamics in 7 different dimensions, but the same imaginary world. Minkowski space-time is realized using SU(6) and SU(10), in all these applications we should note that there is only one imaginary time dimension, different dimensions are used to explore different dynamics. When we describe dodecanion [37], with 11 imaginary worlds nested one inside another, we explore a kind of dynamics that communicates across different imaginary worlds. We repeatedly note that in our formulation, we need only 2 × 2 tensor, one real and one imaginary world to explain quantum mechanics and Minkowski space-time. For Minkowski space-time we need only 2 × 2 tensor, one real and one imaginary world [33], just like quantum mechanics, a pair of the real or imaginary world could share space and time parts of the tensor, together and separately simultaneously.

10.7. Introduction of New Mechanics to Explain the Brain, Was It Essential? Does Time Crystal Model Propose the Brain as a Quantum Device or a Classical Device?

Since entire time crystal architecture representing the human brain or any brain component is made of singularity point and there is no real space, we cannot argue for classical or quantum mechanics. Figure 14 and Figure 15 may appear finite architecture of clocks. However, during operation, it builds an infinite series of geometric patterns via projection to infinity and feedback from infinity [32,33]. Therefore, the observer builds reality in its own system; the undefined network of clocks building the human brain model cannot be analysed using classical and quantum mechanics. The mechanics of singularity inside a singularity [48,49] requires special care. We proposed it as fractal mechanics [18,41], and it requires a provision of the interaction of many imaginary worlds. Moreover, it requires unique morphogenesis. Finally, the proposed time crystal model of the human brain requires a stereographic projection to infinity, and then feedback from infinity [33]. Both classical and quantum mechanics [2] bridge the singularity using various ways. Here, we explore that universe inside the singularity.

10.8. Introduction of Non-Computability in Brain Operation, Was It Essential?

Anything that is defined is computable by a Turing machine. In 2014, Ghosh et al. proposed Fractal tape to introduce a new kind of decision making without a logic gate or executing a computing [20]. Two key features deliver non-computability in the brain. First, within an above assembly of clocks through singularity turns the entire time crystal map of the brain an undefined architecture. Second, the stereographic projections to infinity and feedback from infinity are two events that govern decision output, i.e., human thoughts in our brain model. These are brilliant mathematical tools to explore the infinite topological series in decision synthesis through a network of undefined points [32,33]. Non-computability helps us in understanding decision making where infinite possibilities are taken into account collectively. It helps in estimating conformal effects on human perception. Scale-free geometric structure transmission in decision making helps us in affecting unrelated sensory information and share hidden intelligence from one part to another.

10.9. How Many Different Kinds of Brain Maps Do We Create? Which Brain Map Is Absolute?

Earlier brain maps were spatial [96], we introduce three new kinds of maps, temporal map or time crystal map of the whole brain. Then, by removing the circular paths and connecting the singularity points, we get a 3D topological map of the whole brain. Advancing further, we map the whole brain in terms of primes and primes alone wherefrom we create PPM assembly architecture of the whole brain. These four maps, namely spatial, temporal, topological, and prime, represent the self-operational human brain model that we present here. Therefore, we do not discard the spatial map movement, however, we argue that starting from information architecture and demands of detailed information processing, we can regenerate intricate details of the human brain architecture, i.e., the spatial map. None of the four maps are absolute. All four maps hold key information on brain dynamics and evolve uniquely and collectively at the same time.

10.10. If Some Components Get Destroyed, Does the Brain Loses Memory or the Processing Ability?

As it is well known in physics, that symmetry is the order or arrangement protocol, how many numbers of elements participate in defining the order is not important in building a clock. Therefore, as long as the clock architecture remains intact, it does not matter how many elements get destroyed. There are a large number of clocks keeping a fixed time. In other words, in the time crystal model of an organ, we may notice one clock. However, the corresponding number of elements is plenty. Each element is keeping the same time. Since all are identical, if a few of the clocks are destroyed, it does not change the clock architecture.

Trillions of microtubule oscillators, if produce one kind of identical clock, it contributes as a single clock in the time crystal model. Similarly, hundreds to thousands of neurons hold one memory in a single clock in the memory time crystal. Therefore, if a few neurons die or thousands of microtubules get destroyed, the time crystal architecture representing the brain does not change. There are always redundant elements that are running the same clock.

10.11. Would There Be Any Other Applications of the STts Metric Built Exclusively for Modeling the Human Brain?

While modeling the human brain and building a time crystal architecture, Singh et al. [28] and Ghosh et al. [20] found 12 layers one inside another. It explains life cycles with 10⁹ s (100 years, heart cell regeneration cycle) to 10⁻¹⁶ s faster oscillation of atomic bonds in amines and totally that 10²⁵ order changes in the time scale could be analyzed using GML. The hierarchy problem for the universe is not much different. Now, one could try solving the gravitational quantum problems, renormalization problems [97], which were historical hallmarks for the development of new protocols in physics that could solve long-unsolved mysteries. Time crystal with clockwise and anti-clockwise rotating singularity spheres [98] and [99] could represent spin network [100] or spin foam, to provide space-time architecture required in quantum.

10.12. Is There Any Other Human Brain Model That Argues for the 11D Information Processing? What Are the Differences with the Proposed Time Crystal Model of the Human Brain?

Recently 11D structures are found in the brain. It is claimed that the neurons arrange in the brain in the shape of triangle, square, pentagon like geometric shapes. Moreover, these shapes were linked to human cognition and consciousness [101]. One of the major differences between the discovery of 11D physical structure and our 11D dynamics in clock arrangement is that for our system, it is the arrangement of vibrational peaks in the frequency spectrum where we observe self-similarities [32]. The geometric shapes are not physical. They are to be found in the temporal domain. Moreover, the shapes of brain constituent cavities follow peculiar geometric morphogenesis, e.g., the transition from ellipsoid to teardrop shape, or exhibiting electric, magnetic, and mechanical resonance frequency distribution following an identity $e^2+{\varphi }^2={\pi }^2$.

11. Conclusion: A Global Effort Required to Perfect the time Crystal Map of the Whole Brain

Brodmann asked how the cells look in different parts of the brain? In our terminology, the question would be reframed to consider how the cavity resonators made of neurons look in different parts of the brain. He derived one kind of brain map. Consequently, the connectome introduced where the water flows in the brain, and they derived another kind of brain map. Different questions deliver different maps of the brain. So, we asked, how does it operate by itself, so we get another temporal or time crystal map of the whole brain we present here.

The origin of consciousness is represented as the ability to create a triplet of dodecanion manifolds. Still, there are 12 components in the brain, at least, which are capable of doing this independently. Therefore, the human brain could compose manifold triplets in three different ways simultaneously, by choosing grouping 12 components in three different ways (2 × 2 × 3, 2 × 3 × 2, 3 × 2 × 2) it’s a hierarchy of manifolds. Thus, an entire brain turns out to be a timekeeper that primarily manages time crystals of a few femtoseconds to a few million years by adjusting precise motions of the oscillators within the framework of its frequency fractal network. Cognitive behavior is the output of time adjustment by which external and internal rhythms undergo precise changes at all spatial scales, from a few atoms to the centimeter-scale ranges, to make each other’s PPMs similar. The human brain model is based on three fundamental discoveries: First, a new kind of fourth circuit element, namely H inductor, H, which is inspired by the design of $\alpha$-helix, microtubule, DNA, etc. Second, the pattern of primes that links discretely apparent symmetries, which is called the phase prime metric (PPM), this is based on the experimental measurement of electromagnetic resonance of microtubules. Third, geometric musical language (GML), where a special kind of time crystal is used to write information, GML was also found in the resonant oscillations of microtubules. The human brain model proposed here is an extension of scale-free electromagnetic resonance of the single tubulin protein, microtubule nanowire, and a single hippocampal neuron [26].

A set of 19 classes of tensors powered by space-time-topology-prime build new metrics for the brain. If we want to transmit a triangle across the imaginary worlds, then the three angles of a triangle would remain constant, we squeeze or expand the triangle to fit it in different imaginary worlds. Therefore, the conformal feature is ensured in our brain model. One could switch off consciousness simply by deactivating the integration clocks of 12 major brain components we have identified. If one searches for the right component for consciousness, they would experimentally find 12 factors, and all the answers would be right at the same time. Therefore, it is of utmost importance to advance our work by meticulously checking the intricate details of the clocks at every single domain that we have investigated. We have built the first and the most primitive time crystal model or temporal map of the human brain, considering all major components that actively edit the neural network and decision making of the brain. Therefore, we hope that other researchers would follow up and give it the shape of a global movement just like the connectome brain mapping project. There may be a complete map or catalog of the human brain or a complete life form.