Position Control of Cable-Driven Robotic Soft Arm Based on Deep Reinforcement Learning
Abstract
:1. Introduction
2. System Architecture
2.1. Design of Cable-Driven Soft Arm
2.2. Overall Design of Control System
3. MLP Model of Cable-Driven Soft Arm
| Algorithm 1. Event-Triggered Distributed Optimization Approach | |
| 1 | For episode do |
| 2 | reset start position and target position |
| 3 | While not terminal do |
| 4 | state, reward, terminal = ENV.observe |
| 5 | action = DQN.chooseAction(state) |
| 6 | ENV.executeAction(action) |
| 7 | stateNext, reward, terminal = ENV.observe |
| 8 | DQN.store(state, action, reward, stateNext) |
| 9 | DQN.learn |
| 10 | End while |
| 11 | End for |
3.1. State Design
3.2. Action Design
3.3. Reward Design
| Algorithm 2. Reward function | |
| Input: | The end coordinates of the current soft arm Xc, the last round Xl and the target position Xt |
| Output: | The reward value R of the current state and the termination flag terminal of a single loop |
| 1 | for sequence do |
| 2 | for episode do |
| 3 | Disc = ∥Xc − Xt∥, Disl = ∥Xl − Xt∥, Terminal = False |
| 4 | else if Disc < ϵ then |
| 5 | Terminal = True, R = 2 |
| 6 | else if Disc − Disl > 0 then |
| 7 | R = 1 |
| 8 | else |
| 9 | R = 0 |
| 10 | end for |
4. Simulation and Experiment
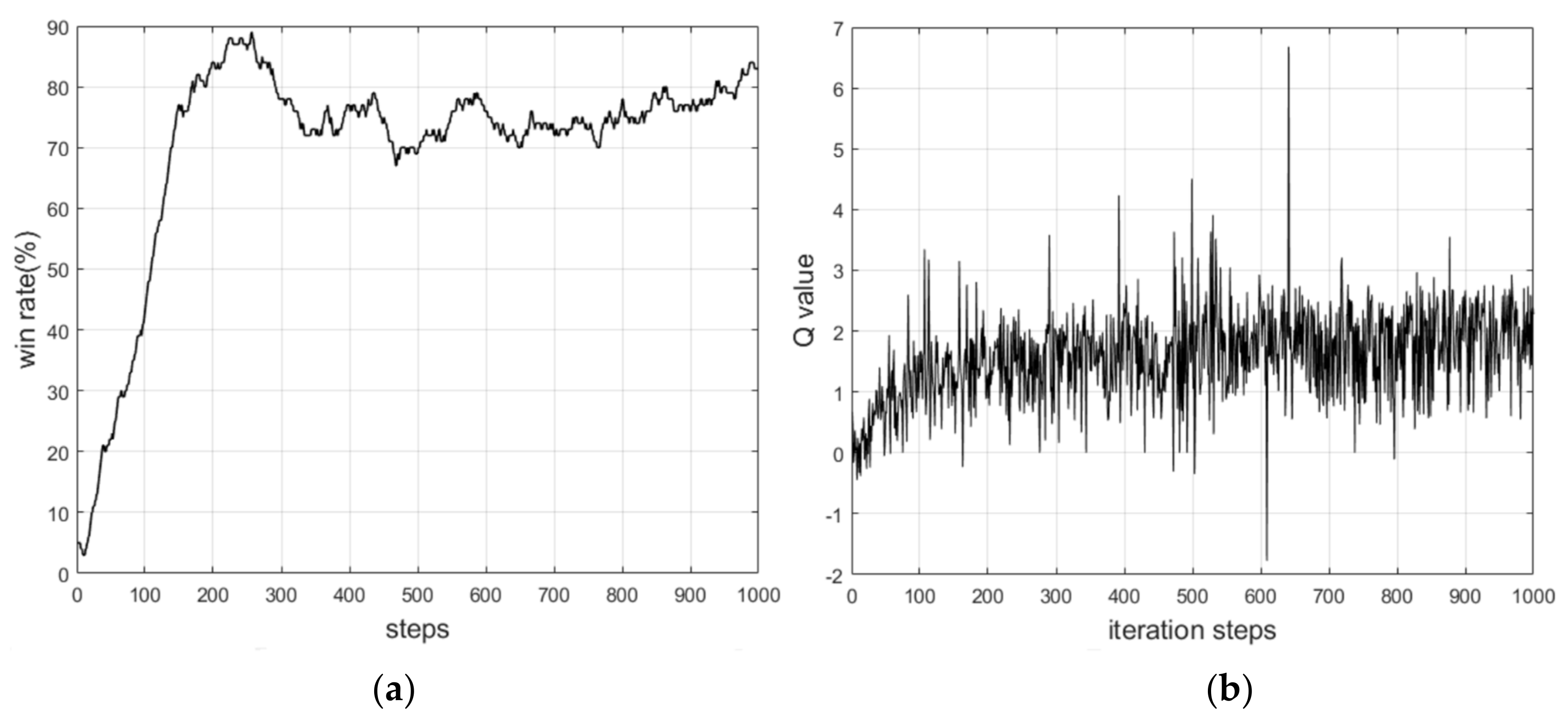
4.1. Train in Simulation Environment
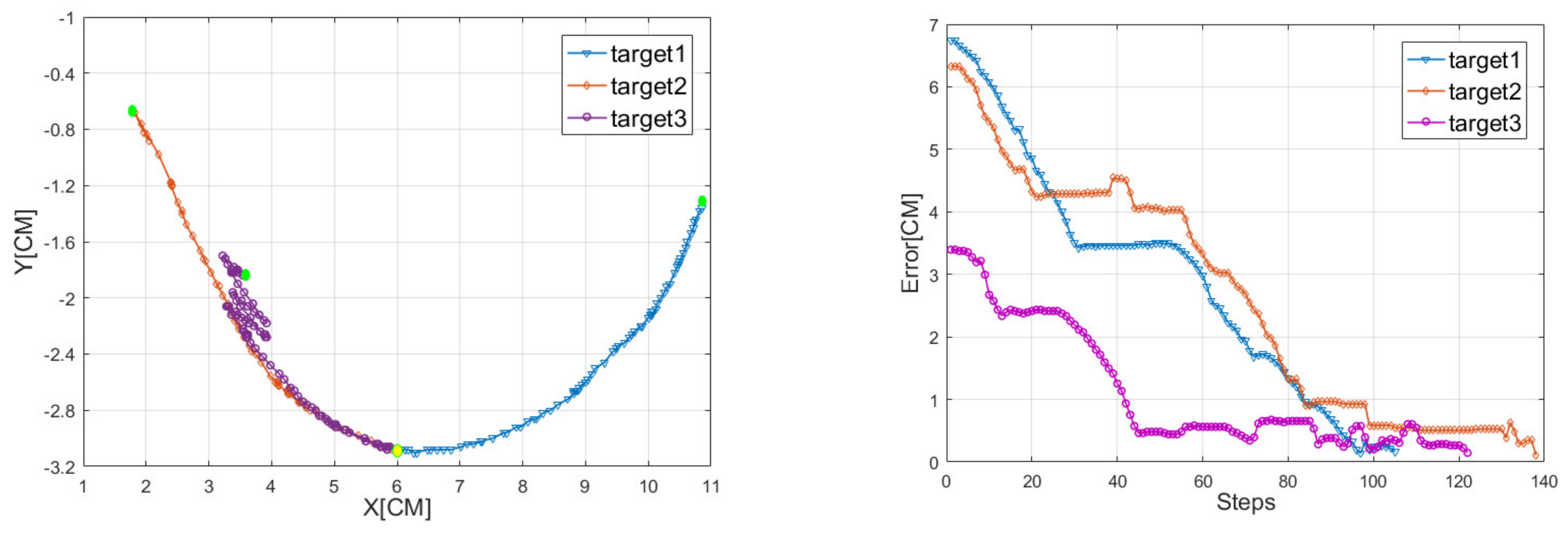
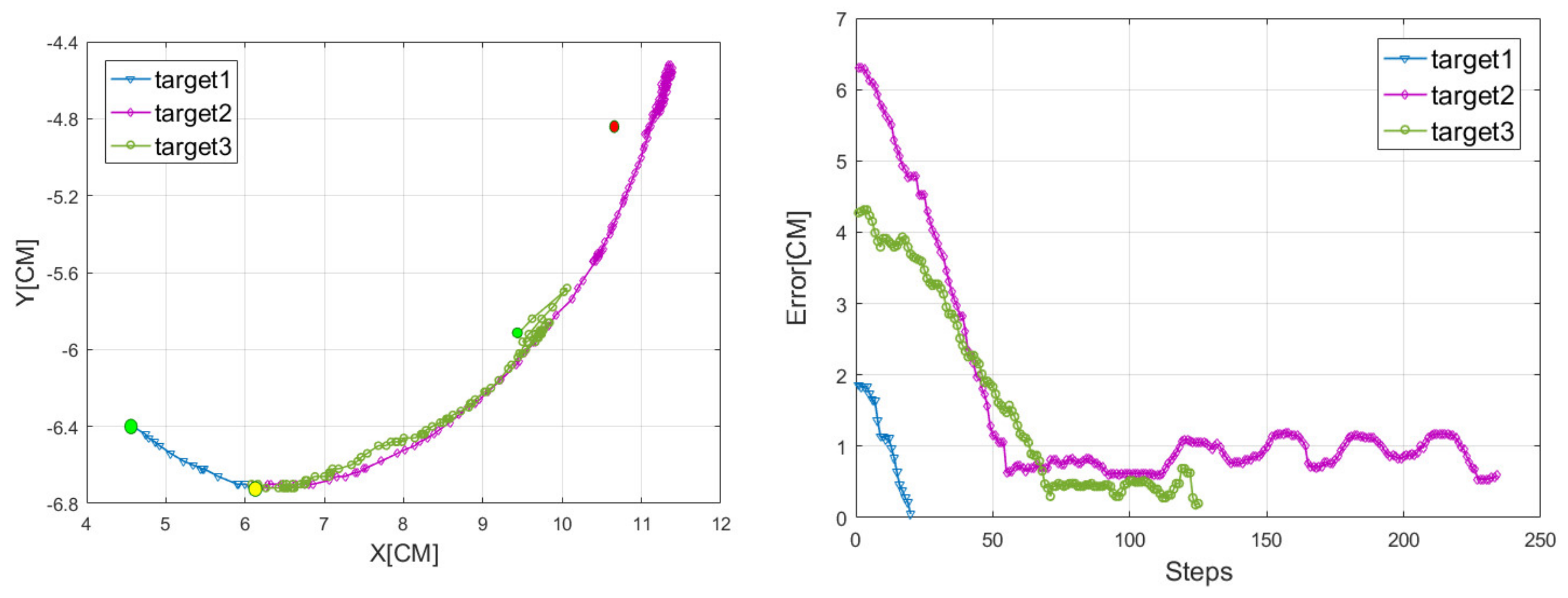
4.2. Test in Real World
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anton, Z.; Oleg, K.; Sergei, C.; Anatoliy, N.; Sergei, S. Numerical Methods for Solving the Problem of Calibrating a Projective Stereo Pair Camera, Optimized for Implementation on FPGA. Procedia Comput. Sci. 2020, 167, 2229–2235. [Google Scholar] [CrossRef]
- Phung, A.S.; Malzahn, J.; Hoffmann, F.; Bertram, T. Data Based Kinematic Model of a Multi-Flexible-Link Robot Arm for Varying Payloads. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Phuket, Thailand, 7–11 December 2011; pp. 1255–1260. [Google Scholar]
- Satheeshbabu, S.; Uppalapati, N.K.; Chowdhary, G.; Krishnan, G. Open Loop Position Control of Soft Continuum Arm Using Deep Reinforcement Learning. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- You, X.; Zhang, Y.; Chen, X.; Liu, X.; Wang, Z.; Jiang, H.; Chen, X. Model-Free Control for Soft Manipulators Based on Reinforcement Learning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2909–2915. [Google Scholar]
- Ivanov, A.; Zhilenkov, A. The Use of IMU MEMS-Sensors for Designing of Motion Capture System for Control of Robotic Objects. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow/St. Petersburg, Russia, 29 January–1 February 2018. [Google Scholar]
- Snderhauf, N.; Brock, O.; Scheirer, W.; Hadsell, R.; Fox, D.; Leitner, J.; Corke, P. The limits and potentials of deep learning for robotics. Int. J. Robot. Res. 2008, 37, 405–420. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Yang, B.; Liu, Y.; Chen, W.; Liang, X.; Pfeifer, R. Model-based reinforcement learning for closed-loop dynamic control of soft robotic manipulators. IEEE Trans. Robot. 2017, 35, 124–134. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; Van Hasselt, H.; Lanctot, M.; De Freitas, N. Dueling network architectures for deep reinforcement learning. arXiv 2015, arXiv:1511.06581. [Google Scholar]
- Zhilenkov, A.; Chernyi, S.; Sokolov, S.; Nyrkov, A. Intelligent autonomous navigation system for UAV in randomly changing environmental conditions. J. Intell. Fuzzy Syst. 2020, 1–7. [Google Scholar] [CrossRef]
- Zhang, F.; Leitner, J.; Milford, M.; Upcroft, B.; Corke, P. Towards vision-based deep reinforcement learning for robotic motion control. arXiv 2015, arXiv:1511.03791. [Google Scholar]
- Kim, J.I.; Hong, M.; Lee, K.; Kim, D.; Park, Y.; Oh, S. Learning to Walk a Tripod Mobile Robot Using Nonlinear Soft Vibration Actuators With Entropy Adaptive Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 2317–2324. [Google Scholar] [CrossRef]
- Feng, N.; Wang, H.; Hu, F.; Gouda, M.; Gong, J.; Wang, F. A fiber-reinforced human-like soft robotic manipulator based on sEMG force estimation. Eng. Appl. Artif. Intell. 2019, 86, 56–67. [Google Scholar] [CrossRef]






| Subjects | Numbers | Unit |
|---|---|---|
| length | 150 | mm |
| Diameter (small) | 6 | mm |
| Diameter (big) | 14 | mm |
| Shore hardness | 20 | AO |
| density | 1.1 | g/cm3 |
| elongation | 150 | % |
| viscosity | 2000 | Pa·s |
| Subjects | Numbers |
|---|---|
| total steps | 1000 |
| Memory size | 20,000 |
| optimizer | RMSPropOptimizer |
| learning rate | 0.0005 |
| ε-greedy | 0.4–0.9 |
| Maximum steps in round | 300 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Gu, Y.; Li, Y.; Zhang, B.; Chepinskiy, S.A.; Wang, J.; Zhilenkov, A.A.; Krasnov, A.Y.; Chernyi, S. Position Control of Cable-Driven Robotic Soft Arm Based on Deep Reinforcement Learning. Information 2020, 11, 310. https://doi.org/10.3390/info11060310
Wu Q, Gu Y, Li Y, Zhang B, Chepinskiy SA, Wang J, Zhilenkov AA, Krasnov AY, Chernyi S. Position Control of Cable-Driven Robotic Soft Arm Based on Deep Reinforcement Learning. Information. 2020; 11(6):310. https://doi.org/10.3390/info11060310
Chicago/Turabian StyleWu, Qiuxuan, Yueqin Gu, Yancheng Li, Botao Zhang, Sergey A. Chepinskiy, Jian Wang, Anton A. Zhilenkov, Aleksandr Y. Krasnov, and Sergei Chernyi. 2020. "Position Control of Cable-Driven Robotic Soft Arm Based on Deep Reinforcement Learning" Information 11, no. 6: 310. https://doi.org/10.3390/info11060310
APA StyleWu, Q., Gu, Y., Li, Y., Zhang, B., Chepinskiy, S. A., Wang, J., Zhilenkov, A. A., Krasnov, A. Y., & Chernyi, S. (2020). Position Control of Cable-Driven Robotic Soft Arm Based on Deep Reinforcement Learning. Information, 11(6), 310. https://doi.org/10.3390/info11060310







