Abstract
An accurate short-term load forecasting (STLF) is one of the most critical inputs for power plant units’ planning commitment. STLF reduces the overall planning uncertainty added by the intermittent production of renewable sources; thus, it helps to minimize the hydrothermal electricity production costs in a power grid. Although there is some research in the field and even several research applications, there is a continual need to improve forecasts. This research proposes a set of machine learning (ML) models to improve the accuracy of 168 h forecasts. The developed models employ features from multiple sources, such as historical load, weather, and holidays. Of the five ML models developed and tested in various load profile contexts, the Extreme Gradient Boosting Regressor (XGBoost) algorithm showed the best results, surpassing previous historical weekly predictions based on neural networks. Additionally, because XGBoost models are based on an ensemble of decision trees, it facilitated the model’s interpretation, which provided a relevant additional result, the features’ importance in the forecasting.
1. Introduction
The electric power system operation is a continuous work that requires real-time coordination from the power plants to distribution substations to operate within a secure range and conclusively deliver the electricity service with quality and without interruptions. Before the real-time operational job arrives, planning should be done to consider the renewable energy production sources’ behavior, the power plants and grid maintenance, and weight the hydrothermal resources, so the electricity production meets a projected demand. This real-time balance between energy generation and load should be sustained to avoid damages to the grid [1].
A power system operation’s planning time scope can be decomposed into three frames, and each of these frames focuses on specific tasks [2]: short-term, mid-term, and long-term. The short-term timeframe goes from 1 day to 1 week, focusing more on the power system’s operational and security aspects. The mid-term timeframe typically considers several weeks to several months, focusing more on managing the production resources and avoiding the energy deficits with the existing power plants. Consequently, the long-term timeframe focuses on years to decades, intending to define the installation of new power plants or changes on the transmission system. These criteria can vary from region to region; nevertheless, the concept should remain.
Generic and multi-site electricity demand data is difficult to obtain. Since the authors are familiar with Panama’s electricity infrastructure and because Panama makes its electricity load data publicly available, the authors decided to use the Panama electricity load data to build the models. In Panama, the National Dispatch Center (CND) is in charge of the power system planning and operation. According to CND methodologies [3], the goal of forecasting with an acceptable level of deviation is to anticipate and supply the demand with minimum costs. Short-term forecasting (following week) is needed to cover security aspects in the electrical system operation. As stated in the short-term and mid-term methodologies [3], CND does this forecast planning every week. For short-term scheduling, CND uses an hourly basis optimization software [4]. This optimization tool solves the weekly minimal dispatch cost, and it requires data about the load forecast, the power plants, and the power grid on an hourly basis. CND is currently using the Nostradamus tool by HITACHI ABB [5] to forecast the hourly load and feed the short-term optimization tool, to plan the following week’s hourly dispatch [6].
This research focuses mainly on predicting the short-term electricity load: this forecasting problem is known in the research field as short-term load forecasting (STLF), particularly, the STLF problem for the Panama power system, in which the forecasting horizon is one week, with hourly steps, which is a total of 168 h. An accurate STLF will help reduce the planning uncertainty added by the intermittent electricity production from renewable sources. Afterward, it will determine the optimum opportunity costs for hydro-electrical power plants with reservoirs. Consequently, an efficient thermal power plant dispatch can be achieved by minimizing the unit commitment production-transmission costs for the power system [7,8]. Ultimately, the operational costs associated with dispatching the best set of power plants in real-time dispatch will also be reduced.
The electricity consumption patterns evolve, and new machine learning (ML) approaches are emerging, motivating the exploration to update the forecasting tools with the most efficient and robust methods to minimize errors. In this sense, the current research aims to develop better STLF models. The models will be evaluated with the Nostradamus’ historical weekly forecasts for Panama’s power grid to benchmark the models’ performance against the Nostradamus forecasts in an effort to show that it is possible to improve the 168 h STLF. This research’s dataset includes historical load, a vast set of weather variables, holidays, and historical load weekly forecast features to compare the proposed ML approaches and achieve the above-declared objectives.
The Extreme Gradient Boosting Regressor (XGBoost) algorithm showed the best performance from the ML algorithms set, surpassing the historical weekly forecasts predicted by an artificial neural network (ANN) tool and providing information about features’ importance.
In addition to this introduction, this paper includes a section with a literature review on the STLF field, followed by a section with the materials and methods employed. Results are presented and discussed in the following section. Finally, the last section presents the conclusions along with limitations and future works recommendations.
Literature Review
The short-term electricity load forecasting is implemented to solve a wide range of needs, providing a wide range of applications. The most evident difference between research is the load scale, from a single transformer [9] to buildings [10], to cities [11], regions [12], and even countries [13]. The second most crucial distinction among the research field is the forecasting horizon. Varying from very short-term applications, like forecasting the next 900 s for machine tools [14], moving to a few hours [15], predicting the day-ahead, which is the most common [16], and 48 h ahead [17], to weekly forecasts [18]. The forecasting granularity also varies among the research field. Having granularities from 15 or 30 min, but most of the approaches consider hourly granularity forecasting. Despite the variety of forecasting applications, the current research will focus on covering implemented methodologies, chosen variables, algorithms, and evaluation criteria, since the forecast success will heavily depend on the decisions made through these development stages.
A wide variety of methodologies and algorithms have been implemented to address STLF. From the most straightforward persistence method, proposed in Reference [19], which follows the basic rule of “today equals tomorrow”, until the most recent deep learning algorithms, as exposed in the review article of Reference [20]. In this article, the authors compare traditional ML approaches with deep learning methods on the electricity forecasting field and the most trending algorithms in Scopus-indexed publications from 2005 to 2015.
Time-series analysis is considered one of the most widely discussed forecasting methodologies in which the Box-Jenkins and Holt-Winters procedures are extensively used. For example, the authors of Reference [21] used those methods to forecast the weekly load for Riyadh Power System in Saudi Arabia, concluding that these approaches give insights to decompose the electric load forecast. The autoregressive integrated moving average (ARIMA) model is proposed to forecast the next 24 h in Iran [22]. This modified ARIMA combines the estimation with temperature and load data, producing an enhancement to the traditional ARIMA model. The ARIMA model by itself does not significantly improve the forecast accuracy and is computationally more expensive, demonstrating the need to complement these models with external inputs to enhance the results.
Overall, in most recent research, these models are less used for electricity STLF since ML methods provide better results, as demonstrated in References [23,24], and more recently in Reference [25]. Particularly, in this last cited study, the authors compare the performance of six classical data-driven regression models and two deep learning models to deliver a day-ahead forecast for Jiangsu province, China, concluding that the ARIMA model had several limitations to solve the STLF problem. First, it can only consider time-series data to forecast based on the electrical load. Second, the determination of the model order is either computationally expensive or empirical. Lastly, to make residuals uncorrelated, several trials are required. At the same time, autocorrelation function (ACF) and partial autocorrelation function (PACF) graphs need to be iteratively checked to tune the model.
In contrast with the classical statistical time-series models, ML models can handle more valuable factors, such as weather conditions, to improve the STLF accuracy. Multiple linear regression (MLR) has been widely used for STLF. For example, the authors of Reference [26] used it to forecast the hourly weekly load in Thailand, obtaining an average mean absolute percentage error (MAPE) of 7.71% for 250 testing weeks and pointing out that temperature is a primary factor to predict load. Similarly, the authors of Reference [13] utilized MLR to forecast electricity consumption 24 h ahead for 14 west-African countries, considering weather variables like temperature, humidity, and daylight hours. The researchers that have implemented MLR agreed on the fast training and interpretability this model offers, although it shows poor performance for irregular load profiles.
Another approach that has been widely used for STLF during the last decades is the artificial neural network (ANN), mainly due to the algorithm flexibility. For example, in the 2006 study of Reference [10], an ANN is proposed with a Levenberg-Marquardt training algorithm to forecast hourly, daily, and weekly load in Ontario, Canada, presenting good results without comparing with other algorithms. Furthermore, the authors of Reference [9] predicted a single transformer hourly load, using quarter-hour load records and weather data with hourly records, obtaining a MAPE performance below 1% with ANN for summer and winter seasons. In more recent research, the authors of Reference [27] apply STLF for urban smart grid systems in Australia, commenting that ANN has good generalization ability for the task. However, this approach still has many disadvantages such as quickly falling into a local optimum, over-fitting, and exhibiting a relatively low convergence rate. Nevertheless, forecasting smart grid loads with increasing renewable energy sources is challenging and deserves complex solutions to obtain good results.
The support vector regression (SVR) model is another popular model for STLF, mainly with a linear kernel, due to the linearity between the inputs and the forecast, as concluded by the authors of Reference [25], who obtained a MAPE under 2.6% for the day-ahead prediction, performing better than MLR and multivariate adaptive regression splines. Similarly, the authors of Reference [17] proposed forecasting the 48 h of Portuguese electricity consumption by using SVR as a better alternative after previously submitting the ANN’s use for the same task in Reference [28]. The main reason for preferring SVR was the efficiency of the hyperparameter tuning on the daily online forecast. The SVR achieved a MAPE between 1.9% and 3.1% for the first-day forecast and between 3.1% and 4% for the second day. A variant of SVR is compared against ANN by the authors of Reference [29] to forecast the south-Iranian day-ahead hourly load. They proposed the nu-SVR, which improves upon SVR by changing the algorithm optimization problem and automatically allowing the epsilon tube width to adapt to data. They evaluated both models for each season: the average MAPE was 2.95% for nu-SVR and 3.24% for ANN.
The random forest (RF) ensemble technique combines independent learners to improve the overall model forecasting ability. The research presented in Reference [30] took advantage of this principle to forecast the day-ahead hourly consumption in office buildings. They used many ensemble algorithms, with RF being one of them, including environmental variables such as temperature and humidity and lagged load records to improve the results. Finally, they obtained a 6.11% MAPE for RF.
Similarly, the authors of Reference [31] submitted a comparative study between many models to forecast smart buildings’ electricity load. ARIMA, Seasonal ARIMA (SARIMA), RF, and extreme gradient boosting (XGB) were on this set of models. Their experiments demonstrated that RF showed decent results, but XGB outperformed the other methods, concluding that XGB gives better accuracy and better performance in terms of execution time. The study from Reference [32] compares RF solely with XGB to forecast the next 24 h load and concludes that XGB, as an emerging ensemble learning algorithm, can achieve higher prediction accuracy, producing a root mean squared error (RMSE) of 3.31 for RF and 2.01 for XGB.
The authors of Reference [33] suggest using XGB, including weather variables and historical load, to forecast the hourly weekly load of a power plant. A remark is made on the complexity of the XGB hyperparameter phase. For this reason, the fireworks algorithm is proposed as a solution to obtain the global minimum on the hyperparameter space, and for instance, getting a more accurate load forecast. STLF for holidays is one of the most challenging tasks within the field due to their irregular load profile, though, in Reference [16], the authors argue that there are many matured predictive methods for STLF such as SVR, ANN, and deep learning (DL). However, those methods have some issues: SVR is not robust to outliers, ANN has the weakness of setting the correct number of hidden layers or can be easily trapped into a local minimum, and DL approaches require massive high-dimensional datasets for good performance. XGB lacks these issues and outperforms the others for solving STLF. Their results are based on averaging the daily profile curves for similar holidays plus the use of XGB, where this averaging plus XGB outperforms RF, SVR, ANN, and even the sole-use XGB.
Despite the good XGB performance, some authors recommend training the model based on similar days to enhance the forecast [34,35]. A comparison between a traditional XGB and the similar days XGB is demonstrated in Reference [34]. The similar days approach showed a noticeable improvement, emphasizing that the accurate selection of similar days will directly affect the STLF.
Because XGB provides the feature importance property, the authors of Reference [36] proposed a hybrid algorithm to classify similar days with K-means clustering fed by XGB feature importance results. Once the classification is done, an empirical mode method is used to decompose similar days’ data into several intrinsic mode functions to train separated long short-term memory (LSTM) models, and finally, a time-series reconstruction from individual LSTM model predictions. This hybrid model using LSTM performed better for STLF over 24 and 168 h horizons, after comparing with ARIMA, SVR, or a back-propagation neural network using the same similar day approach as initial input.
The authors of Reference [37] proposed a multi-step-ahead forecasting methodology using XGB and SVR to forecast hourly heat load, where a “direct” and “recursive” forecasting strategy are compared. The direct method involves an independent model to predict each period on the forecasting horizon, while the “recursive” method considers a unique model that iterates one step at a time over the forecasting horizon, using the previous predicted steps as an input variable for the following forecasting step. Performance is the main disadvantage of the direct strategy because it needs to train as many models as desired periods to forecasts. The recursive strategy is sensitive to prediction errors, meaning that prediction errors will propagate along the forecasting horizon.
A study to forecast the 10-day streamflow for a hydroelectric dam used a decomposition-based methodology to compare XGB and SVR [38]. In this study, the streamflow time-series were decomposed into seven contiguous frequency components using the Fourier Transform. Then, each component was forecasted independently by the SVR or XGB. The study results showed that SVR outperformed XGB in terms of evaluation criteria through the Fourier decomposition methodology.
Another solution joining ANN with ensemble approaches is presented in Reference [39], where the authors seek to improve ANN generalization ability using bagging-boosting. When training ensembles of ANNs in parallel, each ensemble uses a bootstrapped sample of the training data and consists of training the ANNs sequentially, and this method reduces the STLF error but increases the computational time because of the several training procedures. Alternatively to training several ANN sequentially, the authors of Reference [40] propose an evolutionary novel optimization procedure for tuning an ANN. For instance, avoiding the issues related to ANN tuning like overfitting and selecting the best ANN architecture. Their results achieved a 4.86% MAPE. Based on the results from References [10,36], ANN for STLF can outperform other forecasting methods if a robust hyperparameter optimization is performed to avoid the issues related to ANN tuning.
Recurrent neural networks (RNN) are taking an important place in the STLF field from all neural network approaches, especially LSTM. Contrary to standard feedforward neural networks, LSTM feedback connections are beneficial to deal with time-series forecasting applications. An example of forecasting the next 24 h load from a smart grid, comparing LSTM results with a back-propagation ANN and SVR, demonstrates that LSTM can offer a MAPE of 1.9% against 3.3% from ANN and 4.8% of SVR [41]. Similarly, the authors of Reference [42] address the STLF for a furniture company with a method based on a multi-layer LSTM and compare it to other models like ARIMA, exponential smoothing, k-nearest neighbors regressor, and ANN. Moreover, their results showed that LSTM performed better in both RMSE and MAPE, followed by SVM and ANN. According to Reference [43], deep learning methods have a superior performance in electricity STLF. However, the potential of using these methods has not yet been fully exploited in terms of the hidden layer structures. For this reason, they evaluate deep-stacked LSTM with multiple layers for both unidirectional LSTM (Uni-LSTM), bidirectional LSTM (Bi-LSTM), and SVR as the baseline. Their results showed that Bi-LSTM returned a MAPE of 0.22% against MAPE scores above 2% for Uni-LSTM and SVR.
The hybridization of the successive geometric transformations model (SGTM) neural-like structure is another promising approach for STLF, as used in Reference [44] to predict Libya’s solar radiation. This approach demonstrated a higher accuracy than MLR, SVR, RF, and multilayer perceptron neural network, besides having a faster training time due to the non-iterative training procedure.
2. Materials and Methods
Regarding the hardware and software, this research was developed in a computer with an i5-9300H processor and 8 Gigabytes of RAM. Colab [45] hosted Jupyter notebooks service. All the experiments were developed with Python [46].
2.1. Data Sources, Data Extraction, and Data Preparation
All data sources to develop this research are publicly available, and the data is available in hourly records from January 2015 until June 2020. The data composition is the following:
- Historical electricity load, available on daily post-dispatch reports [47], and historical weekly forecasts available on weekly pre-dispatch reports [48], both from CND.
- Calendar information related to holidays, and school period, provided by Panama’s Ministry of Education through Official Gazette [49] and holidays websites [50].
- Weather variables, such as temperature, relative humidity, precipitation, and wind speed, from three main cities in Panama, are gathered from EarthData satellite data [51].
The load datasets are available in Excel files on a daily and weekly basis, with hourly granularity. Holidays and school periods data is sparse, along with websites and PDF files. These periods are represented with binary variables, and date ranges are manually inputted into Excel files. Both Excel datasets are imported and converted into data frames [52]. Weather data is available on daily NetCDF files, which can be treated with netCDF [53] and xarray [54] to select the desired variables and subsequently merge all the datasets into a unique modeling dataset.
Finally, the results of these steps are a time-series with the historical forecast along with its date–time timestamp as the index, and a data frame with the same timestamp index and 15 columns, one for each of the following variables in Table 1. Both objects have 48,048 records.

Table 1.
Variables’ description and units of measure.
There are no missing values on the datasets, and an initial outlier’s revision was made by normalizing each variable. Only a few low values on the load were detected due to hourly blackouts and damages in the power grid, but all records were kept.
The set of variables used to train the ML models, also called features, are treated in this section. New variables related to the date–time index are created to feed the ML models with this extra information about time, with this being one of the most critical steps for STLF [22,48]. The new features added to the datasets are year, month number, day of the month, week of the year, day of the week, the hour of the day, the hour of the week, and a weekend indicator. Since all are integer variables, except for the binary weekend indicator, it is essential to clarify that Saturday is considered the first day of the week. For instance, the first week of each year is the first complete week starting on Saturday, and this is respected to keep the CND reports calendar structure for further comparisons.
Load weekly lags, load weekly moving average (LMA), and weekly moving standard deviation features were newly calculated features that helped capture the most recent load changes [30], keeping the hourly granularity. These were calculated from the immediately preceding week until the fourth week, adding 12 more features to the current dataset.
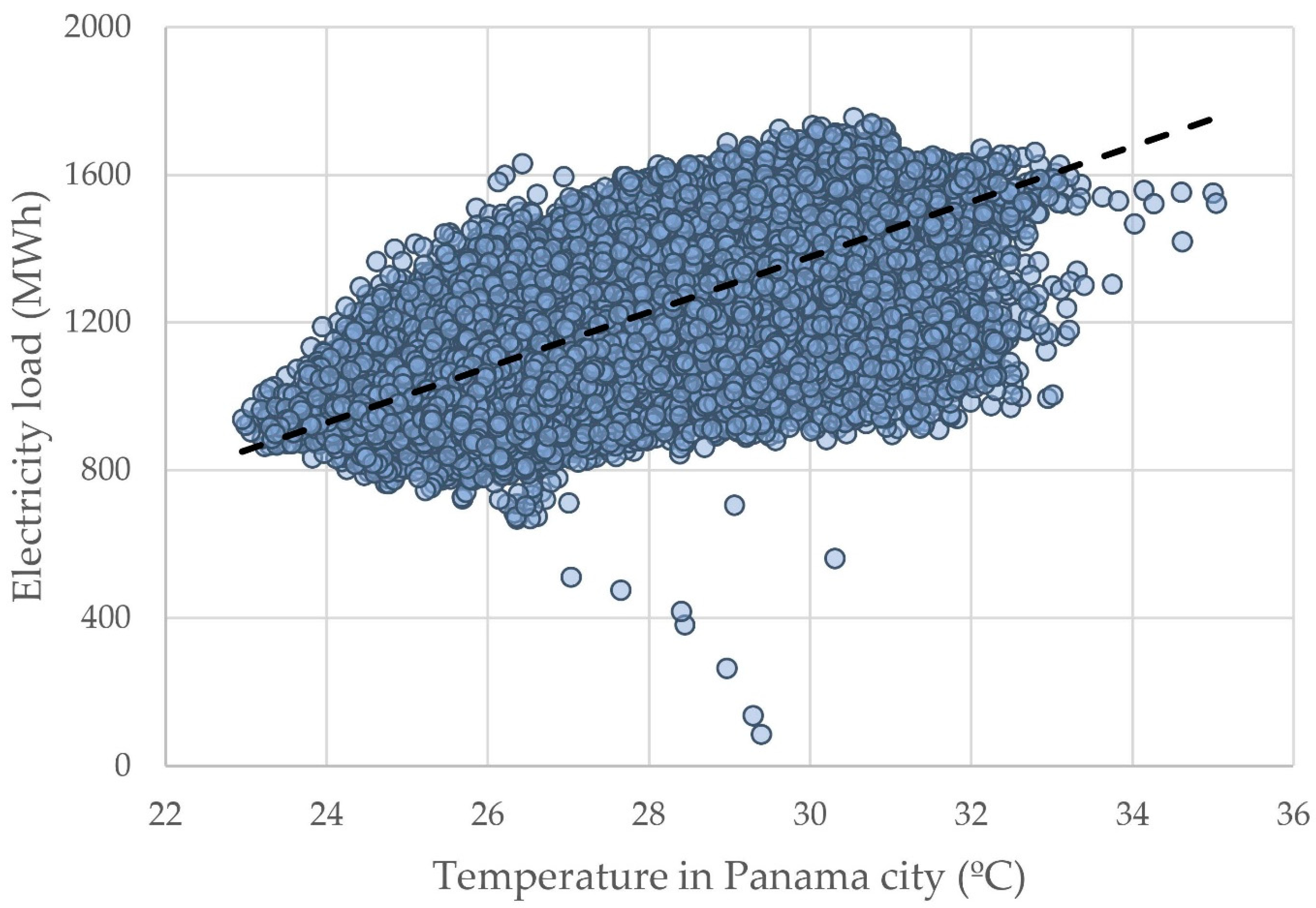
The decision of which variables should be used to train the ML models is critical to obtain good results. This process, known as feature selection (FS), also reduces computation time, decreases data storage requirements, simplifies models, evades the curse of dimensionality, and enhances generalization, avoiding overfitting [55]. For these reasons, several FS techniques were performed along with the STLF state-of-the-art [7,22,50]. The explored FS techniques were: feature variance, correlation with the target, redundancy among regressors [56], and feature importance [57], according to the default models multiple linear regression, decision tree regressor, random forest regressor, and extreme gradient boosting regressor. After having 35 regressors and a defined target, the FS analysis showed that 13 regressors would significantly contribute to the forecast. Given an hour, , to forecast the load, , at this hour, , and denoting lags in historical load by , where remains in the hourly granularity, the best regressor is expressed as: , , , , , , , , , , , and , with temperature being the most important weather variable due to its positive relationship with electricity load [58], as illustrated in Figure 1. This figure shows the typical load range, from 800 to 1600 MWh, and a temperature range between 23 and 35 °C. The dashed line identifies the linear equation: = , which indicates that a 1 °C increase in temperature represents a 74.8 MWh electricity demand increase.
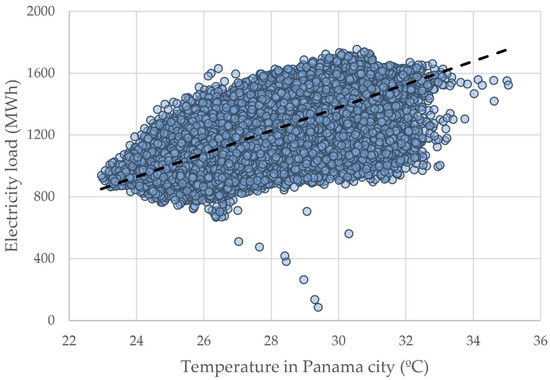
Figure 1.
National electricity load vs. temperature in Panama City.
2.2. Modeling
Before splitting the data into training and test datasets, the hourly records at the beginning and the end of the horizon are dropped if they do not belong to a complete 168 h weekly block for consistency on training, validation, and testing. After this, 284 weeks are available with hourly records. The dataset is split into train and test, keeping the chronological records. Records are sorted by date–time index, always leaving the last week for testing and the remaining older data for training. Based on this logic, there are 14 pairs of train–test datasets selected. Twelve pairs, having a testing week for each month of the last year of records before the 2020 quarantine started (due to the COVID-19 pandemic), and two more after the quarantine began. To note, the official lockdown in Panama began on Wednesday, 25 March of 2020 (week 12—2020) [59]. These criteria test the models under regular and irregular conditions since the quarantine period presented a lower demand with atypical hourly profiles. The selected testing weeks also included typical days and holidays to test the models on different conditions throughout the year.
Studies have shown that many decision-makers exhibit an inherent distrust of automated predictive models, even if they are proven to be more accurate than human forecasters [60]. One way to overcome “algorithm aversion” is to provide them with interpretability [61]. For these reasons, the current research explores a set of candidate ML models that have been proven as forecasters within the STLF state-of-the-art, but also models that can offer a certain level of interpretability.
The candidate ML models considered in this research are multiple linear regression (MLR), k-nearest neighbors regressor (KNN), epsilon-support vector regression (SVR), random forest regressor (RF), and extreme gradient boosting regressor (XGB). All these estimators were executed using a pipeline with a default Min–Max scaler as the first step. These ML models, the pipeline structure, and the scalers were from sci-kit learn [62], except for XGB [63].
MLR uses two or more independent variables to predict a dependent variable by fitting a linear equation. This method’s assumptions are that: the dependent variable and the residuals are normally distributed, there are linear relationships between the dependent and independent variables, and no collinearity should exist between regressors. Since MLR can include many independent variables, it can provide an understanding of the relationships [55], but it presents the disadvantage of being sensitive to outliers.
KNN is not typical for STLF. Nevertheless, their results can be interpreted, and some researchers used it as a baseline model [64]. The KNN method searches for the k most similar instances; when the k most similar samples are found, the target is obtained by local interpolation of the targets associated with the k found instances [42]. The main disadvantage of this method is that it tends to overfit, and it has few hyperparameters to change this situation.
SVR is a regression version of the support vector machine (SVM), which was initially designed for classification problems [65]. In contrast to ordinary least squares of MLR, the objective function of SVR is to minimize the L2-norm of the coefficient vector, not the squared error. The error term is then constrained by a specified margin ε (epsilon). SVR is frequently used for STLF with the linear [25] or radial basis function (RBF) kernel [66], identifying load patterns better than other linear models [67].
RF is an ensemble learning method with generalization ability. It fits many decision trees on various sub-samples of the dataset and uses averaging to improve the forecast and avoid over-fitting. For these reasons, it seems suitable for STLF, but the few researchers that consider this model have demonstrated a weak performance on their results [28,68].
XGB is another ensemble ML algorithm, based on the gradient boosting library, but enhanced and designed to be highly efficient, flexible, and portable [65], providing a forward stage-wise additive model that fits regression trees on many stages while the regression loss function is minimized [69]. Due to its recent development, XGB is not a matured STLF method [16]. Nevertheless, researchers are starting to use it, showing outstanding performances against traditional methods [29,30].
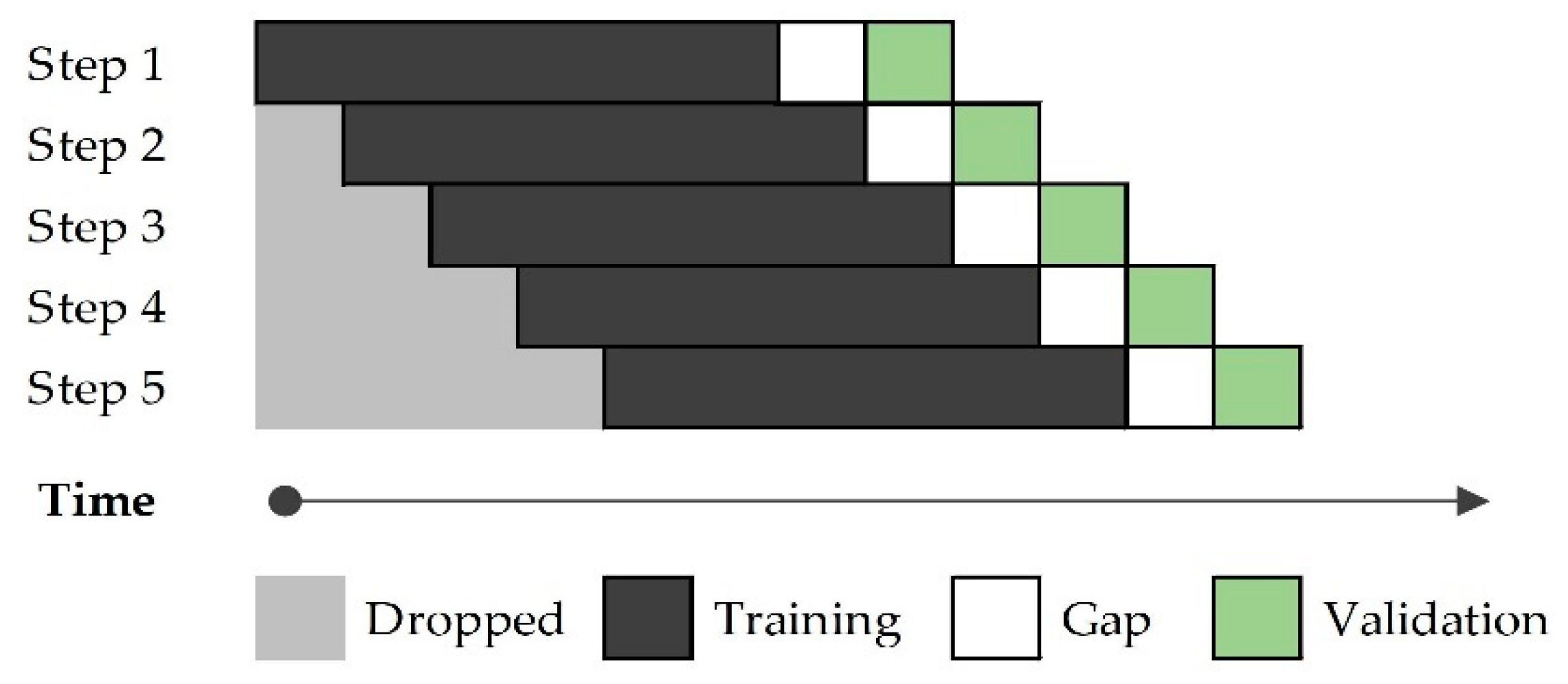
Once the training and testing week pairs were defined, models were trained with the earliest train–test pair, following the forward sliding window approach [70] for time-based cross-validation [71]. The idea for time-based cross-validation is to iteratively split the training set into two folds at each step, always keeping the validation set ahead of the training set. This process of defining folds, training the model, predicting the validation fold, and evaluating the model performance while changing hyperparameters and moving the training/validation sets further into the future is illustrated in Figure 2. The sliding window characteristics are 149 weeks (2.8 years) for training/validation. Within those, 64 are validation weeks, excluding the last 72 h from each validation fold to comply with the three-day unknown gap when forecasting the weekly demand on real conditions; finally, the forward step on the training/validation process is one week.
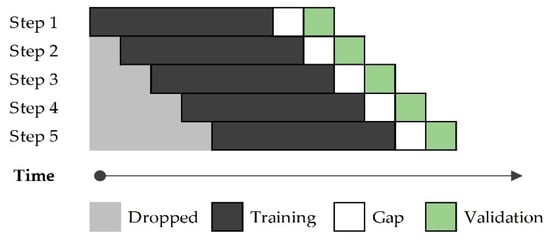
Figure 2.
Sliding window time-based cross-validation.
The hyperparameter tuning was performed using the sci-kit learn package with the sliding window attributes with randomized search and grid search cross-validation [63]. First, a randomized search was conducted to explore a vast hyperparameter space. A grid search was then conducted to explore a finer hyperparameter space based on the randomized search results. This two-step approach [14] attempts to find a global optimum without digging through all the hyperparameter grids in the first step, reducing computational time, and refining the result by searching the second step.
The hyperparameter search results are shown in Table 2, except for MLR, which does not possess a hyperparameter space to enhance the predictions. The absent parameters were considered with their default value. As exposed in the Results and Discussion Section, XGB demonstrated the best performance. For this reason, only a description of these parameters will be addressed. For the ‘eval_metric’ parameter, ‘rmse’ was the most suitable option to penalize large errors. The default ‘gbtree’ booster was kept to take advantage of the generalization ability of the ensemble of trees instead of the weighted sum of linear functions provided by ‘gblinear’. The ‘n_estimators’ is the number of iterations the model will perform, in which a new tree is created per iteration. For this reason, values above hundreds of trees are considered to make a sizeable iterative process that can adapt to the problem. The ‘max_depth’ parameter was kept with low values to avoid overfitting by training weak tree learners. The ‘learning_rate’ had the most extensive search to adapt the hyperparameter search during each boosting step, preventing overfitting. The parameters ‘subsample’, ‘colsample_bytree’, ‘colsample_bynode’, and ‘col_sample_bylevel’ were reduced to provide generalization ability to the model, restricting the training process with sub-samples of the data. A range of larger values and the default zero were explored for ’gamma’, to control partitions on the leaves’ nodes, making the algorithm more conservative. Similarly, because ‘min_child_weight’ controls the number of instances needed to be in each node, for this reason, values above the zero-default setting were explored.

Table 2.
Hyperparameter space search and results.
This research addresses many evaluation metrics to systematically evaluate the ML models’ performance, including the traditional metrics for ML forecasting, RMSE, and MAPE, as well as other specific metrics for STLF. Where MAPE and RMSE metrics express the average model prediction error, both metrics can range from zero to infinity and are indifferent to the direction of errors, with MAPE being easier for interpretation and comparison, and RMSE having the benefit of penalizing large errors. The rest of the metrics focus on the weekly deviation of the forecasts, evaluating the highest load “Peak”, the lowest load “Valley”, and the sum of the 168 load periods “Energy”. All those metrics are negatively oriented, which means that lower values are better. These evaluation metrics and their formulation are listed in Table 3. is a weekly set of actual hourly load values, is a weekly set of forecasted hourly values, and subindex stands for a specific hour. For this research, all testing sets were whole weeks with 168 h, so is 168.

Table 3.
Evaluation metrics.
3. Results and Discussion
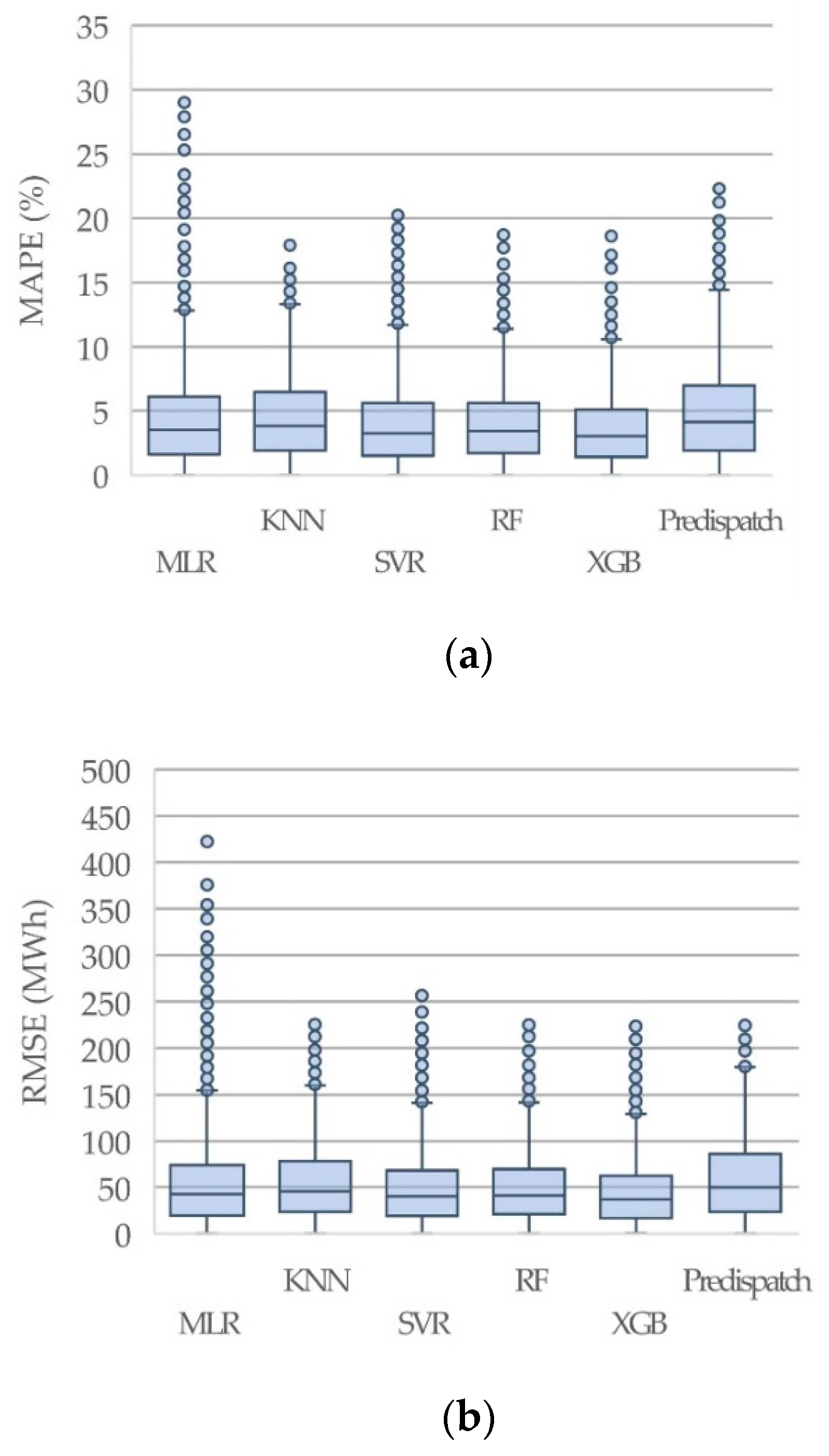
The overall hourly evaluation along the 14 testing weeks is displayed in Figure 3, showing the MAPE and RMSE error distributions with box-whiskers plots by ML candidate model and the historical weekly pre-dispatch forecast. The lower end of each boxplot represents the 25th percentile, the upper end shows the 75th percentile, and the central line depicts the 50th percentile or the median value. In this case, the lower whiskers are zero for all forecasts. In contrast, the upper whiskers represent the upper boundaries for errors distribution, calculated as 1.5 times the inter-quartile range plus the 75th percentile value. The values outside these boundaries are considered outliers, which means large errors. A statistics summary to complement the error’s distribution is shown in Table 4.
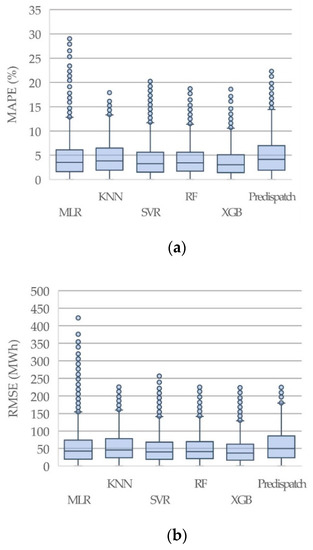
Figure 3.
Box-whisker plots for each candidate model and the pre-dispatch load forecast: (a) MAPE evaluation results, (b) RMSE evaluation results.

Table 4.
Errors distribution by model, by metric. SD = standard deviation, Perc. = percentile.
This overall evaluation shows that the pre-dispatch forecast, also abbreviated as Pre-Disp., has a larger standard deviation on both metrics, which implies that the ML candidates’ models improve the STLF task. Nevertheless, MLR shows several outliers with a high magnitude. The best ML models were XGB, RF, and SVR with RBF kernel, having a similar performance by looking at these two metrics. Considering a reasonable computational time for training and predicting, XGB is more efficient than RF and SVR but even more flexible in hyperparameter tuning. RF showed the slowest computational performance, followed by SVR, XGB, KNN, and MLR, the faster model but the least accurate.
Moreover, all models were also evaluated by testing week, knowing that each week has a different context, hence a different load profile. These models’ results are displayed in Table 5.

Table 5.
Evaluation metrics by model, for each testing week, and average.
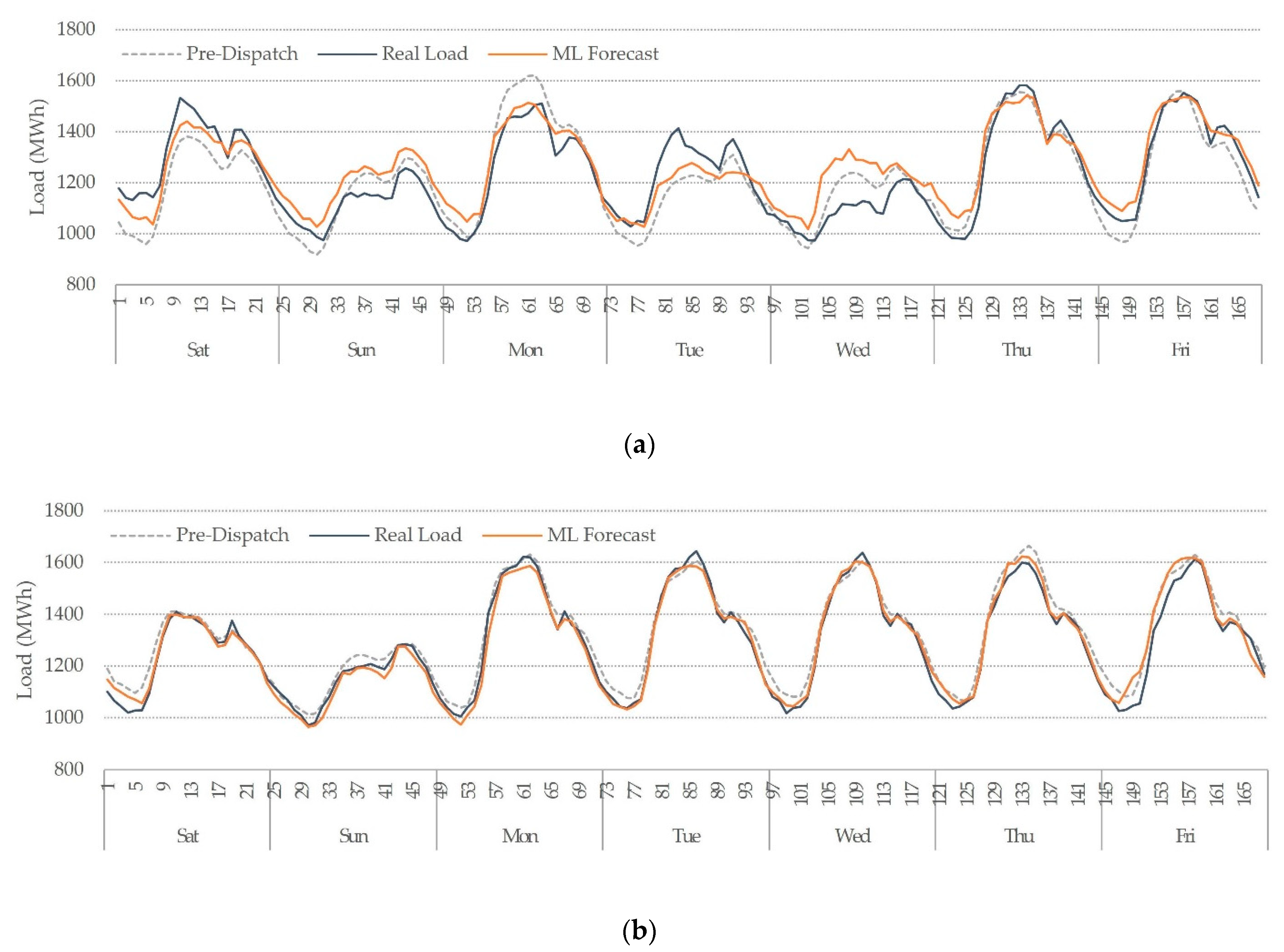
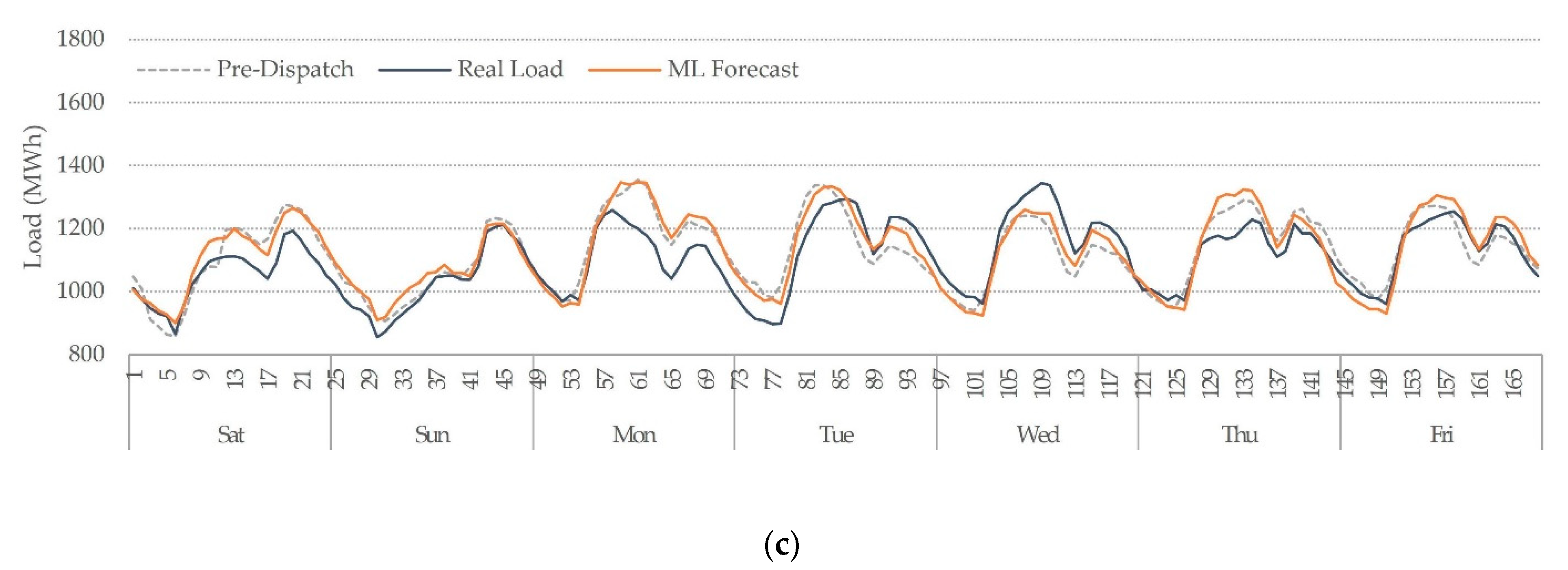
The weekly evaluation demonstrates that XGB improved MAPE and RMSE for all the testing weeks. XGB was also accurate in predicting the peak load, valley load, and weekly energy. MLR is the simplest model, thus for some holidays with low demand, it predicted high loads, adding errors to the weekly evaluation, but it also showed the smallest peak deviation overall, followed by XGB. KNN did not expose this issue, but it predicted unusual hourly load profiles on holidays. It also tends to forecast lower demands. For instance, it was the best model to predict load valleys, followed by XGB, but the worst to predict load peaks. RF showed a good performance for peaks and valleys and had the smallest energy deviation along all testing weeks, followed by XGB. The RF forecast’s negative side was the irregular spikes that do not follow the typical hourly profile. Since XGB demonstrated the best performance, providing an average MAPE of 3.74%, only hourly results from this model are plotted along with the pre-dispatch forecast and the real load, illustrated in Figure 4. These testing weeks include holidays, regular days, and periods with quarantine restrictions due to the COVID-19 pandemic. Figure 5 shows another testing week, with all the candidates’ ML models forecast.
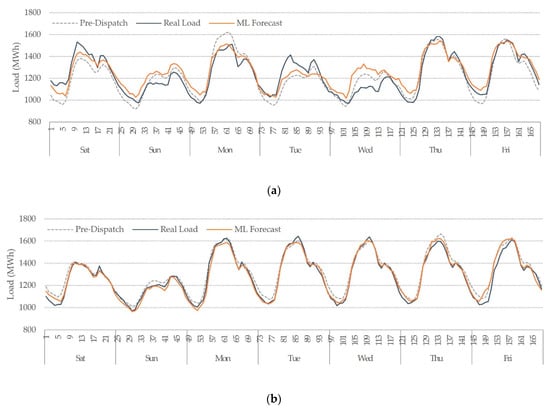
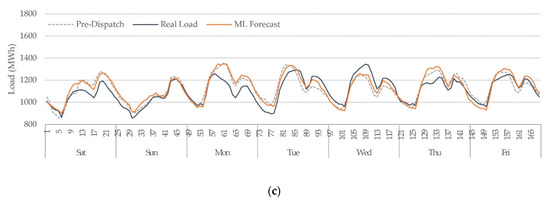
Figure 4.
Weekly pre-dispatch and XGB forecast comparison with the real load. (a) Week 51, 2019 (21–27 December 2019), (b) Week 10, 2020 (7–13 March 2019), (c) Week 24, 2020 (13–19 June 2019).
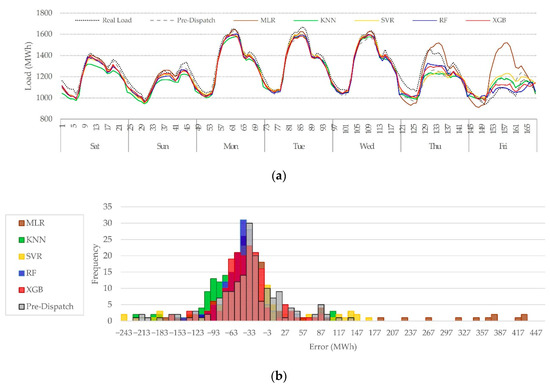
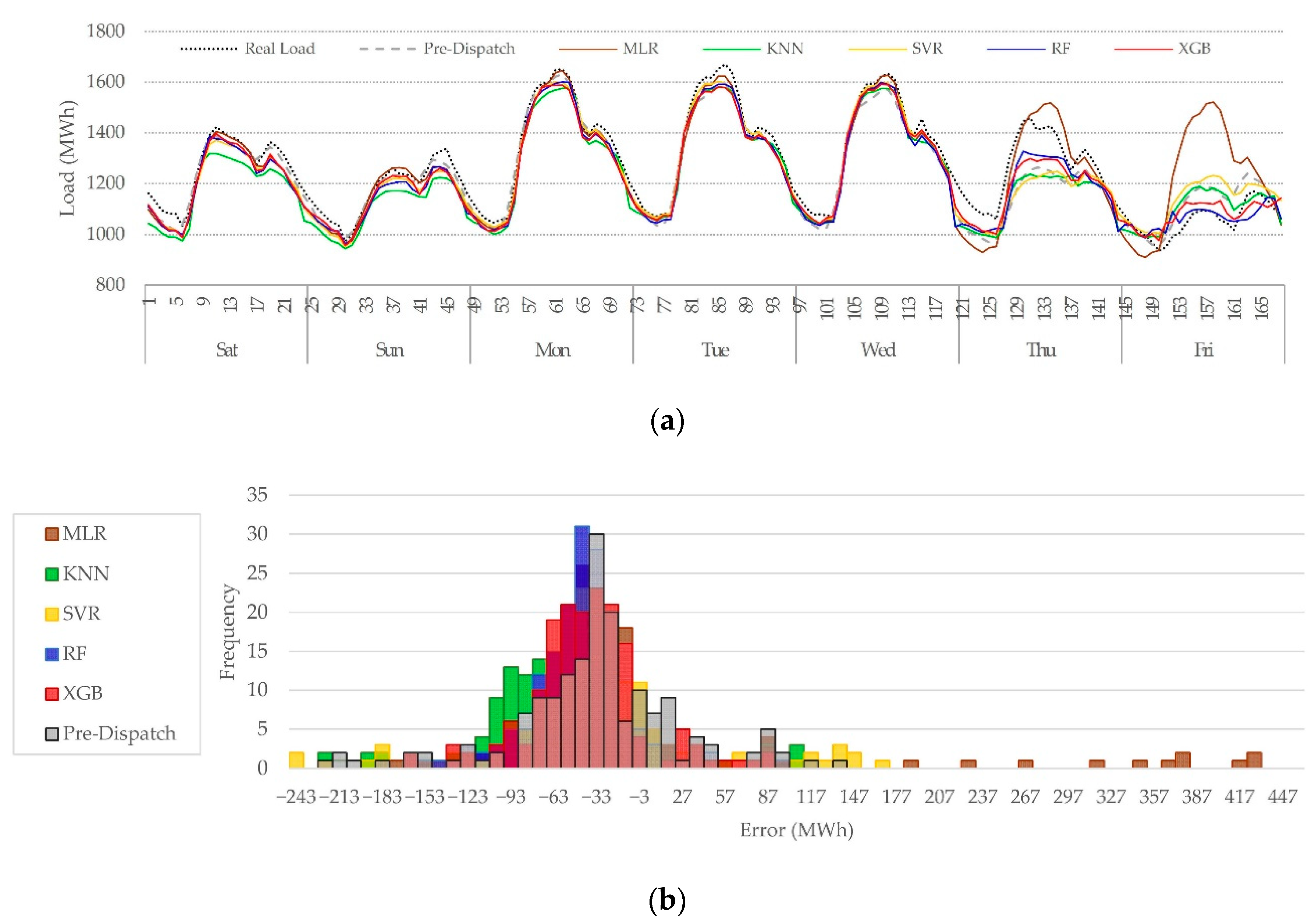
Figure 5.
Weekly pre-dispatch vs. ML candidates’ models. (a) Hourly forecast for Week 15, 2019 (13–19 April 2019). (b) Frequency distribution of error by forecast, for Week 15, April 2019.
Overall, all models distinguished between weekends and weekdays load. Since weekends had a lower demand with low variance, all models showed a decent performance for these periods. For periods with similar characteristics, like the early morning, most of the forecasts were reasonably good. The most difficult periods to forecast were daytime periods during working days due to their high variance. The most challenging was holidays due to fewer records, different contexts, and the natural randomness of consumers’ demand. Examples of holiday forecasting are shown in Figure 4a, on Tuesday 24 and Wednesday 25 December 2019, and another holiday example is illustrated in Figure 5a for Thursday 18 and Friday 19 April 2019. The quarantine period brings another challenge for STLF since the load profiles changed abruptly for this period, and fewer records are available for training. Besides, the load profiles do not follow a steady pattern. Differences between the quarantine period and no quarantine are shown in Figure 4b,c, respectively.
Beyond having an accurate forecast, it is relevant to know the factors contributing to a specific STLF task. Some of the ML candidates’ models proposed in this research provide a straightforward way to check the feature importance, except for KNN and SVR, which only provide coefficients for the linear kernel. Still, feature permutation importance [72] is applied to those two models with ten permutation rounds to estimate their feature importance. For MLR, feature importance is obtained through the coefficient property by multiplying each coefficient by the feature standard deviation to reduce all coefficients to the same measurement unit. Then, the absolute value of each feature importance is scaled to get the contribution percentage. For RF and XGB, the feature importance property directly returns contribution percentage by feature. Table 6 shows the feature importance by ML model, where each value is the average from evaluating each model on the 14 testing weeks.

Table 6.
Average feature importance by ML model.
The feature importance results show that the load lags have a strong influence on the forecasting, especially the most recent week. The hour of the day is also a crucial feature, especially for KNN; also, temperature resulted in an essential feature for SVR and a secondary feature for the rest of the models. Relative humidity does not show a significant weight for all models. Lastly, the binary indicators for holidays and weekends show minor importance but still relevant, mainly to mark the difference between a higher load peak for working days and a lower peak for non-working days. The least essential variable was the month, indicating that monthly trends are not significant for STLF. For research reasons, it is valuable to see the feature’s contribution by model, but the model’s less significant features can be neglected for performance and simplicity for deployment reasons.
The results obtained in the current research can be interpreted from the perspective of any time-series forecasting research using ML techniques since the standard ML methodologies for STLF were applied to train and evaluate results, as exposed in the literature review. For example, the selected features across the STLF field of study match this research’s best features: the load lags, the hour of the day, and temperature. Holidays and weekends’ binary indicators also contribute since they help determine a high or low range of load.
In contrast with most of the studies where researchers forecast 24 or 48 h, this research addressed a 168 h horizon, considering a 72 h gap before the first forecasting period. Besides the typical MAPE and RMSE evaluation metrics, this research proposed load peak, load valley, and energy evaluation as secondary, practical metrics that analysts can easily monitor. Another distinction of this research is the diversity for testing periods, presenting STLF for regular working days, holidays, and irregular periods during the 2020 quarantine. This research’s most important distinction is comparing the official weekly pre-dispatch forecast as a baseline and validating the results.
4. Conclusions
This research presented a novel model that improves weekly STLF forecast with a 72 h gap. The model was developed and benchmarked with data and previous forecasts from Panama’s power system. Results along 14 testing weeks confirmed the suitability of the XGB algorithm. First, for time efficiency on training and predicting, second, for flexibility due to the hyperparameter space, and third, for providing certain interpretability through its feature importance property.
For the above-exposed reasons, this research makes several important contributions to the field of study. First, it shows that models built with XGB have superior performance to models built with other algorithms. Second, it confirms that temperature plays a critical role in STLF. Third, it demonstrates the excellent performance of ML models by forecasting for a longer horizon than typical research, and even with a three-day gap of data before the forecast. Lastly, this research identifies public data that can be used by other researchers to improve STLF forecasting or be used as a benchmark.
This research also has several practical implications. First, it created a model that Panama can use to replace of the current one, thus allowing Panama to reduce costs and improve STLF performance. Second, this model could be trained and applied in other countries or regions with similar conditions. Furthermore, the positive impacts of providing a more accurate STLF will reduce the planning uncertainty added by the intermittent renewable production and subsequently be closer to the optimal hydrothermal costs scheduled in the weekly unit commitment. This third practical implication leads to a fourth: for the specific case of the Panama energy spot market, because it is a marginalist market, accurate STLF can also reduce the hourly energy price uncertainty in the wholesale electricity market.
Limitations and Future Work
Future work within this specific research can include more historical load records to train models in particular situations, like holidays. Another approach to enhance the holidays’ forecast is to develop a specific model for holidays and merge the predictions with a regular days model [16] and use stacking techniques to enhance the forecast accuracy, even though it increases the training and predicting time [73].
In the particular case study of Panama’s national load, there are special consumers named auto-generators (Panama Canal and Minera Panama [74]). These consumers have a significant load, but as their agent’s name suggests, they supply their own demand with their own power plants most of the time, except for scheduled maintenance periods on their power plants or unforeseen unavailability on their power plants [75]. Those agents will consume energy from the national power system during those events, causing an extra increase in the national load. If this additional load can be scheduled, it is better to track the electricity load by consumer and forecast only the residential, commercial, and industrial load, then add auto-generators if needed. This load segregation avoids distortions on the load forecast, as stated in auto-generators methodology [3]. In this context, another research avenue to develop STLF by consumers emerges, but it requires data with this segregation.
Since DL models are out of this research scope, and DL models require more records than ML models, unidirectional and bidirectional LSTM were not compared in the research. However, future studies should evaluate these algorithms’ performance that have proven good for STLF [44]. Similarly, non-iterative ANN-based algorithms can be explored due to their good performance and low training time, like Reference [45] compared with a set of ML models.
Although there are currently several weather forecasts available with hourly granularity [76], because the temperature is crucial for STLF, it is advisable to count with an accurate temperature forecast to feed this STLF model. Hence, a temperature forecast model can complement this research.
It is advised to do a weekly load patterns revision since consumption patterns can change in the future. An example of abrupt changes on the hourly load profile was exposed in this research during the 2020 quarantine period. However, other trending consumption patterns [77], like recharging more electric vehicles and having more solar production behind-the-meter, will produce residential and commercial hourly consumption changes. This revision implies that forecasting models should be updated more often, and even that they need to be more robust.
A possible solution to overcome these issues is to automatically enabling the models to learn with new data every week by deploying the “Champion-Challenger” approach [78]. A weekly hyperparameter tuning is executed to update the models and make them compete to ensure the best performance along time.
The final goal of STLF is to reduce the uncertainty on real-time dispatch of hydrothermal power plants because the wind and solar farms are non-dispatchable power plants. Consequently, another way to reduce this uncertainty and complement the STLF is by providing an accurate forecast for wind and solar production and other non-dispatchable power plants, if any.
Author Contributions
E.A.M. has contributed to the conceptualization, data curation, formal analysis, methodology, software and writing the original draft. N.A. has contributed to the conceptualization, supervision, reviewing and editing the original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available at http://doi.org/10.17632/tcmmj4t6f4.1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wood, A.J.; Wollenberg, B.; Sheblé, G. Power Generation, Operation, and Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 63–302. [Google Scholar]
- Hossein, S.; Mohammad, S.S. Electric Power System Planning; Springer: Berlin/Heidelberg, Germany, 2011; p. 10. [Google Scholar]
- CND—ETESA, Metodologías de Detalle. Available online: https://www.cnd.com.pa/images/doc/norm_metodologiasdetalle_nov2020.pdf (accessed on 15 December 2020).
- PSR, NCP—Short Term Operation Programming. Available online: https://www.psr-inc.com/softwares-en/?current=p4034 (accessed on 4 November 2020).
- ABB HITACHI, Nostradamus. Available online: https://www.hitachiabb-powergrids.com/latam/es/offering/product-and-system/enterprise/energy-portfolio-management/trading-and-risk-management/nostradamus (accessed on 30 December 2020).
- CND—ETESA, Sistema de Información en Tiempo Real (SITR). Available online: http://sitr.cnd.com.pa/m/pub/sin.html (accessed on 2 September 2020).
- Aguilar, M.E.; Valdés, B.L. Impacto de La Entrada de La Generación Eólica y Fotovoltaica en Panamá. I+D Tecnológico. 2017, 13, 71–82. Available online: https://revistas.utp.ac.pa/index.php/id-tecnologico/article/view/1440 (accessed on 6 December 2020).
- Morales-Espana, G.; Latorre, J.M.; Ramos, A. Tight and Compact MILP Formulation of Start-Up and Shut-Down Ramping in Unit Commitment. IEEE Trans. Power Syst. 2012, 28, 1288–1296. [Google Scholar] [CrossRef]
- Becirovic, E.; Cosovic, M. Machine learning techniques for short-term load forecasting. In Proceedings of the 2016 4th International Symposium on Environmental Friendly Energies and Applications (EFEA), Belgrade, Serbia, 14–16 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Li, C. Designing a short-term load forecasting model in the urban smart grid system. Appl. Energy 2020, 266, 114850. [Google Scholar] [CrossRef]
- Fernandes, R.S.S.; Bichpuriya, Y.K.; Rao, M.S.S.; Soman, S.A. Day ahead load forecasting models for holidays in Indian context. In Proceedings of the 2011 International Conference on Power and Energy Systems, Las Vegas, NV, USA, 12–14 November 2012. [Google Scholar] [CrossRef]
- Sarmiento, H.O.; Valencia, J.A.; Villa, W. Load forecasting with Neural Networks for Antioquia-Choco region. In Proceedings of the 2010 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), Sao Paulo, Brazil, 8–10 November 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Adeoye, O.; Spataru, C. Modelling and forecasting hourly electricity demand in West African countries. Appl. Energy 2019, 242, 311–333. [Google Scholar] [CrossRef]
- Dietrich, B.; Walther, J.; Weigold, M.; Abele, E. Machine learning based very short term load forecasting of machine tools. Appl. Energy 2020, 276, 115440. [Google Scholar] [CrossRef]
- Lebotsa, M.E.; Sigauke, C.; Bere, A.; Fildes, R.; Boylan, J.E. Short term electricity demand forecasting using partially linear additive quantile regression with an application to the unit commitment problem. Appl. Energy 2018, 222, 104–118. [Google Scholar] [CrossRef]
- Zhu, K.; Geng, J.; Wang, K. A hybrid prediction model based on pattern sequence-based matching method and extreme gradient boosting for holiday load forecasting. Electr. Power Syst. Res. 2021, 190, 106841. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Cuambe, I.D.; Ruano, A.; Pestana, R. Forecasting the Portuguese Electricity Consumption using Least-Squares Support Vector Machines. IFAC Proc. Vol. 2013, 46, 411–416. [Google Scholar] [CrossRef]
- Zou, M.; Fang, D.; Harrison, G.; Djokic, S. Weather Based Day-Ahead and Week-Ahead Load Forecasting using Deep Recurrent Neural Network. In 2019 IEEE 5th International forum on Research and Technology for Society and Industry (RTSI); Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2019; pp. 341–346. [Google Scholar]
- Dutta, S.; Li, Y.; Venkataraman, A.; Costa, L.M.; Jiang, T.; Plana, R.; Tordjman, P.; Choo, F.H.; Foo, C.F.; Puttgen, H.B. Load and Renewable Energy Forecasting for a Microgrid using Persistence Technique. Energy Procedia 2017, 143, 617–622. [Google Scholar] [CrossRef]
- Paterakis, N.; Mocanu, E.; Gibescu, M.; Stappers, B.; Van Alst, W. Deep learning versus traditional machine learning methods for aggregated energy demand prediction. In 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe); Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Barakat, E.H.; Al-Qasem, J.M. Methodology for weekly load forecasting. IEEE Trans. Power Syst. 1998, 13, 1548–1555. [Google Scholar] [CrossRef]
- Amjady, N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power Syst. 2001, 16, 798–805. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Adamowski, J.; Li, Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inform. 2018, 35, 1–16. [Google Scholar] [CrossRef]
- Al Amin, M.A.; Hoque, M.A. Comparison of ARIMA and SVM for short-term load forecasting. In Proceedings of the IEMECON 2019-9th Annual Information Technology Electromechanical Eng. Microelectron Conference, Lisbon, Portugal, 14–17 October 2019; pp. 205–210. [Google Scholar]
- Chapagain, K.; Kittipiyakul, S. Short-Term Electricity Demand Forecasting with Seasonal and Interactions of Variables for Thailand. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018. [Google Scholar] [CrossRef]
- Liu, F.; Findlay, R.D.; Song, Q. A Neural Network Based Short Term Electric Load Forecasting in Ontario Canada. In Proceedings of the 2006 International Conference on Computational Inteligence for Modelling Control and Automation and International Conference on Intelligent Agents Web Technologies and International Commerce (CIMCA’06), Sydney, Australia, 9 November–1 December 2006; p. 119. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Ruano, A.; Pestana, R. Improving the Identification of RBF Predictive Models to Forecast the Portuguese Electricity Consumption. IFAC Proc. Vol. 2010, 43, 208–213. [Google Scholar] [CrossRef]
- Omidi, A.; Barakati, S.M.; Tavakoli, S. Application of nusupport vector regression in short-term load forecasting. In 2015 20th Conference on Electrical Power Distribution Networks Conference (EPDC); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2015; pp. 32–36. [Google Scholar]
- Pinto, T.; Praça, I.; Vale, Z.; Silva, J. Ensemble learning for electricity consumption forecasting in office buildings. Neurocomputing 2021, 423, 747–755. [Google Scholar] [CrossRef]
- Hadri, S.; NaitMalek, Y.; Najib, M.; Bakhouya, M.; Fakhri, Y.; El Aroussi, M. A Comparative Study of Predictive Approaches for Load Forecasting in Smart Buildings. Procedia Comput. Sci. 2019, 160, 173–180. [Google Scholar] [CrossRef]
- Cai, J.; Cai, H.; Cai, Y.; Wu, L.; Shen, Y. Short-term Forecasting of User Power Load in China Based on XGBoost. In 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2020; Volume 3, pp. 1–5. [Google Scholar]
- Suo, G.; Song, L.; Dou, Y.; Cui, Z. Multi-dimensional Short-Term Load Forecasting Based on XGBoost and Fireworks Algorithm. In Proceedings of the 2019 18th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Wuhan, China, 8–10 November 2019; pp. 245–248. [Google Scholar] [CrossRef]
- Liao, X.; Cao, N.; Li, M.; Kang, X. Research on Short-Term Load Forecasting Using XGBoost Based on Similar Days. In 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 675–678. [Google Scholar]
- Liu, Y.; Luo, H.; Zhao, B.; Zhao, X.; Han, Z. Short-Term Power Load Forecasting Based on Clustering and XGBoost Method. In 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 536–539. [Google Scholar]
- Zheng, H.; Yuan, J.; Chen, L. Short-Term Load Forecasting Using EMD-LSTM Neural Networks with a Xgboost Algorithm for Feature Importance Evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Xue, P.; Jiang, Y.; Zhou, Z.; Chen, X.; Fang, X.; Liu, J. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms. Energy 2019, 188, 116085. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Wu, L.; Chen, G.; Wang, L.; Qin, H. Comparison of support vector regression and extreme gradient boosting for decomposition-based data-driven 10-day streamflow forecasting. J. Hydrol. 2020, 582, 124293. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Anpalagan, A.; Naeem, M.; Venkatesh, B. Joint bagged-boosted artificial neural networks: Using ensemble machine learning to improve short-term electricity load forecasting. Electr. Power Syst. Res. 2020, 179, 106080. [Google Scholar] [CrossRef]
- Singh, P.; Dwivedi, P. Integration of new evolutionary approach with artificial neural network for solving short term load forecast problem. Appl. Energy 2018, 217, 537–549. [Google Scholar] [CrossRef]
- Yan, G.; Han, T.; Zhang, W.; Zhao, S. Short-Term Load Forecasting of Smart Grid Based on Load Spatial-Temporal Distribution. In 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia); Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2019; pp. 781–785. [Google Scholar]
- Abbasimehr, H.; Shabani, M.; Yousefi, M. An optimized model using LSTM network for demand forecasting. Comput. Ind. Eng. 2020, 143, 106435. [Google Scholar] [CrossRef]
- Atef, S.; Eltawil, A.B. Assessment of stacked unidirectional and bidirectional long short-term memory networks for electricity load forecasting. Electr. Power Syst. Res. 2020, 187, 106489. [Google Scholar] [CrossRef]
- Vitynskyi, P.; Tkachenko, R.; Izonin, I.; Kutucu, H. Hybridization of the SGTM Neural-Like Structure Through Inputs Polynomial Extension. In 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 386–391. [Google Scholar]
- Google Colaboratory. Available online: https://research.google.com/colaboratory/faq.html (accessed on 19 November 2020).
- Guido, V.R.; Drake, F.L., Jr. Python 3 Reference Manual. Available online: https://docs.python.org/2/reference/lexical_analysis.html (accessed on 19 November 2020).
- CND—ETESA, Post-dispatch—Operating Reports. Available online: https://www.cnd.com.pa/index.php/informes/categoria/informes-de-operaciones?tipo=60 (accessed on 17 October 2020).
- CND—ETESA, Weekly pre-dispatch—Operating Reports. Available online: https://www.cnd.com.pa/index.php/informes/categoria/informes-de-operaciones?tipo=68&anio=2019&semana=0 (accessed on 17 October 2020).
- Gaceta Oficial—Ministerio de la Presidencia. Busqueda Avanzada. Available online: https://www.gacetaoficial.gob.pa/Busqueda-Avanzada (accessed on 19 November 2020).
- When on Earth? Calendar for Panama. Available online: https://www.whenonearth.com/calendar/panama/2020 (accessed on 19 November 2020).
- Goddard Earth Sciences Data and Information Services Center (GES DISC). Global Modeling and Assimilation Office (GMAO) (2015), MERRA-2 tavg1_2d_slv_Nx: 2d,1-Hourly, Time-Averaged, Single-Level, Assimilation, Single-Level Diagnostics V5.12.4, Greenbelt, MD, USA. Available online: https://disc.gsfc.nasa.gov/datasets/M2T1NXSLV_5.12.4/summary (accessed on 2 September 2020). [CrossRef]
- Wes McKinney and the Pandas Development Team. Pandas: Powerful Python Data Analysis Toolkit. Available online: https://pandas.pydata.org/docs/pandas.pdf (accessed on 6 December 2020).
- Nadh, K. netCDF4 API documentation. Available online: https://unidata.github.io/netcdf4-python/netCDF4/index.html (accessed on 19 November 2020).
- Hoyer, S.; Hamman, J.J. xarray: N-D labeled Arrays and Datasets in Python. J. Open Res. Softw. 2017, 5, 10. [Google Scholar] [CrossRef]
- Zhang, N.; Li, Z.; Zou, X.; Quiring, S.M. Comparison of three short-term load forecast models in Southern California. Energy 2019, 189, 116358. [Google Scholar] [CrossRef]
- Eseye, A.T.; Lehtonen, M.; Tukia, T.; Uimonen, S.; Millar, R.J. Machine Learning Based Integrated Feature Selection Approach for Improved Electricity Demand Forecasting in Decentralized Energy Systems. IEEE Access 2019, 7, 91463–91475. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Reduction. In Data Mining, Concepts and Techniques, 3rd ed.; The Morgan Kaufmann Series; Data Management Systems: Waltham, MA, USA, 2011; pp. 99–110. [Google Scholar]
- Geéron, A. Hands-on Machine Learning with Scikit-Learn and Tensor Flow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2017. [Google Scholar]
- Boya, C. Analyzing the Relationship between Temperature and Load Demand in the Regions with the Highest Electricity Consumption in the Republic of Panama. In 2019 7th International Engineering, Sciences and Technology Conference (IESTEC); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 132–137. [Google Scholar]
- La Estrella de Panamá. “Cuarentena en Panamá,” Calles Desiertas en el Primer día de Cuarentena Total en Panamá por COVID-19. Available online: https://www.laestrella.com.pa/nacional/200325/calles-desiertas-primer-dia-cuarentena-total-panama-covid-19 (accessed on 30 September 2020).
- Dietvorst, B.J.; Simmons, J.P.; Massey, C. Algorithm aversion: People erroneously avoid algorithms after seeing them err. J. Exp. Psychol. Gen. 2015, 144, 114–126. [Google Scholar] [CrossRef]
- Bertsimas, D.; Delarue, A.; Jaillet, P.; Martin, S. The Price of Interpretability. 2019. Available online: https://arxiv.org/pdf/1907.03419.pdf (accessed on 21 November 2020).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P; Weiss, R; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 39. Available online: https://jmlr.csail.mit.edu/papers/volume12/pedregosa11a/pedregosa11a.pdf (accessed on 10 December 2020).
- XGB Developers. XGBoost Documentation. Available online: https://xgboost.readthedocs.io/en/latest/ (accessed on 3 November 2020).
- Johannesen, N.J.; Kolhe, M.; Goodwin, M. Relative evaluation of regression tools for urban area electrical energy demand forecasting. J. Clean. Prod. 2019, 218, 555–564. [Google Scholar] [CrossRef]
- Alex, J.S.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. Available online: https://alex.smola.org/papers/2004/SmoSch04.pdf (accessed on 21 November 2020).
- Cao, L.; Li, Y.; Zhang, J.; Jiang, Y.; Han, Y.; Wei, J. Electrical load prediction of healthcare buildings through single and ensemble learning. Energy Rep. 2020, 6, 2751–2767. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Song, Z. A comparative study of the data-driven day-ahead hourly provincial load forecasting methods: From classical data mining to deep learning. Renew. Sustain. Energy Rev. 2020, 119, 109632. [Google Scholar] [CrossRef]
- Al Amin, M.A.; Hoque, A. Comparison of ARIMA and SVM for Short-term Load Forecasting. In 2019 9th Annual Information Technology, Electromechanical Engineering and Microelectronics Conference (IEMECON); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Scikit-learn Developers. GradientBoostingRegressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html (accessed on 21 November 2020).
- Time Series Data Prediction using Elman Recurrent Neural Network on Tourist Visits in Tanah Lot Tourism Object. Int. J. Eng. Adv. Technol. 2019, 9, 314–320. [CrossRef]
- Herman-Saffar, O. Time Based Cross Validation. Available online: https://towardsdatascience.com/time-based-cross-validation-d259b13d42b8 (accessed on 21 November 2020).
- Raschka, S. Feature Importance Permutation—mlxtend. Available online: http://rasbt.github.io/mlxtend/user_guide/evaluate/feature_importance_permutation/ (accessed on 2 December 2020).
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- CND—ETESA. Informe de Planeamiento Operativo—Semestre I. 2020. Available online: https://sitioprivado.cnd.com.pa/Informe/Download/36121?key=VXd9e23Z9JRA5aIUR21R-P8gocoGOMqdvSo79FduN (accessed on 6 December 2020).
- CND—ETESA. Reglas Comerciales. Available online: https://www.cnd.com.pa/images/doc/norm_regcomerciales_enero2018.pdf (accessed on 1 December 2020).
- Visual Crossing. Historical Weather Data & Weather Forecast Data. Available online: https://www.visualcrossing.com/weather-data (accessed on 2 September 2020).
- Andersen, F.; Henningsen, G.; Møller, N.F.; Larsen, H.V. Long-term projections of the hourly electricity consumption in Danish municipalities. Energy 2019, 186, 115890. [Google Scholar] [CrossRef]
- Abbott, D. Applied Predictive Analytics. Principles and Techniques for the Professional Data Analyst; John Wiley & Sons, Inc.: Indianapolis, IN, USA, 2014; p. 372. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).